运筹学教程清华第三版课后答案(第一章,第五章部分)
运筹学课后习题答案

第一章 线性规划1、由图可得:最优解为2、用图解法求解线性规划: Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解:由图可得:最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解:由图可得:最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得:最大值⎪⎩⎪⎨⎧==+35121x x x , 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示,在(4,2)这一点达到最大值为26将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束,321321321321,00632442392-x x x x x x x x x x x x解:令Z ’ = -z ,引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。
清华大学《运筹学教程》胡运权主编课后习题答案
st
8x1 3x1
x2 x6
4x3 0
2 x5
10
x j 0(, j 1,,6)
基可行解
x1 x2 x3 x4 x5 x6 Z 0 3 0 0 3.5 0 3
0 0 1.5 0 8 0 3
0003500
page 10
0.7 0 0 0 2 2.2 2.2 10
5 13 April 2021
5 5 School of Management
运筹学教程
第一章习题解答
min Z 5x1 2x2 3x3 2x4
(2)
st
2x1x1 22x2x23xx33
4 x4 2 x4
7 3
x j 0, ( j 1,4)
x1 0 0 2/5
page 11 13 April 2021
基可行解
6 x2 2 x2
6 4
x1, x2 0
无穷多最优解,
x1
1, x2
1,Z 3
3是一个最优解
max Z 3x1 2x2
(2)
st.32xx11
x2 2 4x2 12
x1, x2 0
该问题无解
4
School of Management
运筹学教程
page 5 13 April 2021
a=3, j=5, k= -1.5
page 23 13 April 2021
23
School of Management
运筹学教程
第一章习题解答
1.9 若X(1)、X(2)均为某线性规划问题的
最优解,证明在这两点连线上的所有点也是
该问题的最优解。 max Z CT X
设X (1)和X (2)满足: AX b
运筹学教程(第三版)习题答案(第一章)

b 3/2 1
c x1 0 1 0
d x2 1 0 0
0 x3 5/14
0 x4 -3/4
-2/14 10/35 -5/14d+2/14c 3/14d-10/14c
School of Management
运筹学教程
第一章习题解答
之间时最优解为图中的A点 当c/d在3/10到5/2之间时最优解为图中的 点 ; 当 在 到 之间时最优解为图中的 c/d大于 且c大于等于 时最优解为图中的 点;当c/d 大于5/2且 大于等于 时最优解为图中的B点 大于等于0时最优解为图中的 大于 小于3/10且 d大于 时最优解为图中的 点 ; 当 c/d大于 大于0时最优解为图中的 小于 且 大于 时最优解为图中的C点 大于 5/2且c小于等于 时或当 小于 小于等于0时或当 小于3/10且d小于 时最优解 小于0时最优解 且 小于等于 时或当c/d小于 且 小于 为图中的原点。 为图中的原点。
page 7 14 March 2012
School of Management
运筹学教程
第一章习题解答
对下述线性规划问题找出所有基解, 1.3 对下述线性规划问题找出所有基解,指出哪 些是基可行解,并确定最优解。 些是基可行解,并确定最优解。
max Z = 3 x1 + x 2 + 2 x 3 12 x1 + 3 x 2 + 6 x 3 + 3 x 4 = 9 8 x + x − 4 x + 2 x = 10 1 2 3 5 st 3 x1 − x 6 = 0 x j ≥ 0( j = 1, L , 6) ,
School of Management
运筹学第三版课后习题答案 (2)

运筹学第三版课后习题答案第一章:引论1.1 课后习题习题1a)运筹学是一门应用数学的学科,旨在解决实际问题中的决策和优化问题。
它包括数学模型的建立、问题求解方法的设计等方面。
b)运筹学可以应用于各个领域,如物流管理、生产计划、流程优化等。
它可以帮助组织提高效率、降低成本、优化资源分配等。
c)运筹学主要包括线性规划、整数规划、指派问题等方法。
习题2运筹学的应用可以帮助组织提高效率、降低成本、优化资源分配等。
它可以帮助制定最佳的生产计划,优化供应链管理,提高运输效率等。
运筹学方法的应用还可以帮助解决紧急情况下的应急调度问题,优化医疗资源分配等。
1.2 课后习题习题1运筹学方法可以应用于各个领域,如物流管理、生产计划、供应链管理、流程优化等。
在物流管理中,可以使用运筹学方法优化仓储和运输的布局,提高货物的运输效率。
在生产计划中,可以使用运筹学方法优化产品的生产数量和生产周期,降低生产成本。
在供应链管理中,可以使用运筹学方法优化订单配送和库存管理,提高供应链的效率。
在流程优化中,可以使用运筹学方法优化业务流程,提高整体效率。
习题2在物流管理中,可以使用运筹学方法优化车辆的调度和路线规划,以提高运输效率和降低成本。
在生产计划中,可以使用运筹学方法优化生产线的安排和产品的生产量,以降低生产成本和提高产能利用率。
在供应链管理中,可以使用运筹学方法优化供应链各个环节的协调和调度,以提高整体效率和减少库存成本。
在流程优化中,可以使用运筹学方法优化业务流程的排布和资源的分配,以提高流程效率和客户满意度。
第二章:线性规划基础2.1 课后习题习题1线性规划是一种数学优化方法,用于解决包含线性约束和线性目标函数的优化问题。
其一般形式为:max c^T*xs.t. Ax <= bx >= 0其中,c是目标函数的系数向量,x是决策变量向量,A是约束矩阵,b是约束向量。
习题2使用线性规划方法可以解决许多实际问题,如生产计划、供应链管理、资源分配等。
清华大学《运筹学教程》胡运权主编课后习题答案

运筹学教程
第一章习题解答
1.3 对下述线性规划问题找出所有基解, 指出哪些是基可行解,并确定最优解。
max Z 3x1 x2 2x3
12x1 3x2 6x3 3x4 9
(1)
st
8 3
x1 x1
x2 x6
4x3 0
2 x5
10
x j 0(, j 1,,6)
min Z 5x1 2x2 3x3 2x4
第一章习题解答
max Z x1 x2 6x1 10x2 120 (3) st. 5 x1 10 5 x2 8
唯一最优解,x1 10, x2 6, Z 16
max Z 5x1 6x2
(4)
st.22xx11
x2 3x2
2
2
x1, x2 0
该问题有无界解
5
School of Management
X
0
对于任何0 a 1, 两点连线上的点X满足:
X aX (1) (1 a) X (2)也是可行解,且
CT X CT aX (1) CT (1 a) X (2)
C T aX (1) aCT X (2) C T X (2)
CT X (2) , 所以X也是最优解。
page 24 13 April 2021
(1)
st
x12x1x23xx23
2x4 x3
14 x4
. 2
x1, x2, x3 0, x4无约束
max Z 3x1 4x2 2x3 5x41 5x42
4x1 x2 2x3 x41 x42 2
st
x1 x2 x3 2x1 3x2
2x41 2x42 x3 x41 x42
运筹学教程
清华_第三版_运筹学教程_课后答案~(_第一章_第五章部分)

清华第三版 运筹学 答案[键入文字] [键入文字] [键入文字]运筹学教程1. 某饲养场饲养动物出售,设每头动物每天至少需700g 蛋白质、30g 矿物质、100mg 维生素.现有五种饲料可供选用,各种饲料每kg 营养成分含量及单价如表1所示. 表1要求确定既满足动物生长的营养需要,又使费用最省的选用饲料的方案。
解:设总费用为Z.i=1,2,3,4,5代表5种饲料.i x 表示满足动物生长的营养需要时,第i 种饲料所需的数量.则有:⎪⎪⎩⎪⎪⎨⎧=≥≥++++≥++++≥++++++++=5,4,3,2,1,01008.022.05.0305.022.05.07008623..8.03.04.07.02.0min 54321543215432154321i x x x x x x x x x x x x x x x x t sx x x x x Z i2. 某医院护士值班班次、每班工作时间及各班所需护士数如表2所示。
每班护士值班开始时间向病房报道,试决定:(1) 若护士上班后连续工作8h ,该医院最少需要多少名护士,以满足轮班需要; (2) 若除22:00上班的护士连续工作8h 外(取消第6班),其他班次护士由医院排定上1~4班的其中两个班,则该医院又需要多少名护士满足轮班需要.表2解:(1)设i x 第i 班开始上班的人数,i=1,2,3,4,5,6⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥≥+≥+≥+≥+≥+≥++++++=且为整数6,5,4,3,2,1,0302050607060..min 655443322161654321i x x x x x x x x x x x x x t s x x x x x x Z i 解:(2)在题设情况下,可知第五班一定要30个人才能满足轮班需要。
则设设i x 第i 班开始上班的人数,i=1,2,3,4。
⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=≥=+++=≥+++=+++=≥+++=+++=≥+++=+++=≥+++++++=4,3,2,1,1002150216021702,160..30min i44434241444443342241143433323133443333223113242322212244233222211214131211114413312211114321j i y x y y y y y x y x y x y x y y y y y y x y x y x y x y y y y y y x y x y x y x y y y y y y x y x y x y x y t s x x x x Z ij 变量,—是,,,第四班约束,,第三班约束,,第二班约束,第一班约束3. 要在长度为l 的一根圆钢上截取不同长度的零件毛坯,毛坯长度有n 种,分别为ja (j=1,2,…n )。
运筹学1至6章习题参考答案
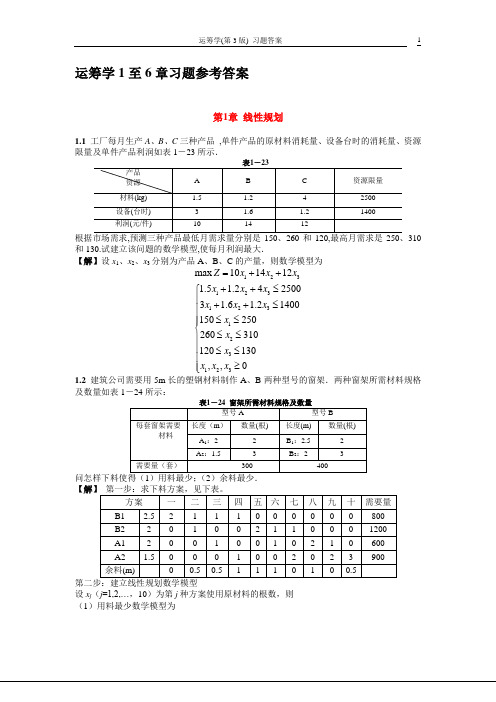
运筹学1至6章习题参考答案第1章 线性规划1.1 工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1-23所示.310和130.试建立该问题的数学模型,使每月利润最大.【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量,则数学模型为123123123123123max 1014121.5 1.2425003 1.6 1.21400150250260310120130,,0Z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤≤⎪⎨≤≤⎪⎪≤≤⎪≥⎪⎩ 1.2 建筑公司需要用5m 长的塑钢材料制作A 、B 两种型号的窗架.两种窗架所需材料规格及数量如表1-24所示:【解设x j (j =1,2,…,10)为第j 种方案使用原材料的根数,则 (1)用料最少数学模型为10112342567368947910min 28002120026002239000,1,2,,10jj j Z x x x x x x x x x x x x x x x x x x j ==⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩∑ (2)余料最少数学模型为2345681012342567368947910min 0.50.50.52800212002*********0,1,2,,10j Z x x x x x x x x x x x x x x x x x x x x x x x x j =++++++⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩1.3某企业需要制定1~6月份产品A 的生产与销售计划。
已知产品A 每月底交货,市场需求没有限制,由于仓库容量有限,仓库最多库存产品A1000件,1月初仓库库存200件。
1~6月份产品A 的单件成本与售价如表1-25所示。
(2)当1月初库存量为零并且要求6月底需要库存200件时,模型如何变化。
清华版《运筹学》(第三版)课后习题详解、...

解:用决策变量 x1, x2 , x3 , x4 , x5 , x6 分别表示 2:00~6:00, 6:00~10:00 ,10:00~14:
00 ,14:00~18:00,18:00~22:00, 22:00~ 2:00 时间段的服务员人数。
其数学模型可以表述为: min Z = x1 + x2 + x3 + x4 + x5 + x6
x1 + x6 >= 3 x1 + x2 >= 9 x2 + x3 >= 12 x3 + x4 >= 5 x4 + x5 >= 18 x5 + x6 >= 4 x1, x2 , x3, x4 , x5 , x6 ≥ 0
3、现要截取 2.9 米、2.1 米和 1.5 米的元钢各 100 根,已知原材料的长度是 7.4 米,问应如 何下料,才能使所消耗的原材料最省。试构造此问题的数学模型。
(0, 0, 0, 5, 2, 6)T ,Z=5。
初始单纯行表为:
cj
2
-1
1
1
CB
XB
x1
x2
x3
x4
1
x4
-1
1
1
1
0
x5
1
1
0
0
0
0
b
x5
x6
0
0
5
1
0
2
0
x6
2
1
1
0
0
1
6
σj
3
-2
0
0
0
0 z=0
(2)非基变量 x2 , x3 仍然取零, x1 由 0 变为 1,即 x1 =1, x2 =0, x3 =0,代入约束条件得一个可 行解 X= (1, 0, 0, 6,1, 4)T 。其目标函数值为 Z=8
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.某饲养场饲养动物出售,设每头动物每天至少需700g蛋白质、30g矿物质、100mg
维生素。
现有五种饲料可供选用,各种饲料每kg营养成分含量及单价如表1所示。
表1
要求确定既满足动物生长的营养需要,又使费用最省的选用饲料的方案。
x表示满足动物生长的营养需要时,解:设总费用为Z。
i=1,2,3,4,5代表5种饲料。
i
第i种饲料所需的数量。
则有:
2.某医院护士值班班次、每班工作时间及各班所需护士数如表2所示。
每班护士值班
开始时间向病房报道,试决定:
(1)若护士上班后连续工作8h,该医院最少需要多少名护士,以满足轮班需要;
(2)若除22:00上班的护士连续工作8h外(取消第6班),其他班次护士由医院排定上1~4班的其中两个班,则该医院又需要多少名护士满足轮班需要。
表2
x第i班开始上班的人数,i=1,2,3,4,5,6
解:(1)设
i
x第i 解:(2)在题设情况下,可知第五班一定要30个人才能满足轮班需要。
则设设
i
班开始上班的人数,i=1,2,3,4。
a 3.要在长度为l的一根圆钢上截取不同长度的零件毛坯,毛坯长度有n种,分别为
j (j=1,2,…n)。
问每种毛坯应当截取多少根,才能使圆钢残料最少,试建立本问题的数学模型。
解:设
x表示各种毛坯的数量,i=1,2,…n。
i
4.一艘货轮分前、中、后三个舱位,它们的与最大允许载重量如表3.1所示。
现有三
种货物待运,已知有相关数据列于表3.2。
表3.1
表3.2
又为了航海安全,前、中、后舱实际载重量大体保持各舱最大允许载重量的比例关系。
具体要求:前、后舱分别与中舱之间载重量比例的偏差不超过15%,前、后舱之间不超过10%。
问该货轮应该载A,B,C各多少件运费收入才最大?试建立这个问题的线性规划模型。
x表示第i件商品在舱j的装载量,i,j=1,2,3
解:设
ij
1)商品的数量约束:
2)商品的容积约束:
3)最大载重量约束:
4)重量比例偏差的约束:
5.篮球队需要选择5名队员组成出场阵容参加比赛。
8名队员的身高及擅长位置见表
5.
表5
出场阵容应满足以下条件: (1) 只能有一名中锋上场; (2) 至少一名后卫;
(3) 如1号和4号均上场,则6号不出场; (4) 2号和8号至少有一个不出场。
问应当选择哪5名队员上场,才能使出场队员平均身高最高,试建立数学模型。
解:设1 i x 表示第i 个队员出场,i=1,2…8.
6. 时代服装公司生产一款新的时装,据预测今后6个月的需求量如表4所示,每件时装用工2h 和10元原材料费,售价40元。
该公司1月初有4名工人,每人每月可工作200h ,月薪2000元。
该公司可于任一个月初新雇工人,但每雇1人需一次性额外支出1500元,也可辞退工人,但每辞退1人需补偿1000元。
如当月生产数超过需求,可留到后面月份销售,但需付库存费每件每月5元,当供不应求时,短缺数不需补上。
试帮组该公司决策,如何使用6个月的总利润最大。
表4 单位:件
解:设1i x 为第i 月现有工人人数,2i x 为新雇工人人数,3i x 为辞退工人人数,i y 为每月的需求。
i=1,2,…,6。
则有:
7. 童心玩具厂下一年度的现金流(万元)如表6所示,表中负号表示该月现金流出大于流入,为此该厂需借款。
借款有两种方式:一是于上一年末借一年期贷款,一次得全部贷款额,从1月底起每月还息1%,于12月归还本金和最后一次利息;二是得到短期贷款,每月初获得,于月底归还,月息1.5%。
当该厂有多余现金时,可短期存款,月初存入,月末取出,月息0.4%。
问该厂应如何进行存贷款操作,既能弥补可能出现的负现金流,又可使年末现金总量为最大。
表6
解:设长期存款为y ,i w 为第i 个月的短期贷款额,i z 为第i 个月短期存款额,i=1,2,…,
n 。
则有:
8. 某地准备投资D 元建民用住宅,可以建住宅的地点有n 处:n 21A A A ,
,。
n A 处每幢住宅的造价为d ,最多可造a 幢。
问应当在哪几处建住宅,分别建几幢,才能使建造的住宅总数最多,试建立问题的数学模型。
解:设i x 表示在A 处所建住宅的数量,i=1,2,…n 。
9. 有一批每根长度为l 的圆钢,需截取n 种不同长度的零件毛坯。
长度为j a 的毛坯必须有j m 段(j=1,2,…n ),为了方便,每根圆钢只截取一种长度的毛坯。
应当怎样截取,才能使动用的圆钢数目最少,要求建立数学模型。
解:设i x 表示各种毛坯使用圆钢的数量,i y 表示各种毛坯在一根圆钢上可得到的数量。
i=1,2,…n 。
10. 一个旅行者要在其背包里装一些最有用的旅行用品。
背包容积为a ,携带物品总重量最多为b 。
现有物品m 件,第i 件物品体积为i a ,重量为i b (i=1,2,m )。
为了比较物品的有用程度,假设第i 件物品的价值为i c (i=1,2,m )。
若每件物品只能整件携带,每件物品都能放入包中,并且不考虑物品放入包后相互的间隙。
问旅行者应当携带几件物品,才能使携带物品的总价值最大,要求建立数学模型。
解:设1 i x 表示携带第i 件物品,i=1,2,…,m 。
11. 宏银公司承诺为谋建设项目从2003年起的4年中每年初分别提供以下数额贷款:2003年——100万元,2004年——150万元,2005年——120万元,2006——110万元。
以上贷款资金均需2002年底前筹集齐。
但为了充分发挥这笔资金的作用,在满足每年贷款额情况下,可将多余资金分别用于下列投资项目:
(1) 于2003年初购买A 种债卷,期限3年,到期后本息合计为投资额的140%,
但限购60万元。
(2) 于2003年初购买B 种债卷,期限2年,到期后本息合计为投资额的125%,
且限购90万元。
(3) 于2004年初购买C 种债卷,期限2年,到期后本息合计为投资额的130%,
但限购50万元。
(4) 于每年初将任意数额的资金存放于银行,年息4%,于每年底取出。
求宏银公司应如何运用好这笔筹集到的资金,使2002年底需要筹集到的资金数额为最少。
解:设x 为2002年底该公司需要筹集到的资金额;321y y y ,,分别为2003、2004、2005年初存放到银行的资金数;C B A w w w ,,分别为购买A 、B 、C 债卷的数额。
则有:。
