第四章 马尔可夫型排队系统的性能分析
马尔可夫过程与排队论

马尔可夫过程与排队论马尔可夫过程与排队论是数学中重要的两个概念,它们在统计学、概率论、运筹学等领域中有着广泛的应用。
本文将分别介绍马尔可夫过程和排队论的基本概念和应用。
马尔可夫过程是一个随机过程,其特点是未来的状态只与当前状态有关,与过去的状态无关。
这种性质被称为马尔可夫性。
马尔可夫过程是由状态空间和转移概率矩阵组成的。
状态空间是一组离散或连续的状态,转移概率矩阵描述了不同状态之间的转移概率。
马尔可夫过程的一个重要应用是在排队系统中的模拟和分析。
排队论是研究排队系统的数学方法和技术的学科。
排队系统是指由顾客和服务员组成的系统,顾客需要接受服务,而服务员有一定的处理能力。
排队论主要关注以下几个方面的问题:平均等待时间、系统繁忙率、系统的稳定性等。
排队论通过数学建模,提供了一种分析和优化排队系统的方法。
在排队系统中,马尔可夫过程可以用来描述系统的状态变化。
例如,一个银行的柜台服务系统可以看作是一个排队系统。
顾客到达银行后,根据柜台服务员的繁忙情况,决定是否需要排队等待。
排队等待时,顾客处于等待状态;当柜台服务员空闲时,顾客进入服务状态。
这个过程可以用马尔可夫过程来描述,其中状态空间包括顾客的等待状态和服务状态,转移概率矩阵描述了顾客在不同状态之间的转移概率。
马尔可夫的应用广泛,不仅在排队系统中有着重要作用,还在许多其他领域中有着广泛应用。
例如,马尔可夫链被用于自然语言处理中的语言模型,通过学习上下文的转移概率来预测下一个词的概率。
马尔可夫过程还被用于金融领域的风险管理,通过建立市场模型来预测金融资产的价格变动。
排队论也有许多重要的应用。
在制造业中,排队论可以用于优化生产线的运作效率,减少等待时间,提高资源利用率。
在交通领域,排队论可以用于交通信号控制系统的优化,减少拥堵现象。
在电信业中,排队论可以用于优化无线网络的资源分配,提高用户的通信质量。
总结来说,马尔可夫过程与排队论是数学中重要的两个概念。
马尔可夫过程描述了一个随机过程的状态变化,而排队论则应用了马尔可夫过程来分析和优化排队系统。
通信系统的马尔可夫过程模型

通信系统的马尔可夫过程模型现代通信系统的设计和性能分析越来越依赖于马尔可夫过程模型。
马尔可夫过程是一种数学模型,可以描述系统状态随时间的变化,特别适用于具有随机特性的系统,例如通信系统中的信道状态和数据流量等。
本文将介绍通信系统中常用的马尔可夫过程模型及其应用,旨在帮助读者理解通信系统的性能分析方法和技术。
1. 引言通信系统是信息传输和交换的关键组成部分,其性能直接影响到用户体验和系统效率。
为了有效地分析和优化通信系统的性能,需要建立准确的数学模型。
马尔可夫过程作为一种常用的建模工具,能够描述系统状态的演化规律,是通信系统性能分析的重要手段。
2. 马尔可夫链马尔可夫链是马尔可夫过程的基本模型,用于描述具有马尔可夫性质的随机系统。
马尔可夫链的核心思想是“未来仅取决于当前状态,与过去状态无关”。
在通信系统中,常用的马尔可夫链模型有信道状态和用户行为等。
2.1 信道状态马尔可夫链通信系统中的信道状态常常是不确定的,例如无线通信中的信道衰落和干扰等。
为了描述这种不确定性,可以使用信道状态马尔可夫链模型。
该模型将信道状态定义为一系列离散的状态,通过状态间的转移概率描述信道状态的演化过程。
基于该模型,可以进一步分析通信系统的传输性能和容量等。
2.2 用户行为马尔可夫链在移动通信系统中,用户的行为常常具有随机特性,例如用户的移动模式和通信需求等。
为了更好地理解和满足用户的需求,可以使用用户行为马尔可夫链模型。
该模型将用户的行为抽象为一系列离散的状态,通过状态间的转移概率描述用户行为的演化过程。
基于该模型,可以优化通信资源分配和调度策略,提高用户的通信质量和系统效率。
3. 马尔可夫过程的性能分析通过建立马尔可夫过程模型,可以对通信系统的性能进行量化和分析。
常用的性能指标包括系统吞吐量、平均延迟和丢包率等。
3.1 稳态性能分析马尔可夫过程的稳态分析用于计算系统在长期运行中的平均性能。
通过求解状态转移方程或离散时间平稳分布,可以获得系统的稳态性能指标。
排队论大学课件11-马尔科夫排队网络

pn
D n (t ) D (t )
t
lim
D n (t ) D (t ) D n (t ) D (t )
An (t ) D (t )
t
An (t ) A(t ) 1
lim 0
t
lim
An (t ) A (t ) A (t ) D (t )
t
pn pn
axbx指各种供人食用或者饮用的成品和原料以及按照传统既是食品又是药品的物品但是不包括以治疗为目的的物品在餐饮业和集体用餐配送单位中主要指原料马尔可夫排队网络马尔可夫排队网络一个二节点的级联网络一个二节点的级联网络两顾客离开的间隔时间是后面顾客到达的间隔时间后面顾客服务的时间后一个顾客前一个顾客前一个顾客后一个顾客指各种供人食用或者饮用的成品和原料以及按照传统既是食品又是药品的物品但是不包括以治疗为目的的物品在餐饮业和集体用餐配送单位中主要指原料马尔可夫排队网络马尔可夫排队网络一个二节点的级联网络一个二节点的级联网络情况一出现的概率顾客离开时发现系统中有顾客的概率顾客到达时发现系统中有顾客的概率统计平衡时系统队长不为0的概率可见mm1排队系统的顾客输出流是泊松流并且强度与其输入流强度相同指各种供人食用或者饮用的成品和原料以及按照传统既是食品又是药品的物品但是不包括以治疗为目的的物品在餐饮业和集体用餐配送单位中主要指原料burkeburke在平稳状态下mmn排队系统的顾客离开的过程为泊松过程离开率等于到达率
t 0
t 0
因为输入流是泊松流,所以A(t, t+∆t)发生的概率是 ∆t+o(∆t),与 N(t)=n这个事件无关。所以
P [ A ( t , t t ) | N ( t ) n ]= P [ A ( t , t t ) 】 p n ( t ) lim p n ( t ) p n ( t )
第四章 马尔科夫排队系统-mmmm

λ = the arrival intensity (rate) of the customers µ = the service rate of the server (the mean service time is 1/µ) Denote
N = number of elements reserved (number of customers in system) πj = P{N = j } the equilibrium probability of state j
J. Virtamo
38.143 Queueing Theory / Loss system
6
The required capacity as a function of the load The following table gives the required number of trunks n as a function of the offered traffic intensity a when the allowed blockin is 1 %. The last column gives the required relative oversizing n/a, i.e. the ratio of the number of trunks to the load. a (erl) n 3 8 10 18 30 42 100 117 300 324 1000 1029 n/a 2.7 1.8 1.4 1.17 1.08 1.03
The state variable Nt constitutes a Markov process of the birth-death type - the state can change only stepwise
马尔可夫性质

泊松过程与排队论应用
01
泊松过程在排队论中的角色
泊松过程是一种重要的随机过程,在排队论中广泛应用于描述顾客到达
的规律。
02
排队系统的性能指标
排队系统的性能指标包括平均队长、平均等待时间、系统利用率等,这
些指标可以通过泊松过程和其他随机过程进行建模和分析。
03
排队论在实际应用中的价值
排队论在实际应用中具有广泛的价值,如电信网络中的呼叫中心、交通
03
序列生成与预测
利用马尔可夫模型对序列数据的建模 能力,结合深度学习等技术,可以实 现更加准确的序列生成和预测。
THANKS
感谢观看
稳态概率分布求解
对于非齐次、非遍历性马尔可夫模型,如何求解稳态概率分布是一 个重要的问题。
深度学习等新技术融合创新
01
深度学习与马尔可夫 模型融合
利用深度学习强大的特征提取和表示 学习能力,可以改进传统马尔可夫模 型的性能。
02
强化学习与马尔可夫 决策过程
将强化学习算法与马尔可夫决策过程 相结合,可以实现更加智能的决策和 控制。
马尔可夫性质
汇报人: 2024-02-06
目录 CONTENTS
• 马尔可夫性质概述 • 马尔可夫链基本概念 • 马尔可夫性质在随机过程中应用 • 马尔可夫性质在信息科学中应用 • 马尔可夫性质在金融领域应用 • 马尔可夫性质挑战与未来发展
01
马尔可夫性质概述
CHAPTER
定义与基本思想
马尔可夫性质是指在给定现在状 态下,过去的信息与未来状态无 关,即未来只依赖于现在,而与
非线性、非高斯问题
复杂系统往往呈现出非线性和非 高斯特性,这使得基于线性高斯 假设的马尔可夫模型不再适用。
马尔可夫排队模型

第一节 状态转移图
• 状态:系统的某种可以稳定存在的形态。
– 从随机过程角度去看,则为随机过程的取值
• 变迁:状态间的有向弧,描述状态间可能的变化。
– 变迁没有延迟,发生的时间为0
• 状态转移图:用来描述系统状态和变迁情况的有 向图 • 实例:一个机械系统由A、B两部分构成,各自有 修理工。若运行时间和修理时间均为服从独立的 指数分布的随机变量,求状态转移图。
例题的求解
• 定义状态:
– S0=AB,S1=AB,S2=AB,S3=AB
• 变迁和强度:
– S0→S1:A系统发生故障强度λ1=1/t1 – S1→S0:A的平均修复强度μ1=1/t1’
• t1’:A的平均修复时间
• t1:A的平均无故障时间。( λ1指数分布参数)
– 同样可能的变迁S1→S3,S3→S1,S0→S2,S2→S0, S2→S3,S3→S2,强度分别为:λ2、μ2、λ2、μ2、λ1、 μ1
• 试证
M|M|1|0的普通解
• 对应的哥氏方程组:
– p0‘(t) = -λp0(t) +μp1(t) – p1‘(t) = - μp1(t) + λp0(t)
• 解得:
– p0(t) =μ/(μ+λ)+Ce -(μ+λ)t – 若 t=0 p0(t) =1,则 C= λ/(μ+λ) – ∴ p0(t) =μ/(μ+λ)+ λ/(μ+λ) e -(μ+λ)t – p1(t)=1-p0(t) = λ/(μ+λ)-λ/(μ+λ) e -(μ+λ)t
07:排队网络模型的性能分析
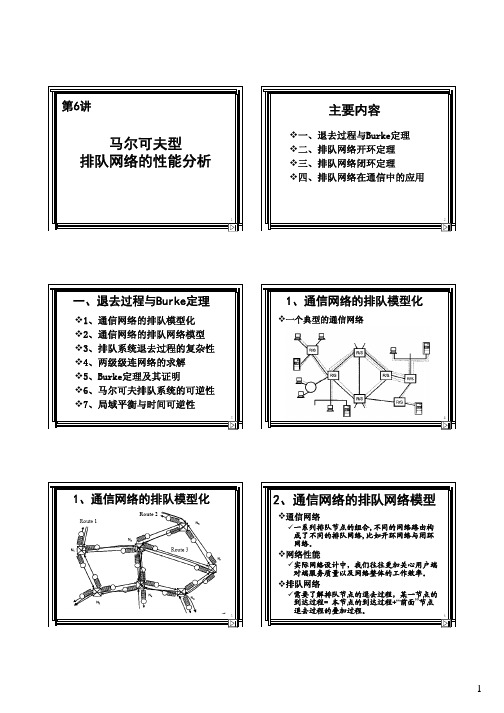
一个典型的通信网络8泊松分布过程的一个例子。
10111522 237、局部平衡与时间可逆性30312、Jackson网络-独立性假设几点独立性假设9相互独立的外部到达、泊松过程9相互独立的服务时间、负指数分布•同一个顾客在不同的排队节点遵循相互独立、且有可能不同参数的负指数分布。
9相互独立的路由策略•在某一节点接受完服务后独立地决定下一节点的路由、或者退出该排队网络。
322、Jackson网络-稳态概率()()()111212,,,,mi i j jij m m i r P I Q r r r λλλγλλλγ−=+Λ−Λ∑L L =对于节点,顾客到达率如下:用矩阵形式可以表示为:=其中:==33111212122212m m m mm m P P P P P P QPP P ⎛⎞⎜⎟⎜⎟=⎜⎟⎜⎟⎜⎟⎝⎠L L M M M M L Q矩阵的性质9对于开环网络来说,至少存在一个节点i有ri>0或者mij 1P 0>∑j=0-343、Jackson定理Jackson 定理9对于一个平稳状态的Jackson网络,在任一节点内的顾客数与其它节点的存在的顾客数无关。
9队长的概率分布Pn=P(n1,n2,…n m )等于每个单个节点队列长度概率分布的积。
353、Jackson定理()()()()()()()121122001100,,,!!!!iii i i i i i mm mn ii i i i i sn s i i i i n s s i i in i i i i ii i iP n n n p n p n p n ap n s n p n a p n s s a a s p n s s a s i a ρλµ−−−==⋅⎧≤⎪⎪=⎨⎪>⎪⎩⎛⎞=+⋅⎜⎟−⎝⎠=∑L L ,,为第个排队节点的服务者数,363、杰克逊网络通信量方程解)非奇异性,存在唯一()=-(则=令稳态总体流量:通信量方程:Q -I Q I }{},{11γλλλλγλγλij i Mi i j Mi jij i i q Q q q ==+=∑∑==iiλiγiq 11λMiM q λ38399虽然外部顾客以泊松过程到达节点i,但实际到达于第i个节点的顾客为非泊松分布过程。
随机过程习题集-第四章马尔可夫过程

1第四章 马尔可夫过程内容提要1. 马尔可夫过程的概念 (1)马尔可夫过程给定随机过程{}(),X t t T ∈,如果对122,∀≥∀<<<∈n n t t t T ,有11221111{()|(),(),,()}{()|()}n n n n n n n n P X t x X t x X t x X t x P X t x X t x ----<====<=则称{}(),X t t T ∈为马尔可夫过程。
称(){}:,==∈E x X t x t T 为状态空间。
参数集和状态空间都是离散的马尔可夫过程称为离散参数马氏链. 参数连续、状态空间离散的马尔可夫过程称为连续参数马氏链. (2)k 步转移概率设{}(),0,1,2,=X n n 为离散参数马氏链,称()(),(,){|},0,1=+==≥≥i j p n k P X n k j X n i n k为{}(),0,1,2,=X n n 在时刻n 的k 步转移概率,称(),(,)((,)),P =∈i j n k p n k i j E为{}(),0,1,2,=X n n 在时刻n 的k 步转移概率矩阵. 特别地,当1k =时,在时刻n 的一步转移概率和一步转移概率矩阵分别简记为()ij p n 和()n P . (3)初始分布、绝对分布称((0)),,==∈i p P X i i E 为离散参数马氏链{}(),0,1,2,=X n n 的初始分布,记为0P ,称()(){},,==∈j p n P X n j j E 为马尔可夫链{}0n X n ≥的绝对分布,记为P n . (4)离散参数齐次马氏链设{}(),0,1,2,=X n n 是一离散参数马氏链,如果其一步转移概率()ij p n 恒与起始时刻n 无关,记为ij p ,则称{}(),0,1,2,=X n n 为离散参数齐次马氏链。
若{}(),0,1,2,=X n n2是离散参数齐次马氏链,则其k 步转移概率记为(),i j p k ,一步转移概率矩阵和k 转移概率矩阵分别记为P 和().P k(5) 离散参数齐次马氏链的遍历性离散参数齐次马氏链{X (n ) ,n=0,1,2… },若对一切状态i ,j ,存在与i 无关的极限()()lim 0,ij j n p n i j E →+∞=π>∈则称此马氏链具有遍历性.0,1j j j Ej E ππ∈>∈=∑若且则称{},j j E π∈为离散参数齐次马氏链{X (n ) ,n=0,1,2… }的极限分布,或称为最终分布,记为{},j j E ∏=∈π(6)离散参数齐次马氏链的平稳分布离散参数齐次马氏链{X (n ) ,n=0,1,2… },若存在{v j , j ∈E } 满足条件:1)0,2)13)j jj Ej i iji Ev j E vv v p ∈∈≥∈==∑∑则称此马氏链是平稳的,称 { v j , j ∈E } 为此马氏链的平稳分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
aA? B ? 50erl
E62 (50) ? 0.01388 ? 0.01
E63 (50) ? 0.00844 ? 0.01
S ? 64 2001-3-14 A? B
? ? ? @? 华? ?
26
马尔可夫型排队系统的应用(2)
? 例题:有限等待空间排队系统与无限等待空间排队系统 的性能比较
? ? ? @? 华? ?
12
M/M/1排队系统的性能分析
? 等待/滞留时间的概率分布
2001-3-14
? ? ? @? 华? ?
13
M/M/1排队系统的扩展(1)
? 顾客到达率和服务率可变的M/M/1排队系统
? 分组交换网中 window-based flow control ? ATM网中用于ABR业务的 rate-based flow control ? 电路/分组交换网中的 dynamic bandwidth assignment
9
2001-3-14
? ? ? @? 华? ?
10
M/M/1排队系统的性能分析
? 全局平衡方程式(Global Balance Equation)
其中:
? 平稳状态概率的求解
?局域平衡方程式(local balance equation):
pi
?平稳状态概率:
i
2001-3-14
? ? ? @? 华? ?
s?
s?
s?
? ? ? @? 华? ?
15
M/M/s/K排队系统的性能分析
? 被截断的M/M/s排队系统
?
?
?
?
?
?
?
0
1
. . . .
s-1
s
s+1
. . . .
s+k
?
2?
(s ? 1)?
s?
s?
s?
s?
? 排队系统性能
2001-3-14
? ? ? @? 华? ?
16
其他变型的马尔可夫排队系统
28
马尔可夫型排队系统的应用(3)
? 例题4-4:三种排队模型的性能比较
模型III: 综合网络/集中排队
模型II: 分散网络/集中排队
模型I: 分散网络/独立排队
2001-3-14
? ? ? @? 华? ?
29
三种排队模型的性能比较
2001-3-14
? ? ? @? 华? ?
30
三种排队模型的性能比较
2001-3-14
? ? ? @? 华? ?
36
课外练习(2)
? M(N)/M/s(0) Queueing Systems (Engset Formula)
2001-3-14
? ? ? @? 华? ?
37
马尔可夫型排队系统的总结
2001-3-14
? ? ? @? 华? ?
38
马尔可夫型排队系统的总结
2001-3-14
? ? ? @? 华? ?
3
连续时间马尔可夫过程的状态转移
2001-3-14
? ? ? @? 华? ?
4
离散时间马尔可夫链
2001-3-14
? ? ? @? 华? ?
5
离散时间马尔可夫链
2001-3-14
? ? ? @? 华? ?
6
连续时间马尔可夫过程
2001-3-14
? ? ? @? 华? ?
11
M/M/1排队系统的性能分析
? 排队系统的性能参数
? 队列长度的均值、方差
? 等待/滞留时间的均值
? 队列长度的概率分布与?和µ本身无关,只与两者的比? 有关;但是,平均等待/滞留时间不仅与?有关,而且 与平均服务时间成正比
? 同等负载(ρ)情况下的快速服务系统与慢速服务系统的例 子
2001-3-14
? {Nt}:一维马尔可夫型排队系统 ? {N1t,N2t,… ,Nkt}:k 维马尔可夫型排队系统
? 由于排对系统的随机特性主要来源于顾客的到达和所 需的服务时间,不难想象,如果顾客的到达和服务时 间均没有记忆性,则该排队系统的状态变量也必然没
有记忆性,或称马尔可夫性
? 对于马尔可夫型排对系统的性能分析,只要针对该排
2001-3-14
? ? ? @? 华? ?
33
马尔可夫排队系统的过渡过程(续)
2001-3-14
? ? ? @? 华? ? Nhomakorabea34
M(N)/M/N模型的过渡解
2001-3-14
? ? ? @? 华? ?
35
课外练习(1)
? M/M/s Random Service Queueing System
2001-3-14
? ? ? @? 华? ?
39
多维马尔可夫排队系统的解析
? 例题:M1+M2/M1,M2/s(0,infty)
1
令 N_1=j 表示平稳状态下业务1
1
2
在排队系统中的顾客数;
2
N_2=i 表示平稳状态下业务2
s
在排队系统中的顾客数;
2001-3-14
? ? ? @? 华? ?
40
《通信网理论基础》
第4章 马尔可夫型排队系统的性能分析
2001-3-14
? ? ? @? 华? ?
1
马尔可夫型排队系统
? 定义:
? 可用当前状态变量或变量组(例如,任意时刻的队列长度)完 全描述的排队系统,即给定当前时刻的状态概率就完全可以
求解出将来时刻的状态概率
? 排队系统的状态变量本身是一个马尔可夫过程
(impatient customers)
2001-3-14
? ? ? @? 华? ?
17
到达率随队列长度变化的M/M/1排队系统
2001-3-14
? ? ? @? 华? ?
18
M/M/1/K Loss Performance
2001-3-14
? ? ? @? 华? ?
19
M/M/s(0)排队系统与Erlang-B公式
2001-3-14
? ? ? @? 华? ?
21
Erlang Loss Performance
2001-3-14
? ? ? @? 华? ?
22
Erlang-B Formula’s Application
2001-3-14
? ? ? @? 华? ?
23
Erlang-C Formula
2001-3-14
2001-3-14
? ? ? @? 华? ?
31
三种排队模型的性能比较
注:平均等待时间的比较会得出不同的结论
2001-3-14
? ? ? @? 华? ?
32
马尔可夫排队系统的过渡过程
? 过渡过程的分析是非常重要的(了解达到平稳 状态的过程和时间)
? 过渡过程的分析是非常困难的,即使是最简单 的M/M/1排队系统,其过渡过程解也非常复杂
? ? ? @? 华? ?
24
马尔可夫型排队系统的应用(1)
2001-3-14
? ? ? @? 华? ?
25
电路交换网的设计
单方向中继线:
aA? B ? 0.05x1000x(1000/1999) ? 25erl aB? A ? 0.05x1000x(1000/1999) ? 25erl E35 (25) ? 0.01165? 0.01 E36 (25) ? 0.00802? 0.01 S A? B ? 36 SB? A ? 36
对系统的当前状态建立起马尔可夫状态转移方程式就
可以求解出该排队系统的状态概率
2001-3-14
? ? ? @? 华? ?
2
排队系统的马尔可夫过程描述
队列长度Nt
K
t
? 马尔可夫型排队系统在任意时刻的队列长度实际 上是一个最简单的马尔可夫过程,即生灭过程。
? 生灭过程的状态转移只在相邻状态之间发生
? 多维状态变量可以构成一个多维生灭过程
? 一般来讲,求解无限等待空间排队系统比较容易 ? 但是,能否用无限等待空间排队系统的队列长度的尾分布来
近似有限等待空间排队系统的阻塞率性能? ? 一般来讲是不行的,但对于马尔可夫排队系统有如下结果:
2001-3-14
? ? ? @? 华? ?
27
马尔可夫型排队系统的应用(2)
2001-3-14
? ? ? @? 华? ?
?M/M/s(k)中若k=0, 则
或
(Erlang-B公式)
? Erlang-B公式的鲁棒性
?只与a有关,与?,µ本身无关
?与服务时间的概率分布无关(M/G/s(0)也适用)
? Erlang-B公式的迭代计算
2001-3-14
? ? ? @? 华? ?
20
Erlang Loss Performance
? 平稳状态概率
? 例:M/M/s排队系统的平稳状态概率
2001-3-14
? ? ? @? 华? ?
14
M/M/s排队系统的性能分析
? 等待概率:
? 平均队列长度:
Erlang-C Formula
? 平均等待时间:
? 等待时间的概率分布:
?
0
?
2001-3-14
?
1
2?
?
?
?
?
s-1
s
s+1
(s ? 1)?
多维马尔可夫排队系统的解析
2001-3-14
? ? ? @? 华? ?
41
本章小节
