第九章马尔可夫概型分析
马尔可夫分析法
马尔可夫分析法马尔可夫分析法是俄国数学家马尔可夫在1907年提出, 并由蒙特·卡罗加以发展而建立起的一种分析方法。
它主要用于分析随机事件未来发展变化的趋势, 即利用某一变量的现在状态和动向去预测该变量未来的状态及动向, 以便采取相应的对策。
1马尔可夫过程及马尔可夫链 [3]定义1设随机序列{X(n) ,n=0, 1, 2, …}的离散状态空间为E, 若对于任意m个非负整数n1,n2, …,nm(0≤n1<n2<…<nm) 和任意自然数k, 以及任意i1,i2, …,im,j∈E满足 [3]P{X(nm+k) =j|X(n1) =i1,X(n2) =i2, …,X(nm)=im}=P{X(nm+k) =j|X(nm) =im} (1) [3]则称X(n) ,n=0, 1, 2, …}为马尔可夫链。
[3]在式(1) 中, 如果nm表示现在时刻,n1,n2, …,nm-1表示过去时刻,nm+k表示将来时刻, 那么此式表明过程在将来nm+k时刻处于状态j仅依赖于现在nm时刻的状态im, 而与过去m-1个时刻n1,n2, …,nm-1所处的状态无关, 该特性称为马尔可夫性或无后效性。
式(1) 给出了无后效性的表达式。
[3]2齐次马尔可夫链和k步转移概率 [3]P{X(nm+k) =j|X(nm) =im},k≥1称之为马尔可夫链在n时刻的k 步转移概率, 记为Pij(n,n+k) 。
转移概率表示已知n时刻处于状态i, 经k个单位时间后处于状态j的概率。
若转移概率Pij(n,n+k) 是不依赖于n的马尔科夫链, 则称为齐次马尔可夫链。
这种状态只与转移出发状态i、转移步数k及转移到达状态j有关, 而与n无关。
此时,k 步转移概率可记为Pij(k) , 即 [3]Pij(k) =Pij(n,n+k) =P{X(n+k) =j|X(n) =i},k>0 (2) [3]式中,0≤Ρij(k)≤1,∑j∈EΡij(k)=10≤Ρij(k)≤1,∑j∈EΡij(k)=1。
如何利用马尔可夫模型进行网络数据分析(九)
马尔可夫模型是一种用来描述随机过程的数学模型，它可以用来预测未来的状态或事件。
在网络数据分析中，马尔可夫模型可以用来分析用户行为、网络流量、社交网络传播等方面。
下面将介绍如何利用马尔可夫模型进行网络数据分析，包括模型原理、应用案例和未来发展方向。
马尔可夫模型是一种描述随机过程的数学模型，它假设系统的未来状态只与当前状态有关，与过去状态无关。
这种假设在网络数据分析中有着广泛的应用，比如在用户行为分析中，可以用马尔可夫模型来预测用户下一步的行为，从而提高推荐系统的准确度；在网络流量分析中，可以用马尔可夫模型来预测网络流量的变化趋势，从而优化网络资源的分配。
在实际应用中，马尔可夫模型通常分为有限状态马尔可夫模型和隐马尔可夫模型两种形式。
有限状态马尔可夫模型假设系统的状态是有限的，每个状态之间存在状态转移的概率；而隐马尔可夫模型假设系统的状态是不可观测的，只能通过观测到的结果来推断系统的状态。
这两种模型都在网络数据分析中有着重要的应用。
在用户行为分析中，可以利用有限状态马尔可夫模型来建模用户的行为轨迹，从而预测用户下一步的行为。
比如在电子商务网站中，可以根据用户的浏览、搜索、点击等行为来建立马尔可夫模型，从而根据用户当前的状态来预测用户下一步可能感兴趣的商品，从而提高推荐系统的准确度。
在这个案例中，用户的行为可以看作是系统的状态，而用户之间的行为转移可以看作是状态之间的转移概率。
在网络流量分析中，可以利用隐马尔可夫模型来建模网络流量的变化趋势，从而预测网络流量的未来状态。
比如在网络运营商中，可以根据历史网络流量数据来建立隐马尔可夫模型，从而根据当前的网络流量观测值来预测未来网络流量的变化趋势，从而优化网络资源的分配。
在这个案例中，网络流量的变化可以看作是系统的状态，而观测到的网络流量数据可以看作是系统状态的观测值。
总的来说，马尔可夫模型在网络数据分析中有着重要的应用，可以用来预测用户行为、网络流量变化等方面。
马尔可夫分析
1、 已知马氏链X 的状态空间I={0,1,2,3}及一步转移概率矩阵为1100221000120033110022⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦求其平稳分布 解：由=ππP 及31i i π==∑得001310222333011221123213201i i ππππππππππππ=⎧=++⎪⎪⎪=+⎪⎪⎪=+⎨⎪=⎪⎪⎪=⎪⎪⎩∑ 求解得012321,,0.33ππππ====2、 已知6月底，甲乙丙3种型号的某商品在某地区有相同的销售额。
7月份甲保持原有客户的60%，分别获得乙丙的客户15%和30%；乙保持原有顾客的70%，分别获得甲丙顾客的10%和20%；丙保持原有顾客的50%，分别获得甲乙顾客的30%和15%。
求8月份初各型号商品的占有率及稳定状态时的占有率。
解：由于6月份甲乙丙有相同的销售额，故在市场的占有率为（1/3，1/3，1/3）；7月份的转移概率矩阵为0.60.10.30.150.70.150.30.20.5⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦故8月初各商品的占有率为0.60.10.3111(,,)=0.150.70.15(0.350,0.333,0.317)3330.30.20.5p p p ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦甲乙丙（，，）由=ππP 及31i i π==∑得1123212331231230.60.150.30.10.70.20.30.150.51πππππππππππππππ=++⎧⎪=++⎪⎨=++⎪⎪++=⎩ 解得 1230.359,0.327,0.314.πππ===3. 110.10.050.850.050.050.90.030.050.920.950.010.04R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦4110.66860.18580.00.00040.01150.13370.89670.092000.00050.01080.95800.0417000.000.00030.98960.01040.0R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦一年级学生四年内退学概率为0.1858 4.（1）初始概率矩阵稳态概率为（0.2778，0.3889，0.3333） （2）广告后的稳态概率（0.3333，0.3333，0.3333），（0.4375，0.25，0.3125） 5.0.40.30.30.30.50.20.20.30.5R ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦平稳概率（0.2969，0.375，0.3281）6. 已知随机游动的质点构成一个马氏链，其状态空间为I={1，2，3，4，5}，而一步转移概率矩阵为11116231116231116231P ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦试求质点从状态2出发，分别被吸收于状态1、状态5的概率。
马尔可夫性质
泊松过程与排队论应用
01
泊松过程在排队论中的角色
泊松过程是一种重要的随机过程，在排队论中广泛应用于描述顾客到达
的规律。
02
排队系统的性能指标
排队系统的性能指标包括平均队长、平均等待时间、系统利用率等，这
些指标可以通过泊松过程和其他随机过程进行建模和分析。
03
排队论在实际应用中的价值
排队论在实际应用中具有广泛的价值，如电信网络中的呼叫中心、交通
03
序列生成与预测
利用马尔可夫模型对序列数据的建模 能力，结合深度学习等技术，可以实 现更加准确的序列生成和预测。
THANKS
感谢观看
稳态概率分布求解
对于非齐次、非遍历性马尔可夫模型，如何求解稳态概率分布是一 个重要的问题。
深度学习等新技术融合创新
01
深度学习与马尔可夫 模型融合
利用深度学习强大的特征提取和表示 学习能力，可以改进传统马尔可夫模 型的性能。
02
强化学习与马尔可夫 决策过程
将强化学习算法与马尔可夫决策过程 相结合，可以实现更加智能的决策和 控制。
马尔可夫性质
汇报人： 2024-02-06
目录 CONTENTS
• 马尔可夫性质概述 • 马尔可夫链基本概念 • 马尔可夫性质在随机过程中应用 • 马尔可夫性质在信息科学中应用 • 马尔可夫性质在金融领域应用 • 马尔可夫性质挑战与未来发展
01
马尔可夫性质概述
CHAPTER
定义与基本思想
马尔可夫性质是指在给定现在状 态下，过去的信息与未来状态无 关，即未来只依赖于现在，而与
非线性、非高斯问题
复杂系统往往呈现出非线性和非 高斯特性，这使得基于线性高斯 假设的马尔可夫模型不再适用。
马尔可夫分析法
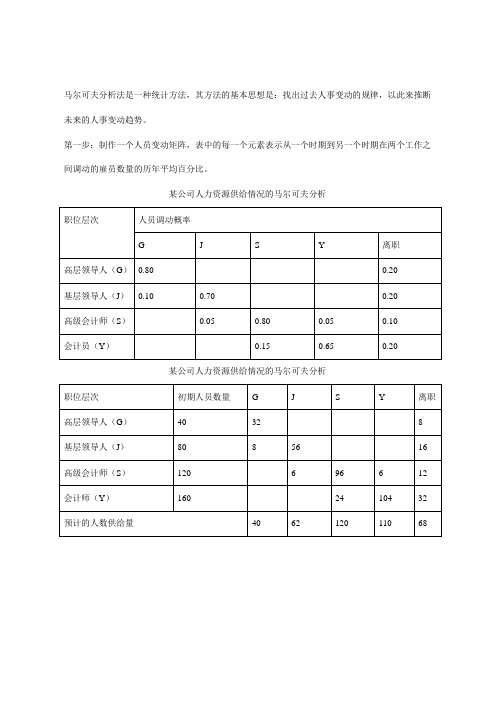
24
104
32
预计的人数供给量
40
62
120
110
68
马尔可夫分析法是一种统计方法，其方法的基本思想是：找出过去人事变动的规律，以此来推断未来的人事变动趋势。
第一步：制作一个人员变动矩阵，表中的每一个元素表示从一个时期到另一个时期在两个工作之间调动的雇员数量的历年平均百分比。
某公司人力资源供给情况的马尔可夫分析
职位层次
人员调动概率
G
JSBiblioteka Y离职高层领导人（G）
0.80
0.20
基层领导人（J）
0.10
0.70
0.20
高级会计师（S）
0.05
0.80
0.05
0.10
会计员（Y）
0.15
0.65
0.20
某公司人力资源供给情况的马尔可夫分析
职位层次
初期人员数量
G
J
S
Y
离职
高层领导人（G）
40
32
8
基层领导人（J）
80
8
56
16
高级会计师（S）
120
6
96
6
12
会计师（Y）
第9章马尔可夫分析
9.3 马尔科夫分析在管理工作中的应用 Page 12
参考上面解题方法，对照教材例题，熟练掌握即可。其中 P172页例1和P173页例2为重点。
本章总结
Page 13
本章内容选择、填空和名词解释都会涉及（马尔科夫基本概 念、概率向量和概率矩阵特殊注意）；计算题考察主要有两 个知识点：1、预测下一周期或下二周期的市场份额；2、计 算最终的市场份额，本章9.3中例题特殊注意，考原题考过 若干次。
当
n
，必有：Pn
Hale Waihona Puke z1...z2 ...
... ...
zn
称作平衡（固定）概率矩阵
...
z1
z2
...
zn
9.2 马尔科夫分析问题的要求
Page 5
1、马尔科夫问题的阶：一阶马尔科夫过程在确定事件周期 的选择概率时，只考虑前一周期的选择情况，二阶马尔科夫 过程在确定事件周期的选择概率时，考虑前两 周期的选择 情况。 2、转移概率：某个销售者保持、获得或失去消费者的概率。 3、转移概率矩阵：把转移概率排列成矩阵。 4、未来市场份额的确定★ 设第一周期的市场份额为T1,转移概率矩阵为P, 则第二周期的市场份额为T2=T1*P,以此类推可以得出任意 周期的市场份额。
C.迭代过程
D.渐趋过程
Page 16
5、（09年7月）下列矩阵属于概率矩阵的是（ B ）
6、（09年4月）任意一个方阵，如果其各行都是概率向 量，则该方阵称之为( D )
Page 10
【答案】由已知的该问题的转移概率矩阵为：
0.75 0.10 0.15
0.20 0.05
0.60 0.05
0.20 0.90
设最终这三种品牌服装的市场占有率分别为X1,X2,X3
案例九马尔科夫预测
案例九 马尔科夫预测一、 市场占有率的预测重点例1：在北京地区销售鲜牛奶主要由三个厂家提供。
分别用1，2，3表示。
去年12月份对2000名消费者进行调查。
购买厂家1，2和3产品的消费者分别为800，600和600。
同时得到转移频率矩阵为：3202402403601806036060180N ⎛⎫ ⎪= ⎪ ⎪⎝⎭其中第一行表示，在12月份购买厂家1产品的800个消费者中，有320名消费者继续购买厂家1的 产品。
转向购买厂家2和3产品的消费者都是240人。
N 的第二行与第三行的含义同第一行。
（1） 试对三个厂家1~7月份的市场占有率进行预测。
（2） 试求均衡状态时，各厂家的市场占有率。
解：（1）用800，600和600分别除以2000，得到去年12月份各厂家的市场占有率，即初始分布0(0.4,0.3,0.3)p =。
用800，600和600分别去除矩阵N 的第一行、第二行和第三行的各元素，得状态转移矩阵：0.40.30.30.60.30.10.60.10.3P ⎛⎫ ⎪= ⎪ ⎪⎝⎭于是，第k 月的绝对分布，或第 月的市场占有率为：00()(1,2,3,,7)k k P p P k p P =⋅=1k =时，()()10.40.30.30.40.30.30.60.30.10.520.240.240.60.10.3p ⎛⎫⎪== ⎪ ⎪⎝⎭2k =时，()()()220.40.30.30.520.240.240.4960.2520.252p P P ===3k =时,()()()330.40.30.30.4960.2520.2520.50080.24960.2496p P P === 类似的可以计算出4p ，5p ，6p 和7p 。
现将计算结果绘制成市场占有率变动表，如表所示：从表中可以看到，厂家1的市场占有率随时间的推移逐渐稳定在50%，而厂家2和厂家3的市场占有率随都逐渐稳定在25%.由于转移概率矩阵P 是正规矩阵，因此P 有唯一的均衡点μ。
马尔科夫分析法
特殊预测法：马尔可夫分析法定义：马尔可夫分析法是应用俄国数学家马尔可夫发现系统状态概率转移过程规律的数学方程，通过分析随机变量的现时变化情况，预测这些变量未来变化趋势及可能结果，为决策者提供决策信息的一种分析方法。
•单个生产厂家的产品在同类商品总额中所占的比率，称为该厂产品的市场占有率。
在激烈的竞争中，市场占有率随产品的质量、消费者的偏好以及企业的促销作用等因素而发生变化，企业在对产品种类与经营方向做出决策时，需要预测各种商品之间不断转移的市场占有率。
•市场占有率的预测可采用马尔可夫分析法，也就是运用转移概率矩阵对市场占有率进行市场趋势分析的方法。
俄国数学家马尔可夫在20世纪初发现：一个系统的某些因素在转移中，第N次结果只受第N－1次结果影响，只与当前所处状态有关，与其他无关。
例如：研究一个商店的累计销售额，如果现在时刻的累计销售额已知，则未来某一时刻的累计销售额与现在时刻以前的任一时刻的累计销售额都无关。
•在马尔可夫分析中，引入状态转移这个概念。
所谓状态是指客观事物可能出现或存在的状态；状态转移是指客观事物由一种状态转移到另一种状态的概率。
•马尔可夫分析法的一般步骤为：•1、调查目前的市场占有率情况；•2、调查消费者购买产品时的变动情况；•3、建立数学模型；•【•4、预测未来市场的占有率。
例一：一个800户居民点，提供服务的A、B、C三家副食品店，从产品、服务等方面展开竞争，各自原有稳定的居民户购买者开始出现了变化。
经过调查获得上月与本月三家商店的居民资料如表1；两个月中三商店都失去一些客户，同时也都赢得了一些客户，其转移变化资料如表2。
用马尔科夫法预测稳定状态下三商店的市场占有率。
表1表2例二：假定某小区有1000户居民，每户居民每月用一块香皂，并且只购买A牌、B牌、C牌。
8月份使用A牌香皂居民有500户，使用B 牌居民有200户，使用C牌居民有300户。
据调查9月份使用A牌香皂仍在使用的有360户，50户表示要改买B牌，90户表示要改买C牌；在使用B牌的用户中，120户仍在使用B牌，表示改买A牌的有40户，改买C牌的有40户；在使用C牌的用户中，表示仍在使用的有230户，有30户表示改买A牌，有40户表示改买C牌。
第9章马尔可夫预测方法讲述案例
指尽力保留公司原有顾客的各种经营方针与对策，譬 如采用提供优质服务或对连续两期购货的顾客实行折 价优惠等方法。
假设甲公司采用保留策略后，减少了其原有顾客向乙、丙 两公司的流失，使保留率从原来的63.16％提高到80％，同 时向乙、丙两公司的转移概率分别为9%和11%，此时程序 中第（2）步的一步转移概率矩阵变为：
第9章 马尔可夫预测方法
9.1 马尔可夫链基本理论 9.2 案例分析
9.2.1市场占有率预测 9.2.2 股票价格走势预测 9.2.3 加权马氏链法预测证券指数走势 9.2.4 期望利润预测
9.1 马尔可夫链基本理论
9.1.1马尔可夫链基本概念 （1）马尔可夫链
设随机过程{ X (t) ,t T }，
（2） 争取策略
指从竞争者拥有的顾客中争取顾客的各种经营方针 与对策。如：通过广告等方法。
设甲公司采用争取策略后，能从上一期内向另外两 家公司购货的顾客中分别争取20％与15％，此时程 序中第（2）步的一步转移概率矩阵又变为：
0.6316 0.1579 0.2105
P
0.2
0.5759 0.2241
( j) 1 的唯一解
j0
注1
定理表明不论从链中哪一状态i出发，都能以正概率经 有限次转移到达链中预先指定的其它任一状态。
注2 定理给出了求平稳分布 ( j)的方法。
3．马尔可夫链预测基本步骤
（1）划分状态区间，确定状态空间I =[1, 2，…，N]；
（2）按步骤（1）所划分状态区间，确定资料序列中各时段指 标值所对应的状态；
设有限马氏链{ X n , n 0 }的状态空间为 I={0,1,2,…,s}
如果存在正整数n0 ，使对一切i, j I 都有pi(jn0 ) 0 ，
马尔可夫模型
马尔可夫模型简介马尔可夫模型（Markov Model）是一种描述随机过程的数学模型，它基于“马尔可夫性质”假设，即未来的状态只与当前状态有关，与过去的状态无关。
马尔可夫模型在许多领域中得到了广泛的应用，如自然语言处理、机器学习、金融等。
历史发展马尔可夫模型最早由俄国数学家马尔可夫在20世纪初提出。
马尔可夫通过研究字母在俄文中的出现概率，发现了一种有规律的模式，即某个字母出现的概率只与之前的字母有关。
他将这种模式抽象为数学模型，即马尔可夫模型。
后来，马尔可夫模型被广泛应用于其他领域，并得到了不断的发展和完善。
基本概念状态（State）在马尔可夫模型中，状态是指系统可能处于的一种情况或状态。
每个状态都有一个特定的概率，表示系统处于该状态的可能性。
状态可以是离散的，也可以是连续的。
例如，对于天气预测，状态可以是“晴天”、“阴天”、“雨天”等。
转移概率（Transition Probability）转移概率表示从一个状态转移到另一个状态的概率。
在马尔可夫模型中，转移概率可以用转移矩阵表示，其中每个元素表示从一个状态转移到另一个状态的概率。
例如，对于天气预测，转移概率可以表示为：晴天阴天雨天晴天0.6 0.3 0.1阴天0.4 0.4 0.2雨天0.2 0.3 0.5上述转移矩阵表示了从一个天气状态到另一个天气状态的转移概率。
初始概率（Initial Probability）初始概率表示系统在初始时刻处于每个状态的概率。
它可以用一个向量表示，向量中每个元素表示系统处于对应状态的概率。
例如，对于天气预测，初始概率可以表示为：晴天阴天雨天0.3 0.4 0.3上述向量表示了系统初始时刻处于不同天气状态的概率。
观测概率（Observation Probability）观测概率表示系统处于某个状态时观测到某个观测值的概率。
观测概率可以用观测矩阵表示，其中每个元素表示系统处于某个状态观测到某个观测值的概率。
例如，对于天气预测，观测概率可以表示为：晴天阴天雨天温度高0.7 0.2 0.1温度低0.3 0.6 0.1上述观测矩阵表示了在不同天气状态下观测到不同温度的概率。
9.马尔可夫预测方法
（8.3）
8
例 1 ：不可越壁（反 弹壁）的随机游动
1
2
3
4
5
设一质点在线段[1，5 ]上随机游动，状态空间I={1，2， 3，4，5}，每秒钟发生一次随机游动，移动的规则是： 1 （1）若移动前在2，3，4处，则均以概率 向左 或向右移动一单位，或停留在原处；3 （2）若移动前在1处，则以概率1移到2处； （3）若移动前在5处，则以概率1移到4处。
齐次马尔柯夫链
如果马氏链的一步转移概率 pij (n) 与 n 无关，
即
P{X n1 j | X n i} pij
则称此马尔柯夫链为齐次马尔柯夫链（即关于时间为齐次）。
设 p0 (i) P{X 0 i} ，i I ，
初始分布
如果对一切 i I 都有
p0 (i) 0
马尔柯夫链在时刻n处于状态 i 的条件下，到时刻n+1转 移到状态 j 的条件概率，
即
P{X n1 j | X n i}
记作 pij (n)
称为在时刻n的一步转移概率，
注:
由于概率是非负的，且过程从一状态出发，经过一步 转移后，必到达状态空间中的某个状态 一步转移概率满足
（1） pij (n) 0 , i, j I
（2）
一步转移矩阵
p (n) 1 ,
jI ij
iI
如果固定时刻n T
则由一步转移概率为元素构成的矩阵 P 1 ：
称为在时刻n的一步转移矩阵
即 有
p00 ( n) p ( n) 10 P 1 pn 0 ( n )
p01 ( n) p11 ( n) pn1 ( n)
马尔科夫分析
1） Pij ≥ 0,i,j = 1,2, ……, N 非负性性质
2） ∑ Pij = 1 行元素和为1 ,i=1,2,…N
如： W1 = [1/4, 1/4, 1/2, 0]
概率向量 W2 = [1/3, 0, 2/3] W3 = [1/4, 1/4, 1/4, 1/2] 非概率向量 W4 = [1/3, 1/3, -1/3,0, 2/3] 3）若A和B分别为概率矩阵时，则AB为概率 矩阵。
i,j = 1,2, ……, N
定义：k步状态转移矩阵为： P11(k) P12(k) …… P1N(k) [k] P = : : : PN1(k) PN2(k) …… PNN (k) 当系统满足稳定性假设时 k [k] P = P = P• P• …… P 其中P为一步状态转移矩阵。 即当系统满足稳定性假设时，k步状态转移矩阵为一步 状态转移矩阵的k次方.
在试验过程中，随机变量可能随某一参数（不一定 是时间）的变化而变化. 如测量大气中空气温度变化x = x(h),随高度变化。 这种随参变量而变化的随机变量称为随机函数。而以时 间t作参变量的随机函数称为随机过程。 也就是说：随机过程是这样一个函数，在每次试 验结果中，它以一定的概率取某一个确定的，但预先未 知的时间函数。
0.4 0.3 0.3 0.6 0.3 0.1 0.6 0.1 0.3 = [U1 U2 U3]
[U1 U2 1－U1－U2]
即
-0.2U1 + 0.6 = U1 → U1 = 0.5 0.2U1 + 0.2U2 + 0.1 =U2 → U2 = 0.25 -0.2U2 + 0.3 = U3 → U3 = 0.25 ∴ U = [0.5 0.25 0.25] 则 0.5 0.25 0.25 T= 0.5 0.25 0.25 0.5 0.25 0.25 说明： 不管系统的初始状态如何，当系统运行时间较长时，转 移到各个状态的概率都相等。（列向量各元素相等） 即 各状态转移到1状态都为0.5; 2状态都为0.25 ; 3状态都为0.25
马尔可夫模型简介及应用(九)
马尔可夫模型简介及应用马尔可夫模型是一种用来描述一系列随机变量的数学模型，其基本思想是当前时刻的状态只依赖于前一个时刻的状态，与更早的状态无关。
马尔可夫模型在自然语言处理、金融、生态学等领域有着广泛的应用。
马尔可夫链马尔可夫链是马尔可夫模型的最基本形式。
它是一种离散时间的随机过程，具有无记忆性和状态转移性。
在一个马尔可夫链中，每个状态都有一个特定的概率，表示从当前状态转移到下一个状态的概率。
这些概率可以用一个状态转移矩阵来描述，矩阵的每一个元素表示从一个状态转移到另一个状态的概率。
马尔可夫链的应用马尔可夫链在自然语言处理领域有着广泛的应用。
例如，在语音识别中，可以使用马尔可夫链来建模语音的特征序列，从而识别出不同的语音单元。
在文本生成中，可以利用马尔可夫链来模拟语言的生成过程，从而生成类似真实语言的文本。
此外，在金融领域，马尔可夫链也被广泛应用。
例如，在股票价格的预测中，可以使用马尔可夫链来建模股票价格的波动，从而预测未来的价格走势。
在风险管理中，也可以利用马尔可夫链来建立信用风险模型，评估不同投资组合的风险水平。
马尔可夫随机场除了马尔可夫链，马尔可夫模型还有一个重要的扩展形式，即马尔可夫随机场。
马尔可夫随机场是一种无向图模型，用来描述一组随机变量之间的关系。
在马尔可夫随机场中，每个节点表示一个随机变量，每条边表示两个随机变量之间的关系。
马尔可夫随机场的应用马尔可夫随机场在计算机视觉、自然语言处理等领域有着广泛的应用。
例如，在图像分割中，可以使用马尔可夫随机场来建立像素之间的关系，从而实现对图像的分割。
在自然语言处理中，可以利用马尔可夫随机场来建立单词之间的关系，从而实现对文本的标注和分类。
总结马尔可夫模型是一种简单而强大的数学模型，具有广泛的应用价值。
通过建立状态转移矩阵，可以描述随机变量之间的动态演变过程。
在实际应用中，马尔可夫模型能够帮助我们更好地理解和预测复杂系统的行为，为决策和规划提供科学依据。
马尔可夫过程详解
平均正常工作时间为1/λ；
损坏后的修复时间： 典型地也是一个负指数分布的随机变量 平均修复时间为 1/μ；
问： 1) 一个系统正常启动后, 10小时以后正常工作的概率？
2) 系统平均无故障时间MTBF？平均修复时间MTTR？…
典型问题：排队论
N(t)
t
到达某个服务台的顾客流是一个强度为 λ 的泊松过程，单位 时间到达服务台的平均人数为λ； 服务台只有一个服务员，顾客所需服务时间是负指数分布的
w (t) w0 (t), w1 (t), ，wn (t)
例
例1：确定跳跃强度
λΔt+o(Δt) 1 μΔt+o(Δt) 2 3 4 5
1
x
在[1,5]上有个质点在整数点上作随机游动。
质点任何时刻都可能发生移动 若在时刻 t 质点位于2~4，则在(t+Δt)中以概率λΔt+o(Δt)
离散马尔可夫过程的无穷小转移率 或 跳跃强度。
性质：
q
j
ij
0
qi1 1+qii
qi2 i qi4
qi3
马尔可夫过程的数学描述：跳跃强度矩阵
跳跃强度(转移率)矩阵：
q00 Q q10 q n0 q01 q11 qn1 q0n q1n qnn
马尔可夫过程的数学描述：跳跃强度Q
定 对于一个很小的正的Δt 义 P ( Δt) P (0) q Δt o( Δt) δ q Δt o( Δt) ij ij ij ij ij
lim 其中： qij Δ to
Pij ( Δt) δi j Δt
称为参数连续状态
Ft
n 1 /t1 ,t2 tn
第09讲 计算机地质学---马尔科夫概型分析(28页)
9 马尔科夫概型分析
•学习重点、难点
重点：是马尔可夫概型、转移概率概念
和对实际地质问题的正确分析
难点：在于实际地质概念模型是否具有
马尔可夫概型性质的判断
•问题的提出
9 马尔科夫概型分析
对于地层序列的沉积旋回、油气藏中河
9 马尔科夫概型分析
计算转移概率的目的
转移概率矩阵完全描述了马尔可夫链的概 率统计特性，可以用它对未来时刻出现状态的
种类进行预报。
9 马尔科夫概型分析
转移频数矩阵[nij]的求法 1 2 3 4 5
1 0 2 0 3 1 4 1 5 1
列和 3
1 0 0 2 1
4
1 2 0 2 0mmN nij
i 1 j 1
m
9 马尔科夫概型分析
当给定检验水平α 之后，如果由上式 算出的X2 >X2α [(m-1)2],则否定原假设， 认为系统具有马尔可夫概型的性质。
以例一给出的岩性状态序列，计算
X2=28.6。若取信度α=0.05，自由度f=(5-
1)2=16,查X2分布表，得X20.05=26.3，X2>
9 马尔科夫概型分析
马氏概型检验 根据频数矩阵中列出的数据，计算
出X2=180.17，自由度f=(7-1)2=36，查
表得X20.05=60，显然，X2>> X20.05，说
明该序列为马氏链。
9 马尔科夫概型分析
从转移频数矩阵计算出岩性的转移概率矩阵：
1
1 2 3 P= 4 5 6 7
2
3
0.125 0.857 0 0.048
第九章马尔可夫概型分析讲解
求出
p
j
m i 1
pi
p(1) ij
( j 1, 2,
, m)
m
j 1
pj
1
( p j 0)
19
对于本例为
p1 p2
0.79 p1 0.21p1
0.59 0.41
p2 p2
p1 p2 1
( p1, p2 0)
最后得到p2=0.26，p1=0.74。所以，其极限概率矩阵为
p
0.74 0.74
0.26 0.26
20
如果从公式P（k）=（P（1））k出发，计算其高阶转移概率
第九章马尔可夫概型分析
§1 概述 §2马尔可夫概型 §3马儿可夫链的转移概率 §4遍历定理与极限分布 §5马儿可夫概型检验 §6 应用简例
1
§1 概述
任何一个地质过程都可认为是某些确定性地质因素和 随机性地质因素相互作用的产物。也就是说，地质过程 都应是确定型和随机型地质过程在时间上和空间上叠加 的结果，因此在地质研究工作中，应重视上述两类地质 过程的作用。但是，由于产生随机地质过程的机理十分 复杂，甚至连随机性地质因素也不容易或不可能观察， 这就给用数学校型(一个或几个)来描述随机型地质过程带 来了极大的、甚至是在目前条件下不可能克服的困难。 这样以来，人们自然就会侧重于确定型地质过程的研究， 而使随机型地质过程的研究成为地质工作中的一个薄弱 环节。
m
p p (1) (1) 1k k 2
m
p(1) 1k
p(1) km
k 1
k 1
k 1
马尔可夫分析
0
P
1
2
1 1 2
,P
2
1 2 1 4
1
2
3 4
正规概 率矩阵
1 0
1 0
1 0
Q
1
2
1
,
Q
2
3
2
4
1 4
，
，Qm
2m 1 2m
1 2m
非正规概 率矩阵
概率矩阵具有一下性质：
若A是一个正规概率矩阵，则有
① 一定存在一个概率向量X，使得AT X X 成立，
且X的各分量皆为正数；
pCA 25 / 300 0.083, pAA 160 / 200 0.800 pAB 20 / 200 0.100, pBB 450 / 500 0.900 pCB 20 / 300 0.067, pAC 20 / 200 0.100 pBC 15 / 500 0.030, pCC 255 / 300 0.850
i1、i2、 in-1、i、j及一切n 0，有 p( X n1 j | X n i, X k ik , k 1, 2, p( X n1 j | X n i) pij (n),
则称{X n}是一个马尔可夫链。
n -1)
例如，有一位顾客每天向一家商店买一包香烟。他购买香烟 并不固定于一种牌号，商店中A、B、C、D、E五种牌号的香 烟他都有可能购买。设X m表示他在第m天购买的香烟牌号。 若这个人只记得昨天抽烟的味道，以前的都记不得了，那么 X m取什么值，只与X m1取什么值有关，则{X m}构成一个马尔 可夫链。
例3 ：（天气预报问题）
如果明日是否有雨仅与今日天气（是否有雨）有关，而 与过去的天气无关，并设今日下雨，则明日下雨的概率
马尔可夫网络的参数估计方法(九)
马尔可夫网络的参数估计方法马尔可夫网络是一种用于建模随机过程的图模型，它的应用涵盖了很多领域，包括自然语言处理、生物信息学、社交网络分析等。
在马尔可夫网络中，节点表示随机变量，边表示变量之间的依赖关系。
参数估计是马尔可夫网络中的一项重要任务，它的目的是从观测数据中估计出网络中节点之间的条件概率分布。
本文将介绍几种常见的马尔可夫网络参数估计方法，并对它们进行比较和分析。
一、极大似然估计极大似然估计是一种常用的参数估计方法，它的基本思想是选择一组参数，使得观测数据出现的概率最大化。
对于离散型的马尔可夫网络，参数估计可以转化为计算条件概率分布的频率。
假设我们有一个包含n个样本的数据集，每个样本都是由d个离散型随机变量组成。
对于每一个节点，我们可以统计其在每个取值下出现的频率，然后将其归一化得到条件概率分布。
这样就得到了马尔可夫网络的参数估计结果。
极大似然估计的优点是简单易实现，但是当数据稀疏时，估计结果可能会出现严重的过拟合问题。
二、贝叶斯估计贝叶斯估计是一种基于贝叶斯理论的参数估计方法，它的目的是在观测数据的基础上推断参数的分布。
对于马尔可夫网络的参数估计，贝叶斯估计可以通过引入先验分布来解决数据稀疏的问题。
假设我们对参数的先验分布有一定的先验知识，那么我们可以通过贝叶斯定理来更新参数的后验分布。
与极大似然估计相比，贝叶斯估计可以更好地利用先验信息，从而在数据稀疏的情况下得到更稳健的估计结果。
然而，贝叶斯估计的计算复杂度要高于极大似然估计，而且对先验分布的选择也会对估计结果产生影响。
三、EM算法EM算法是一种常用的参数估计方法，它的基本思想是通过交替优化来估计模型参数。
对于马尔可夫网络的参数估计，EM算法可以通过交替进行E步和M步来更新参数的估计。
在E步中，我们可以通过当前参数的估计来估计隐变量的期望，而在M步中，我们可以通过最大化期望似然函数来更新参数的估计。
EM算法的优点是可以处理隐变量的情况，而且对于数据稀疏的情况也有较好的性能。
马尔可夫分析法
谢谢大家
人力资源中的运用 预测未来组织中规模和分布的演变情况。
举例：未来的升迁、转职、调配或离职等情况。
具体步骤
① 根据历史数据推算各类人员的转移率，迁出转移 率的转移矩阵P； ② 统计作为初始时刻点的各类人员分布状况S0； ③ 建立马尔可夫模型，预测未来各类人员供给状况S。
实例分析 了解企业岗位设置
假设某企业的岗位设置如下高级经理、部门经理、业务主管 和技术人员, 则N=4
Company Logo
为什么他们都能采用马尔可夫分析法？ 为什么他们都能采用马尔可夫分析法？ 答案： 答案： 其一，他们都具有马尔可夫性的时间序列 马尔可夫性的时间序列（ ） 其一，他们都具有马尔可夫性的时间序列（T）， 并且各时刻的状态转移概率(P)保持稳定。 保持稳定。 并且各时刻的状态转移概率 保持稳定 其二，马尔可夫分析法是用来稳定预测的 分析法是用来稳定预测的。 其二，马尔可夫分析法是用来稳定预测的。
了解企业各岗位人员分布
通过调查, 期初该企业各岗位 企业各岗位的人员数量P1，P2，P3，P4分别 企业各岗位 为10，25，35，50。 那么（P1，P2，P3，P4）=（10，25，35，50）为不同岗位 人员的初始分布矩阵。
实例分析 了解企业内部各岗位人员流动情况
调查得出企业内部人员流动情况如下本年度高级经理留 任的有70%、离职的有30%；部门经理晋升为高级经理的有 10%、留任部门经理的有70%、离职的有20%；业务主管晋 升为部门经理的有20%、留任业务主管的有60%、调换担任 技术人员的有10%、离职的有10%；技术人员晋升为业务主 管的有20%。留任技术人员的有60%，离职的有20%。
使用原理——概率矩阵 概率矩阵 使用原理
由概率向量构成的方阵即行和列相同的矩 阵称为概率矩阵。马尔可夫分析法预测用 的全部为正概率矩阵。
马尔可夫 主方程
马尔可夫主方程【原创版】目录1.马尔可夫的简介2.马尔可夫方程的定义3.马尔可夫方程的应用4.马尔可夫方程的求解方法5.马尔可夫方程在现代科学中的重要性正文1.马尔可夫的简介马尔可夫（Andrey Markov，1896-1984）是一位俄罗斯数学家，他的研究领域涉及概率论、统计学和信息论等多个领域。
马尔可夫方程，以其名字命名，是概率论中的一种重要方程，描述了一个系统的时间序列的统计特性。
2.马尔可夫方程的定义马尔可夫方程，又称马尔可夫过程，是一种随机过程，描述了一个系统随时间变化的状态转移规律。
它的基本特征是系统的下一状态只依赖于当前状态，而与过去的状态无关，这就是马尔可夫性质。
用数学公式表示，可以写为：P(X(t+1)|X(t)) = P(X(t+1)|X(t), X(t-1),..., X(1))。
3.马尔可夫方程的应用马尔可夫方程在实际应用中有广泛的应用，例如在语言处理、模式识别、金融分析、网络流量预测等领域。
其中最著名的应用是马尔可夫链在自然语言处理中的应用，通过分析语料库中的词频和词序列，可以构建出一个马尔可夫链模型，用于预测一段文本的下一个词。
4.马尔可夫方程的求解方法马尔可夫方程的求解方法主要包括矩阵幂法、迭代法和随机模拟法等。
矩阵幂法是求解马尔可夫链的主要方法，通过计算矩阵的幂次，可以得到系统在任意时刻的状态概率分布。
迭代法则是通过迭代计算，逐步逼近系统的稳态概率分布。
随机模拟法则是通过大量的模拟实验，估计系统的稳态概率分布。
5.马尔可夫方程在现代科学中的重要性马尔可夫方程在现代科学中具有重要的地位，它不仅为理论研究提供了一种重要的工具，也为实际应用提供了一种有效的方法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0
p(k ) ij
1；
p(k ) ij
1。
j 1
因而有
p(2)
[
p(2) ij
]mm
p(2) 11
p(2) 21
p(2) 12
p(2) 22
p(2) m1
p(2) m2
p(2) 1m
p(2) 2m
p(2) mm
m
p p (1) (1) 1k k1
p p (1) (1) 22 22
p p (1) (1) 23 32
j 1
0.4 0.5 0.4 0.4 0.2 0.6 0.36
16
9.4遍历定理与极限分布 马尔可夫链遍历性的直观意义是：不论从哪个初始状 态Ei出发，当转移步数k充分大后，它到达状态Ej的概率 是一个不随时间变化的常数pj。
2
1949年，维斯捷列马斯在研究复式沉积层形成问题时， 首先应用了马尔可夫链。1984年，在莫斯科举行的第27 届国际地质会议上，维斯短列乌斯、阿柑特伯格 (F．P．Agterbers)等数学地质学家发表了莫斯科宣言，其 基本思想是；随机型模型应作为数学地质模型的基础，并 且肯定了马尔可夫过程(特别是马尔可夫链)在地质学中应 占有特殊的地位。
1251454524543541343423545454231454 545
9
解： 首先由上面的状态序列统计出转移频数矩阵[nij] 如下
1 2 3 4 5 列和ni·
1 2
0 0
1 0
1 2
2 1
0 1
n1 4 n2 4
3 4
1 1
0 2
0 2
2 0
2 8
n3 5 n4 13
{xt ,t 0,1, 2, }
马尔可夫链适用于时间离散、状态离散的时间序列。 但是，在研究地质过程时，有时能直接确定过程在时间 上的先后顺序，有时则只能间接地以空间上的上下、前 后、左右关系宋代替；也就是说，在地质过程研究中， 有时可以挨到确定的时间序列，有时只能间接地用距离 来代替时间参数：但是，只要空间序列有类似于马尔可 夫性质的关系存在，则仍然可以应用马尔可夫链对这种 序列进行研究。在此，我们将既适用于时间序列又适用 于空间序列的马尔可夫概率模型统称为“马尔可夫概 型”。
目前，常用马尔可夫概型分析研究沉积旋回，进行 地层对比，查明火山岩系的喷出顺序和侵入杂岩体中 各个侵入体形成的先后顺序，划分矿床的成矿期和成 矿阶段、揭示各个成矿阶段的空间分布等。
到目前为止，研究随机型地质过程所涉及的数学 方法也仅限于马尔可夫概型分析。
3
9.2马尔可夫概型
随机过程是概率论的基本概念之一，它是依赖于参数t 的一族随机变量，记为
p(k)
[
p(k ij
)
]mm
p(k) 11
p(k) 21
p(k) 12
p(k) 22
p(k) m1
p(k) m2
p(k) 1m
p(k) 2m
p(k) mm
称为K阶转移概率矩阵，其中
13
p(k ) ij
Ei后的第k步是E
的次数
j
Ei出现的次数
m
且有性质
6
若马尔可夫过程的转移概率随着时间的推移而发生变 化，则称其为非齐次或非乎稳马尔可夫过程，转移概率不 随时间而变的马尔可夫过程就称为齐次或平稳马尔可夫过 程。目前在地质研究中，主要是应用平稳马尔可夫过程。
7
9.3马儿可夫链的转移概率
设马尔可夫链中可列个发生状态转移的时刻为t1， t2，…tn，…，在已知时刻t＝tn时随机过程xi所处状态为i 的条件下，把经过一步转移，即在时刻t＝tn+1(tn+1＞tn)转 移到状态j上的概率记为pij，
由条件分布律的性质，知转
p (1)
p (1) 11
p (1) 21
p (1) m1
p (1) 11
p (1) 22
p (1) m2
p(1) 1m
p (1) 2m
p(1) mm
移概率有如下性质：
0
p(1) ij
1
m
p(1) ij
1
也就是说，无论初始状态如何，经过若干步转移以后， 系统将处于平衡状态，因而当k充分大时，可用pj作为pij（k） 的近似值。
遍历性可以解决当k很大时高阶转移概率的计算问 题。pj称为马尔可夫链的极限概率。
遍历性需要确定的中心问题在什么样的条件下，转移
概率的极限才是存在的；极限概率是否构成一个概率分布；
F (xn；tn / xn1；tn1)
则称x(t)为马尔可夫过程,条件分布函数
F(xn；tn / xn1；tn1) P{x(tn ) xn / x(tn1) xn1} (tn tn1)
是马尔可夫过程的概率模型,上式为马尔可夫过程的转移
概率。
马尔可夫过程又称为“无后效随机过程”。所谓无后
p
0.74 0.74
0.26 0.26
20
如果从公式P（k）=（P（1））k出发，计算其高阶转移概率
p (1) 25
0
0
0.25 0.25 0.5 0
0
0.5
0.25
0.25
p (1)
p (1) 31
p (1) 41
p (1) 32
p (1) 42
p (1) 33
p (1) 43
p (1) 34
p (1) 44
p (1) 35
p (1) 45
0.2 0.077
p(2) 21
p(2) 12
p(2) 22
p(2) m1
p(2) m2
p(2) 1m
p(2) 2m
p(2) mm
这个矩阵称为二阶转移概率矩阵，其中元素pij可以 由实际资料统计出来，即
12
p(2) ij
Ei后的第二步是E
的次数
j
Ei出现的次数
更一般地，由状态Ei经k步转移到状态Ej，的概率pij称 为k阶转移概率，其转移概率矩阵
i 1
m
在满足条件pj>0，
p (1) j
1
时的唯一解
i 1
18
例，有一马尔可夫链，其转移状态有两种：E1，E2。 经计算得出它的一阶转移概率矩阵为
p(1)
0.79 0.59
0.21 0.41
当s=1时，对一切i，j，pij（1）〉0满足遍历性定理，故有。 而pj可由方程组
x(t),t T
这里的参数t一般是时间，T是它的变化范围，随机变
量x(ti)也称作随机过程 x(t)在t＝ti ∈T时的状态。
当随机过程在时刻t1所处的状态x(t1)为已知的条件下， 若随机过程在时刻t(t＞t1)所处的状态x(t)与随机过程在t1 时刻之前发生的状态无关，那么这样的随机过程就称为
链的一个重要问题。转移概率在理论上是条件概率，而实
际应用时则是以转移频率nij/ni．作为条件概率的估计值，
即
pˆ ij
nij ni
例：一地层段由五种岩性状态组成，以1表示砾状砂岩
和粗砂岩，2表示细砂岩，3表示粉砂岩，4表示粘土岩，
5表示灰岩，下面列出了自下而上的岩性状态转移序列，
求其转移概率。
求出
p
j
m i 1
pi
p(1) ij
( j 1, 2,
, m)
m
j 1
pj
1
( p j 0)
19
对于本例为
p1 p2
0.79 p1 0.21p1
0.59 0.41
p2 p2
p1 p2 1
( p1, p2 0)
最后得到p2=0.26，p1=0.74。所以，其极限概率矩阵为
p(1) k1
p p (1) (1) mk k 2 k 1
k 1
p(1) mk
p(1) km
14
从而，对于高阶转移概率矩阵有
m
p(k ) ij
p p (r ) (k r ) ij ij
i 1
也就是说，从状态Ei出发经过k步到达状态Ej这一过 程，可以看作它是先经过r(o＜r＜k)步转移到某一状态
0 0.154
0 0.154
0.4 0
0.4 0.615
p (1) 51
p (1) 52
p (1) 53
p (1) 54
p (1) 55
0.1
0.1
0 0.8 0
如果过程的状态不是5种而是m种，即E1，E2，…，
Em ,那么由状态Ei经过一步转移到状态Ej的一阶转移概率
矩阵为
j 1
(i 1, 2,
, m)
11
二、高阶转移概率
如果马尔可夫链有，m 种状态EI，E2，…，Em，从状 态Ei出发经两步转移到状态Ej的概率(不管第一步是什么状 态)称为二阶转移概率，记为此pij(2)，用二阶转移概率排成 的矩阵为
p(2)
[
p(2) ij
]mm
p(2) 11