六年级行程问题习题及答案 (1)之欧阳数创编
(2021年整理)六年级行程问题练习及答案

六年级行程问题练习及答案编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(六年级行程问题练习及答案)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为六年级行程问题练习及答案的全部内容。
行程问题(1)一、填空题1。
两车同时从甲乙两地相对开出,甲每小时行48千米,乙车每小时行54千米,相遇时两车离中点36千米,甲乙两地相距千米。
2.小明从甲地到乙地,去时每小时走6公里,回来时每小时走9公里,来回共用5小时.小明来回共走了公里.3。
一个人步行每小时走5公里,如果骑自行车每1公里比步行少用8分钟,那么他骑自行车的速度是步行速度的倍。
4。
一位少年短跑选手,顺风跑90米用了10秒钟。
在同样的风速下,逆风跑70米,也用了10秒钟。
在无风的时候,他跑100米要用秒.5。
A、B两城相距56千米。
有甲、乙、丙三人。
甲、乙从A城,丙从B城同时出发.相向而行.甲、乙、丙分别以每小时6千米、5千米、4千米的速度行进。
求出发后经小时,乙在甲丙之间的中点?6.主人追他的狗,狗跑三步的时间主人跑两步,但主人的一步是狗的两步,狗跑出10步后,主人开始追,主人追上狗时,狗跑出了步.7。
兄妹二人在周长30米的圆形水池边玩,从同一地点同时背向绕水池而行,兄每秒走1.3米,妹每秒走1。
2米,他们第十次相遇时,妹妹还需走米才能回到出发点。
8.骑车人以每分钟300米的速度,从102路电车始发站出发,沿102路电车线前进,骑车人离开出发地2100米时,一辆102路电车开出了始发站,这辆电车每分钟行500米,行5分钟到达一站并停车1分钟,那么需要分钟,电车追上骑车人.9.一个自行车选手在相距950公里的甲、乙两地之间训练,从甲地出发,去时每90公里休息一次,到达乙地并休息一天后再沿原路返回,每100公里休息一次.他发现恰好有一个休息的地点与去时的一个休息地点相同,那么这个休息地点距甲地有公里。
相遇及追及问题(含答案)之欧阳理创编

相遇及追击问题(一)一.填空题(共12小题)1.五羊公共汽车公司的555路车在A,B两个总站间往返行驶,来回均为每隔x分钟发车一次.小宏在大街上骑自行车前行,发现从背后每隔6分钟开过来一辆555路车,而每隔3分钟则迎面开来一辆555路车.假设公共汽车与小宏骑车速度均匀,忽略停站耗费时间,则x= _________分钟.2.在一条街AB上,甲由A向B步行,乙骑车由B向A行驶,乙的速度是甲的速度的3倍,此时公共汽车由始发站A开出向B行进,且每隔x分发一辆车,过了一段时间,甲发现每隔10分有一辆公共汽车追上他,而乙感到每隔5分就碰到一辆公共汽车,那么在始发站公共汽车发车的间隔时间x=_________分钟.3.小王沿街匀速行走,发现每隔6分钟从背后驶过一辆18路公交车,每隔3分钟从迎面驶来一辆18路公交车.假设每辆18路公交车行驶速度相同,而且18路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是_________分钟.4.小锋骑车在环城路上匀速行驶,每隔5分钟有一辆公共汽车从对面向后开过,每隔20分钟又有一辆公共汽车从后向前开过,若公共汽车也匀速行驶,不计中途耽误时间,则公交车车站每隔_________分钟开出一辆公共汽车.5.某人在公共汽车上发现一个小偷向反方向步行,10秒钟后他下车去追小偷,如其速度比小偷快一倍,比汽车慢,则追上小偷要(_________)秒.6.某人沿电车路线行走,每12分钟有一辆电车从后面赶上,每4分钟有一辆电车迎面开来,若行人与电车都是匀速前进的,则电车每隔_________分钟从起点开出一辆.7.某公交公司停车场内有15辆车,从上午6时开始发车(6时整第一辆车开出),以后每隔6分钟再开出一辆.第一辆车开出3分钟后有一辆车进场,以后每隔8分钟有一辆车进场,进场的车在原有的15辆车后依次再出车.问到_________点时,停车场内第一次出现无车辆?8.通讯员从队伍末尾追赶至队伍前头时用全速进行,其速度为队伍的3倍,当他从队伍前面返回队伍末尾时每分钟减少100米.在队伍前进过程中,通讯员连续三次往返执行任务,途中花费时间共1小时,其中三次往返队伍末尾时间比三次追赶队伍前头时间共少用12分钟,则队伍的长为_________.9.男女运动员各一名,在环行跑道上练习长跑,男运动员比女运动员速度快,如果他们从同一起跑点沿相反方向同时出发,那么每隔25秒相遇一次,现在他们从同一起跑点沿相同方向同时出发,男运动员经过15分钟追上女运动员,并且比女运动员多跑了16圈,女运动员跑了_________圈.10.有甲、乙两辆小汽车模型,在一个环形轨道上匀速行驶,甲的速度大于乙.如果它们从同一点同时出发沿相反方向行驶,那么每隔1分钟相遇一次.现在,它们从同一点同时出发,沿相同方向行驶,当甲第一次追上乙时,乙已经行驶了4圈,此时它们行驶了_________分钟.11.一路电车的起点和终点分别是甲站和乙站,每隔5分钟有一辆电车从甲站发车开往乙站,全程要走15分钟,有一个人从乙站出发沿电车路线骑车前往甲站,他出发的时候,恰好有一辆电车到达乙站,在路上他又遇到了10辆迎面开来的电车,才到达甲站,到甲站时恰好又有一辆电车从甲站开出,问他从乙站到甲站用了_________分钟.12.如图,在矩形ABCD中,AB=4cm,AD=12cm,点P从点A向点D以每秒1cm的速度运动,Q以每秒4cm 的速度从点C出发,在B、C两点之间做往返运动,两点同时出发,点P到达点D为止,这段时间内线段PQ 有_________次与线段AB平行.13.(巴蜀初2012级第一次月考16题)某人从甲地走往乙地,甲、乙两地之间有定时的公共汽车往返,且两地发车的时间间隔都相等。
六年级高难度奥数题及答案之行程问题

六年级高难度奥数题及答案之行程问题
六年级高难度奥数题及答案之行程问题
六年级奥数题及答案:行程问题(高等难度)
行程问题:(高等难度)
有甲、乙、丙三辆汽车,各以一定的速度从A地开往B地,乙比丙晚出发10分钟,出发后40分钟追上丙;甲比乙又晚出发20分钟,出发后1小时40分钟追上丙,那么甲出发后需多少分钟才能追上乙。
行程问题答案:
由已知条件可知,乙用40分钟所走的路程与丙用50分钟所走的路程相等;甲用100分钟所走的.路程与丙用130分钟所走的路程相等。
故丙用130分钟所走的路程,乙用了40×(130÷50)=104(分钟),即甲用100分钟走的路程,乙用104分钟走完。
多用4分钟,由于甲比乙晚出发20分钟,所以甲出发500分钟才能追上乙。
下载全文。
六年级下册奥数试题 行程问题(一) 全国通用(含答案)-精编

第11讲行程问题(一)在人们的生活中离不开“行”,“行”中有三个重要的量:路程、速度、时间。
研究这三个量的典型应用题叫做行程问题。
这三个量之间的关系可以用下面的公式来表示:路程=速度×时间速度=路程÷时间时间=路程÷速度相遇问题和追及问题是行程问题的两个重要的类型。
相遇问题是指两个物体在行进过程中相向而行,然后在途中某点相遇的行程问题。
其主要数量关系式为:总路程=速度和×相遇时间追及问题是指两个物体在行进过程中同向而行,快行者从后面追上慢行者的行程问题。
其主要数量关系式为:路程差=速度差×追及时间例1 姐姐放学回家,以每分钟80米的速度步行回家,12分钟后妹妹骑车以每分钟240米的速度从学校往家中骑,经过几分钟妹妹可以追上姐姐?分析:经过12分钟,姐姐到达A地,妹妹骑车回家。
如下图所示:从图中可以看出妹妹从出发到追上姐姐这段时间里,妹妹要比姐姐多行的路程就是姐姐12分钟所走的路程,也就是妹妹与姐姐的路程差。
有了路程差,再求出速度差,根据追及问题的数量关系式追及时间=路程差÷速度差就可求出妹妹追上姐姐的时间。
解答:妹妹与姐姐的路程差80×12=960(千米)妹妹与姐姐的速度差240-80=160(千米)妹妹追上姐姐的时间960÷160=6(分)答:经过6分钟妹妹追上姐姐。
例2 一辆公共汽车和一辆小轿车同时从相距360千米的两地相向而行,公共汽车每小时行35千米,小轿车每小时行55千米,几小时后两车相距90千米?分析:两车从相距360千米的两地同时出发相向而行,距离逐渐缩短,在相遇前某一时刻两车相距90千米。
如下图这时两车共行的路程为360-90=270(千米)值得注意的是,当两车相遇后继续行驶时,两车之间的距离又从零逐渐增大,到某一时刻,两车再一次相距90千米。
如下图所示从图中可知,这时两车共行的路程为360+90=450(千米)根据相遇问题的数量关系式相遇时间=总路程÷速度和所求的问题就可以解答。
(完整版)六年级行程问题习题及答案(1)
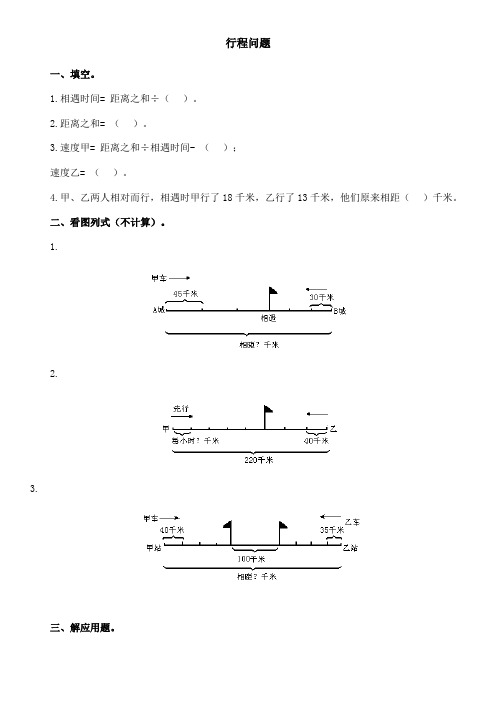
行程问题一、填空。
1.相遇时间= 距离之和÷()。
2.距离之和= ()。
3.速度甲= 距离之和÷相遇时间- ();速度乙= ()。
4.甲、乙两人相对而行,相遇时甲行了18千米,乙行了13千米,他们原来相距()千米。
二、看图列式(不计算)。
1.2.3.三、解应用题。
1.一列客车和一列货车同时从两个车站相对开出,货车每小时行35千米,客车每小时行45千米,2.5小时相遇,两车站相距多少千米?2.两个县城相距52.5千米,甲、乙二人分别从两城同时相对而行,甲每小时行5千米,乙每小时比甲快0.5千米,几小时后相遇?3.甲、乙二人分别从相距110千米的两地相对而行。
5小时后相遇,甲每小时行12千米,问乙每小时行多少千米?4.甲、乙两站相距486千米,两列火车同时从两站相对开出,5小时相遇。
第一列火车比第二列火车每小时快1.7千米,两列火车每小时的速度各是多少?5.两列火车同时从相距650千米的两地相向而行,甲列火车每小时行50千米,乙列火车每小时行52千米,4小时后还差多少千米才能相遇?6.大陈庄和小王庄相距90千米。
小刚和小牛分别由两庄同时反向出发。
2小时24分后两人相距46.6千米,如果小刚每小时行9.9千米,小牛每小时行多少千米?7.学校距活动站670米,小明从学校前往活动站每分钟行80米,2分钟后,小丽从活动站往学校走,每分钟行90米,小明出发多少分钟后和小丽相遇?相遇时二人各行了多少米?8.甲、乙两队合挖一条水渠,甲队从东往西挖,每天挖65米,乙队从西往东挖,每天比甲多挖2.5米。
两队合挖8天后还差52米,这条水渠全长多少米?9.张、李两位叔叔计划共同生产一种零件300个,二人一起生产了5小时后还差40个没完成。
已知张叔叔每小时生产24个,李叔叔每小时生产多少个?10.甲、乙两队合修一条长2400米的路,甲队每小时修126米,乙队每小时比甲队多修48米,求完工时两队各修路多少米?11.东西两村相距64千米。
小升初数学压轴题(打印版)之欧阳索引创编

第一篇一般应用题欧阳家百(2021.03.07)1、一桶油,连桶共重8千克,倒出一半的油后,连桶重4.4千克,桶中原有油多少千克?2、一瓶酒,连瓶共重0.7千克,喝了一半的酒后,连瓶重0.5千克,原有酒多少千克?3、有一桶水,每次倒出桶中水的一半,倒了2次后连桶重12千克。
已知桶重1.5千克,求桶中原有水多少千克?4、7袋大米和3袋面粉共重425千克,同样的3袋大米和7袋面粉共重325千克。
每袋大米重多少千克?每袋面粉重多少千克?5、小明买2支笔和4本练习本用去10元,小丽买同样的3支笔和3本练习本用去12元。
一支笔多少元?一本练习本多少元?6、甲买了8盒糖和5盒饼干共用去171元,乙买了5盒糖和2盒饼干共用去90元。
每盒糖多少元?每盒饼干多少元?7、小明和小丽到商店买作业本,他们所付的钱一样多,共买了20本作业本。
小丽比小明多拿4本作业本,因此小丽还给小明1.2元钱。
小明和小丽共花了多少钱?8、王大伯和李大伯带同样多的钱买了一批化肥,结果王大伯比李大伯多拿了2袋,因此王大伯又给了李大伯82元。
每袋化肥多少钱?9、甲、乙、丙三人用了同样多的钱合买西瓜。
分西瓜时,甲和丙都比乙多拿西瓜7.5千克。
结果甲、丙两人各给乙2元。
每千克西瓜多少元?10、李丽前六次测验的平均分是93分,她第七次测验成绩比这七次测验的平均分高出3分。
李丽第七次测验得了多少分?11、某班一次英语测验的平均分为88分,其中小明因病没有参加考试。
第二天,小明补考,其不靠成绩是79分,加上小明的成绩后该班平均分为87.8分。
这个班共有学生多少名?12、五年级(4)班有40名学生,期末数学测验,有两名同学因病缺考,班级平均分为89分,缺考的两名同学补考的成绩分别是98分、100分。
全班同学的平均分又是多少分?13、某工厂有93名工人,因经济危机,工厂施行减员增效方案,安排男工的一半和30名女工上班,剩下的工人在家待岗,待岗的男、女工人数相等。
六年级小升初数学行程问题精编WORD版

六年级小升初数学行程问题精编W O R D版 IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】六年级(小升初)总复习行程问题行程问题常用的解题方法有⑴公式法 S=V*T ⑵图示法⑶比例法行程问题中有很多比例关系,在只知道和差、比例时,用比例法可求得具体数值.更重要的是,在一些较复杂的题目中,有些条件(如路程、速度、时间等)往往是不确定的,在没有具体数值的情况下,只能用比例解题;⑷分段法⑸方程法模块一、时间相同速度比等于路程比【例 1】甲、乙二人分别从 A、 B 两地同时出发,相向而行,甲、乙的速度之比是4 : 3,二人相遇后继续行进,甲到达 B 地和乙到达 A地后都立即沿原路返回,已知二人第二次相遇的地点距第一次相遇的地点 30千米,则 A、 B 两地相距多少千米?【解析】两个人同时出发相向而行,相遇时时间相等,路程比等于速度之比,即两个人相遇时所走过的路程比为 4 : 3.第一次相遇时甲走了全程的4/7;第二次相遇时甲、乙两个人共走了 3个全程,三个全程中甲走了453177⨯=个全程,与第一次相遇地点的距离为542(1)777--=个全程.所以 A、 B两地相距2301057÷= (千米).【例 2】B地在A,C两地之间.甲从B地到A地去送信,甲出发10分后,乙从B地出发到C地去送另一封信,乙出发后10分,丙发现甲、乙刚好把两封信拿颠倒了,于是他从B地出发骑车去追赶甲和乙,以便把信调过来.已知甲、乙的速度相等,丙的速度是甲、乙速度的3倍,丙从出发到把信调过来后返回B地至少要用多少时间。
【解析】根据题意当丙发现甲、乙刚好把两封信拿颠倒了此时甲、乙位置如下:因为丙的速度是甲、乙的3倍,分步讨论如下:(1)若丙先去追及乙,因时间相同丙的速度是乙的3倍,比乙多走两倍乙走需要10分钟,所以丙用时间为:10÷(3-1)=5(分钟)此时拿上乙拿错的信当丙再回到B点用5分钟,此时甲已经距B地有10+10+5+5=30(分钟),同理丙追及时间为30÷(3-1)=15(分钟),此时给甲应该送的信,换回乙应该送的信在给乙送信,此时乙已经距B地:10+5+5+15+15=50(分钟),此时追及乙需要:50÷(3-1)=25(分钟),返回B地需要25分钟所以共需要时间为5+5+15+15+25+25=90(分钟)(2)同理先追及甲需要时间为120分钟【例 3】 (“圆明杯”数学邀请赛) 甲、乙两人同时从A、B两点出发,甲每分钟行80米,乙每分钟行60米,出发一段时间后,两人在距中点的C处相遇;如果甲出发后在途中某地停留了7分钟,两人将在距中点的D 处相遇,且中点距C 、D距离相等,问A 、B 两点相距多少米?【分析】 甲、乙两人速度比为80:604:3=,相遇的时候时间相等,路程比等于速度之比,相遇时甲走了全程的47,乙走了全程的37.第二次甲停留,乙没有停留,且前后两次相遇地点距离中点相等,所以第二次乙行了全程的47,甲行了全程的37.由于甲、乙速度比为4:3,根据时间一定,路程比等于速度之比,所以甲行走期间乙走了3374⨯,所以甲停留期间乙行了43317744-⨯=,所以A 、B 两点的距离为1607=16804⨯÷(米). 【例 4】 甲、乙两车分别从 A 、 B 两地同时出发,相向而行.出发时,甲、乙的速度之比是 5 : 4,相遇后甲的速度减少 20%,乙的速度增加 20%.这样当甲到达B 地时,乙离 A 地还有 10 千米.那么 A 、B 两地相距多少千米?【解析】 两车相遇时甲走了全程的59,乙走了全程的49,之后甲的速度减少 20%,乙的速度增加 20%,此时甲、乙的速度比为5(120%):4(120%)5:6⨯-⨯+= ,所以甲到达 B 地时,乙又走了4689515⨯=,距离 A 地58191545-=,所以 A 、 B 两地的距离为11045045÷= (千米). 【例 5】 早晨,小张骑车从甲地出发去乙地.下午 1 点,小王开车也从甲地出发,前往乙地.下午 2 点时两人之间的距离是 15 千米.下午 3 点时,两人之间的距离还是 l5 千米.下午 4 点时小王到达乙地,晚上 7 点小张到达乙地.小张是早晨几点出发?【解析】从题中可以看出小王的速度比小张块.下午 2 点时两人之间的距离是 l5 千米.下午 3 点时,两人之间的距离还是 l5 千米,所以下午 2 点时小王距小张 15 千米,下午 3 点时小王超过小张 15千米,可知两人的速度差是每小时30 千米.由下午 3 点开始计算,小王再有 1 小时就可走完全程,在这 1 小时当中,小王比小张多走 30 千米,那小张 3 小时走了15 30 45? ? 千米,故小张的速度是45 ÷3 =15千米/时,小王的速度是15 +30 =45千米/时.全程是45 ×3 =135千米,小张走完全程用了135 +15= 9小时,所以他是上午 10 点出发的。
(完整版)六年级行程问题练习及答案

行程问题(1)一、填空题1.两车同时从甲乙两地相对开出,甲每小时行48千米,乙车每小时行54千米,相遇时两车离中点36千米,甲乙两地相距 千米.2.小明从甲地到乙地,去时每小时走6公里,回来时每小时走9公里,来回共用5小时.小明来回共走了 公里.3.一个人步行每小时走5公里,如果骑自行车每1公里比步行少用8分钟,那么他骑自行车的速度是步行速度的 倍.4.一位少年短跑选手,顺风跑90米用了10秒钟.在同样的风速下,逆风跑70米,也用了10秒钟.在无风的时候,他跑100米要用 秒.5.A 、B 两城相距56千米.有甲、乙、丙三人.甲、乙从A 城,丙从B 城同时出发.相向而行.甲、乙、丙分别以每小时6千米、5千米、4千米的速度行进.求出发后经 小时,乙在甲丙之间的中点?6.主人追他的狗,狗跑三步的时间主人跑两步,但主人的一步是狗的两步,狗跑出10步后,主人开始追,主人追上狗时,狗跑出了 步.7.兄妹二人在周长30米的圆形水池边玩,从同一地点同时背向绕水池而行,兄每秒走1.3米,妹每秒走1.2米,他们第十次相遇时,妹妹还需走 米才能回到出发点.8.骑车人以每分钟300米的速度,从102路电车始发站出发,沿102路电车线前进,骑车人离开出发地2100米时,一辆102路电车开出了始发站,这辆电车每分钟行500米,行5分钟到达一站并停车1分钟,那么需要 分钟,电车追上骑车人.9.一个自行车选手在相距950公里的甲、乙两地之间训练,从甲地出发,去时每90公里休息一次,到达乙地并休息一天后再沿原路返回,每100公里休息一次.他发现恰好有一个休息的地点与去时的一个休息地点相同,那么这个休息地点距甲地有 公里.10.如图,是一个边长为90米的正方形,甲从A 出发,乙同时从B 出发,甲每分钟行进65米,乙每分钟行进72米,当乙第一次追上甲时,乙在 边上.二、解答题11.动物园里有8米的大树.两只猴子进行爬树比赛,一只稍大的猴子爬上2米时,另一只猴子才爬了1.5米.稍大的猴子先爬到树顶,下来的速度比原来快了2倍.两只猴子距地面多高的地方相遇?12.三个人自A 地到B 地,两地相距36千米,三个人只有一辆自行车,这辆车只能坐两人,自行车的速度比步行速度快两倍.B C他们三人决定:第一个人和第二个人同乘自行车,第三个人步行.这三个人同时出发,当骑车的二人到达某点C 时,骑车人放下第二个人,立即沿原路返回去接第三个人,到某处D 与第三个人相遇,然后两人同乘自行车前往B ;第二个人在C 处下车后继续步行前往B 地.结果三个人同时到达B 地.那么,C 距A 处多少千米?D 距A 处多少千米?13.铁路旁一条平行小路上,有一行人与一骑车人同时向南行进,行人速度为每小时3.6公里,骑车人速度为每小时10.8公里.这时有一列火车从他们背后开过来,火车通过行人用22秒钟,通过骑车人用26秒钟.这列火车的车身长多少米?14.一条小河流过A 、B 、C 三镇.A 、B 两镇之间有汽船来往,汽船在静水的速度为每小时11千米.B 、C 两镇之间有木船摆渡,木船在静水中的速度为每小时3.5千米.已知A 、C 两镇水路相距50千米,水流速度为每小时1.5千米.某人从A 镇上乘汽船顺流而下到B 镇,吃午饭用去1小时,接着乘木船又顺流而下到C 镇,共用8小时,那么A 、B 两镇的水路路程是多少米.———————————————答 案——————————————————————1. 1224乙每小时比甲多行54-48=6(千米),而乙相遇时比甲多行36⨯2=72(千米),故相遇时的时间为72÷6=12(小时),从而甲乙两地相距12⨯(48+54)=1224(千米).2. 36设甲、乙两地相距x 公里,则596=+x x ,故x =18,于是小明共行了18⨯2=36(公里)3. 3这个人步行每小时5公里,故每12分钟1公里,故他骑车每12-8=4(分钟)1公里,即每小时15公里,故他骑车速度是步行速度的15÷5=3(倍).4. 12.5顺风时速度为90÷10=9(米/秒),逆风时速度为70÷10=7(米/秒).故在无风时该选手的速度为(9+7)÷2=8(米/秒),他跑100米要100÷8=12.5(秒).5. 7设经过x 小时后,乙在甲、丙之间的中点,依题意得6x -5x =5x +4x -56,解得x =7.6. 30设狗跑3步的时间为单位时间,则狗的速度为每单位时间3步,主人的速度为每单位时间2⨯2=4(步),主人追上狗需要10÷(4-3)=10(单位时间),从而主人追上狗时,狗跑了3⨯10=30(步).7. 6第一次相遇的时间为:30÷(1.3+1.2)=12(秒);兄妹第十次相遇时走的距离为1.2⨯12⨯10=144(米);因144÷30=4…24(米),故妹妹离出发点的距离为30-24=6(米).8. 15.5不考虑停车时间,电车追上骑车人所用时间为2100÷(500-300)=10.5(分),这期间,电车需要经过两站,停车2分钟.骑车人在2分钟内所走的距离为300⨯2=600(米).这样,考虑停车时间,电车追上骑车人所用时间为:(2100+600) ÷(500-300)+2=15.5(分).9. 450这个选手去时休息的地点与甲地距离依次为:90公里,180公里,270公里,360公里,450公里,540公里,630公里,720公里,810公里和900公里,而他返回休息地点时距甲的距离为850公里,750公里,650公里,450公里,350公里,250公里,150公里和50公里.故这个相同的休息地点距甲地450公里.10. DA乙追上甲时所用的时间是(90⨯3)÷(72-65)=7270(分);乙追上甲时所走的距离为907216727072⨯=⨯(米);这时乙走过了763090907216=÷⨯(条)边,因762747630=⨯-,故乙追了7圈后,还需走762条边便可追上甲,显然乙在DA 边上.11. 设大猴爬2米和小猴爬1.5米都用时1秒.当大猴爬上树稍时,小猴爬的距离为8÷2⨯1.5=6(米);两猴相遇的时间为(8-6)÷[1.5+2⨯(2+1)]=154(秒).两猴相遇时,距地面高度为4.61545.16=⨯+(米). 12. 如图,第一、二两人乘车的路程AC ,应该与第一、三两人骑车的路程DB 相等,否则三人不能同时到达B 点.同理AD =BC .当第一人骑车在D 点与第三人相遇时,骑车人走的路程为AD +2CD ,第三人步行路程为AD .因自行车速度比步行速度快2倍,即自行车速度是步行的3倍,故AD +2CD =3CD ,从而AD =CD =BC .因AB =36千米,故AD =CD =BC =12千米,故C 距A 24千米,D 距A 12千米.13. 行人速度为3.6公里/时=1米/秒,骑车人速度为1.8公里/时=3米/秒.设车身长为x 米,依题得326122+=+x x ,故x =286.即车长286米. 14. 设某人从A 镇到B 镇共用x 小时,依题意得,(11+1.5)x +(3.5+1.5)(8-1-x )=50.解得x =2,故A 、B 两镇的水路距离为(11+1.5)⨯2=25(千米).A D CB 第二人步行第三人步行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
行程问题
一、填空。
1.相遇时间= 距离之和÷()。
2.距离之和= ()。
3.速度甲= 距离之和÷相遇时间- ();
速度乙= ()。
4.甲、乙两人相对而行,相遇时甲行了18千米,乙行了13千米,他们原来相距()千米。
二、看图列式(不计算)。
1.
2.
3.
三、解应用题。
1.一列客车和一列货车同时从两个车站相对开出,货车每小时行35千米,客车每小时行45千米,
2.5小时相遇,两车站相距多少千米?
2.两个县城相距52.5千米,甲、乙二人分别从两城同时相对而行,甲每小时行5千米,乙每小时比甲快0.5千米,几小时后相遇?
3.甲、乙二人分别从相距110千米的两地相对而行。
5小时后相遇,甲每小时行12千米,问乙每小时行多少千米?
4.甲、乙两站相距486千米,两列火车同时从两站相对开出,5小时相遇。
第一列火车比第二列火车每小时快1.7千米,两列火车每小时的速度各是多少?
5.两列火车同时从相距650千米的两地相向而行,甲列火车每小时行50千米,乙列火车每小时行52千米,4小时后还差多少千米才能相遇?
6.大陈庄和小王庄相距90千米。
小刚和小牛分别由两庄同时反向出发。
2小时24分后两人相距46.6千米,如果小刚每小时行9.9千米,小牛每小时行多少千米?
7.学校距活动站670米,小明从学校前往活动站每分钟行80米,2分钟后,小丽从活动站往学校走,每分钟行90米,小明出发多少分钟后和小丽相遇?相遇时二人各行了多少米?
8.甲、乙两队合挖一条水渠,甲队从东往西挖,每天挖65米,乙队从西往东挖,每天比甲多挖2.5米。
两队合挖8天后还差52米,这条水渠全长多少米?
9.张、李两位叔叔计划共同生产一种零件300个,二人一起生产了5小时后还差40个没完成。
已知张叔叔每小时生产24个,李叔叔每小时生产多少个?
10.甲、乙两队合修一条长2400米的路,甲队每小时修126米,乙队每小时比甲队多修48米,求完工时两队各修路多少米?
11.东西两村相距64千米。
甲、乙二人同时骑车从东西两地相对出发,2.5小时相遇。
甲每小时行12.5千米,乙每小时比甲快多少千米?
12.一列客车和一列货车分别从甲、乙两地相向而行。
客车每小时行50千米,货车每小时比客车慢8千米,客车先行1小时后,货车从乙地出发,经过3小时后两车相遇。
甲、乙两地相距多少千米?
13.东西两城相距254千米,甲、乙两辆汽车相对开出,甲车每小时行27千米,先行2小时后,乙车开始出发,速度为每小时23千米。
乙车出发几小时后两车相遇?
14.甲、乙两个工程队开凿一条隧道。
甲队每天开凿1.5千米,乙队比甲队的2倍少0.5千米.半个月完成了任务,这条隧道有多长?
15.两个车站相距360千米,两列火车相对行驶,第一列火车每小
16.两艘客轮同时从两港相对行驶,甲轮每小时行40千米,乙轮每小时行36千米,早上8时开出,晚上11时相遇,两港口相距几千米?
17.甲、乙两个工程队同时从公路的一点向两头铺沥青,甲队每天比乙队多铺20米。
已知4天后两队相距880米,两队每天各铺多少米?
18.小明和小华相距50步远,同时反向出发,小明每分钟走80步,小华每分钟走85步。
当两人相距1700步时,出发了多少分钟?
19.两辆摩托车分别从相距440千米的两地同时相向而行,因雪后路滑,5小时后才相遇。
甲车比原计划每小时
少行15千米,乙车比原计划每小时少行7千米。
已知原计划甲车每小时的速度是乙车的1.2倍,求两车原计划每小时各行多少千米?
行程问题答案
一、略
二、1.(45+30)×3 2.(220-40×3)÷5 3.
(35+40)×4+100
三、1.(35+45)×2.5=200(千米)
2. 52.5÷(5+5+0.5)=5(小时)
3. (110-12×5)÷5=10(千米)
4. (486-1.7×5)÷5÷2=47.75(千米)
47.75+1.7=49.45(千米)
5. 650-(50+52)×4=242(千米)
6. (90-46.6)÷2.4-9.9≈8.18(千米)
7. (670-80×2)÷(80+90)+2=5(分钟)
80×5=400(米)
90×(5-2)=270(米)
8. (65+65+2.5)×8+52=1112(米)
9. (300-40)÷5-24=28(个)
10. 2400÷(126+126+48)=8(小时)
126×8=1008(米)
(126+48)×8=1392(米)
11. 64÷2.5-12.5-12.5=0.6(千米)
12. (50+50-8)×3+50=326(千米)
13. (254-27×2)÷(27+23)=4(小时)
14. (1.5+1.5×2-0.5)×15=60(千米)50×4=200(千米)
16. (40+36)×(12-8+11)=1140(千米)
17. (880÷4+20)÷2=120(米)
120-20=100(米)
18. (1700-50)÷(80+85)=10(分钟)
19. (440÷5+15+7)÷(1.2+1)=50(千米)50×1.2=60(千米)。
