2019安徽数学中考一轮复习阶段性测试卷(1)有答案-推荐
2019安徽数学中考一轮复习阶段性测试卷(1)有答案

阶段性测试卷(一)(考查内容:数与式、方程(组)与不等式(组)、函数 时间:45分钟 满分:100分) 一、选择题(每小题4分,共20分) 1.8的相反数的立方根是( C ) A .±2 B .12 C .-2D .-122.下列运算正确的是( D ) A .a 3·a 2=a 6B .a 12÷a 3=a 4C .(m -n )2=m 2-n 2D .(-b 3)2=b 63.在创建文明城市的进程中,合肥市为美化城市环境,计划种植树木30万棵,由于志愿者的加入,实际每天植树比原计划多20%,结果提前5天完成任务,设原计划每天植树x 万棵,可列方程是( B )A .30x -3020%x =5B .30x-30+x =5C .3020%x +5=30xD .30+x-30x=54.下列命题为假命题...的是( C ) A .若a =b ,则a -2018=b -2018 B .若a =b ,则a c 2+1=bc 2+1C .若a >b ,则a 2>abD .若a <b ,则a -2c <b -2c5.二次函数y =ax 2+bx +c 的图象如图所示,则反比例函数y =a x与一次函数y =ax +b 在同一坐标系内的大致图象是( C )A B C D 二、填空题(每小题5分,共20分)6.亚洲陆地面积约为4 400万平方千米,则“4 400万”用科学记数法记作__4.4×107__. 7.分解因式(a -b )(a -4b )+ab 的结果是__(a -2b )2__.8.写出不等式组⎩⎪⎨⎪⎧x +x +10,x -5<x -83的所有非负整数解.....__0,1,2,3__. 9.如图的抛物线是二次函数y =ax 2+bx +c 图象的一部分,图象过点A (-3,0),对称轴为直线x=-1,给出四个结论:①b 2>4ac ;②2a +b =0;③a +b +c =0;④若点B ⎝ ⎛⎭⎪⎫-52,y 1,C ⎝ ⎛⎭⎪⎫-12,y 2为函数图象上的两点,则y 1<y 2,其中正确结论有__①③④__(填序号).三、解答题(共60分) 10.(8分)计算:(-1)2 018-8+(π-3)0+4cos 45°解:原式=1-22+1+22=2.11.(8分)先化简再计算:x 2-1x 2+x ÷⎝ ⎛⎭⎪⎫x -2x -1x ,其中x 是一元二次方程x 2-2x -2=0的正数根. 解:原式=x +1x -1x x+1÷x 2-2x +1x =x -1x ·x x -12=1x -1.解方程x 2-2x -2=0,解得x 1=1+3>0,x 2=1-3<0,所以原式=11+3-1=33.12.(8分)化简代数式:⎝ ⎛⎭⎪⎫3x x -1-x x +1÷x x 2-1,再从不等式组⎩⎪⎨⎪⎧x -x -①,6x +10>3x +1②的解集中取一个合适的整数值代入,求出代数式的值.解:原式=3xx +1-x x -1x-1x +1·x -1x +1x=3(x +1)-(x -1)=2x +4.解不等式①,得x≤1,解不等式②,得x>-3,故原不等式组的解集为-3<x≤1.∵x≠0,±1,∴x 可取-2.当x =-2时,原式=2×(-2)+4=0.13.(10分)观察下列等式:4-11=3,9-12=4,16-13=5,25-14=6,…. (1)写出第5个等式:__36-15=7__;(2)猜想并写出第n 个等式,请证明你所猜想的等式是正确的.(2)第n 个等式:n +12-1n=n +2.证明:左边=n 2+2n +1-1n =n 2+2n n=n +2=右边,所以猜想n +12-1n=n +2是正确的.14.(12分)某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:(1)计算这5(2)通过对上面表格中的数据进行分析,发现销量y (件)与单价x (元/件)之间存在一次函数关系,求y 关于x 的函数关系式;(不需要写出函数自变量的取值范围)(3)预计在今后的销售中,销量与单价仍然存在(2)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少?解:(1)30×40+34×32+38×24+40×20+42×165=934.4;(2)设所求一次函数关系式为y =kx +b (k≠0),将(30,40),(40,20)代入y =kx +b ,得⎩⎪⎨⎪⎧30k +b =42,40k +b =20,解得⎩⎪⎨⎪⎧k =-2,b =100,∴y =-2x +100;(3)设利润为w 元,根据题意,得w =(x -20)(-2x +100)=-2x 2+140x +2 000=-2(x -35)2+450,则当x =35时,w 取最大值.即当该产品的单价为35元/件时,工厂获得最大利润450元.15.(14分)如图,抛物线y =x 2+bx +c 与直线y =12x -3交于A ,B 两点,其中点A 在y 轴上,点B坐标为(-4,-5),点P 为y 轴左侧的抛物线上一动点,过点P 作PC ⊥x 轴于点C ,交AB 于点D .(1)求抛物线的解析式;(2)以O ,A ,P ,D 为顶点的平行四边形是否存在?如存在,求点P 的坐标;若不存在,说明理由. 解:(1)∵直线y =12x -3交于A ,B 两点,其中点A 在y 轴上,∴A (0,-3),∵B (-4,-5),⎩⎪⎨⎪⎧c =-3,16-4b +c =-5.∴⎩⎪⎨⎪⎧b =92,c =-3.∴抛物线解析式为y =x 2+92x -3;(2)存在,设P (m ,m 2+92m -3),(m <0),∴D (m ,12m -3),∴PD =|m 2+4m|.∵PD∥AO ,∴当PD =OA=3时,|m 2+4m|=3.①m 2+4m =3时,∴m 1=-2-7,m 2=-2+7(舍),∴m 2+92m -3=-1-72,∴P ⎝ ⎛⎭⎪⎫-2-7,-1-72; ②当m 2+4m =-3时,∴m 1=-1,m 2=-3.若m 1=-1,∴m 2+92m -3=-132,∴P ⎝⎛⎭⎪⎫-1,-132;若m 2=-3,∴m 2+92m -3=-152,∴P ⎝⎛⎭⎪⎫-3,-152,∴点P 的坐标为⎝ ⎛⎭⎪⎫-2-7,-1-72,⎝⎛⎭⎪⎫-1,-132,⎝ ⎛⎭⎪⎫-3,-152.。
2019年安徽省初中学业水平考试数学阶段检测试卷(一)含答案

2019年安徽省初中学业水平考试阶段检测卷一代数综合检测(时间:120分钟,满分:150分)一、选择题(本大题共10小题,每小题4分,满分40分) 每小题都给出A 、B 、C 、D 四个选项,其中只有一个是正确的. 1.2的倒数是( ) A .-2B.12C .-12D .22.下列实数中的无理数是( ) A .0.7B.12C .πD .-83.温度由-4 ℃上升7 ℃是( ) A. 3 ℃B. -3 ℃C. 11 ℃D. -11 ℃4.一条数学信息在一周内被转发了2 180 000次,将数据2 180 000用科学记数法表示为( ) A .2.18×106B .2.18×105C .21.8×106D .21.8×1055.下列算式中,结果等于a 6的是( ) A .a 3+a 4 B .a 2+a 2+a 2 C .a 2·a 3D .a 2·a 2·a 26.下列分解因式正确的是( ) A .-ma -m =-m (a -1) B .a 2-1=(a -1)2 C .a 2-6a +9=(a -3)2 D .a 2+3a +9=(a +3)27.不等式组⎩⎪⎨⎪⎧2x <6,x +1≥-4的解集是( )A .-5<x ≤3B .-5≤x <3C .x ≥-5D .x <38.已知关于x 的一元二次方程4mx 2-4(m +2)x +m =0有两个不相等的实数根,则m 的值可以是( ) A .2或-1 B .-1 C .2D .不存在9.某小区为了排污,需铺设一段全长为720米的排污管道,为减少施工对居民生活的影响,需缩短施工时间,实际施工时每天的工作效率比原计划提高20%,结果提前2天完成任务,设原计划每天铺设x 米,下面所列方程正确的是( )A.720x -720(1+20%)x =2B.720(1-20%)x -720x =2C.720(1+20%)x -720x=2 D.720x +2=720(1+20%)x10.如图,菱形ABCD 的边长是4 cm ,∠B=60°,动点P 以1 cm/s 的速度自A 点出发沿AB 方向运动至B 点停止,动点Q 以2 cm/s 的速度自B 点出发沿折线BCD 运动至D 点停止.若点P 、Q 同时出发运动了t s ,记△B PQ 的面积为S cm 2,下面图象中能表示S 与t 之间的函数关系的是( )二、填空题(本大题共4小题,每小题8分,满分20分) 11.计算:12×3=________.12.方程组⎩⎪⎨⎪⎧x -y =4,2x +y =-1的解是____________.13.方程12x =1x +1的解是__________.14.如图,正比例函数y =x 的图象与反比例函数y =kx的图象相交于A ,B 两点,且点B 的横坐标为-2.若点E 是反比例函数在第一象限内图象上一点,S △A OE =3,则点E 的坐标为__________________________.三、(本大题共2小题,每小题8分,满分16分)15.计算:π0+2cos 30°+︱2-3︱-(12)-2.16.先化简,再求值:x 2+2x +1x 2-1-xx -1,其中x =2.四、(本大题共2小题,每小题8分,满分16分)17.先化简,再求值:(-x2+3-7x)+(5x-7+2x2),其中x=2+1.18.《九章算术》中有一题:今有二马、一牛价过一万,如半马之价.一马、二牛价不满一万,如半牛之价.向牛、马价各几何?译文为:现有二匹马加一头牛的价钱超过一万,超过的部分正好是半匹马的价钱;一匹马加上二头牛的价钱则不到一万,不足部分正好是半头牛的价钱,求一匹马、一头牛各多少钱.请解答上述问题.五、(本大题共2小题,每小题10分,满分20分)19.阅读下列材料解决问题:材料:古希腊著名数学家毕达哥拉斯发现把数1,3,6,10,15,21…这些数量的(石子),都可以排成三角形,则称像这样的数为三角形数.把数1,3,6,10,15,21…换一种方式排列,即1=11+2=31+2+3=61+2+3+4=101+2+3+4+5=15…从上面的排列方式看,把1,3,6,10,15…叫做三角形数“名副其实”.(1)设第一个三角形数a1=1,第二个三角形数为a2=3,第三个三角形数为a3=6,请直接写出第n个三角形数为a n的表达式(其中n为正整数);(2)根据(1)的结论判断66是三角形数吗?若是,请说出66是第几个三角形数?若不是,请说明理由;(3)根据(1)的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由.20.某校为打造书香校园,计划购进甲乙两种规格的书柜放置新购买的图书,调查发现,若购买甲种书柜3个,乙种书柜2个,共需资金1 020元;若购买甲种书柜4个,乙种书柜3个,共需资金1 440元.(1)甲乙两种书柜每个的价格分别是多少元?(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多提供资金4 320元,请设计几种购买方案供这个学校选择.六、(本题满分12分) 21.如图,点M在函数y=3x(x>0)的图象上,过点M分别作x轴和y 轴的平行线交函数y=1x(x>0)的图象于点B、C.(1)若点M坐标为(1,3).①求B、C两点的坐标;②求直线BC的表达式.(2)求△B M C的面积.七、(本题满分12分)22.如图,已知点O(0,0),A(-5,0),B(2,1),抛物线l:y=-(x-h)2+1(h为常数)与y轴的交点为C.(1)当l经过点B,求它的表达式,并写出此时l的对称轴及顶点坐标;(2)当线段O A被l只分为两部分,且这两部分的比是1∶4时,求h的值.第22题图八、(本题满分14分)23.为响应某市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18 m,另外三边由36 m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=x m,面积为y m2(如图).(1)求y与x之间的函数关系式,并写出自变量x的取值范围;(2)若矩形空地的面积为160 m2,求x的值;(3)若该单位用8 600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.参考答案1.B 2.C 3.A 4.A 5.D 6.C 7.B 8.C 9.A 10.D11.6 12.⎩⎪⎨⎪⎧x =1,y =-313.x =1 14.(4,1)或(1,4)15.解:原式=-2.16.解: 原式=1x -1.当x =2时,原式=12-1=1.17.解: 原式=x 2-2x -4.当x =2+1时,原式=(2+1)2-2(2+1)-4=-3. 18.解:一匹马的价钱为6 00011,一头牛的价钱是20 00011.19.解:(1)a n =n (n +1)2(n 为正整数);(2)66是三角形数,理由如下:当n (n +1)2=66时,解得:n =11或n =-12(舍去),则66是第11个三角形数;(2)T =11+13+16+115+…+2n (n +1)=21×2+22×3+23×4+24×5+…+2n (n +1)=2(1-12+12-13+13-14+…+1n -1n +1)=2nn +1∵n 为正整数,∴0<n n +1<1,则T <2.20.解:(1)甲种书柜单价为180元,乙种书柜单价为240元, (2)学校的购买方案有以下三种:方案一:甲种书柜8个,乙种书柜12个, 方案二:甲种书柜9个,乙种书柜11个, 方案三:甲种书柜10个,乙种书柜10个.21.解:(1)①点C 坐标为(1,1),点B 坐标为(13,3).②直线BC 的表达式为:y =-3x +4. (2)设点M 坐标为(a ,t),∵点M 在函数y =3x (x >0)的图象上,∴at=3.由(1)知C 点坐标为(a ,1a ),B 点坐标为(1t ,t),∴BM=a -1t =at -1t ,MC =t -1a =at -1a ,∴S △BMC =12·at -1t ·at -1a =23.22.解:(1)把B(2,1)代入y =-(x -h)2+1,得h =2, ∴函数表达式为y =-(x -2)2+1, ∴对称轴为x =2,顶点坐标为B(2,1).(2)把OA 分为1∶4两部分的点为(-1,0)或(-4,0), 把x =-1,y =0代入y =-(x -h)2+1,得h =0或h =-2, 但h =-2时,OA 被分为三部分,不合题意,舍去,同样,把x =-4,y =0代入y =-(x -h)2+1,得h =-5或h =-3(舍去),∴h 的值为0或-5.23.解:(1)∵四边形ABCD 是矩形,垂直于墙的边AB =x , ∴CD=AB =x ,BC =(36-2x), ∴y=x(36-2x),即y =-2x 2+36x ,由矩形的任一边都大于0,⎩⎪⎨⎪⎧36-2x >0,36-2x≤18,解得9≤x<18,∴y 与x 之间的函数关系式为y =-2x 2+36x(9≤x<18). (2)∵矩形空地的面积为160 m 2,即y =160, ∴-2x 2+36x =160,解得x 1=10,x 2=8, ∵9≤x<18,∴x 2=8舍去, 答:x 的值为10.(3)设甲、乙、丙三种植物分别购买了m 棵、n 棵、k 棵,由题意得:⎩⎪⎨⎪⎧m +n +k =400①,14m +16n +28k =8 600②,①×16-②得:m =6k -1 100.②-①×14得:n =1 500-7k , ∵m 、n 、k 分别表示三种植物的数量,∴m、n 、k 为正整数,∴⎩⎪⎨⎪⎧6k -1 100>0,1 500-7k >0,解得5503<k <1 5007,∵k 为正整数,∴k 能取的最大正整数为214,即丙种植物最多可以购买214棵,当k =214时,m =6k -1 100=6×214-1 100=184,n =1 500-7k =1 500-7×214=2,∵y=-2x 2+36x =-2(x -9)2+162,∴当x =9时,y 有最大值,最大值为162,即当垂直于墙的一边长为 9 m 时,矩形空地的面积最大,最大为162 m 2. ∵0.4×184+2+0.4×214=161.2<162, ∴这批植物可以全部栽种到这块空地上.。
2019年最新安徽省中考第一次数学模拟试卷含答案解析

安徽省第一次中考(数学)模拟试卷(含答案)数 学本试题卷分第一部分(选择题)和第二部分(非选择题),共8页.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效.满分150分.考试时间120分钟.考试结束后,将本试题卷和答题卡一并交回.考生作答时,不能使用任何型号的计算器.第一部分(选择题 共30分)注意事项:1.选择题必须使用2B 铅笔将答案标号填涂在答题卡对应题目标号的位置上. 2.本部分共10小题,每小题3分,共30分.一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项符合题目要求.1. 2-的倒数是)A ( 21-)B (21)C (2 )D (2-2.随着经济发展,人民的生活水平不断提高,旅游业快速增长,2016年国民出境旅游超过120 000 000人次,将120 000 000用科学记数法表示为)A ( 91021⨯. )B ( 71012⨯ )C ( 910120⨯. )D (81021⨯.3. 下列图形中,既是轴对称图形又是中心对称图形的是)A ( )B ( )C ( )D (4.含︒30角的直角三角板与直线1l 、2l 的位置关系如图1所示,已知21//l l ,A ACD ∠=∠,则1∠=)A (︒70 )B (︒60 )C (︒40 )D (︒305. 下列说法正确的是)A (打开电视,它正在播广告是必然事件)B (要考察一个班级中的学生对建立生物角的看法适合用抽样调查 )C (在抽样调查过程中,样本容量越大,对总体的估计就越准确)D (甲、乙两人射中环数的方差分别为2S 2=甲,4S 2=乙,说明乙的射击成绩比甲稳定6. 若02=-ab a ()0≠b ,则=+ba a)A (0 )B (21)C (0或21)D (1或 27. 图2是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,250.CD AB ==米,51.BD =米,且AB 、CD 与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离 地面的距离是)A (2米 )B (52.米 )C (42.米)D (12.米8. 已知31=+x x ,则下列三个等式:①7122=+xx ,②51=-x x ,③2622-=-x x 中,正确的个数有)A ( 0个)B (1个)C ( 2个)D (3个图1图29. 已知二次函数mx x y 22-=(m 为常数),当21≤≤-x 时,函数值y 的最小值为2-,则m 的值是)A (23)B (2)C (23或2)D (23-或2 10. 如图3,平面直角坐标系xOy 中,矩形OABC 的边OA 、OC 分别落在x 、y 轴上,点B 坐标为()46,, 反比例函数xy 6=的图象与AB 边交于点D ,与BC 边交于点E ,连结DE ,将BDE ∆沿DE 翻折至DE B '∆处,点B '恰好落在正比例函数kx y =图象上,则k 的值是 )A ( 52-)B (211-)C (51-)D (241-第二部分(非选择题 共120分)注意事项1.考生使用0.5mm 黑色墨汁签字笔在答题卡上题目所指示的答题区域内作答,答在试题卷上无效.2.作图时,可先用铅笔画线,确认后再用0.5mm 黑色墨汁签字笔描清楚.3.解答题应写出文字说明、证明过程或推演步骤. 4.本部分共16小题,共120分.二、填空题:本大题共6小题,每小题3分,共18分.11.计算:=-23 ____. 12.二元一次方程组2322+=-=+x yx y x 的解是____. 13.如图4,直线b a 、垂直相交于点O ,曲线C 关于点O 成中心对称,点A 的对称点是点'A ,a AB ⊥于点B ,b D A ⊥'于点D .若3=OB ,2=OC , 则阴影部分的面积之和为____.14.点A 、B 、C 在格点图中的位置如图5所示,格点小正方形的边长为1,则点C 到线段AB 所在直线的距离是_____.15. 庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将 事物无限分割的思想,用图形语言表示为图6.1, 按此图分割的方法,可得到一个等式(符号语言):⋅⋅⋅++⋅⋅⋅+++=n 32212121211. 图6.2也是一种无限分割:在ABC ∆中, 90=∠C ,30=∠A ,过点C 作AB CC ⊥1于点1C ,再过点1C 作BC C C ⊥21于点2C ,又过点2C 作AB C C ⊥32于点3C ,如此无限继续下去,则可将利ABC ∆分割成1ACC ∆、21C CC ∆、321C C C ∆、432C C C ∆、…、n n n C C C 12--∆、….假设2=AC ,这些三角形的面积和可以得到一个等式是_________.16.对于函数m n x x y +=,我们定义11--+='m n mx nx y (n m 、为常数). 例如24x x y +=,则x x y 243+='. 已知:()x m x m x y 223131+-+=. (1)若方程0='y 有两个相等实数根,则m 的值为___________; (2)若方程41-='m y 有两个正数根,则m 的取值范围为__________. 三、本大题共3小题,每小题9分,共27分.17. 计算:272017316020-+-+︒sni .18. 求不等式组⎪⎩⎪⎨⎧≥--+<+02251,312x x x x 的所有整数解.19. 如图7, 延长□ABCD 的边AD 到点F ,使DC DF =,延长CB 到点E ,使BA BE =,分别连结点A 、E 和点C 、F . 求证:CF AE =.四、本大题共3小题,每小题10分,共30分.20. 化简:12121222222-÷⎪⎪⎭⎫ ⎝⎛+----+a aa a a a a a a .21. 为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图8所示.请根据图表信息解答下列问题: (1)在表中:=m ,=n ; (2)补全频数分布直方图;FEDCB A(3)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在 组;(4)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A 、C 两组学生的概率是多少?并列表或画树状图说明.22. 如图9,在水平地面上有一幢房屋BC 与一棵树DE ,在地面观测点A 处测得屋顶C 与树梢D 的仰角分别是︒45与︒60,︒=∠60CAD ,在屋顶C 处测得︒=∠90DCA .若房屋的高6=BC 米.求树高DE 的长度.五、本大题共2小题,每小题10分,共20分.23、某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:EDCBA律,给出理由,并求出其解析式; (2)按照这种变化规律,若已投入资金5万元.①预计生产成本每件比2016年降低多少万元?②若打算在把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).24.如图10,以AB 边为直径的⊙O 经过点P ,C 是⊙O 上一点,连结PC 交AB 于点E ,且 60=∠ACP ,PD PA =.(1)试判断PD 与⊙O 的位置关系,并说明理由;(2)若点C 是弧AB 的中点,已知4AB =,求CP CE ⋅的值.六、本大题共2小题,第25题12分,第26题13分,共25分.25.在四边形ABCD 中,︒=∠+∠180D B ,对角线AC 平分BAD ∠.(1)如图11.1,若︒=∠120DAB ,且︒=∠90B ,试探究边AD 、AB 与对角线AC 的数量关系并说明理由.A(2)如图11.2,若将(1)中的条件“︒=∠90B ”去掉,(1)中的结论是否成立?请说明理由. (3)如图11.3,若︒=∠90DAB ,探究边AD 、AB 与对角线AC 的数量关系并说明理由.26.如图12.1,抛物线1C :ax x y +=2与2C :bx x y +-=2相交于点O 、C ,1C 与2C 分别交x 轴于点B 、A ,且B 为线段AO 的中点.(1)求ba的值; (2)若AC OC ⊥,求OAC ∆的面积;(3)抛物线2C 的对称轴为l ,顶点为M ,在(2)的条件下:①点P 为抛物线2C 对称轴l 上一动点,当PAC ∆的周长最小时,求点P 的坐标; ②如图12.2,点E 在抛物线2C 上点O 与点M 之间运动,四边形OBCE 的面积是否存在最大值?若存在,求出面积的最大值和点E 的坐标;若不存在,请说明理由.DCBAD CB ADCBA第一次中考(数学)模拟试卷数学参考答案及评分意见第一部分(选择题 共30分)一、选择题:本大题共10小题,每小题3分,共30分.1. )(A2. )(D3. )(D4. )(B5. )(C6. )(C7. )(B8. )(C9. )(D 10.)(B第二部分(非选择题 共120分)二、填空题:本大题共6小题,每小题3分,共18分.11.91;12.⎩⎨⎧-=-=15y x ;13. 6; 14.553; 15.⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++= n434343431233232;16.(1)21=m ;(2)43≤m 且21≠m . 注:(1)第14题,若给出的是化简后正确的等式,也视为正确; (2)第16题,第(1)问1分,第(2)问2分.三、本大题共3小题,每小题9分,共27分.17.解:原式33113232-+-+⨯=……………………………………(8分) =3-.………………………………(9分)18.解:解不等式①得:1->x ……………………………………(3分)解不等式②得:4≤x ……………………………………(6分)所以,不等式组的解集为41≤<-x ……………………………………(8分) 不等式组的整数解为43210,,,,. ……………………………………(9分)19. 证明:□ABCD 中,CD AB =,BE AB =,DF CD =,∴DF BE =.BC AD =, ∴EC AF =………………(6分)又 AF ∥EC ,∴四边形AECF 是平行四边形. ………………(8分) ∴CF AE =………………………(9分)四、本大题共3小题,每小题10分,共30分.20. 解:原式=()()()()()121111122-÷⎥⎦⎤⎢⎣⎡----++a aa a a a a a a ………………(2分)=12112-÷⎪⎭⎫⎝⎛---a a a a a a………………(4分) =121-÷-a a a a ………………(6分) =aa a a 211-⋅-………………(8分) =21…………………………(10分) 21.解:(1)120=m ,30.n =………………(2分)(2);如图2 ………………(4分) (3)C ;………………(6分) (4)FED CBACB A D B A DC AD C B DC BA………………(9分)∴抽中A ﹑C 两组同学的概率为122=P =61…………(10分) 22.解:如图3,在ABC Rt ∆中,︒=∠45CAB ,m BC 6=, ∴26=∠=CABsin BCAC ()m ;…………………(3分)在ACD Rt ∆中,︒=∠60CAD , ∴212=∠=CADcos ACAD ()m ;…………………(6分)在DEA Rt ∆中,︒=∠60EAD ,()m sin AD DE 662321260=⋅=︒⋅=…………………(9分) 答:树DE 的高为66米.…………………(10分) 五、本大题共2小题,每小题10分,共20分 23.解:(1)设b kx y +=,(b k 、为常数,0≠k )∴⎩⎨⎧+=+=645436k .b k ,解这个方程组得⎩⎨⎧=-=51051.b .k ,∴51051.x .y +-=. 当52.x =时,4756≠=.y .∴一次函数不能表示其变化规律. ……………………………………(2分) 设x k y =,(k 为常数,0≠k ),∴5227.k.=, ∴18=k ,∴xy 18=. EDCBA当3=x 时,6=y ;当4=x 时,54.y =;当54.x =时,4=y ; ∴所求函数为反比例函数xy 18=……………………………………(5分) (2)①当5=x 时,63.y =; 40634..=-(万元)∴比2016年降低40.万元. ……………………………………(7分) ②当23.y =时,6255.x =; 630625056255...≈=-(万元) ∴还需要投入技改资金约630.万元. ……………………………………(9分)答:要把每件产品的成本降低到23.万元,还需投入技改资金约630.万元. …………………(10分)24.解:(1)如图4,PD 是⊙O 的切线.证明如下:……………………………………(1分)连结OP ,60=∠ACP ,∴120=∠AOP , OP OA = ,∴ 30=∠=∠OPA OAP ,PD PA =,∴ 30=∠=∠D PAO , ∴ 90=∠OPD ,∴PD 是⊙O 的切线. ……………………………………(4分) (2)连结BC ,AB 是⊙O 的直径, ∴90=∠ACB ,又C 为弧AB 的中点, ∴45=∠=∠=∠APC ABC CAB ,4=AB ,2245== sin AB AC .APC CAB C C ∠=∠∠=∠, ,∴CAE ∆∽CPA ∆,……………………………………(8分)∴CACECP CA =,∴82222===⋅)(CA CE CP .……………………………………(10分)六、本大题共2小题,第25题12分,第26题13分,共25分 25.解:(1)AB AD AC +=.证明如下:在四边形ABCD 中,︒=∠+∠180B D ,︒=∠90B , ∴ ︒=∠90D . ︒=∠120DAB ,AC 平分DAB ∠,∴ 60=∠=∠BAC DAC ,︒=∠90B ,∴AC AB 21=,同理AC AD 21=.∴AB AD AC +=.……………………………(4分) (2)(1)中的结论成立,理由如下:以C 为顶点,AC 为一边作60=∠ACE ,ACE ∠的另一边交AB 延长线于点E , 60=∠BAC ,∴AEC ∆为等边三角形,∴CE AE AC ==,︒=∠+∠180B D ,︒=∠120DAB ,∴60=∠DCB ,∴BEC DAC ∆≅∆,∴BE AD =,∴AB AD AC +=.……………………………………(8分) (3)AC AB AD 2=+.理由如下:过点C 作AC CE ⊥交AB 的延长线于点E ,︒=∠+∠180B D ,︒=∠90DAB ,∴ 90=DCB ,90=∠ACE ,∴BCE DCA ∠=∠,又AC 平分DAB ∠,∴ 45=∠CAB ,∴45=∠E .∴CE AC =.又︒=∠+∠180B D ,CBE D ∠=∠,ACC∴CBE CDA ∆≅∆,∴BE AD =,∴AE AB AD =+. 在ACE Rt ∆中, 45=∠CAB ,∴AC cos ACAE 245==,∴AC AB AD 2=+. ……………………………………(12分)26.解:(1)ax x y +=2,当0=y 时,02=+ax x ,01=x ,a x -=2,∴()0,a B -bx x y +-=2,当0=y 时,02=+-bx x ,01=x ,b x =2,∴()b ,A 0 ∵B 为OA 的中点,∴a b 2-=.∴21-=b a .……………………………………(2分) (2)解⎪⎩⎪⎨⎧--=+=axx y ax x y 222得:ax x ax x 222--=+ ,0322=+ax x , 01=x ,a x 232-=,当a x 23-=时,243a y =, ∴⎪⎭⎫ ⎝⎛-24323a ,a C . ……………………………(3分) 过C 作x CD ⊥轴于点D ,∴⎪⎭⎫⎝⎛-023,a D . ∵︒=∠90OCA ,∴OCD ∆∽CAD ∆,∴CDODAD CD =, ∴OD AD CD ⋅=2,即⎪⎭⎫ ⎝⎛-⋅-=⎪⎭⎫⎝⎛a a a 23214322,∴01=a (舍去),3322=a (舍去),3323-=a ……………………………(5分) ∴3342=-=a OA ,1432==a CD,∴33221=⋅=∆CD OA S OAC ……………………………………(6分) (3)①x x y C 334:22+-=,对称轴332:2=x l , 点A 关于2l 的对称点为)0,0(O ,)1,3(C ,则P 为直线OC 与2l 的交点,设OA 的解析式为kx y =,∴k 31=,得33=k ,则OA 的解析式为x y 33=,当332=x 时,32=y ,∴),(P 32332. ……………………………………(8分)②设)3320(),334,(2≤≤+-m m m E ,则m m m S OBE 3433)334(3322122+-=+-⋅⨯=∆, 而)0,332(B ,)1,3(C ,设直线BC 的解析式为b kx y +=,由⎪⎩⎪⎨⎧+=+=b k b k 332031,解得2,3-==b k , ∴直线BC 的解析式为23-=x y .分)过点E 作x 轴的平行线交直线BC 于点N ,则233342-=+-x m m , 即=x 33234332++-m m ,∴=EN 3323133332343322++-=-++-m m m m m ,∴336163332313312122++-=++-⋅⋅=∆m m )m m (S EBC∴EBC O BE O BCE S S S ∆∆+=四边形)336163()3433(22++-++-=m m m m 24317)23(2333232322+--=++-=m m m ,……………………………………(11分)3320≤≤m ,∴当23=m 时,24317=最大S ,当23=m 时,4523334)23(2=⋅+-=y ,∴),(E 4523,24317=最大S . ……………………………………(13分)。
(课标通用)安徽省2019年中考数学总复习学业水平模拟考试试题及参考答案

2019年安徽省初中学业水平模拟考试数学(考试用时:120分钟满分:150分)一、选择题(本大题共10小题,每小题4分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(-3)×2的结果是()A.-5B.1C.-6D.6答案C2.计算x8÷x2(x≠0)的结果是()A.x-4B.x4C.x-6D.x6答案D3.下列几何体中,俯视图为三角形的是()答案C4.大量事实证明,治理垃圾污染刻不容缓.据统计,全球每分钟约有8 500 000吨污水排入江河湖海,这个排污量用科学记数法表示为()A.8.5×105B.8.5×106C.85×105D.85×106答案B5.如图,已知平行线a,b,一个直角三角板的直角顶点在直线a上,另一个顶点在直线b上,若∠1=70°,则∠2的大小为()A.15°B.20°C.25°D.30°答案B6.为了解居民用电情况,小陈在小区内随机抽查了30户家庭的月用电量,结果如下表:月用40 50 60 80 90 100电量/度户数 6 7 9 5 2 1则这30户家庭的月用电量的众数和中位数分别是() A.60,60 B.60,50 C.50,60 D.50,70答案A7.计算:的结果是()A. B.C. D.答案B8.某公司第4月份投入1 000万元科研经费,计划6月份投入科研经费比4月多500万元.设该公司第5、6个月投放科研经费的月平均增长率为x,则所列方程正确的为()A.1 000(1+x)2=1 000+500B.1 000(1+x)2=500C.500(1+x)2=1 000D.1 000(1+2x)=1 000+500答案A9.一直角三角形放置在如图所示的平面直角坐标系中,直角顶点C刚好落在反比例函数y=的图象的一支上,两直角边分别交y、x轴于A、B两点.当CA=CB时,四边形CAOB的面积为()A.4B.8C.2D.答案B10.如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=1,AD=3,DC=5.点S沿A→B→C运动到C点停止,以S 为圆心,SD为半径作弧交射线DC于T点,设S点运动的路径长为x,等腰△DST的面积为y,则y与x 的函数图象应为()〚导学号16734168〛答案A解析分别过点S、B作SE⊥DC于E点,BF⊥DC于F点.∵AB∥CD,∠A=90°∴BF=AD=3,DF=AB=1.在Rt△BCF中,CF=DC-DF=5-1=4,BC==5.当S点在AB上时,0<x≤1;DT=2DE=2AS=2x,y=×DT×SE=×2x×3=3x.当S点在BC上时,1<x≤6,SC=AB+BC-x=6-x.∵SE⊥DC,BF⊥DC.∴△SCE∽△BCF,∴.∴SE=6-x,CE=(6-x).∴DT=2DE=2(DC-CE)=x+.∴y=×DT×SE=x+×(6-x)=-x-2+.故选A.二、填空题(本大题共4小题,每小题5分,满分20分)11.分解因式:x3-4x=.答案x(x+2)(x-2)12.已知关于x的一元二次方程ax2+(a-3)x-3=0有两个实数根,则a的取值为.答案a≠013.如图,AB为☉O的直径,D为的中点,若∠CAD=25°,则∠CAB=.答案40°14.如图,某同学在一张硬纸板的中间画了一条4 cm长的线段AB,过AB的中点O画直线CO,使∠AOC=60°,在直线CO上取一点P,作△PAB并剪下(纸板足够大),当剪下的△PAB为直角三角形时,AP的长为.答案2或2或2解析如图1,当∠APB=90°时,∵AO=BO,∴OP=AB=OA.∵∠AOC=60°,∴△AOP是等边三角形,∴AP=OP=AB=2.如图2,当∠APB=90°时,∵AO=BO,∴OP=AB=OA.∵∠AOC=60°,∴∠BOP=60°,∴△BOP是等边三角形,∴BP=OP=AB=2.∴AP==2.如图3,当∠PAB=90°时.∵∠AOC=60°,∴∠APO=30°,∴OP=2OA=4,∴AP==2.如图4,当∠ABP=90°时,∵∠BOP=∠AOC=60°,OA=OB=AB=2,∴BP=2.在Rt△ABP中,AB==2.故答案为2或2或2.三、(本大题共2小题,每小题8分,满分16分)15.计算:|1-|--3-2cos 30°+(π-3)0.解原式=-1-8-2×+1=-8.16.《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪.现在传本的《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木长多少尺?”请解答上述问题.解设绳长x尺,则长木为(x-4.5)尺.依题意可得(x-4.5)-x=1.解得x=11,则x-4.5=6.5.答:长木长6.5尺.四、(本大题共2小题,每小题8分,满分16分)17.如图,在边长为1个单位长度的小正方形组成的网格中,按要求完成下面的问题:(1)以图中的O为位似中心,将△ABC作位似变换且缩小到原来的一半,得到△A'B'C',再把△A'B'C'绕点B'逆时针旋转90°得到△A″B'C″;(2)求点A→A'→A″所经过的路线长.解(1)如图所示:(作出每个图形变换3分)(2)点A→A'→A″所经过的路线长为:2+=2+.18.观察下列关于自然数的等式:(1)32-4×1=4+1(1)(2)52-4×2=16+1 (2)(3)72-4×3=36+1 (3)……根据上述规律解决下列问题:(1)完成第四个等式:()2-4×()=()+1;(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.解(1)9,4,64 2分(2)(2n+1)2-4n=(2n)2+1 6分验证:左边=(2n+1)2-4n=4n2+4n+1-4n=4n2+1,左边=右边.8分五、(本大题共2小题,每小题10分,满分20分)19.已知,如图,在铅直高度为200 m的小山上建有一座电视转播塔,某数学兴趣小组为测量电视转播塔的高度,在山脚的点C处测得山顶B的仰角为30°(即∠BCD=300),测得塔顶A的仰角为45°(即∠ACD=45°),请根据以上数据求塔高AB(精确到1 m)(备用数据:≈1.414,≈1.732)解在Rt△BCD中,由tan30°=,得CD=BD=200.3分在Rt△ACD中,由tan45°=,得AD=CD=200, 6分所以AB=AD-BD=200-200=200×1.732-200≈146(m).10分20.如图,AB是☉O的直径,点C在☉O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB.(1)求证:PC是☉O的切线;(2)点M是弧AB的中点,CM交AB于点N,若MN·MC=8,求☉O的直径.(1)证明∵OA=OC,∴∠A=∠ACO.∴∠COB=2∠ACO.又∵∠COB=2∠PCB,∴∠ACO=∠PCB.2分∵AB是☉O的直径,∴∠ACO+∠OCB=90°.∴∠PCB+∠OCB=90°,即OC⊥CP.∵OC是☉O的半径,∴PC是☉O的切线.4分(2)解连接MA、MB.(如图)∵点M是弧AB的中点,∴∠ACM=∠BAM.∵∠AMC=∠AMN,∴△AMC∽△NMA.6分∴.∴AM2=MC·MN.∵MC·MN=8,∴AM=2.8分∵AB是☉O的直径,点M是弧AB的中点,∴∠AMB=90°,AM=BM=2.∴AB==4.10分〚导学号16734169〛六、(本题满分12分)21.为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:(1)请把折线统计图补充完整;(2)求扇形统计图中,网络文明部分对应的圆心角的度数;(3)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.解(1)该班全部人数:12÷25%=48人.社区服务的人数为48×50%=24,补全折线统计如图所示:(2)网络文明部分对应的圆心角的度数为360°×=45°.(3)分别用A,B,C,D表示“社区服务、助老助残、生态环保、网络文明”四个服务活动,画树状图得:∵共有16种等可能的结果,他们参加同一服务活动的有4种情况,∴他们参加同一服务活动的概率为.七、(本题满分12分)22.某厂家生产一种产品,月初需要一次性投资25 000元,每生产一件产品需增加投入100元.设x(件)是月生产量,y(元)是销售完x件产品所得的总销售额,y与x的关系如图中的图象所示,图象中从点O到点A的部分是抛物线的一部分,且点A是抛物线的顶点,点A后面的部分与x轴平行.(1)求y关于x的函数关系式;(2)设月纯利润为z,求z关于x的函数关系式;(3)当月产量为多少件时,厂家所获利润最大?最大利润为多少元?解(1)y=4分(2)z=y-25000-100x=8分(3)当x>400时,z<-100×400+55000=15000(元);当0≤x≤400时,z=-x2+300x-25000=-(x-300)2+20000.所以,当x=300时,z最大=20000(元).答:当月产量为300台时,利润最大,最大利润为20000元.12分八、(本题满分14分)23.如图,矩形纸片ABCD,P是AB的中点,Q是BC上一动点,△BPQ沿PQ折叠,点B落在点E处,延长QE 交AD于M点,连接PM.(1)求证:△PAM≌△PEM;(2)当DQ⊥PQ时,将△CQD沿DQ折叠,点C落在线段EQ上点F处.①求证:△PAM∽△DCQ;②如果AM=1,sin∠DMF=,求AB的长.解(1)∵四边形ABCD是矩形,∴∠A=∠B=90°,根据折叠的性质可知:PE=PB,∠PEM=∠B=90°;∵P点为AB中点,∴PA=PB=PE.又∵PM=PM,∴△PAM≌△PEM.4分(2)①由(1)知△PAM≌△PEM,∴∠APM=∠EPM.根据折叠的性质可知:∠EPQ=∠BPQ,∴∠APM+∠BPQ=∠EPM+∠EPQ=90°,∵∠APM+∠AMP=90°,∴∠BPQ=∠AMP,∵∠B=90°,DQ⊥PQ,∴∠BPQ+∠PQB=90°,∠BPQ+∠DQC=180°-∠PQD=90°.∴∠BPQ=∠DQC.∴∠AMP=∠DQC.又∵∠A=∠C=90°,∴△AMP∽△CQD.8分②设AP=x,则,BP=AP=EP=x,AB=DC=2x,∵由①知∠BPQ=∠AMP,∠A=∠B=90°,∴△AMP∽△BPQ.∴,即BQ=x2.10分由△AMP∽△CQD得,,即CQ=2.12分AD=BC=BQ+CQ=x2+2.∵在Rt△FDM中,sin∠DMF=,DF=DC=2x,∴,变形得3x2-10x+3=0,解方程得,x1=3,x2=(不合题意,舍去)∴AB=2x=6.14分。
2019年安徽省中考数学试卷含答案解析

数学试卷 第1页(共18页) 数学试卷 第2页(共18页)绝密★启用前安徽省2019年初中学业水平考试数 学本试卷满分150分,考试时间120分钟.第Ⅰ卷(选择题 共40分)一、选择题(本大题共10小题,每小题4分,满分40分。
在每小题给出的四个选项中,只有一项是符合要求的)1.在2-,1-,0,1这四个数中,最小的数是 ( )A .2-B .1-C .0D .1 2.计算3()a a ⋅-的结果是( )A .2aB .2a -C .4 aD .4a - 3.一个由圆柱和长方体组成的几何体如图水平放置,它的俯视图是( )ABCD4.2019年“五一”假日期间,某省银联网络交易总金额接近161亿元,其中161亿用科学记数法表示为( )A .91.6110⨯B .101.6110⨯C .111.6110⨯D .121.6110⨯5.已知点(13)A -,关于x 轴的对称点A '在反比例函数ky x=的图像上,则实数k 的值为( ) A . 3B .13C . 3-D .13-6.在某时段由50辆车通过一个雷达测速点,工作人员将测得的车速绘制成如图所示的条形统计图,则这50辆车的车速的众数(单位:km/h )为( )A . 60B .50C . 40D .157.如图,在Rt ABC △中,90ACB ∠=︒,6AC =,12BC =,点D 在边BC 上,点E 在线段AD 上,EF AC ⊥于点F ,EG EF ⊥交AB 于点G ,若EF EG =,则CD 的长为( )A. 3.6B.4C. 4.8D.58.据国家统计局数据,2018年全年国内生产总值为90.3万亿,比2017年增长6.6%.假设国内生产总值的年增长率保持不变,则国内生产总值首次突破100万亿的年份是( )A .2019年B .2020年C .2021年D .2022年 9.已知三个实数a b c ,,满足20a b c -+=,20a b c ++<,则( )A .200b b ac >-,≤B .2 00b b ac -<,≤C .200b b ac >-,≥D .200b b ac -<,≥10.如图,在正方形ABCD 中,点E ,F 将对角线AC 三等分,且12AC =,点P 在正方形的边上,则满足9PE PF +=的点P 的个数是( )A. 0B.4C.6D.8毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共18页) 数学试卷 第4页(共18页)第Ⅱ卷(非选择题 共110分)二、填空题(本大题共4小题,每小题5分,满分20分。
2019年安徽中考数学试卷(详解版)
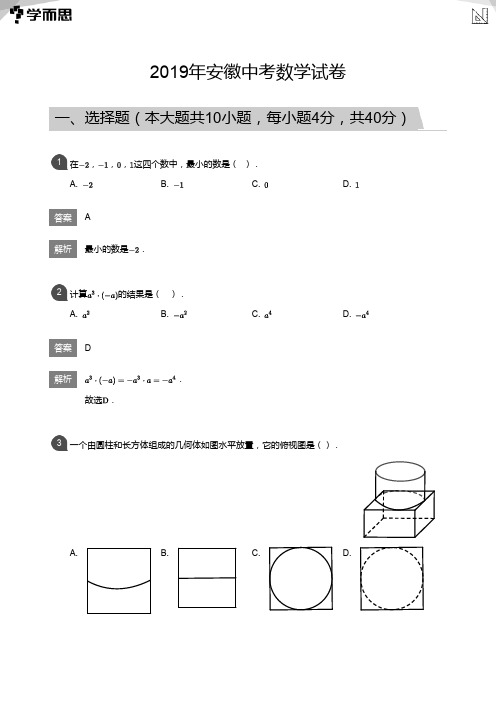
1在2计算3一个由圆柱和长方体组成的几何体如图水平放置,它的俯视图是().45已知点6在某时段由7如图,在答案解析A.年B.年C.年D.年.据国家统计局数据,年全年国内生产总值为万亿,比年增长.假设国内生产总值的年增长率保持不变,则国内生产总值首次突破万亿的年份是().8B年全年国内生产总值为:(万亿),年全年国内生产总值为:(万亿),∴国内生产总值首次突破万亿的年份是年.故选.答案解析A.,B.,C.,D.,已知三个实数,,满足,,则().9D ∵,,∴,,∴,∴,∴即,.故选.10如图,在正方形11计算12命题13如图,14在平面直角坐标系中,垂直于15解方程16如图,在边长为17为实施乡村振兴战略,解决某山区老百姓出行难的问题,当地政府决定修建一条高速公路.其中观察以下等式:18筒车是我国古代发明的一种水利灌溉工具.如图1920如图,点答案解析证明见解析.(1).(2)∵四边形是平行四边形,∴,,∴,∵,∴,∴,同理得,在和中,∵,∴≌.(1)∵点在平行四边形内部,∴平行四边形,由()知:≌,∴,∴四边形平行四边形,∵平行四边形的面积为,四边形的面积为,∴.(2)六、解答题(共12分)为监控某条生产线上产品的质量,检测员每隔相同时间抽取一件产品,并测量其尺寸,在一天的抽检结束后,检测员将测得的各数据按从小到大的顺序整理成如下表格:编号①②③④⑤⑥⑦⑧⑨⑩⑪⑫⑬⑭⑮尺寸21∴抽到两种产品都是特等品的概率.七、解答题(共12分)答案解析一次函数与二次函数的图象的一个交点坐标为,另一个交点是该二次函数图象的顶点22求,,的值.(1)过点且垂直于轴的直线与二次函数的图象相交于,两点,点为坐标原点,记,求关于的函数解析式,并求的最小值.(2);;.(1).(2)由题意得,,解得,又∵二次函数顶点为,∴,把带入二次函数表达式得,解得.(1)由()得二次函数解析式为,令,得∴,设,两点的坐标分别为,,则,∴,,∴当时,取得最小值.(2)八、解答题(共14分)如图,中,,,为内部一点,且.23∴,,,∵,∴,∴,又∵,∴,∴,∴,即,∴,∵,∴,∴,∴.即:.。
安徽省2019中考数学决胜一轮复习阶段性测试卷 (2)

阶段性测试卷(二)(考查内容:三角形、四边形、圆时间:45分钟满分:100分)一、选择题(每小题5分,共40分)1.(改编题)如图,AB∥CD,CE交AB于点F.∠A=20°,∠E=30°,则∠C的度数为( A)A.50°B.55°C.60°D.65°2.(2018·蜀山区二模)如图,平行四边形ABCD中,∠ABC的角平分线交边CD于点E,∠A=130°,则∠BEC的度数是( B)A.20°B.25°C.30°D.50°3.(2018·宿州月考)在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( D)A.若AD⊥BC,则四边形AEDF是矩形B.若AD垂直平分BC,则四边形AEDF是矩形C.若BD=CD,则四边形AEDF是菱形D.若AD平分∠BAC,则四边形AEDF是菱形4.(改编题)正方形ABCD的边长为2,对角线相交于点O,点O又是长方形MNPO的一个顶点,且OM=4,OP=2,长方形绕O点转动的过程中,长方形与正方形重叠部分的面积等于( D)A.6 B.4C.2 D.15.(2018·衢州)如图,AC 是⊙O 的直径,弦BD ⊥AO 于E ,连接BC ,过点O 作OF ⊥BC 于F ,若BD =8 cm ,AE =2 cm ,则OF 的长度是( D )A .3 cmB . 6 cmC .2.5 cmD . 5 cm6.(2018·明光市二模)如图,AB 与⊙O 相切于点B ,OA =2,∠OAB =30°,弦BC ∥OA ,则劣弧BC ︵的长是( B )A .π2B .π3C .π4D .π67.(2018·河南)如图,已知▱AOBC 的顶点O (0,0),A (-1,2),点B 在x 轴正半轴上,按以下步骤作图:①以点O 为圆心,适当长度为半径作弧,分别交边OA ,OB 于点D ,E ;②分别以点D ,E 为圆心,大于12DE 的长为半径作弧,两弧在∠AOB 内交于点F ;③作射线OF ,交边AC 于点G .则点G 的坐标为( A )A .(5-1,2)B .(5,2)C .(3-5,2)D .(5-2,2)8.(改编题)如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,过点B 作⊙O 的切线,交AC 的延长线于点F .已知3AE =BE =6,则CF 的长是( C )A.12 3 B.16 3C.12 D.16二、填空题(每小题5分,共15分)9.(改编题)如图,已知矩形ABCD的对角线AC的长为10 cm,连接各边中点E,F,G,H得四边形EFGH,则四边形EFGH的周长为__20__cm.10.(2018·青岛模拟)如图,在△ABC中,D,E分别是AB,AC的中点,F是线段DE上一点,连接AF,BF,若AB=16,EF=1,∠AFB=90°,则BC的长为__18__.11.(原创题)如图,PA,PB是⊙O的切线,A,B为切点,AC为⊙O的直径,BD⊥AC.下列结论:①∠P+2∠D=180°;②∠BOC=∠BAD;③∠DBO=∠ABP;④∠ABP=∠ABD.其中正确结论有__①②④__(只填序号).三、解答题(共40分)12.(10分)(2018·朝阳区二模)如图,平行四边形ABCD的对角线AC,BD相交于点O,延长CD到E,使DE=CD,连接AE.(1)求证:四边形ABDE是平行四边形;(2)连接OE,若∠ABC=60°,且AD=DE=4,求OE的长.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵DE=CD,∴AB綊DE,∴四边形ABDE是平行四边形;(2)解:∵AD =DE =4,∴AD =AB =4,∴▱ABCD 是菱形,∴AB =BC ,AC ⊥BD ,BO =12BD ,∠ABO =12∠ABC ,又∵∠ABC =60°,∴∠ABO =30°,在Rt △ABO 中,AO =AB ·sin ∠ABO =2,BO =AB ·cos ∠ABO=23,∴BD =43,∵四边形ABDE 是平行四边形,∴AE ∥BD ,AE =BD =43,又∵AC ⊥BD ,∴AC ⊥AE ,在Rt △AOE 中,OE =AE 2+AO 2=213.13.(15分)(2018·霍邱县二模)已知:如图,四边形ABCD 是⊙O 的内接四边形,直径DG 交边AB 于点E ,AB ,DC 的延长线相交于点F .连接AC ,若∠ACD =∠BAD .(1)求证:DG ⊥AB ;(2)若AB =6,tan ∠FCB =3,求⊙O 半径.(1)证明:连接AG ,∵∠ACD 与AGD 是同弦所对圆周角,∴∠ACD =∠AGD ,∵∠ACD =∠BAD ,∴∠BAD =∠AGD ,∵DG 为⊙O 的直径,A 为圆周上一点,∴∠DAG =90°,∴∠BAD +∠BAG =90°,∴∠AGD+∠BAG =90°,∴∠AEG =90°,即DG ⊥AB ;(2)解:∵四边形ABCD 是⊙O 的内接四边形,∴∠FCB =∠BAD ,∵tan ∠FCB =3,∴tan ∠BAD =DEAE=3,连接OA ,由垂径定理得AE =12AB =3,∴DE =9,在Rt △OEA 中,OE 2+AE 2=OA 2,设⊙O 半径为r ,则有(9-r )2+32=r 2,解得,r =5,∴⊙O 半径为5.14.(15分)(2018·安徽四模)如图,⊙O 的直径AD 长为6,AB 是弦,∠DAB =30°,CD ∥AB ,且CD = 3.(1)求∠C 的度数;(2)求证:BC 是⊙O 的切线.(1)解:如图,连接BD ,∵AD 为圆O 的直径,∴∠ABD =90°,∴BD =12AD =3,∵CD ∥AB ,∠ABD=90°,∴∠CDB =∠ABD =90°,在Rt △CDB 中,tan C =BD CD=33=3,∴∠C =60°; (2)证明:连接OB ,∵BD =3,AD =6,∴∠A =30°,∵OA =OB ,∴∠OBA =∠A =30°,∵CD ∥AB ,∠C =60°,∴∠ABC =180°-∠C =120°,∴∠OBC =∠ABC -∠ABO =120°-30°=90°,∴OB ⊥BC ,∴BC为圆O的切线.。
2019届安徽省中考第一次模试考数学试卷【含答案及解析】

2019届安徽省中考第一次模试考数学试卷【含答案及解析】姓名___________ 班级____________ 分数__________一、单选题1. 下面的数中,比0小的是()A. B. C. D. -20162. 如果我们都能改掉餐桌上的陋习,珍惜每一粒粮食,合肥市每年就能避免浪费30.1亿元,将30.1亿用科学计数法表示为()A. B. C. D.3. 计算的结果是()A. B. C. - D.4. 下图中的几何体的左视图是()A. B. C. D.5. 不等式组的解集是()A. B. C. D. 无解6. 寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图。
观察这个频数分布直方图,给出如下结论,正确的是()A. 小明调查了100名同学B. 所得数据的众数是40小时C. 所得数据的中位数是30小时D. 全区有七年级学生6000名,寒假阅读总时间在20小时(含20小时)以上的约有5000名7. 如图,在△ABC中,从A点向∠ACB的角平分线作垂线,垂足为D,E是AB的中点,已知AC=4,BC=6,则DE的长为()A. 1B.C.D. 28. 已知⊙O的半径为,弦AB=2,以AB为底边,在圆内画⊙O的内接等腰△ABC,则底边AB边上的高CD长为()A. B. C. 或 D. 或9. 某企业积极相应政府号召,今年提出如下目标,和去年相比,在产品的出厂价增加10%的前提下,将产品成本降低20%,使产品利润率(利润率=×100%)较去年翻一番.则今年该企业产品利润率为()A. 40%B. 80%C. 120%D. 160%10. 如图,菱形ABCD的边长为4,∠A=30°,点P从起点D出发,沿DC、CB向终点B匀速运动.设点P所走过的路程为,△ADP的面积为,则关于的函数图象是()A. B. C. D.二、填空题11. __________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阶段性测试卷(一)
(考查内容:数与式、方程(组)与不等式(组)、函数 时间:45分钟 满分:100分)
一、选择题(每小题4分,共20分) 1.8的相反数的立方根是( C ) A .±2 B .1
2
C .-2
D .-12
2.下列运算正确的是( D ) A .a 3·a 2=a 6 B .a 12÷a 3=a 4 C .(m -n )2=m 2-n 2
D .(-b 3)2=b 6 3.在创建文明城市的进程中,合肥市为美化城市环境,计划种植树木30万棵,由于志愿者的加入,实际每天植树比原计划多20%,结果提前5天完成任务,设原计划每天植树x 万棵,可列方程是( B )
A .30x -3020%x =5
B .30x -30
(1+20%)x =5
C .
3020%x +5=30
x
D .30(1+20%)x -30
x
=5
4.下列命题为假命题...的是( C ) A .若a =b ,则a -2018=b -2018 B .若a =b ,则a c 2+1=b
c 2+1
C .若a >b ,则a 2>ab
D .若a <b ,则a -2c <b -2c
5.二次函数y =ax 2+bx +c 的图象如图所示,则反比例函数y =a
x 与一次函数y =ax +b 在同一坐标系内
的大致图象是( C )
A B C D
二、填空题(每小题5分,共20分)
6.亚洲陆地面积约为4 400万平方千米,则“4 400万”用科学记数法记作__4.4×107__. 7.分解因式(a -b )(a -4b )+ab 的结果是__(a -2b )2__.
8.写出不等式组⎩
⎪⎨⎪
⎧
4(x +1)≤7x +10,x -5<x -83的所有非负整数解.....__0,1,2,3__. 9.如图的抛物线是二次函数y =ax 2+bx +c 图象的一部分,图象过点A (-3,0),对称轴为直线x =-1,给出四个结论:①b 2>4ac ;②2a +b =0;③a +b +c =0;④若点B ⎝⎛⎭⎫-52,y 1,C ⎝⎛⎭⎫-1
2,y 2为函数图象上的两点,则y 1<y 2,其中正确结论有__①③④__(填序号).
三、解答题(共60分)
10.(8分)计算:(-1)2 018-8+(π-3)0+4cos 45° 解:原式=1-22+1+22=2.
11.(8分)先化简再计算:x 2-1x 2+x ÷⎝⎛⎭⎫
x -2x -1x ,其中x 是一元二次方程x 2-2x -2=0的正数根.
解:原式=(x +1)(x -1)x (x +1)÷x 2-2x +1x =x -1x ·x (x -1)2=1
x -1.解方程x 2-2x -2=0,解得x 1=1+3>0,x 2=1-3<0,所以原式=11+3-1=33
.
12.(8分)化简代数式:⎝⎛⎭⎫3x x -1-x x +1÷x
x 2-1,再从不等式组⎩
⎪⎨⎪⎧
x -2(x -1)≥1①,6x +10>3x +1②的解集中取一个合适
的整数值代入,求出代数式的值.
解:原式=3x (x +1)-x (x -1)(x -1)(x +1)·(x -1)(x +1)
x =3(x +1)-(x -1)=2x +4.解不等式①,得x ≤1,解不等式
②,得x>-3,故原不等式组的解集为-3<x ≤1.∵x ≠0,±1,∴x 可取-2.当x =-2时,原式=2×(-2)+4=0.
13.(10分)观察下列等式:
4-11=3,9-12=4,16-13=5,25-1
4=6,…. (1)写出第5个等式:__36-15
=7__;
(2)猜想并写出第n 个等式,请证明你所猜想的等式是正确的.
(2)第n 个等式:(n +1)2-1n =n +2.证明:左边=n 2+2n +1-1n =n 2+2n
n =n +2=右边,所以猜想
(n +1)2-1
n
=n +2是正确的.
14.(12分)某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:
单价(元/件) 30 34 38 40 42 销量(件)
40
32
24
20
16
(1)计算这5(2)通过对上面表格中的数据进行分析,发现销量y (件)与单价x (元/件)之间存在一次函数关系,求y 关于x 的函数关系式;(不需要写出函数自变量的取值范围)
(3)预计在今后的销售中,销量与单价仍然存在(2)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少?
解:(1)30×40+34×32+38×24+40×20+42×16
5
=934.4;
(2)设所求一次函数关系式为y =kx +b (k ≠0),将(30,40),(40,20)代入y =kx +b ,得⎩⎨⎧
30k +b =42,
40k +b =20,解
得⎩
⎨⎧
k =-2,b =100,∴y =-2x +100;
(3)设利润为w 元,根据题意,得w =(x -20)(-2x +100)=-2x 2+140x +2 000=-2(x -35)2+450,则当x =35时,w 取最大值.即当该产品的单价为35元/件时,工厂获得最大利润450元.
15.(14分)如图,抛物线y =x 2+bx +c 与直线y =1
2x -3交于A ,B 两点,其中点A 在y 轴上,点B 坐
标为(-4,-5),点P 为y 轴左侧的抛物线上一动点,过点P 作PC ⊥x 轴于点C ,交AB 于点D .
(1)求抛物线的解析式;
(2)以O ,A ,P ,D 为顶点的平行四边形是否存在?如存在,求点P 的坐标;若不存在,说明理由. 解:(1)∵直线y =1
2x -3交于A ,B 两点,其中点A 在y 轴上,∴A (0,-3),∵B (-4,-5),
⎩⎨⎧
c =-3,16-4b +c =-5.∴⎩
⎪⎨⎪⎧
b =92,
c =-3.∴抛物线解析式为y =x 2+9
2x -3; (2)存在,设P (m ,m 2+92m -3),(m <0),∴D (m ,1
2m -3),∴PD =|m 2+4m|.∵PD ∥AO ,∴当PD =
OA =3时,|m 2+4m|=3.
①m 2+4m =3时,∴m 1=-2-7,m 2=-2+7(舍),∴m 2+92m -3=-1-7
2
,
∴P ⎝⎛⎭
⎫-2-7,-1-
72; ②当m 2+4m =-3时,∴m 1=-1,m 2=-3.若m 1=-1,∴m 2+92m -3=-13
2,∴P ⎝⎛⎭⎫-1,-132;若m 2=-3,∴m 2+92m -3=-152,∴P ⎝⎛⎭⎫-3,-152,∴点P 的坐标为⎝
⎛⎭⎫-2-7,-1-7
2,⎝⎛⎭⎫-1,-132,⎝
⎛⎭⎫-3,-152.。
