最新2018山东春季高考数学试题
2018年山东省春季高考数学真题

山东省 2018 年普通高校招生(春季)考试 数学试题参考答案
卷一(选择题,共 60 分)
一、选择题(本大题 20 个小题,每小题 3 分,共 60 分)
1 2 3 4 5 6 7 8 9 10 BDAACDBCBC 11 12 13 14 15 16 17 18 19 20 BAADDACCBA
(1)若函数 f(x)在区间( ,0)上单调递减,求实数 m 的取值范围;
(2)若 xR,都有 f(x)>0,求实数 m 的取值范围
27.(本小题
8
分)已知在等比数列
an
中,a2=
1 4
,a5=
1 32
。
(1)求数列an 的通项公式;
(2)若数列bn 满足 bn an n ,求bn 的前 n 项和 Sn.
30.(本小题 10 分)双曲线 x2 y2 =1(a>0,b>0)的左、右焦点分别是
a2 b2
F1,F2,抛物线 y2=2px(p>0)的焦点与点 F2 重合,点 M(2, 2 6 )是抛 物线与双曲线的一个交点,如图所示。 (1)求双曲线及抛物线的标准方程; (2)设直线 l 与双曲线的过一、三象限的渐近线平行,且交抛物线于 A,B 两点,交双曲线于点 C,若点 C 是线段 AB 的中点,求直线 l 的 方程.
其中,正确结论的序号是
.
(第 23 题图)
24.已知椭圆 C 的中心在坐标原点,一个焦点的坐标是(0,3),若点(4,0)在椭圆 C 上,则椭圆 C
的离心率等于
。
25.在一批棉花中随机抽测了 500 根棉花纤维的长度(精确到 1mm)作为样本,并绘制了如图所示的 频率分布直方图,由图可知,样本中棉花纤维长度大于 225mm 的频数是
2018年春季高考数学真题完整

2018春季高考真题一、选择题1、已知集合M ={a,b},N ={b,c},则M ∩N 等于A 、?B 、{b}C 、{a,c}D 、{a,b,c}2、函数f (x )=√??+1+????-1的定义域是A 、(-1,+∞)B 、(-1,1)∪(1,+∞)C 、[ -1,+∞)D 、 [ -1,1)∪(1,+∞)3、奇函数y =f(x)的布局如图所示,则A 、f(2)>0>??(4) B 、f(2)<0<??(4)C 、f(2)> ??(4)>0D 、f(2)<??(4)<04、已知不等式1+lg|x|<0的解集是A 、(-110,0)∪(0,110)B 、(-110,110)C 、(-10,0)∪(0,10)D 、(-10,10)5、在数列{????}中,??1=-1 , ??2=0,????+2=????+1+????,则??5等于A 、0B 、-1C 、-2D 、-36、在如图所示的平面直角坐标系中,向量AB????? 的坐标是A 、(2,2)B 、(-2,-2)C 、(1,1)D 、(-1,-1)7、圆(??+1)2+(??-1)2=1的圆心在A 、第一象限B 、第二象限C 、第三象限D 、第四象限8、已知a 、b ∈R ,则“a>??”是“2??>2??”的A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件9、关于直线l:x -√3??+2=0,下列说法正确的是A 、直线l 的倾斜角为60。
B 、向量??=(√??,??)是直线l 的一个方向向量C 、直线l 经过点(1,√3)D 、向量??=(??,√??)是直线l 的一个法向量10、景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同的走法的种数是A 、6B 、10C 、12D 、2011、在平面直角坐标系中,关于x,y 的不等式Ax +By +AB >0(AB ≠0)表示的区域(阴影部分)可能是12、已知两个非零向量a 与b 的夹角为锐角,则A 、?????>0B 、?????<0C 、?????≥0D 、?????≤013、若坐标原点(0,0)到直线x -y +sin 2??=0的距离等于√22,则角θ的取值集合是A 、{θ|θ=k π±??4,??∈??} B 、{θ|θ=k π±??2,??∈??} C 、{θ|θ=2k π±??4,??∈??}D 、{θ|θ=2k π±??2,??∈??}14、关于x,y 的方程??2+????2=a 2(a ≠0),表示的图形不可能是15、在(x -2y )2的展开式中,所有项的系数之和等于A 、32B 、-32C 、1D 、-116、设命题p:5≥3,命题q:{1}?{0,1,2},则下列命题中为真命题的是A 、p ∧q B 、?p ∧qC 、p ∧?qD 、?p ∨?q17、已知抛物线??2=????(??≠0)的焦点为F ,准线为l,该抛物线上的点M 到x 轴的距离为5,且|MF|=7,则焦点F 到准线l 距离是A 、2B 、3C 、4D 、518、某停车场只有并排的8个停车位,恰好全部空闲,现有3辆汽车依次驶入,并且随机停放在不同车位,则至少有2辆汽车停放在相邻车位的概率是A 、514B 、1528C 、914D 、6719、已知矩形ABCD ,AB=2BC ,把这个矩形分别以AB ,BC 所在直线为轴旋转一周,所围成集合体的侧面积分别记为S 1、S 2 ,则S 1、S 2的比值等于A 、12B 、1C 、2D 、420、若由函数y =sin(2??+??2)图像变换得到y =sin(??2+??3)的图像,则可以通过以下两个步骤完成:第一步,把y =sin(2??+??2)上所有点的横坐标变为原来的4倍,纵坐标不变;第二步,可以把图像沿x 轴A 、向右平移??3个单位B 、向右平移5π12个单位C 、向左平移??3个单位D 、向左平移5π12个单位二、填空题21、已知函数f (x )={x 2+1,??>0-5,??≤0,则f[f(0)]的值等于。
山东省2018年普通高校招生(春季)考试 数学试题-答案

三 、解 答 题 (本 大 题 5 个 小 题 ,共 40 分 ) 26.(本 小 题 6 分 )
文
博 解:(1)函数f(x)=x2+(m -1)x+4的对称轴为x=-m2-1,……………………… (1分) 东 因为函数f(x)在区间(-∞,0)上单调递减,
所以-m2-1≥0,…………………………………………………………………………… (1分)
(2 7)2=(3 7)2+72-2×3 7×7×cos∠B,
解 得 cos∠B =277,
媒
传 所以sin∠B=
1-
æç2
7
ö2
÷
=
è7ø
21,… … … … … … … … … … … … … … … … … … … … … 7
(1 分 )
化 sin∠APB
=sin(180°-30°-
∠B
)=sin150°cos∠B
山东省2018年普通高校招生(春季)考试 数学试题答案及评分标准
卷 一 (选 择 题 ,共 60 分 )
一 、选 择 题 (本 大 题 20 个 小 题 ,每 小 题 3 分 ,共 60 分 )
题号
1
2
3
4
5
6
7
8
9 10
答案
B
D
A
A
C
D
B
C
B
C
题号
11 12 13 14 15 16 17 18 19 20
-cos150°sin∠B
=
1 2
27 ×7-
æ
ç
è
-
3ö÷ 2ø
×
文 721=5147,………………………………………………………………………………… (1分)
高三数学-2018年春季高考题(文) 精品

2018年普通高等学校春季招生考试数学(文史类)第I 卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.不等式组⎪⎩⎪⎨⎧<-<-030122x x x 的解集是 A }11|{<<-x x B }30|{<<x xC }10|{<<x xD }31|{<<-x x2.已知三条直线m 、n 、l ,三个平面α、β、γ,下面四个命题中,正确的是A αγβγ⇒⎭⎬⎫⊥⊥a ∥βB ββ⊥⇒⎭⎬⎫⊥l m l m // Cn m m //////⇒⎭⎬⎫γβγ D n m n m //⇒⎭⎬⎫⊥⊥γγ 3.已知椭圆的焦点是F 1、F 2,P 是椭圆上的一个动点,如果延长F 1P 到Q ,使得||||2PF PQ =,那么动点Q 的轨迹是A 圆B 椭圆C 双曲线的一支D 抛物线4.如果),2(ππθ∈,那么复数)sin )(cos 1(θθi i ++的辐角的主值是 A 49πθ+ B 4πθ+ C 4πθ- D 47πθ+ 5.若角α满足条件02sin <α,0sin cos <-αα,则α在A 第一象限B 第二象限C 第三象限D 第四象限6.若从6名志愿者中选出4人分别从事翻译、导游、导购、保法四项不同工作,则选派方案共有A 180种B 360种C 15 种D 30种7.7.在△ABC 中,AB=2,BC=1.5,∠ABC=120º(如图),若将△ABC 绕直线BC 旋转一周,则所形成的旋转体的体积是 Aπ29 B π27 C π25 D π23 8.到两坐标轴距离相等的点的轨迹方程是A 0=-y xB 0=+y xC 0||=-y xD 0||||=-y x9.函数的单调增区间是 A )](22,22[Z k k k ∈+-ππππ B )](232,22[Z k k k ∈++ππππ C )](2,2[Z k k k ∈-πππ D )](2,2[Z k k k ∈+πππ10.在62)1(x x+的展开式中,x 3的系数和常数项依次是 A 20,20 B 15,20 C 20,15 D 15,1511.若一个等差数列前3项的和为34,最后3项的和为146,且所有项的和 为390,则这个数列有A 13项B 12项C 11项D 10项12.用一张钢板制作一个容积为4m 3的无盖长方体水箱,可用的长方形钢板有四种 同的规格(长宽的尺寸如各选项所示,单位均为m ),若既要够用,又要所剩最少,则应选择钢板的规格是A 2×5B 2×5.5C 2×6.1D 3×5第II 卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
2018年春季高考数学真题(精品资料).doc

2018春季高考真题一、选择题1、已知集合M={a,b},N={b,c},则M∩N等于A、∅B、{b}C、{a,c}D、{a,b,c}2、函数f(x)=√x+1+xx−1的定义域是A、(−1,+∞)B、(−1,1)∪(1,+∞)C、[ −1,+∞)D、 [ −1,1)∪(1,+∞)3、奇函数y=f(x)的布局如图所示,则A、f(2)>0>f(4)B、f(2)<0<f(4)C、f(2)> f(4)>0D、f(2)<f(4)<04、已知不等式1+lg|x|<0的解集是A、(−110,0)∪(0,110)B、(−110,110)C、(−10,0)∪(0,10)D、(−10,10)5、在数列{a n}中,a1=-1 , a2=0,a n+2=a n+1+a n,则a5等于A、0B、−1C、−2D、−36、在如图所示的平面直角坐标系中,向量AB⃗⃗⃗⃗⃗ 的坐标是A、(2,2)B、(−2,−2)C、(1,1)D、(−1,−1)7、圆(x+1)2+(y−1)2=1的圆心在A、第一象限B、第二象限C、第三象限D、第四象限8、已知a、b∈R,则“a>b”是“2a>2b”的A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件9、关于直线l:x−√3y+2=0,下列说法正确的是A、直线l的倾斜角为60。
B、向量v=(√3,1)是直线l的一个方向向量C、直线l经过点(1,√3)D、向量n=(1,√3)是直线l的一个法向量10、景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同的走法的种数是A、6B、10C、12D、2011、在平面直角坐标系中,关于x,y的不等式Ax+By+AB>0(AB≠0)表示的区域(阴影部分)可能是12、已知两个非零向量a与b 的夹角为锐角,则A、a∙b>0B、a∙b<0C、a∙b≥0D、a∙b≤013、若坐标原点(0,0)到直线x−y+sin2θ=0的距离等于√22,则角θ的取值集合是A、{θ|θ=kπ±π4,k∈Z} B、{θ|θ=kπ±π2,k∈Z}C、{θ|θ=2kπ±π4,k∈Z} D、{θ|θ=2kπ±π2,k∈Z}14、关于x,y的方程x2+ay2=a2(a≠0),表示的图形不可能是15、在(x−2y)2的展开式中,所有项的系数之和等于A、32B、-32C、1D、-116、设命题p:5≥3,命题q:{1}⊑{0,1,2},则下列命题中为真命题的是A、p∧qB、¬p∧qC、p∧¬qD、¬p∨¬q17、已知抛物线x2=ay(a≠0)的焦点为F,准线为l,该抛物线上的点M到x轴的距离为5,且|MF|=7,则焦点F到准线l距离是A、2B、3C、4D、518、某停车场只有并排的8个停车位,恰好全部空闲,现有3辆汽车依次驶入,并且随机停放在不同车位,则至少有2辆汽车停放在相邻车位的概率是A、514B、1528C、914D、6719、已知矩形ABCD,AB=2BC,把这个矩形分别以AB,BC所在直线为轴旋转一周,所围成集合体的侧面积分别记为S1、S2 ,则S1、S2的比值等于A、12B、1C、2D、420、若由函数y=sin(2x+π2)图像变换得到y=sin(x2+π3)的图像,则可以通过以下两个步骤完成:第一步,把y=sin(2x+π2)上所有点的横坐标变为原来的4倍,纵坐标不变;第二步,可以把图像沿x轴A、向右平移π3个单位B、向右平移5π12个单位C、向左平移π3个单位D、向左平移5π12个单位二、填空题21、已知函数f(x)={x 2+1,x>0−5,x≤0,则f[f(0)]的值等于。
山东省青岛市2018年春季高考第二次模拟考试数学试题(含答案)

⼭东省青岛市2018年春季⾼考第⼆次模拟考试数学试题(含答案)青岛市2018年春季⾼考第⼆次模拟考试数学试题第Ⅰ卷(选择题,共60分)⼀、选择题(本⼤题共20个⼩题,每⼩题3分,共60分.在每⼩题给出的四个选项中,只有⼀项是符合题⽬要求的,请将符合题⽬要求的选项选出)1.已知{|10}A x x =+>,{2,1,0,1}B =--,则()R C A B =()A .{2,1}--B .{2}-C .{1,0,1}-D .{0,1}2.命题“对任意x R ∈,都有20x ≥”的否定为()A .对任意x R ∈,都有20x <B .存在0x R ∈,使得200x <C .存在0x R ∈,使得200x ≥D .不存在x R ∈,使得20x < 3.已知x a b -<的解集是{|39}x x -<<,则实数a ,b 的值是()A .3a =-,6b =B .3a =-,6b =-C .6a =,3b =D .3a =,6b =4.已知244(2)log 3x f x +=,则(1)f =() A .1- B .0 C .1 D .25.下列函数是偶函数的是()A .sin y x x =B .244y x x =++ C .sin cos y x x =+ D .23()log (1)f x x x =++ 6.已知⽅程2310x x -+=的两个根为1x ,2x ,则1222x x ?=()A .3B .6C .8D .27.已知等差数列{}n a 中,415a =,若,则它的前7项和为()A .120B .115C .110D .1058.已知(5,3)AB =-,(1,3)C -,2CD AB =,则点D 的坐标是()A .(11,3)-B .(9,3)-C .(9,3)D .(4,0)9.要得到函数sin 2y x =的图象,需要将函数sin(2)6y x π=+的图象作怎样的平移才能得到() A .向左平移6π B .向右平移6π C .向左平移12π D .向右平移12π10.如图所⽰,设A ,B 两点在河的两岸,⼀测量者在A 所在的同侧河岸边选定⼀点C ,测出AC 的距离为50m ,45ACB ∠=,105CAB ∠=后,就可以计算出A ,B 两点的距离为()A .502mB .503mC .252mD .2522m 11.已知直线经过两条直线1l :2x y +=,2l :21x y -=的交点,且直线l 的⼀个⽅向向量(3,2)v =-,则直线l 的⽅程是()A .3210x y -++=B .3210x y -+=C .2350x y +-=D .2310x y -+=12.已知圆的⽅程22290x y ax +++=圆⼼坐标为(5,0),则它的半径为()A .3B .5C .5D .413.下列命题中是真命题的个数是()(1)垂直于同⼀条直线的两条直线互相平⾏(2)与同⼀个平⾯夹⾓相等的两条直线互相平⾏(3)平⾏于同⼀个平⾯的两条直线互相平⾏(4)两条直线能确定⼀个平⾯(5)垂直于同⼀个平⾯的两个平⾯平⾏A .0B .1C .2D .314.函数()2sin()f x x ω?=+(0,)22ππω?>-<<的部分图象如图所⽰,则ω,?的值分别是()A .2,3π-B .2,6π-C .4,6π-D .4,3π 15.设x ,y 满⾜24122x y x y x y +≥??-≥-??-≤?,则Z x y =+()A .有最⼩值2,最⼤值3B .有最⼤值3,⽆最⼩值C .有最⼩值2,⽆最⼤值D .既⽆最⼤值也⽆最⼩值16.过双曲线2213y x -=的右焦点且与x 轴垂直的直线交该双曲线的两条渐近线于A 、B 两点,则AB =() A .433B .23C .6D .43 17.从1,2,3,4,5中任意取出两个不同的数,其和为5的概率是()A .15B .14C .13D .1218.在⼀次马拉松⽐赛中,35名运动员的成绩(单位:分钟)如图所⽰:若将运动员按成绩由好到差编为135号,再⽤系统抽样⽅法从中抽取7⼈,则其中成绩在区间[139,151]上的运动员⼈数为()A .3B .4C .5D .619.设(1,2)a =,(1,1)b =,c a kb =+.若b c ⊥,则实数k 的值等于()A .53B .53-C .32-D .3220.若1(3)n x x -的展开式各项系数之和为64,则展开式的常数项为() A .540- B .162- C .162 D .540⼆、填空题(本⼤题5⼩题,每题4分,共20分.请将答案填在答题卡相应题号的横线上)21.若集合{1,2,3}A =,{1,3,4}B =,则A B 的⼦集个数为. 22.设02πθ<<,向量(sin 2,cos )a θθ=,(1,cos )b θ=-,若0a b ?=,则sin θ= .23.若⼀个圆锥的轴截⾯是等边三⾓形,其⾯积为3,则这个圆锥的全⾯积等于.24.已知抛物线28y x =的准线过双曲线22221(0,0)x y a b a b -=>>的⼀个焦点,且双曲线的离⼼率为2,则该双曲线的⽅程为.25.若直⾓坐标平⾯内两点P ,Q 满⾜条件:①P 、Q 都在函数()f x 的图象上;②P Q 、关于原点对称,则称点对()P Q 、是函数()f x 的⼀个“友好点对”(点对()P Q 、与点对(,)Q P 看作同⼀个“友好点对”).已知函数2241,0()2,0x x x x f x x e++三、解答题(本⼤题共5⼩题,共40分请在答题卡相应的题号处写出解答过程)26.在等⽐数列{}n a 中,212a a -=,且22a 为13a 和3a 的等差中项,求数列{}n a 的⾸项、公⽐.27.⼭东省寿光市绿⾊富硒产品和特⾊农产品在国际市场上颇具竞争⼒,其中⾹菇远销⽇本和韩国等地.上市时,外商李经理按市场价格10元/千克在本市收购了2000千克⾹菇存放⼊冷库中.据预测,⾹菇的市场价格每天每千克将上涨0.5元,但冷库存放这批⾹菇时每天需要⽀出各种费⽤合计340元,⽽且⾹菇在冷库中最多保存110天,同时,平均每天有6千克的⾹菇损坏不能出售.(1)若存放x 天后,将这批⾹菇⼀次性出售,设这批⾹菇的销售总⾦额为y 元,试写出y 与x 之间的函数关系式;(2)李经理如果想获得利润22500元,需将这批⾹菇存放多少天后出售?(提⽰:利润=销售总⾦额-收购成本-各种费⽤)(3)李经理将这批⾹菇存放多少天后出售可获得最⼤利润?最⼤利润是多少?28.已知向量1cos ,2a x ?=- ,(3sin ,cos 2)b x x =,x R ∈,设函数()f x a b =?. (1)求()f x 的最⼩正周期;(2)求函数()f x 的单调递减区间;(3)求()f x 在0,2π上的最⼤值和最⼩值. 29.如图,三棱柱111ABC A B C -中,侧棱1AA ⊥底⾯ABC ,且各棱长均相等.D ,E ,F 分别为棱AB ,BC ,11A C 的中点.(1)证明://EF 平⾯1A CD ;(2)证明:平⾯1ACD ⊥平⾯11A ABB ;(3)求直线EF 与直线11A B 所成⾓的正弦值.30.已知椭圆22221(0)x y a b a b +=>>经过点(0,3),离⼼率为12,左右焦点分别为1(,0)F c -,2(,0)F c .(1)求椭圆的⽅程;(2)若直线l :12y x m =-+与椭圆交于A ,B 两点,与以12F F 为直径的圆交于C ,D 两点,且满⾜534ABCD =,求直线l 的⽅程. 青岛市2018年春季⾼考第⼆次模拟考试数学试题答案⼀、选择题1-5: ABDCA 6-10: CDBDA 11-15:CDAAC 16-20:DABCA⼆、填空题21. 4 22. 55 23. 3π 24. 2213y x -= 25. 2 三、解答题26.【解析】由212a a -=,得112a q a -=;由21343a a a =+,得211143a q a a q =+,得2430q q -+=,得1q =(不合题意,舍去),3q =,当3q =时,11a =.27.【解析】(1)由题意得,y 与x 之间的函数关系式为:(100.5)(20006)y x x =+-2394020000(1110)x x x =-++≤≤;(2)由题意得,2(394020000)(102000340)22500x x x -++-?+=;化简得,220075000x x -+=;解得,150x =,2150x =(不合题意,舍去);因此,李经理如果想获得利润22500元,需将这批⾹菇存放50天后出售.(3)设利润为W ,则由(2)得,2(394020000)(102000340)W x x x =-++-?+ 2236003(100)30000x x x =-+=--+;因此当100x =时,max 30000W =;⼜因为100(0,110)∈,所以李经理将这批⾹菇存放100天后出售可获得最⼤利润为30000元.28.【解析】试题分析: 1()cos ,2f x x ?=-(3sin ,cos 2)x x ? 13cos sin cos 22x x x =- 31sin 2cos 222x x =- cos sin 2sin cos 266x x ππ=-sin 26x π??=- ??. (1)()f x 的最⼩正周期为222T πππω===,即函数()f x 的最⼩正周期为π.(2)函数sin(2)6y x π=-单调递减区间:3222262k x k πππππ+≤-≤+,k Z ∈,得:536k x k ππππ+≤≤+,k Z ∈,∴所以单调递减区间是5,36k k ππππ??++?,k Z ∈. (3)∵02x π≤≤,∴52666x πππ-≤-≤. 由正弦函数的性质,当262x ππ-=,即3x π=时,()f x 取得最⼤值1. 当266x ππ-=-,即0x =时,1(0)2f =-,当5266x ππ-=,即2x π=时,122f π??= ,∴()f x 的最⼩值为12-. 因此,()f x 在0,2π上的最⼤值是1,最⼩值是12-. 29.(1)证明:连接ED ,∵D 、E 分别是AB 、BC 的中点,∴//DE AC ,12DE AC =,∵三棱柱111ABC A B C -中,∴11//AC A C ,11AC A C =,⼜F 为棱11A C 的中点,∴1A F DE =,1//A F DE ,∴四边形1A DEF 是平⾏四边形,∴1//EF DA ,⼜∵1DA ?平⾯1A CD ,EF ?平⾯1A CD ,∴//EF 平⾯1A CD .(2)证明:∵D 是AB 的中点,∴CD AB ⊥,⼜∵1AA ⊥平⾯ABC ,CD ?平⾯ABC ,∴1AA CD ⊥,⼜∵1AA AB A =,∴CD ⊥⾯11A ABB ,⼜CD ?⾯1A CD ,∴平⾯1ACD ⊥平⾯11A ABB ;(3)解:∵1//EF DA ,11//AB A B ,∴1A DA ∠为直线EF 与直线11A B 所成的⾓. 设三棱柱111ABC A B C -的棱长为a ,则12AD a =,∴221152A D A A AD a =+=,∴11125sin 5A A A DA A D ∠==. 即直线EF 与直线11AB 所成⾓的正弦值为255. 30.【解析】(1)由题意可得222312b c a a b c ?=??==+?,解得2a =,3b =,1c =,∴椭圆的⽅程为22143x y +=. (2)由题意可得以12F F 为直径的圆的⽅程为221x y +=,∴圆⼼到直线l 的距离为25md =,由1d <,即215m<,可得52m <,∴22421215m CD d =-=-22545m =-,设()11,A x y ,()22,B x y ,联⽴2212143y x m x y ?=-++=??,整理得2230x mx m -+-=,可得:12x x m +=,2123x x m =-,∴22211()4(3)2AB m m =+-?--21542m =-. ∵534ABCD =,∴224154m m -=-,解⽅程得33m =±,且满⾜52m <,∴直线l 的⽅程为1323y x =-+或1323y x =--.。
(完整版)2018山东春季高考数学试题
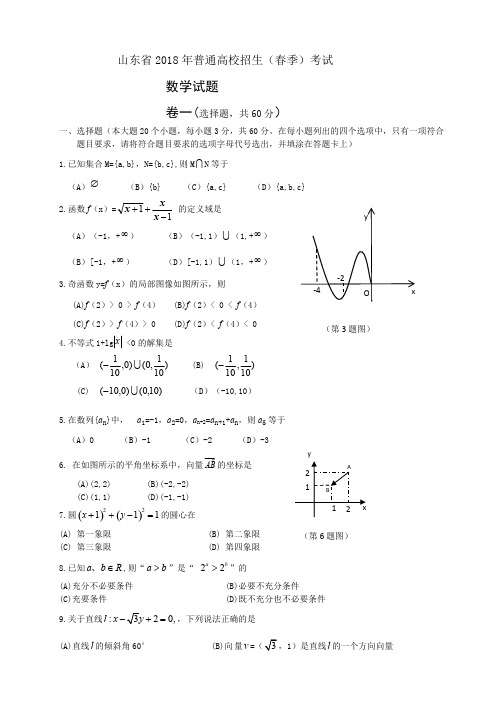
山东省2018年普通高校招生(春季)考试数学试题卷一(选择题,共60分)一、选择题(本大题20个小题,每小题3分,共60分。
在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项字母代号选出,并填涂在答题卡上)1.已知集合M={a,b},N={b,c},则M N等于(A)∅(B){b} (C){a,c} (D){a,b,c}2.函数f(x)=的定义域是11-++xxx(A)(-1,+∞)(B)(-1,1)(1,+∞)(B)[-1,+∞)(D)[-1,1)(1,+∞)3.奇函数y=f(x)的局部图像如图所示,则(A)f(2)> 0 > f(4) (B)f(2)< 0 < f(4)(C)f(2)> f(4)> 0 (D)f(2)< f(4)< 04.不等式1+lg <0的解集是(A) (B)101,0()0,101(-101,101(-(C) (D)(-10,10))10,0()0,10(-5.在数列{a n}中,a1=-1,a2=0,a n+2=a n+1+a n,则a5等于(A)0 (B)-1 (C)-2 (D)-36. 在如图所示的平角坐标系中,向量的坐标是AB(A)(2,2) (B)(-2,-2)(C)(1,1) (D)(-1,-1)7.圆的圆心在()()22111x y++-=(A) 第一象限 (B) 第二象限(C) 第三象限 (D) 第四象限8.已知,则“”是“ ”的a b R∈、a b>22a b>(A)充分不必要条件 (B)必要不充分条件(C)充要条件 (D)既不充分也不必要条件9.关于直线,下列说法正确的是:20,l x-+=(A)直线的倾斜角60° (B)向量=,1)是直线的一个方向向量l v lxy(第6题图)(第3题图)e ae i r(C)直线经过(1,) (D)向量=(1)是直线的一个法向量l n l 10.景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同走发的种数是(A) 6 (B) 10 (C) 12 (D) 2011.在平面直角坐标系中,关于x ,y 的不等式Ax+By+AB>0(AB ≠0)表示的区域(阴影部分)可能是12.已知两个非零向量a 与b 的夹角为锐角,则(A)0a b ⋅> (B )0a b ⋅< (C )0a b ⋅≥(D )0a b ⋅≤13.若坐标原点(0,0)到直线 的距离等于,则角θ的取值集合是(A) (B)(C) )(D)14.关于x,y 的方程 ,表示的图形不可能是15.在 的展开式中,所有项的系数之和等于(A )32 (B )-32 (C )1 (D )-116. 设命題p: 53,命題q: {1} ⊆{0, 1, 2},则下列命題中为真命題的是≥ (A) p ∧q (B) ﹁p ∧q (C) p ∧﹁q (D) ﹁p ∨﹁q17.己知抛物线x²=ay(a≠0)的焦点为F,准线为l,该抛物线上的点M 到x 轴的距离为5,且|MF |=7,则焦点F 到准线l 的距离是(A) 2 (B) 3 (C) 4 (D) 518.某停车场只有并排的8个停车位,恰好全部空闲,现有3辆汽车依次驶入,并且随机停放在不同车位,则至少有2辆汽车停放在相邻车位的概率是 (A)(B) (C) (D)1452815149762,2k k Z πθθπ⎧⎫|=±∈⎨⎬⎩⎭sin 0x y θ-+=()2220x ay a a +=≠,2k k Z πθθπ⎧⎫|=±∈⎨⎬⎩⎭,4k k Z πθθπ⎧⎫|=±∈⎨⎬⎩⎭2,4k k Z πθθπ⎧⎫|=±∈⎨⎬⎩⎭5(2)x y -19.已知矩形ABCD,AB= 2BC,把这个矩形分别以AB、BC所在直线为轴旋转一周,所围成几何体的侧面积分别记为S1、S2,则S1与S2的比值等于(A) (B) 1 (C) 2 (D) 42120.若由函数y= sin(2x+)的图像变换得到y=sin()的图像,则可以通过以下两个步骤完3π32π+x成:第一步,把y= sin(2x+)图像上所有点的横坐标变为原来的4倍,纵坐标不变;第二步,可以把3π所得图像沿x轴 (A)向右平移个单位 (B)向右平移个单位3π125π(C) 向左平移个单位 (D)向左平移个单位3π125π二、填空题(本大题5个小题,每小题4分,共20分。
(完整版)2018年春季高考数学真题

2018春季高考真题一、选择题1、已知集合M={a,b},N={b,c},则M∩N等于A、∅B、{b}C、{a,c}D、{a,b,c}2、函数f(x)=√x+1+xx−1的定义域是A、(−1,+∞)B、(−1,1)∪(1,+∞)C、[ −1,+∞)D、 [ −1,1)∪(1,+∞)3、奇函数y=f(x)的布局如图所示,则A、f(2)>0>f(4)B、f(2)<0<f(4)C、f(2)> f(4)>0D、f(2)<f(4)<04、已知不等式1+lg|x|<0的解集是A、(−110,0)∪(0,110)B、(−110,110)C、(−10,0)∪(0,10)D、(−10,10)5、在数列{a n}中,a1=-1 , a2=0,a n+2=a n+1+a n,则a5等于A、0B、−1C、−2D、−36、在如图所示的平面直角坐标系中,向量AB⃗⃗⃗⃗⃗ 的坐标是A、(2,2)B、(−2,−2)C、(1,1)D、(−1,−1)7、圆(x+1)2+(y−1)2=1的圆心在A、第一象限B、第二象限C、第三象限D、第四象限8、已知a、b∈R,则“a>b”是“2a>2b”的A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件9、关于直线l:x−√3y+2=0,下列说法正确的是A、直线l的倾斜角为60。
B、向量v=(√3,1)是直线l的一个方向向量C、直线l经过点(1,√3)D、向量n=(1,√3)是直线l的一个法向量10、景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同的走法的种数是A、6B、10C、12D、2011、在平面直角坐标系中,关于x,y的不等式Ax+By+AB>0(AB≠0)表示的区域(阴影部分)可能是12、已知两个非零向量a与b 的夹角为锐角,则A、a∙b>0B、a∙b<0C、a∙b≥0D、a∙b≤013、若坐标原点(0,0)到直线x−y+sin2θ=0的距离等于√22,则角θ的取值集合是A、{θ|θ=kπ±π4,k∈Z} B、{θ|θ=kπ±π2,k∈Z}C、{θ|θ=2kπ±π4,k∈Z} D、{θ|θ=2kπ±π2,k∈Z}14、关于x,y的方程x2+ay2=a2(a≠0),表示的图形不可能是15、在(x−2y)2的展开式中,所有项的系数之和等于A、32B、-32C、1D、-116、设命题p:5≥3,命题q:{1}⊑{0,1,2},则下列命题中为真命题的是A、p∧qB、¬p∧qC、p∧¬qD、¬p∨¬q17、已知抛物线x2=ay(a≠0)的焦点为F,准线为l,该抛物线上的点M到x轴的距离为5,且|MF|=7,则焦点F到准线l距离是A、2B、3C、4D、518、某停车场只有并排的8个停车位,恰好全部空闲,现有3辆汽车依次驶入,并且随机停放在不同车位,则至少有2辆汽车停放在相邻车位的概率是A、514B、1528C、914D、6719、已知矩形ABCD,AB=2BC,把这个矩形分别以AB,BC所在直线为轴旋转一周,所围成集合体的侧面积分别记为S1、S2 ,则S1、S2的比值等于A、12B、1C、2D、420、若由函数y=sin(2x+π2)图像变换得到y=sin(x2+π3)的图像,则可以通过以下两个步骤完成:第一步,把y=sin(2x+π2)上所有点的横坐标变为原来的4倍,纵坐标不变;第二步,可以把图像沿x轴A、向右平移π3个单位B、向右平移5π12个单位C、向左平移π3个单位D、向左平移5π12个单位二、填空题21、已知函数f(x)={x 2+1,x>0−5,x≤0,则f[f(0)]的值等于。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省2018年普通高校招生(春季)考试
数学试题
卷一(选择题,共60分)
一、选择题(本大题20个小题,每小题3分,共60分。
在每小题列出的四个选项中,只有一项符合
题目要求,请将符合题目要求的选项字母代号选出,并填涂在答题卡上) 1.已知集合M={a,b},N={b,c},则M N 等于
(A )∅ (B ){b} (C ){a,c} (D ){a,b,c} 2.函数f (x )=
1
1-+
+x x
x 的定义域是 (A )(-1,+∞) (B )(-1,1) (1,+∞) (B )[-1,+∞) (D )[-1,1) (1,+∞) 3.奇函数y=f (x )的局部图像如图所示,则
(A)f (2)> 0 > f (4) (B)f (2)< 0 < f (4) (C)f (2)> f (4)> 0 (D)f (2)< f (4)< 0
4.不等式1+lg <0的解集是
(A ) )101,0()0,101( -
(B) )10
1
,101(- (C) )10,0()0,10( - (D )(-10,10) 5.在数列{a n }中, a 1=-1,a 2=0,a n+2=a n+1+a n ,则a 5等于 (A )0 (B )-1 (C )-2 (D )-3
6. 在如图所示的平角坐标系中,向量AB 的坐标是 (A)(2,2) (B)(-2,-2)
(C)(1,1) (D)(-1,-1) 7.圆()()2
2
111x y ++-=的圆心在
(A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限 8.已知a b R ∈、,则“a b >”是“ 22a
b
>”的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件 9.
关于直线:20,l x +=,下列说法正确的是
(A)直线l 的倾斜角60° (B)向 量v =
,1)是直线l 的一个方向向量
x
y
(第6题图)
(第3题图)
(C)直线l经过(1,
(D)向量n=(1
)是直线l的一个法向量
10.景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同走发的种数是
(A) 6 (B) 10 (C) 12 (D) 20
11.在平面直角坐标系中,关于x,y的不等式Ax+By+AB>0(AB≠0)表示的区域(阴影部分)可能是
12.已知两个非零向量a与b的夹角为锐角,则
(A)0
a b⋅>(B)0
a b⋅<(C)0
a b⋅≥(D)0
a b⋅≤
13.若坐标原点(0,0)到直线的距离等于,则角θ的取值集合是
(A) (B)
(C) )(D)
14.关于x,y的方程,表示的图形不可能是
15.在的展开式中,所有项的系数之和等于
(A)32 (B)-32 (C)1 (D)-1
16. 设命題p: 5≥3,命題q: {1} ⊆{0, 1, 2},则下列命題中为真命題的是
(A) p∧q (B) ﹁p∧q (C) p∧﹁q (D) ﹁p∨﹁q
17.己知抛物线x²=ay(a≠0)的焦点为F,准线为l,该抛物线上的点M到x轴的距离为5,且|MF |=7,则焦点F到准线l的距离是
(A) 2 (B) 3 (C) 4 (D) 5
18.某停车场只有并排的8个停车位,恰好全部空闲,现有3辆汽车依次驶入,并且随机停放在不同车
位,则至少有2辆汽车停放在相邻车位的概率是 (A)
14
5
(B)
28
15
(C)
14
9
(D)
7
6
2
2,
2
k k Z
π
θθπ
⎧⎫
|=±∈
⎨⎬
⎩⎭
sin0
x yθ
-+=
()
2220
x ay a a
+=≠
,
2
k k Z
π
θθπ
⎧⎫
|=±∈
⎨⎬
⎩⎭
,
4
k k Z
π
θθπ
⎧⎫
|=±∈
⎨⎬
⎩⎭
2,
4
k k Z
π
θθπ
⎧⎫
|=±∈
⎨⎬
⎩⎭
5
(2)
x y
-
19.已知矩形ABCD ,AB= 2BC ,把这个矩形分别以AB 、BC 所在直线为轴旋转一周,所围成几何体的侧面积分别记为S 1、S 2,则S 1与S 2的比值等于
(A)
2
1
(B) 1 (C) 2 (D) 4 20.若由函数y= sin(2x+3π)的图像变换得到y=sin(3
2π
+x )的图像,则可以通过以下两个步骤完成:
第一步,把y= sin(2x+3π
)图像上所有点的横坐标变为原来的4倍,纵坐标不变;第二步,可以把所得图像沿x 轴 (A)向右平移
3π个单位 (B)向右平移125π
个单位 (C) 向左平移3π个单位 (D)向左平移12
5π
个单位
二、填空题(本大题5个小题,每小题4分,共20分。
请将答案填在答题卡相应题号的横线上)
21.已知函数f (x)= 2x 1x > 0
-5 , x 0
⎧+⎨≤⎩,,则f [f (0)]的值等于 .
22.已知,02πθ⎛⎫
∈-
⎪⎝⎭
, 若3cos 2θ=,则sin θ等于 .
23.如图所示,已知正方体1111ABCD A B C D -,E ,F 分别是
11D B A C ,上不重合的两个动点,给出下列四个结论:
○
11CE D F ; ○211AFD B EC 平面平面
○31AB EF ⊥; ○4 11平面AED 平面ABB A
其中,正确结论的序号是 .
24.已知椭圆C 的中心在坐标原点,一个焦点的坐标是(0,3),若点(0,4) 在椭圆C 上,则椭圆C 的离心率等于
25.在一批棉花中随机抽测了500根棉花纤维的长度(精确到1mm )作为样本,并绘制了如图所示的频率分布直方图,由图可知,样本中棉花纤维长度大于225mm 的频数是
0.0038
0.0022 0.0020
0.0026
0.0044
0.0050
0.001
0.002
0.003 0.004 0.005 组距
(第23题图)
三、解答题(本大题5个小题,共40分)
26.(本小题6分)已知函数f(x)=x 2+(m-1)x+4,其中m 为常数
(1)若函数f(x)在区间(-∞,0)上单调递减,求实数m 的取值范围; (2)若∀x ∈R ,都有f(x)>0,求实数m 的取值范围 27.(本小题8分)已知在等比数列{}n a 中,a 2=14,a 5=132。
(1) 求数列{}n a 的通项公式;
(2) 若数列{}n b 满足n n b a n =+,求{}n b 的前n 项和S n.
28.(本小题8分)如图所示的几何体中,四边形ABCD 是矩形,MA ⊥平面ABCD ,NB ⊥平面ABCD , 且AB=NB=1,AD=MA=2 (1) 求证:NC ║平面MAD ; (2)求棱锥M -NAD 的体积.
29.(本小题8分)如图所示,在△ABC 中,BC=7,2AB=3AC,点P 在BC 上,且∠BAP=∠
PAC=30°.求线段AP 的长.
30.(本小题10分)双曲线22
22x y a b
-=1(a>0,b>0)
的左、右焦点分别是F 1,F 2,抛物线y 2
=2px (p>0) 的焦点与点F 2重合,点M (2
,)是抛物线 与双曲线的一个交点,如图所示.
(1) 求双曲线及抛物线的标准方程;
(2) 设直线l 与双曲线的过一、三象限的渐近线平行,
且交抛物线于A ,B 两点,交双曲线于点C , 若点C 是线段AB 的中点,求直线l 的方程.
(第25题图)
25.5
75.5
125.5 225.5 175.5 275.5
325.5
(第28题图) (第29题图)
A
C
D B
M
N
A
C P B
l
(第30题图)。
