卡氏第二定理
材料力学能量法第3节 卡式定理
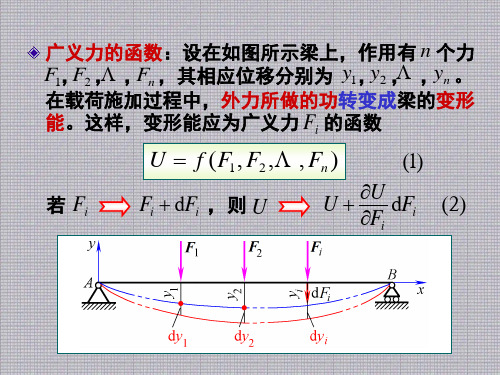
q 2 M ( x) (l x) M e 2
M 1 M e
(2)计算 B 截面转角 B
M q 2 1 M ( x) (l x) M e M e 2 M ( x) M ( x) Bq M e dx EI M e 1 l q 2 [ ( l x ) M ] ( 1 ) d x e EI 0 2 3 l ql 顺时针转向 Me EI 6 ql 3 顺时针转向 B 令 Me 0 6 EI
2
1 dFi dyi U dFi yi 2
(3)
比较(2)(3)式
1 dFi dyi U dFi yi (3) 2 U ( F1 , F2 , Fn ) yi i 1,2,3,... Fi
U U dFi Fi
(Hale Waihona Puke 2)梁的变形能对某一载荷 Fi 的偏导数,等于 在该载荷处沿载荷方向的位移,这就是卡氏定理, 也称卡氏第二定理。由意大利工程师 A 卡斯蒂利亚 诺(1847-1884)于1873年提出的。卡氏定理对其他 线弹性结构也是适用的。
广义力的函数:设在如图所示梁上,作用有 n 个力 y2 , , yn 。 F1, F2 , , Fn ,其相应位移分别为 y1, 在载荷施加过程中,外力所做的功转变成梁的变形 能。这样,变形能应为广义力 Fi 的函数
U f ( F1, F2 ,, Fn )
若 Fi
(1) ( 2)
Fi dFi , 则 U
U U dFi Fi
卡式定理的推导 —— 改变加力的次序 (1)先施加 dFi :在施加 dFi 时,其作用点沿 dFi 方向的 1 dF dy 位移为 dyi ,梁的变形能为 i i;
能量法

1
3Eh2 10GL2
It is therefore customary in engineering practice to neglect the effect of shear in computing the strain energy of slender beams.
F 广义力
1
广义位移
基本变形下杆的应变能:(线弹性范围内)
F
V
1 2
Fl
FN2l 2EA
l
FN2 x dx
2EA
Me
V
1 2
M e
T 2l 2GI P
T 2 xdx
l 2GIP
M
V
1 M
2
M 2l 2EI
横力弯曲
M 2 x dx
2EI 0
2GI p 0
4EI 4GI p
外力功
V
W
1 2
P
A
A
PR3
2EI
3PR3
2GI p
互等定理 (Reciprocal theorems)
1. 功的互等定理
设有两组外力F1和F2分别作用于同一线弹性结构上,如 图所示,(a)、(b)分别称为结构的第一状态和第二状态。
F1 Δ11 1
F1 dF
0
线弹性范围内:
1
1
Vc
V
F 2
➢ 余能仅具有与应变能相同的量纲,无具体 的物理意义。线弹性材料,余能数值上等 于应变能,应区分两者的概念。
应变能的普遍表达式
材料力学卡式定理
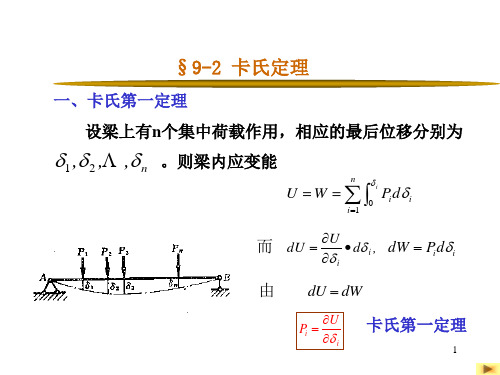
l
(2)
于是(1)式改写为
y / l
(3)
3
梁内任一点处的比能
u
1 2
E 2
1 2
E 2
l2
y2
(4)
梁的应变能
l
U VudV 0 (AudA)dx
l 1 E 2
( 02
l2
y2dA)dx 1 EI 2
A
2l
(5)
由卡氏第一定理
m U 1 EI (2 ) EIθ
(6)
2 lx)
2
dx
1 ( 5PL3 RC L3 ) 0
EI 48
3
RC
5P 16
能量法求解超静定结构,适 用任意荷载作用下、线性或 非线性弹性杆系、刚架或曲 杆等超静定系统。
14
2.求 wB
① 求内力
M
AB ( x)
5P 16
(L
x)
P(0.5L
x)
M BC ( x)
5P 16
Px L EI Px
1 EI
x 0
P(L
x1 ) ( x1
x)dx1
P
x3 [
(L
x)x2
Lx 2 ]
EI 3
2
12
例6 等截面梁如图,用卡氏定理求B 点的挠度。
P 0.5 L
B
A
L
解:1.依 wC 0 求多余反力,
卡氏定理解 ① 取静定基如图 C 超静定结构
② 求内力
M AB ( x) RC (L x) P(0.5L x)
L x1
O
x
w
①求内力 M AB ( x1) P(L x1) Px ( x x1) M BC ( x1) P(L x1)
卡氏第二定理

卡氏第二定理卡氏第二定理(KummerSecondTheorem)又称为卡氏二元定理,它是由德国数学家卡氏于1852年提出的一种数论定理,是多个古老定理的总结,是一个重要的代数结构之一。
卡氏第二定理涉及了几何射影以及椭圆曲线的投影,是一项重要的数学理论,被广泛应用在数论、组合数学、多元代数和特殊函数的研究中。
卡氏第二定理的主要原理可以归结为三点:(1)设f(x)为一种单个变量的多项式,一般地,一个多项式具有n次不同的根,不论是实根还是复根,他们出现的次数总是n次。
(2)设P(x,y)为一个二元多项式,其中x和y是连续变量,该多项式的根是一个椭圆曲线E上的点的坐标。
若F(x,y)是P(x,y)的一个不可约因子,那么F(x,y)在E上的根也是E上的点的坐标,而且出现次数等于P(x,y)的根的出现次数。
(3)对于任意的二元多项式P(x,y),如果F(x,y)是P(x,y)的一个不可约因子,则P(x,y)的根总是满足如下条件:P(x,y)是一个整数关系。
卡氏第二定理在数论、组合数学、多元代数研究和计算数学中有着重要的应用价值。
它不仅用于解决多变量多项式的求根问题,而且还可以用来寻找椭圆曲线上有趣点的坐标,以及在数论中研究质素数和平方数等问题。
此外,在数据加密领域,卡氏第二定理的应用也是非常广泛的。
其中,最重要的应用是RSA加密算法,它是目前世界上最常用的公钥加密算法,而RSA算法的安全性完全依赖于卡氏第二定理的应用。
因此,卡氏第二定理的研究可以说是数学的“金矿”,在数学领域有着重要的应用价值,且极具前景。
现代数学家们仍一直在探索和研究卡氏第二定理,并发现了它具有良好的应用价值,为世界各地的科研人员提供了难以估量的帮助。
卡氏第二定理的研究不仅对数学的发展至关重要,而且对实际的应用也具有极大的意义,是数学巨人卡氏的一项重要成就。
第10章 能量法

EI L x
2
P A O
U =
∫
[M n ( x)]
L
2 EI
P 2 L2 dx = 6 EI
∂U PL3 = ③求位移 δ A = ∂P 3EI
例5(续): 求 A点的转角 解: ①求弯矩 M n ( x) = −(M 0 + Px) ②求变形能
U =
EI L x
P A O
N1 = N 2 cos α = Pctgα , N 2 =
对每个杆内能
2 2
P sin α
2
L
A N1 α
2
P
U =∫
L
[ N ( x)] dx + [ M T ( x)] dx + [ M n ( x)] dx = N
2 EA
∫
L
2GI p
∫
L
2 EI
L 2 EA
C
对整个杆系内能 N 12 l1 N 22 l 2 1 U = + = W = P yc 2 E A1 2 E A2 2 1 ( Pctg α ) 2 l1 l2 P 2 Py c = + ( ) 2 2 EA 1 2 EA 2 sin α
δ1 δi δn
δ2
Fi
Fn
1 n U = ∑ Fiδ i 2 i =1
二. 互等定理
1.功互等定理 Fi δ′ = Fjδ′ji ij
i 力在 j 力引起的位移δ’ij上 做的功等于j 力在 i 力引起 的位移δ’ji上做的功。
Fi
δ i′
i
0 Fj j
δ i′
i Fi
0
δ ij ′
δ j′
材料力学第8章-能量法3-1

d
FN dx d(l) = EA
0 N
Mdx d EI
0
Tdx d GI p
0 S 0
1 F d l M d F d T d
F FN T T M M dx dx dx EA EI GI p
0 N 0 0
2.力和位移应理解为广义力和广义位移。
能量法/虚功原理 单位力法 图乘法
上节回顾
1、可能内力,可能位移,虚位移 2、虚功原理
在外力作用下处于平衡的结构,任意给它一个虚位移, 则外力在虚位移上所做的虚功,等于结构内力在虚变形上所 作的功。
W Wi
* e
e
*
外力虚功
内力虚功
l
W
Fi
5 M a 3
0 1c
2 Fa a
M
0 2c
3 a 2
Fa a 3 2 2 0 M 3c a 3
能量法/虚功原理 单位力法 图乘法
A
EI1
a
C
EI 2
a
F B
1
2Fa Fa
1
2a 5a/3
2
3a/2
-
2a/3
3
根据图乘法,自由端的挠度为:
1 1 0 0 yB 1M1c 2 M 2c EI 3M 30c EI1 2 1 Fa a 5 3 1 Fa a 2a a Fa a a EI1 2 3 2 EI 2 2 3
能量法/超静定问题 力法 例 如图超静定梁, EI为常数,试求B点的约束反力。
第八章
一、杆件的应变能
材料力学常用基本公式

面积A,拉应力为正)d,拉伸后试样直径 d1)纵向线应变和横向线应变外力偶P 功率, n 转速)弯矩、剪力和荷载集度之间的关系式轴向拉压杆横截面上正应力的计算公式杆件横截面轴力F N,横截面1.2.3.4.5.6.7.8.9.10.11.12.泊松比胡克定律受多个力作用的杆件纵向变形计算公式轴向拉压杆斜截面上的正应力与切应力计算公式夹角a 从x 轴正方向逆时针转至外法线的方位角为正)纵向变形和横向变形(拉伸前试样标距l ,拉伸后试样标距 l1 ;拉伸前试样直径承受轴向分布力或变截面的杆件,纵向变形计算公式轴向拉压杆的强度计算公式许用应力,脆性材料延伸率截面收缩率剪切胡克定律拉压弹性模量,塑性材料切变模量G,切应变gE、泊松比和切变模量圆截面对圆心的极惯性矩( a)实心圆b)空心圆)G之间关系式圆轴扭转时横截面上任一点切应力计算公式圆截面周边各点处最大切应力计算公式扭转截面系数,( a)实心圆扭矩T,所求点到圆心距离r )13.14.15.16.17.18.19.20.21.22.23.24.薄壁圆管(壁厚 δ≤ R 0 /10 ,R 0 为圆管的平均半径)扭转切应力计算公式圆轴扭转角 与扭矩 T 、杆长 l 、 扭转刚度 GH p 的关系式 同一材料制成的圆轴各段内的扭矩不同或各段的直径不同(如阶梯轴)时等直圆轴强度条件受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式平面应力状态下斜截面应力的一般公式b )空心圆25.26. 27. 28. 29. 30.31.32.33.或 塑性材料或 扭转圆轴的刚度条件 ? ;脆性材料平面应力状态的三个主应力 主平面方位的计算公式 ,面内最大切应力 三向应力状态最大切应力 广义胡克定律 四种强度理论的相当应力34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44.任意截面图形对一点的极惯性矩与以该点为原点的任意两正交坐标轴的惯性矩之 和的关系式平行移轴公式(形心轴 z c 与平行轴 z 1的距离为 a ,图形面积为 A )纯弯曲梁的正应力计算公式45. 46.47.48.49. 50.51.52.53.54., 组合图形的形心坐标计算公式 截面图形对轴 z 和轴y 的惯性半径 ?矩形、圆形、空心圆形的弯曲截面系数几种常见截面的最大弯曲切应力计算公式( 轴 z 的静矩, b 为横截面在中性轴处的宽度)为中性轴一侧的横截面对中性横力弯曲最大正应力计算公式工字形截面梁腹板上的弯曲切应力近似公式轧制工字钢梁最大弯曲切应力计算公式 圆形截面梁最大弯曲切应力发生在中性轴处弯曲正应力强度条件弯曲梁危险点上既有正应力 σ 又有切应力 τ 作用时的强度条件 或,梁的挠曲线近似微分方程 轴向荷载与横向均布荷载联合作用时杆件截面底部边缘和顶部边缘处的正应力计弯扭组合变形时圆截面杆按第三和第四强度理论建立的强度条件表达式55.56.57.58.59. 60.61.62.63.64.65. 66.算公式偏心拉伸(压缩) 圆环形薄壁截面梁最大弯曲切应力发生在中性轴处 几种常见截面梁的弯曲切应力强度条件梁的转角方程梁的挠曲线方程圆截面杆横截面上有两个弯矩 和 同时作用时,合成弯矩为圆截面杆横截面上有两个弯矩和同时作用时强度计算公式弯拉扭或弯压扭组合作用时强度计算公式剪切实用计算的强度条件挤压实用计算的强度条件 等截面细长压杆在四种杆端约束情况下的临界力计算公式 压杆的约束条件:( a )两端铰支 μ =l( b )一端固定、一端自由 μ =2( c )一端固定、一端铰支d )两端固定 μ =0.567.68.69.70.71.72.73. 74. 75. 76. 77.μ=0.778.压杆的长细比或柔度计算公式79.细长压杆临界应力的欧拉公式80.欧拉公式的适用范围81.压杆稳定性计算的安全系数法82.压杆稳定性计算的折减系数法83. 关系需查表求得3截面的几何参数4应力和应变5应力状态分析6内力和内力图7强度计算刚度校核9 压杆稳定性校核10 动荷载11 能量法和简单超静定问题材料力学公式汇总、应力与强度条件1、拉压maxmax2、剪切max3、4、挤压挤压圆轴扭转P挤压A挤压TWtmax平面弯曲①maxM maxy t maxI z*③ Q max S z max②t max5、斜弯曲max M z M yW z W yW z maxtmaxt maxmax注意:“5”与“ 6”两式仅供参考 ②第四强度理论r4w 2 3 n 2M w 20.75M n 2r4 w 3 n WWz二、变形及刚度条件1拉压LNLNLN i L iN ( x) dxEA EA LEA2扭转TLT i L i T x dx T 180 0( /GI pGI pGI pL GI p3弯曲(1) 积分法 : EIy ''( x) M(x) E Iy '(x) EI (x) M(x)dx CEIy ( x) [ M (x)dx]dx Cx D(2)叠加法 : f P 1,P 2 ⋯= f P 1 f P 2 +⋯, P 1, P 2 = P 1 P 2 ⋯M 2L =M i 2L i =M 2xdx2EI 2EI i 2EI(5)卡氏第二定理 ( 注:只给出线性弹性弯曲梁的公式 ) 三、应力状态与强度理论 1、 二向应力状态斜截面应力2、 二向应力状态极值正应力及所在截面方位角 3、 二向应力状态的极值剪应力注:极值正应力所在截面与极值剪应力所在截面夹角为 4504、 三向应力状态的主应力: 1 2 36、拉(压)弯组合 maxNM7、圆轴弯扭组合:①第三强度理论M w 2 M n2Wz(3)基本变形表 ( 注意:以下各公式均指绝对值,使用时要根据具体情 况赋予正负号 )ML3EI, A MLA6EIBA PL 216EI qL3 24EI (4)弹性变形能 ( 注:以下只给出弯曲构件的变形能 响, 其他变形与此相似 ,不予写出 ) 并忽略剪力影 B最大剪应力 : max1 325、二向应力状态的广义胡克定律(1)、表达形式之一(用应力表示应变) (2)、表达形式之二(用应变表示应力) 6、三向应力状态的广义胡克定律 强度理论 1) r1 1 1 bnb2)r 3 1 3五、动载荷(只给出冲击问题的有关公式)能量方程TVU7、 sn s8、平面应力状态下的应变分析sin 2x y x y1)2 2xys i n222tg2 0 xyxy四、压杆稳定1、临界压力与临界应力公式(若把直杆分为三类) ① 细长受压杆 p ② 中长受压杆 p ③ 短粗受压杆s2EI minPcr 2PcrL2cr a b“ cr ”2Ecr22、关于柔度的几个公式 或 b2Epasb3、惯性半径公式 i I Az短边长度 ))圆截面 i d4,矩形截面 i min b12(b 为2cos 2xyc o 2s2冲击系数 K d 1 1 2hst (自由落体冲击)K dgv0st(水平冲击)六、截面几何性质1、 惯性矩(以下只给出公式,不注明截面的形状) 442 d D 4 d132 DI P 2dA =2、惯性矩平移轴公式32。
材料力学13能量法

功的互等定理:
F1 12 F2 21
即:F1 力在由F2力引起的位移上所作的功,等于F2 力在由F1力引起的位移上所作的功。
若F1 = F2 ,则得
位移互等定理:
12 21
即: F2引起的F1 作用点沿 F1方向的位移,等于同 样大小的力F1 引起的F2作用点沿 F2方向的位移。
( F1 F2 ) L F1 L F2 L F1F2 L V 2 EA 2 EA 2 EA EA
2
2
2
L
2) F1 单独作用下:
F1 F2
F1 L V 1 2 EA
3)F2 单独作用下:
F22 L V 2 2 EA
2
L F1 F2
L
V1 V 2 V
证毕。
b Px1 l ( 0 ≤x1 ≤ a) a CB段: M(x2 ) = RB x2 = Px2 l ( 0 ≤x2≤ b) 2
AC段:M(x1 ) = RA x1 =
13-3 应变能的普遍表达式
基础知识
广义
线弹性结构上受一个外力作用,任一点的位移与该力成正比。
线弹性结构上任意一点的广义位移与各广义力成线性 齐次关系。 比例加载时,线弹性结构上任一外力作用点沿外力方 向的位移与该点的广义力成正比。
P12 l1 P1作功为 V 3 2 EA
(5)应变能是可逆的。(跳板跳水)
总功仍为上述表达式。
直接利用功能原理求位移的实例
利用能量法求解时,所列 例 求简支梁外力P作用点C的挠度。 弯矩方程应便于求解。
解:
A x1 RA l a
P
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F3
F1
3 1
1 , 2 , , i ,
结构的变形能
11 1 V ε W 2 F 1 δ 1 2 F 2 δ 2 2 F 3 δ 3
只给 Fi 一个增量 Fi .
引起所有力的作用点沿力方向的位
移增量为 Δ1,δ Δ2,δ Δ3,δ
在作用Fi 的过程中, Fi 完成 F1
的功为
1 2
ΔFi
氏定理)(Castigliano’s Theorem)
说明 (Directions):
(1)卡氏第二定理只适用于线性弹性体( Applying only to linearly elastic bodies)
δi
Vε Fi
(2)Fi 为广义力(generalized force) i为相应的位移
(displacement corresponding to force Fi )
一个力
一个力偶
一对力
一对力偶
一个线位移
一个角位移
相对线位移 相对角位移
(3)卡氏第二定理的应用 ( Application of castigliano’s second theorem ) (a) 轴向拉,压(Axial tension and compression)
δ i V F ε i F i F N 2 2 ( E x )x d A F E N (x )A F N F ( ix )d x
Δδi
原有的所有力完成的功为
2
F2
F3
3 1
F 1 Δ 1 F 2 δ Δ 2 δ F iΔ i δ
结构应变能的增量为
Δ ε 1 2 V Δ iΔ i F F δ 1 Δ 1 F δ 2 Δ 2 δ F iΔ i δ
略去高阶微量
1 2
ΔFi
Δδi
Δ ε F 1 Δ V 1 F 2 Δ δ 2 δ F i Δ i δ
F N ( x ) F N ( x ) d x T ( x ) T ( x ) d x M ( x ) M ( x ) d x E A F i G p F I i E I F i
例 2.6
• 已知 EI, 求 C 端挠 度及 A 截面的转角
解:பைடு நூலகம்
• 根据卡氏定理,有
AB段
BC段
卡氏定理
卡氏定理(Castigliano's Theorem),是意大利工 程师卡斯蒂利亚诺(A.Castigliano )于1873年提出 的,故得其名.
卡氏第二定理
卡氏第一定理
卡氏定理的证明
设弹性结构在支座的约束下无 任何刚性位移.
作用有外力:
F1 ,F2 , ,Fi ,
相应的位移为:
2
F2
例2.7
• 图示刚架EI为常 量,B截面受m作 用。求C截面转
角qC及D点的水 平位移x。轴力
及剪力不计。
aa
2a
C
D
B
m
A
C点施以附加力 偶矩m2,支反力为
RAy=
—m—+m—2 2a
RD=
—m—+m—2 2a
aa
2a
C
m2
B
m
A
RAy
D
RD
RAy=
—m—+m—2 2a
RD=
—m—+m—2 2a
ds
=
—PR—3p—
4EI
再在B点施加水平力Pa
M=PrcosfPaR(1-sinf)
— M—=R(1- sinf) Pa
Af
B P Pa
[ ] x=
S
—M— —M EI Pa
ds
= —PR—3— Pa=0 2EI
例 求A点位移A和B点位移B
解
• 先求A点位移
由卡氏定理
因为 所以
求B点位移
(b) 扭转(Torsion)
δ i V F ε i F i T 2 2 (G x )px d I T G (x p )I T F (x i)d x
(c) 弯曲 (Bending)
δ i V F ε i F i M 2 2 ( E x )x d I M E (x ) I M F (ix )d x
(4) 平面桁架 (Plane truss)
δi V Fεi jn 1F E NjljAF FN ij
(5) 组合变形(Combined deformation)
δi
Vε Fi
[F N 2(x )x d T 2(x )x d M 2(x )x d ] F i l 2 EAl 2 G pI l 2 EI
求AB,BC,CD各段的弯 矩方程,并对m2求偏导, 最后由卡氏定理求得C 截面的转角qC。
qC=
2a —3E—I (m+m2)
x3
x2
x1
C
m2
B
m
D
RD
A
RAy
实际上并无m2 ,所以令m2 =0得
qC=
—2a—m 3EI
通常在积分前即令m2 =0,可使积分简单
为求D点水平位
移 x , 在D点加水平
如果把原来的力看作第一组力,而把 Fi 看作第二组力.
根椐互等定理
F 1 Δ 1 F 2 Δ δ 2 δ F i Δ i δ Δ i δ i F
ΔεV ΔiF δi 或者
ΔV ε ΔF i
δi
当 Fi 趋于零时,上式为
Vε Fi
δi
这就是卡氏第二定理(Castigliano’s Second Theorem )(卡
加入虚载荷P’ AB段
BC段
所以
事实上并无P’,因此令P’=0有 其实可在进行以下积分前令P’=0
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
力Pa ,求AB,BC,CD各 段的弯矩方程,并对
x2
x1
C
D Pa
B
RD
m
Pa求偏导,最后由卡 氏定理求得D点水平
位移x。
x3
RAx
A
RAy
x=
17ma2 —— 6EI
例2.8
EI=常量,求B点水平和 垂直位移
先求垂直位移y
B
M=PRcosf
P
—M—=Rcosf P
Af
y=
S
—MEI— —PM
