高中数学框图
高中数学第四章框图4.1流程图同步新人教A版选修

到
的全部步骤,在日常生活和工作的很多领域都得到广泛应用.
知识点二 工序流程图
用于描述 工业生产
的流程的流程图通常称为工序流程图.常见的
一种画法是:将一个工作或工程从头至尾依先后顺序分为若干道工序(即
所谓自上向下),每一道工序用矩形框表示,并在该矩形框内注明此工序
的名称或代号.两相邻工序之间用流程线相连.有时为合理安排工程进度,
解答
达标检测
1.要描述一个工厂某种产品的生产步骤,应用 A.程序框图
√B.工序流程图
C.程序框图或工序流程图 D.以上都不正确 解析 工序流程图是描述产品生产工序的流程图.
12345
解析 答案
2.下列说法正确的是 A.流程图只有一个起点和一个终点
√B.程序框图只有一个起点和一个终点
C.工序流程图只有一个起点和一个终点 D.以上都不对
第四章 框 图
§4.1 流程图
学习目标 1.通过实例,进一步认识程序框图. 2.理解流程图的概念,并掌握流程图的特征. 3.了解流程图的分类,并会画各类流程图. 4.理解画流程图的步骤,绘制简单问题的流程图,体会流程图 在解决实际问题中的作用.
内容索引
问题导学 题型探究 达标检测
问题导学
知识点一 流程图 思考 在流程图中,基本元素之间用什么线连接? 答案 用流程线连接.
本课结束
解答
类型二 绘制工序流程图 例2 某药厂生产某产品的过程如下: (1)备料、前处理、提取、制粒、压片、包衣、颗粒分装、包装; (2)提取环节经检验合格,则进入下一工序,否则返回前处理; (3)包衣、颗粒分装两环节分别检验合格才进入下一工序,否则为废品. 画出生产该产品的工序流程图. 解 工序流程图如图所示.
人教版 高中数学 第一章 循环结构的程序框图(共16张PPT)教育课件
凡 事都 是多棱 镜, 不同 的角 度会
凡 事都是 多棱 镜, 不同 的角度 会看 到不 同的 结果 。若 能把一 些事 看淡 了, 就会 有个好 心境 ,若 把很 多事 看开 了 ,就会 有个 好心 情。 让聚散 离合 犹如 月缺 月圆 那样 寻常, 让得 失利 弊犹 如花 开花谢 那样 自然 ,不 计较 ,也 不 刻意执 着; 让生 命中 各种的 喜怒 哀乐 ,就 像风 儿一 样,来 了, 不管 是清 风拂 面,还 是寒 风凛 冽, 都报 以自 然 的微笑 ,坦 然的 接受 命运的 馈赠 ,把 是非 曲折 ,都 当作是 人生 的
i<100? 否 是 i=i+1
S=S+ i
输出S 结束
开始 i=0,S=0
i=i+1 S=S+ i 否 i>=100?
是 输出S 结束
当型循环与直到循环的区别:
①当型循环可以不执行循环体,直到 循环至少执行一次循环体. ②当型循环先判断后执行,直到型循 环先执行后判断. ③对同一算法来说,当型循环和直到 循环的条件互为反条件.
开始 i=0,S=0
否 i<100? 是 i=i+1 S=S+ i
输出S 结束
思考:将步骤A和步骤B交换位 置,结果会怎样?能达到预期结果 吗?为什么?要达到预期结果,还 需要做怎样的修改?
步骤A
步骤B 答:达不到预期结果;
当i = 100时,退出循环,i 的值未能加入到S中;修 改的方法是将判断条件改 为i<101
i=i+1 S=S+ i
i=i+1 S=S + i
当型结构
i<100? 是
否
i=i+1
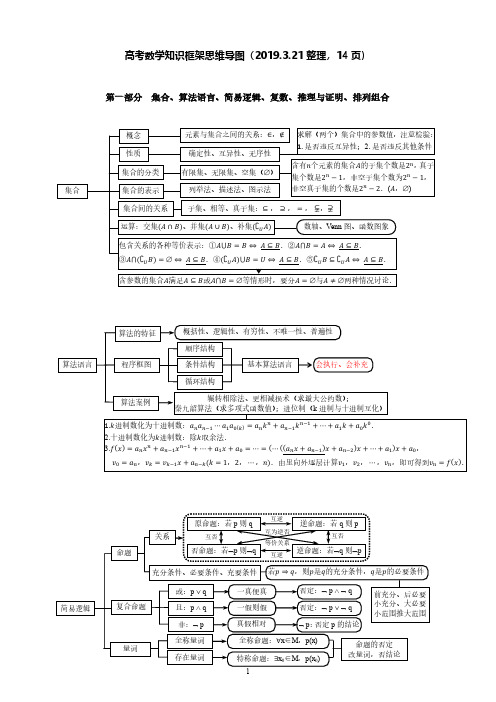
高中数学知识框架思维导图
i.
①(1 ± i)2 = ±2i;
②1+i = i;1−i = −i;
1−i
1+i
③������ + ������i = i(������ − ������i),
如3+4i = i(4−3i) = i;
4−3i 4−� = ������ + ������i、复平面内点 Z(������, ������)、向量���⃗⃗���⃗⃗���⃗��� = (������, ������)的一一对应关系; 复数模的几何意义:|������| = |������ + ������i| = √������2 + ������2 = |���⃗⃗���⃗⃗���⃗���|
2.对数的运算性质(������>0,且������ ≠1,������>0,������>0):①log������(������ ∙ ������) = log������������ + log������������;
简易逻辑
命题
关系
原命题:若 p 则 q
互否
否命题:若p 则q
互逆
互为逆否 等价关系
互逆
逆命题:若 q 则 p
互否
逆命题:若q 则p
充分条件、必要条件、充要条件 若������ ⇒ ������,则������是������的充分条件,������是������的必要条件
复合命题 量词
或:p q 且:p q 非: p 全称量词 存在量词
2
映射
函数
函数图象 及其变换
第二部分 函数、导数及微积分
������: ������ → ������:一对一,或多对一
高中数学知识结构框图(人教版)

高中数学知识结构框图(人教版)高中数学知识结构框图(必修1)第一章集合与函数概念第二章基本初等函数(Ⅰ)数学二第一章空间几何体的知识结构框架第二章点、直线、平面之间的位置关系的知识结构框架第三章直线与方程的知识结构框架第四章圆与方程的知识结构框架数学三数学四本章知识结构如下:本章知识结构如下:本章知识结构如下:英语(课程)书信的常见写作模板开头部分:How nice to hear from you again. Let me tell you something about the activity. I’m glad to have received your letter of Apr. 9th. I’m pleased to hear that you’re coming to China for a visit. I’m writing to thank yo u for your help during my stay in America.结尾部分:With best wishes. I’m looking forward to your reply. I’d appreciate it if you could reply earlier.口头通知常见写作模板开场白部分:Ladies and gentlemen, May I have your attention, please? I have an announcement to make.正文部分:All the teachers and students are required to attend it. Please take your notebooks and make notes. Please listen carefully and we’ll have a discussion in groups. Please come on time and don’t be late.结束语部分:Please come and join in it. Everybody is welcome to attend it. I hope you’ll have a nice time here. That’s all. Thank you.议论文模板1.正反观点式议论文模板:导入:第1段:Recently we’ve had a discussion about whether we should... (导入话题) Our opinions are divided on this topic.(观点有分歧) 正文:第2段:Most of the students are in favour of it.(正方观点) Here are the reasons. First... Second... Finally...(列出2~3个赞成的理由) 第3段:However, the others are strongly against it. (反方观点) Their reasons are as follows. In the first place... What’s more... In addition...(列出2~3个反对的理由) 结论:第4段:Personally speaking, the advantages overweigh the disadvantages, for it will do us more harm than good, so I support it.(个人观点)2.“A或者B”类议论文模板:导入:第1段:Some people hold the opinion that A is superior to B in many ways. Others, however, argue that B is much better. Personally, I would prefer A because I think A has more advantages. 正文:第2段:There are many reasons why I prefer A. The main reason is that ... Another reason is that...(赞同A 的原因) 第3段: Of course, B also has advantages to some extent... (列出1~2个B的优势) 结论:第4段: But if all these factors are considered, A is much better than B. From what has been discussed above, we may finally draw the conclusion that ...(得出结论)3.观点论述类议论文模板:导入:第1段:提出一种现象或某个决定作为议论的话题 As a student, I am strongly in favour of the decision. (亮明自己的观点是赞成还是反对) The reasons for this may be listed as follows. (过渡句,承上启下) 正文:第2段:First of all... Secondly... Besides...(列出2~3个赞成或反对的理由) 结论:第3段:In conclusion, I believe that... (照应第1段,构成"总—分—总"结构)4."How to"类议论文模板:导入:第1段:提出一种现象或某种困难作为议论的话题正文:第2段: Many ways can help to solve this serious problem, but the following may be most effective. First of all... Another way to solve the problem is ... Finally...(列出2~3个解决此类问题的办法) 结论:第3段:These are not the best but the only two/ three measures we can take. But it should be noted that we should take action to...(强调解决此类问题的根本方法)图表作文写作模板The chart gives us an overall picture of the 图表主题.The first thing we notice is that 图表最大特点 .This means that as 进一步说明.We can see from the statistics given that 图表细节图表细节一 . After 动词-ing :细节一中的第一个变化, the动词-ed+幅度+时间(紧跟着的变化) .The figures also tell us that图表细节二 .In the column, we can see that accounts for (进一步描述).Judging from these figures, we can draw the conclusion that (结论).The reason for this, as far as I am concerned is that (给出原因). b或是It is high time that we (发出倡议).图画类写作模板1.开头Look at this picture./The picture shows that.../From this picture, we can see.../As is shown in the picture.../As is seen in the picture...2.衔接句 As we all know, .../As is known to all,.../It is well known that.../In my opinion,.../As far as I am concerned,.../This sight reminds me of something in my daily life.3.结尾句 In conclusion.../In brief.../On the whole.../In short.../In aword.../Generally speaking.../As has been stated..一、有关语言修辞的题型描绘类提问方式:某句话中某个词换成另一个行吗?为什么?或:文章的某个句子说成另一个句子好不好?为什么?答题模式:不行。
高中数学第四章框图4.1流程图同步课件新人教B版

解答
反思与感悟
要画工序流程图,首先要弄清整项工程应划分为多少道
工序;其次是仔细考虑各道工序之间的先后顺序及相互联系、制约的 程度;最后要考虑哪些工序可以平行进行,哪些工序可以交叉进行.总 之,画工序流程图,应统筹兼顾,符合逻辑上的先后顺序,这样在照 图执行时才能减少、甚至杜绝“窝工”现象的发生.
跟踪训练3
外一些工作或工序可以穿插进行.
(3)根据各工作或各工序所需要的工时进行统筹安排.
(4)开始时流程图可以画得粗疏,然后再对每一环节进行逐步细化.
识程序框图,了解工序流程图. 2.能绘制简单实际问题的流程图,体会流程图在解决问题中的 作用.
内容索引
问题导学
题型探究
达标检测
问题导学
知识点一
流程图
思考 在流程图中,基本元素之间用什么线连接? 答案 用流程线连接.
梳理 流程图 (1)构成元素: 图形符号 , 文字说明 ,流程线. (2)起点与终点:通常会有 一个 “起点”, 一个或多个 “终点”. (3)顺序:从 左 到右,从上到 下 . (4)常见的流程图:程序框图和 工序流程图 . (5)优点:流程图可以 直观 、明确地表示动态过程从 开始 到 结束 的全 部步骤,在日常生活和工作的很多领域都得到广泛应用.
机床的大修有如下的工作项目:拆卸清洗、部件检查、零
件加工、零件修理、床身和工作台研合、部件组装 (不含电器)、变速器 组装、试车.试画出其工序流程图. 解 工序流程图如图所示.
解答
达标检测
1.要描述一个工厂某种产品的生产步骤,应用 A.程序框图 C.知识结构图
B.工序流程图 √ D.组织结构图
解析 工序流程图是描述产品生产工序的框图.
知识点二
高中数学(必修5)知识结构框图
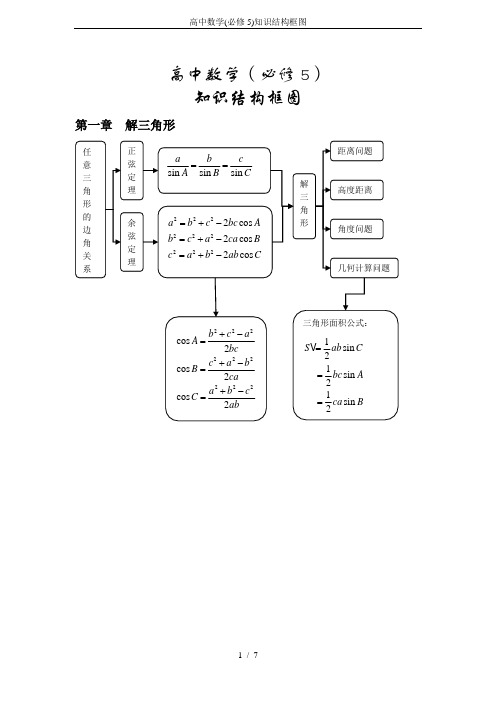
高中数学(必修5) 知识结构框图第一章 解三角形1sin 21sin 2S ab bc == 第二章数列第三章不等式¤例题精讲:【例1】在四棱锥的四个侧面中,直角三角形最多可有( ).A. 1个B. 2个C. 3个D. 4个 选D. 【例2】已知球的外切圆台上、下底面的半径分别为,r R ,求球的半径.解:圆台轴截面为等腰梯形,与球的大圆相切,由此得梯形腰长为R +r ,梯形的高即球的直径为=.第4讲 §1.2.3 空间几何体的直观图¤知识要点:“直观图”最常用的画法是斜二测画法,由其规则能画出水平放置的直观图,其实质就是在坐标系中确定点的位置的画法. 基本步骤如下:(1) 建系:在已知图形中取互相垂直的x 轴和y 轴,得到直角坐标系xoy ,直观图中画成斜坐标系'''x o y ,两轴夹角为45︒.(2)平行不变:已知图形中平行于x 轴或y 轴的线段,在直观图中分别画成平行于x ’或y ’轴的线段.(3)长度规则:已知图形中平行于x 轴的线段,在直观图中保持长度不变;平行于y 轴的线段,长度为原来的一半.第5讲 §1.3.1 柱体、锥体、台体的表面积¤学习目标:了解棱柱、棱锥、台的表面积的计算公式(不要求记忆公式);能运用柱、锥、台的表面积进c 直截面周长h 高S h 底高2. 当台体的上底面逐渐扩展到与下底面全等时,它就成了柱体. 因而体积会有以下的关系:13V S h =锥 '0S =←−−− 1(')3V S S h =台 'S S=−−−→ V S h =柱. 第7讲 §1.3.2球的体积和表面积¤知识要点:1. 表面积:24S R π=球面 (R :球的半径). 2. 体积:343V R π=球面. 第8讲 §2.1.1 平面¤知识要点:1. 点A 在直线上,记作A a ∈;点A 在平面α内,记作A α∈;直线a 在平面α内,记作a α⊂.ll β=∈推论1 经过一条直线和这条直线外的一点,有且只有一个平面; 推论2 经过两条相交直线,有且只有一个平面; 推论3 经过两条平行直线,有且只有一个平面. 第9讲 §2.1.2 空间中直线与直线之间的位置关系¤知识要点:1.空间两条直线的位置关系:⎧⎧⎪⎨⎨⎩⎪⎩相交直线:同一平面内,有且只有一个公共点;共面直线平行直线:同一平面内,没有公共点;异面直线:不同在任何一个平面内,没有公共点.2. 已知两条异面直线,a b ,经过空间任一点O 作直线//,//a a b b '',把,a b ''所成的锐角(或直角)叫异面直线,a b 所成的角(或夹角). ,a b ''所成的角的大小与点O 的选择无关,为了简便,点O 通常取在异面直线的一条上;异面直线所成的角的范围为(0,90]︒,如果两条异面直线所成的角是直角,则叫两条异面直线垂直,记作a b ⊥. 求两条异面直线所成角的步骤可以归纳为四步:选点→平移→定角→计算.第19讲 §3.1.2 两条直线平行与垂直的判定¤知识要点:1. 对于两条不重合的直线1l 、2l ,其斜率分别为1k 、2k ,有:(1)12//l l ⇔12k k =;(2)12l l ⊥⇔121k k ⋅=-.2. 特例:两条直线中一条斜率不存在时,另一条斜率也不存在时,则它们平行,都垂直于x 轴;….第20讲 §3.2.1 直线的点斜式方程¤知识要点:1. 点斜式:直线l 过点000(,)P x y ,且斜率为k ,其方程为00()y y k x x -=-.2. 斜截式:直线l 的斜率为k ,在y 轴上截距为b ,其方程为y kx b =+.3. 点斜式和斜截式不能表示垂直x 轴直线. 若直线l 过点000(,)P x y 且与x 轴垂直,此时它的倾斜角为90°,斜率不存在,它的方程不能用点斜式表示,这时的直线方程为00x x -=,或0x x =.4. 注意:y y k x x -=-与00()y y k x x -=-是不同的方程,前者表示的直线上缺少一点000(,)P x y ,后者才是整条直线.第21讲 §3.2.2 直线的两点式方程¤知识要点:1. 两点式:直线l 经过两点111222(,),(,)P x y P x y ,其方程为112121y y x x y y x x --=--, 2. 截距式:直线l 在x 、y 轴上的截距分别为a 、b ,其方程为1x ya b+=.3. 两点式不能表示垂直x 、y 轴直线;截距式不能表示垂直x 、y 轴及过原点的直线.4. 线段12P P 中点坐标公式1212(,)22x x y y ++. 第22讲 §3.2.3 直线的一般式方程¤知识要点:1. 一般式:0Ax By C ++=,注意A 、B 不同时为0. 直线一般式方程0(0)Ax By C B ++=≠化为斜截式方程A Cy x B B=--,表示斜率为A B -,y 轴上截距为C B -的直线.2 与直线:0l Ax By C ++=平行的直线,可设所求方程为'0Ax By C ++=;与直线0Ax By C ++=垂直的直线,可设所求方程为'0Bx Ay C -+=. 过点00(,)P x y 的直线可写为00()()0A x x B y y -+-=.经过点0M ,且平行于直线l 的直线方程是00()()0A x x B y y -+-=; 经过点0M ,且垂直于直线l 的直线方程是00()()0B x x A y y ---=.3. 已知直线12,l l 的方程分别是:1111:0l A x B y C ++=(11,A B 不同时为0),2222:0l A x B y C ++=(22,A B 不同时为0),则两条直线的位置关系可以如下判别: (1)1212120l l A A B B ⊥⇔+=; (2)1212211221//0,0l l A B A B AC A B ⇔-=-≠; (3)1l 与2l 重合122112210,0A B A B AC A B ⇔-=-=; (4)1l 与2l 相交12210A B A B ⇔-≠. 如果2220A B C ≠时,则11112222//A B C l l A B C ⇔=≠;1l 与2l 重合111222A B CA B C ⇔==;1l 与2l 相交1122A B A B ⇔≠. 第23讲 §3.3.1 两条直线的交点坐标¤知识要点:1. 一般地,将两条直线的方程联立,得到二元一次方程组1112220A x B y C A x B y C ++=⎧⎨++=⎩. 若方程组有惟一解,则两条直线相交,此解就是交点的坐标;若方程组无解,则两条直线无公共点,此时两条直线平行;若方程组有无数解,则两条直线有无数个公共点,此时两条直线重合.2. 方程111222()()0A x B y C A x B y C λ+++++=为直线系,所有的直线恒过一个定点,其定点就是1110A x B y C ++=与2220A x B y C ++=的交点.第24讲 §3.3.2 两点间的距离两点111(,)P x y ,222(,)P x y ,则两点间的距离为:.特别地,当12,P P 所在直线与x 轴平行时,1212||||PP x x =-;当12,PP 所在直线与y 轴平行时,1212||||PP y y =-;当12,PP 在直线y kx b =+上时,1212|||PP x x -. 2. 坐标法解决问题的基本步骤是:(1)建立坐标系,用坐标表示有关量;(2)进行有关代数运算;(3)把代数运算的结果“翻译”成几何关系.第25讲 §3.3.3 点到直线的距离及两平行线距离¤知识要点:1. 点00(,)P x y 到直线:0l Ax By C ++=的距离公式为d .2. 利用点到直线的距离公式,可以推导出两条平行直线11:0l Ax By C ++=,22:0l Ax By C ++=之间的距离公式d =,推导过程为:在直线2l 上任取一点00(,)P x y ,则0020A x B y C ++=,即002A x B y C +=-. 这时点00(,)P x y 到直线11:0l Ax By C ++=的距离为d ==第26讲 第4章 §4.1.1 圆的标准方程¤知识要点:1. 圆的标准方程:方程222()()(0)x a y b r r -+-=>表示圆心为A (a ,b ),半径长为r 的圆.2. 求圆的标准方程的常用方法:(1)几何法:根据题意,求出圆心坐标与半径,然后写出标准方程;(2)待定系数法:先根据条件列出关于a 、b 、r 的方程组,然后解出a 、b 、r ,再代入标准方程.第27讲 §4.1.2 圆的一般方程¤知识要点:1. 圆的一般方程:方程220x y Dx Ey F ++++= (2240D E F +->)表示圆心是(,)22D E --的圆. 2. 轨迹方程是指点动点M 的坐标(,)x y 满足的关系式.第28讲 §4.2.1 直线与圆的位置关系¤知识要点:1. 直线与圆的位置关系及其判定: 方法一:方程组思想,由直线与圆的方程组成的方程组,消去x 或(y ),化为一元二次方程,由判别式符号进行判别;方法二:利用圆心(,a b )到直线0Ax By C ++=的距离d =,比较d 与r 的大小.(1)相交d r ⇔<⇔ 0∆>;(2)相切d r ⇔=⇔0∆=;(3)相离d r ⇔>⇔0∆<.2. 直线与圆的相切研究,是高考考查的重要内容. 同时,我们要熟记直线与圆的各种方程、几何性质,也要掌握一些常用公式,例如点线距离公式d =第29讲 §4.2.2 圆与圆的位置关系¤知识要点:两圆的位置关系及其判定: 设两圆圆心分别为12,O O ,半径分别为12,r r ,则: (1)两圆相交121212||||r r O O r r ⇔-<<+;(2)两圆外切1212||O O r r ⇔=+;(3)两圆内切1212||||O O r r ⇔=-;第30讲 §4.2.3 直线与圆的方程的应用¤知识要点:坐标法:建立适当的直角坐标系后,借助代数方法把要研究的几何问题,转化为坐标之间的运算,由此解决几何问题。
高中数学教你画程序框图

高中数学教你画程序框图程序框图(又叫流程图)是算法的一种表示形式,具有直观形象、结构清晰和简洁明了的效果,但难点是怎样才能熟练而准确地画出程序框图,为此教你“抓特征,明规则,依步骤”九字诀,让你即可拥有画程序框图的基本功.一、抓特征组成任何一个程序框图的三要素是“四框”、“一线”加“文字说明”,所以首先要抓住它们各自的特征与意义.“四框”的特征与意义:①终端框(起止框)的特征是圆角矩形,表示算法的开始和结束,是任何流程不可缺少的;②输入、输出框的特征是平行四边形,表示算法中输入和输出的信息,可放在任何需输入、输出的位置;③处理框(执行框)的特征是方角矩形,表示赋值和计算等,算法中要处理的数据或计算可分别写在不同的处理框内;④判断框的特征是菱形,用在当算法要求对两个不同的结果进行判断时.“一线”的特征与意义:流程线的特征是带有方向箭头的线,用以连接程序框,直观地表示算法的流程,任意两个程序框之间都存在流程线.“文字”的特征与意义:在框图内加以说明的文字、算式等,也是每个框图不可缺少的内容.二、明规则程序框图的画法规则是:①用标准,即使用标准的框图符号;②按顺序,即框图一般从上到下、从左到右的顺序画;③看出入,即大多数程序框图的图形符号只有一个入口和一个出口,判断框是唯一具有超过一个出口的符号,条件结构中要在出口处标明“是”或“否”;④明循环,即循环结构要注意变量的初始值及循环终止条件;⑤辨流向,即流程线的箭头表示执行的方向,不可缺少;⑥简说明,即在图形符号内的描述语言要简练清晰.三、依步骤画程序框图的总体步骤是:第一步,先设计算法,因为算法的设计是画程序框图的基础,所以在画程序框图前,首先写出相应的算法步骤,并分析算法需要哪种基本逻辑结构(顺序结构、条件结构、循环结构);第二步,再把算法步骤转化为对应的程序框图,在这种转化过程中往往需要考虑很多细节,是一个将算法“细化”的过程. 具体画法步骤请看例题.例1 某商场进行优惠促销:若购物金额x 在500元以上,打8折;若购物金额x 在300元以上,打9折;否则,不打折. 设计算法的程序框图,要求输入购物金额x ,即能输出实际交款额.算法分析:由题意,实际交款额y 与购物金额x 之间的函数关系是⎪⎩⎪⎨⎧=,8.0,9.0,x x x y500500300300>≤<≤x x x ,因为它需对x 进行三次判断,所以算法含有两个条件结构,写出算法步骤如下:第一步,输入购物金额x .第二步,判断300≤x 吗?若是,则x y =;否则,进入第三步.第三步,判断500≤x 吗?若是,则x y 9.0=;否则,x y 8.0=.第四步,输出y ,结束算法.画法步骤:①画顺序结构图,即起止框及输入框,并用流程线连接(如图①);②画条件结构图,即画判断框并判断300≤x ?若是,则画处理框并填入②);“x y =”,否则流向下一个判断框(如图③再画条件结构图,即画判断框并判断500≤x ?若是, 则画处理框(如“x y 9.0=”,否则画处理框“x y 8.0=”以及图③);④画一个总的输出框并输出y ,起止框表示算法结束(如图④).最后,合成整个算法程序框图如图1. 点评:画程序框图的关键是分析算法步骤,因为程序框图是算法步骤的图形表示,所以算法步骤越明确画图就越容易;另外,如分段函数这种需要对条件进行判断的算法设计中,宜使用条件结构.例2 若2008531>++++n ,试设计算法的程序框图,寻找满足条件的最小奇数n .算法分析:因为涉及类加问题,所以算法含有循环结构,写出直到型循环结构的算法步骤如下:第一步,令1,0==i S .第二步,计算i S S +=,2+=i i .第三步,判断2008>S 吗?若是,则输出2-n ,结束算法;否则,返回第二步.画法步骤:①画顺序结构图,即起止框及两个处理框,并分别填入循环初始条件(如图①);②画循环结构图,先画循环体即两个处理框(一个累加,一个计数),再画循环终止条件,即判断框并判断2008>S ?若是,则输出2-n ,否则,流向循环体之前进行再循环(如图②);③画输出框输出2-n ,以及起止框表示算法结束(如图③).最后,合成整个算法程序框图如图2.点评:循环结构必包含顺序结构和条件结构,所以本题具有一定的典型性和示范性;如累加、类乘等需要反复执行的算法设计中,宜使用循环结构,这时要密切注意“循环体”、“循环变量”和“循环终止条件”三个重要组成部分的框图设计.程序框图错误面面观程序框图中若有一处错误,就可能导致执行后的结果出错。
高中数学知识点框图
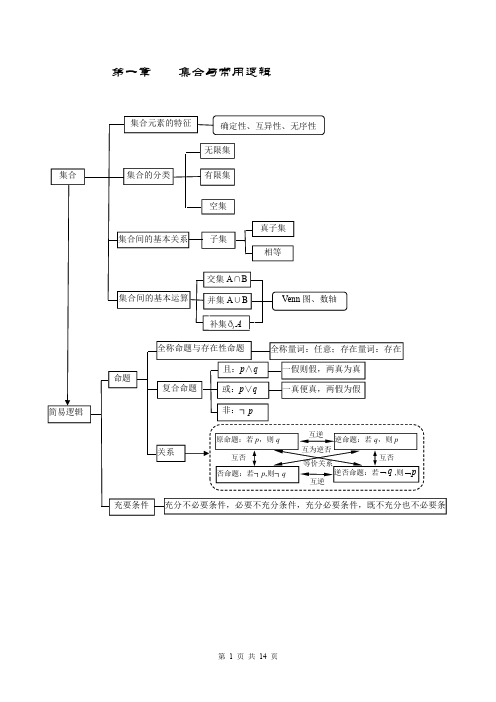
相交 平行
平行 相交
只有一个公共点 没有公共点 没有公共点
有公共点
平行关系的 相互转化
线线 平行
线面 平行
面面 平行
空间直角坐标系
垂直关系的 相互转化
线线 垂直
线面 垂直
面面 垂直
空间的角 空间的距离
异面直线所成的角 直线与平面所成的角 二面角
点到面的距离 直线与平面的距离 平行平面之间的距离
第九章 直线与圆的方程
本章知识结构图
倾斜角和斜率
k
tan
y2 x2
y1 x1
,
0,
2
2
,
,当
=
2
时,k不存在
直线的方程
位置关系
重合 平行
A1B2-A2B1=0
截距
相交
A1B2-A2B1≠0
注意:截距可正、可负,也可为 0.
点斜式:y-y0=k(x-x0) 斜截式:y=kx+b
②图象也可以用五点作图法;③用整体代换求单调区间(注意的符号);
④最小正周期
T= |
2 ;⑤对称轴 |
x=(2k+1)-2,对称中心为(k-,b)(k∈Z).
2
解三角形
正弦定理 余弦定理
面积
实际应用
解的个数的讨论 三角形形状的判定
S△=1ah=1absinC= p(p-a)(p-b)(p-c)(其中 p=a+b+c)
逐差累加法 逐商累积法 构造等比数列{an+ q }
p-1
④pan+1an=an-an+1
构造等差数列
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
框图
教学目的:巩固本章节学习的内容,提高学生解决问题的能力
教学过程:
1、.结构图一般由构成系统的和表达各要素之间构成.连线通常按照、的方向(方向箭头按照箭头所指的方向)表示要素的或
2.在表达逻辑先后关系的结构图中从上至下反映的是要素之间的,从属关系通常是“”形结构,然而有时也经常出现一些“”形结构.在组织结构图中一般都呈“”形结构,这种图直观,易于理解.被应用很多领域.
【例1 :某班有 50 名学生,现将某科的成绩分为三个等级, 80 一 100 分为 A , 60 一79 分为 B , 60 分以下为 C ,试设计一程序框图来表示输出每一个学生成绩等级.解析:学生成绩的三个等级由是否小于等于 60 分的和是否小于等于 79 分这两个条件控制,因此可以将其分为两部分来设计框图,即判断框的选择问题,还应注意将全部学生的相应成绩等级全部显示.答案:依题意设计以下程序框图:
启示:该题也可以先用判断条件“是否小于等于 79 分”先行判断,再根据“是否小于等于 60 分”,从而将成绩分成三个等级.
【例 2 ]某工厂加工某种零件有三道工序:粗加工、返修加工和精加工.每道工序完成时,都要对产品进行检验.粗加工的合格品进人精加工,不合格品进人返修加工;返修加工的合格品进人精加工,不合格品作为废品处理;精加工的合格品为成品,不合格品为废品. ( 1 )用流程图表示这个零件的加工过程. ( 2 )一件成品在哪几个环节可导致废品产生.解析:( l )本题是一个工序流程图,分为三道工序:粗加工、返修加工和精加工,在每道工序完成时须检
验,即有一个判断环节. ( 2 )导致废品出现的环节在于检验工序,即判断是否合格.答案:( l )按照工序要求,可以画出下面的工序流程图:
( 2 )产品在返修加工和精加工可导致废品,这两道工序检验不合格则即成废品.而粗加工检验环节,若不合格则可以返修加工.启示:工序流程图是描述工农业生产过程的流程图,是一个动态过程,其中有时常见判断、循环等环节,依具体问题加以分析,主要线索是生产的工序.本题中废品的产生在于返修加工和精加工.最初的粗加工检验,若不合格则加以返
修加工,经再检验合格则进入下道工序,不合格才成为废品,应加以明确,这也是符合生产实际情况的.
【例 3 ]对于《数学·必修 3 ) )第一章《算法初步》,画出本章知识结构图.解析:对于《算法初步》这一章来讲,主要有算法与程序框图、基本算法语句和中国古代算法案例三部分,分部分又可再细分,大致可以将本章知识分块加以解决.答案:
启示:知识结构图可采用“树”形或“环”形结构,反映各要素间的逻辑先后关系或从属关系一般是从上到下.从左到右顺序画图.本题知识结构图采用从左向右的方向画出,当然出可采用其他方向,或对某部分再加以细分.
强化练习:1、北京获得2008 年第 29 届奥林匹克运动会主办权.国际奥委会是通过对遴选出的 5 个申办城市进行表决而决定主办权的.表决的操作程序是:首先进行第一轮投票,如果一个城市得票超过总票数的一半.那么该城市将获得举办权;如果所有申办城市得票数都不超过总票数的一半,则将得票最少的城市淘汰,然后重复上述过程,直到选出一个中办城市为止.请设计一个算法表述上述过程,并画出程序流程图.
2、某大学远程教育学院网上学习流程: ( 1 )学生凭录取通知书到当地远程教育中心报到.交费注册.领取网上学习注册码,
( 2 )网上选课,课程学习.完成网上平时作业.获得平时作业成绩.
( 3 )预约考试,参加期末考试获得期末考试成绩,获得综合成绩,成绩合格获得学分,否则重修.
试画出该远程教育学院网上学习流程图.
3、对于《数学·必修II》中的“圆与方程”这一章.试画出本章知识结构图.。
