第一章 矢量分析重点内容总结资料
合集下载
第1章 矢量分析53050
ax ay az Ax Ay Az
Bx By Bz
2020/7/30
2 圆柱坐标系和球坐标系
2.1 圆柱坐标系 空间任一点P的位置可以用圆柱坐标系中的三个变量(ρ, φ, z)来表示，
如下图示。 其中，ρ是位置矢量OP在xy面上的投影， φ是从+x轴到
位置矢量OP在xy面上的投影之间的夹角，z是OP在z轴上的投影。
aρ×aρ=aφ×aφ=az×az= 0 aρ·aφ=aφ·az=aρ·az=0 aρ·aρ=aφ·aφ=az·az=1
z
z
az
r P(, , z)
O
y a
x
a
圆柱坐标系的位置矢量r可以表示为
r=aρρ+azz
2020/7/30
O
x
y
aycos
a
－axs in
a xcos
ays in
a
2020/7/30
由图可以看出，圆柱坐标与直角坐标之间的关系为 x=ρcosφ y=ρsinφ z=z
如同直角坐标系一样， 圆柱坐标系也具有三个相互垂直的坐标面，
2020/7/30
z
z
az
r P(, , z)
O
x
y a
a
圆柱坐标系一点的投影
z z＝ 常 数
＝ 常 数
O
y ＝ 常 数
x
圆柱坐标系三个互相垂直的坐标
2020/7/30
圆柱坐标系单位矢量的变换
圆柱坐标系中的单位矢量aρ和aφ在单位矢量ax和ay上的投影示.显然 aρ=ax cosφ+ay sinφ aφ=ax(-sinφ)+ay cosφ
所以，直角坐标系中的单位矢量变换到圆柱坐标系中的单位矢量的 表达式写成矩阵形式为
Bx By Bz
2020/7/30
2 圆柱坐标系和球坐标系
2.1 圆柱坐标系 空间任一点P的位置可以用圆柱坐标系中的三个变量(ρ, φ, z)来表示，
如下图示。 其中，ρ是位置矢量OP在xy面上的投影， φ是从+x轴到
位置矢量OP在xy面上的投影之间的夹角，z是OP在z轴上的投影。
aρ×aρ=aφ×aφ=az×az= 0 aρ·aφ=aφ·az=aρ·az=0 aρ·aρ=aφ·aφ=az·az=1
z
z
az
r P(, , z)
O
y a
x
a
圆柱坐标系的位置矢量r可以表示为
r=aρρ+azz
2020/7/30
O
x
y
aycos
a
－axs in
a xcos
ays in
a
2020/7/30
由图可以看出，圆柱坐标与直角坐标之间的关系为 x=ρcosφ y=ρsinφ z=z
如同直角坐标系一样， 圆柱坐标系也具有三个相互垂直的坐标面，
2020/7/30
z
z
az
r P(, , z)
O
x
y a
a
圆柱坐标系一点的投影
z z＝ 常 数
＝ 常 数
O
y ＝ 常 数
x
圆柱坐标系三个互相垂直的坐标
2020/7/30
圆柱坐标系单位矢量的变换
圆柱坐标系中的单位矢量aρ和aφ在单位矢量ax和ay上的投影示.显然 aρ=ax cosφ+ay sinφ aφ=ax(-sinφ)+ay cosφ
所以，直角坐标系中的单位矢量变换到圆柱坐标系中的单位矢量的 表达式写成矩阵形式为
《电磁场与电磁波》第一章 矢量分析
ey Ay By
ez Az Bz
显然，矢量的矢积不满足交换律。 两个矢量的矢积仍是矢量。
矢积的几何意义 设 则
A A ex
B Bxex By ey
z
A B y B
A B ez A B sin
A
可见，矢积A×B的方向与矢量A及 矢量B构成的平面垂直，由A旋转到B成 右手螺旋关系；大小为 A B sin 。
S
E dS
0
可见，当闭合面中存在正电荷时，通量为正。当闭合面中存在负电 荷时，通量为负。在电荷不存在的无源区中，穿过任一闭合面的通 量为零。
㊀
㊉
二、散度(divergence)
通量仅能表示闭合面中源的总量，不能显示源的分布特性。为 此需要研究矢量场的散度。
如果包围点P的闭合面S所围区域V以任意方式缩小为点P 时, 矢量A通过 该闭合面的通量与该闭合面包围的体积之比的极限称为矢量场A在该点的散度， 以divA表示，即
结合律： ( A B) C A ( B C )
标量乘矢量：
A Ax ex Ay e y Az ez
§1-3 矢量的标积和矢积
一、矢量的标积
A Axex Ay e y Az ez
矢量A与矢量B的标积定义为：
B Bxex By ey Bz ez
则： A A ea ex A cos ey A cos ez A cos 标积的几何意义
y B
设 其中
A A ex
B Bxex By ey
Bx B cos By B cos( ) B sin 2
A
x
所以
A B A B cos
大学物理 第一章 矢量分析资料
电磁场与电磁波
第1章 矢量分析
17
1.3 标量场的梯度
标量场和矢量场 确定空间区域上的每一点都有确定物理量与之对应，称在
该区域上定义了一个场。
如果物理量是标量，称该场为标量场。
例如：温度场、电位场、高度场等。
如果物理量是矢量，称该场为矢量场。
例如：流速场、重力场、电场、磁场等。
如果场与时间无关，称为静态场，反之为时变场。 从数学上看，场是定义在空间区域上的函数：
eφ dz
er
y
φ dφ
电磁场与电磁波
第1章 矢量分析
14
电磁场与电磁波
第1章 矢量分析
15
球坐标系
rsinθdφ rsinθdφ z rdθ
θ
er
rdθ
dr
eφ
dL
dr eθ
r
θ
dr
rdθ
y
rsinθdφ
o
x
φ dφ
rsinθdφ
电磁场与电磁波
第1章 矢量分析
16
4. 坐标单位矢量之间的关系
电磁场与电磁波
第1章 矢量分析
10
电磁场与电磁波
第1章 矢量分析
11
直角坐标系
dx dy
ez
z
dx
dL
dz
dy dz ex
y
dx dz ey
dy
o
x
电磁场与电磁波
第1章 矢量分析
12
电磁场与电磁波
第1章 矢量分析
13
圆柱坐标系
p pdφ dL dy o
x
pdφ dr
ezzdz来自dr dzpdφ电磁场与电磁波
第01章 矢量分析
( A B )C A (B C )
矢量，标量与矢量相乘。
标量，标量三重积。
矢量，矢量三重积。
A (B C )
a. 标量三重积 法则：在矢量运算中,先算叉积,后算点积。
（ 定义：B C） A | A || B || C | sin cos
•矢量与矢量的乘积
a
•标量积（数量积、内积、点积）
a b | a | | b | co s
b
a
两矢量点积的含义： 一矢量在另一矢量方向上的投影与另一矢量模的乘 积，其结果是一标量。 推论1：满足交换 律 推论2：满足分配律
a b b a a (b c ) a b a c
( x, y, z )
5 ( x 1) ( y 2 ) z
2 2 2
标量场
如温度场、电位场、势场…
2 2 F ( x , y , z ) 2 xy e x x z e y xy z e z
矢量场
如速度场、电场、磁场…
1.1.3、矢量的运算法则
（1）加法: 矢量加法是矢量的几何和,服从平行四边形法则。
Ay A B By
Az Ax ex Bz Bx
Ax Az ey Bx Bz
Ay ez By
设( A B ) C xe x ye y ze z
x
Ax Bx
Az Bz
cx
Ax Bx
Ay By
cy
见课本P6
例： 设
r1 2 e x e y e z , r2 e x 3 e y 2 e z r3 2 e x e y 3 e z , r4 3 e x 2 e y 5 e z
矢量，标量与矢量相乘。
标量，标量三重积。
矢量，矢量三重积。
A (B C )
a. 标量三重积 法则：在矢量运算中,先算叉积,后算点积。
（ 定义：B C） A | A || B || C | sin cos
•矢量与矢量的乘积
a
•标量积（数量积、内积、点积）
a b | a | | b | co s
b
a
两矢量点积的含义： 一矢量在另一矢量方向上的投影与另一矢量模的乘 积，其结果是一标量。 推论1：满足交换 律 推论2：满足分配律
a b b a a (b c ) a b a c
( x, y, z )
5 ( x 1) ( y 2 ) z
2 2 2
标量场
如温度场、电位场、势场…
2 2 F ( x , y , z ) 2 xy e x x z e y xy z e z
矢量场
如速度场、电场、磁场…
1.1.3、矢量的运算法则
（1）加法: 矢量加法是矢量的几何和,服从平行四边形法则。
Ay A B By
Az Ax ex Bz Bx
Ax Az ey Bx Bz
Ay ez By
设( A B ) C xe x ye y ze z
x
Ax Bx
Az Bz
cx
Ax Bx
Ay By
cy
见课本P6
例： 设
r1 2 e x e y e z , r2 e x 3 e y 2 e z r3 2 e x e y 3 e z , r4 3 e x 2 e y 5 e z
第1章 矢量分析
第一章 矢量分析
矢量的直角坐标分量表示
r v v v A= A ex + A ey + A ez x y z
s A = Aco α x s A = Aco β y A = Aco γ s z
2 A = Ax2 + Ay + Az2
z
A z
r A
A y
A x
y
r v A= A A e
x
v v v v eA = ex cosα +ey cos β +ez cosγ
r r r eρ × eφ = ez r r r eφ × e z = e ρ r r r e z × e ρ = eφ
2 2
x = ρ cos φ y = ρ sin φ z=z
ρ = x + y ， φ = y/ x tan
第一章 矢量分析
位置矢量
v r r r 线元矢量 dl = eρ dρ + eφ ρ dφ + ez dz
第一章 矢量分析
2、矢量的加减运算
v A
v B
直角坐标系下：
v v A+B
v v A− B
v −B
v A
v v A− B
v B
v v v v v v C = A + B = ( Ax + Bx )i + ( Ay + By ) j + ( Az + Bz )k
v v v v v v C = A − B = ( Ax − Bx )i + ( Ay − By ) j + ( Az − Bz )k
性质：
r B
AB sin θ
v v v v A× B = −B × A v v v v A × B = 0 ⇔ A // B
第一章 矢量分析
电磁场与电磁波
电子信息工程系 高 飞
第一章
矢量分析
主 要 内 容 梯度、散度、旋度、 梯度、散度、旋度、亥姆霍兹定理
1. 标量场的方向导数与梯度 方向导数:标量场在某点的方向导数表示标量场自该点沿某一方向 方向导数: 上的变化率。 上的变化率。 l 数 例如标量场 Φ 在 P 点沿 l 方向上的方向导
由物理得知， 由物理得知，真空中的电场强度 E 通过任一闭合曲面的通量 之比， 等于该闭合面包围的自由电荷的电量 q 与真空介电常数 ε 0 之比， 即，
∫
S
E ⋅ dS =
q
ε0
可见，当闭合面中存在正电荷时，通量为正。当闭合面中存在负电 可见，当闭合面中存在正电荷时，通量为正。 荷时，通量为负。在电荷不存在的无源区中， 荷时，通量为负。在电荷不存在的无源区中，穿过任一闭合面的通 量为零。这一电学实例充分地显示出闭合面中正源、 量为零。这一电学实例充分地显示出闭合面中正源、负源及无源的 通量特性。但是，通量仅能表示闭合面中源的总量， 通量特性。但是，通量仅能表示闭合面中源的总量，它不能显示源 分布特性 为此需要研究矢量场的散度 特性。 散度。 的分布特性。为此需要研究矢量场的散度。
∆S →0
的缩写， 式中 rot 是英文字母 rotation 的缩写，en 为最大环量强度的方向上 的单位矢量， 包围的面积。上式表明， 的单位矢量，∆S 为闭合曲线 l 包围的面积。上式表明，矢量场的 旋度大小可以认为是包围单位面积的闭合曲线上的最大环量。 旋度大小可以认为是包围单位面积的闭合曲线上的最大环量。
4. 无散场和无旋场 散度处处为零的矢量场称为无散场，旋度处处为零 散度处处为零的矢量场称为无散场，旋度处处为零的 无散场 矢量场称为无旋场。 矢量场称为无旋场。 无旋场 两个重要公式： 两个重要公式：
电子信息工程系 高 飞
第一章
矢量分析
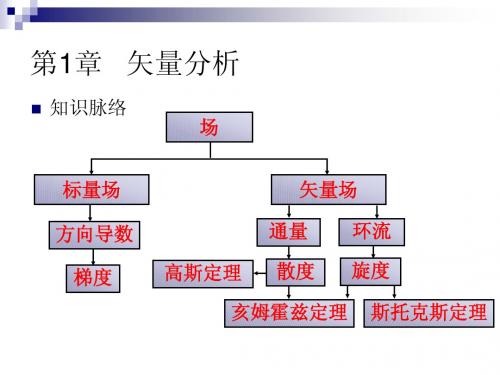
主 要 内 容 梯度、散度、旋度、 梯度、散度、旋度、亥姆霍兹定理
1. 标量场的方向导数与梯度 方向导数:标量场在某点的方向导数表示标量场自该点沿某一方向 方向导数: 上的变化率。 上的变化率。 l 数 例如标量场 Φ 在 P 点沿 l 方向上的方向导
由物理得知， 由物理得知，真空中的电场强度 E 通过任一闭合曲面的通量 之比， 等于该闭合面包围的自由电荷的电量 q 与真空介电常数 ε 0 之比， 即，
∫
S
E ⋅ dS =
q
ε0
可见，当闭合面中存在正电荷时，通量为正。当闭合面中存在负电 可见，当闭合面中存在正电荷时，通量为正。 荷时，通量为负。在电荷不存在的无源区中， 荷时，通量为负。在电荷不存在的无源区中，穿过任一闭合面的通 量为零。这一电学实例充分地显示出闭合面中正源、 量为零。这一电学实例充分地显示出闭合面中正源、负源及无源的 通量特性。但是，通量仅能表示闭合面中源的总量， 通量特性。但是，通量仅能表示闭合面中源的总量，它不能显示源 分布特性 为此需要研究矢量场的散度 特性。 散度。 的分布特性。为此需要研究矢量场的散度。
∆S →0
的缩写， 式中 rot 是英文字母 rotation 的缩写，en 为最大环量强度的方向上 的单位矢量， 包围的面积。上式表明， 的单位矢量，∆S 为闭合曲线 l 包围的面积。上式表明，矢量场的 旋度大小可以认为是包围单位面积的闭合曲线上的最大环量。 旋度大小可以认为是包围单位面积的闭合曲线上的最大环量。
4. 无散场和无旋场 散度处处为零的矢量场称为无散场，旋度处处为零 散度处处为零的矢量场称为无散场，旋度处处为零的 无散场 矢量场称为无旋场。 矢量场称为无旋场。 无旋场 两个重要公式： 两个重要公式：
矢量分析报告
对于无散场Fc, ▽·Fc=0, 但这个场的旋度不会处处为零, 根矢量恒等式▽ ·(▽ ×A)=0, 可令
第一章 矢量分析
静电场的基本方程是
(1-52) 对于各向同性的媒质, 电通量密度和电场强度的关系为
D=εE, 因而式(1-52)可改写为
假设在无限空间中有两个矢量函数F和G，它们具有相同的散 度和旋度。但这两个矢量函数不等，可令
第一章 矢量分析
由于矢量F和矢量G具有相同的散度和旋度, 根据矢量场由其 散度和旋度唯一确定, 那么矢量g应该为零矢量, 也就是矢量 F 与矢量G是同一个矢量。
因为▽·F= ▽ ·G, 所 以
同样由于▽ ×G= ▽ ×F, 所 以
拉普拉斯微分算子▽ 2的表示式为
第一章 矢量分析
例1-14 在一对相距为l的点电荷+q和-q的静电场中, 当距 r>>l离时, 其空间电位的表达式 为
求其电场强度E(r, θ, φ)。 解: 在球面坐标系中，哈密顿微分算子▽的表达式为
第一章 矢量分析
因为
第一章 矢量分析
1.6 亥姆霍兹定理
亥姆霍兹定理的简单表达是: 若矢量场F在无限空间中处处单 值，且其导数连续有界，而源分布在有限空间区域中，则矢量场 由其散度和旋度唯一确定，并且可以表示为一个标量函数的梯度 和一个矢量函数的旋度之和， 即
图 1-6 例 1-11 图
第一章 矢量分析
解: 由于在曲线l上z=0，所以dz=0。
第一章 矢量分析
例1-12 求矢量场A=x(z-y) ex+y(x-z)ey+z(y-x)ez在点 M(1，0 1)处的旋度以及沿n=2ex+6ey+3ez方向的环量面密度。
解: 矢量场A的旋度
第一章 矢量分析
静电场的基本方程是
(1-52) 对于各向同性的媒质, 电通量密度和电场强度的关系为
D=εE, 因而式(1-52)可改写为
假设在无限空间中有两个矢量函数F和G，它们具有相同的散 度和旋度。但这两个矢量函数不等，可令
第一章 矢量分析
由于矢量F和矢量G具有相同的散度和旋度, 根据矢量场由其 散度和旋度唯一确定, 那么矢量g应该为零矢量, 也就是矢量 F 与矢量G是同一个矢量。
因为▽·F= ▽ ·G, 所 以
同样由于▽ ×G= ▽ ×F, 所 以
拉普拉斯微分算子▽ 2的表示式为
第一章 矢量分析
例1-14 在一对相距为l的点电荷+q和-q的静电场中, 当距 r>>l离时, 其空间电位的表达式 为
求其电场强度E(r, θ, φ)。 解: 在球面坐标系中，哈密顿微分算子▽的表达式为
第一章 矢量分析
因为
第一章 矢量分析
1.6 亥姆霍兹定理
亥姆霍兹定理的简单表达是: 若矢量场F在无限空间中处处单 值，且其导数连续有界，而源分布在有限空间区域中，则矢量场 由其散度和旋度唯一确定，并且可以表示为一个标量函数的梯度 和一个矢量函数的旋度之和， 即
图 1-6 例 1-11 图
第一章 矢量分析
解: 由于在曲线l上z=0，所以dz=0。
第一章 矢量分析
例1-12 求矢量场A=x(z-y) ex+y(x-z)ey+z(y-x)ez在点 M(1，0 1)处的旋度以及沿n=2ex+6ey+3ez方向的环量面密度。
解: 矢量场A的旋度
最新最全的矢量分析与场论讲义(必考)
矢量分析与场论第一章 矢量分析一 内容概要1 矢量分析是场论的基础，本章主要包括以下几个主要概念：矢性函数及其极限、连续，有关导数、微分、积分等概念。
与高等数学研究过的数性函数的相应概念完全类似，可以看成是这些概念在矢量分析中的推广。
2 本章所讨论的，仅限于一个自变量的矢性函数()t A ，但在后边场论部分所涉及的矢性函数，则完全是两个或者三个自变量的多元矢性函数()y x ,A 或者()z y x ,,A ，对于这种多元矢性函数及其极限、连续、偏导数、全微分等概念，完全可以仿照本章将高等数学中的多元函数及其有关的相应概念加以推广而得出。
3 本章的重点是矢性函数及其微分法，特别要注意导矢()t 'A 的几何意义，即()t 'A 是位于()t A 的矢端曲线上的一个切向矢量，其起点在曲线上对应t 值的点处，且恒指向t 值增大的一方。
如果将自变量取为矢端曲线的弧长s ，即矢性函数成为()s A A =，则()dsd s A A ='不仅是一个恒指向s 增大一方的切向矢量，而且是一个单位切向矢量。
这一点在几何和力学上都很重要。
4 矢量()t A 保持定长的充分必要条件是()t A 与其导矢()t 'A 互相垂直。
因此单位矢量与其导矢互相垂直。
比如圆函数()j i e t t t sin cos +=为单位矢量，故有()()t t 'e e ⊥，此外又由于()()t t 1'e e =，故()()t t 1e e ⊥。
（圆函数还可以用来简化较冗长的公式，注意灵活运用）。
5 在矢性函数的积分法中，注意两个矢性函数的数量积和两个矢性函数的矢量积的分部积分法公式有所不同，分别为：dt dt ''⎰⎰⋅-⋅=⋅A B B A B Adt dt ''⎰⎰⨯+⨯=⨯A B B A B A前者与高等数学种数性函数的分部积分法公式一致，后者由两项相减变为了求和，这是因为矢量积服从于“负交换律”之故。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Bx By Bz
若
A
A
BB，则B
A
A
ห้องสมุดไป่ตู้ B
AB
若 A // B ，则 A B 0
A B
B
AB sin
A
矢量A 与B 的叉积
电磁场与电磁波
第1章 矢量分析
3
（5）矢量的混合运算
A(B C) B (C A) C (A B) —— 标量三重积
A (B C) (AC)B (A B)C
dS
en ——面积元的法向单位矢量；
面积元矢量
dψ F endS ——穿过面积元 dS 的通量；
如果曲面 S 是闭合的，则规定曲面法矢由闭合曲面内指向
外，矢量场对闭合曲面的通量是：
F dS
S
S F endS
电磁场与电磁波
第1章 矢量分析
13
通量的物理意义 矢量场通过闭合曲面通量的三种可能结果
2(x x)ex (x x)2 ( y y)2 (z z)2
2( y y)ey
2(z z)ez
R
2 (x x)2 ( y y)2 (z z)2 2 (x x)2 ( y y)2 (z z)2 R
1 R
ex
x
(1) R
ey
y
(1) R
ez
z
(1) R
0
直角坐标与 球坐标系
ex
ey
ez
er sin cos sin sin cos
e cos sin cos sin sin
e sin
cos
0
y
e
6
ey
e
ex
o
单位圆
x
直角坐标系与柱坐标系之间
坐标单位矢量的关系
z
ez
er
e
单位圆
e
o
柱坐标系与球坐标系之间
坐标单位矢量的关系
第1章 矢量分析
10
梯度的性质：
• 标量场的梯度是矢量场，它在空间某
点的方向表示该点场变化最大（增大）
的方向，其数值表示变化最大方向上
场的空间变化率。
• 标量场在某个方向上的方向导数，是
梯度在该方向上的投影。 • 标量场的梯度垂直于通过该点的等值面（或切平面）
C 0
梯度运算的基本公式：((uCu)v)
Cu u
v
(uv) uv vu
f (u) f (u)u
电磁场与电磁 波
第1章 矢量分析
11
例题：
R
ex
(
x
x)
ey
(
y
y)
ez
(
z
z)
R R
证明
(1)R R R
(2)
1 R
R R3
证明： R R (x x)2 ( y y)2 (z z)2
R R R R ex x ey y ez z 2
8
小结
1）不同的位置上，圆柱和圆球坐标轴单位矢量方向不同。
2）当矢量场的方向为圆柱面的法向或切向时，用圆柱 坐标表 示不但形式简单，而且形象，更易理解。
3）当矢量场的方向为圆球面的法向或切向时，用圆球坐标表 示不但形式简单，而且形象，更易理解。
电磁场与电磁波
第1章 矢量分析
9
1.3 标量场的梯度
1、标量场的梯度（ gradu 或 u ）
(x x)ex ( y y)ey (z z)ez
3
(x x)2 ( y y)2 (z z)2
R R3
电磁场与电磁波
第1章 矢量分析
12
1.4 矢量场的通量与散度
2、矢量场的通量
F(x, y, z)
通量的概念：ψ
dψ F dS S
S F endS
en
其中：dS endS ——面积元矢量；
电磁场与电磁波
第1章 矢量分析
1
1.1 矢量代数
（1） 矢量的标积（点积）
A B AB cos AxBx Ay By Az Bz
AB
A B 0 A// B
ex ey ey ez ez ex 0
ex ex ey ey ez ez 1
A B AB
B
A
电磁场与电磁波
第1章 矢量分析
7
4、柱坐标和球坐标系与直角坐标系的关系
柱坐标与直角坐标微分关系
e
ex sin ey cos
e
e
ex cos ey sin
e
球坐标与直角坐标微分关系
er
e
e
er
e 0
er
e
sin
e
e cos
e
er sin e cos
电磁场与电磁波
第1章 矢量分析
矢量 A与 B 的夹角
电磁场与电磁波
第1章 矢量分析
2
（2数）值矢大量小的：矢A积（B叉 积en A）Bsin 方向：右手螺旋法则
用坐标分量表示为
A B ex ( Ay Bz Az By ) ey ( Az Bx AxBz ) ez ( AxBy Ay Bx )
写成行列式形式为
ex ey ez A B Ax Ay Az
—— 矢量三重积
电磁场与电磁波
第1章 矢量分析
4
1.2 三种常用的正交坐标系
1、圆柱面坐标系
坐标变量
,, z
坐标单位矢量
e , e , ez
位置矢量
r e ez z
线元矢量
dl ed e d ezdz
面元矢量
dS
e dldlz
e ddz
dS
e dl dlz
e ddz
dSz ezdldl ez dd
球面坐标系
体积元
dV r2sindrdd
球坐标系中的线元、面元和体积元
电磁场与电磁波
第1章 矢量分析
3、坐标单位矢量之间的关系
直角坐标与
e
ex
cos
圆柱坐标系 e sin
ez
0
圆柱坐标与
er
球坐标系
e
e
e
sin cos
0
ey
sin cos
0
e
0 0 1
ez
0 0 1
ez
cos sin
体积元
dV dddz
电磁场与电磁波
第1章 矢量分析
5
2、球面坐标系
坐标变量
r ,,
坐标单位矢量 er , e , e
位置矢量 线元矢量
r err
dl erdr e rd ersind
面元矢量
dSr
er dl dl
er
r
2sin
dd
dS e dlrdl e rsindrd
dS edlrdl erdrd
| 概念：
u
en
u l
max
，其中en
u 取得最大值的方向
l
意义：描述标量场在某点的最大变化率及其变化最大的方向
梯度的表达式： 直角面坐标系 圆柱面坐标系 球面坐标系
u
ex
u x
ey
u y
ez
u z
u
e
u
e
1
u
ez
u z
u
er
u r
e
1 r
u
e
1
r sin
u
电磁场与电磁波
0
0
0
通过闭合曲面有 净的矢量线穿出
有净的矢 量线进入
进入与穿出闭合曲 面的矢量线相等
闭合曲面的通量从宏观上建立了矢量场通过闭合曲面的通 量与曲面内产生矢量场的源的关系。
电磁场与电磁波
第1章 矢量分析
14
3、矢量场的散度 F