矢量分析与场论
矢量分析与场论

A B 'dt
A B 'dt
AB
B A ' dt
B A ' dt
A B
前者与高等数学种数性函数的分部积分法公式一致, 后者由两项相减变为了求和,这是因为矢量积服积分
矢性函数的定积分概念也和数性困数的完全类似.因此,也相应地具有数 性函数定积分的基本性质。
又
cos ( sin ) sin cos 0
。
所以
e ( ) e1 ( )
容易看出,( ) 为一单位矢量,故其矢端曲线为一单位圆, e e1 ( ) 因此 又叫圆函数;与之相伴出现的 亦为单位矢 e ( ) 量,其矢端曲线亦为单位圆
第三节 矢性函数的积分
r ( t ) ( e cos t ) i ( e sin t ) j e k
t t t
e (cos t sin t ) i e (sin t cos t ) j e k
t t t
例 3 设 e ( ) cos i sin j , e1 ( ) sin i cos j 证明 证:
矢量分析与场论
西北工业大学 航空学院 张 强
关于矢量分析与场论的简单介绍
• 矢量分析是矢量代数和微积分运算的结合和推广, 主要研究矢性函数的极限、连续、导数、微分、 积分等。而场论则是借助于矢量分析这个工具, 研究数量场和矢量场的有关概念和性质。通过这 门课的学习,可使我们掌握矢量分析和场论这两 个数学工具,并初步接触到算子的概念及其简单 用法,为以后学习有关专业课程和解决实际问题, 打下了必要的数学基础。
1 矢性函数的不定积分 定义:若B’(t)=A(t),则称B(t)为A(t)的一个原函数。A(t)的原函数的全体, 叫做A(t)的不定积分,记作 A ( t ) dt 由于矢性函数的不定积分和数性函数的不定积分在形式上完全类似,因此, 数性函数不定积分的基本性质对矢性因数来说仍然成立。
1-矢量分析与场论

ex ex 0, ey ey 0, ez ez 0
ex ey ez , ey ez ex , ez ex ey
A B A B en AB
A// B A B 0
A B Axex Ayey Azez Bxex Byey Bzez
如果要了解场的局部特性,即考虑场在空间每 个点沿各个方向的变化情况,
对于标量场,需要引入方向导数和梯度的概念;
对于矢量场,需要引入散度和旋度的概念。
从数学上看,场是定义在空间区域上的函数:
静态标量场和矢量场可分别表示为:
u(x, y, z)、F(x, y, z)
时变标量场和矢量场可分别表示为:
矢量的叉积不符合交换律,但符合分配律 A B B A A(B C) A B AC
两个矢量的叉积为矢量
矢量运算恒等式
A (B C) B (C A) C (A B) A(BC) B(AC) C(A B)
混合积 双重矢量积
几个特殊结论
假设 M(x, y, z) 为矢量线上任一点,则过点 M沿矢量 线的位移元 dl 与矢量 A(x, y, z)共线。
共线矢量dl 与 A(x, y, z) 满足方程
dl A 0 或
dx dy dz Ax Ay Az
矢量形式
标量形式
A
M
dl r r dr
上面这两个方程称为矢量线方程
M0
而 l 的方向余弦为 cos
2
2
12 22 22 3
cos cos
2
2
12 22 22 3
1
1
12 22 22 3
矢量分析与场论

矢量分析与场论矢量分析是矢量代数和微机分运算的结合和推广,主要研究矢性函数的极限、连续、导数、微分、积分等。
而场论则是借助于矢量分析这个工具,研究数量场和矢量场的有关概念和性质。
通过这一部分的学习,可使读者掌握矢量分析和场论这两个数学工具,并初步接触到算子的概念及其简单用法,为以后学习有关专业课程和解决实际问题,打下了必要的数学基础。
第1章 矢量分析在矢量代数中,曾经讨论过模和方向都保持不变的矢量,这种矢量称为常矢。
然而,在科学和技术的许多问题中,也常遇到模和方向改变或其中之一会改变的矢量,这种矢量称为变矢。
如非等速及非直线运动物体的速度就是变矢量的典型例子。
变矢量是矢量分析研究的重要对象。
本章主要讨论变矢与数性变量之间的对应关系——矢函数及微分、积分和它们的一些主要性质。
§1.1 矢函数与普通数量函数的定义类似,我们引进矢性函数(简称矢函数)的概念,进而结出矢函数的极限与连续性等概念。
1、矢函数的概念定义1.1.1 设有数性变量t 和变矢A ,如果对于t 在某个范围D 内的每一个数值,A 都以一个确定的矢量和它对应,则称A 为数性变量t 的矢量函数,记作A =A )(t (1.1.1)并称D 为矢函数A 的定义域。
在Oxyz 直角坐标系中,用矢量的坐标表示法,矢函数可写成A {})(),(),()(t A t A t A t z y x = (1.1.2) 其中)(),(),(t A t A t A z y x 都是变量t 的数性函数,可见一个矢函数和三个有序的数性函数构成一一对应关系。
即在空间直角坐标系下,一个矢函数相当于三个数性函数。
本章所讲的矢量均指自由矢量,所以,以后总可以把A )(t 的起点取在坐标原点。
这样当t 变化时,A )(t 的终点M 就描绘出一条曲线l (图1.1),这样的曲线称为矢函数A )(t 的矢端曲线,也称为矢函数A )(t 的图形。
同时称(1.1.1)式或(1.1.2)式为此曲线的矢量方程。
矢量分析和场论讲义

曲面S。 试求矢量场r从S内穿出S的通量。
P55 3. 求矢量场 A (x3 yz)i (y2 xz)j (z3 +xy)k
的散度。
• 假如曲面s是闭合旳,并要求曲面法矢由闭合 曲面内指向外,矢量场对闭合曲面旳通量是:
A
0
l 当 (G, lˆ) 0
,即
lˆ
与
G
方向一致时,
u l
为最大。
u l
0 ,沿l增加
u
l
0 ,沿l降低
G
n
u l lˆ c2 c1
u c1
梯度、方向导数与等值面
总结:数量场梯度旳性质
(1)数量场沿任一方向旳方向导数等于梯度在 该方向旳投影。
(2)数量场在任一点旳梯度垂直于过该点旳等 值面,且指向场增大旳一方。(注意:等值面 旳法向有两个)
直接从散度旳定义出发,不难得到矢量场 在空间任意闭合曲面旳通量等于该闭合曲 面所包括体积中矢量场散度旳积分。
A ds divAdV
s
V
上式称为矢量场旳Gauss定理。
注:它能把一种闭合曲面旳面积分转为对 该曲面所包围体积旳体积分,反之亦然。
§4 矢量场旳环量及旋度(Rotation)
1. 矢量场旳环量
以温度场为例:
等温面
热源
能够看出:数量场旳函数是单值函数,各等值面 是互不相交旳。
矢量场旳矢量线:直观描述矢量在场中旳分布情况。
矢量线上每一点处曲线与相应于该点旳矢量相切。
A
M
z
r
l
y
o
x
观察:
图2 矢量线
1.在曲线上旳每一点M处, 场旳矢量都位于该点处旳 切线上(如图所示),称其为矢量线。例:静电场电力 线、磁场旳磁力线、流速场中旳流线等。
第1章 矢量分析与场论基础
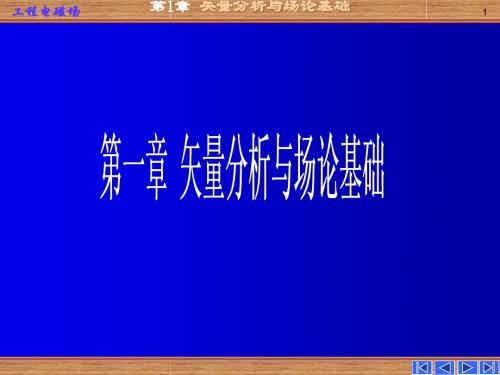
ex e y e y ez ez ex 0 ex ex e y e y ez ez 1
(4)矢量的矢积(叉积) 两矢量的叉积是一个矢量,其大小为两个矢量的大小与它们之
用单位矢量 en 表示。
间夹角 的正弦之积,它的方向垂直于包含两个矢量的平面,
工程电磁场
第1章 矢量分析与场论基础
10
1.2 三种常用的正交曲线坐标系
三维空间任意一点的位置可通过三条相互正交曲线的交点来 确定。 三条正交曲线组成的确定三维空间任意点位置的体系,称为
正交曲线坐标系;三条正交曲线称为坐标轴;描述坐标轴的量称
为坐标变量。 在电磁场与波理论中,三种常用的正交曲线坐标系为:直角 坐标系、圆柱坐标系和球坐标系。
矢量的加减符合交换律和结合律 交换律 A B B A 结合律 A ( B C ) ( A B) C
B B
A B
矢量的减法
A
工程电磁场
第1章 矢量分析与场论基础
6
(2)标量乘矢量
B sA ex sAx e y sAy ez sAz
第1章 矢量分析与场论基础
17
(3)圆柱坐标系与球坐标系的坐标变量之间的转换
r柱 r球 sin r球 r柱 z 2
2
z r cos r柱 z
arctg
工程电磁场
第1章 矢量分析与场论基础
18
1.3场的基本概念和可视化 1场的概念 “场”是指某种物理量在空间的分布。具有标量特征的物理量在空间 的分布是标量场,具有矢量特征的物理量在空间的分布是矢量场。 例如,温度场、能量场、电位场是标量场;电场、磁场、流速场与 重力场都是矢量场。 定义了场量的空间点称为场点。
工程电磁场-第1章-矢量分析和场论基础

04
电磁2
03
静电场
由静止电荷产生的电场, 其电场线不随时间变化。
恒定磁场
由恒定电流产生的磁场, 其磁场线是闭合的,且不 随时间变化。
时变电磁场
由变化的电流或变化的电 荷产生的电场和磁场,其 电场线和磁场线都随时间 变化。
电磁场的分类
按存在形式分类
有源场和无源场。有源场是指其散度非零的场,如静电场和恒定 磁场;无源场是指其散度为零的场,如时变电磁场。
根据场的来源,可以将场分为自然场 和人工场。
场量和场强
场量是描述场中物理量分布的量,如电场强度、磁场强度等 。
场强是描述场作用的强度和方向的物理量,如电场线、磁场 线等。
03
矢量场和标量场
矢量场的性质
02
01
03
矢量场由矢量线组成,具有方向和大小。
矢量场具有旋度或散度,分别表示场中的旋涡或电荷 分布。 矢量场的变化遵循斯托克斯定理和格林定理。
80%
斯托克斯定理
斯托克斯定理是矢量积分的重要 定理之一,它描述了矢量场中某 点处的散度与该点处单位球体体 积内的积分之间的关系。
矢量函数和场
矢量函数
矢量函数是描述空间中矢量场 变化的数学工具,其定义域和 值域都是矢量。
矢量场
矢量场是由空间中一系列点构 成的集合,每个点都有一个与 之相关的矢量。
梯度、散度和旋度
在磁场的边界上,磁场线切线方向的 分量连续,即磁场强度不突变。
05
电磁场的能量和动量
电磁场的能量
电磁场能量的定义
01
电磁场能量是指存在于电磁场中的能量,它与电场和磁场的变
化率有关。
电磁场能量的计算
02
通过计算电场和磁场的能量密度,可以得出整个电磁场的总能
矢量分析与场论

矢量分析与场论矢量分析与场论第一章矢理分析1.1 矢性函数1.矢性函数的定义:数性变量t 在一范围G 内,对于任意的t 都有唯一确定的矢量A与其对应则称A 是t 的矢性函数,并称G 为A 的定义域,记作:()A A t =2.矢性函数的极限和连续性(1)矢性函数极限的定义:()A t在0t 某领域内有定义,对于0ε?>,0δ?>,常矢量0A ,只要为0<0t t δ-<就有0()A t A ε-< ,则称0A 为()A t 当0t t →的极限,记作:00lim ()t t A t A →=;极限的性质:(有界性)若00lim ()t t A t A →=,则0δ?>,M>0,0(;)t U t δ?∈ 都有()A t M <。
证明:0lim ()1,0,..(;)t t A t A s t t U t εδδ→=∴=?>?∈都有0()1A t A ε-<= ,00()()1A t A A t A ∴-<-<,0()1A t A ∴<+ ,取M=01A +极限的则运算:0lim ()()lim ()lim ()t t t t t t u t A t u t A t →→→=?000l i m (()())l i m ()l i m()t tt tt tA tB t A t B t →→→±=±lim(()())lim ()lim ()t t t t t t A t B t A t B t →→→?=?lim(()())lim ()lim ()t t t t t t A t B t A t B t →→→?=?其中()u t ,()A t ,()B t当0t t →时极限均存在。
证明:设00lim ()t t A t A →= ,00lim ()t t u t u →=,00lim ()t t B t B →=;000000()()()()()()u t A t u A u t A t u A t u A t u A -=-+-,00000000000()()()()()()()()()()()u t A t u A t u A t u A u t A t u A t u A t u A u t u A t u A t A -+-≤-+-=-?+?- 00000()()()()()u t A t u A u t u A t u A t A ∴-≤-?+?-而11010,0,..(;)M s t t U t δδ?>>?∈有1()A t M <;对于任意给定的ε>o ,101010,..(;),()2s t t U t u t u M εδδ''?>?∈-<; 同理20,s tt U t δδ?>?∈有00()2A t A u ε-<所以取{}112m i n ,,δδδδ'=,则有0(;)t U t δ?∈,00()()u t A t u A -<10122M u M u εε+?=ε其他证明方法类似,可参看数学分析中相关证明。
第3章 矢量分析和场论

y
ˆ ax A B Ax Bx
ˆ ay Ay By
ˆ az Az Bz
12
(3)三重积:
三个矢量相乘有以下几种形式:
( A B)C
矢量,标量与矢量相乘。
A ( B C ) 标量,标量三重积。 A ( B C ) 矢量,矢量三重积。
A A
A A
a.满足交换律: A B B A
b.满足结合律: ( A B) (C D) ( A C ) ( B D)
5
在直角坐标系下的矢量表示:
三个方向的单位矢量用 ax , a y , az 表示。 ˆ ˆ ˆ 根据矢量加法运算:
பைடு நூலகம்
在直角坐标系中两矢量的减法运算:
ˆ ˆ ˆ A B ( Ax Bx ) ax ( Ay By )a y ( Az Bz ) az
8
3.乘法: (1)标量与矢量的乘积:
ˆ kA k | A | a k 0 方向不变,大小为|k|倍 k 0 k 0 方向相反,大小为|k|倍
16
例4:
和 已知A点和B点对于原点的位置矢量为 a b
求:通过A点和B点的直线方程。
解:在通过A点和B点的直线方程上,
任取一点C,对于原点的位置 矢量为
z
a
,则 c
A
c
C
b
c a k (b a )
B y
x
c (1 k )a kb
h BC
注意:先后轮换次序。
推论:三个非零矢量共面的条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矢量分析与场论第一章 矢理分析1.1 矢性函数1. 矢性函数的定义:数性变量t 在一范围G 内,对于任意的t 都有唯一确定的矢量A 与其对应则称A 是t 的矢性函数,并称G 为A 的定义域,记作:()A A t = 2. 矢性函数的极限和连续性(1) 矢性函数极限的定义:()A t 在0t 某领域内有定义,对于0ε∀>,0δ∃>,常矢量0A ,只要为0<0t t δ-<就有0()A t A ε-<,则称0A 为()A t 当0t t →的极限,记作:00lim ()t t A t A →= ;极限的性质:(有界性)若00lim ()t t A t A →=,则0δ∃>,M>0,0(;)t U t δ∀∈都有()A t M <。
证明:0lim ()1,0,..(;)t t A t A s t t U t εδδ→=∴=∃>∀∈都有0()1A t A ε-<=,00()()1A t A A t A ∴-<-<, 0()1A t A ∴<+,取M=01A +极限的则运算:0lim ()()lim ()lim ()t t t t t t u t A t u t A t →→→=⋅lim(()())lim ()lim ()t t t t t t A t B t A t B t →→→±=±lim(()())lim ()lim ()t t t t t t A t B t A t B t →→→⋅=⋅lim(()())lim ()lim ()t t t t t t A t B t A t B t →→→⨯=⨯其中()u t ,()A t ,()B t 当0t t →时极限均存在。
证明:设00lim ()t t A t A →=,00lim ()t t u t u →=,00lim ()t t B t B →=;000000()()()()()()u t A t u A u t A t u A t u A t u A -=-+-,00000000000()()()()()()()()()()()u t A t u A t u A t u A u t A t u A t u A t u A u t u A t u A t A -+-≤-+-=-⋅+⋅- 00000()()()()()u t A t u A u t u A t u A t A ∴-≤-⋅+⋅-而11010,0,..(;)M s t t U t δδ∃>>∀∈有1()A t M <;对于任意给定的ε>o ,101010,..(;),()2s t t U t u t u M εδδ''∃>∀∈-<; 同理2020,,..(;)s t t U t δδ∃>∀∈有00()2A t A u ε-<所以取{}112min ,,δδδδ'=,则有0(;)t U t δ∀∈,00()()u tA t u A -<10122M u M u εε⋅+⋅= ε其他证明方法类似,可参看数学分析中相关证明。
极限(0lim ()t t A t →)存在的充要条件:()A t 的三个分量()x A t ,()y A t ,()z A t 当0t t →时极限均存在。
且0ˆˆˆlim ()(lim ())(lim ())(lim ())x y z t t t t t t t t A t A t iA t j A t k →→→→=++ 证明:充分性由极限运算第一条可知:0ˆˆˆlim(()),lim(()),lim(())x y z t t t t t t A t iA t j A t k →→→均存在,所以 0ˆˆˆlim(()()())x y z t t A t i A t j A t k→++也存在且0ˆˆˆˆˆˆlim(()()())lim ()lim ()lim ()x y z x y zt t t t t t t t A t i A t j A t k i A t j A t k A t →→→→++=++即ˆˆˆlim ()(lim ())(lim ())(lim ())x y z t t t t t t t t A t A t i A t j A t k→→→→=++必要性:不妨设00lim ()t t A t A →=,则对于0,0,εδ∀>∃>只要0(;)t U t δ∈就有0()A t A ε-< ;而00,0,0,ˆˆˆˆˆˆ()()()()()x y z x y z A t A A t i A t j A t k A i A j A k -=++-++所以0,0,0,ˆˆˆ(())(())(())x x y y z z A t A i A t A j A t A kε-+-+-<;考虑:0,0,0,0,0,ˆˆˆ(())(())(())ˆ(())()x x y y z z x x x x A t A i A t A j A t A k A t A iA t A -+-+-≥-=-所以:0,()x x A t A ε-<,所以00,lim ()x x t t A t A →=; 其他分量极限存在的证明类似。
综上所述:lim ()t t A t →存在,则0lim (),lim (),lim ()x y z t t t t t t A t A t A t →→→均存在,且00,lim ()x x t t A t A →=0,lim ()y y t t A t A →= ,00,lim ()z z t t A t A →=;自然0ˆˆˆlim ()(lim ())(lim ())(lim ())x y z t t t t t t t t A t A t i A t j A t k→→→→=++由此求矢性函数的极限可转化为求其三分量的极限。
(2) 矢性函数连续性的定义:若()A t 在0(;)U t δ内有定义,且00lim ()()t t A t A t →=则称()A t 在0t 处连续;如果()A t 在t 的I 区间上都连续则称()A t 在I 上连续。
连续(()A t 在0t 处)的充要条件:()A t 的三个分量()x A t ,()y A t ,()z A t 在0t 处均连续。
充分性:0lim ()()x x t t A t A t →=,00lim ()()y y t t A t A t →=,00lim ()()z z t t A t A t →=。
000ˆˆˆlim ()()()()()x y z t t A t A t i A t j A t k A t →∴=++=必要性:若0lim ()t t A t →=0()A t ,显然00lim ()()x x t t A t A t →= ,00lim ()()y y t t A t A t →= ,0lim ()()z z t t A t A t →=;1.2 矢性函数的导数与微分1. 矢性的导数定义:()A t 在0(;)U t δ内有定义,若0000()()()limlimt t t A t t A t A t t t t→∆→+∆-∆=-∆存在则称此极限为()A t 在0t 处的导数。
记为:()dA t dt 或()A t ';即()dA t dt=0()lim t A t t ∆→∆∆导数存在的充要条件:()A t 的三个分量()x A t ,()y A t ,()z A t 的导数均存在。
且()dA t dt=()()()ˆˆˆy x z dA t dA t dA t i j k dt dt dt ++充分性:因为00()()()()ˆˆˆlimlim()y x z t t A t A t A t A t i j k t t t t ∆→∆→∆∆∆∆=++∆∆∆∆,而0()lim x t A t t∆→∆∆ ,()limy t A t t∆→∆∆,0()limz t A t t ∆→∆∆均存在。
所以:0()limt A t t∆→∆∆=0()ˆ(lim )x t A t i t ∆→∆∆+0()ˆ(lim )y t A t j t ∆→∆∆+0()ˆ(lim )z t A t k t ∆→∆∆=()()()ˆˆˆy x z dA t dA t dA t i j k dt dt dt++ 必要性:因为00()()()()ˆˆˆlimlim()y x z t t A t A t A t A t i j k t t t t ∆→∆→∆∆∆∆=++∆∆∆∆存在所以0()lim x t A t t∆→∆∆ ,()limy t A t t ∆→∆∆,0()limz t A t t ∆→∆∆也都存在。
且()dA t dt=()()()ˆˆˆy x z dA t dA t dA t i j k dt dt dt ++导矢的几何意义:由定义可知导矢表示的是位矢()A t 末端所画的曲线的切线。
2. 矢性函数的微分:()A t 在0(;)U t δ内有定义,如果00()()()A t t A t C t t +∆-=∆+∆,其中C 为常矢量则称()A t 在0t 处可微,C t ∆为()A t 在0t 处的微分记作dA |0t t ==Cdt可微与可导之间的关系:()A t 在0(;)U t δ内有定义,若()A t 在0t 处可微则它在0t 必可导;反之若()A t 在0t 处可导则()A t 在0t 处可微。
且dA |0t t ==0()A t dt '。
证明:若()A t 在0t 处可微,由定义可知:00()()()A t t A t C t t +∆-=∆+∆; 所以00()lim limt t t t C t t A C t→→∆+∆∆==∆,即若()A t 在0t 处可导并有:0()A t '=C 。
若()A t 在0t 处可导则: 0limt t A t →∆∆=0()A t ',所以00lim(())0t t AA t t→∆'-=∆,从而0()(1)AA t t∆'-=∆,即0()()A A t t t '∆=∆+∆所以()A t 在0t 处可微。
且dA |0t t ==0()A t dt '由导数存在的充要条件及可微与可导之间的关系,可以得到:()A t 在0t 处可微当且仅当它的三分量在0t 处可微。
(可微的充要条件)微分的意义:由微分的定义可知,当0t ∆→时,dA =A ∆。
