第一章矢量分析与场论基础题解
第01章 矢量分析和场论基础

cos ϕ e y
− sin ϕ e x
cos ϕ e x ϕ
e ρ cos ϕ sin ϕ 0 e x e = − sin ϕ cos ϕ 0 e ϕ y ez 0 0 1 e z − sin ϕ cos ϕ 0 0 e ρ 0 eϕ 1 e z
第一章 矢量分析与场论基础
电磁场与电磁波理论基础
3.体、面和线微分元 体 体微分元 dV = ρ d ρ dϕ dz
dS ρ = ρ dϕ dze ρ 面微分元 dSϕ = d ρ dz eϕ dS = ρ d ρ dϕ e z z
Z
ez
线微分元 dl = d ρ e ρ + ρ dϕ eϕ + dze z
P( ρ ,θ , ϕ )
er eϕ
θ是位矢 与正 轴之间的夹角, 是位矢r与正 轴之间的夹角, 与正Z轴之间的夹角
θ
in rs
eθ
r sin θ sin ϕ
(1-17)
式中 n 是一垂直于由矢量 A 和 B 构成的平面的单位矢量, 构成的平面的单位矢量,并遵循 右手螺旋法则,见图1-3。 右手螺旋法则,见图 。
图1-3 矢量的标积和矢积
矢量的矢积不满足交换律: 矢量的矢积不满足交换律: A × B = −B × A (1-18) 矢积满足分配律和数乘, 矢积满足分配律和数乘,即
ϕ
ez
P( ρ , ϕ , z )
ρ
eϕ
eρ
图1-10 圆柱坐标
0 ≤ ρ < +∞ 取值范围 0 ≤ ϕ ≤ 2π −∞ < z < +∞
z = 常数
(优选)第一矢量分析与场论

2.矢量的运算
(1)加法和减法
➢任意两个矢量 A 与B 相加等于两个矢量对 应分量相加,它们的和仍然为矢量.
➢常用作图的方法来求矢量的加减法。 ➢加减法服从交换律和结合律。 (2) 乘积运算
①标量与矢量的乘积 B kA
②两个矢量的标量积
➢两矢量的点积定义为一个矢量在另一个矢量 方向上的投影与另一个矢量模的乘积,结果
B
A
➢两矢量叉积,结果得一新矢量,其大小为这两个
矢量组成的平行四边形的面积,方向为该面的法线
方向,且三者符合右手螺旋法则。
➢两矢量叉积满足分配律,但不满足交换律和结合 律。
A(B C) A B AC A B B A
A(BC) (A B)C
➢当两个非零矢量叉积为零,则这两个矢量必平行。
➢在直角坐标系中,两矢量的叉积运算可以用行列式
(2)拉普拉斯(Laplace)算子
属于一阶微分算子,而在场论的研究中还
会用到二阶微分算子,即拉普拉斯算子:
2
1 h1h2h3
u1
( h2h3 h1
)
u1
u2
( h1h3 h2
u2
)
u3
( h1h2 h3
u3
)
显然,它是一个标量算子.
例如在直角坐标系中
2 2 2 2 x2 y2 z2
是个标量。
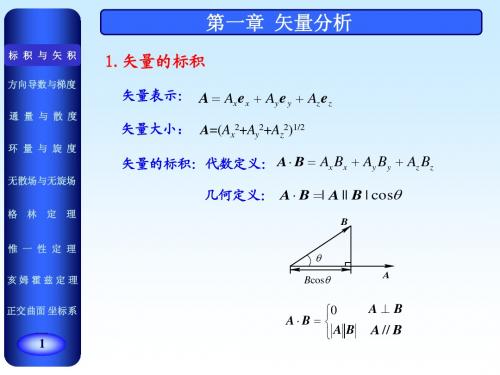
A• B ABcos
➢两矢量点积等于对应分量的乘积之和。
A B AxBx Ay By Az Bz
➢两矢量点积满足交换律和分配律。
A B B A
A(B C) A B AC
➢当两个非零矢量点积为零,则这两个矢量必正 交。
③两个矢量的矢量积
一、 矢量分析与场论基础

根据散度定理,上式左边等于
(C A) ds ( A ds) C C A ds
S S S
于是得
C ( A)dv C A ds
V S
由于上式中常矢C是任意的,故式必成立。
1 .5 方向导数与梯度, 格林定理
1 .5 .1 方向导数与梯度 ; 标量场u(x, y, z)在某点沿l方向的变化率称为u沿该方向的方 向导数 u / l 它的值与所选取的方向 。
4 3 rds rdv 3 dv 3 r 4r 3 S V V 3
1.4 环量与旋度, 斯托克斯定理
1 .4 .1 环量
矢量A沿某封闭曲线的线积分, 定义为A沿该曲线的环量(或
旋涡量), 记为
A dl
l
图 1 -5 矢量场的环量
1 .4 .2 旋度的定义和运算
即
ˆ x
ˆ y
ˆ z
rot A A x y z Ax Ay Az
旋度运算符合如下规则:
( A B) A B (A) A A ( A B) B A A B ( A) 0 A ( A) A
V
Adv A ds
上式称为散度定理, 也称为高斯公式。 利用散度定理可将矢量 散度的体积分化为该矢量的封闭面积分, 或反之。
例1 .1 球面S上任意点的位置矢量为 r 试利用散度定理计算 ds r
S
ˆ ˆ ˆ ˆ xx yy zz rr,
[解]
x y z r 3 x y z
荷Q。 若Q为正电荷, Ψe为正, 有电通量流出; 反之, 若Q为负电荷,
场论典型例题汇编

场论典型例题第一章 矢量分析 例题1、(基本矢量计算)已知两个矢量j i 2+=A ,j i 34+=B ,求(1)B A + (2)B A - (3)B A •(4)B A ⨯ (5)若A 和B 两矢量夹角为α,求αcos 。
解:(1)B A +=)34()2(j i j i +++=j i )32()41(+++=j i 55+ (2)B A -=)34()2(j i j i +-+=j i )32()41(-+-=j i --3 (3)B A •=)34()2(j i j i +•+=)32()41(⨯+⨯=64+=10(4)B A ⨯=)34()2(j i j i +⨯+=0 3 4 0 21 kj i =k 5- (5)根据内积的定义有:B A •=αcos B A ,其中A ,B 为矢量的模。
所以:BΑBA •=αcos 其中B A •在(2)中已经得到B A •=10,而A =5021222=++,B =5034222=++ 因此B ΑB A •=αcos =5510=52说明:此题可以用于掌握矢量运算法则。
例题2、(矢性函数的极限)设t t t cos sin )(B A F += )20(π<≤t ,式中A ,B 为矢量,分别为j i -=A ,j i +=B 。
求下列极限。
(1))(lim 3/t F t π→ (2)|)(|lim 3/t F t π→解:(1)整理)(t F 。
t j i t j i t t t F cos )(sin )(cos sin )(++-=+=B A=j t t i t t )sin (cos )sin (cos -++而 3/|)sin (cos π→+t t t =231+ 3/|)sin (cos π→-t t t =231- 所以)(lim 3/t F t π→=i 231++j 231- (2)|)(|t F =|j t t i t t )sin (cos )sin (cos -++| =22)sin (cos )sin (cos t t t t -++ =2=→|)(|lim 3/t F t π2说明:对矢性函数的极限,归结为对各坐标分量求极限,因此,需要温习高等数学中微积分中关于“函数极限”的内容,特别是一些常用极限的求法。
第一章 矢量分析
立了面积分和线积分的关系。从物理角度可以理解为斯托克 立了面积分和线积分的关系。从物理角度可以理解为斯托克 斯定理建立了区域 S 中的场和包围区域 S 的闭合曲线 l 上的 场之间的关系。因此, 中的场, 场之间的关系。因此,如果已知区域 S 中的场,根据斯托克 上的场,反之亦然。 斯定理即可求出边界 l 上的场,反之亦然。
Ψ = ∫ A ⋅ dS
S
通量可为正、或为负、或为零 当矢量穿出某个闭合面时, 通量可为正、或为负、或为零。当矢量穿出某个闭合面时, 认为该闭合面中存在产生该矢量场的源 认为该闭合面中存在产生该矢量场的源;当矢量进入这个闭合 面时,认为该闭合面中存在汇聚该矢量场的洞 )。闭合 面时,认为该闭合面中存在汇聚该矢量场的洞(或汇)。闭合
惟 一 性 定 理 亥姆霍兹定理 正交曲面 坐标系
10
第一章 矢量分析
标 积 与 矢 积 方向导数与梯度 通 量 与 散 度 环 量 与 旋 度 环 量 与 旋 度 无散场与无旋场 格 林 定 理
2. 旋度:旋度是一个矢量。若以符号 rot A 表示矢量 A 的旋 旋度:旋度是一个矢量。 具有最大环量强度的方向, 度, 则其方向是使矢量 A 具有最大环量强度的方向, 其大小等于对该矢量方向的最大环量强度, 其大小等于对该矢量方向的最大环量强度,即
惟 一 性 定 理 亥姆霍兹定理 正交曲面 坐标系
1
0 A⋅ B = A B
A⊥B
A // B
第一章 矢量分析
标 积 与 矢 积 方向导数与梯度
2.矢量的失积 2.矢量的失积
矢量的失积:代数定义: 矢量的失积:代数定义:
ex A × B = Ax Bx ey Ay By ez Az Bz
矢量分析与场论(定理一及例题)

而全体势函数为 v sin y x2 yz 2 c
例2. 用不定积分法求例1中矢量场的势函数.
解:在例1中已经证得A为有势场,故存在函数u满足
ur A gradu, 即有
由第一个方程对x积分,得
与 代入
比较,得 得
从而,势函数
v
v
v
v
例3. 证明 A 2xyz3i x2z3 jur 3xr2 yz2k
所以
vv A dl
x2 yz3
B
12 4
8
»AB
A
代入公式
v
v
v
v
例4. 若 A P(x, y, z)i Q(x, y, z) j R(x, y, z)k 为保守场,
则存在函数u(M )使
vv
B
A dl u(M ) u(B) u( A)
AB
A
得
z
R(x, y, z)dz z0
例1. 证明矢量场
v
r
r
ur
A 2xyz2i (x2z2 cos y) j 2x2 yzk
为有势场,并求其势函数.
解:由
2 yz2
D
uv A
2xz
2
4xyz
2 xz 2 sin y 2x2z
4xyz
2
x
2
z
2x2 y
得rotAv 0v, 故Av为有势场。
y
z
ur
定理1. 在线单连域内,矢量场A 为有势场的
ur
充要条件是 A为无旋场.
此性质表明:
ur r A dl Pdx Qdy Rdz
u dx u dy u dz x y zdu即表来自式ur Ar dl
第一章 矢量分析

第一章 矢量分析在这门课程中,我们几乎从头到尾和场打交道。
实际上,人们周围的空间也确实存在着各种各样的场,例如自由落体现象,说明存在一个重力场;人们能感觉到室内外的冷暖,说明我们周围分布着一个温度场,等等。
那么到底什么是场呢?从物理意义上理解,场是遍及一个被界定的或无限扩展的空间内的,能够产生某种物理效应的特殊的物质,场是具有能量的。
从数学意义上理解,场是给定区域内各点数值的集合,这些数值规定了该区域内一个特定量的特性。
例如温度场就由T 描述,只要知道了场中各点T 的大小,该温度场就被确定了,这种只有数值大小的物理量称为标量,该场称为标量场;还有一种场,例如本书中讨论的电磁场,电场强度E 是描述电场的物理量之一,人们不仅需要知道它的数值大小,还要知道它的方向,这样才能完全确定它,这样的物理量称为矢量,该场称为矢量场。
在电磁场和电磁波的学习中,我们始终要用到矢量运算,因此掌握矢量分析是十分必要的。
§1.1 矢量的概念1.1.1 标量在电磁场中遇到的特征量可区分为标量和矢量两类。
一个仅用大小就能够完整描述的物理量称为标量。
如电荷、电位和能量等。
这些量中的每一个量,用单纯的一个数就可以完整地描述。
电荷0.5库伦(C ),电位220伏特(V )等都是标量的例子。
1.1.2 矢量一个不仅有大小而且有方向的物理量称为矢量。
力、速度、力矩、电场强度和加速度都是矢量。
一个矢量常用一个带箭头的线段来图示,其长度按适当比例表示它的大小,方向则用箭头指示,如图 1.1(a)所示。
其中,R 代表一个从O 点指向P 点的矢量。
图1.1(b)表示几个平行矢量有同样的大小和方向,它们都代表同一个矢量。
一个大小为零的矢量称为空矢或零矢。
一个大小为1的矢量称为单位矢量。
一个矢量A 可以表示为A Aa = (1.1)其中A 是A的大小,称为模,由式(1.2)表示||A A = (1.2)a 是A 的单位矢量,即方向与A 的方向相同,大小为1的矢量,由式(1.3)表示||A a A =(1.3)§1.2 矢量运算1.2.1 矢量加法矢量加法是矢量的几何和,两个矢量的几何和服从平行四边形规则,如图1.2(a)所示。
第01讲 矢量分析与场论(1)

第一章矢量分析与场论(1)1.什么是场?重力场、温度场、电磁场、……在许多科学问题中,常常需要研究某种物理量(如温度、密度、电位、力等等)在某一空间区域的分布和变化规律。
为此,在数学上引入了场的概念。
如果在某一空间里的每一点,都对应着某个物理量的一个确定的值,则称在此空间里确定了该物理量的一个场。
如教室中每一点都对应一个确定的温度,教室中确立一个温度场。
地球周围空间任一点对应一个重力加速度值,在此空间就存在一个重力场。
•从数学角度:场是给定区域内各点数值的集合,这些数值规定了该区域内一个特定量的特性。
比如:T是温度场中的物理量,T 就是温度场•从物理角度:场是遍及一个被界定的或无限扩展的空间内的,能够产生某种物理效应的特殊的物质,场是具有能量的。
场的分类:●按物理量的性质分:标量场:描述场的物理量是标量。
温度场、密度场等是数量场矢量场:描述场的物理量是矢量。
力场、速度场等为矢量场。
●按场量与时间的关系分:静态场:场量不随时间发生变化的场。
动态场:场量随时间的变化而变化的场。
动态场也称为时变场。
数量场的等值面一般地,数量场中各点处的数量u是位置的函数,在直角坐标系中,是点的坐标x,y,z的函数,即:),,(z y xuu就是说,一个数量场可以用一个数性函数来表示。
场存在的空间即为其定义域。
此后,我们总假定这个函数单值、连续且一阶可导。
在数量场中,使函数u 取相同数值的所有点所组成的曲面称为该数量场的等值面。
如温度场的等温面,电场的等位面等。
显然,数量场的等值面方程为:c z y x u =),,((常数)给定不同的常数c ,就得到不同的等值面。
如图,c 取遍所有可能的值时,这族等值面就充满数量场所在的空间,而且这族等值面两两互不相2c =1c u =3c =交。
因为数量场中的每一点),,(0000z y x M 都有一个等值面),,(),,(000z y x u z y x u =通过,而且由于函数u 为单值,故一个点只能在一个等值面上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 矢量分析与场论基础1-1 求下列温度场的等温线 1)Txy=,2)Txy=+122解 求等温线即设定相关的方程为常数,因此可得 ⑴ Cxy =,xC y=;⑵ Cyx =+221-2 求下列标量场的等值面 1)ua xb y cz=++1,2) =-uz xy 22+, 3)uxyz =ln(++)222解 据题意可得 ⑴ kcz by ax =++ ⑵ cyxz=+-22,()222c z yx -=+⑶ ()c z y x =++222ln ,c e z y x =++222,2222k z y x =++1-3 求矢量场A e e e =++x y z x y z 2 经过点M (.,.,.)102030的矢量线方程。
解 根据矢量线的定义,可得zz y y x x 2d d d ==解微分方程,可得 x c y 1=,22x c z =将点M (.,.,.)102030的坐标代入,可得 21=c ,32=c 即 x y 2=,23x z = 为所求矢量线方程。
1-4 求矢量场A e e e =++y x x y y z x y z 222的矢量线方程。
解 根据矢量线的定义,可得zy z yx y xy x 222d d d ==解微分方程,可得 122c y x =-,x c z 2= 为所求矢量线方程。
1-5 设u x z yz xz ()M =+-+32222,求:1)u ()M 在点M 0102030(.,.,.)处沿矢量l e e e =++yx zx xy x y z 方向的方向导数,2)u ()M 在点M 0(.,.,.)102030处沿矢量l e e e =+-+-+()()622222x z z z y x x y z 方向的方向导数。
解 l 的方向余弦为1722322cos 222=++=α,1732323cos 222=++=β,1722322cos 222=++=γ;又有12260=+=∂∂MMxzx xu ,620-=-=∂∂MMzyu ,42220=+-=∂∂MMxy z zu据方向导数的定义,可得1714172436212cos cos cos 0=⨯+⨯-⨯=∂∂+∂∂+∂∂=∂∂γβαMMMMzu yu xu lu1-6 求标量场uxy yz zx=++在点M 0(.,.,.)102030 处沿其矢径方向的方向导数。
解 l 的方向余弦为1413211cos 222=++=α,1423212cos 222=++=β,1433213cos 222=++=γ; 又有5=+=∂∂MMzy xu ,4=+=∂∂MMzx yu ,3=+=∂∂MMxy zu据方向导数的定义,可得142214332415cos cos cos 0=⨯+⨯+⨯=∂∂+∂∂+∂∂=∂∂γβαMMMMzu yu xu lu1-7 设有标量场u xy z=-22,求u 在点(.,.,2010 1.0)-处沿该点至(.,.,3010 -1.0)方向的方向导数。
在点(.,., 1.0)2010-沿什么方向的方向导数达到最大值?其值是多少?解 点(.,.,2010 1.0)-至点(.,.,3010 -1.0)的方向余弦为()()()3111112323c o s 222=--+++--=α,()()()3211112311cos 222=--+++-+=β,()()()3211112311cos 222-=--+++---=γ;又有220-==∂∂MMyxu ,420==∂∂MMxyu ,220-=-=∂∂MMzzu据方向导数的定义,可得3103222412cos cos cos 0=⨯+⨯+⨯-=∂∂+∂∂+∂∂=∂∂γβαMMMMzu yu xu lu当方向余弦均为1时,方向导数达到最大值,即沿z y x e e e G242-+-=方向导数达最大值,()()6224242222==-++-=G1-8 求下列标量场的∇u1)u xy =2;2)u x y =+22;3)u y x =e sin ;4)u x y z=234; 5)ux yz=-+323222解 据 zy x z u yu xu u e e e ∂∂+∂∂+∂∂=∇,可得1) y x x y u e e 22+=∇ 2) yx y x u e e 22+=∇3) yxx xy e y e u e e cos sin +=∇4) z y x z y x z y x z xy u e e e 33242243432++=∇5) zy x z y x u e e e 646+-=∇1-9 求标量场u xyzx x y=-+222在点(.,., -2.0)-1030处的梯度。
解()()zyx x y z xxzxy yzu e ee 222222++++-=∇,则所求梯度为()()zy x z y x Mue e e e e e 1234121462120+-=++-+--=∇1-10 求标量场223),(yxy x u +=具有最大方向导数的点及方向,所求的点满足x y 221+=。
(提示:最大的方向导数就是在点(,)x y 处的梯度,模最大,且满足x y 221+=,即求条件极值。
)解yx y x y x yu xu u e e e e 26+=∂∂+∂∂=∇,22436yxu+=∇,将21xy-±=代入,可得()43214362222+=-+=∇x xx u ,即 []43222+=∇x u ,当1±=x、0=y 时,有6max±=∇u,即点()0,1-和()0,1为满足条件的点,又()x ue 60,1-=∇-,()xue 60,1=∇,即最大方向导数的方向分别为xe ±1-11 设re e e r =++x y z r nx y z , =, 为正整数,1)求∇∇∇r r f r n 2,,(),2)证明∇=∙(a r a a),(是常矢量)解 1)()()re e e 22222222=++=++∇=∇z y xz y x zyxr()()()()zy xnn nz y x z y x n zy x re e e2222122222222++++=⎥⎦⎤⎢⎣⎡++∇=∇-rnrrnrn n r r 2122-⎪⎭⎫⎝⎛-==()()()()rr f r r f r r f r f r r '='=∇'=∇-12) 证明 设zz y y x x a a a e e e a ++=,则 za y a x a z y x ++=⋅r a ,因此,可得 ()()zz y y x x z y x a a a z a y a x a e e e r a ++=++∇=⋅∇,证毕。
1-12 设S 为上半球面x y z a 2222++=≥ (z 0),其法向单位矢量e n 与z 轴的夹角为锐角,求矢量场r e e e =++x y z x y z 沿e n 所指的方向穿过S 的通量。
(提示:注意r 与e n 同向)解 将r e e e =++x y z x y z 用球坐标表示,则在S 面上有na e r=,因此,可得3222d aaa sππ=⨯=⋅⎰s r1-13 求均匀矢量场A 通过半径为R 的半球面的通量。
(如图1-1所示)解 设半球面的方程为x y z a 2222++=≥ (z 0),则矢量A 通过S 面的通量等于矢量A 通过S 面在0=z 的平面上的投影的通量,因此,2d R A sπ=⋅⎰s A1-14 计算曲面积分yx x z x z yz yz y xy xSd d )12(d d )2(d d )2(22+-+-+-=Φ⎰⎰,其中S 是球心在原点,半径为a 的球面外侧。
解 设z y x x z yz y xy x e e e A )12()2()2(22+-+-+-=,根据散度定理,可得()()32234d 1222222d d d d )12(d d )2(d d )2(avx z z y y x v y x x z x z yz yz y xy xvvsSπ=+-+-+-=⋅∇=⋅=+-+-+-=Φ⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰A sA1-15 求矢量场A 从内穿出所给闭曲面S 的通量: 1)A e e e =++x y z x y z 333,S 为球面x y z a2222++= 2)Ae e e =-++-++-+(x y z y z x z x y x y z )()(),S 为椭球面x ay bz c2222221++=解 1) 根据散度定理,可得()()522222512d 43d 333d d ar r r v zyxvavvsππ=⨯=++=⋅∇=⋅⎰⎰⎰⎰⎰⎰⎰⎰⎰A s A2) ()()abcabc vvvvsππ4343d 111d d =⨯=++=⋅∇=⋅⎰⎰⎰⎰⎰⎰⎰⎰A s A1-16 求下列空间矢量场的散度: 1)A e e e =-+-+-()()()2332z y x z y x x y z2)A e e e =-+++-()()()3232322xyz y yz xyz xz x y z解 1)=∂∂+∂∂+∂∂=⋅∇z A y A x A z y x A2) xzxy zy x zA yA xA z y x 63622-+++=∂∂+∂∂+∂∂=⋅∇A1-17 求div A 在给定点处的值:1)A e e e =++x y z x y z 333在M (1.0,0.0,-1.0)处; 2)A e e e =-+422x xy z x y z,在M (1.0,1.0,3.0)处;3)A r r e e e ==++xyz x y z x y z ()在M (1.0,3.0,2.0)处。
解 1)222333zy xz A y A x A z y x ++=∂∂+∂∂+∂∂=⋅∇A ,则633=+=⋅∇MA2)zx z A y A x A z y x 224+-=∂∂+∂∂+∂∂=⋅∇A ,则8624=+-=⋅∇MA3)()[]xyzxyz xyz xyz z y x xyz zA yA xA z y x z y x 6222=++=++⋅∇=∂∂+∂∂+∂∂=⋅∇e e e A ,则362316=⨯⨯⨯=⋅∇M A1-18 求标量场u x y z =342的梯度场的散度。
解zy x z y x z y x z y x z y x zu yu xu u e e e e e e 43233242243++=∂∂+∂∂+∂∂=∇()222222243223246322126y x z x z y xy y x z y x z xy u ++=++=∇⋅∇1-19 已知液体的流速场V e e e =++3523x xy xyz x y z ,问点M (1.0,2.0,3.0)是否为源点? 解 2356x y z x x ++=⋅∇v ,由于065≠=∇M v ,所以M 是源点。
