因数和与因数积
因数与积、商与被除数除数的变化规律

例1、因数与积的变化规律复习:小数乘法怎样计算3.2 5 3 2 5×0.6×61 9 5 0找规律:3.5×1.2 =4.2 3.5×1.2 = 4.2 3.5×1.2 = 4.23.5×3.6 = 7× 3.6 = 0.7×3.6 =3.5 × 6 = 14 × 6 = 14 ×0.4 =3.5×0.4 = 0.7 ×0.4 = 14 ×0.3 =小结:因数×因数 = 积因数×(因数×m)= 积因数×(因数÷m)= 积(因数×m)×(因数×n)= 积(因数÷m)×(因数÷n)= 积(因数×m)×(因数÷n)= 积思考:什么时候积不变?例2、被除数、除数与商的变化规律思考:为什么被除数和除数同时乘以(或除以)一个不为0的数,商才不变?找规律:4.2÷3.5 =1.2 4.2÷3.5 =1.2 4.2÷3.5 =1.212.6÷3.5 = 4.2 ÷ 7 = 8.4÷ 7 =21 ÷3.5 = 4.2÷0.7 = 0.6÷0.5 =1.4 ÷3.5 = 4.2÷0.5 = 8.4÷0.7 =1.4÷10.5 =小结:被除数÷除数 = 商(被除数×m)÷除数 = 商(被除数÷m)÷除数 = 商被除数÷(除数×m)= 商被除数÷(除数÷m)= 商(被除数×m)÷(除数×n)= 商(被除数÷m)÷(除数÷n)= 商(被除数×m)÷(除数÷n)= 商(被除数÷m)÷(除数×n)= 商例3:一个两位小数四舍五入到十分位是5.0,那么这个小数最大是多少?最小是多少?还可能是多少?分析:比5.0小的数需要五入,可能是比5.0大的数需要四舍,可能是例4: 2.5×6= 2.5×2.2= 2.5×1.1= 2.5×0.8= 2.5×0.6=小结:一个数(0除外)乘大于1的数,例5: 4.5÷5= 4.5÷1.5= 4.5÷1= 4.5÷0.9= 4.5÷0.5= 小结:一个数(0除外)除以大于1的数,例6: 下面各题的商那些事小于1的?那些是大于1的?4.5÷1.5= 3÷2= 2.4÷2.4= 4÷5= 7.6÷8=小结:例7:一个小数,如果把小数点向右移动一位,所得的数比原来增加了63.9,这个小数是多少?(分析)原数:扩大后的数:扩大后的数是原数的10倍,比原数多9倍,原数的9倍是。
因数和积的乘法运算

因数和积的乘法运算在数学中,因数和积是基本的概念,而乘法运算是将两个数相乘得到一个结果的操作。
因数是能够整除一个数的数,而积是指两个或多个数相乘得到的结果。
因数和积的乘法运算在数学中有着重要的应用。
首先,因数的概念在因式分解和最大公因数的求解中起到了关键作用。
因式分解是将一个数表示为几个因数的乘积的过程,而最大公因数是指能够整除两个或多个数的最大的因数。
通过因式分解和最大公因数的求解,我们可以简化复杂的计算和问题,并找到数的特殊性质。
积的概念在代数中也有着广泛的应用。
代数是数学的一个分支,它研究的是数与数之间的关系。
在代数中,我们经常会遇到多项式的乘法运算。
多项式是由常数和变量通过加减乘除等运算组成的式子,而多项式的乘法运算就是将两个或多个多项式相乘得到一个新的多项式。
通过多项式的乘法运算,我们可以解决各种实际问题,如求解方程、计算面积和体积等。
除了代数中的应用,因数和积的乘法运算在几何中也有重要的作用。
几何是研究空间和图形的形状、大小、相对位置和性质的一门学科。
在几何中,我们经常会遇到图形的面积和体积的计算。
面积是指平面图形所占的空间大小,而体积是指立体图形所占的空间大小。
通过因数和积的乘法运算,我们可以方便地计算出各种图形的面积和体积,进而解决几何问题。
因数和积的乘法运算还在实际生活中有广泛的应用。
例如,在商业中,我们经常会遇到价格、数量和总额的计算。
通过因数和积的乘法运算,我们可以快速计算出商品的总价和折扣优惠等。
在工程中,因数和积的乘法运算也有着重要的应用,如计算力学和电路中的功率、能量和电压等。
因数和积的乘法运算是数学中基本的概念和操作。
它在因式分解、最大公因数、代数、几何和实际生活中都有着重要的应用。
通过因数和积的乘法运算,我们可以解决各种复杂的计算和问题,简化计算过程,找到数的特殊性质,进而推动数学和科学的发展。
因此,深入理解和掌握因数和积的乘法运算对于数学学习和实际应用都具有重要意义。
小学奥数题库《数论》因数和倍数-因数和-4星题(含解析)

数论-因数和倍数-因数和-4星题课程目标知识提要因数和•概念因数和:即一个整数的所有因数的和。
因数和公式:a3×b2×c的因数的和为(1+ a + a2 + a3)×(1+ b + b2)×(1+ c)精选例题因数和1. 2010的全部约数有个,这些约数的和数是.【答案】16;4896【分析】详解:2010=2×3×5×67,约数有(1+1)×(1+1)×(1+1)×(1+1)=16个,约数之和是(1+2)×(1+3)×(1+5)×(1+67)=4896.2. 36的所有约数的和多少?90的所有约数的和是多少?【答案】91;234【分析】简答:提示,牢记求约数和的公式,并能准确分解质因数.3. 10000的所有因数的和为多少?所有因数的积为多少?【答案】24211;1000012×100【分析】10000=24×54,因数和:(20+21+22+23+24)×(50+51+52+53+54)=24211因数积为(1002)n×100,其中n=[(4+1)×(4+1)−1]÷2=12所以因数的积为1000012×1004. 求出所有恰好含有10个因数的两位数,并求出每个数的所有因数之和.【答案】124或186【分析】10=9+1=2×5,表达式为a9或者ab4,29>100,2×34>100,只可能是24×3=48或24×5=80.48的因数之和:(20+21+22+23+24)×(30+31)=124,80的因数之和:(20+21+ 22+23+24)×(50+51)=186.5. 360的所有因数的和为多少?所有因数的积为多少?【答案】1170、36012【分析】360=23×32×5,因数和:(20+21+22+23)×(30+31+32)×(50+51)=1170因数积:360n,n=(3+1)×(2+1)×(1+1)÷2=12所以因数的积为36012.6. 360共有多少个奇约数?所有这些奇约数的和是多少?【答案】6、78【分析】360=23×32×5,奇约数有:(2+1)×(1+1)=6(个),奇约数的和是:(30+ 31+32)×(50+51)=78.7. 2000的所有因数的和为多少?所有因数的积为多少?【答案】4836、200010【分析】2000=24×53,因数和:(20+21+22+23+24)×(50+51+52+53)=4836;因数积为2000n,其中n=(4+1)×(3+1)÷2=10,所以因数的积为200010.。
西师四年级数学下册因数和积的变化规律

因数和积的变化规律教学内容:因数和积的变化规律素质教育目标:(一)知识教学点1.知道“扩大”“缩小”的含义2.理解乘法里一个因数不变,另一个因数扩大(或缩小)若干倍积也扩大(或缩小)相同的倍数的规律。
(二)能力训练点1.能抽象概括:一个因数不变另一个因数扩大(或缩小)若干倍,积也扩大(或缩小)相同倍数的规律。
2.能运用积的变化规律进行简便计算。
(三)德育渗透点通过“因数和积的变化规律”这一数学规律的教学渗透函数思想,培养学生发现规律,进行抽象概括等思维能力。
教学重点:理解“一个因数不变,另一个因数扩大(或缩小)若干倍,积也扩大(或缩小)相同的倍数”这一数学规律。
教学难点:理解因数和积的变化规律,并运用规律计算。
教学步骤一、铺垫孕伏1.口算:24×20 15×30 16×200 18×3002.下面两题,用竖式怎样计算比较简便?28×40 2800×30二、探究新知1.教学“扩大”或“缩小”几倍的含义。
(1)讲授把一个数“扩大”几倍就是把这个数乘以几。
(2)练习:①6扩大4倍是多少?②3扩大10倍是多少?③200缩小20倍是多少?④8缩小8倍是多少?2.教学例6。
(3)想:发现了什么?分组讨论引导学生明确:①第2、3、4、5组的第二个因数同第一组比较,分别扩大5倍、10倍、100倍、500倍,积也随着扩大5倍、10倍、100倍、500倍。
②一个因数不变,另一个因数扩大若干倍,积也扩大相同的倍数。
(4)练习:58页做一做,说说是怎么想的[通过观察—思考—讨论—交流,使学生的认识逐步加深,通过教师必要的点拨,使每位学生透彻理解](5)观察1、2、3、4组第2个因数与5组第2个因数比较,引导学生归纳出:一个因数不变,另一个因数缩小若干倍,积也缩小相同的倍数。
(6)启发学生把发现的两条规律进行概括。
一个因数不变,另一个因数扩大(或缩小)若干倍,积也扩大(或缩小)相同的倍数。
因数的变化引起积的变化规律

因数的变化引起积的变化规律1. 引言:生活中的积的变化嘿,你有没有注意到生活中经常有一些小变化会让结果大相径庭?比如说,你加了多少糖进咖啡里,味道就会完全不同。
这种因数的变化引起的结果变化,其实就是我们今天要聊的“因数和积”的关系。
我们会探讨一下这背后的规律,让你从数学角度理解生活中的这些小妙招。
2. 因数的基本概念2.1 因数是什么?先来个简单的解释,因数就是能整除一个数的那些数字。
比如说,12的因数有1、2、3、4、6和12。
这些数字,都是12的“好朋友”,能把12完完整整地“分开”。
2.2 积的概念当我们把因数相乘的时候,就得到了积。
比如,2和3的积是6。
积就是那些因数结合起来的结果,像拼图一样,拼得好,结果就漂亮。
3. 因数变化对积的影响3.1 变化的规律好啦,接下来我们要聊的是因数变化怎么影响积。
举个简单的例子:如果你把3和4这两个因数变成了4和4,积就从12变成了16。
看到了没?小小的变化,结果就有了大不同。
这说明了什么呢?因数的变化直接决定了积的大小。
3.2 变化的方向我们再深入一点。
假如你把一个因数增加了,比如说把2变成了3,那么积也会变大。
举个例子,2乘以5等于10,3乘以5就等于15。
是不是很简单?如果因数变大,积也会跟着变大。
反之,如果因数变小,积也会缩小。
4. 实际应用:生活中的因数和积4.1 日常生活中的应用让我们把这些数学知识应用到实际生活中去。
比如,你做饭时,增加了几种调料,菜的味道就完全不同了。
这里的调料就是因数,它们的组合就决定了菜的味道,也就是积。
生活中很多时候,我们要学会灵活运用这些因数,使得结果最合适、最美味。
4.2 教育中的应用在学校里,老师经常用因数和积的例子来帮助我们理解数学。
比如,教你们算面积的时候,实际上就是在用因数的变化来展示积的变化。
你可以想象一下,一个正方形的边长变长了,它的面积就会增加。
这就像我们把因数调整了,积也随之变化了。
5. 结论:理解因数变化的意义总的来说,因数的变化直接影响到积的变化,这是数学中的一个基本规律。
因数和积的变化规律

因数和积的变化规律导读:本文是关于因数和积的变化规律,希望能帮助到您!课题:因数和积的变化规律教学目标1.知道“扩大”、“缩小”的含义.2.理解乘法里一个因数不变,另一个因数扩大(或缩小)若干倍积也扩大(或缩小)相同倍数的规律.3.能运用积的变化规律进行简便计算.教学重点理解“一个因数不变,另一个因数扩大(或缩小)若干倍,积也扩大(或缩小)相同的倍数”这一数学规律.教学难点理解因数和积的变化规律并运用规律计算.教学步骤一、铺垫孕伏.1.口算:420×2 9×40 23×30 0×700600×3 80×90 35×20 800×10200×30 70×60 1×190 18×402.下面两题,用竖式怎样计算比较简便?28×40 2800×30二、探究新知.1.教“扩大”或“缩小”几倍的含义.(1)讲授把一个数“扩大”几倍就是把这个数乘几.如5扩大3倍就是5×3=15,板书:,把一个数缩小几倍就是把这个数除以几.如15缩小3倍就是15÷3=5,板书:(2)练习:① 6扩大4倍是多少?② 3扩大10倍是多少?③ 200缩小20倍是多少?④ 8缩小8倍是多少?2.教例6.(1)出示表格:因数1616161616因数241020100积32(2)学生口算填表:(3)想:发现了什么?分组讨论.①第2、3、4、5组的第二个因数同第一组比较,分别扩大2倍、5倍、10倍、50倍,积也随着扩大2倍、5倍、10倍、50倍.②一个因数不变,另一个因数扩大若干倍,积也扩大相同的倍数.(4)练习:12×3= 48×5=24×5=120×3= 48×50= 24×25=1200×3= 48×500=24×75=小结:启发学生把发现的规律进行概括:一个因数不变,另一个因数扩大(或缩小)若干倍,积也扩大(或缩小)相同的倍数.(5)填空练习:①在4×5=20中,如果4不变,5扩大2倍,那么积也()倍.②在6×8=48中,如果8不变,6缩小3倍,那么积也()倍.三、课堂总结.这堂课你学到了什么?四、随堂练习.1.填表:观察每次计算同前一次比较,因数有什么变化?积有什么变化?因数204040200200因数5050100100200积2.填空:(1)一个因数不变,另一个因数(),积也().(2)一个因数不变,另一个因数扩大5倍,积();一个因数缩小7倍,另一个因数不变,积();一个因数不变,要想使积扩大24倍,另一个因数().五、布置作业.(207+99)×32 130×(560-490) 400×(225÷9)(798+486)÷6板书设计因数和积的变化规律因数1616161616因数241020100积32641603201600一个因数不变,另一个因数扩大(或缩小)若干倍,积也扩大(或缩小)相同的倍数.。
因数与积的变化

因数和与积的变化规律请家长先生督促孩子理解并背以下数学知识点。
家长签名---------- 1、请同学们仔细观察下面的一组算式,你能接着写出下面的两个算式吗?(提示:因数有什么变化,积有什么变化。
)第一组:(1)、从上往下看,我的发现是:两数相乘,一个因数不变,(1)6×2=12 另一个因数扩大几倍,积也会扩大相同的倍数。
(2)6×20=120 或第一个因数不变,第二个因数越变越大,积也越变越(3)6×200=1200大。
大。
(4)6×2000=12000(5)6×20000=120000(2)、从下往上看,我的发现是:两数相乘,一个因数不变,另一个因数缩小几倍,积也会缩小相同的倍数。
或第一个因数不变,另一个因数越变越小,积也越变越小。
2、总结:两数相乘,一个因数不变,另一个因数扩大(或缩小)若干倍,积也扩大(或缩小)相同的倍数。
或两数相乘,一个因数不变,另一个因数乘(或除以0除外)几,积也乘(或除以)几。
3、根据8×50=400,直接写出下面各题的积。
(1)16×50=(2)24×50=(3)32×50=从左往右看3个算式的变化规律是:第二个因数不变,第一个因数(),积()。
4:先填得数,后思考:你发现了什么规律?第一组第二组5×10 = 2 ×3=5 ×100 = 4 ×3=5 ×1000 = 10×3=5、我的发现是:1、第一个因数不变,第二个因数扩大多少倍,积也扩大相同的倍数。
2、第二个因数不变,第一个因数扩大多少倍,积也扩大相同的倍数。
3、第一个因数不变,第二个因数缩小多少倍,积也缩小相同的倍数。
4、第二个因数不变,第一个因数缩小多少倍,积也缩小相同的倍数。
6、3×6= 30×6= 300×6= 我的发现是(先不看零相乘,再看两个因数的末尾一共有几个零,就在不看零时乘得的结果后面添上几个零)。
因数与积的变化规律
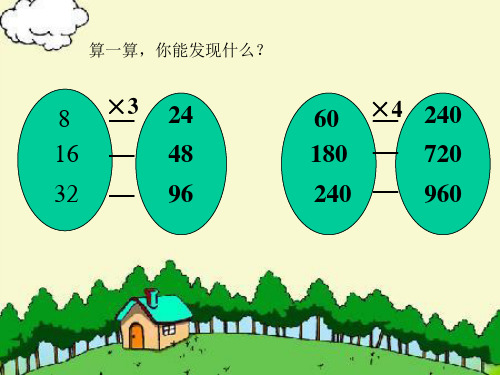
8 16 32
×3
— — —
24 48 96
60 ×4 240 — 180 — 720 240 — 960
四合庄小学
陈虹
计算下面的三道题,你有什么发现吗? 把你的发现写下来。
6× 2=( 12 )
6×20=( 120 )
6×200=( 1200)
6× 2
×10
= 12
×10
先用积的变化规律填空,再用笔算或计 算器验算。 26×48= 1248 26×24=( 624 ) 26×12=( 312 ) 17×48= 816 17×24=( 408 ) 17×12=( 204 )
两数相乘,一个因数不变, 另一个因数扩大(或缩小) 若干倍时,积也扩大(或缩 小)相同的倍数。
同学们安静地各写两组算式 , 一组3个,展现积分别随一个 因数扩大、缩小的变化情况。
×100 =
6 × 20
×10
120
×100
×10
6 × 200
= 1200
因数
16 2
32
不 变 扩大5倍
扩大5倍
… 16
… 10 160 …
因数
积
因数 因数 积
16 2
不 变
扩大100倍
… 16
… 200 … 3200
32 扩大100倍
两数相乘,一个因数不变,另一个因数 扩大若干倍时,积也扩大相同的倍数。
20 × 8=( 160 )
10 × 8=( 80 )
5 × 8=( 40 )
20× 8 ÷2 ÷4
= 160 ÷2 ÷4
10× 8 ÷2
5× 8 =
= 80
÷2 40
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因数和与因数积
在数学中,因数是指能够整除某个数的数,而因数和与因数积则是与因数相关的数学概念。
因数和是指一个数所有因数的和,而因数积则是指一个数所有因数的乘积。
这两个概念在数学中有着广泛的应用。
一、因数和
1.1 定义
一个数的因数和是指该数所有因数的和。
例如,数12的因数和为1+2+3+4+6+12=28。
1.2 计算方法
计算一个数的因数和可以通过以下方法进行:
(1)列出该数的所有因数;
(2)将所有因数相加,得到因数和。
例如,计算数12的因数和,可以列出其因数1、2、3、4、6、12,然后将它们相加,得到28。
1.3 性质
(1)一个数的因数和等于所有小于等于该数的正整数的因数和之和。
(2)一个数的因数和等于该数的约数个数乘以该数的因数平均值。
(3)一个数的因数和等于其所有因数的积除以该数本身再加1。
1.4 应用
因数和在数论中有着广泛的应用,例如:
(1)判断一个数是否为完全数。
完全数是指一个数等于它的因数和减去它本身,例如,6是一个完全数,因为6的因数和为
1+2+3+6=12,减去6得到6。
(2)计算一个数的约数个数。
一个数的约数个数等于其因数和除以该数本身再加1,例如,数12的因数和为28,约数个数为6。
(3)计算一个数的因数平均值。
一个数的因数平均值等于其因数和除以其约数个数,例如,数12的因数平均值为28/6=4.67。
二、因数积
2.1 定义
一个数的因数积是指该数所有因数的乘积。
例如,数12的因数积为1×2×3×4×6×12=1728。
2.2 计算方法
计算一个数的因数积可以通过以下方法进行:
(1)列出该数的所有因数;
(2)将所有因数相乘,得到因数积。
例如,计算数12的因数积,可以列出其因数1、2、3、4、6、12,然后将它们相乘,得到1728。
2.3 性质
(1)一个数的因数积等于该数的因数个数的一半次方乘以该数的平方根。
(2)一个数的因数积等于其所有因数的积的平方根。
2.4 应用
因数积在数论中也有着广泛的应用,例如:
(1)计算一个数的因数个数。
一个数的因数个数等于其因数积
的因数个数,例如,数12的因数积为1728,因数个数为6。
(2)判断一个数是否为平方数。
如果一个数的因数积是一个完
全平方数,那么该数就是一个平方数,例如,数16的因数积为1×2×4×8×16=1024,是一个完全平方数。
(3)计算一个数的因数之和。
一个数的因数之和等于其因数积
除以该数本身再加1,例如,数12的因数之和为1728/12+1=145。
三、结论
因数和与因数积是与因数相关的两个数学概念,在数学中有着广泛的应用。
因数和可以用于判断完全数、计算约数个数和因数平均值等问题,而因数积则可以用于判断平方数、计算因数个数和因数之和等问题。
熟练掌握这两个概念对于数学学习和解题都有着重要的意义。
