高中数学空间中的平行关系考点及例题讲解
考点22 空间几何平行问题(讲解)(解析版)

考点22 空间几何平行问题【思维导图】【常见考法】考法一 平行传递性证线线平行1.四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底面ABCD ,01,90.2AB BC AD BAD ABC ==∠=∠= 证明:直线//BC 平面PAD ;【答案】见解析 【解析】 在平面内,因为,所以又平面平面故平面考法二 三角形中位线证线线平行1.如图,在四棱锥P -ABCD 中,底面ABCD 为平行四边形,E 为侧棱P A 的中点,求证:PC // 平面BDE ;【答案】见解析【解析】证明: 连结AC ,交BD 于O ,连结OE .因为ABCD 是平行四边形,所以OA OC =. 因为E 为侧棱PA 的中点所以OE ∥PC .因为PC ⊄平面BDE ,OE ⊂平面BDE 所以PC ∥平面BDE .2.四棱锥P ABCD -中,底面ABCD 为矩形,PA ABCD ⊥平面,E 为PD 的中点,证明://E PB A C 平面;【答案】见解析【解析】连结BD 交AC 于点O,连结EO 因为ABCD 为矩形,所以O 为BD 的中点 又E 为的PD 的中点,所以EO//PBEO ⊂平面AEC,PB ⊄平面AEC ,所以PB//平面AEC考法三 构造平行四边形证线线平行1.如图,在四棱锥P−ABCD 中,底面ABCD 为平行四边形,E ,F 分别为AD ,PB 的中点,求证:EF ∥平面PCD .【答案】详见解析【解析】如图,取PC 中点G ,连接,FG GD .∵,F G 分别为PB 和PC 的中点,∴FG BC ,且12FG BC =. ∵四边形ABCD 为平行四边形,且E 为AD 的中点, ∴1,2ED BC DE BC =, ∴ED FG ,且ED FG =,∴四边形EFGD 为平行四边形,∴EF GD . 又EF ⊄平面PCD ,GD ⊂平面PCD ,∴EF 平面PCD .2.如图,在直四棱柱1111ABCD A B C D -中,底面ABCD 为梯形,//AB CD ,60BAD ∠=,1CD =,2AD =,4AB =,点G 在线段AB 上,3AG GB =,11AA =,证明:1//D G 平面11BB C C【答案】证明见解析【解析】证明:连接1C B ,因为底面ABCD 为梯形,//AB CD ,44AB CD ==,3AG GB =, 则11////GB CD D C ,且111GB D C ==, 所以四边形11GBC D 为平行四边形,则11//D G C B . 又1C B ⊂平面11BB C C ,1D G ⊄平面11BB C C , 所以1//D G 平面11BB C C .考法四 线面垂直的性质证线线平行1.如图,BCD 与MCD △都是边长为2的正三角形,平面MCD ⊥平面BCD ,AB ⊥平面BCD ,2AB =,证明:直线//AB 平面MCD ;【答案】见解析【解析】证明:取CD 中点O ,连接MO ,MCD 是正三角形,MO CD ∴⊥∵平面MCD ⊥平面BCD ,MO ∴⊥平面BCD ,AB ⊥平面BCD ,∴//MO AB ,又MO ⊂面MCD ,AB ⊄面MCD ,//AB ∴面MCD .2如图,菱形ABCD 与正三角形BCE 的边长均为2,且平面ABCD ⊥平面BCE ,FD ⊥平面ABCD ,FD =//EF 平面ABCD证明:如图,过点E 作EH BC ⊥于H ,连接HD ,∴EH =D ∵平面ABCD ⊥平面BCE ,EH ⊂平面BCE , 平面ABCD ⋂平面BCE BC =, ∴EH ⊥平面ABCD ,又∵FD ⊥平面ABCD ,FD =∴//FD EH ,FD EH =. ∴四边形EHDF 为平行四边形. ∴//EF HD .∵EF ⊄平面ABCD ,HD ⊂平面ABCD , ∴//EF 平面ABCD .考法五 三角形相似比证线线平行1.如图,在四棱锥P ABCD -中,PA =//AB CD ,1AD DC ==,2AB =,E 为侧棱P A 上一点,若13PE PA =,求证://PC 平面EBD【答案】证明见解析【解析】设AC BD G ⋂=,连结EG , 由已知//AB CD ,1DC =,2AB =,得2AG ABGC DC==. 由13PE PA =,得2AEEP =. 在PAC ∆中,由AE AG EP GC=,得//EG PC . 因为EG ⊂平面EBD ,PC ⊄平面EBD ,所以//PC 平面EBD.2.如图,在三棱柱111ABC A B C -中,侧面11ABB A 是菱形,160BAA ∠=︒,E 是棱1BB 的中点,CA CB =,F 在线段AC 上,且2AF FC .证明:1//CB 面1A EF【答案】详见解析【解析】连接1AB 交1A E 于点G ,连接FG . 因为11AGA B GE ∆∆,所以1112AA AG GB EB ==,又因为2AF FC=,所以1AF AG FC GB =,所以1//FG CB ,又1CB ⊄面1A EF ,FG ⊂面1A EF ,所以1//CB 面1A EF .考法六 线面平行性质证明线线平行1.如图,P 为平行四边形ABCD 所在平面外一点,E 为AD 上一点,且13AE ED =,F 为PC 上一点,当//PA 平面EBF 时,PFFC= .【答案】14【解析】连接AC 交BE 于点M ,连接FM . //PA 平面EBF ,PA ⊂平面PAC ,平面PAC 平面EBF FM =,//PA FM ∴,∴14PF AM AE FC MC BC ===,2.如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,M 是PC 的中点,在DM 上取一点G ,过点G 和AP 作平面,交平面BDM 于GH ,点H 在线段BD 上.求证://AP GH .【答案】证明见解析【解析】证明:如图,连接AC ,设AC 交BD 于点O ,连接MO .∵四边形ABCD 是平行四边形, ∴O 是AC 的中点又M 是PC 的中点,∴//MO PA . 又MO ⊂平面BDM ,PA ⊄平面BDM , ∴//PA 平面BDM又PA ⊂平面PAHG ,平面PAHG ⋂平面BDM GH =,∴//AP GH .3.如图所示,在多面体111A B D DCBA -中,四边形11AA B B ,11ADD A ,ABCD 均为正方形,E 为11B D 的中点,过1,,A D E 的平面交1CD 于F .证明:1//EF B C . 【答案】见解析 【解析】证明:11B C A D =且11A B CD =,∴四边形11A B CD 为平行四边形,11//B C A D ∴,又1B C ⊂/平面1A EFD ,1A D ⊂平面1A EFD1//B C ∴平面1A EFD ,又因为平面1A EFD平面11B CD EF =,1B C ⊂平面11B CD ,1//EF B C ∴;考法七 面面平行的性质证线面平行1.如图①所示,在直角梯形ABCP 中,APBC ,12AP AB AB BC AP ⊥==,,D 为AP 的中点,E F G ,,分别为PC PD CB ,,的中点,将PCD 沿CD 折起,得到四棱锥P ABCD -,如图②所示.求证:在四棱锥P ABCD -中,AP ∥平面EFG . 【答案】见解析【解析】∵G 为BC 的中点,E 为PC 的中点,∴GE ∥BP ∵GE ⊄平面PAB ,BP ⊂平面PAB ,∴GE ∥平面PAB , 由F 为PD 的中点,得EF ∥DC ,∵AB ∥DC ,∴EF ∥AB∵EF ⊄平面PAB ,AB ⊂平面PAB ,∴EF ∥平面PAB ,∵EF∩GE =E ∴平面EFG ∥平面PAB ,∵PA ⊂平面PAB ,∴AP ∥平面EFG .2如图,三棱锥P ABC -中, D 是PA 的中点, E 是CD 的中点,点F 在PB 上且14BF PB =,证明://EF 平面ABC ;证明:如图,取AD 中点G ,连接GE ,GF ,如图C 则GE//AC ,GF//AB , 因为GE∩GF=G ,AC∩AB=A ,所以平面GEF//平面ABC ,所以EF//平面ABC考法八:面面平行1.如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,点M ,N ,Q 分别在PA ,BD ,PD 上(不与端点重合),且:::PM MA BN ND PQ QD ==.求证:平面//MNQ 平面PBC .【答案】证明见解析【解析】证明 :::,==PM MA BN ND PQ QD .//,//∴MQ AD NQ BPBP ⊂平面,PBC NQ ⊄平面PBC ,//NQ ∴平面PBC .∵底面ABCD 为平行四边形,//,//BC AD MQ BC ∴∴.BC ⊂平面,PBC MQ ⊂/平面PBC ,//MQ ∴平面PBC .又MQ NQ Q =,根据平面与平面平行的判定定理,所以面//MNQ 平面PBC2.如图所示,在三棱柱111ABC A B C -中,E F G H ,,,分别是1111AB AC A B A C ,,,的中点,求证:(1)B C H G ,,,四点共面;(2)平面1EFA //平面BCHG .【答案】(1)证明见解析;(2)证明见解析.【解析】(1)G H ,分别是1111A B A C ,的中点,GH ∴是111A B C △的中位线,则11//GH B C ,又11////B C BC GH BC ∴,,B C H G ∴,,,四点共面. (2)E F ,分别为AB AC ,的中点,//EF BC ∴,EF ⊄平面BCHG BC ⊂,平面BCHG ,EF ∴平面BCHG ,又G E ,分别是11A B AB ,的中点,11A B AB ⊥,1A G EB ∴⊥,∴四边形1A EBG 是平行四边形,1//A E GB ∴,1A E ⊄平面BCHG GB ⊂,平面BCHG ,1//A E ∴平面BCHG ,又1A E EF E ⋂=,∴平面1EFA //平面BCHG ,考法九:动点问题1.如图,在四棱锥P ﹣ABCD 中,底面ABCD 为边长为2的菱形,点F 为棱PD 的中点,在棱AB 上是否存在一点E ,使得AF ∥面PCE ,并说明理由;【答案】见解析;【解析】在棱AB 上存在点E ,使得AF ∥面PCE ,点E 为棱AB 的中点.理由如下:取PC 的中点Q ,连结EQ 、FQ ,由题意,FQ ∥DC 且1FQ CD 2=,AE ∥CD 且1AE CD 2=,故AE ∥FQ 且AE =FQ .所以,四边形AEQF 为平行四边形.所以,AF ∥EQ ,又EQ ⊂平面PEC ,AF ⊄平面PEC ,所以,AF ∥平面PEC .2.如图,在三棱柱111ABC A B C -中,点,E F 分别是棱11,CC BB 上的点,点M 是线段AC 上的动点,22EC FB ==.若MB 平面AEF ,试判断点M 的位置.【答案】M 是AC 的中点【解析】由题意知//MB 平面AEF ,过,,F B M 作平面FBMN 交AE 于N ,连接,MN NF .因为//BF 平面11,AAC C BF ⊂平面FBMN ,平面FBMN ⋂平面11AAC C MN =,所以BF MN .因为//MB 平面,AEF MB ⊂平面FBMN ,平面FBMN ⋂平面AEF FN =,所以//MB FN ,所以四边形BFNM 是平行四边形,所以1MN BF ==.而//,22EC FB EC FB ==,所以1//,12MN EC MN EC==,故MN是ACE的中位线.所以M是AC的中点时,//MB平面AEF.。
空间中的平行与垂直例题和知识点总结

空间中的平行与垂直例题和知识点总结在立体几何的学习中,空间中的平行与垂直关系是非常重要的内容。
理解和掌握这些关系,对于解决相关的几何问题具有关键作用。
下面我们通过一些例题来深入探讨,并对相关知识点进行总结。
一、平行关系(一)线线平行1、定义:如果两条直线在同一平面内没有公共点,则这两条直线平行。
2、判定定理:如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行。
例 1:在正方体 ABCD A₁B₁C₁D₁中,E,F 分别是 AB,BC 的中点,求证:EF∥A₁C₁。
证明:连接 AC,因为 E,F 分别是 AB,BC 的中点,所以 EF∥AC。
又因为正方体中,AC∥A₁C₁,所以 EF∥A₁C₁。
(二)线面平行1、定义:如果一条直线与一个平面没有公共点,则称这条直线与这个平面平行。
2、判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
例 2:已知四棱锥 P ABCD 的底面是平行四边形,M 是 PC 的中点,求证:PA∥平面 MBD。
证明:连接 AC 交 BD 于 O,连接 MO。
因为四边形 ABCD 是平行四边形,所以 O 是 AC 的中点。
又因为 M 是 PC 的中点,所以MO∥PA。
因为 MO⊂平面 MBD,PA⊄平面 MBD,所以 PA∥平面MBD。
(三)面面平行1、定义:如果两个平面没有公共点,则称这两个平面平行。
2、判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
例 3:在正方体 ABCD A₁B₁C₁D₁中,求证:平面 A₁BD∥平面 B₁D₁C。
证明:因为 A₁B∥D₁C,A₁D∥B₁C,且 A₁B 和 A₁D 是平面A₁BD 内的两条相交直线,D₁C 和 B₁C 是平面 B₁D₁C 内的两条相交直线,所以平面 A₁BD∥平面 B₁D₁C。
二、垂直关系(一)线线垂直1、定义:如果两条直线所成的角为 90°,则这两条直线垂直。
人教高中数学B版必修2 空间中的平行关系 精讲精析
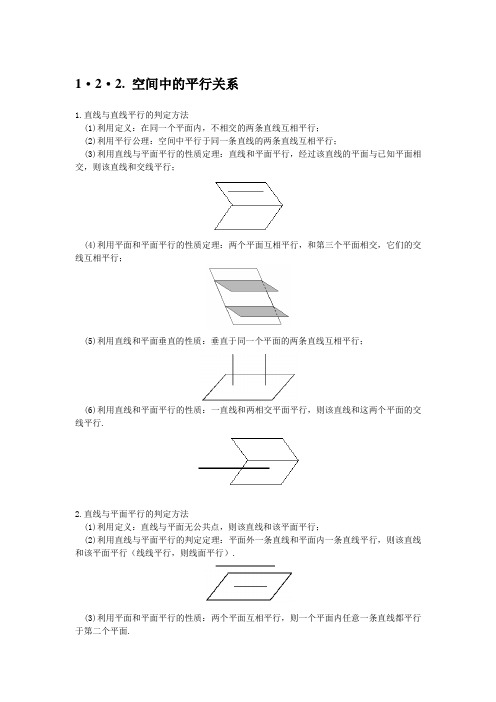
1·2·2. 空间中的平行关系1.直线与直线平行的判定方法(1)利用定义:在同一个平面内,不相交的两条直线互相平行;(2)利用平行公理:空间中平行于同一条直线的两条直线互相平行;(3)利用直线与平面平行的性质定理:直线和平面平行,经过该直线的平面与已知平面相交,则该直线和交线平行;(4)利用平面和平面平行的性质定理:两个平面互相平行,和第三个平面相交,它们的交线互相平行;(5)利用直线和平面垂直的性质:垂直于同一个平面的两条直线互相平行;(6)利用直线和平面平行的性质:一直线和两相交平面平行,则该直线和这两个平面的交线平行.2.直线与平面平行的判定方法(1)利用定义:直线与平面无公共点,则该直线和该平面平行;(2)利用直线与平面平行的判定定理:平面外一条直线和平面内一条直线平行,则该直线和该平面平行(线线平行,则线面平行).(3)利用平面和平面平行的性质:两个平面互相平行,则一个平面内任意一条直线都平行于第二个平面.3.平面和平面平行的判定方法(1)利用定义:两个平面没有公共点,则这两个平面平行;(2)利用平面与平面平行的判定定理:一个平面内有两条相交直线分别与另一个平面内两条相交直线平行,则这两个平面平行;(3)利用平面与平面平行的判定:一个平面内有两条相交直线分别平行于另一个平面,则这两个平面平行;(4)利用平面与平面平行的传递性:平行于同一个平面的两个平面互相平行.(5)利用直线与平面垂直的性质:垂直于同一条直线的两个平面互相平行;4.直线与平面平行的性质(1)性质定理:直线和平面平行,经过该直线的平面与已知平面相交,则该直线和交线平行;(2)直线和平面平行的性质:一直线和两相交平面平行,则该直线和这两个平面的交线平行.5.平面与平面平行的性质(1)平面与平面平行的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.(2)平面与平面平行的性质:两个平面互相平行,则一个平面内任意一条直线均平行于第二个平面.(3)平面与平面平行的性质:两个平面互相平行,那么夹在这两个平面之间的平行线段相等.(4)平面与平面平行的性质:平行平面中的一个垂直于第三个平面,则另一个也垂直于第三个平面.1. 求证:过两条平行直线有且只有一个平面. 已知:直线a ∥b.求证:过a ,b 有且只有一个平面. 【解析】证明:①存在性:由平行线的定义可知,过平行直线a ,b 有一个平面.②唯一性(反证法):假设过a ,b 有两个平面.在直线上任取两点A 、B ,在直线b 上任取一点C ,则A 、B 、C 三点不共线.由于这两个平面都过直线a ,b ,因此由公理1可知:都过点A 、B 、C.由平面的基本性质公理2,过不共线三点的平面唯一存在,因此重合,与假设矛盾.矛盾表明:过平行直线a ,b 只有一个平面. 综上所述:过a ,b 有且只有一个平面.,αβa ,αβ,αβ,αβ2. 已知平面α∩β=m,直线a//α,a//β,求证:a//m.【解析】证明:过a 作一平面与α交于直线b,由线面平行的性质可知:a//b;过a作另一平面与β交于直线c,则:a//c.由平行公理可知:b//c,故b//β.由线面平行的性质可知:b//m.由平行公理,a//m.【说明】判定空间关系的主要思路有三种,一是利用判定定理和相关结论,二是反证法(常利用定义),三是同一法,并且凡是用反证法可以证明的都可以用同一法证明.而且一般地,每个这样的题目都可以同时使用这三种方法.同一法的主要过程是:欲证某几何图形M具备某性质,可以先作一个图形M′具备这种性质,然后证明所作图形M′与待证图形M是同一个图形,因M′具备这种性质,故M也具备该性质.如本题可用同一法证明如下:证明:在m上取一点A,过a、A作一平面分别交α、β于e、f,则e//a,f//a,即过直线外一点有两条直线与之平行,因此e、f重合,记为l;又e在α上,f在β上,且e、f重合于l,故l是α、β的交线,故l与m重合.因l//a,故m//a.3. 平面α外的两条直线a//b,且a//α,求证:b//α.【解析】证明:因a//α,过a作一平面与α交于直线m,则由直线与平面平行的性质可知:a//m. 又因a//b,a//m,故b//m,由线面平行的判定定理可知:b//α.4. 如图,ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP//GH.【解析】证明:连接AC交BD于O,连接MO.因为ABCD是平行四边形,故O是AC中点.又M是PC中点,故AP//OM.又AP在平面BDM外,OM在平面BDM上,故AP//平面BDM.因为平面PAGH∩平面BDM=GH,根据线面平行的性质定理,得PA//GH.5. 如图,三棱柱ABC-A′B′C′,D是BC上一点,且A′B//平面AC′D,D′是B′C′的中点,求证:平面A′BD′//平面AC′D.【解析】证明:连接A′C交AC′于点E,则E是A′C中点.连接ED,因为A′B//平面AC′D,平面A′BC∩平面AC′D=ED,所以A′B∥ED,因为E是A′C中点,所以D是BC中点.又D′是B′C′中点,所以BD′∥C′D,A′D′∥AD.又A′D′∩BD′=D′,所以平面A′BD′∥平面AC′D.6. 已知平面α//γ,γ//β,求证:α//β.【解析】作两个相交平面分别交α、β、γ于a、b、c和a′、b′、c′.因为α//γ,故a//c,a′//c′.因为γ//β,故b//c,b′//c′.从而a//b,a′//b′,即平面α、β内分别有两条相交直线平行,故α//β.。
高考数学总复习---空间中的平行与垂直关系知识点总结及真题训练.doc
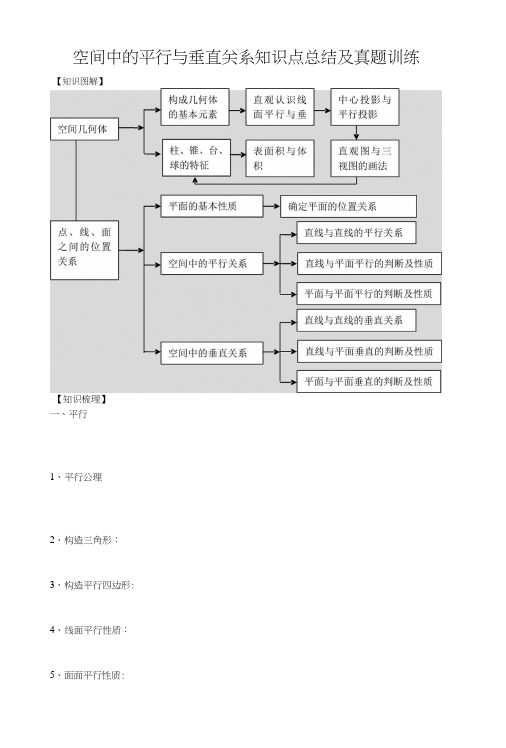
空间中的平行与垂直关系知识点总结及真题训练【知识图解】【知识梳理】一、平行1、平行公理2、构造三角形:3、构造平行四边形:4、线面平行性质:5、面面平行性质:6、线面平行判定:7、面面平行的性质:8、面面平行的判定1:9、面面平行的判定2:【典型例题】例1、正方体ABCD_A、B\GD\屮,E,F分别是的屮点,求ffi: EF〃面ABCD.变式:如图,两个全等的正方形ABCD和M3EF所在的平面相交于AB, M eAC, Nw FB 且AM = FN,求证:MN〃平面BCE.例2、如图,以垂直于矩形ABCD所在的平面,PA=AD f E、F分别是AB、PD 的中点。
(1)求证:AF〃平面PCE;*(2)求证:平面PCE丄平面PCD。
/ \\(1) 求证:BC 】//平面CAD(2) 求证:平面CAJ)丄平面AAiBiBo例3、浙江理20.(本题满分15分)如图,平面PAC 丄平面ABC, \ABCPB, AC 的中点,AC = 16, PA = PC = 10.(I) 设G 是0C 的中点,证明:FG//平面BOE ;(II) 证明:在AABO 内存在一点M ,使FM 丄平面BOE, 并求点M 到Q4, 03的距离.练习:1、(浙江卷文)(本题满分14分)如图,DC 丄平面ABC , EB//DCAC = BC = EB = 2DC = 2 , ZACB = 120 ,只Q 分别为AE.AB 的中点.(I )证明:PQII 平面ACD ; (II )求AD 与平面ABE Wr 成角的.正弦值.2、如图,在直三棱柱ABC-A1B1C1屮,AC=BC,点D 是AB 的屮点。
是以4C 为斜边的等腰直角三角形,匕£0分别为必,(第20(2) 求二面角B-FC!-C 的余眩值。
. Ei D L-.-.♦ E / ■<C 3、如图,在四面体ABCD 中,截而EFGH 是平行四边形•求证:AB 〃平面EFGH.安徽理(19)如图,圆锥定点为P,底面圆心为O,其母线与底而所成的角为22.5°, AB 和 CD 是底面圆0上的两条平行的弦,轴OP 与平面PCD 所成的角为60°-(1) 证明:平面PAB 与平面PCD 的交线平行于底面;(2) 求 cosZCOD4、点P 是平行四边形ABCD 所在的平面外一点,E,F 分别是PA,BD 上的点,且 PE:EA=BF ・・FD,求证:EF//面PBC.5、(山东卷理)(本小题满分12分)如图,在直四棱柱ABCD ・A]B]C]D]中,底面ABCD 为等腰梯形,AB//CD, AB=4, BC=CD=2, AA )=2, E 、E“ F 分别是棱 AD 、AA 【、AB 的中点。
考点22 空间几何平行问题(讲解)(解析版)

考点22 空间几何平行问题【思维导图】【常见考法】考法一平行传递性证线线平行1.四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底面ABCD ,01,90.2AB BC AD BAD ABC ==∠=∠= 证明:直线//BC 平面PAD ;【答案】见解析【解析】 在平面内,因为,所以又平面平面故平面考法二 三角形中位线证线线平行1.如图,在四棱锥P -ABCD 中,底面ABCD 为平行四边形,E 为侧棱P A 的中点,求证:PC // 平面BDE ;【答案】见解析【解析】证明: 连结AC ,交BD 于O ,连结OE .因为ABCD 是平行四边形,所以OA OC =.因为E 为侧棱PA 的中点所以OE ∥PC .因为PC ⊄平面BDE ,OE ⊂平面BDE 所以PC ∥平面BDE .2.四棱锥P ABCD -中,底面ABCD 为矩形,PA ABCD ⊥平面,E 为PD 的中点,证明://E PB A C 平面;【答案】见解析【解析】连结BD 交AC 于点O,连结EO 因为ABCD 为矩形,所以O 为BD 的中点又E 为的PD 的中点,所以EO//PBEO ⊂平面AEC,PB ⊄平面AEC ,所以PB//平面AEC考法三 构造平行四边形证线线平行1.如图,在四棱锥P−ABCD 中,底面ABCD 为平行四边形,E ,F 分别为AD ,PB 的中点,求证:EF ∥平面PCD .【答案】详见解析【解析】如图,取PC 中点G ,连接,FG GD .∵,F G 分别为PB 和PC 的中点,∴FG BC ,且12FG BC =. ∵四边形ABCD 为平行四边形,且E 为AD 的中点, ∴1,2ED BC DE BC =, ∴ED FG ,且ED FG =,∴四边形EFGD 为平行四边形,∴EF GD .又EF ⊄平面PCD ,GD ⊂平面PCD ,∴EF 平面PCD .2.如图,在直四棱柱1111ABCD A B C D -中,底面ABCD 为梯形,//AB CD ,60BAD ∠=,1CD =,2AD =,4AB =,点G 在线段AB 上,3AG GB =,11AA =,证明:1//D G 平面11BB C C【答案】证明见解析【解析】证明:连接1C B ,因为底面ABCD 为梯形,//AB CD ,44AB CD ==,3AG GB =, 则11////GB CD D C ,且111GB D C ==,所以四边形11GBC D 为平行四边形,则11//D G C B .又1C B ⊂平面11BB C C ,1D G ⊄平面11BB C C ,所以1//D G 平面11BB C C .考法四 线面垂直的性质证线线平行1.如图,BCD 与MCD △都是边长为2的正三角形,平面MCD ⊥平面BCD ,AB ⊥平面BCD ,2AB =,证明:直线//AB 平面MCD ;【答案】见解析【解析】证明:取CD 中点O ,连接MO , MCD 是正三角形,MO CD ∴⊥∵平面MCD ⊥平面BCD ,MO ∴⊥平面BCD ,AB ⊥平面BCD ,∴//MO AB ,又MO ⊂面MCD ,AB ⊄面MCD ,//AB ∴面MCD .2如图,菱形ABCD 与正三角形BCE 的边长均为2,且平面ABCD ⊥平面BCE ,FD ⊥平面ABCD ,FD =//EF 平面ABCD证明:如图,过点E 作EH BC ⊥于H ,连接HD ,∴EH =D∵平面ABCD ⊥平面BCE ,EH ⊂平面BCE ,平面ABCD ⋂平面BCE BC =,∴EH ⊥平面ABCD ,又∵FD ⊥平面ABCD ,FD =∴//FD EH ,FD EH =.∴四边形EHDF 为平行四边形.∴//EF HD .∵EF ⊄平面ABCD ,HD ⊂平面ABCD ,∴//EF 平面ABCD .考法五 三角形相似比证线线平行1.如图,在四棱锥P ABCD -中,PA =//AB CD ,1AD DC ==,2AB =,E 为侧棱P A 上一点,若13PE PA =,求证://PC 平面EBD【答案】证明见解析【解析】设AC BD G ⋂=,连结EG ,由已知//AB CD ,1DC =,2AB =,得2AG AB GC DC ==. 由13PE PA =,得2AE EP =. 在PAC ∆中,由AE AG EP GC =,得//EG PC . 因为EG ⊂平面EBD ,PC ⊄平面EBD ,所以//PC 平面EBD.2.如图,在三棱柱111ABC A B C -中,侧面11ABB A 是菱形,160BAA ∠=︒,E 是棱1BB 的中点,CA CB =,F 在线段AC 上,且2AF FC .证明:1//CB 面1A EF【答案】详见解析【解析】连接1AB 交1A E 于点G ,连接FG .因为11AGA B GE ∆∆,所以1112AA AG GB EB ==,又因为2AF FC =,所以1AF AG FC GB =,所以1//FG CB , 又1CB ⊄面1A EF ,FG ⊂面1A EF ,所以1//CB 面1A EF .考法六线面平行性质证明线线平行1.如图,P为平行四边形ABCD所在平面外一点,E为AD上一点,且13AEED=,F为PC上一点,当//PA平面EBF时,PFFC=.【答案】1 4【解析】连接AC交BE于点M,连接FM.//PA平面EBF,PA⊂平面PAC,平面PAC平面EBF FM=,//PA FM ∴,∴14 PF AM AEFC MC BC===,2.如图,在四棱锥P ABCD-中,底面ABCD为平行四边形,M是PC的中点,在DM上取一点G,过点G和AP作平面,交平面BDM于GH,点H在线段BD上.求证://AP GH.【答案】证明见解析【解析】证明:如图,连接AC,设AC交BD于点O,连接MO.∵四边形ABCD 是平行四边形,∴O 是AC 的中点又M 是PC 的中点,∴//MO PA .又MO ⊂平面BDM ,PA ⊄平面BDM ,∴//PA 平面BDM又PA ⊂平面PAHG ,平面PAHG ⋂平面BDM GH =,∴//AP GH .3.如图所示,在多面体111A B D DCBA -中,四边形11AA B B ,11ADD A ,ABCD 均为正方形,E 为11B D 的中点,过1,,A D E 的平面交1CD 于F .证明:1//EF B C .【答案】见解析【解析】证明: 11B C A D =且11A B CD =,∴四边形11A B CD 为平行四边形,11//B C A D ∴,又1B C ⊂/平面1A EFD ,1A D ⊂平面1A EFD1//B C ∴平面1A EFD ,又因为平面1A EFD 平面11B CD EF =,1B C ⊂平面11B CD ,1//EF B C ∴;考法七 面面平行的性质证线面平行1.如图①所示,在直角梯形ABCP 中,AP BC ,12AP AB AB BC AP ⊥==,,D 为AP 的中点,E F G ,,分别为PC PD CB ,,的中点,将PCD 沿CD 折起,得到四棱锥P ABCD -,如图②所示.求证:在四棱锥P ABCD -中,AP ∥平面EFG .【答案】见解析【解析】∵G 为BC 的中点,E 为PC 的中点,∴GE ∥BP∵GE ⊄平面PAB ,BP ⊂平面PAB ,∴GE ∥平面PAB ,由F 为PD 的中点,得EF ∥DC ,∵AB ∥DC ,∴EF ∥AB∵EF ⊄平面PAB ,AB ⊂平面PAB ,∴EF ∥平面PAB ,∵EF∩GE =E∴平面EFG ∥平面PAB ,∵PA ⊂平面PAB ,∴AP ∥平面EFG .2如图,三棱锥P ABC -中, D 是PA 的中点, E 是CD 的中点,点F 在PB 上且14BF PB =,证明: //EF 平面ABC ;证明:如图,取AD 中点G ,连接GE ,GF ,如图C 则GE//AC ,GF//AB , 因为GE∩GF=G ,AC∩AB=A ,所以平面GEF//平面ABC ,所以EF//平面ABC考法八:面面平行1.如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,点M ,N ,Q 分别在PA ,BD ,PD 上(不与端点重合),且:::PM MA BN ND PQ QD ==.求证:平面//MNQ 平面PBC .【答案】证明见解析【解析】证明 :::,==PM MA BN ND PQ QD .//,//∴MQ AD NQ BPBP ⊂平面,PBC NQ ⊄平面PBC ,//NQ ∴平面PBC .∵底面ABCD 为平行四边形,//,//BC AD MQ BC ∴∴.BC ⊂平面,PBC MQ ⊂/平面PBC ,//MQ ∴平面PBC .又MQ NQ Q =,根据平面与平面平行的判定定理,所以面//MNQ 平面PBC2.如图所示,在三棱柱111ABC A B C -中,E F G H ,,,分别是1111AB AC A B A C ,,,的中点,求证:(1)B C H G ,,,四点共面;(2)平面1EFA //平面BCHG .【答案】(1)证明见解析;(2)证明见解析.【解析】(1)G H ,分别是1111A B A C ,的中点,GH ∴是111A B C △的中位线,则11//GH B C ,又11////B C BC GH BC ∴,,B C H G ∴,,,四点共面. (2)E F ,分别为AB AC ,的中点,//EF BC ∴,EF ⊄平面BCHG BC ⊂,平面BCHG ,EF ∴平面BCHG ,又G E ,分别是11A B AB ,的中点,11A B AB ⊥,1A G EB ∴⊥,∴四边形1A EBG 是平行四边形,1//A E GB ∴,1A E ⊄平面BCHG GB ⊂,平面BCHG ,1//A E ∴平面BCHG ,又1A E EF E ⋂=,∴平面1EFA //平面BCHG ,考法九:动点问题1.如图,在四棱锥P ﹣ABCD 中,底面ABCD 为边长为2的菱形,点F 为棱PD 的中点,在棱AB 上是否存在一点E ,使得AF ∥面PCE ,并说明理由;【答案】见解析;【解析】在棱AB 上存在点E ,使得AF ∥面PCE ,点E 为棱AB 的中点.理由如下:取PC 的中点Q ,连结EQ 、FQ ,由题意,FQ ∥DC 且1FQ CD 2=,AE ∥CD 且1AE CD 2=,故AE ∥FQ 且AE =FQ .所以,四边形AEQF 为平行四边形.所以,AF ∥EQ ,又EQ ⊂平面PEC ,AF ⊄平面PEC ,所以,AF ∥平面PEC .2.如图,在三棱柱111ABC A B C -中,点,E F 分别是棱11,CC BB 上的点,点M 是线段AC 上的动点,22EC FB ==.若MB 平面AEF ,试判断点M 的位置.【答案】M 是AC 的中点【解析】由题意知//MB 平面AEF ,过,,F B M 作平面FBMN 交AE 于N ,连接,MN NF .因为//BF 平面11,AAC C BF ⊂平面FBMN ,平面FBMN ⋂平面11AAC C MN =,所以BF MN .因为//MB 平面,AEF MB ⊂平面FBMN ,平面FBMN ⋂平面AEF FN =,所以//MB FN ,所以四边形BFNM 是平行四边形,所以1MN BF ==.而//,22EC FB EC FB ==, 所以1//,12MN EC MN EC ==, 故MN 是ACE 的中位线.MB平面AEF.所以M是AC的中点时,//。
空间直线、平面的平行 高中数学例题课后习题详解

8.5空间直线、平面的平行8.5.1直线与直线平行例1如图8.5-3,空间四边形ABCD 中,E ,F ,G ,H 分别是边AB ,BC ,CD ,DA 的中点.求证:四边形EFGH 是平行四边形.分析:要证明四边形EFGH 是平行四边形,只需证明它的一组对边平行且相等.而EH ,FG 分别是ABD △和CBD 的中位线,从而它们都与BD 平行且等于BD 的一半.应用基本事实4,即可证明EH FG .证明:连接BD .∵EH 是ABD △的中位线,∴//EH BD ,且12EH BD =.同理//FG BD ,且12FG BD =.∴EH FG ∴四边形EFGH 为平行四边形.练习1.如图,把一张矩形纸片对折几次,然后打开,得到的折痕互相平行吗?为什么?【答案】互相平行,理由见解析【解析】【分析】根据对折可知:每对折一次,把矩形纸片分成的部分翻倍,形状还是全等的矩形,即可得到结论.【详解】互相平行,因为根据对折可知:每对折一次,把矩形纸片分成的部分翻倍,形状还是全等的矩形,所有的折痕都与矩形的边平行,故打开后所有折痕是互相平行.【点睛】本题考查了图形的变化,解题的关键是:根据对折把矩形纸片分成的部分翻倍,形状还是矩形,属于基础题.2.如图,在长方体ABCD A B C D ''''-中,与棱AA '平行的棱共有几条?分别是什么?【答案】共3条,分别是,,BB CC DD '''.【解析】【分析】根据图形,AA '是长方体的高的棱,找出其它的表示高的棱即可.【详解】如图,与棱AA '平行的棱有,,BB CC DD ''',共3条.【点睛】本题考查了对长方体的认识,明确表示长的棱,表示宽的棱,表示高的棱是解题的关键,属于基础题.3.如图,,,AA BB CC '''不共面,且//AA BB '',//BB CC '',求证:'ABC A B C ''≅ .【答案】证明见解析【解析】【分析】由已知条件推导出四边形ABB A ''是平行四边形,四边形ACC A ''为平行四边形,由此能证明ABC A B C '''∆≅∆.【详解】//AA '' ,∴四边形ABB A ''是平行四边形,AB A B ''∴=.同理'BC B C '=.'//,//AA BB BB CC ''' .//AA CC ''∴.,AA BB BB CC ''''== .AA CC ''∴=.∴四边形ACC A ''是平行四边形,AC A C ''∴=,ABC A B C '''∴∆≅∆.【点睛】本题考查三角形全等的证明,解题时要认真审题,注意空间思维能力的培养,属于基础题.4.如图,在四面体A BCD -中,E F G ,,分别为AB AC AD ,,上的点.若//EF BC ,//FG CD ,则EFG 和BCD △有什么关系?为什么?【答案】EFG BCD ∽,证明见解析【解析】【分析】利用线线平行,再利用等角定理即可得到EFG BCD ∆∆∽.【详解】EFG BCD ∽,证明如下://EF BC ,AE AF EF AB AC BC∴==.//FG CD ,AF AG FG AC AD CD ∴==,AE AG AB AD∴=,//EG BD ∴.由等角定理可得,,EFG BCD FGE CDB GEF DBC ∠=∠∠=∠∠=∠,EFG BCD ∴ ∽.【点睛】本题考查线线平行,平行线分线段成比例,属于基础题.8.5.2直线与平面平行例2求证:空间四边形相邻两边中点的连线平行于经过另外两边的平面.已知:如图8.5-7,空间四边形ABCD 中,E ,F 分别是AB ,AD 的中点.求证://EF 平面BCD .证明:连接BD .∵AE EB =,AFFD =,∴//EF BD .又EF ⊄平面BCD ,BD ⊂平面BCD ,∴//EF 平面BCD .例3如图8.5-10(1)所示的一块木料中,棱BC 平行于面A C ''.(1)要经过面A C ''内的一点P 和棱BC 将木料锯开,在木料表面应该怎样画线?(2)所画的线与平面AC 是什么位置关系?分析:要经过面A C ''内的一点P 和棱BC 将木料锯开,实际上是经过BC 及BC 外一点P 作截面,也就需要找出所作的截面与相关平面的交线.我们可以依据直线与平面平行的性质定理、基本事实4和推论1画出所需要的线段.解:(1)如图8.5-10(2),在平面A C ''内,过点P 作直线EF ,使//EF B C '',并分别交棱A B '',DC '于点E ,F ,连接BE ,CF ,则EF ,BE ,CF 就是应画的线.(2)因为棱BC 平行于平面A C '',平面BC '与平面A C ''相交于B C '',所以//BC B C '''.由(1)知,//EF B C '',所以//EF BC .而BC 在平面AC 内,EF 在平面AC 外,所以//EF 平面AC .显然,BE ,CF 都与平面AC 相交.练习5.如图,在长方体ABCD A B C D ''''-的六个面所在的平面中,(1)与AB 平行的平面是______;(2)与AA '平行的平面是______;(3)与AD 平行的平面是______.【答案】①.平面A B C D '''',平面DCC D ''②.平面BCC B '',平面DCC D ''③.平面A B C D '''',平面BCC B ''【解析】【分析】(1)根据线面平行的判定定理填写出正确结论.(2)根据线面平行的判定定理填写出正确结论.(3)根据线面平行的判定定理填写出正确结论.【详解】(1)由于''//AB A B ,AB ⊂/平面''''A B C D ,''A B ⊂平面''''A B C D ,所以//AB 平面''''A B C D .同理证得//AB 平面''DCC D .(2)由于''//AA BB ,'AA ⊂平面''BCC B ,'BB ⊂平面''BCC B ,所以'//AA 平面''BCC B .同理证得'//AA 平面''DCC D .(3)由于''//AD A D ,AD ⊂平面''''A B C D ,''A D ⊂平面''''A B C D ,所以//AD 平面''''A B C D .同理证得//AD 平面''BCC B .故答案为:(1).平面A B C D '''',平面DCC D '';(2).平面BCC B '',平面DCC D '';(3).平面A B C D '''',平面BCC B ''.【点睛】本小题主要考查线面平行的判定定理,属于基础题.6.如图,在正方体1111ABCD A B C D -中,E 为1DD 的中点,判断1BD 与平面AEC 的位置关系,并说明理由.【答案】1//BD 平面AEC .见解析【解析】【分析】通过三角形的中位线以及线面平行的判定定理,证得1//BD 平面AEC .【详解】1//BD 平面AEC 理由如下:如图,在正方体1111ABCD A B C D -中,连接BD 交AC 于点F ,则F 为BD 中点.连接EF ,又∵E 为1DD 的中点,∴EF 是1B D D ∆的中位线,1//EF BD ∴.1BD ⊄ 平面AEC ,EF ⊂平面AEC ,1//BD ∴平面AEC .【点睛】本小题主要考查线面平行的证明,考查空间想象能力和逻辑推理能力,属于基础题.7.判断下列命题是否正确,正确的在括号内画“√”,错误的画“×”.(1)如果直线//a b ,那么a 平行于经过b 的任何平面.()(2)如果直线a 与平面α满足//a α,那么a 与α内的任何直线平行.()(3)如果直线a b ,和平面α满足//a α,//b α,那么//a b .()(4)如果直线a b ,和平面α满足//a b ,//a α,b α⊄,那么//b α.()【答案】①.×②.×③.×④.√【解析】【分析】(1)根据“a 在以,a b 确定的平面内”,由此判断(1)错误.(2)根据a 与α内直线可能异面,判断(2)错误.(3)根据,a b 可能平行、相交或异面,判断(3)错误.(4)根据线面平行的性质定理和判定定理,以及平行公理,证得//b α,由此判断(4)正确.【详解】(1)α不平行于同时过a b ,这两条直线的平面.(2)a 与α内的直线有平行和异面两种位置关系.(3)a 与b 可能出现三种位置关系:平行、相交、异面.(4)已知//a α,//a b ,b α⊄,过a 作平面β交α于直线c ,则//a c ,所以//b c ,所以//b a .故答案为:(1)×(2)×(3)×(4)√【点睛】本小题主要考查线线、线面平行的有关命题真假性的判断,属于基础题.8.如图,a αβ⋂=,b α⊂,c β⊂,//b c ,求证////a b c .【答案】见解析【解析】【分析】首先根据线面平行的判定定理,证得b β//;再根据线面平行的性质定理证得//b a ,由平行公理证得//a c ,从而证得////a b c .【详解】,b a ααβ⊂⋂= ,b β∴⊄.//,,//b c c b ββ⊂∴ ,,b a ααβ⊂⋂=,//,//b a a c ∴∴,////a b c ∴.【点睛】本小题主要考查线面平行的判定定理和性质定理,考查平行公理,属于基础题.8.5.3平面与平面平行例4已知正方体1111ABCD A B C D -(图8.5-16),求证:平面11//AB D 平面1BC D .证明:∵1111ABCD A B C D -为正方体,∴1111D C A B ,11AB A B .∴11D C AB .∴四边形11D C BA 为平行四边形.∴11//D A C B .又1D A ⊄平面1BC D ,1C B ⊂平面1BC D ,∴1//D A 平面1BC D .同理11//D B 平面1BC D .又1111D A D B D ⋂=,∴平面11//AB D 平面1BC D .例5求证:夹在两个平行平面间的平行线段相等.如图8.5-19,//αβ,//AB CD ,且A α∈,C α∈,B β∈,D β∈,求证AB CD =.证明:过平行线AB ,CD 作平面γ,与平面α和β分别相交于AC 和BD .∵//αβ,∴//BD AC .又//AB CD ,∴四边形ABDC 是平行四边形.∴AB CD =.练习9.判断下列命题是否正确.若正确,则说明理由;若错误,则举出反例.(1)已知平面,αβ和直线m n ,,若m α⊂,n ⊂α,//m β,//n β则//αβ.(2)若一个平面α内两条不平行的直线都平行于另一个平面β,则//αβ.(3)平行于同一条直线的两个平面平行.(4)平行于同一个平面的两个平面平行.(5)一条直线与两个平行平面中的一个相交,则必与另一个相交.【答案】(1)×(2)√(3)×(4)√(5)√.【解析】【分析】(1)缺少条件:m n P = ;(2)符合判定定理;(3)两个平面也可以相交;(4)(5)均符合.【详解】解:(1)已知平面,αβ和直线m n ,,若m α⊂,n ⊂α,//m β,//n β则//αβ,缺少条件:m n P = ,故错误;(2)若一个平面α内两条不平行的直线都平行于另一个平面β,则//αβ,符合平面与平面平行的判定定理,故正确;(3)平行于同一条直线的两个平面平行,次两个平面也可以相交,故错误;(4)平行于同一个平面的两个平面平行,正确;(5)一条直线与两个平行平面中的一个相交,则必与另一个相交;正确.【点睛】本题主要考查直线与平面平行的判定与性质、平面与平面平行的判定与性质,注意灵活运用定理进行判断.10.平面α与平面β平行的充分条件可以是()A.α内有无穷多条直线都与β平行B.直线//a α,//a β,且直线a 不在α内,也不在β内C.直线a α⊂,直线b β⊂,且//a β,//b αD.α内的任何一条直线都与β平行【答案】D【解析】【分析】利用平面与平面平行的判定定理一一进行判断,可得正确答案.【详解】解:A 选项,α内有无穷多条直线都与β平行,并不能保证平面α内有两条相交直线与平面β平行,这无穷多条直线可以是一组平行线,故A 错误;B 选项,直线//a α,//a β,且直线a 不在α内,也不在β内,直线a 可以是平行平面α与平面β的相交直线,故不能保证平面α与平面β平行,故B 错误;C 选项,直线a α⊂,直线b β⊂,且//a β,//b α,当直线a b ∥,同样不能保证平面α与平面β平行,故C 错误;D 选项,α内的任何一条直线都与β平行,则α内至少有两条相交直线与平面β平行,故平面α与平面β平行;故选:D.【点睛】本题主要考查平面与平面平行的判断,解题时要认真审题,熟练掌握面与平面平行的判定定理,注意空间思维能力的培养.11.如图所示,正方体1111ABCD A B C D -中,M 、N 、E 、F 分别是棱11A B 、11A D 、11B C 、11C D 的中点.求证:平面//AMN 平面EFDB .【答案】证明见解析.【解析】【分析】连接MF ,由线面平行的判定可得//AM 平面EFDB ,同理可得//AN 平面EFDB ,再由面面平行的判定即可得证.【详解】证明:连接MF ,如图,∵M 、F 是11A B 、11C D 的中点,四边形1111D C B A 为正方形,∴11//MF A D 且11MF A D =,又11//A D AD 且11A D AD =,∴//MF AD 且MF AD =,∴四边形AMFD 是平行四边形.∴//AM DF .∵DF ⊂平面EFDB ,AM ⊄平面EFDB ,∴//AM 平面EFDB ,同理//AN 平面EFDB ,又AM ⊂平面ANM ,AN ⊂平面ANM ,AM AN A = ,∴平面//AMN 平面EFDB .12.如图,平面//,,,,//a b c c b αβγαγββ⋂=⋂=⊂.判断c 与a ,c 与α的位置关系,并说明理由.【答案】见解析.【解析】【分析】由题意//,,,,a b c αβγαγββ⋂=⋂=⊂,由平面与平面平行的性质定理可得//a b ,由//c b 可得//c a ,由直线与平面平行的判定定理可得//c α.【详解】解://,//c a c α.理由如下:∵平面//,,,//a b a b αβγαγβ⋂=⋂=∴.又//,//c b c a ∴.又,,//a c c ααα⊂⊄∴.【点睛】本题主要考查平面与平面平行的性质定理及直线与平面平行的判定定理,需注意定理的灵活运用.习题8.5复习巩固选择题13.若直线a 不平行于平面,则下列结论成立的是A.内的所有直线都与直线a 异面 B.内不存在与a 平行的直线C.内的直线都与a 相交D.直线a 与平面有公共点【答案】D【解析】【详解】试题分析:直线不平行于,包括两种情况:或,当时,内的所有直线都与直线共面,A 错;当时,内必然有直线与直线平行,B 错;从而C 也错;当,直线和平面有无数个公共点,当,直线与平面有唯一公共点,D 正确.考点:直线和平面的位置关系.14.已知直线l 和平面α,若l ∥α,P ∈α,则过点P 且平行于l 的直线()A.只有一条,不在平面α内B.只有一条,且在平面α内C.有无数条,一定在平面α内D.有无数条,不一定在平面α内【答案】B【解析】【分析】通过假设过点P 且平行于l 的直线有两条m 与n ,由平行公理可得//m n ,这与m n P = 矛盾.【详解】假设过点P 且平行于l 的直线有两条m 与n ,∴//m l 且//n l ,由平行公理得//m n ,这与两条直线m 与n 相交与点P 相矛盾.故选:B .15.已知平面,αβ和直线a ,b ,c ,////,,,a b c a b c αββ⊂⊂⊂,则α与β的位置关系是________.【答案】平行或相交【解析】【分析】可通过对两平面α,β位置关系分类讨论,研究符合题意的位置关系.【详解】若α//β,可以保证存在直线a ,b ,c ,且a //b //c ,a ⊂α,b ,c ⊂β,故平行关系有可能;若α∩β=l ,且a //b //c //l ,此种情况下也能保证存在直线a ,b ,c ,且a //b //c ,a ⊂α,b ,c ⊂β,故两面相交也有可能,由上讨论知,在题设条件下,α与β的关系是平行或相交,故答案为:平行或相交.【点睛】本题主要考查平面与平面的位置关系的判断,考查了分类讨论思想与空间想象能力,属于基础题.16.如图,在长方体木块1111ABCD A B C D -中,面11A C 上有一点P ,怎样过点P 画一条直线与棱CD 平行?【答案】见解析【解析】【分析】根据平行公理,只需在面11A C 内,过点P 作直线11//EF C D 即可.【详解】在面11A C 内,过点P 作直线EF ,使11//EF C D ,分别交棱1111,A D B C 于点E ,F ,因为11//CD C D ,所以//CD EF ,即EF 就是过点P 与棱CD 平行的直线.【点睛】本题主要考查平行公理的应用,考查了空间想象能力,意在考查灵活应用所学知识解答问题的能力,属于基础题.17.如图,在长方体ABCD A B C D ''''-中,E ,F 分别是AB ,BC 的中点,求证//''EF A C .【答案】见解析【解析】【分析】根据平行四边形的性质证明//A C AC '',根据三角形中位线证明//,EF AC 再由平行公理可得结论.【详解】连接AC .∵在长方体ABCD A B C D ''''-中,//AA CC ''.∴四边形ACC A ''为平行四边形.//A C AC ''∴.又∵E ,F 分别是AB ,BC 的中点,//,//EF AC EF A C ''∴∴.【点睛】本题主要考查长方体的性质,考查了平行公理的应用,意在考查对基础知识的掌握情况,属于基础题.18.如图,在四面体D -ABC 中,E ,F ,G 分别是AB ,BC ,CD 的中点,求证:(1)//BD 平面EFG ;(2)//AC 平面EFG .【答案】(1)证明见解析(2)证明见解析【解析】【分析】(1)由三角形中位线的性质可得//FG BD ,再由线面平行的判定定理可得结论;(2)由三角形中位线的性质可得//EF AC ,再由线面平行的判定定理可得结论.【详解】(1)F ,G 分别是BC ,CD 的中点,//FG BD ∴.BD ⊄ 平面EFG ,FG ⊂平面EFG ,//BD ∴平面EFG .(2)E .F 分别是AB ,BC 的中点,//EF AC ∴,AC ⊄ 在平面EFG ,EF ⊂平面EFG ,//AC ∴平面EFG .【点睛】证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面.19.如图,a ,b 是异面直线,画出平面α,使a α⊂,且//b α,并说明理由.【答案】见解析【解析】【分析】在直线a 上取一点O ,过点O 作'//b b ,则由a 与'b 确定的平面α即为所求,利用线面平行的判定定理可证明结论.【详解】在直线a 上取一点O ,过点O 作'//b b ,则由a 与b '确定的平面α即为所求.理由:如答图,,,//a b b b αα''⊂⊂且b α⊄,所以//b α.【点睛】本题主要考查作图能力,考查了线面平行的判定定理,意在考查灵活应用所学知识解答问题的能力,属于基础题.20.如图,,,,//CD EF AB AB αβαγβγα⋂=⋂=⋂=,求证//CD EF .【答案】证明见解析【解析】【分析】直接利用线面平行的性质定理证明//AB CD ,//AB EF ,再利用平行公理可得结论.【详解】证明:,AB AB βγβ⋂=∴⊂ .//,,//AB CD AB CD αβα⋂=∴ .同理//AB EF ,于是//CD EF .【点睛】本题主要考查线面平行的性质定理以及平行公理的应用,意在考查对基本定理掌握的熟练程度,属于中档题.21.如图,直线,,AA BB CC '''相交于点O ,',,AO AOBO B O CO C O ''===,求证:平面ABC //平面A B C '''.【答案】证明见解析【解析】【分析】利用全等三角形的性质以及平行线的判定定理可得//''AC A C ,从而由线面平行的判定定理可得//AC 平面'''A B C ,同理可证AB //平面'''A B C ,进而由面面平行的判定定理可得结论.【详解】AA ' 与'CC 相于点O ,''AOC AOC ∴∠=∠.又'',,AO AO CO C O OAC OAC ''==∴≅ .'''',//CAO C AO AC AC ∴∠=∠∴.又AC ⊄平面'''A B C ,''AC ⊂平面'''A B C .//AC ∴平面'''A B C .同理可证AB //平面'''A B C .又AB Ì平面ABC ,AC ⊂平面ABC ,AB AC A ⋂=,∴平面//ABC 平面'''A B C .【点睛】本题主要考查线面平行的判断、面面平行的判断,解答过程中一定要注意线面平行的判定定理与面面平行的判定定理的应用条件,本题属于中档题.综合运用22.如图,,'E E 分别为长方体ABCD A B C D ''''-的棱AD ,A D ''的中点,求证BEC B E C '''∠=∠.【答案】证明见解析【解析】【分析】分别利用平行四边形的性质可证明''//,//BE B E CE C E ',结合BEC B E C '''∠=∠方向相同,从而可得结论.【详解】证明:连接'EE ',E E ∵分别是,AD A D ''的中点,''//EE AA ∴.又在长方体''''ABCD A B C D -中,////AA BB CC '''.'//,//EE BB EE CC '''∴.∴四边形BEE B ''与''CEE C 都是平行四边形.'''//,//BE B E CE C E '∴.又因为BEC B E C '''∠=∠方向相同,'BEC B E C ''∴∠=∠.【点睛】本题主要考查长方体的结构特征,考查了等角定理的应用,同时考查了空间想象能力,属于基础题.23.如图//,//,,AB AC BD C D ααα∈∈,求证AC BD =.【答案】证明见解析【解析】【分析】连接CD ,则平面ABDC CD α⋂=,由线面平行的性质定理可得//AB CD ,从而得四边形ABDC 是平行四边形,进而可得结果.【详解】如图,连接CD .//,,,,AC BD A B C D ∴ 共面,C ∴∈面ABDC ,D ∈平面ABDC ,CD ⊂平面ABDC .,,C D CD ααα∈∈∴⊂ ,∴平面ABDC CD α⋂=.//,//AB AB CD α∴ ,∴四边形ABDC 是平行四边形.AC BD∴=【点睛】本题主要考查线面平行的性质定理的应用,属于基础题.应用线面平行的性质定理时,一定要注意线面平行与线线平行的转换.24.如果平面外的两条平行直线中的一条直线平行于这个平面,那么另一条直线也平行于这个平面.【答案】详见解析【解析】【分析】根据题意,利用线面平行的性质,得到线线平行,再利用线面平行的判定,可得线面平行.【详解】过两条平行直线中的一条直线a 作平面β,与平面α交于直线c .//a α ,//a c ∴.//a b ,//b c ∴.b α⊄ ,c α⊂,//b α∴【点睛】本题考查了线面平行的性质定理和判定定理,解决相关问题时,我们常利用辅助平面把空间问题转化为平面问题.25.一木块如图所示,点P 在平面VAC 内,过点P 将木块锯开,使截面平行于直线VB 和AC ,应该怎样画线?【答案】画线见解析.【解析】【详解】试题分析:利用线面平行的判定定理去确定.试题解析:过平面内一点作直线,交于,交于;过平面内一点作直线,交于,则,所确定的截面为所求.考点:棱锥的结构特征,线面平行的判定和实际应用.26.如图,////αβγ,直线a 与b 分别交,,αβγ于点A ,B ,C 和点D ,E ,F ,求证AB DEBC EF=.【答案】见解析【解析】【分析】连接AF 交β于点M ,连接MB ,CF ,ME ,AD ,由面面平行的性质定理可得BM CF //,所以AB AM BC MF =,同理可得AM DEMF EF=,从而可得结果.【详解】证明:如图,连接AF 交β于点M ,连接MB ,CF ,ME ,AD .因为//,βγβ⋂平面ACF BM =,γI 平面ACF CF =,所以BM CF //,所以AB AMBC MF=.同理//ME AD ,且AM DEMF EF=,所以AB DEBC EF=.【点睛】本题主要考查面面平行的性质定理的应用,考查了空间想象能力,证明过程要注意线面平行的性质定理应用的条件,本题属于中档题.拓广探索27.如图,a b ,是异面直线,,//,,//a a b b αββα⊂⊂,求证://αβ.【答案】证明见解析【解析】【分析】如图,过直线b 作平面γ,平面γ与α相交于直线c ,c 与a 交于点P .先证明//c β,又//a β且,a c P ⋂=所以//αβ得证.【详解】如图,过直线b 作平面γ,平面γ与α相交于直线c ,c 与a 交于点P .,,//,//c b b b c αγβγα⋂=⋂=∴ .又b ⊂平面,c β⊄平面β,//c β∴.又//a β且,//a c P αβ⋂=∴.【点睛】本题主要考查空间直线平面平行位置关系,意在考查学生对这些知识的理解掌握水平.28.如图,透明塑料制成的长方体ABCD﹣A 1B 1C 1D 1内灌进一些水,固定容器底面一边BC 于水平地面上,再将容器倾斜,随着倾斜度不同,有下面五个命题:①有水的部分始终呈棱柱形;②没有水的部分始终呈棱柱形;③水面EFGH 所在四边形的面积为定值;④棱A1D1始终与水面所在平面平行;⑤当容器倾斜如图(3)所示时,BE•BF是定值.其中所有正确命题的序号是____.【答案】①②④⑤【解析】【分析】根据题意,结合棱柱的特征进行判断,观察即可得到答案.【详解】根据棱柱的定义知,有两个面是互相平行且是全等的多边形,其余每相邻两个面的交线也互相平行,而这些面都是平行四边形,所以①②正确;因为水面EFGH所在四边形,从图2,图3可以看出,有两条对边边长不变而另外两条对边边长随倾斜度变化而变化,所以水面四边形EFGH的面积是变化的,③不对;因为棱11A D始终与BC平行,BC与水面始终平行,所以④正确;因为水的体积是不变的,高始终是BC也不变,所以底面积也不会变,即BE•BF是定值,所以⑤正确;综上知①②④⑤正确,故填①②④⑤.【点睛】本题主要考查了棱柱,棱柱的几何特征,线面平行,棱柱体积,属于中档题.变式练习题29.如图,E,F分别是长方体ABCD-A1B1C1D1的棱A1A,C1C的中点.求证:四边形B1EDF为平行四边形.【答案】证明见解析【解析】【分析】结合线线平行以及平行四边形的知识来证得结论成立.【详解】由于,E F 分别是长方体1111ABCD A B C D -的中点,设G 是1DD 的中点,连接1C G ,根据长方体的性质可知1B E DF ==且11////B E C G DF ,所以四边形1B EDF 是平行四边形.30.如图所示,OA ,OB ,OC 为不共面的三条线段,点1A ,1B ,1C 分别是OA ,OB ,OC 上的点,且111OA OB OC OA OB OC==成立.求证:111~A B C ABC .【答案】见解析【解析】【分析】根据111OA OB OC OA OB OC==,可得11A B AB ∥,11A C AC ∥,11B C BC ∥进而通过平行线得两个角111C A B CAB ∠=∠和111A B C ABC ∠=∠对应相等,即可证明111~A B C ABC ∆∆.【详解】证明;在OAB 中,因为111OA OB OA OB =,所以11A B AB ∥.同理可证11A C AC ∥,11B C BC ∥.所以111C A B CAB ∠=∠,111A B C ABC ∠=∠.所以111~A B C ABC ∆∆.【点睛】本题考查了通过线段成比例,证明线线平行,根据空间中角的两边分别平行判断两个角的关系,属于基础题.31.如图,在正方体ABCD -A 1B 1C 1D 1中,E ,F ,G 分别是BC ,CC 1,BB 1的中点,求证:EF ∥平面AD 1G.【答案】证明见解析.【解析】【分析】连接BC 1,由四边形ABC 1D 1是平行四边形,可得BC 1∥AD 1,进而EF ∥BC 1,利用线面平行的判定定理证得命题成立.【详解】连接BC 1,则由E ,F 分别是BC ,CC 1的中点,知EF ∥BC 1.又AB //A 1B 1//D 1C 1,所以四边形ABC 1D 1是平行四边形,所以BC1∥AD1,所以EF∥AD1.又EF⊄平面AD1G,AD1⊂平面AD1G,所以EF∥平面AD1G.【点睛】本题考查线面平行的判定定理,考查学生的直观想象能力与逻辑思维能力,属于基础题.32.如图所示,ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,AP GH.在DM上取一点G,过G和AP作平面交平面BDM于GH,求证://【答案】见解析【解析】【分析】连接AC交BD与O,可证PA//平面BDM,再利用线面平行的性质定理即可GH AP.证得//【详解】证明:如图,连接AC交BD于点O,连接MO.在△APC 中,MO 是△APC 的中位线,∴MO ∥PA又 PA ⊄平面MBD ,MO ⊂平面MBD,∴PA//平面MBD又 平面GAP∩平面BDM =GH ,PA ⊂平面GAP∴PA//GH33.如图所示,已知正方体ABCD -A 1B 1C 1D 1.(1)求证:平面A 1BD ∥平面B 1D 1C .(2)若E ,F 分别是AA 1,CC 1的中点,求证:平面EB 1D 1∥平面FBD .【答案】(1)见解析;(2)见解析【解析】【详解】试题分析:(1)由11//BB DD ,得11//B D BD ,进而证得平面1//A BD 平面1B CD .(2)由1//AE B G ,得1//B E AG ,再由//AG DF ,则1//B E DF ,进而证得//DF 平EB D,即可得到结论.面11试题解析:BB//DD,所以四边形BB1D1D是平行四边形,(1)因为11所以B1D1∥BD,又BD⊄平面B1D1C,B1D1⊂平面B1D1C,所以BD∥平面B1D1C.同理A1D∥平面B1D1C,又A1D∩BD=D,所以平面A1BD∥平面B1D1C.(2)由BD∥B1D1,得BD∥平面EB1D1,取BB1的中点G,连接AG,GF,易得AE∥B1G,又因为AE=B1G,所以四边形AEB1G是平行四边形,所以B1E∥AG.易得GF∥AD.又因为GF=AD,所以四边形ADFG是平行四边形,所以AG∥DF,所以B1E∥DF,DF⊄平面EB1D1,B1E⊂平面EB1D1,所以DF∥平面EB1D1.又因为BD∩DF=D,所以平面EB1D1∥平面FBD.点睛:本题主要考查了平面与平面平行的判定与证明问题,其中解答中涉及到直线与平面平行的判定定理,平面与平面平行的判定定理的综合应用,此类问题的解答中要证“面面平行”只要证明“线面平行”,只要证“线线平行”,把问题最终转化为线与线的平行问题,着重考查了学生的转化思想的应用.34.如图所示,两条异面直线BA,DC与两平行平面α,β分别交于点B,A和D,MN平面αC,点M,N分别是AB,CD的中点,求证://【答案】证明见解析【解析】【分析】过点A 作//AE CD 交α于点E ,取AE 的中点P ,连接MP ,PN ,BE ,ED ,BD ,AC ,根据面面平行的性质得到//PN α,MP//α,即可得到平面//MPN α,再利用面面平行的性质即可得到//MN 平面α。
原创1:1.2.2 空间中的平行关系(三)(讲授式)

C'
观察:观察右边的长方体,平面B′D′与平面BD
平行,平面ABCD内的直线BD与平面B′D′内的直线
有哪些位置关系呢?它们满足什么条件时平行?
D'
A'
B'
C
B
D
A
观察猜想:平面B′D′与平面BD内的直线只有两种位置关系:平行或异面.
平面B′D′∩平面CD′ = C′D′ ,平面BD∩平面CD′=CD,由长方体的性质可知,
平面相交.
④夹在两个平行平面间的所有平行线段相等.
第
一
章
立
体
几
何
初
步
例2 如图,在长方体 − ′′′′中,
求证:平面′//平面’’.
分析:只要证明一个平面内有两条相交直线
和另一个平面平行即可.
− ′ ′ ′ ′ 是正方体,
证明: ∵
∴AB//DC//D’C’且AB=DC=D’C’.
⟹ 是平行四边形.
⟹ BC′//AD′.
线平行的转化策略.
课堂练习
一.判断下列命题的真假;
1.如果两个平面不相交,那么它们就没有共公点;
2.如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行;
3.如果一个平面内的任何一条直线都平行于另一个平面,那么这两个平面平行;
4.已知两个平行平面中的一个平面内有一条直线,
则在另一个平面内有且只有一条直线与已知直线平行;
面面平行⇌线线平行
典例精讲
平面与平面平行判定定理的应用
例5 已知三个平行平面α、β、γ与两条异面直线l,m分别交于
A、B、C 和D、E、F.求证:
高中数学《空间的平行关系》复习和习题课件PPT

巩固练习
过关练习
ห้องสมุดไป่ตู้固练习
过关练习
同学们!再见!
课后一定要多练习哦!
(2)直线与平面平行的判定定理:平面α外的一条直线l与平面α内的一条直线m
平行,则直线l与平面α平行.(线线平行 线面平行)
(3)直线与平面平行的性质定理:已知直线l与平面α平行,且经过直线l的平面β
与平面α相交于直线m,则直线l与直线m平行.(线面平行 线线平行)
知识清单
知识点四 平面与平面的平行
典例精析
例
变式训练
变式训练3
下列说法正确的是(). A.经过平面外一点有且仅有一条直线平行于这个平面 B.经过平面外一点有且仅有一条直线垂直于这个平面 C.经过直线外一点有且仅有一个平面平行于这条直线 D.经过直线外一点有且仅有一条直线垂直于这条直线
巩固练习
过关练习
巩固练习
过关练习
巩固练习
知识清单
知识点二 直线与平面的位置关系
直线与平面的三种位置关系:直线在平面内、直线与平面相交、直线与平面平 行.
(1)直线在平面内:直线上的所有点都在平面内. (2)直线与平面相交:直线与平面只有唯一一个公共点. (3)直线与平面平行:直线与平面没有公共点.
知识清单
知识点三 直线与平面的平行
(1)直线与平面平行的定义:若直线l与平面α没有公共点,则称直线l与平面α平 行.
线都与另一个平面平行.(面面平行 线面平行)
典例精析
例
变式训练
变式训练1
如图92所示,AB、CD是夹在两个平行平面α、β之间的 线段,M、N分别为AB、CD的中点. 求证:MN∥平面α.
典例精析
例
变式训练
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间中的平行关系考纲解读 1.以立体几何的定义、公理和定理为出发点,判定常见几何体中的平行关系;2.以常见几何体为模型,进行空间平行关系的转化.[基础梳理]1.直线与平面平行的判定定理和性质定理[三基自测]1.下列命题中正确的是()A.若a,b是两条直线,且a∥b,那么a平行于经过b的任何平面B.若直线a和平面α满足a∥α,那么a与α内的任何直线平行C.平行于同一条直线的两个平面平行D.若直线a,b和平面α满足a∥b,a∥α,b⊄α,则b∥α答案:D2.下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是()A.①③B.②③C.①④D.②④答案:C3.(必修2·2.2练习改编)在正方体ABCD A1B1C1D1中,点E是DD1的中点,则BD1与平面ACE的位置关系为________.答案:平行4.(2017·高考全国卷Ⅰ改编)如图,正方体ABCD A1B1C1D1中,M、N、E、F分别为棱的中点,则面AMN与面DBEF的关系为________.答案:平行考点一直线与平面平行的判定与性质|方法突破[例1](1)如图,在三棱台DEF ABC中,AB=2DE,点G,H分别为AC,BC的中点.求证:BD∥平面FGH.(2)正方形ABCD与正方形ABEF所在平面相交于AB,在AE,BD上各有一点P,Q,且AP=DQ.求证:PQ∥平面BCE.[证明] 如图,连接DG ,CD ,设CD ∩FG =O ,连接OH .在三棱台DEF ABC 中,AB =2DE ,点G 为AC 的中点,可得DF ∥GC ,DF =GC , 所以四边形DFCG 为平行四边形,所以点O 为CD 的中点.又因为点H 为BC 的中点,所以OH ∥BD .又因为OH ⊂平面FGH ,BD ⊄平面FGH , 所以BD ∥平面FGH .(2)法一:(判定定理法)如图所示.作PM ∥AB 交BE 于点M ,作QN ∥AB 交BC 于点N ,连接MN .∵正方形ABCD 和正方形ABEF 有公共边AB ,∴AE =BD . 又AP =DQ ,∴PE =QB .又PM ∥AB ∥QN ,∴PM AB =PE AE =QB BD ,QN DC =BQBD .∴PM AB =QNDC.∴PM 綊QN ,即四边形PMNQ 为平行四边形.∴PQ ∥MN . 又MN ⊂平面BCE ,PQ ⊄平面BCE , ∴PQ ∥平面BCE .法二:(判定定理法)如图,连接AQ 并延长交BC 的延长线于点K ,连接EK ,∵AE =BD ,AP =DQ , ∴PE =BQ .∴AP PE =DQBQ .又AD ∥BK ,∴DQ BQ =AQQK .∴AP PE =AQQK.∴PQ ∥EK . 又PQ ⊄平面BCE ,EK ⊂平面BCE , ∴PQ ∥平面BCE .法三:(性质定理法)如图,在平面ABEF 内,过点P 作PM ∥BE ,交AB 于点M ,连接QM .∵PM ⊄平面BCE ,∴PM ∥平面BCE ,且AP PE =AM MB ,又AE =BD ,AP =DQ ,PE =BQ , ∴AP PE =DQ BQ .∴AM MB =DQ QB.∴MQ∥AD.又AD∥BC,∴MQ∥BC.又MQ⊄平面BCE,∴MQ∥平面BCE.又PM∩MQ=M,∴平面PMQ∥平面BCE.又PQ⊂平面PMQ,∴PQ∥平面BCE.[方法提升]方法关键适用题型利用线面平行的判定定理证线面平行在该平面内找或作一直线,证明其与已知直线平行平行线易作出利用面面平行的性质证线面平行过该线找或作一平面,证明其与已知平面平行面面平行较明显利用线面平行性质证线线平行过线作平面,产生交线已知线面平行[跟踪训练]如图,四棱锥P ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°.P A⊥平面ABCD,且P A=3.F在棱P A上,(1)若F为P A的中点,求证PC∥平面BDF;(2)若AF=1,E在棱PD上,且CE∥平面BDF,求PE∶ED的值.解析:(1)证明:连接AC、AC∩BD=O,由ABCD为菱形知O为AC的中点,F为P A的中点,∴OF∥PC.OF⊂平面BDF,PC⊄平面BDF.∴PC∥平面BDF.(2)过E 作EG∥FD交AP于G,连接CG,FO.∵EG∥FD,EG⊄平面BDF,FD⊂平面BDF,∴EG∥平面BDF,又EG∩CE=E,CE∥平面BDF,EG,CE⊂平面CGE,∴平面CGE∥平面BDF,又CG⊂平面CGE,∴CG∥平面BDF,又平面BDF∩平面P AC=FO,CG⊂平面P AC,∴FO∥CG.又O为AC的中点,∴F 为AG 中点,∴FG =GP =1, ∴E 为PD 的中点,PE ∶ED =1∶1.考点二 平面平行的判定与性质|方法突破[例2] (1)如图所示,正方体ABCD A 1B 1C 1D 1的棱长为a ,点P 是棱AD 上一点,且AP =a3,过B 1、D 1、P 的平面交平面ABCD 于PQ ,Q 在直线CD 上,则PQ =________.(2)在正方体ABCD A 1B 1C 1D 1中,M ,N ,P 分别是C 1C ,B 1C 1,C 1D 1的中点,求证:平面PMN ∥平面A 1BD .[证明] (1)∵平面A 1B 1C 1D 1∥平面ABCD ,而平面B 1D 1P ∩平面ABCD =PQ ,平面B 1D 1P ∩平面A 1B 1C 1D 1=B 1D 1,∴B 1D 1∥PQ .又∵B 1D 1∥BD ,∴BD ∥PQ .设PQ ∩AB =M ,∵AB ∥CD ,∴△APM ∽△DPQ . ∴PQ PM =PDAP=2,即PQ =2PM . 又知△APM ∽△ADB ,∴PM BD =AP AD =13,∴PM =13BD ,又BD =2a ,∴PQ =223a .(2)法一:(判定定理法)如图,连接B 1D 1,B 1C .∵P ,N 分别是D 1C 1,B 1C 1的中点, ∴PN ∥B 1D 1.又B 1D 1∥BD ,∴PN ∥BD .又PN ⊄平面A 1BD ,∴PN ∥平面A 1BD . 同理MN ∥平面A 1BD ,又PN ∩MN =N ,∴平面PMN ∥平面A 1BD .法二:(性质定理法)如图,连接AC 1,AC . ∵ABCD A 1B 1C 1D 1为正方体, ∴AC ⊥BD .又CC 1⊥平面ABCD ,∴AC 为AC 1在平面ABCD 上的射影. ∴AC 1⊥BD .同理可证AC 1⊥A 1B ,∴AC 1⊥平面A 1BD .同理可证AC 1⊥平面PMN , ∴平面PMN ∥平面A 1BD . [答案] (1)223a[方法提升]方法关键适合题型 判定定理证明面面平行 证出面内的两条相交线平行平面 线面平行关系明显 线面垂直性质证面面平行 证出两个面垂直于同一条直线 线面垂直关系明显 面面平行性质得线面平行、线线平行 作辅助面得出面的交线已知面面平行[跟踪训练]如图,在正方体ABCD A 1B 1C 1D 1中,O 为底面ABCD 的中心,P 是DD 1的中点,若Q 是CC 1的中点.证明:平面D 1BQ ∥平面P AO .证明:∵Q 为CC 1的中点,P 为DD 1的中点,∴QB ∥P A . ∵P ,O 分别为DD 1,DB 的中点, ∴D 1B ∥PO .又∵D 1B ⊄平面P AO ,PO ⊂平面P AO ,QB ⊄平面P AO ,P A ⊂平面P AO , ∴D 1B ∥平面P AO ,QB ∥平面P AO , 又D 1B ∩QB =B ,D 1B ,QB ⊂平面D 1BQ , ∴平面D 1BQ ∥平面P AO .考点三 平行关系的探索问题|思维突破[例3] 如图所示,在斜三棱柱ABC A 1B 1C 1中,D ,D 1分别是AC ,A 1C 1上的点,当AD DC ,A 1D 1D 1C 1分别为何值时,平面BC 1D ∥平面AB 1D 1.[解析] 如图所示,连接A 1B 与AB 1交于点O ,连接OD 1.因为平面BC 1D ∥平面AB 1D 1,且平面A 1BC 1∩平面BDC 1=BC 1,平面A 1BC 1∩平面AB 1D 1=OD 1,所以BC 1∥OD 1.同理AD 1∥DC 1.由BC 1∥OD 1,得A 1D 1D 1C 1=A 1OOB =1,即A 1D 1=D 1C 1.由AD 1∥DC 1,AD ∥D 1C 1, 得四边形ADC 1D 1是平行四边形, 所以AD =D 1C 1,所以A 1D 1=DC . 所以DC AD =A 1D 1D 1C 1=1,即当AD DC =A 1D 1D 1C 1=1时,平面BC 1D ∥平面AB 1D 1.[思维升华]对于此类问题往往采取逆向思维(1)对命题条件的探索常采用以下三种方法: ①先猜后证,即先观察与尝试给出条件再证明;②先通过命题成立的必要条件探索出命题成立的条件,再证明其充分性; ③把几何问题转化为代数问题,探索命题成立的条件. (2)对命题结论的探索常采用以下方法:首先假设结论存在,然后在这个假设下进行推理论证,如果通过推理得到了合乎情理的结论,就肯定假设,如果得到了矛盾的结论,就否定假设.[跟踪训练]在三棱柱ABC A 1B 1C 1中,设D ,E 分别是线段BC ,CC 1的中点,在线段AB 上是否存在一点M ,使直线DE ∥ 平面A 1MC ?请证明你的结论.解析:存在一点M ∈AB ,使DE ∥平面A 1MC . 证明如下:取AB 的中点M ,A 1C 的中点N , 连接EN ,DM ,MN (图略).∴DM 綊12AC ,NE 綊12A 1C 1,∴NE 綊DM .∴四边形DENM 为平行四边形,∴MN ∥DE , 又DE ⊄平面A 1MC ,MN ⊂平面A 1MC , ∴DE ∥平面A 1MC .故存在点M 为AB 的中点,使DE ∥平面A 1MC .1.[考点一](2017·高考全国卷Ⅰ)如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 不平行的是( )解析:对于选项B ,如图所示,连接CD ,因为AB ∥CD ,M ,Q 分别是所在棱的中点,所以MQ ∥CD ,所以AB ∥MQ ,又AB ⊄平面MNQ ,MQ ⊂平面MNQ ,所以AB ∥平面MNQ .同理可证选项C ,D 中均有AB ∥平面MNQ .故选A.答案:A2.[考点一](2017·高考全国卷Ⅱ)如图,四棱锥P ABCD 中,侧面P AD 为等边三角形且垂直于底面ABCD ,AB =BC =12AD ,∠BAD =∠ABC=90°.(1)证明:直线BC ∥平面P AD ;(2)若△PCD 的面积为27,求四棱锥P ABCD 的体积. 解析:(1)证明:在平面ABCD 内,因为∠BAD =∠ABC =90°,所以BC ∥AD .又BC ⊄平面P AD ,AD ⊂平面P AD ,故BC ∥平面P AD .(2)如图,取AD 的中点M ,连接PM ,CM .由AB =BC =12AD 及BC ∥AD ,∠ABC =90°得四边形ABCM 为正方形,则CM ⊥AD .因为侧面P AD 为等边三角形且垂直于底面ABCD ,平面P AD ∩平面ABCD =AD ,所以PM ⊥AD ,PM ⊥底面ABCD .因为CM ⊂底面ABCD ,所以PM ⊥CM .设BC =x ,则CM =x ,CD =2x ,PM =3x ,PC =PD =2x . 如图,取CD 的中点N ,连接PN ,则PN ⊥CD ,所以PN =142x . 因为△PCD 的面积为27, 所以12×2x ×142x =27,解得x =-2(舍去)或x =2.于是AB =BC =2,AD =4,PM =2 3.所以四棱锥P ABCD 的体积V =13×2×(2+4)2×23=4 3.3.[考点二](2013·高考陕西卷)如图,四棱柱ABCD A 1B 1C 1D 1的底面ABCD 是正方形,O 是底面中心,A 1O ⊥底面ABCD ,AB =AA 1= 2.(1)证明:平面A 1BD ∥平面CD 1B 1; (2)求三棱柱ABD A 1B 1D 1的体积.解析:(1)由题设知BB 1綊DD 1,∴四边形BB 1D 1D 是平行四边形,∴BD ∥B 1D 1. 又BD ⃘平面CD 1B 1,∴BD ∥平面CD 1B 1. ∵A 1D 1綊B 1C 1綊BC ,∴四边形A 1BCD 1是平行四边形,∴A 1B ∥D 1C . 又A 1B ⃘平面CD 1B 1,∴A 1B ∥平面CD 1B 1. 又BD ∩A 1B =B ,∴平面A 1BD ∥平面CD 1B 1. (2)∵A 1O ⊥平面ABCD ,∴A 1O 是三棱柱ABD A 1B 1D 1的高.∵AO =12AC =1,AA 1=2,∴A 1O =AA 21-OA 2=1. ∵S △ABD =12×2×2=1,∴VABD A 1B 1D 1=S △ABD ×A 1O =1.。
