控制工程第3章习题解答
控制工程基础习题解答3
控制工程基础习题解答第三章3-1.已知二阶系统的闭环传递函数为()()2222nn n s s s R s C ωςωω++=,其中ζ=0.6,ωn =5rad/s ,试求在单位阶跃输入下的瞬态响应指标t r 、t p 、σp %、和t s 。
解:srad radn d /46.0151927.013.536.06.01tan1tan222121=-=-==︒=-=-=--ςωωςςβ 0.55(s)4927.0=-=-=πωβπd r t ()s t d p 79.04===πωπ %5.9%226.016.01===----πςςπσe e p()()s t s t ns ns 33.156.044156.033=⨯===⨯==ςωςω3-2.已知某系统的框图如图3-16所示,要求系统的性能指标为σp%=20%,t p =1s ,试确定系统的K 值和A 值,并计算t r 和t s 之值。
解:()()KAK K Ks AK s Ks n 2112+==+++=ςωφ45.02.0%21===--ςσςςπe p()s rad s t n n d p /52.3145.012==-==ωωπωπ17.039.12145.039.1221239.122=-⨯⨯=-===K K A K n ςωsrad radn d /14.345.0152.311.145.045.01tan1tan222121=-=-==-=-=--ςωωςςβ 0.65(s)14.31.1=-=-=πωβπd r t ()()%252.252.345.044%589.152.345.033±=⨯=±=⨯==, =, s s t nns ςωςω3-3.某系统的开环传递函数为()ss s G n n ςωω222+=,为使单位反馈的闭环系统对单位阶跃输入的瞬态响应具有σp %=5%的超调量和t s =2s 的调整时间,试确定系统的ζ和ωn 的值。
《控制工程基础》课程作业习题(含解答)
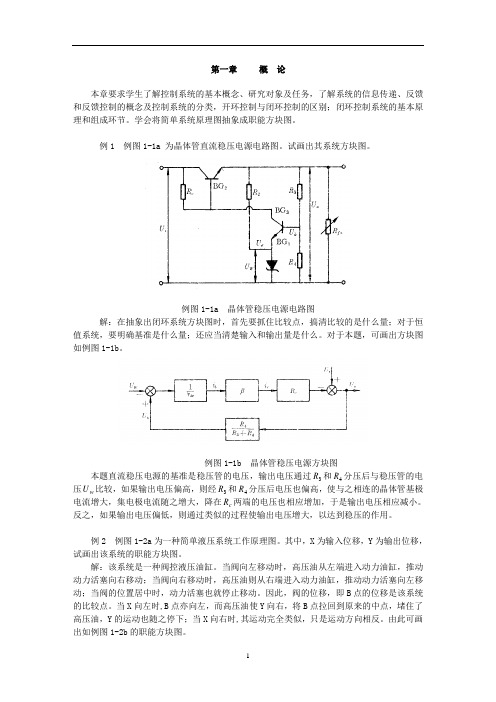
第一章概论本章要求学生了解控制系统的基本概念、研究对象及任务,了解系统的信息传递、反馈和反馈控制的概念及控制系统的分类,开环控制与闭环控制的区别;闭环控制系统的基本原理和组成环节。
学会将简单系统原理图抽象成职能方块图。
例1 例图1-1a 为晶体管直流稳压电源电路图。
试画出其系统方块图。
例图1-1a 晶体管稳压电源电路图解:在抽象出闭环系统方块图时,首先要抓住比较点,搞清比较的是什么量;对于恒值系统,要明确基准是什么量;还应当清楚输入和输出量是什么。
对于本题,可画出方块图如例图1-1b。
例图1-1b 晶体管稳压电源方块图本题直流稳压电源的基准是稳压管的电压,输出电压通过R和4R分压后与稳压管的电3压U比较,如果输出电压偏高,则经3R和4R分压后电压也偏高,使与之相连的晶体管基极w电流增大,集电极电流随之增大,降在R两端的电压也相应增加,于是输出电压相应减小。
c反之,如果输出电压偏低,则通过类似的过程使输出电压增大,以达到稳压的作用。
例2 例图1-2a为一种简单液压系统工作原理图。
其中,X为输入位移,Y为输出位移,试画出该系统的职能方块图。
解:该系统是一种阀控液压油缸。
当阀向左移动时,高压油从左端进入动力油缸,推动动力活塞向右移动;当阀向右移动时,高压油则从右端进入动力油缸,推动动力活塞向左移动;当阀的位置居中时,动力活塞也就停止移动。
因此,阀的位移,即B点的位移是该系统的比较点。
当X向左时,B点亦向左,而高压油使Y向右,将B点拉回到原来的中点,堵住了高压油,Y的运动也随之停下;当X向右时,其运动完全类似,只是运动方向相反。
由此可画出如例图1-2b的职能方块图。
例图1-2a 简单液压系统例图1-2b 职能方块图1.在给出的几种答案里,选择出正确的答案。
(1)以同等精度元件组成的开环系统和闭环系统,其精度比较为_______ (A )开环高; (B )闭环高; (C )相差不多; (D )一样高。
(2)系统的输出信号对控制作用的影响 (A )开环有; (B )闭环有; (C )都没有; (D )都有。
控制工程期末试题 (3)

第3章补充习题一、填空题1.系统分析是指对系统的___稳定性____、____误差_____和___动态特性______三方面的性能指标进行分析。
2.控制系统分析的目的是确定系统的___稳定性____、___误差______和___动态特性______。
3.在控制系统分析时,人们经常选用的典型信号有__阶跃信号___、__速度信号___、___加速度信号___、__脉冲信号___和__正弦信号_____。
4.如果系统的实际输入信号具有突变的性质,可以选用___单位阶跃____信号作为输入信号进行试验。
5.如果系统的实际输入信号具有随时间逐渐变化的性质,可以选用_______信号作为输入信号进行试验。
6.凡能够用一阶微分方程描述的系统称为___一阶系统________。
7.一阶系统的典型环节也称为____惯性环节___________。
8.系统在单位阶跃信号作用下的输出称为__单位阶跃响应_____________。
9.一阶惯性环节的单位阶跃响应的时域数学表达式是___________。
10.一阶惯性环节一定是稳定的和___无__振荡的。
11.一阶惯性环节的时间常数可以用实验测出的单位阶跃响应曲线达到__0.632__高度点时所对应的时间来确定。
12.一阶惯性环节的时间常数越小,系统的惯性_越小_______。
13.一阶惯性环节的时间常数越小,系统的响应___快_____。
14.一阶惯性环节的阶跃响应在半对数坐标纸上是__t 1-x0(t)______。
15.一阶惯性环节的单位速度响应的时域数学表达式是___________。
16.系统在单位速度信号作用下的输出称为____单位速度响应___________。
17.一阶惯性环节在单位速度信号作用下的稳态误差是____T_______。
18. 系统在单位脉冲信号作用下的输出称为_____单位脉冲响应_________。
19.一阶惯性环节的单位脉冲响应的时域数学表达式是___________。
现代控制工程基础第三章习题解答

解:
s5
1
2 11
s4
2
4 10
s3 0(ε)
6
4ε −12
s2
ε
10
s1
−10ε 2 + 24ε − 72 4ε −12
s0
10
当ε→0+时,第一列变了两次符号,故在右半平面
有两个正根。
10
(5) D(s)=s6+2s5+8s4+12s3+20s2+16s+16=0
解: s6 s5 s4 s3 s2 s1 s0
5
s0 K-8
第一列元素全部大于零,可得
8<K<18
13
3.14 已知单位负反馈的开环传递函数如下,试求系统在
输入信号分别为r(t)=1,t和t2时的稳态误差ess。
(1)
G(s) =
100
(0.1s +1)(0.5s +1)
解:闭环系统特征方程 D(s) = 0.01s2 + 0.6s +101 = 0 稳定的。
Hale Waihona Puke ess=1 1+ Kp
=1 1+ KK1
18
Vr
−
K1
+
K2 s
K Ts +1
Vc
(2) 当K2≠0时,求Vr(t)=1(t)时的稳态误差ess; I型系统,开环传递函数 G(s) = K(K1s + K2)
s(Ts +1)
当Vr(t)=1(t)时,静态位置误差系数
Kp
=
lim G(s)
s→0
=
∞
时速度误差系数为Kv=6?此时的ess为多少?
机械控制工程基础第3章习题解答

由于前述 K h 0.116
101 0.116 s 则系统的传递函数为: G s 2 s 3.16 s 10
输入单位阶跃 X i s
101 0.116 s X o s Gs X i s s 2 3.16 s 10 s 0.42 2.74 1 s 1.58 2.74 X o s s s 1.582 2.742 s 1.582 2.742
单位反馈,开环传递函数为:
Ⅱ 型,开环增益为
an K an 2
an 2 e ss an
3.16
101 K h s G s 2 s 2 10K h s s 10
K h 0.116
n 10 1 / s 3.161 / s 0.5 M p 16.3% 直接代入公式: t s 2.53 s 2% t 1.897 s 5% s
单位阶跃响应:x
ou
t 201 e
t / 2.5
xou t wt
3.8
3.12
微分关系
9 3 G s 2 s s 9 s 2 2 1 3s 32 6 n 31 / s M 58.8% p 0.167
求导,得到最大值
M p 17. 7%
clear all; close all; t=0:0.01:5; y=1-exp(-1.58*t).*cos(2.74.*t) -0.1533.*exp(-1.58*t).*sin(2.74.*t); %output express figure; h=plot(t,y,’r’); set(h,’linewidth’,5) set(gca, ’fontsize’,16) [mp_abs ,tp_space]=max(y(:)); %0.1772 mp= mp_abs–1; %计算最大超调量0.1772 tp= tp_space.*0.01; %计算峰值时间 grid on; i=tp_space; while abs(y(i)-1)>0.02 i=i+1; end ts=i.*0.01; %计算调整时间ts=1.69s
控制工程基础第三章参考答案

第三章 习题及答案传递函数描述其特性,现在用温度计测量盛在容器内的水温。
发现需要时间才能指示出实际水温的98%的数值,试问该温度计指示出实际水温从10%变化到90%所需的时间是多少?解: 41min, =0.25min T T = 1111()=1-e0.1, =ln 0.9t h t t T -=-T21T22()=0.9=1-e ln 0.1t h t t T -=-,210.9ln2.20.55min 0.1r t t t T T =-===2.已知某系统的微分方程为)(3)(2)(3)(t f t f t y t y +'=+'+'',初始条件2)0( , 1)0(='=--y y ,试求:⑴系统的零输入响应y x (t );⑵激励f (t ) (t )时,系统的零状态响应y f (t )和全响应y (t );⑶激励f (t ) e 3t(t )时,系统的零状态响应y f (t )和全响应y (t )。
解:(1) 算子方程为:)()3()()2)(1(t f p t y p p +=++)()e 25e 223()()()( )()e 21e 223()()()( )()e e 2()(2112233)( )2(;0 ,e 3e 4)( 34221e e )( 2x 2222x 212121221x t t y t y t y t t t h t y t t h p p p p p p H t t y A A A A A A A A t y t t t t t t f f t t ttεεεε------------+=+=+-==-=⇒+-+=+++=-=⇒⎩⎨⎧-==⇒⎩⎨⎧--=+=⇒+=∴* )()e4e 5()()()( )()e e ()(e )()( )3(2x 23t t y t y t y t t t h t y ttt t t f f εεε------=+=-==*3.已知某系统的微分方程为)(3)(')(2)(' 3)(" t f t f t y t y t y +=++,当激励)(t f =)(e4t tε-时,系统2的全响应)()e 61e 27e314()(42t t y t t tε-----=。
机械控制工程基础第三章 复习题及答案

题目:时间响应由 和 两部分组成。
分析与提示:时间响应由瞬态响应和稳态响应两部分组成。
答案:瞬态响应、稳态响应题目:系统的输出量从初始状态到稳定状态的响应过程,称为 。
分析与提示:瞬态响应,指系统在某一输入信号作用下,系统的输出量从初始状态到稳定状态的响应过程。
答案:瞬态响应题目:系统的时间响应可从两方面分类,按振动性质可分为 与 。
分析与提示:系统的时间响应可从两方面分类,按振动性质可分为自由响应与强迫响应。
答案:自由响应、强迫响应题目:系统的时间响应可从两方面分类,按振动来源可分为 与 。
分析与提示:系统的时间响应可从两方面分类,按振动性质可分为自由响应与强迫响应;按振动来源可分为零输入响应(即由“无输入时系统的初态”引起的自由响应)与零状态响应(即仅由输入引起的响应)。
答案:零输入响应、零状态响应题目:系统微分方程的特解就是系统由输入引起的输出(响应),工程上称为 。
分析与提示:初始条件及输入信号产生的时间响应就是微分方程的全解。
包含通解和特解两个部分。
通解完全由初始条件引起的,它是一个瞬态过程,工程上称为自然响应 (如机械振动中的自由振动)。
特解只由输入决定,特解就是系统由输入引起的输出(响应),工程上称为强迫响应 (如机械振动中的强迫振动)。
答案:强迫响应题目:系统的瞬态响应不仅取决于系统本身的特性,还与外加 的形式有关。
分析与提示:系统的瞬态响应不仅取决于系统本身的特性,还与外加输入信号的形式有关。
答案:输入信号题目:单位阶跃信号⎩⎨⎧<>=000t t t u1)(的拉氏变换为【 】A 、s 1 B 、21sC 、1D 、s 分析与提示:熟练掌握典型信号的拉氏变换。
B 为单位斜坡信号的拉氏变换,C 为单位冲击信号的拉是变换。
答案:A题目:选取输入信号应当考虑以下几个方面,输入信号应当具有 ,能够反映系统工作的大部分实际情况。
分析与提示:选取输入信号应当考虑以下几个方面,输入信号应当具有典型性,能够反映系统工作的大部分实际情况。
大气污染控制工程(郝吉明版) 课后习题答案:Unlock-3

dP = −g ρ ⋅dZ (1)
将空气视为理想气体,即有
PV = m RT 可写为 ρ = m = PM (2)
M
V RT
将(2)式带入(1),并整理,得到以下方程:
dP gM = − dZ
P RT
假定在一定范围内温度 T 的变化很小,可以忽略。对上式进行积分得:
gM ln P = − Z + C
=
−0.72K
/
100m
,故γ
2
= −G2
= 0.72K / 100m < γ d ,稳定;
G3
=
∆T3 ∆z3
=
8.9 −15.6 580
= −1.16K
/100m ,故γ 3
= −G3
= 1.16K / 100m
> γ d ,不稳定;
G4
=
∆T4 ∆z4
=
5.0 − 25.0 2000
= −1K / 100m ,故 γ 4
放后陆续发回相应的气温和气压记录如下表所给。1)估算每一组数据发出的高度;2)以高
度为纵坐标,以气温为横坐标,作出气温廓线图;3)判断各层大气的稳定情况。
测定位置 2
3
4
5
6
7
8
9
10
气温/。C 9.8
12.0 14.0 15.0 13.0 13.0 12.6 1.6
0.8
气压/hPa 1012 1000 988 969 909 878 850 725 700
=
3.33m / s
u5
=
u
0
(
Z Z
5 0
) 0.15
=
2 × ( 400) 0.15 10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.5 使用温度计对水温进行测量,若水温为恒定值,该温度计能在1分钟时指示出实际温度值的98%。
假定温度计为一个一阶系统,求该系统的时间常数T 。
解:恒定的水温可以视为一个阶跃输入信号,温度计的测量输出可以视为对该阶跃输入信号的响应。
一阶系统的单位阶跃响应的时间函数为:)0(1)(/>-=-t e t x T t o (P82,3.3.2) 根据题意可知:98.01)(/11=-=-=Tt o e t x→02.0/1=-T e →256.050ln 1==T (min)若测量开始后,实际水温从零度起,以10°C/min 的速度线性升温,求温度计在1分钟时的示值与实际水温的误差是多大?(帮助公式:11111222++-=+⋅Ts T s T sTs s ) 根据题意,实际的温度输入信号为:t t x i ⋅=10)(其拉氏变换为:210)(ss X i =测量误差的时间函数为:]1110[)()]()([)()]([)()()()(2111+⋅⋅-=⋅-=-=-=---s T sL t x s G s X L t x s X L t x t x t x t e i i i o i o i其中:)(10]11[10]111[10]1110[/2212121T t e T T t Ts T s T s L Ts s L s T s L ----⋅+-=++-=+⋅=+⋅⋅所以:)1(56.2)1(10)(1010)(256.0///t T t T t e e T e T T t t t e ----=-=⋅+--=当t=1时,测量误差为:5.2)1(56.2)(256.0/11=-=-=e t e t3.7已知控制系统的微分方程为)(20)()(5.2t x t y t y =+',试用拉氏变换法求该系统的单位脉冲响应)(t w 和单位阶跃响应)(t x ou ,并讨论二者之间的关系解:由传递函数的定义和系统的微分方程(P34,2.2.2~2.2.3),可得系统的传递函数为4.0815.220)()()(+=+==s s s X s Y s G 系统的单位脉冲响应为(P81)t e s L s X s G L t w 4.0118]14.08[)]()([)(---=⋅+==系统的单位阶跃响应为(P82):)1(20]4.011[4.08]14.08[)]()([)(4.0111t ou e s s L s s L s X s G L t x -----=+-=⋅+==比较)(t x ou 和)(t w ,有)(t w =)(t x ou' 即系统的单位脉冲响应等于系统的单位阶跃响应的微分。
3.12下图为某数控机床系统的位置随动系统的方框图,试求:(1)阻尼比ξ及无阻尼固有频率n ω解:由图可知,该系统为一个单位反馈系统,其系统的闭环传递函数为:99)1(191)1(19)(1)()()(1)()(2++=+⋅++⋅=+=+=s s s s s s s G s G s H s G s G s G B 对比二阶系统传递函数的标准形式(P83,3.4.1)2222nn ns ωξωω++可得该系统的阻尼比ξ及无阻尼固有频率n ω为:61,3==ξωn (2)该系统的p M ,p t ,s t ,N13611312≈-=-==πξωπωπn d p t (P90,3.4.15)%53%100%1003611/6121/≈⨯=⨯=----πξξπe eM p (P90,3.4.17)9=a K )1(1+s s +-)(s X i )(s X o若令02.0=∆,84=≈ns t ξω(P91,3.4.22), 7.3122≈-=πξξN (P91,3.4.25)若令05.0=∆,63=≈ns t ξω(P91,3.4.23),8.215.12≈-=πξξN (P91,3.4.26)3.15 要使下图所示系统的单位阶跃响应的最大超调量等于25%,峰值时间p t 为2秒,试确定K 和f K 的值解:由图可知,该系统的闭环传递函数为:Ks K K s K s K sK s K s H s G s G s G f f B +⋅+=+⋅⋅+⋅=+=222)1(111)()(1)()( 对比二阶系统传递函数的标准形式2222nn n s ωξωω++可得该系统的阻尼比ξ及无阻尼固有频率n ω为:2,KK K fn ==ξω由题意, 令:%2521/==--ξξπeM p ,即4ln 12=-ξξπ解得:4.0=ξ令:()24.01122=-=-==K t nd p πξωπωπ 解得:93.2=K再由:293.22f fK K K ==4.0=ξ 解得:467.0=f K3.16如图所示系统,试求 (1)h K 为多少时,5.0=ξ;K21s+ -)(s X i )(s X os K f +1(2)单位阶跃响应的超调量和调整时间;(3)比较加入)1(s K h +与不加入)1(s K h +时系统的性能;解:(1)h K 为多少时,5.0=ξ;由图可知,该系统为一个单位反馈系统,其系统的闭环传递函数为:10)102(1010)2(10)1(1)2(10)1()(1)()()(1)()(2++++=+⋅+++⋅+=+=+=s K s s K s s s K s s s K s G s G s H s G s G s G h h h h B 其无阻尼自由频率为:10=n ω 又因为h n K 1022+=ξω,即102102-⋅=ξh K由题意,要求5.0=ξ,解得所需的h K 为:116.01025.0102=-⋅=h K(2)单位阶跃响应的超调量和调整时间;将该系统的闭环传递函数10)102(1010)(2++++=s K s s K s G h h B对比二阶系统传递函数的标准形式:2222nn ns ωξωω++可知该系统不是一个标准的二阶系统其s p t M ,无法利用P90页公式3.4.17以及P91页公式3.4.22~2.4.23直接求得 需要利用s p t M ,的定义求得。
令输入信号为单位阶跃信号,即)()(t u t x i =,其拉氏变换为:ss X i 1)(= 输出信号的拉氏变换为:⎥⎦⎤⎢⎣⎡++⋅+⎥⎦⎤⎢⎣⎡++⋅=+++⋅=++++⋅=⋅=1016.31011016.3101116.01016.31016.1110)102(10101)()()(2222s s s s s s s s s s s s K s s K s s G s X s X h h B s os K h +1)2(10+s s+-)(s X i)(s X o令:()()⎥⎥⎦⎤⎢⎢⎣⎡++⋅=⎥⎦⎤⎢⎣⎡++⋅=--2111221121211016.3101)(n n n s s s L s s s L t z ωωξω, 可以求得:74.25.0110,5.010216.3,16.3102111=-==⋅===d n ωξω由P86页公式(3.4.8~3.4.9),可得:)74.2sin 58.074.2(cos 1)74.2sin 5.015.074.2(cos 1)sin 1(cos 1)(58.1216.35.0121111t t e t t e t t e t z t t d d t n +-=-+-=-+-=-⋅--ωξξωωξ则,[][])74.2sin 155.074.2(cos 1)74.2sin 58.074.2(cos 1)74.2sin 74.274.2cos 74.258.0()74.2sin 58.074.2(cos 58.1116.0)()(116.01016.31011016.3101116.0)]([)(58.158.158.158.12211t t e t t et t e t t e t z dtt dz s s s s s s s L s X L t x t tt t o o +-=+-+-⋅-+=+=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++⋅+⎪⎪⎭⎫ ⎝⎛++⋅==------由上式可知,1)(lim )(==∞∞→t x x o t o由峰值时间p t 的定义,令:0)(==ptt o dt t dx0)74.2cos 15.174.2sin 89.2(58.1=+-p p pt t t e即:0)89.215.1arctan 74.2sin(=+p t 14.33787.074.2=+p t 解得:s t p 01.1≈将s t p 01.1≈代入)(t x o ,求得响应的第一个峰值为:177.1)01.174.2sin 155.001.174.2(cos 1)(01.158.1=⋅+⋅-=⋅-e t x p o由超调量的定义,得%7.17%10011177.1%100)()()(=⨯-=⨯∞∞-=o o p o p x x t x M 由调整时间的定义:)()()()(s o o o t t x x t x ≥∞⋅∆≤∞-即:)()74.2sin 155.074.2(cos 58.1s t t t t t e ≥∆≤+-由于1)74.2sin 155.074.2(cos ≤+t t 上式等价为:)(58.1s t t t e ≥∆≤-解得∆=1ln 58.11s t 若取02.0=∆,则sec 45.202.01ln 58.11==s t 若取05.0=∆,则sec 9.105.01ln 58.11==s t(2)若没有串联环节)1(s K h +,即则系统的闭环传递函数为:10210)2(101)2(10)(2++=+++=s s s s s s s G B 对比二阶系统传递函数的标准形式2222nn ns ωξωω++可得该系统的阻尼比ξ及无阻尼固有频率n ω为:316.0,10==ξωn其超调量及调整时间为:()%35%100%1002316.01316.021≈⨯=⨯=----πξξπe eM p若令02.0=∆,414=≈s t , 若令05.0=∆,313=≈s t ,由此可见,串联环节)1(s K h +的作用使得系统的性能改善了,即超调量和过渡时间都减小了。
)(s X i)(s X o)2(10+s s+ -3.17单位反馈系统的开环传递函数为)5)(1()(++=s s s Ks G K其输入为单位斜坡输入(单位恒速输入)时,系统的稳态误差01.0=ss e ,求所需的K 值 解:由于系统为单位反馈系统,其稳态偏差与稳态误差相同(P98,3.6.4),即ss ss e ε=将)(s G K 写为标准形式)12.0)(1(5/)(++=s s s K s G K (P100,3.6.12)当输入为单位斜坡输入时,其稳态偏差为:01.05/1==K e ss (P101,P102,表3.6.1)求得所需的K 值为500。
