如何快速找正方体的展开面和相对面复习过程
找正方体展开图的相对面的方法总结

找正方体展开图的相对面的方法总结
都昌县第五小学:段国镇
正方体的展开图是数学问题中经常遇到的问题,也一直是学生们总难以想明白的问题,为了学生更好的理解这一问题,我带领孩子们合作交流,对于如何快速准确地正方体展开图的相对面,和孩子们一起总结一些方法,现在分享给大家,希望能帮到大家。
第一种情况:一四一”型展开图;
(相同颜色为相对面)
像这种情况,在同层中有连续的四个正方形, 那么,间隔一个为对面。
剩下的上下两个为对面。
第二种情况:“二三一”型展开图
这种情况含有同层连续三个正方形,我们也可以利用“同层隔一面”
第三种情况:“二二二”型展开图
图中不存在同层连续三个或四个正方形的情况,利用“异层隔两面”的方法找到“1”和“4”隔着“2”、“3”是对面,“2”和“5”隔着“3”、“4”是对面,剩下的“3”和“6”是对面。
第四种情况:“三三”型展开图
图中含有同层连续的三个正方形,利用“同层隔一面”的方法,找到“1”和“3”是对面,“4”和“6”是对面,剩下的“2”和“5”是对面。
2019年9月。
巧记正方体展开图

巧记正方体展开图一、先用排除法
口诀:一排最多不过四,去掉田凹等臂7
1
2
3凹
4等臂
图1中4个面构成田字,剩余2个面无论放到哪里都不能构成正方体。
图2图4中剩余1个面无论放到哪里都不能构成正方体。
也就是说,只要展开图中包含田、凹、等臂7,就不能构成正方体。
二、分类记忆:横着看,分两大类,三排和二排(其余情况没有)(一)展开是三排的,以中间一排为准,又分成三小类。
第一类,中间一排是四连方,有以下6种:
口诀:中间4个一连串,两边各一一随便。
解释:中间一排是四连方的,两边必须各一个(A和B),并且这一个可以前后随便移动。
总之,只要两边各有一个就一定是展开图。
第二类,中间一排三连方,有以下3种:
口诀:中间3个一连串,三二错一一随便。
解释:中间一排是三连方的,两连方必须和中间的三连方有一个错开(三二错一),剩下的一个面(B)在中间三连方的另一边,并且可以前后随便移动。
第三类,中间一排二连方的,就一种:
口诀:三排各二一相连。
解释:分三排,每排两个,每排之间要有一个相连。
(二)展开是两排的,就一种:
口诀:二排各三一相连。
解释:分两排,每排三个,每排之间要有一个相连。
共8句口诀,两句一组,记住之后,正方体展开图的所有问题迎刃而解。
一排最多不过四,去掉田凹等臂7。
中间4个一连串,两边各一一随便。
中间3个一连串,三二错一一随便。
三排各二一相连,二排各三一相连。
口诀识别正方体展开图

口诀识别正方体展开图正方体有六个面,沿其中七条棱剪开可以得到一个由六个相同的正方形组成的平面图形,该图形虽然千姿百态,但六个正方形的排列是有一定规律的,并非胡乱拼接。
因此,在判断由六个正方形组成的图形中哪个是正方体展开图,哪个不是往往令人眼花缭乱。
为解决这个问题我们对正方体所有展开图用口诀归纳如下:首先,把六个正方形排列的行数和列数中较小的规定为行(当行数大于列数时,将图形旋转90°,列数便成了行数),则行数最小是2,最大是3。
行数二或三,个个边相连,不论何排列,去掉凹和田。
行二唯一见,每行三个现。
三行比大小,中间不能少。
“行数二或三”,指的是正方体展开图中的六个正方形要么排成两行,要么三行。
比如图1的行数是2,图2、图3的行数都是3,图4、图5的行数都是4,把它们旋转90°后行数就变成了3.“个个边相连”是指每个正方形都至少有一边与其他正方形是公共的。
否则它一定不是正方体展开图。
比如图3不是正方体展开图;“不论何排列,去掉凹和田”的意思是:不管六个正方形如何排列,一旦出现“凹”字型(如图6)或“田”字型(如图7)的,一定不是正方体展开图。
“行二唯一见,每行三个现”指的是排成两行的只有图1这种情形,每行都是3个正方形。
“三行比大小,中间不能少”说的是六个正方形排成三行的最多,而且排列方式五花八门,在这些排列中只要中间一行的个数不少于其他行的个数,再去掉图3、6、7这三种情形,那么它们都是正方体展开图。
显然,上述图1、图2、图4、图5都满足口诀条件,所以它们都是正方体展开图。
练习:下列由六个相同的正方形组成的图形中,哪些是正方体展开图?答案:(1)(3)(5)是,(2)(4)不是。
正方体相对面分布规律
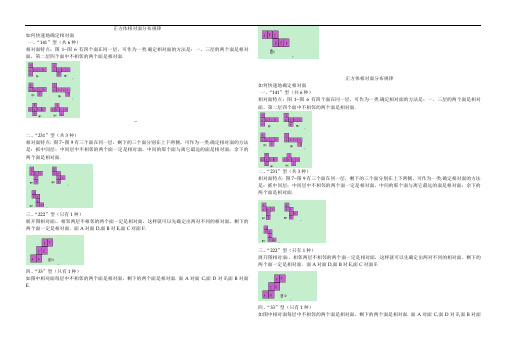
正方体相对面分布规律如何快速地确定相对面一、“141”型(共6种)相对面特点:图1~图6有四个面在同一层,可作为一类.确定相对面的方法是:一、三层的两个面是相对面,第二层四个面中不相邻的两个面是相对面.二、“231”型(共3种)相对面特点: 图7~图9有三个面在同一层,剩下的三个面分别在上下两侧,可作为一类.确定相对面的方法是:抓中间层;中间层中不相邻的两个面一定是相对面,中间的那个面与离它最远的面是相对面;余下的两个面是相对面.三、“222”型(只有1种)展开图相对面:,相邻两层不相邻的两个面一定是相对面,这样就可以先确定出两对不同的相对面,剩下的两个面一定是相对面.面A对面D,面B对E,面C对面F.四、“33”型(只有1种)如图中相对面每层中不相邻的两个面是相对面,剩下的两个面是相对面. 面A对面C,面D对F,面B对面E.正方体相对面分布规律如何快速地确定相对面一、“141”型(共6种)相对面特点:图1~图6有四个面在同一层,可作为一类.确定相对面的方法是:一、三层的两个面是相对面,第二层四个面中不相邻的两个面是相对面.二、“231”型(共3种)相对面特点: 图7~图9有三个面在同一层,剩下的三个面分别在上下两侧,可作为一类.确定相对面的方法是:抓中间层;中间层中不相邻的两个面一定是相对面,中间的那个面与离它最远的面是相对面;余下的两个面是相对面.三、“222”型(只有1种)展开图相对面:,相邻两层不相邻的两个面一定是相对面,这样就可以先确定出两对不同的相对面,剩下的两个面一定是相对面.面A对面D,面B对E,面C对面F.四、“33”型(只有1种)如图中相对面每层中不相邻的两个面是相对面,剩下的两个面是相对面. 面A对面C,面D对F,面B对面E.。
有关正方体表面展开图的解题规律

有关正方体表面展开图的解题规律新课标数学课本中新添了正方体展开图,中考题也多次出现,这种题有利于培养学生的空间观念,也有利于培养学生的实践、探索、交流能力.本文对几种常见类型的解题规律,作初步的探讨.一、判断给定的平面图形是否属正方体表面展开图1.如以最长的正方形链横排为准,展开图一般是三行,个别是两行,•不能是一行或四行,最长的一行(或列)在中间,可为2、3、4个,超过4•个或长行不在中间的不是正方体表面展开图.如都不是.2.在每一行(或列)的两旁,每旁只能有1个正方形与其相连,超过1个就不是.如都不是.中间的长行可折作正方体侧面,它两旁(或一旁)的正方形,与中间一行相连的折作底面,不相连的再下折作侧面.具体说可有以下4类11种图形,如作旋转或翻折后,方向会不同,但相对位置不变,这些不重复计算.1.“一·四·一”,中间一行4个作侧面,两边各1个分别作上下底面,•共有6种.2.“二·三·一”(或一·三·二)型,中间3个作侧面,上(或下)边2•个那行,相连的正方形作底面,不相连的再下折作另一个侧面,共3种.3.“二·二·二”型,成阶梯状.4.“三·三”型,两行只能有1个正方形相连.二、找正方体相邻或相对的面1.从展开图找.(1)正方体中相邻的面,在展开图中有公共边或公共顶点.如,•或在正方形长链中相隔两个正方形.如中A与D.(2)在正方体中相对的面,在展开图中同行(或列)中,中间隔一个正方形.如ABCD中,A与C,B与D,或和中间一行(或列)•均相连的两正方形亦相对.例1 右图中哪两个字所在的正方形,在正方体中是相对的面.解“祝”与“似”,“你”和“程”,“前”和“锦”相对.例2在A、B、C内分别填上适当的数.使得它们折成正方体后,对面上的数互为倒数,则填入正方形A、B、C•的三数依次是:(A)12,13,1 (B)13,12,1 (C)1,12,13(D)12,1,13分析A与2,B与3中间都隔一个正方形,C与1分处正方形链两边且与其相连,选(A).例3 在A、B、C内分别填上适当的数,使它们折成正方体后,对面上的数互为相反数.分析A与0,B与2,C和-1都分处正方形链两侧且与其相连,∴A─0,B─-2,C ─1.例4 代出折成正方体后相对的面.解A和C,D和F,B和E是相对的面.2.从立体图找.例5 正方体有三种不同放置方式,问下底面各是几?分析先找相邻的面,余下就是相对的面.上图出现最多的是3,和3相连的有2、4、5、6,余下的1就和3相对.再看6,•和6相邻的有2、3、4,和3相对的是1,必和6相邻,故6和5相对,余下是4和2相对,•下底面依次是2、5、1.例6由下图找出三组相对的面.分析和2相连的是1、3、5、6,相对的是4,和3相连的是2、4、5、6,相对的是1,和6相连的是1、2、3、4,相对的是5.三、由带标志的正方体图去判断是否属于它的展开图例7 如下图,正方体三个侧面分别画有不同图案,它的展开图可以是().分析基本方法是先看上下,后定左右,图A图B都是□和+两个面相对,不合题意,图C“□”和“○”之上,从立体图看“+”在右,符合要求.图D•“□”和“+”之上,“○”在右,而立体图“○”应在左,不合要求,故选(C).例8 下面各图都是正方体的表面展开图,若将它们折成正方体,•则其中两个正方体各面图案完全一样,它们是().分析首先找出上下两底,(1)是+和*,(2)是+和*,(3)(4)都是□和×,排除(1)(2),再检查侧面,(3)(4)顺序相同,所以选(3)(4).十一种展开图找对面的规律首先拿到一个展开图时,先看清楚它的结构。
巧记口诀确定正方体表面展开图

巧记口诀确定正方体表面展开图6个相连的正方形组成的平面图形,经折叠能否围城正方体问题,是近年来中考常考题型。
同学们在学习这一知识时常感到无从下手,现将确定正方体展开图的方法以口诀的方式总结出来,供大家参考:正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明:四方成线两相卫,六种图形巧组合; 跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
现将口诀的内涵解释如下:将一个正方体盒的表面沿某些棱剪开,展开成平面图形,需剪7刀,故平面展开图中周围有14条边长共有十一种展开图:一、四方成线两相卫,六种图形巧组合(1) (2) (3) (4)(5) (6)以上六种展开图可归结为四方连线,即 ,另外两个小方块在四个方块的上下两侧,共六种情况。
二、跃马失蹄四分开解析:本题可用“识图巧排‘7’、‘田’、‘凹’”来解决。
A 、D 都有“凹”形结构,B 有“田”形结构,故应选C例2.(2004扬州)马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如右图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示.) 解析:本题可用“跃马失蹄四分开”来解决。
图中具备了三二相连的结构,故本题有四种答案,即小方块的位置有图中 所示的四种情况之一。
试一试:1.(2004浙江金华)下列图形中,不是立方体表面展开图的是( )2.(2004镇江)如图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和圆,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图可以是( )3.(2004海南)如图是一个正方体包装盒的表面展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个表面展开图沿虚线折成正方体后,相对面上的两数互为相反数,则填在A、B、C内的三个数依次是().(A)0,-2,1(B)0,1,-2(C)1,0,-2(D)-2,0,1(2005济南中考题)在正方体的表面上画有如图(1)中所示的粗线,图(2)是其展开图的示意图,但只在A面上画有粗线,那么将图(1)中剩余两个面中的粗线画入图(2)中,画法正确的是(如果没有把握,还可以动手试一试)。
正方体123456面找对面口诀

正方体123456面找对面口诀1、一面连六:五四两面搭,三面连一搭配。
2、六面连三:四一两边相接,五六面连着它。
3、三面连五:六四搭一边,一二三面要相依。
4、五面连二:三六一边对应,二五四面重合。
5、二面连四:五一六面相结,三二四面并联。
6、四面连一:三五二面搭档,六四一面搭配。
一、总体综述正方体口诀便是小学生学习数学时常会碰见的语言,按照数值与方位确定,给出一到六面之间相互搭配的口诀,可以让学生更加准确的理解正方体的面的关系。
二、正方体123456面找对面口诀1、一面连六:五四两面搭,三面连一搭配。
从正方体的上角开始数,从第一面连到最后的第六面,中间有五面四面连接,三面与第一面搭配。
2、六面连三:四一两边相接,五六面连着它。
从第六面开始连到第三面,中间有第四面与第一面相连,五面和第六面由它们连接,把三面与它们连接起来。
3、三面连五:六四搭一边,一二三面要相依。
从第三面往五面搭档,中间有六面与四面搭配在一边,一面二面三面要彼此之间相依,将六面、四面与它们连接起来。
4、五面连二:三六一边对应,二五四面重合。
往五面连到二面,三面六面一边对应,而二五四面重合合而为一,将三六一边与它们联接起来。
5、二面连四:五一六面相结,三二四面并联。
将二面向四面连接,五面一面六面相互搭配结合,三面二面四面合而为一,将五一六面与它们接上。
6、四面连一:三五二面搭档,六四一面搭配。
从四面开始连至第一面,三面五面二面搭档,而六面四面一面共同搭配,再将三五二面与它们相结合起来。
三、正方体123456面找对面口诀的意义1、正方体口诀能够更加直观的展示出正方体各面之间的相互关系与组合,更好地引导学生思维。
2、口诀在学习中,能够让学生流畅的记忆数学知识,增强数学思维能力,提高学习乐趣性。
3、口诀一句,不仅能够记忆大量数学知识,而且能够深入理解,尤其在学习初期,更能够帮助学习者便捷的记忆。
4、借助口诀,将书中记忆的杂乱的数学概念形成一句句的口诀,就能够较为省力的把学到的知识搞定,而且容易记忆,而且更容易理解,文字统一,不易有遗漏。
正方体的11种展开图及判断方法教案

正方体的11种展开图及判断方法教案今天这节课我分成了两大块,前一部分:学习正方体的展开图;后一部分:动手操作、验证。
因为我在课前已经布置了学生预习,“找几个正方体纸盒,把它剪开,看看可以有哪些不同的展开图?”我在检查预习作业时,我就发现有的同学已经能找出10种不同的展开图。
但有也一些学生根本就没有完成预习作业。
为了,使不同的学生在本课上都能得到不同的发展,所以我把这节课分成了上面两大板块,第一板块:我直接就将11种不同的情况的展开图出示给学生,因为好学生在课前已经完成过“剪”的操作活动,如果课上再安排去剪,对于他们来说本课对他们来说没有什么收获。
而那些没有认真去做预习的同学,往往是那些成绩暂差生,如果上课再慢慢地安照教材给他们去动手再剪,一节课下来可能无法完成“11种”不同展开图的教学任务。
我直接告诉他们这些不同的展开图,至少可以应付后面的练习,有的学生虽然没有动手剪,但是在课堂上他们可以去想象,我想这样同样也可以培养学生的空间观念。
到了六年级,我个人认为有的操作是可有可无的。
我想操作的目的也是为了不操作,最后终归要回到抽象中,比如今天的“展开图教学”,一般的教学顺序应该是找一个正方体实物剪开,观察、认识展开图;然后把几种展开图动手折叠判断看看哪些展开图能做成正方体。
最后,运用获得的一些展开图的知识去判断、练习。
我在备课时,就产生了这样的疑问:1、通过剪的操作能不能找全部11种不同的展开图吗?2、通过什么活动能让学生发现11种不同的展开图?第一个问题:我想通过剪的操作不可能得全11种展开图,难道要学生去准备11个正方体纸盒吗?况且课堂时间也不允许,因为这部分知识只有1课时。
所以,我认为正方体的11种展开图用自主探索的方法可能不太可能,所以,我就运用讲授法,直接将这个结果告诉学生。
但是我在教学这个知识点的时候并不是生硬的直接出示,我是这样教学第一部分知识的:第一板块:师:如果给你一张硬纸板,你能做成一个正方体纸盒吗?怎么做?教学长方体展开图:(这时,我先教学长方体的展开图,拿出事先准备好的长方体的展开图,重点是让学生能判断,“谁和谁是对面?”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如何快速找正方体的展开面和相对面
正方体的展开与折叠是《图形的初步认识》这一章的重要内容,也是近几年中考的热点,而探索正方体的展开图的相对面分布的规律就是其中的一个考点.下面就谈一谈如何快速地确定相对面,供同学们学习时参考.
一、“141”型(共6种)
展开图特点:在这类展开图中,最长的一行(或列)有四个正方形(如图1~6所示)
在这种类型中,有4个正方形“直线”相连,其余2个正方形分别在“直线”两旁,位置任意。
相对面特点:图 1~图6有四个面在同一层,可作为一类.确定相对面的方法是:一、三层的两个面是相对面,第二层四个面中不相邻的两个面是相对面.
二、“231”型(共3种)
展开图特点:在这类展开图中,最长的一行(或列)有3个正方形(如图7~9).在“231”型中,“3”所在的行(或列)必须在中间,“2”、“1”所在行(或列)分属两边(前后不分).也就是正方体展开后,如有三个面在“直线”相连,另2个面在“直线”相连面一旁,另一面在它另一旁.故该种情况有3种。
相对面特点: 图7~图9有三个面在同一层,剩下的三个面分别在上下两侧,可作为一类.确定相对面的方法是:抓中间层;中间层中不相邻的两个面一定是
三、“222”型(只有1种)
展开图特点:在展正如
开图中,最多只有2个正方形“直线”相连.正如“二面三行,像楼梯”.如图
10所示
展开图相对面:,相邻两层不相邻的两个面一定是相对面,这样就可以先确定出两对不同的相对面,剩下的两个面一定是相对面.面A对面D,面B对E,面C 对面F.
四、“33”型(只有1种)
犹如“三面两行,两台阶”
如图中相对面每层中不相邻的两个面是相对面,剩下的两个面是相对面. 面A对面C,面D对F,面B对面E.。
