计算全距平均差方差和标准差
4差异量数

N
z 1
•标准分数(Z分数)
标准分数的优点
(1)可比性; (2)可加性; (3)明确性; (4)稳定性。
标准分数的应用
(1)用于比较分属性质不同的观测值在各自数据分布中相对位置的高低; (2)计算不同质的观测值的总和或平均值,以表示在团体中的相对位置; (3)表示标准测验分数。
例: 假定甲、乙两生高考入学考试成绩如下表所示,试问根
(2)一组原始分数转换得到的Z 分数可以是正值,也可以是负值。
(3)一组原始分数中,各个Z 分数的标准差为1,即 sZ 1
(4)若原始分数呈正态分布,则转换得到的所有Z 分数值的均值为0, 标准差为1的标准正态分布。即将原始分数标准化后不改变原来数据的分布。
• 证明 Z 0, z 1
解: Z X X σ
与最小值而求得,易受两极端数值影响。不考虑中间数值的 差异,它反应不灵敏,因此,它只是一种低效的差异量数。 它的用处一般只用于研究的预备阶段,用它检查数据的大概 散布范围,以便确定如何进行统计分组。
•二、百分位数 百分等级 百分位差
百分位数的概念
百分位数是位于依一定顺序排列的一组数据中某一百分位 置的数值。百分位数一般用 表示。 百分位数的计算方法
则有 Z
X
σ
X
N
1 σ
(X X)
N
1 Nσ
(X
X)
1 Nσ
[(X1
X)
(X2
X) ......
(Xn
X)]
1 Nσ
[(X1
X2
...
Xn)
NX]
1 Nσ
0
0
Z 0
解: ( X X )2 N
则有 z
数理统计_方差与标准差

心理和教育方面的实验或调查所得到的数据,大都具有随机变量的性质。
而对这些随机变量的描述,仅有前一章所讲集中趋势的度量是不够的。
集中量数只描述数据的集中趋势和典型情况,它还不能讲明一组数据的全貌。
数据除典型情况之外,还有变异性的特点。
关于数据变异性即离中趋势进行度量的一组统计量,称作差异量数,这些差异量数有标准差或方差,全距,平均差,四分差及各种百分差等等。
第一节方差与标准差方差(Variance)也称变异数、均方。
作为统计量,常用符号S2表示,作为总体参数,常用符号σ2表示。
它是每个数据与该组数据平均数之差乘方后的均值,即离均差平方后的平均数。
方差,在数理统计中又常称之为二阶中心矩或二级动差。
它是度量数据分散程度的一个特别重要的统计特征数。
标准差(Standarddeviation)即方差的平方根,常用S或SD表示。
假设用σ表示,那么是指总体的标准差,本章只讨论对一组数据的描述,尚未涉及总体咨询题,故本章方差的符号用S2,标准差的符号用S。
符号不同,其含义不完全一样,这一点瞧读者能够给予充分的注重。
一、方差与标准差的计算(一)未分组的数据求方差与标准差全然公式是:〔3—la〕〔3—1b〕表3—1讲明公式3—1a与3—1b的计算步骤表3—1未分组的数据求方差与标准差应用3—1公式的具体步骤:①先求平均数X=36/6=6;②计算X i-X;③求(Xi-X)2即离均差x2;④将各离均差的平方求和(∑x2);⑤代进公式3—1a与3—1b求方差与标准差。
具体结果如下:S2(二)已分组的数据求标准差与方差数据分组后,便以次数分布表的形式出现,这时原始数据不见了,假设计算方差与标准差可用下式:(3—3a)(3—3b)式中d=(Xc-AM)/i,AM为估量平均数Xc为各分组区间的组中值f为各组区间的次数N=Σf为总次数或各组次数和i为组距。
下面以表1—8数据为例,讲明分组数据求方差与标准差的步骤:表3—2次数分布表求方差与标准差具体步骤:①设估量平均数AM,任选一区间的Xc充任;②求d⑧用f乘d,并计算Σfd;④用d与fd相乘得fd2,并求Σfd2;⑤代进公式计算。
标志变异指标

方差: 2 (x x)2
n
标准差: (x x)2
n
标志变异指标
方差和标准差的计算
(2)由分组资料计算方差和标准差
在分组资料的条件下,计算方差用加权平均式,其计算公式为:
方差: 2 (x x)2 f f
标准差:
x
2
x
f
f
标志变异指标
【例4.22】 某企业200名工人工资的资料如表所示 :
二、标志变异指标的种类
(二)四分位差
1、什么是四分位差
是指在四分位数中,第三四分位数与第一四分位数之差。用 Q.D.表示,公式为:
Q.D.=Q3 -Q1 2、什么是四分位数
在一组标志值由小到大排列的数列中,将该数列等分成四个 部分,处在分界点上的标志值称为四分位数,其中:第一个分界 点上的标志值称为第一四分位数Q1;第二个分界点上的标志值 称为第二四分位数Q2;第三个分界点上的标志值称为第三四分 位数Q3。
标志变异指标
二、标志变异指标的种类
(一)全距 1、什么是全距
是指总体中最大的标志值与最小的标志值之差,用以说明单 位标志值的变动范围。 2、全距的计算 (1)由未分组资料、单项式变量分配数列计算全距
全距=最大的标志值—最小的标志值 (2)由组距式变量分配数列计算全距
全距≈最高组的上限最低组的下限
标志变异指标
200
1606.25 11x06x.25 606.25 106.25 393.75 1143.75 2143.75
—
计算工资的平均差。
16062.50 19x912x.5f 0 18793.75 7968.75 12993.75 24018.75 25725.00
125475.00
比较甲乙两学生平均成绩的代表性

变异指标的概念与作用
概念:变异指标是反映总体各单位标志值差 别大小程度的综合指标,又称为标志变动度。
平均指标说明总体各单位标志值的集中趋 势,而变异指标则说明总体各单位标志值 的分散程度或离中趋势。
变异指标的作用
(1)变异指标是衡量平均指标代表性的尺度。 一般情况下,数据分布越分散,变异指标越
大,平均指标的代表性越差;数据分布越集中, 变异指标越小,平均指标的代表性就越好。 (2)变异指标可以反映社会经济活动过程的均 衡程度和稳定性。
某车间50名工人日加工零件标准差计算表
按零件数分组
105~110 110~115 115~120 120~125 125~130 130~135 135~140
组中值(Xi)
107.5 112.5 117.5 122.5 127.5 132.5 137.5
频数(fi)
3 5 8 14 10 6 4
| Xi-x |
用 2 表示,标准差用 表示。在实际工作中,
标准差是测定总体离散程度最常用的指标。
方差的计算公式为:
未分组数据
n
(xi x)2
2 i1
n
标准差只需在方 差基础上开平方 根即可得到。
已分组数据
n
(xi x)2 fi
2 i1 n
fi
i 1
【例】根据表中的数据,计算标准差。
某车间50名工人日加工零件标准差计算表
2班的平x均 8成 5( 绩分);1 标 2准 (差 分σ ) Vσσ x1 82 51
THANKS
THANKS
感谢收看
谢谢!
23
汇报结束
谢谢大家! 请各位批评指正
15.7 10.7 5.7 0.7 4.3 9.3 14.3
第四章 差异量数

三、由各部分的标准差合成总标准差的计算方式
已知总体中各部分的标准差,若求其总标准 差,可用下面公式进行合成: (4.6) 式中: t为总标准差; N t 为总体中数据的个 d 数; i为各部分数据的标准差;i 为各部分平 均数与总平均数之差,即 di X i X t 。其中
Nt
t
例6.某小学四年级248名学生的平均身高为 143.52厘米,标准差是6.48厘米;平均体重
30.28千克,标准差4.56千克,试比较身高与体
重两变量的离散程度。
解:
CV身高
6.48 100= 100 4.52 X 143 00 15.06 X 30.28
=
50 90 52 85 48 88 51 92 50 52 48 51
= 89
d1 X 1 X t 90 89 1 d 2 X 2 X t 85 89 4 d 3 X 3 X t 88 89 1 d 4 X 4 X T 92 89 3
第四章
差异量数
第一节 标准差 第二节 四分差 第三节 差异系数 第四节 相对地位量数 习 题与思考题
描述一组数据离中趋势(波动性)的量数,称 为差异量数。
差异量数有:绝对差异量数和相对差异量数 两种。绝对差异量数包括全距、平均差、四分差 、方差、标准差等,相对差异量数有差异系数和 峰态量数、偏态量数。
本章重点介绍标准差、四分差、差异系数, 并学习标准分数和百分等级两个相对地位量数。
第一节 标准差
一、标准差的概念 二、标准差的计算方法
1、对原始数据计算标准差
2、对次数分布表计算标准差
统计心理-第四章 差异量数

25% 25% 25% 25%
Q1
Q2
Q3
Q = (Q3 – Q1)/2
排序后处于25%和75%位置上的值
三、四分位差
1. 也称为内距或四分间距 2. 反映了中间50%数据的离散程度 3. 不受极端值的影响 4. 用于衡量中位数的代表性
5. 可用于顺序数据、数值型数据,但不 能用于分类数据
顺序数据的四分位数
i 1
N
i 1
N
i
(三)总标准差的合成
St
N 1
S
2 1
d
2 1
N2
S
2 2
d
2 2
Nk
S
2 k
d
2 k
N1 N2 Nk
k
k
N
i
S
2 i
N
i
d
2 i
i1
i1
k
Ni
i1
S
:
t
总
标
准差
注意:只有应用同一种观测手段,测量同一 个特质,只是样本不同时,才能应用该公式 合成方差和标准差。
二、百分位差
3.百分位数的计算
Pp
Lb
1p00NFb f
i
4.百分位差
(1)P90 P10 (2)P93 P7
Pp为所求的第P个百分位数 Lb为百分位数所在组的精确下限 f为百分位数所在组的次数
Fb为小于Lb的各组次数的和 N为总次数
i为组距。
【例】:用下面的次数分布表计算该分布的百分位差P90-P10。
方差 标准差

方差标准差方差和标准差是统计学中常用的两个概念,它们都是用来衡量数据的离散程度的。
在实际的数据分析中,我们经常会用到这两个指标来描述数据的分布情况。
接下来,我们将详细介绍方差和标准差的概念、计算方法以及它们在实际应用中的意义。
首先,让我们来了解一下方差的概念。
方差是衡量数据离散程度的一个重要指标,它是各个数据与平均值之差的平方的平均数。
方差越大,说明数据的离散程度越大,反之则离散程度较小。
在统计学中,方差通常用σ^2来表示,其中σ代表总体标准差。
接下来,让我们来介绍一下标准差。
标准差是方差的平方根,它也是衡量数据离散程度的一个重要指标。
标准差的计算方法是先计算方差,然后对方差进行开方运算。
标准差的大小和数据的离散程度成正比,离散程度越大,标准差越大,反之则标准差越小。
在统计学中,标准差通常用σ来表示,其中σ代表总体标准差。
在实际应用中,方差和标准差都有着重要的意义。
它们可以帮助我们更好地理解数据的分布情况,从而进行更准确的数据分析和决策。
例如,在投资领域,我们可以利用标准差来衡量投资组合的风险程度,从而选择更合适的投资组合。
在质量控制方面,我们可以利用方差来衡量产品质量的稳定程度,从而及时发现和解决质量问题。
此外,方差和标准差还可以帮助我们进行数据的比较和评估。
通过比较不同数据集的方差和标准差,我们可以更好地了解它们的差异和特点。
在科学研究中,方差和标准差也经常被用来评估实验数据的稳定性和可靠性。
总之,方差和标准差是统计学中非常重要的概念,它们可以帮助我们更好地理解和分析数据。
通过对方差和标准差的深入了解,我们可以更加准确地把握数据的特点和规律,从而为实际应用提供有力的支持。
希望本文能够帮助读者更好地理解方差和标准差的概念和意义,为实际应用提供参考和指导。
统计计算练习题
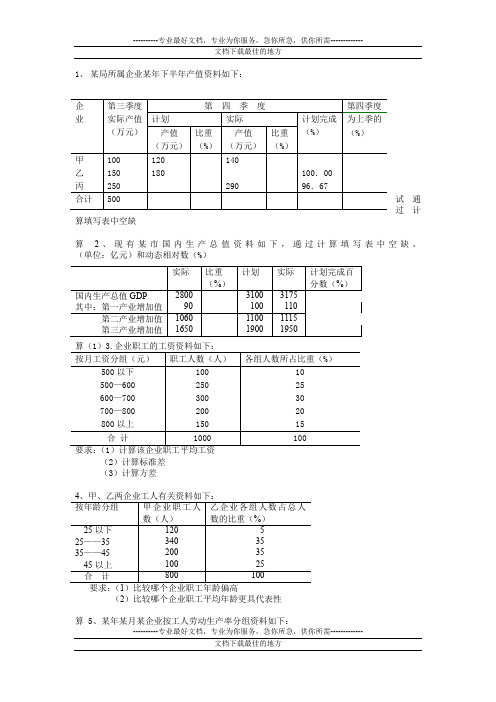
----------专业最好文档,专业为你服务,急你所急,供你所需-------------1、 某局所属企业某年下半年产值资料如下:试通过计算填写表中空缺算 2、现有某市国内生产总值资料如下,通过计算填写表中空缺。
(单位:亿元)和动态相对数(%)(2)计算标准差 (3)计算方差(2)比较哪个企业职工平均年龄更具代表性算 5、某年某月某企业按工人劳动生产率分组资料如下:7、甲、乙两企业工人有关资料如下:要求:(1)比较哪个企业职工工资偏高(2)比较哪个企业职工平均工资更具代表性10、甲、乙两钢铁生产企业某月上旬的钢材供货量资料如下:----------专业最好文档,专业为你服务,急你所急,供你所需-------------11、某校甲、乙两班学生的统计学原理考试成绩分组情况如下:要求:(1)计算各班学生的平均成绩(2)通过计算说明哪个班学生平均成绩的代表性强12求平均利润率。
13、设甲乙两公司进行招员考试,甲公司用百分制记分,乙公司用五分制记分,有关资料如问哪一个公司招员考试的成绩比较整齐?(用标准差)----------专业最好文档,专业为你服务,急你所急,供你所需-----------------------专业最好文档,专业为你服务,急你所急,供你所需-------------3、(1)平均工资=655元 (组中值:450 550 650 750 850。
450*100+550*250+650*300+750*200+850*150=655000。
655000/1000) (2)标准差=120.3元 (3)方差=144754、(1)甲、乙两企业的平均年龄分别为34元、38元,乙企业职工年龄偏高(2)甲、乙两企业的平均差系数分别为22.35%、19.47%,所以乙企业职工的平均年龄更具代表性5、该企业工人平均劳动生产率为67.6件/人 (组中值:55 65 75 85 95。
8250/55+6500/65+5250/75+2550/85+1520/95=366。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算全距、平均差、方差和标准差
一、全距 R(range)
全距是一组数据中的最大值(maximum)与该组数据中最小值(minimum)之差,又称极差。
R=Xmax-Xmin
一般用于研究的预备阶段,用它检查数据的分布范围,以便确定如何进行统计分析
原始数据计算公式
三、四分位差(Quartile)
四分位差是第一个四分位数与第三个四分位数之差计算公式为
Q=Q
3-Q
1
四、方差与标准差
方差:又称为变异数、均方,是每个数据与该组数据平均数之差乘方后的均值,是表示一组数据离散程度的统计指标。
样本的方差用表示,总体的方差用表示。
标准差是方差的算术平方根。
一般样本的标准差用 S 表示,总体的标准差用表示。
标准差和方差是描述数据离散程度的最常用的差异量。
分组数据方差与标准差的计算公式
方差与标准差的性质
•方差是对一组数据中各种变异的总和的测量,具有可加性和可分解性特点。
•标准差是一组数据方差的算术平方根,它不可以进行代数计算,但有以下特性:
总体方差、标准差或者方差、标准才差的合成
•方差具有可加性的特点。
当已知几个小组数据的方差或标准差时,可
以计算几个小组联合在一起的总的方差或标准差。
•需要注意的是,只有在应用同一种观测手段,测量的是同一种特质,只是样本不同的数据时,才能计算合成方差或标准差。
方差和标准差的优点:
方差与标准差是表示一组数据离散程度的最好指标,其值越大,离散程度越大。
应用方差和标准差表示一组数据的离散程度,须注意必须是同一类数据(即同一种测量工具的测量结果),而且被比较样本的水平比较接近。
优点:
•反应灵敏。
每个数据发生变化,方差与标准差也随之变化
•有一定计算公式的严密确定
•容易计算
•受抽样变动的影响小
•简单明了
•方差具有可加性(区分变异源,组间/组内)
五、差异系数(coefficient of variation)
差异系数指标准差与其算术平均数的百分比,它是没有单位的相对数。
用CV表示。
何种情况下运用差异系数:
•两个或两个以上样本所测特质不同,即所使用的观测工具不同,如何比较两者的离散程度?
•即使使用同一种观测量具,但样本水平相差较大,如何比较其离散程度?
差异系数的作用
•比较不同单位资料的差异程度
•比较单位相同而平均数相差较大的两组资料的差异程度
•可判断特殊差异情况
根据经验,一般CV值常在5%-35%之间。
如果CV大于35%时,可怀疑所求得的平均数是否失去了意义;如果CV小于5%时,可怀疑平均数与标准差是否计算有误。
六、标准分数(standard score)
1、概念
标准分数,又称为基分数或Z分数(Z-score),是以标准差为单位,反映一个原始分数在团体中所处位置。
具体来说,Z分数表示原始分数在以平均数为中心时的相对位置。
•标准分数从分数对平均数的相对地位、该组分数的离中趋势两个方面来表示原始分数的地位。
•Z分数可以表明原始分数在团体中的相对位置,因此称为相对位置量数。
2、计算
把原始分数转换成Z分数,就把单位不等距的和缺乏明确参照点的分数转换成以标准差为单位、以平均数为参照点的分数。
线性变换
标准分数带有小数和负值,为了克服标准分数出现的小数、负数和不易为人们所接受等缺点,常常是将其转换成正态标准分数。
例如:早期智力测验中运用智力商数表示智力测查的指标这种表示智力的方法后来被离差智商取代:
标准分数的性质
•Z分数无实际单位,是以平均数为参照点、以标准差为单位的相对量。
•一组原始分数得到的Z分数既有正值,也有负值,所有原始分数的Z分数之和为零。
•一组原始数据中,各个Z分数的标准差为1。
标准分数的应用
•用于比较几个分属性质不同的观测值在各自数据分布中相对位置的高低。
•表示标准测验分数。
经过标准化的心理和教育测验,常常用标准分数表示测验结果。
标准分数的优点
•可比性:标准分数以团体的平均数为基准,以标准差为单位,因而具有可比性。
•可加性:标准分数使不同的原始分数具有相同的参照点,因而具有可加性。
•明确性:标准分数较原始分数的意义更为明确。
•合理性:标准分数保证了不同性质的分数在总分数中的权重相同,使分数更合理地反映事实。
七、百分位数与百分位差
把一个次数分布排序后,分为100个单位。
百分位数就是次数分布中相对于某个特定百分点的原始分数,它表明在次数分布中特定个案百分比低于该分数。
百分位数用P m表示
百分位差(距)
•百分位差是指两个百分位数(percentile)之差。
•常用的百分位距有两种:
P90-P10和 P93-P7。
第三节数据的分布形状
一、正态分布
二、偏态系数(skewness SK)
•当数据较多的出现在均值的一侧时,数据分布左右不对称,此时,数据分布称为偏态分布。
•描述变量非对称分布的数字特征是偏态系数,也称为偏度。
•偏态分布有正偏态分布和负偏态分布两种。
当N>200以上时,计算的偏态系数才是可靠的。
SK>0为正偏态,SK<0为负偏态,SK=0 为正态。
•如果偏态系数的绝对值大于1,则说明数据的分布与正态分布有明显的不同
三、峰态系数(kurtosis Ku)
Ku以为判断值,小于为高狭峰,大于为低阔峰
四、偏态系数与峰态系数的计算方法
1、皮尔逊偏态量数法
2、峰度、偏度检验法。
