长方体的元素
第1讲 长方体的元素及其直观图的画法
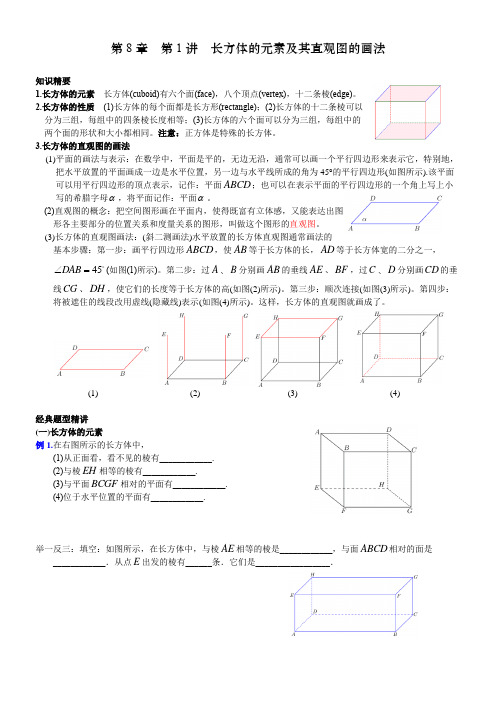
第8章第1讲长方体的元素及其直观图的画法知识精要1.长方体的元素长方体(cuboid)有六个面(face),八个顶点(vertex),十二条棱(edge)。
2.长方体的性质(1)长方体的每个面都是长方形(rectangle);(2)长方体的十二条棱可以分为三组,每组中的四条棱长度相等;(3)长方体的六个面可以分为三组,每组中的两个面的形状和大小都相同。
注意:正方体是特殊的长方体。
3.长方体的直观图的画法(1)平面的画法与表示:在数学中,平面是平的,无边无沿,通常可以画一个平行四边形来表示它,特别地,把水平放置的平面画成一边是水平位置,另一边与水平线所成的角为45°的平行四边形(如图所示).该平面可以用平行四边形的顶点表示,记作:平面ABCD;也可以在表示平面的平行四边形的一个角上写上小写的希腊字母α,将平面记作:平面α。
(2)直观图的概念:把空间图形画在平面内,使得既富有立体感,又能表达出图形各主要部分的位置关系和度量关系的图形,叫做这个图形的直观图。
(3)长方体的直观图画法:(斜二测画法)水平放置的长方体直观图通常画法的基本步骤:第一步:画平行四边形ABCD,使AB等于长方体的长,AD等于长方体宽的二分之一,∠=(如图(1)所示)。
第二步:过A、B分别画AB的垂线AE、BF,过C、D分别画CD的垂DAB45线CG、DH,使它们的长度等于长方体的高(如图(2)所示)。
第三步:顺次连接(如图(3)所示)。
第四步:将被遮住的线段改用虚线(隐藏线)表示(如图(4)所示)。
这样,长方体的直观图就画成了。
(1) (2) (3) (4)经典题型精讲(一)长方体的元素例1.在右图所示的长方体中,(1)从正面看,看不见的棱有____________.(2)与棱EH相等的棱有____________.(3)与平面BCGF相对的平面有____________.(4)位于水平位置的平面有____________.举一反三:填空:如图所示,在长方体中,与棱AE相等的棱是____________,与面ABCD相对的面是____________.从点E出发的棱有______条.它们是_________________.例2.用一根长100厘米的塑料管和橡皮泥做一个棱长为5厘米,6厘米,7厘米的长方体架子,应该如何截取?材料够吗?举一反三:一个长方体的长、宽、高之比为4:3:2,已知这个长方体的棱长之和是108厘米,求这个长方体的表面积和体积.例3.要做一个棱长分别为3厘米、5厘米和7厘米的无盖的长方体纸盒,最少需要多大的纸?最多需要多少纸? 107cm2, 127 cm2举一反三:一个正方体的所有棱长之和为60cm,则这个正方体的所有面的面积之和是_________cm2.例4.如图,将一个长方体的木块,沿线段CD从右侧截去一个长方体,成为一个正方体后,表面积减少了84cm2,已知新长方体的棱AB长3cm。
8.1长方体的元素8.2长方体直观图的画法

长方体有12条棱,相对的四条棱为一组,可以分为三组, 每组中的棱长度相等.
三条棱相交的点叫结: 1.长方体的每个面都是长方形.
2.长方体的十二条棱可以分为三组, 每组中的四条棱的长度相等. 3.长方体的六个面可以分为三组, 每组中的两个面的形状和大小都相等.
在数学中,我们约定把水平放置地平面画成一边是水平位置, 另一边与水平线所成的角为45度的平行四边形.
如何表示一个平面?
1. 依次用平行四边形四个顶点的字母来表示,记作:平面ABCD;
2 .用平行四边形相对的两个顶点的字母来表示, 记作:平面AC 或 平面BD ;
3.在表示平面的平行四边形的一个角上写上小写的希腊字母α, 记作:平面α.
自主小结
长方体、正方体的特征;
平面的画法及表示法;
长方体的斜二侧画法及表示法.
如何将长方体直观图画在纸上 ?
1. 画平行四边形ABCD,使AB等于长方体 的长,AD等于长方体宽的二分之一, ∠DAB = 45°. 2 . 过A、B分别画AB的垂线AE、BF, 过C、D分别画CD的垂线CG、DH, 使它们的长度都等于长方体的高. 3. 顺次连接EFGH. 4. 将被遮住的线段改用虚线表示 . 长方体ABCD—FFGH 斜二侧画法 平面ABCD、平面FFGH
8.1 长方体的元素
8.2 长方体直观图的画法
平面图形
立体图形
长方体有几个面? 每个面是什么形状? 相对的两个面有什么特点?
长方体有6个面. 每个面都是长方形. 相对的两个面形状、 大小相同. 相对的两个面为一组,长方体的六个面可以分为三组, 每组中的两个面的形状和大小都相同.
长方体有多少条棱,相对的棱长短怎样? 长方体有十二条棱,相对的棱长相等.
长方体正方体的特征

长方体正方体的特征一、长方体的特征长方体是一种立体图形,具有以下特征:1. 定义:长方体是指六个矩形面围成的立体图形。
其中,相对的两个面是相等的矩形,且所有顶点都是直角。
2. 元素:长方体由六个面、十二条棱和八个顶点组成。
3. 每个面都是矩形,有两对相等的边。
其中,相邻两个面共享一条边。
4. 所有棱都相等,并且每条棱都与四个面相邻。
5. 所有顶点都是直角,并且每个顶点都与三条棱和三个面相邻。
6. 长方体有三条对称轴,分别为通过中心的三条互相垂直的轴线。
其中,任意两条对称轴在中心交汇。
7. 长方体的表面积公式为2(ab+bc+ac),其中a、b、c分别为长方体的三条边长。
8. 长方体的体积公式为abc,其中a、b、c分别为长方体的三条边长。
9. 长方体具有稳定性好、容量大等优点,在日常生活中广泛应用于建筑、家具制造、运输等领域。
二、正方体的特征正方体是一种立体图形,具有以下特征:1. 定义:正方体是指六个正方形面围成的立体图形。
其中,相对的两个面是相等的正方形,且所有顶点都是直角。
2. 元素:正方体由六个面、十二条棱和八个顶点组成。
3. 每个面都是正方形,边长相等。
其中,相邻两个面共享一条边。
4. 所有棱都相等,并且每条棱都与四个面相邻。
5. 所有顶点都是直角,并且每个顶点都与三条棱和三个面相邻。
6. 正方体有四条对称轴,分别为通过中心的两条互相垂直的轴线和通过中心的两条对角线。
其中,任意两条对称轴在中心交汇。
7. 正方体的表面积公式为6a²,其中a为正方体的边长。
8. 正方体的体积公式为a³,其中a为正方体的边长。
9. 正方体具有稳定性好、容量大、造型美观等优点,在日常生活中广泛应用于建筑、家具制造、运输等领域。
三、长方体与正方体的区别长方体和正方体都是立体图形,但它们的特征存在一些区别:1. 定义不同:长方体是由六个矩形面围成的立体图形,其中相对的两个面是相等的矩形;而正方体是由六个正方形面围成的立体图形,其中相对的两个面是相等的正方形。
长方体的认识(一)

长方体的认识(一)引言长方体是我们日常生活中常见的一种几何体,它具有一些独特的性质和特征。
本文将对长方体进行全面介绍,包括它的定义、特征、计算公式以及一些常见的应用场景等。
定义长方体是一种有六个面的多面体,在几何学中属于一种特殊的柱状体。
长方体的六个面都是矩形,它的相邻面是矩形,且对应的边长度相等。
特征1. 面的性质长方体的六个面都是矩形,因此具有以下特性: - 面积:长方体的每个面的面积可通过长度、宽度和高度计算得出,且相邻两个面的面积相等。
- 对角线:长方体的每个面都有两条对角线,它们的长度也可以通过长度、宽度和高度计算得出。
2. 体积长方体的体积是指其所占的三维空间大小,也就是长方体内部的容积。
计算长方体的体积公式为:体积 = 长度 × 宽度 × 高度其中,长度、宽度和高度均为长方体相应边的长度。
3. 表面积长方体的表面积是指长方体各个面的总面积,计算长方体的表面积公式为:表面积 = 2 × (长度 × 宽度 + 长度 × 高度 + 宽度 × 高度)其中,长度、宽度和高度均为长方体相应边的长度。
4. 对角线长方体的对角线是指连接长方体相对角的线段,一个长方体共有四条对角线。
计算长方体的对角线的长度公式为:对角线= √(长度² + 宽度² + 高度²)其中,长度、宽度和高度均为长方体相应边的长度。
应用场景长方体作为一种常见的几何体,在我们的日常生活中有着广泛的应用,下面介绍几个常见的应用场景。
1. 建筑与构造在建筑与构造领域中,长方体经常被用作建筑物的基本形状。
例如,房屋、办公楼和大型建筑等都可以使用长方体作为基本结构来设计和建造。
2. 家具设计长方体的形状使得它在家具设计方面具有很大的灵活性。
很多家具,例如桌子、椅子和柜子等,都可以使用长方体作为基本构件进行设计和制造。
3. 货物包装由于长方体具有规则的形状和可测量的体积,因此它被广泛用于货物包装行业。
长方体和正方体统一的体积计算公式

长方体和正方体统一的体积计算公式一、长方体体积计算公式推导。
1. 长方体的基本元素。
- 长方体有长、宽、高这三个维度。
设长方体的长为a,宽为b,高为h。
2. 体积的意义及计算方法。
- 体积是指物体所占空间的大小。
对于长方体来说,我们可以通过数小正方体的个数来计算它的体积。
- 我们把长方体看作是由若干个单位体积(棱长为1的小正方体)组成的。
沿着长的方向,可以摆放a个小正方体;沿着宽的方向,可以摆放b个小正方体;沿着高的方向,可以摆放h个小正方体。
- 那么长方体所含小正方体的总个数(也就是长方体的体积V)就等于长、宽、高的乘积,即V = a×b×h。
二、正方体体积计算公式推导。
1. 正方体的特点。
- 正方体是特殊的长方体,它的长、宽、高都相等,设正方体的棱长为a。
2. 正方体体积计算。
- 由于正方体的长、宽、高都为a,根据长方体体积公式V=a×b×h,此时b = a,h=a,所以正方体的体积V=a×a×a=a^3。
1. 统一公式的原理。
- 我们可以把长方体和正方体的体积公式统一起来。
对于长方体V = a×b×h,而正方体是特殊的长方体,当a=b = h时,正方体体积V=a^3。
- 如果我们把长方体底面的面积S = a×b(底面积就是长乘宽),那么长方体的体积V=S×h(体积等于底面积乘高)。
- 对于正方体,它的底面积S = a×a=a^2,体积V = S×a=a^2×a=a^3,也符合V = S×h这个公式(这里h=a)。
用1.1.1构成空间几何体的基本元素

练 3.在空间中,下列说法正确的是( B ) 习 (A)一个点运动形成直线 (B)直线平行移动形成平面或曲面 (C)直线绕定点运动形成锥面 (D)矩形上各点沿同一方向移动形成长方体 解:A错误,一个点运动形成线, 若运动方向保持不变则形成直线,运 动方向发生变化则形成曲线; C错误,直线绕定点转动形成锥面,而不是直线绕定点“ 运动”形成锥 面; D错误,矩形上各点沿同一方向移动,没有具体说明移动的具体方向及 移动的距离的大小,故而不一定形成长方体。 故选B
几何体的相关概念: 1.异面直线 2.直线与平面平行 3.直线与平面垂直 4.点到平面的距离 5.两个平面互相垂直 6.两个平面互相平行
D1 B1 D
C1
A1
C B
A
以上概念只要求在形象感觉的基础上理解即可,在后面的各个小节中 还会具体地进行研究和学习.
六、点、线、面的位置关系及表示
空间看成点的集合,点是空间的基本元素,直线和平面都是点的集合.
A1 B1 D C B
C1
A
异面直线的画法 如图,通常以平面α为依托,将一条直线a画在平面α内,另一条直线不 在平面α内,且经过平面α内、直线a外一点,来画异面直线a,b.
b
a
异面直线a,b
五、相关概念
2.直线和平面平行: 如果直线和平面没有公共点,我们就说直线和平面平行。 如图,在长方体ABCD-A1B1C1D1中,直线A1B1平行于平面ABCD。 记作A1B1//平面ABCD.
四、长方体
观察长方体中的线和面,并思考以下问题: 存在!
D' A' B' C'
(1)存在平行的直线吗?
AB∥CD∥C′D′∥A′B′; D∥BC∥B′C′∥A′D′; AA′∥ DD′ ∥ CC′∥ B B′. (2)存在既不平行也不相交的直线吗? 存在! AB与CC′;AB与DD′;AD与BB′;AD与CC′;等等. 这样的直线叫做异面直线! (3)存在直线与平面没有公共点的情况吗? 存在! A′B′与平面ABCD;B′C′与平面ABCD;等等. 这时称直线与平面平行,记作A′B′∥平面ABCD;B′C′∥平面ABCD.
长方体正方体.知识点总结
长方体的再认识一、 概念1、 长方体的元素:六个面、八个顶点、十二条棱2、 长方体的三元素的特点:(主要是外观特征和数量关系)①长方体的每个面都是长方形;②长方体的十二条棱可以分为三组,每组中的四条棱的长度相等。
③长方体的六个面可以分为三组,每组中的两个面形状大小都相同。
3、 正方体是特殊的长方体。
4、 平面是平的,无边无沿,没有厚度和大小,一般用平行四边形来表示。
记作:平面ABCD 或平面α。
5、 将水平放置的平面画成一边是水平位置,另一边与水平线成45度角的平行四边形。
6、 斜二侧画法画长方体时要注意:宽画成标注尺寸的一半;看不到的线画成虚线;要标字母和尺寸,要写结论。
长方体ABCD-EFGH 、平面ABCD 、棱AB 、顶点A 。
7、 空间中两直线的位置关系有三种:相交、平行、异面① 如果两条直线在同一平面内,有唯一公共点,称这两条直线的位置关系是相交; ② 如果两条直线在同一平面内,没有唯一公共点,称这两条直线的位置关系是平行; ③ 如果两条直线既不平行也不相交,称这两条直线的位置关系是异面。
8、直线垂直于平面记作:直线P Q ⊥平面ABCD ;直线平行于平面记作:直线P Q ∥平面ABCD 。
9、 计算公式之一:(三条棱长分别是a 、b 、c 的长方体)① 棱长和 = 4()a b c ++ ; ② 体积 = abc ;③ 表面积 = 2()ab bc ac ++ ; ④ 无盖表面积 = S ab -、S bc -、S bc - 10、计算公式之二:(边长是a 正方体)① 棱长和= 12a ;②体积= 3a ;③表面积= 26a ;④无盖表面积 =25a 。
11、长方体不一定是正方体;正方体一定是长方体。
12、长方体中棱与棱的位置关系有3种,分别是平行、相交、异面。
13、长方体中棱与面的位置关系有2种,分别是:平行、垂直。
14、长方体中面与面的位置关系有2种,分别是:平行、垂直。
长方体的知识点整理
长方体的知识点整理长方体是三维空间中最基本的几何体之一,它的特点是有六个面,每个面都是一个矩形。
在日常生活和学习中,长方体是非常常见的,因此对长方体的知识点进行整理和学习掌握,能够帮助我们更好地认识和应用长方体,下面就来仔细学习长方体吧。
一、长方体的定义和性质长方体是一种六个面都是矩形的立体图形,其中任意相邻两个面彼此垂直,每个面的对边长度相等。
除此之外,长方体还具有以下几个性质:1. 所有的棱和面都是直角。
2. 任意两个相对的面互为平行面。
3. 所有的对面积相等。
4. 所有的顶点的维数都是 $3$。
二、长方体的元素长方体的面、棱、顶点构成了长方体的元素,接下来分别介绍一下。
1. 面:长方体有六个面,其中三对面互为平行面,共有三种不同的面:上下底面、前后底面和左右底面,三对相对的底面都是矩形。
2. 棱:长方体有 $12$ 条棱,每条棱都是两个相邻面的交线,其中任意两条垂直的棱互为正交棱,还有任意两个相邻棱的长度相等。
3. 顶点:长方体有$8$ 个顶点,每个顶点是三个相邻面的交点,每个顶点的维数都是 $3$。
三、长方体的表面积和体积长方体的表面积可以用公式 $S=2ab+2bc+2ac$ 来计算,其中$a$、$b$、$c$ 分别为长方体的三条边长,横截面积也可以用$S=ah$ 来计算。
长方体的体积可以用公式 $V=abc$ 来计算,其中 $a$、$b$、$c$ 分别为长方体的三条边长。
四、长方体的投影和展开图长方体的三个不同方向的投影都是矩形,分别称为正视投影、俯视投影和侧视投影。
展开图就是将长方体拆开后展开成一个平面的二维图形,可以用来计算长方体的面积和体积等。
五、长方体的应用长方体在日常生活中应用非常广泛,例如:建筑中的砖、石等都是长方体,以及一些器具、家具等也是长方体。
此外,长方体还有很多科学和数学应用,例如计算机图形学中的三维图形处理、微积分中的三重积分等。
以上就是关于长方体的一些基本知识点的整理,希望对大家有所帮助。
1.1.1构成空间几何体的基本元素
平静的水面
平面式处处平直的面,而曲面就不是处处平直的.
曲面
曲面的形成
生活中的平面与曲面
从运动的观点,理解空间基本图形之间 的关系.
流星“点动成线”
动态观察几何体
直线平行移动,可以形成平面或曲面.
面动成体
结论
在集合中,可以把线看成点运动的轨迹, 如果点运动的方向始终不变,那么他的轨迹 就是一条直线或线段;如果点运动的方向时 刻在变化,则运动的轨迹是一条曲线或曲线 的一段. 同样,一条线运动的轨迹可以是一个面, 面运动的轨迹(经过的空间部分)可以形成 一个几何体.
过程与方法
通过让学生探究点、线、面 之间的相互关系,掌握文字语言、 符号语言、图示语言之间的相互 转化.
情感态度与价值观
通过用集合论的观点和运动的观 点讨论点、线、面、体之间的相互关 系培养学生会从多角度,多方面观察 和分析问题,体会将理论知识和现实 生活建立联系的快乐,从而提高学生 学习数学的兴趣.
各种形状的玩具
实际存在的几何图形
后来又通过学习几何知识,认识 了许多几何图形,如:长方形、长 方体、圆、球等.同学们有没有想过, 为什么画在纸上的各种各样的物体, 你一看就能认出它是某种物体呢?
三角形和半圆
1.1.1构成空间几何体的基本元素
教学目标
知识与能力
掌握空间点、线、面之间的 相互关系以及相互之间的位置 关系.
D`
A` B`
C`
D
A B连线 段中最短的一条,线段AA`的长称作点A` 到平面AC的距离.
D`
A` B`
C`
D
A B
C
平面AC∥平面A`C`
如果两个平面没有公共点,则说这两个平面平行.
8.1 长方体的元素
2)数一数长方体有多少条棱.相对的棱长短怎样?
长方体有12条棱,相对的棱长相等.
3)3条棱相交的点叫做顶点.数一数 长方体有几个顶点.
长方体有8个顶点.
分组
面:长方体有六个面,
相对的两个面为一组,可以分为三组, 每组中的两个面的形状和大小都相同.
棱:长方体有12条棱,
相对的四条棱为一组,可以分为三组, 每组中的棱长度相等.
想一想:
有没有六个面都一样的长方体?
正方体
A D B C
正方体各个元素有什么特征呢?
正方体的12条棱的长度都一样, 6个面的形状都一样,都是正方形.
E
H G F
练习1:
1)长方体有(6)个面,每个面都是(长方形), 相对的面的( 形状和大小 )相等;
正方体的表面积、体积怎样计算?
S表=6a2
V=a3
练习3:
一个正方体的棱长的和是60厘米, 求正方体的表面积是多少平方厘米 ?
体积是多少立方厘米?
练习4:
如图,是边长为10厘米的三个小正方体 拼成的图形,这个图形共有几个面? 求出它的表面积和体积. 把一个棱长为3cm的正方体的六个面如图都涂上颜色, 将它的棱三等分,然后从等分点把正方体锯开。 27 1)能得到________ 个棱长为1cm的小正方体。 8 个。 2)三个面涂有黄色的小正方体有_____ 12 个。 3)两个面涂有绿色的小正方体有_____ 6 个。 4)一个面涂有红色的小正方体有_____ 5)有没有各面都没有涂颜色的小正方体? 1 个。 如果有,那么有______
2)这是一个( 长方体 ),它的长( 8 )厘米,
宽( 4 )厘米,高( 3 )厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长方体的元素
教学目标
1、进一步认识长方体的元素及其特征。
2、通过观察、操作,初步具备认识长方体等几何体的能力及空间想象能力。
3、能熟练计算长方体的表面积和体积。
4、体会数学与生活的联系,学会与人合作,获得在活动中克服困难,运用知识
解决问题的成功体验。
教学重点
长方体的元素及其特征。
教学难点
运用所学知识(什么具体知识?)解决问题。
教学过程
一、创设情境,导入新课
1、比较平面图形和立体图形的差别,由平面图形过渡到立体图形,特别是
其中的长方体。
强调正方体是特殊的长方体。
2、列举生活中的长方体。
感性认识长方体,让学生体会到长方体图形来源
于生活。
本节课我们将对长方体进行进一步的认识,引出课题——长方
体的元素。
二、尝试发现,探索新知
1、长方体是由哪些元素组成的?顶点、棱和面。
2、学生自行讨论得出长方体的主要特征。
提高学生识图能力,渗透分类思想。
(1)数一数长方体有几个顶点?
(2)数一数长方体的棱有多少条?量一量相对(讲法确切吗?)的棱的长短有什么关系?
(3)长方体有多少个面?分别是是什么形状?相对的两个面有什么特点?
3、试一试:
结合身边长方体模型,概括长方体的面、棱、顶点的特点。
4 、探讨长方体和正方体的关系。
让学生知道正方体是特殊的长方体,强化识图能力。
(1)正方体也是长方体吗?
(2)正方体的棱与棱之间、面与面之间有什么特点?
三、巩固新知,及时反馈
判断题
(1)长方体的每个面都是长方形。
( )
(2)长方体有十二条棱,并且每条棱都相等。
( )
(3)六个面,十二条棱和八个顶点组成的图形都是长方体。
( )
(教具演示)
(4)长方体相对的面的面积都相等。
( )
(5)长方体的任一个顶点都可以引出四条棱。
( )
(6)存在一个八条棱长相等的长方体。
( )
四、动手实践,增强体验
1、考考你:
小明想用一些长度为16厘米的塑料管和橡皮泥做一个棱长分别为6厘米、8
厘米和10厘米的长方体架子。
请问至少需要几根这样的塑料管?应如何裁
截?
2、动手操作,小组搭建长方体。
对长方体有更感性的认识,进一步掌握长
方体的特点,培养学生团结互助的良好个性品质。
前后四名同学组成一个小
组,制作一个长方体艺术品。
看看哪个小组做的又快又好!
五、复习旧知,熟练应用
1、长方体的表面积和体积
长方体六个面的总面积,叫做它的表面积。
长方体的容积,叫做它的体积。
2、长方体的表面积、体积怎样来计算哪?
长方体的表面积=(长×宽+长×高+宽×高)×2
长方体的体积=长×宽×高
3、熟练计算
(1)已知一个长方体的纸盒,棱长分别是6厘米,3厘米和4厘米,那么,这个纸
盒的表面积和体积各是多少?(提醒学生注意单位)
(2)一个正方体的棱长的和是60厘米,求正方体的表面积是多少平方厘米?
体积是多少立方厘米?
六、问题探究,拓展思维
思考:由4个边长为2cm的正方体拼接而成的长方体的表面积是多少?
七、总结归纳,提升认识
谈谈你今天的收获。
八、回家作业
1、预习6.10
2、订正并完成练习册8.1。
