上海市沪教版六年级第二学期易错题整理 8.1长方体的元素(原卷版)
沪教版数学六年级(下)第八章长方体的再认识8.1长方体的元素练习卷一和参考答案

数学六年级(下)第八章长方体的再认识8.1 长方体的元素(1)一、填空题1. 长方体有个面,条棱,个顶点。
2. 长方体的面可分为组,每组中面的相同,相等。
3. 如果长方体的每一条棱的长短都一样,则这个长方体就是,它的每个面都是形状大小相同的。
4. 长方体的每个面都是。
5. 长方体的条棱可以分为组,每组中的条棱的相等。
6. 如图所示的长方体中,与棱AB长度相等的棱是.7. 如图所示,长方体中,与平面ABEH相对的面是,它上面的底面用字母表示是 .8. 如图所示,长方体中被遮住的棱是,从点F出发的棱是 .第1、2、3题9. 当长方体的所有棱长都相等时,长方体就变成.10. 如果正方体的棱长为a,那么这个正方体的表面积为,体积为 .二、选择题11. 长方体中,棱长相等的至少有()A.2条B.4条C.8条D.12条12.用长96cm的铁丝围成一个最大的正方体,这个正方体的棱长是()A.4cmB.12cmC.8cmD.48cm13.如果一个长方体的长、宽、高都扩大到原来的2倍,那么这个长方体的体积就扩大到原来的()A.2倍B.4倍C.6倍D.8倍14.下列说法中正确的个数有()(1)正方体是特殊的长方体;(2)长方体的表面中不可能有正方形(3)棱长为6cm 的正方体的表面积和体积的数值相等(4)具有6个面,12条棱和8个顶点的图形都是长方体A.1个B.2个C.3个D. 4个三、解答题15.如图,在长方体EFGH ABCD -中,cm BF cm BC cm AB 8,10,12===.求四边形ADHE 、四边形EFGH 、四边形DCGH 的面积,并求出此长方体的体积.16.把一根长72分米的木条截开后刚好能搭成一个正方体架子,求这个正方体的表面积和体积.17.长方体的棱长分别为4cm 、5cm 、6cm ,求这个长方体的棱长和、表面积和体积18. 如图,是边长为5厘米的三个小正方体拼成的图形,这个图形共有几个面?求出它的表面积和体积.19.如图,把一个棱长8厘米的正方体的六个面都涂上红色,再将它的棱四等分,然后从等分点把正方体锯开.(1)能得到多少个棱长为2厘米的小正方体?(2)三个面有红色的小正方体有多少个?(3)两个面有红色的小正方体有多少个?(4)一个面有红色的小正方体有多少个?(5)有没有各面都没有红色的小正方体?如果有,那么有多少个?质量QQ交流群:467235124课外辅导热线:132******** (微信)数学六年级(下)第八章长方体的再认识8.1 长方体的元素(1)参考答案一、1. 6 12 82. 3 形状大小3. 正方体正方形4 长方形5. 十二三四长度6. CD、FG、EH7.平面CDGF ADGH8. BE、EF、EH EF、FG、CF9. 正方体6a3a10. 2二、11. B 12. C 13. D 14. A三、15. 四边形ADHE的面积为80cm2,,四边形EFGH面积为120cm2,,四边形DCGH的面积为96cm2,,长方体的体积为960cm3,.16. 正方体的表面积216平方分米,体积为216立方分米17. 棱长和: 60cm,表面积:148cm2,体积:120cm318. 图形共有8个面,它的表面积350平方厘米,体积为375立方厘米19. (1)64个;(2)8个;(3)24个;(4)24个;(5)有,8个。
上海市沪教版六年级第二学期易错题整理 8.1长方体的元素(原卷版)

8.1长方体的元素易错点归纳1. 长方体有6个面,8个顶点,12条棱.2. 长方体的特点(正方体是特殊的长方体).(1)长方体的每个面都是长方形;(2)长方体的十二条棱可以分为3组,每组中的4条棱的长度都相等.(3)长方体的六个面可以分为3组,每组中的2个面的形状和大小相同.3.若一个长方体的三条棱长分别是a,b,h,则这个长方体的总棱长可以表示为4(a+b+h );它的表面积可以表示为2ab+2ah+2bh ;它的体积可以表示为abh .一、填空题1.已知一个长方体的长、宽、高分别是7厘米、5厘米、3厘米,那么这个长方体的棱长和为_厘米.2.将三个棱长为4cm 的小正方体拼成一个大长方体,表面积比原来减少了_____cm².3.一个长方体平均截成5个正方体,表面积增加了40cm 2,原长方体的表面积是______cm².4. 棱长分别为3厘米、5厘米、7厘米的两个长方体拼成一个长方体, 它们的表面积最多减少_____________平方厘米.5.如果一根24米的铁丝剪开后刚好能搭成一个长方体框架模型,这个长方体的长、宽、高的长度均为整数米,且互不相等,那么这个长方体的体积是 立方米.6.某长方体中,一个公共顶点的三条棱长度之比为5:8:10,长方体中最小的一个面的面积是1202cm ,则最大的一个面的面积是 2cm .7.有12个棱长为1cm 的完全相同的小正方体,用它们拼成一个长方体,这个长方体的表面积最小是 平方厘米.二.选择题8.一个长方体的棱长总和是108厘米,且长:宽:高是4:3:2,则长方体的体积( )立方厘米。
A.216B.324C.432D.6489.下列说法中正确的个数有( )①正方体是特殊的长方体,②长方体的表面中不可能有正方形,③楼长为6cm的正方体的表面积和体积的数值相等,④具有6个面,12条棱和8个项点的图形都是长方体.A.1个B.2个C.3个D.4个二、解答题10.制作一个无盖的长方体玻璃鱼缸,底面长为115米,宽为35米,高为45米,如果不计拼缝,那么至少需要多少平方米的玻璃?11.如图所示,在一张长8cm、宽6cm的长方形纸处的四角分别剪去1个边长为1.5cm的正方形,然后沿虚线折成一个无盖的长方体盒子,求这个长方体盒子的体积.12.已知一个长方体无盖容器,它的棱长分别为5厘米、8厘米、10厘米,问:这个容器的表面积和容积各是多少?13.一根长为36分米的铁丝截开后刚好能够搭成一个长方体架子,这个长方体架子的长、宽、高的长度均为整数分米,且互不相等,求这个长方体的体积.14.(青浦2017期末27)如图,是一个长方体的一部分,虚线表示被遮住的线段,按要求完成下列问题.(1)补画出这个长方体.【画图时,请使用2B铅笔,不写画法】(2)在补画出的长方体中,若长是宽的2倍,高比宽多4厘米,用96厘米长的铁丝制作这个长方体框架.问:这个长方体框架的长、宽、高应分别是多少?(3)如果给出一个与(2)中所作的长方体形状、大小相同的木块,并在这个木块上切下一个棱长是1厘米的正方体,求剩余木块的表面积(要求:切下的正方体木块中至少有一个面是原来长方体木块表面的一部分).。
沪教版 六年级数学下册 第八章 8.1 长方体的元素

1 沪教版 六年级数学下册 8.1 长方体的元素
1.以下说法中正确的是( )
A .一个长方体有8个面
B .一个长方体有12条棱
C .一个长方体有6个顶点
D .一个长方体有10个顶点
2.如图,在长方体ABCD -EFGH 中,与面ABCD 相对的面是( )
A .面CDHG
B .面ABFE
C .面EFGH
D .面AEHD
3、在一个长方体中,相对两个面的周长和面积都
4、如图,在长方体 ABCD -EFGH 中.
(1)与面ABCD 相对的面是
(2)与棱CD 的长度相等的棱是
5.已知一个正方体的棱长总和是48厘米,那么这
个正方体的每条棱长为 厘米。
6.已知一个长方体的长、宽、高分别为5厘米、4厘米和3厘米,
那么这个长方体的体积是 立方厘米,表面积为 平方厘米。
7如图,把三个大小相等的小正方体叠放在一起,已知小正方体的棱长为2厘米,求这个组合体的表面积。
8.已知一个长方体的棱长总和为64厘米,且长∶宽∶高=5∶1∶2,求这个长方体的长、宽及高分别是多少厘米;这个长方体的最大占地面积是多少平方厘米?
9.已知一个无盖的长方体纸盒的棱长分别为4厘米、6厘米和8厘米,求这个纸盒的表面积和 容积。
上海市沪教版六年级第二学期易错题整理 8.3长方体中棱与棱的位置关系的认识(原卷版)
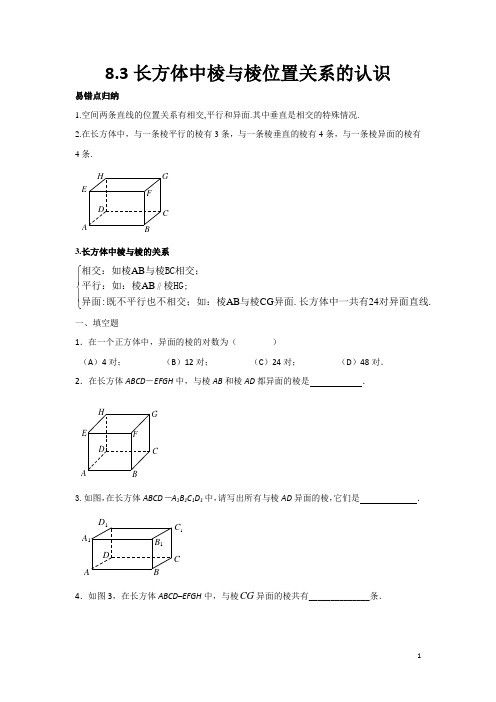
8.3长方体中棱与棱位置关系的认识易错点归纳1.空间两条直线的位置关系有相交,平行和异面.其中垂直是相交的特殊情况.2.在长方体中,与一条棱平行的棱有3条,与一条棱垂直的棱有4条,与一条棱异面的棱有4条.D H GFEC B A3.长方体中棱与棱的关系AB AB AB CG 24⎧⎪⎨⎪⎩相交:如棱与棱BC 相交;平行:如:棱棱HG;异面:既不平行也不相交;如:棱与棱异面.长方体中一共有对异面直线.∥一、填空题1.在一个正方体中,异面的棱的对数为( ) (A )4对;(B )12对;(C )24对;(D )48对.2.在长方体ABCD -EFGH 中,与棱AB 和棱AD 都异面的棱是 .H GFED C B A3.如图,在长方体ABCD -A 1B 1C 1D 1中,请写出所有与棱AD 异面的棱,它们是 .A 1D 1B 1C 1D CB A4.如图3,在长方体ABCD –EFGH 中,与棱CG 异面的棱共有______________条.5.如图在长方体ABCD-EFGH 中,与棱EF 在同一平面内且垂直的棱是 .(写出符合题意的所有棱)H GFED C B A6.如下图是一张长方形纸处ABCD 对折后翻开所成的图形.(1)与AE 所在直线平行的直线是______________________. (2)与AE 所在直线相交的直线是__________________________. (3)与AE 所在直线异面的直线是__________________________. (4)图中有____对异面直线.它们分别是_____________________. 7. 如右图,长方体ABCD-EFGH 中,下列各对棱的位置关系:(1)棱AD 与棱BC:_______.AFECB GH DEFD CAB(2)棱EH 与棱EF:_______. (3)棱AB 与棱FG:________. (4)棱CD 与棱BF:________. (5)棱AB 与棱EF:_______.8.如右图,在长方体ABCD-EFGH 中, (1)与棱AC 相交的棱有____________________. (2)与棱AC 异面的棱有_____________________. (3)与棱AC 平行的棱有___________________. (4)与棱BF 平行的棱有___________________. 9.如图所示,在长方体ABCD -EFGH 的12条棱中, (1)与AC 平行的棱有______条; (2)与AC 相交的棱有____条; (3)与AC 异面的棱有______条. 二.选择题10. 如图1,在长方体-ABCD EFGH 中,与棱EF 异面的棱是( )(A )棱HD ;(B )棱BF ; (C )棱HG ; (D )棱AB .11.如图1,在长方体ABCD -EFGH 中,与棱AD 所在的直线既不相交也不平行的棱共有( ) (A )1条; (B )2条; (C )3条; (D )4条.三.解答题12.如图, 在长方体ABCD –EFGH 中,(1)写出所有与棱AB 异面的棱:______________________________;(图1)ABC GH E FD ABC EG H FD图1AFECBGH DAFEC B GH D(2)写出所有与棱AB平行的棱:___________________________________;(3)写出所有与棱AB相交的棱:_______________________________.H GEFD CABABCD 中,13. 如图,在长方体EFGH(1)与棱BC平行的棱有______________________________;(2)与棱AB垂直的平面有 _____________________________;(3)与平面ABFE平行的平面有__________________________.H GFED CAB14. 把11块相同的砖拼成了一个大长方体,已知大长方体的棱长总和是188厘米,求每一块砖的体积.(6分)。
2022年必考点解析沪教版(上海)六年级数学第二学期第八章长方体的再认识专题练习试卷(含答案解析)

六年级数学第二学期第八章长方体的再认识专题练习考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图的几何体是由一平面将一圆柱体截去一部分后所得,则该几何体的俯视图是()A.B.C.D.2、如图,该几何体的三视图中面积相等的是()A.主视图与俯视图B.主视图与左视图C.俯视图与左视图D.三个视图都不相等3、如图所示的几何体由六块相同的小正方体搭成,若移走一块小正方体,几何体的左视图发生了改变,则移走的小正方体是()A.①B.②C.③D.④4、如图,这个几何体由5个大小相同的小立方块搭成,它的主视图是()A. B.C. D.5、将如图所示的图形绕着给定的直线L旋转一周后形成的几何体是()A.B.C.D.6、下列四个几何体中,主视图是三角形的是()A.B.C.D.7、如图所示的一个六角螺帽毛坯底面正六边形的边长、高和内孔直径都相等,其主视图是()A.B.C.D.8、如图是某几何体放置在水平面上,则其俯视图是()A.B.C.D.9、分别观察下列几何体,其中主视图、左视图和俯视图完全相同的是()A.B.C.D.10、如图是由5个相同的小立方块搭成的几何体,则从左面看这个几何体的形状图是()A.B.C.D.第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、一根80分米长的铁条,剪断后刚好可焊接成一个长8分米、宽5.5分米的长方体框架,那么这个长方体的高是_______分米.2、如图所示是一个正方体的展开图,在原正方体中与平面1平行的面是______,与平面5垂直的平面是_______.3、一块长方体的木块,从左面和右面分别裁去长为2厘米和5厘米的长方体,成为一个正方体后,表面积减少了84平方厘米,那么原来长方体的体积为_______.4、如图所示是某种型号的正六角螺母毛坯的三视图,则它的侧面积为2cm.5、已知正方体的一个平面展开图如图所示,则在原正方体上“百”的对面是 __.三、解答题(5小题,每小题10分,共计50分)1、如图是某几何体的三种形状图.(1)说出这个几何体的名称;(2)若从正面看到的形状图的长为15cm,宽为4cm;从左面看到的形状图的宽为3cm,从上面看到的形状图的最长边长为5cm,求这个几何体的所有棱长的和为多少?它的侧面积为多少?它的体积为多少?2、已知长方体无盖纸盒的棱长分别是4cm、6cm和8cm,这个纸盒的外表面积是多少?3、将下面的长方体补画完整.4、已知如图是边长为2cm的小正方形,现小正方形绕其对称轴线旋转一周,可以得到一个几何体,求所得的这个几何体的体积.5、如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.(1)制作这样的包装盒需要多少平方厘米的硬纸板?(2)若1平方米硬纸板价格为5元,则制作10个这样的包装盒需花费多少钱?(不考虑边角损耗)-参考答案-一、单选题1、A【分析】根据从上面看得到的图形是俯视图,可得答案.【详解】∵该几何体是由一平面将圆柱体截去一部分后所得,∴从上往下看,得到该几何体的俯视图是一个圆.故选:A.【点睛】本题考查了简单组合体的三视图,从上面看得到的视图是俯视图.2、A【分析】作出该几何体的三视图,根据三视图的面积求解即可.【详解】解:该几何体的三视图为:可得出主视图与俯视图的面积相等.故选:A.【点睛】本题考查了简单组合体的三视图,解答本题的关键在于熟练掌握三视图的概念,并能找出正确的三视图.3、D【分析】根据左视图的特点即可判断.【详解】解:当移走的小正方体是①、②、③时,左视图为没有发生变化当移走的小正方体是④时,左视图为故发生变化故选D.【点睛】此题主要考查三视图,解题的关键是熟知左视图的定义.4、A【分析】从正面看:共有3列,从左往右分别有1,2,1个小正方形,据此可画出图形.【详解】解:如图所示的几何体的主视图是,故选:A.【点睛】考查简单组合体的三视图;用到的知识点为:主视图,左视图,俯视图分别是从物体的正面,左面,上面看得到的图形.5、B【分析】根据面动成体的原理以及空间想象力可直接选出答案.【详解】解:将如图所示的图形绕着给定的直线L旋转一周后形成的几何体是圆台,故选:B.【点睛】此题主要考查了点、线、面、体,关键是同学们要注意观察,培养自己的空间想象能力.6、C【分析】直接根据三视图中主视图的定义即可判断.【详解】根据几何体三视图中主视图的定义;正方体的主视图是矩形,不符合题意;圆柱体的主视图是矩形,不符合题意;圆锥的主视图是三角形,符合题意;B、球的主视图是圆,不符合题意;故选:C.【点睛】本题考查了几何体的三视图的主视图,解题的关键是:掌握三视图中主视图的定义,是由正面往后看.7、C【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.【详解】解:从正面看,是一行三个矩形,中间的矩形的长较大,两边的矩形相同.故选:C.【点睛】本题考查了三视图的知识,主视图是从物体的正面看得到的视图,解题关键是明确主视图的概念,准确识图.8、B【分析】根据从上面看得到的图象是俯视图,可得答案.【详解】从上面看得到的图象如下故选:B.【点睛】本题考查了简单组合体的三视图,从上面看的到的视图是俯视图.9、D根据正方体、三棱柱、圆锥、圆柱的三视图的形状进行判断即可.【详解】解:根据三视图的定义可知,选项A主视图和左视图都是三角形,但俯视图是有圆心的圆;选项B主视图和左视图都是矩形,但俯视图是圆;选项C主视图是一个矩形,中间有一条线段,左视图是矩形,俯视图是三角形;选项D的主视图、左视图和俯视图都是正方形,完全相同.故选D.【点睛】本题考查简单几何体的三视图,掌握简单几何体三视图的形状是正确判断的前提.10、D【分析】观察图形可知,从左面看到的图形是2列,分别有2,1个正方形,据此即可判断.【详解】解:从左面看这个几何体的形状图如图所示:故选D.【点睛】此题考查了从不同方向观察物体和几何体和画简单图形的三视图的方法,是基础题型.二、填空题1、6.5根据长方体棱长和棱长的知识点准确计算即可;【详解】()÷-+=(分米).8048 5.5 6.5故答案是6.5.【点睛】本题主要考查了长方体棱与棱的位置关系和长方体认识,准确分析计算是解题的关键.2、平面3 平面1、2、3、4【分析】根据正方体中与平面1平行的面是与平面1相对的面,和平面5相交的面与平面5垂直.根据这一特点作答.【详解】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,与平面1平行的面是与平面1相对的面,所以与平面1平行的面是:平面3在正方体中和平面5相交的面与平面5垂直所以与平面5垂直的平面是:平面1、2、3、4故答案为:平面3,平面1、2、3、4,【点睛】本题主要考查了正方体的展开图认识立体图形的知识,属于基础题,解答本题的关键是掌握长方体的特点,从相对面和邻面入手,分析及解答问题.3、90立方厘米【分析】设正方体棱长为x 厘米,根据题意列方程可求得x 的值,进而得到原长方体的长、宽、高的值,再计算体积即可.【详解】设正方体棱长为x 厘米,依题意得245484x x ⋅⋅+⋅⋅=,解得3x =,则原长方体的宽为3厘米,高为3厘米,长为32510++=厘米,则331090V =⨯⨯=立方厘米.【点睛】此题主要考查长方体的表面积公式、体积公式的灵活运用,解题的关键是熟记公式.4、36【分析】正六角螺母侧面为6个相同的长方形,求出每个长方形的面积,即可得出它的侧面积.【详解】2×3=6cm 2,6×6=36cm 2.故答案为:36.【点睛】本题主要考查正六棱柱的三视图,将三视图上边的长度转化为正六棱柱对应边的长度是解题关键.5、建【分析】根据正方体表面展开图的特征进行判断即可.【详解】解:正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,所以在原正方体上“百”的对面是“建”.故答案为:建.【点睛】本题考查正方体的展开与折叠,掌握正方体表面展开图的特征是正确判断的前提.三、解答题1、(1)直三棱柱;(2)所有棱长的和69cm,侧面积180cm2,体积90cm3【分析】(1)只有棱柱的主视图和左视图才能出现长方形,根据俯视图是三角形,可得到此几何体为三棱柱;(2)这个几何体的所有棱长的和为2个3cm、2个4cm、2个5cm,3个15cm的和;三个长为15cm,宽分别为3cm、4cm、5cm的长方形的面积即是几何体的侧面积;先求出俯视图的面积,再乘高15cm,即为体积.【详解】解:(1)直三棱柱;⨯+++⨯=.(2)这个几何体所有棱长的和:153345269cm⨯=180cm2;它的侧面积:(3+4+5)15×3×4×15=90cm3它的体积:12故这个几何体的所有棱长的和为69cm,它的侧面积为180cm2,它的体积为90cm3.【点睛】此题考查从三视图判断几何体,掌握棱柱的侧面都是长方形,上下底面是几边形就是几棱柱是解决问题的关键.2、184或176或160【分析】由题意分别以4cm ,6cm 为底面,以8cm 为高和以4cm ,8cm 为底面,以6cm 为高以及以6cm ,8cm 为底面,以4cm 为高进行计算即可.【详解】解:以4cm ,6cm 为底面,以8cm 为高,则外表面积为()246(64)82184cm ⨯++⨯⨯=;以4cm ,8cm 为底面,以6cm 为高,则外表面积为()248(84)62176cm ⨯++⨯⨯=; 以6cm ,8cm 为底面,以4cm 为高,则外表面积为()286(68)42160cm ⨯++⨯⨯=. 【点睛】本题主要考查长方体的表面积公式的灵活应用,注意掌握分类讨论思维进行分析分三种情况进行解答.3、见解析【分析】根据长方体的定义直接作图.【详解】如图所示:【点睛】本题主要考查长方体的定义,关键是根据定义作图.4、2πcm 3【分析】由图可知小正方形绕其对称轴线旋转一周得到一个底面半径为1cm ,高为2cm 的圆柱,故可求解.【详解】由旋转体可知小正方形绕其对称轴线旋转一周得到一个底面半径为1cm ,高为2cm 的圆柱, ∴这个几何体的体积为22122r h πππ=⨯⨯= cm 3.【点睛】此题主要考查旋转体的体积,解题的关键是熟知圆柱体的体积公式.5、(1)360平方厘米;(2)花费1.8元钱.【分析】(1)根据长方体表面积公式计算即可;(2)根据题意列式计算即可.【详解】解:(1)由题意得,()()2212612666360cm ⨯⨯+⨯+⨯=;答:制作这样的包装盒需要360平方厘米的硬纸板;(2)1平方米10000=平方厘米,36010000510 1.8÷⨯⨯=(元),答:制作10个这的包装盒需花费1.8元钱.【点睛】本题考查了几何体的表面积,正确的计算长方体的表面积是解题的关键.。
2022年沪教版(上海)六年级数学第二学期第八章长方体的再认识必考点解析练习题(无超纲)

六年级数学第二学期第八章长方体的再认识必考点解析考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“中”字所在面相对的面上的汉字是()A.梦B.聚C.力D.凝2、如所示简单几何体从正面看到的形状图是()A.B.C.D.3、如图为某几何体的三视图,则该几何体是()A.圆锥B.圆柱C.三棱柱D.四棱柱4、如图,该几何体的三视图中面积相等的是()A.主视图与俯视图B.主视图与左视图C.俯视图与左视图D.三个视图都不相等5、下列几何体中,截面不可能是三角形的是()A.长方体B.正方体C.圆柱D.圆锥6、如图,这个几何体由5个大小相同的小立方块搭成,它的主视图是()A. B.C. D.7、下列图形中,能折叠成正方体的是()A.B.C.D.8、下列几何体不可以展开成一个平面图形的是()A.三棱柱B.圆柱C.球D.正方体9、下列几何体中,每个面都是由同一种图形组成的是()A.圆柱B.圆锥C.三棱柱D.正方体10、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数()V、面数()F、棱数()E之间存在的一个有趣的关系式:2V F E+-=,被称为欧拉公式.若某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,求x y+的值为()A.12 B.14 C.16 D.18第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、一个棱柱的棱数是15,则这个棱柱的面数是________.2、在长方体中,已知它的宽为8cm,长是宽的2倍少6cm,高是宽的35,则这个长方体的体积是_______.3、正方体的表面展开图如图所示,“遇”的相对面上的字为___________.4、如果把骰子看作是一个正方体,点数1的对面是6,点数5的对面是2,点数4的对面是3,则与点数是3的面垂直的所有的面的点数和是_______.5、一个棱长为2厘米、6厘米、8厘米的长方体,最多可切割出棱长为1厘米、2厘米、3厘米的长方体_______个.三、解答题(5小题,每小题10分,共计50分)1、如图所示是一个透明的长方体容器1111ABCD A B C D ,里面装着水,从里面量长AB 、宽BC 、高1BB 分别是16厘米、4厘米、8厘米,水深6厘米.如果把长方体的左侧面11ADD A 作为底面,放在桌子上,那么水深多少厘米?2、经过长方体一个顶点的两条棱长分别是3cm 、4cm ,与长3cm 的棱垂直的面的面积是220cm ,求这个长方体的体积.3、如图是由若干个相同的正方体组成的立体图形从上往下看所得到的平面图形,正方形上标注的数字表示该位置上正方体的个数.请画出这个立体图形从左面看所得到的平面图形.4、画出下列几何体的主视图、左视图与俯视图.5、小明用一根长为24分米的铅质角铁,截开后刚好可以搭一个长方体小鱼缸架子,这个长方体的长、宽、高的长度均为整数分米,且互不相等,求这个长方体的体积.-参考答案-一、单选题1、D【分析】根据正方体表面展开图的特征进行判断即可.【详解】解:由正方体的表面展开图的特点可知,“中”与“凝”是对面,“国”与“聚”是对面,“梦”与“力”是对面,故选:D.【点睛】本题考查正方体的展开与折叠,掌握正方体表面展开图的特征是正确判断的前提.2、C【分析】画出从正面看所得到的图形即可.【详解】解:这个组合体从正面看所得到的图形如下:故选:C.【点睛】本题考查了从不同方向看几何体,解题关键是树立空间观念,准确识图.3、C【分析】根据三视图判断该几何体即可.【详解】解:根据该几何体的主视图与左视图均是矩形,主视图中还有一条棱,俯视图是三角形可以判断该几何体为三棱柱.故选:C.【点睛】本题考查三视图,解题的关键是理解三视图的定义,属于中考常考题型.4、A【分析】作出该几何体的三视图,根据三视图的面积求解即可.【详解】解:该几何体的三视图为:可得出主视图与俯视图的面积相等.故选:A.【点睛】本题考查了简单组合体的三视图,解答本题的关键在于熟练掌握三视图的概念,并能找出正确的三视图.5、C【分析】根据各个几何体截面的形状进行判断即可得.【详解】解:A、长方体的截面可能是三角形,则此项不符题意;B、正方体的截面可能是三角形,则此项不符题意;C、圆柱的截面可能是圆形、长方形、梯形、椭圆形,不可能是三角形,则此项符合题意;D、圆锥的截面可能是三角形,则此项不符题意;故选:C.【点睛】本题考查了截一个几何体,熟练掌握常见几何体的截面特征是解题关键.6、A【分析】从正面看:共有3列,从左往右分别有1,2,1个小正方形,据此可画出图形.【详解】解:如图所示的几何体的主视图是,故选:A.【点睛】考查简单组合体的三视图;用到的知识点为:主视图,左视图,俯视图分别是从物体的正面,左面,上面看得到的图形.7、C【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.【详解】A折叠后不可以组成正方体;B折叠后不可以组成正方体;C折叠后可以组成正方体;D折叠后不可以组成正方体;故选C.【点睛】本题考查几何体的展开图,解题的关键是熟练掌握几何体的展开图的特征,属于中考常考题型.8、C【分析】首先想象三棱柱、圆柱、正方体的平面展开图,然后作出判断.解:A、三棱柱可以展开成一个矩形和2个三角形,故此选项错误;B、圆柱可以展开成两个圆和一个矩形,故此选项错误;C、球不能展开成平面图形,故此选项符合题意;D、正方体可以展开成一个矩形和两个小正方形,故此选项错误;故选:C.【点睛】本题主要考查了图形展开的知识点,根据几何体的形状特点求解是解题关键.9、D【分析】分别找出每个图形的每个面是由什么图形组成的即可.【详解】解:A、圆柱是由长方形和圆组成的,故此选项不符合题意;B、圆锥是由扇形和圆组成,故此选项不符合题意;C、三棱柱是由三角形和长方形组成,故此选项不符合题意;D、正方体是由正方形组成,故此选项符合题意;故选:D.【点睛】此题主要考查了认识立体图形,关键是掌握各立体图形的形状.10、B【分析】得到多面体的棱数,求得面数即为x+y的值.解:∵有24个顶点,每个顶点处都有3条棱,两点确定一条直线;∴共有24×3÷2=36条棱,那么24+F−36=2,解得F=14,∴x+y=14.故选B.【点睛】本题考查多面体的顶点数,面数,棱数之间的关系及灵活运用.难点是熟练掌握欧拉定理.二、填空题1、7【详解】解:一个直棱柱有15条棱,这是一个五棱柱,有7个面;故答案为:7【点睛】本题考查五棱柱的构造特征.棱柱由上下两个底面及侧面组成,五棱柱上下底面共有10条棱,侧面有5条棱.2、3384cm【分析】先根据题意得到长方体的长和高,然后根据体积计算公式直接求解即可.【详解】解:由题意得:长为82610cm⨯-=,高为3248=55cm⨯,则有长方体的体积为324810384cm5⨯⨯=.故答案为3384cm.【点睛】本题主要考查长方体的体积,熟练掌握计算公式是解题的关键.3、中【分析】根据正方体表面展开图的特征进行判断即可.【详解】解:由正方体表面展开图的“相间、Z端是对面”可知,“遇”与“中”是对面,“见”与“纷”是对面,“缤”与“附”是对面,故答案为:中.【点睛】本题考查正方体的展开与折叠,掌握正方体表面展开图的特征是正确判断的前提.4、14【分析】根据正方体中面与面的位置关系知道除了点数是4的面,其他的面都与点数是3的面垂直.【详解】+++=.解:与点数是3的面垂直的所有的面的点数和是165214故答案是:14.【点睛】本题考查正方体中面与面的位置关系,解题的关键是搞清楚正方体中各个面的位置关系.5、16【分析】先分别求出原长方体和需要切割的小长方体的体积,再相除计算即可.【详解】∵()326896cm ⨯⨯=,()31236cm ⨯⨯=, ∴96616÷=(个).故答案为:16.【点睛】此题考查长方体的体积,解题的关键是抓住长方体切割成小正方体的特点进行计算.三、解答题1、12厘米【分析】根据题意可直接列式计算求解即可.【详解】解:由题意得:水量一定,水的体积为1646384⨯⨯=(立方厘米),左侧面的面积为8432⨯=(平方厘米),水深为3843212÷=(厘米).答:水深为12厘米.【点睛】本题主要考查长方体的体积计算,关键是根据题意得到水量一定时水的体积,然后可求出问题答案. 2、360cm【分析】根据题意易得长方体的长,然后根据长方体的体积计算公式求解即可.【详解】解:由题意得:()2045cm ÷=,∴这个长方体的长为5cm ,宽是4cm ,高是3cm ,∴()334560cm ⨯⨯=. 答:这个长方体的体积为360cm .【点睛】本题主要考查长方体的体积,熟练掌握长方体的体积计算公式是解题的关键.3、图见解析.【分析】由已知条件可知,左视图有2列,每列小正方形数目分别为2,3.据此可画出图形.【详解】解:如图【点睛】本题考查几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.4、见解析【分析】 主视图是从物体的正面看得到的视图,左视图是从物体的左面看得到的视图,俯视图是从物体的上面看得到的视图.【详解】如图所示:主视图左视图俯视图【点睛】本题考查简单组合体的三视图,掌握三视图的画法是正确判断的前提,画三视图时应注意“长对正,宽相等、高平齐”.5、6立方分米【分析】根据题意易得长宽高的和为6分米,然后可直接根据体积计算公式进行求解即可.【详解】=++,解:2446÷=(分米),∴6321∴长、宽、高分别为3分米、2分米、1分米,体积为3216⨯⨯=(立方分米).答:这个长方体的体积为6立方分米.【点睛】本题主要考查长方体的体积计算,关键是根据题意得到长方体的长宽高,然后直接进行求解即可.。
2022年沪教版(上海)六年级数学第二学期第八章长方体的再认识重点解析试题(名师精选)
六年级数学第二学期第八章长方体的再认识重点解析考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、四棱柱中,棱的条数有()A.4条B.8条C.12条D.16条2、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数()V、面数()F、棱数()E之间存在的一个有趣的关系式:2+-=,被称为欧拉公式.若某个玻璃饰品的外形是简单多面体,它的外表面是V F E由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表+的值为()三角形的个数为x个,八边形的个数为y个,求x yA.12 B.14 C.16 D.183、四个相同的小正方体组成的立体图形如图所示,它的主视图为()A.B.C.D.4、在“爱国、爱党”主题班会上,小颖特别制作了一个正方体玩具,其表面展开图如图所示,则原正方体中与“有”字相对的字是()A.少B.年C.强D.国5、图中所示几何体从上面看,得到的平面图形为()A.B.C.D.6、如图是由5个相同的小正方体和1个圆锥组成的立体图形,这个立体图形的主视图是()A.B.C.D.7、下列四个图形中,主视图、左视图和俯视图相同的是()A.B.C.D.8、有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图+的值为()所示.如果记6的对面的数字为a,2的对面的数字为b,那么a bA.3 B.7 C.8 D.119、若要使图中的平面展开图折叠成正方体后,相对面上两个数之和为6,则y x=()A.625 B.64 C.125 D.24310、如图是某几何体的三视图,该几何体是()A.圆柱B.三棱锥C.三棱柱D.正方体第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、把一根长为32米的木条截开后刚好能搭一个长方体架子,这个长方体的长、宽、高的长度均为整米数,且互不相等,那么这个长方体体积是_______立方米.2、如图,与棱EH平行的面是_______.3、凡与铅垂线重合的直线必与平面_______(填“垂直”或“平行”).4、正方体的表面展开图如图所示,“遇”的相对面上的字为___________.5、如果把骰子看作是一个正方体,点数1的对面是6,点数5的对面是2,点数4的对面是3,则与点数是3的面垂直的所有的面的点数和是_______.三、解答题(5小题,每小题10分,共计50分)1、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式,请你观察下列几种简单多面体模型,解答下列问题:(1)根据上面多面体模型,完成表格中的空格:(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是___________;(3)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是___________;(4)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.该多面体外表面三角形的个数为x个,八边形的个数为y 的值.个,求x y2、已知长方体无盖纸盒的长、宽、高分别为9cm、7cm、5cm,这个纸盒的外表面积和容积各是多少?3、用长为108cm的铜丝做一个棱长之比为2:3:4的长方体,它的体积是多少?4、四个完全相同的小长方体拼成一个大长方体,小长方体的长、宽、高分别为3、2、1,求这个大长方体表面积的最小值.5、我们从不同的方向观察同一物体时,可以看到不同的平面图形,如图是一个由7个相同的小正方体搭成的几何体,请从图的正面、左面和上面看这个几何体,并在所给的图中画出各自的图形.-参考答案-一、单选题1、C【分析】根据棱柱的概念和特性即可解.【详解】解:四棱柱有4×3=12条棱.故选C.【点睛】本题主要考查四棱柱的棱的条数,解题的关键是熟知n棱柱共有3n条棱.2、B【分析】得到多面体的棱数,求得面数即为x+y的值.【详解】解:∵有24个顶点,每个顶点处都有3条棱,两点确定一条直线;∴共有24×3÷2=36条棱,那么24+F−36=2,解得F=14,∴x+y=14.故选B.【点睛】本题考查多面体的顶点数,面数,棱数之间的关系及灵活运用.难点是熟练掌握欧拉定理.3、A【分析】根据几何体的三视图解答即可.【详解】根据立体图形得到:主视图为:,左视图为:,俯视图为:,故选:A【点睛】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.4、B【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.【详解】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,∴“有”与“年”相对,“强”与“少”相对,“我”与“国”相对,故选:B.【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.5、D【分析】根据从上面可以看到三个矩形判断即可.【详解】解:从上面看,可以看到三个矩形,如图,故选:D.【点睛】本题考查了从不同方向看几何体,解题关键是建立空间想象能力.6、C【分析】从正面看所得到的图形即为主视图,注意所有的看到的棱都应表现在主视图中.【详解】解:从正面看易得第一层有3个正方形,第二层最左边有一个正方形,右边是一个三角形.故选:C.【点睛】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.7、A【分析】分别分析正方体、圆柱、三棱柱、圆锥的主视图、左视图、俯视图,并判断各图形三视图是否相同,即可得到结论.【详解】解:A、正方体的主视图、左视图、俯视图都是正方形,故本选项符合题意;B、圆柱的主视图、左视图是矩形,俯视图是圆,故本选项不合题意;C、三棱柱的主视图、左视图是矩形,俯视图是三角形,故本选项不合题意;D、圆锥的主视图、左视图是等腰三角形,俯视图是带圆心的圆,故本选项不合题意;故选:A.【点睛】本题考查三视图,熟练掌握常见几何体的三视图,是解决问题的关键.8、B【分析】由图一和图二可看出1的对面的数字是5;再由图二和图三可看出3的对面的数字是6,从而2的对面的数字是4.【详解】解:从3个小立方体上的数可知,与写有数字1的面相邻的面上数字是2,3,4,6,所以数字1面对数字5,同理,立方体面上数字3对6.故立方体面上数字2对4.则a=3,b=4,那么a+b=3+4=7.故选B.【点睛】本题考查灵活运用正方体的相对面解答问题,立意新颖,是一道不错的题.解题的关键是按照相邻和所给图形得到相对面的数字.9、C【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点可得答案.【详解】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,1与x 是相对面, 3与y 是相对面,∵相对面上两个数之和为6,∴x=5,y=3,∴35125,y x ==故选:.C【点睛】本题主要考查了正方体相对两个面上的文字或数字,注意正方体是空间图形,掌握“正方体的表面展开图,相对的面之间一定相隔一个正方形.”是解题的关键.10、C【分析】根据主视图和左视图都是高度相等的长方形,可判断该几何体是柱体,进而根据俯视图的形状,可判断柱体底面形状,得到答案.【详解】解:∵几何体的主视图和左视图都是高度相等的长方形,故该几何体是一个柱体,又∵俯视图是一个三角形,故该几何体是一个三棱柱,故选:C .【点睛】题考查的知识点是三视图,如果有两个视图为三角形,该几何体一定是锥,如果有两个矩形,该几何体一定柱,其底面由第三个视图的形状决定.二、填空题1、10或12【分析】根据长方体的棱长总和=(长+宽+高)×4,求出长、宽、高的和是8米,在根据题意可求出长、宽、高的长,即可求解;【详解】解:3248÷=(米),8521=++或8431=++,所以长、宽、高分别为5米、2米、1米或4米、3米、1米,体积:52110⨯⨯=(立方米)或43112⨯⨯=(立方米).故答案为:10或12【点睛】本题主要考查了立体图形的认识和截一个几何体,准确分析是解题的关键.2、面BCGF ,面ABCD【分析】根据长方体中棱与面的位置关系直接作答即可.【详解】由图可知:与棱EH 平行的面是面BCGF ,面ABCD ;故答案为面BCGF,面ABCD.【点睛】本题主要考查长方体中棱与平面的位置关系,正确理解概念是解题的关键.3、垂直【分析】根据铅垂线法可直接作答.【详解】因为凡与铅垂线重合的直线必与平面垂直;故答案为垂直.【点睛】本题主要考查长方体中棱与面的位置关系,熟练掌握位置关系解题的关键.4、中【分析】根据正方体表面展开图的特征进行判断即可.【详解】解:由正方体表面展开图的“相间、Z端是对面”可知,“遇”与“中”是对面,“见”与“纷”是对面,“缤”与“附”是对面,故答案为:中.【点睛】本题考查正方体的展开与折叠,掌握正方体表面展开图的特征是正确判断的前提.5、14【分析】根据正方体中面与面的位置关系知道除了点数是4的面,其他的面都与点数是3的面垂直.【详解】解:与点数是3的面垂直的所有的面的点数和是165214+++=.故答案是:14.【点睛】本题考查正方体中面与面的位置关系,解题的关键是搞清楚正方体中各个面的位置关系.三、解答题1、(1)4,6,6,6;(2)2V F E +=+;(3)20;(4)14【分析】(1)根据上面多面体模型,直接计数可得答案;(2)根据表格中多面体的顶点数(V )、面数(F )、棱数(E )归纳可得答案;(3)设这个多面体的面数为x ,则顶点数为:8,x - 再根据2V F E +=+列方程,解方程可得答案;(4)先求解多面体的棱的总数,再根据2V F E +=+求解多面体的面数,从而可得x y +的值.【详解】解:(1)根据上面多面体模型,可得:故答案为:4,6,6,6; (2)从以上表格数据归纳可得:顶点数(V )+面数(F )=棱数(E )+2,即:2V F E +=+.故答案为:2V F E +=+ (3)设这个多面体的面数为x ,则顶点数为:8,x -8302x x ∴-+=+20x ∴=即这个多面体的面数为20.故答案为:20.(4) 简单多面体的外表面是由三角形和八边形两种多边形拼接而成,有24个顶点,每个顶点处都有3条棱.∴ 共有2432=36⨯÷条棱,设总面数为:,F24+362F ∴=+14,F ∴=即14.x y +=【点睛】本题考查的是简单多面体的顶点数(V ),面数(F ),棱数(E )之间的关系,考查探究规律分基本方法,以及应用规律解决实际问题,掌握从具体到一般探究规律的方法及运用规律是解题的关键.2、外表面积为2223cm ,容积为2315cm【分析】根据长方体的表面积和容积的计算公式计算即可;【详解】纸盒的外表面积为()29795752223cm ⨯+⨯+⨯⨯=;容积为3975315cm ⨯⨯=. 答:这个纸盒的外表面积为2223cm ,容积为2315cm .【点睛】本题主要考查了长方体的棱与棱的关系及面积、体积公式应用,准确分析是解题的关键. 3、3648cm【分析】设长方体的棱长分别为2cm x ,3cm x ,4cm x ,根据总长为108cm 求出各棱长的值,再根据体积公式计算即可.【详解】设长方体的棱长分别为2cm x ,3cm x ,4cm x .根据题意得,()4234108x x x ++=,解得3x =,∴棱长分别为6、9、12,∴36912648cm V =⨯⨯= .答:它的体积为3648cm .【点睛】本题考查长方体棱长和体积的计算,解题的关键是根据题意列方程求出各棱长的值.4、52【分析】要使表面积最小,也就是把这4个小长方体最大的面(3×2)重合,再用长方体表面积公式计算即可.【详解】解:要使表面积最小,也就是把这4个小长方体最大的面(3×2)重合,拼成的大长方体长、宽、高分别为4、3、2,大长方体表面积为(3×4+2×3+4×2)×2=52,这个大长方体表面积的最小值为52.【点睛】此题主要考查长方体的表面积的计算,明确把两个完全相同的长方体拼成一个大长方体,最小的面重合时,拼成的表面积最大,最大的面重合时拼成的表面积最小.5、见解析【分析】主视图有3列,每列小正方形数目分别为1,2,3;左视图有2列,每列小正方形数目分别为3,1;俯视图有3列,每行小正方形数目分别为1,1,2.【详解】解:如图所示:【点睛】此题主要考查了作三视图,根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形是解题关键.。
上海六年级数学下--8.1长方体的元素(含答案)
8.1 长方体的元素 姓名一、填空题1、(1)长方体有 个面, 个顶点, 条棱。
(2)长方体的每个面都是 ,正方体的每个面都是 。
(3)长方体的十二条棱可以分为 组,每组中的四条棱的长度都 。
(4)长方体的六个面可以分为 组,每组中的两个面的 和 都相同。
2、长方体的长是12cm ,宽是8cm ,高是5cm 。
(1)这个长方体所有的棱长和是_______;(2)这个长方体的表面积是 ;(3)这个长方体的体积是 。
3、已知一个正方体的所有棱长之和是48cm ,则这个正方体的体积是 ,表面积是 。
4、把3个棱长1厘米的小正方体拼成长方体,这个长方体的棱长和是 ,体积是 。
★★5、把一个正方体切成两个完全一样的长方体,表面积增加了20平方厘米。
这个正方体的表面积是 。
6、如图,在长方体ABCD-EFGH 中,与棱AE 相等的棱有 ;与面ABCD 形状大小均相同的是 ;从点A 出发的棱有 条,它们是 。
★7、有一长方体的棱长之和为64厘米,长:宽:高=5:1:2,则它的高为 。
二、选择题8、在长方体中,经过同一个顶点的面有………………………………………………( )(A )1个 (B )2个 (C )3个 (D )4个9、在长方体的12条棱中,相等的棱至少有…………………………………………( )(A )12条 (B )8条 (C )4条 (D )2条10、一个长方体木块,无论从哪个角度去观察,最多可以看到的棱有………………( )(A )12条 (B )9条 (C )8条 (D )6条】 A B C D E F G H11、如果想用铁丝弯成一个长、宽、高分别为5cm,3cm,4cm的长方体架子,至少需要铁丝……………………………………………………………………………………()(A)48cm (B)36cm (C)24cm (D)12cm三、简答题12、用总长为100厘米的木条做一个三条棱长分别为10厘米,12厘米和5厘米的长方体木架,木条长够用吗?为什么?★13、一个长方体的六个面都是长方形,其中三个长方形的面积之比是5:7:2,最大的面积比最小的面积大60cm2,求这个长方体的表面积.★14、一个长方体的长、宽、高之比为5︰3︰2,所有棱长之和为120厘米,求它的体积.★★15、某宾馆在楼梯铺红地毯,准备从A点起逐级向上铺到B点为止,所铺地毯的宽度与楼梯的宽度相同,若红地毯的价格为每平方米75元,则购买地毯共要用去多少钱?8.1长方体的元素一、1、6;8;12;长方形;正方形;3;相等;3;大小;形状。
精品试题沪教版(上海)六年级数学第二学期第八章长方体的再认识必考点解析试题(含详解)
六年级数学第二学期第八章长方体的再认识必考点解析考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图所示的立体图形的主视图是()A.B.C.D.2、如图所示,该几何体的俯视图是()A.正方形B.长方形C.三角形D.圆3、下列几何体的俯视图中,其中一个与其他三个不同,该几何体是()A.B.C.D.4、四个相同的小正方体组成的立体图形如图所示,它的主视图为()A.B.C.D.5、如图,该几何体的三视图中面积相等的是()A.主视图与俯视图B.主视图与左视图C.俯视图与左视图D.三个视图都不相等6、如图是一个几何体的展开图,则这个几何体是()A.B.C.D.7、如图是一个由6个相同的正立方块搭成的几何体,其三视图中面积最大的是()A.主视图B.左视图C.俯视图D.左视图与俯视图8、如图是某几何体放置在水平面上,则其俯视图是()A.B.C.D.9、某学习小组送给医务工作者的正方体的六个面上都有一个汉字,如图所示的是它的一种展开图,那么在原正方体中,与“美”字所在面相对的面上的汉字是()A.最B.逆C.行D.人10、如图是某个几何体的展开图,该几何体是()A.三棱柱B.四棱柱C.圆柱D.圆锥第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、一个棱长为2厘米、6厘米、8厘米的长方体,最多可切割出棱长为1厘米、2厘米、3厘米的长方体_______个.2、铅笔在纸上划过会留下痕迹,这种现象说明点动成线;一枚硬币在光滑的桌面上快速旋转,看上去像形成了一个球,这体现的数学知识是______.3、如图,在长方体中要检验面ADHE与面BCGF是否平行的现成的长方形纸片可以是_______.4、如果长方体的长、宽、高之和为12cm,则它的棱长总和为_______cm.5、用一个平面去截下列几何体A球体B圆锥C圆柱D正三棱柱E长方体,得到的截面形状可能是三角形的有 ___(写出正确序号).三、解答题(5小题,每小题10分,共计50分)1、观察下列图中由棱长为1的小立方体摆成的图形,寻找规律:如图①:共有1个小立方体,其中1个看得见,0个看不见.(1)如图②:共有8个小立方体,其中________个看得见,_______个看不见.(2)如图③:共有_______个小立方体,其中________个看得见,_______个看不见.(3)按此规律在第⑥个图中,看不见的小立方体有多少个?2、如图是用六块相同的小立方体搭成的一个几何体,请你在下面相应的位置分别画出从正面、左面和上面观察这个几何体的视图.(在答题卡上画完图后请用黑色水笔描黑).3、如图所示,线段BC垂直于平面ABFE,问:是否存在一个平面过点C,且与平面ABFE平行?若存在,请把这个平面在图中表示出来;反之,说明理由.4、写出下图中各个几何体的名称.①__________;②__________;③__________;④__________;⑤__________;⑥__________.5、已知一个长方体宽是10cm,长比宽的2倍多4cm,高是宽的一半,求这个长方体的所有棱长之和.-参考答案-一、单选题1、A【分析】找出此几何体从正面看所得到的视图即可,看不见的棱用虚线.解:此立体图形从正面看所得到的图形为矩形,中间有两条看不见的棱,故主视图为矩形中有两条竖的虚线.故选:A.【点睛】此题主要考查了简单几何体的三视图,关键是注意所有的看到的棱都应表现在三视图中.2、C【分析】根据俯视图的定义,从上面看该几何体,所得到的图形进行判断即可.【详解】解:从上面看该几何体,所看到的图形是三角形.故选:C.【点睛】本题考查简单几何体的三视图,理解视图的意义,掌握俯视图的概念是正确判断的前提.3、C【分析】根据从上边看得到的图形是俯视图,可得答案.【详解】解:选项A、B、D的俯视图是不带圆心的圆,选项C的俯视图是带圆心的圆,故选:C.【点睛】此题主要考查三视图,解题的关键是熟知俯视图的定义.4、A根据几何体的三视图解答即可.【详解】根据立体图形得到:主视图为:,左视图为:,俯视图为:,故选:A【点睛】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.5、A【分析】作出该几何体的三视图,根据三视图的面积求解即可.【详解】解:该几何体的三视图为:可得出主视图与俯视图的面积相等.故选:A.【点睛】本题考查了简单组合体的三视图,解答本题的关键在于熟练掌握三视图的概念,并能找出正确的三视图.6、B【分析】侧面为三个长方形,底边为三角形,故原几何体为三棱柱或依次分析例题图形与展开图关系即可.【详解】解:A.展开全部是三角形,不符合题意;B.展开图两个三角形与三个长方形,由展开图也可以发现该立体图形是三棱柱,故此项正确;C.展开全部是四个三角形,一个四边形,不符合题意;D.展开全部是四边形,不符合题意;故选:B.【点睛】本题考查的是三棱柱的展开图,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.7、C【分析】找到从物体的正面、上面和左面看,所得到的图形里正方形的个数最多的那个视图即可.【详解】解:小立方块的边长为1,那么看到的一个正方形面积为1.从正面看,得到从左往右3列正方形的个数依次为1,2,1,面积为4;从左面看,得到从左往右3列正方形的个数依次为1,2,1,面积为4;从上面看得到从左往右3列正方形的个数依次为1,3,1,面积为5,∴三视图中面积最大的是俯视图.故选:C.【点睛】本题考查了简单组合体的三视图,从正面看得到的图形是主视图,从左边看得到的图形是左视图,从上边看得到的图形是俯视图.8、B【分析】根据从上面看得到的图象是俯视图,可得答案.【详解】从上面看得到的图象如下故选:B.【点睛】本题考查了简单组合体的三视图,从上面看的到的视图是俯视图.9、B【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点即可作答.【详解】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“美”与“逆”是相对面.故选:B.【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.10、A【分析】根据展开图的侧面与底面图形形状即可判断.【详解】解:由于该几何体的展开图的三个侧面均是长方形,两个底面是三角形,因此可以判定该几何体是三棱柱.故选:A【点睛】本题考查了学生对常见几何体及其展开图的理解与辨别,解决本题的关键是牢记这些几何体的特征,考查了学生对图形的认识与分析的能力.二、填空题1、16【分析】先分别求出原长方体和需要切割的小长方体的体积,再相除计算即可.【详解】∵()326896cm ⨯⨯=,()31236cm ⨯⨯=, ∴96616÷=(个).故答案为:16.【点睛】此题考查长方体的体积,解题的关键是抓住长方体切割成小正方体的特点进行计算.2、面动成体【分析】根据点、线、面、体的关系解答即可.【详解】解:铅笔在纸上划过会留下痕迹,这种现象说明点动成线;一枚硬币在光滑的桌面上快速旋转,看上去像形成了一个球,这体现的数学知识是面动成体.故答案为:面动成体.【点睛】本题考查了点、线、面、体的关系.解题的关键是明确点动成线,线动成面,面动成体.3、面ABFE 和面EFGH (答案不唯一)【分析】直接根据长方体平面与平面的位置关系直接作答即可.【详解】因为在长方体中要检验面ADHE 与面BCGF 是否平行的现成的长方形纸片可以是面ABFE 和面EFGH 等;故答案为面ABFE和面EFGH(答案不唯一).【点睛】本题主要考查长方体中平面与平面的位置关系,正确理解概念是解题的关键.4、48【分析】根据长方体的棱长计算公式计算即可;【详解】长方体的棱长和41248cm=⨯=;故答案是48.【点睛】本题主要考查了长方体的棱长计算,准确计算是解题的关键.5、B,D【分析】当截面的角度和方向不同时,圆柱体的截面无论什么方向截取圆柱都不会截得三角形.【详解】解:A球体不能截出三角形;B圆锥沿着母线截几何体可以截出三角形;C圆柱不能截出三角形;D正三棱柱能截出三角形.故截面可能是三角形的有2个.故答案为:B,D.【点睛】本题考查几何体的截面,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.三、解答题1、(1)7;1;(2)27;19;8;(3)125【分析】(1)根据题意及图①直接求解即可.(2)根据题意及图②直接进行求解即可.(3)根据(1)、(2)及图③可得规律,然后进行求解即可.【详解】解:第①幅图,即1n =,共有小立方体的个数是1,看不见的小立方体的个数是0,看得见的小立方体是101-=(个);(1)第②幅图,即2n =时,共有小立方体2228⨯⨯=(个),看不见的小立方体的个数是()()()2121211111-⨯-⨯-=⨯⨯=,看得见的小立方体的个数是817-=;故答案为7;1;(2)第③幅图,即3n =时,共有小立方体33327⨯⨯=(个),看不见的小立方体的个数是()()()3131318-⨯-⨯-=(个),看得见小立方体的个数是27819-=(个);故答案为27,19,8;(3)第⑥幅图,即6n =时,共有小立方体的个数为666216⨯⨯=(个);看不见的小立方体的个数为()()()616161555255125-⨯-⨯-=⨯⨯=⨯=.答:看不见的小立方体有125个.【点睛】本题主要考查几何图形的规律,关键是根据题目所给图形中得到一定的规律进行求解即可.2、见详解【分析】观察立体图形画出三视图即可.【详解】如图:【点睛】本题考查实物体的三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.本题画几何体的三视图时应注意小正方形的数目及位置.3、存在,画图见解析【分析】把平面ABFE看作是一个长方体的正面,线段BC看作是长方体的宽,补全成一个长方体即可【详解】存在,把平面ABFE看作是一个长方体的正面,线段BC看作是长方体的宽,只要把这个图形补全成一个长方体ABCD EFGH,就可以得到过C点且与平面ABFE平行的平面CGHD.如图【点睛】本题考查了空间中线线、线面、面面间的位置关系等基础知识4、①圆柱;②圆锥;③四棱锥;④五棱柱;⑤三棱锥;⑥长方体(或四棱柱)【分析】分别根据圆柱、圆锥、四棱锥、五棱柱、三棱锥、四棱柱的基本特点即可进行判断得出.【详解】解:圆柱的侧面展开图是一个长方形,两个底面是圆形,由此可得①为圆柱; 圆锥的侧面展开图是一个扇形,底面是一个圆形,可得②为圆锥;四棱锥的侧面是四个三角形,底面是一个四边形,可得③为四棱锥;五棱柱的侧面是五个长方形,底面是两个五边形,可得④为五棱柱;三棱锥的侧面是三个三角形,底面也是一个三角形,可得⑤为三棱锥;四棱柱的侧面是四个长方形,底面是两个四边形,可得⑥为四棱柱或长方体.【点睛】题目主要考查基本立体图形的特点,熟练掌握多种常见的几何体的特点是解题关键. 5、156cm【分析】根据题意易得长方体的长、宽、高的长度,然后直接进行求解即可.【详解】解:由题意得:长:()210424cm ⨯+=,高:()1025cm ÷=,棱长之和:(10245)4156(cm)++⨯=. 故答案为156cm .【点睛】本题主要考查长方体棱长和,关键是根据题意得到长方体的长、宽、高,然后求解即可.。
上海市沪教版六年级第二学期易错题整理 8.1长方体的元素(原卷版)
8.1长方体的元素易错点归纳1. 长方体有6个面,8个顶点,12条棱.2. 长方体的特点(正方体是特殊的长方体).(1)长方体的每个面都是长方形;(2)长方体的十二条棱可以分为3组,每组中的4条棱的长度都相等.(3)长方体的六个面可以分为3组,每组中的2个面的形状和大小相同.3.若一个长方体的三条棱长分别是a,b,h,则这个长方体的总棱长可以表示为4(a+b+h );它的表面积可以表示为2ab+2ah+2bh ;它的体积可以表示为abh .一、填空题1.已知一个长方体的长、宽、高分别是7厘米、5厘米、3厘米,那么这个长方体的棱长和为_厘米.2.将三个棱长为4cm 的小正方体拼成一个大长方体,表面积比原来减少了_____cm².3.一个长方体平均截成5个正方体,表面积增加了40cm 2,原长方体的表面积是______cm².4. 棱长分别为3厘米、5厘米、7厘米的两个长方体拼成一个长方体, 它们的表面积最多减少_____________平方厘米.5.如果一根24米的铁丝剪开后刚好能搭成一个长方体框架模型,这个长方体的长、宽、高的长度均为整数米,且互不相等,那么这个长方体的体积是 立方米.6.某长方体中,一个公共顶点的三条棱长度之比为5:8:10,长方体中最小的一个面的面积是1202cm ,则最大的一个面的面积是 2cm .7.有12个棱长为1cm 的完全相同的小正方体,用它们拼成一个长方体,这个长方体的表面积最小是 平方厘米.二.选择题8.一个长方体的棱长总和是108厘米,且长:宽:高是4:3:2,则长方体的体积( )立方厘米。
A.216B.324C.432D.6489.下列说法中正确的个数有( )①正方体是特殊的长方体,②长方体的表面中不可能有正方形,③楼长为6cm的正方体的表面积和体积的数值相等,④具有6个面,12条棱和8个项点的图形都是长方体.A.1个B.2个C.3个D.4个二、解答题10.制作一个无盖的长方体玻璃鱼缸,底面长为115米,宽为35米,高为45米,如果不计拼缝,那么至少需要多少平方米的玻璃?11.如图所示,在一张长8cm、宽6cm的长方形纸处的四角分别剪去1个边长为1.5cm的正方形,然后沿虚线折成一个无盖的长方体盒子,求这个长方体盒子的体积.12.已知一个长方体无盖容器,它的棱长分别为5厘米、8厘米、10厘米,问:这个容器的表面积和容积各是多少?13.一根长为36分米的铁丝截开后刚好能够搭成一个长方体架子,这个长方体架子的长、宽、高的长度均为整数分米,且互不相等,求这个长方体的体积.14.(青浦2017期末27)如图,是一个长方体的一部分,虚线表示被遮住的线段,按要求完成下列问题.(1)补画出这个长方体.【画图时,请使用2B铅笔,不写画法】(2)在补画出的长方体中,若长是宽的2倍,高比宽多4厘米,用96厘米长的铁丝制作这个长方体框架.问:这个长方体框架的长、宽、高应分别是多少?(3)如果给出一个与(2)中所作的长方体形状、大小相同的木块,并在这个木块上切下一个棱长是1厘米的正方体,求剩余木块的表面积(要求:切下的正方体木块中至少有一个面是原来长方体木块表面的一部分).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.1长方体的元素
易错点归纳
1. 长方体有6个面,8个顶点,12条棱.
2. 长方体的特点(正方体是特殊的长方体).
(1)长方体的每个面都是长方形;
(2)长方体的十二条棱可以分为3组,每组中的4条棱的长度都相等.
(3)长方体的六个面可以分为3组,每组中的2个面的形状和大小相同.
3.若一个长方体的三条棱长分别是a,b,h,则这个长方体的总棱长可以表示为4(a+b+h );它的表面积可以表示为2ab+2ah+2bh ;它的体积可以表示为abh .
一、填空题
1.已知一个长方体的长、宽、高分别是7厘米、5厘米、3厘米,那么这个长方体的棱长和为_厘米.
2.将三个棱长为4cm 的小正方体拼成一个大长方体,表面积比原来减少了_____cm².
3.一个长方体平均截成5个正方体,表面积增加了40cm 2,原长方体的表面积是______cm².
4. 棱长分别为3厘米、5厘米、7厘米的两个长方体拼成一个长方体, 它们的表面积最多减少_____________平方厘米.
5.如果一根24米的铁丝剪开后刚好能搭成一个长方体框架模型,这个长方体的长、宽、高的长度均为整数米,且互不相等,那么这个长方体的体积是 立方米.
6.某长方体中,一个公共顶点的三条棱长度之比为5:8:10,长方体中最小的一个面的面积是1202cm ,则最大的一个面的面积是 2cm .
7.有12个棱长为1cm 的完全相同的小正方体,用它们拼成一个长方体,这个长方体的表
面积最小是 平方厘米.
二.选择题
8.一个长方体的棱长总和是108厘米,且长:宽:高是4:3:2,则长方体的体积( )立方厘米。
A.216
B.324
C.432
D.648
9.下列说法中正确的个数有( )
①正方体是特殊的长方体,
②长方体的表面中不可能有正方形,
③楼长为6cm的正方体的表面积和体积的数值相等,
④具有6个面,12条棱和8个项点的图形都是长方体.
A.1个
B.2个
C.3个
D.4个
二、解答题
10.制作一个无盖的长方体玻璃鱼缸,底面长为
1
1
5
米,宽为
3
5
米,高为
4
5
米,如果不计拼
缝,那么至少需要多少平方米的玻璃?
11.如图所示,在一张长8cm、宽6cm的长方形纸处的四角分别剪去1个边长为1.5cm的正方形,然后沿虚线折成一个无盖的长方体盒子,求这个长方体盒子的体积.
12.已知一个长方体无盖容器,它的棱长分别为5厘米、8厘米、10厘米,问:这个容器的表面积和容积各是多少?
13.一根长为36分米的铁丝截开后刚好能够搭成一个长方体架子,这个长方体架子的长、宽、高的长度均为整数分米,且互不相等,求这个长方体的体积.
14.(青浦2017期末27)如图,是一个长方体的一部分,虚线表示被遮住的线段,按要求完成下列问题.
(1)补画出这个长方体.【画图时,请使用2B铅笔,不写画法】
(2)在补画出的长方体中,若长是宽的2倍,高比宽多4厘米,用96厘米长的铁丝制作这个长方体框架.问:这个长方体框架的长、宽、高应分别是多少?
(3)如果给出一个与(2)中所作的长方体形状、大小相同的木块,并在这个木块上切下一个棱长是1厘米的正方体,求剩余木块的表面积(要求:切下的正方体木块中至少有一个面是原来长方体木块表面的一部分).。
