圆周角的概念及定理
人教版数学九年级上册圆周角的概念和圆周角定理课件
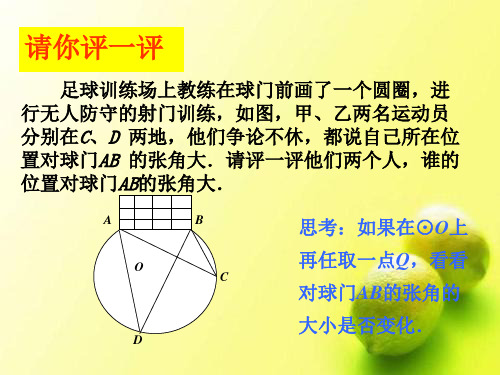
(2)∠BOC=____7_0°,理由是
__同__弧__所__对__的__圆__周__角__等__于__该__弧__所__对_ __的__圆__心__角__的__一__半__.___________.
DAC 1 DOC . 2
∴ DAC DAB 1 (DOC BOD) , 2
即BAC 1 BOC. 2
议一议
一条弧所对的圆周角等于它所 对的圆心角的一半. 同弧或等弧所对的圆周角相等。
思考
C
A
O
B
如图,AB是直径,则∠ACB=_9_0_°。 半圆(或直径)所对的圆周角是直角, 90度的圆周角所对的弦是直径。
∵ ∠BAC=∠BFC (同弧
B
所对的圆周角相等).
A
D
F
E O
C
请你说一说 这节课你有哪些收获和困惑? 圆周角定义及定理。
课后作业 课本P89第3题,P90第14题; 练习册P7∠BAC的内部或外部时, BAC 1 BOC 的关系还成立吗?
2
思考与探索
证明:作直径AD.
∵BAD 1 BOD ,
2
DAC 1 DOC. 2
∴ BAD DAC 1 (BOD DOC ) , 2
即BAC 1 BOC .
2
思考与探索
证明:作直径AD.
∵BAD 1 BOD , 2
思考与探索
3.当圆心O在∠BAC的一边上时,圆周角 ∠BAC与圆心角∠BOC之间有怎样的数量关系? 你能证明你的发现吗?
思考与探索
4.BAC 1 BOC .
证明:
2
圆周角定理 课件

3.关于圆周角定理推论的理解
(1)在推论1中,注意:“同弧或等弧”改为“同弦或等弦” 的话结论就不成立了,因为一条弦所对的圆周角有两种可 能,在一般情况下是不相等的.
(2)圆心角的度数和它所对的弧的度数相等,但并不是 “圆心角等于它所对的弧”.
(3)“相等的圆周角所对的弧也相等”的前提条件是“在 同圆或等圆中”.
【示例2】 如图,D,E分别为△ABC边AB,AC 的中点,直 线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明: (1)CD=BC; (2)△BCD∽△GBD.
证明 (1)因为D,E分别为AB,AC的中点,所以DE∥BC.又 已知CF∥AB,故四边形BCFD是平行四边形,所以CF=BD = AD. 而 CF∥AD , 连 接 AF , 所 以 ADCF 是 平 行 四 边 形 , 故 CD=AF.
证明 连结 CE、CF、EF,∵BC 为⊙O 的直径,∴∠BFC =90°,∠BEC=90°.又∵∠ACB=90°,∴∠BCE=∠A. 又∵∠BFE=∠BCE,∴∠BFE=∠A.又∵∠EBF=∠DBA, ∴△BEF∽△BDA.∴EBFE=ABDD. ∵∠BFC=∠BCA,∠CBD=∠CBD, ∴△CBF∽△DBC.∴CBCF=CBDD. 又∵AD=CD,∴EBFE=CBCF,∴BBCE=CEFF.
(4)在同圆或等圆中,由弦相等⇒弧相等时,这里的弧要求 同是优弧或同是劣弧,一般选劣弧.
题型一 圆中相关角度数的求解
【例 1】 在半径为 5 cm 的圆内有长为 5 3 cm 的弦 AB,求此弦
所对的圆周角.
[思维启迪] 对于弦所对的圆周角要考虑全面.
解 如图所示,过 O 点作 OD⊥AB 于点 D.因为 OD⊥AB,OD
反思感悟 弦所对的圆周角有两个,易丢掉120°导致错误,另外求圆周角时易应用到解三角形的知识.
圆周角的三个定理和三个推论

圆周角的三个定理和三个推论
圆周角是几何学中非常重要的课题,它测量了连续弧线绕圆心一周所形成的面积,它表征了圆弧路径的大小。
圆周角的三个定理和三个推论很重要,下面将对
它们做一些详细的介绍。
第一个定理是“极角定理”,它声明了一个角的圆心角(圆周角),它的大小
是由圆弧的长度和此弧端点从圆心到他们之间的距离决定的。
它可以为求解圆周角提來许多帮助。
第二个定理,“同余角定理”,它认为圆弧A,B,C,D上的三个角相同,即
A=B=C=D,那么圆的圆周必然相同为∠ACD。
这一定理使圆周角更容易求解。
第三个理定,“圆周角定理”,它宣称,对于任意两个圆心角相同的多边形的
每一条边,其角的总和为360°,或等于2π。
这一定理可以用来计算更复杂的圆
上的角度和圆周角。
此外,圆周角有三个重要推论,第一个是“梯形定理”,它保证了梯形是可以
分解为两个相同的三角形,梯形的内角和周围角之和等于360°,即弧度为2π。
第二个推论是“饼图定理”,它保证了由一个圆形分割成多个部分形成的饼图,其总弧度之和等于2π,在此饼图中,各部分所占的弧度数可以根据各部分的大小
来计算。
最后一个推论是“三角形定理”,它给出了一个三角形,它的三条边和三个内
角的总和等于180°,或与弧度等于π。
这三个推论可以用来计算更复杂的圆周角。
总之,圆周角的三个定理和三个推论对于几何学是非常重要的,它们可以帮助
我们很好地计算出更复杂的圆周角,这对于研究几何领域是很有帮助的。
人教版初三数学上册24.1.4圆周角的概念和圆周角定理

1.形成概念
问题5:将圆心角顶点向上移,直至与⊙O 相交于点C?观察并比较∠ACB 与∠AOB 由和异同?
我们知道,∠AOB 叫做AB 所对的圆心角,类似地,我们把∠ACB 叫做AB 所对的圆周角
教材定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角
2.剖析概念、应用概念
问题6:判断下列图形中所画的∠P 是否为圆周角?并说明理由。
探究定理:
问题7:在同一个圆中,一条弧所对的圆心角只有一个,那么一条弧所对的圆周角有几个呢?
结论:(1)一条弧所对的圆周角有无数个;(2)优弧和劣弧所对的圆周角大小不同 问题8:∠ACB 与∠AOB 有怎样的关系?
问题9:当点C 移动到C 1 C 2 C 3 C 4 C 5 时,圆周角与圆心角的数量关系改变没? 结论:无论移动点C 、还是点C 1 始终有
∠ACB=2
1∠AOB ,即一条弧所对的圆周角等于圆心角的一半 问题10:通过观察、猜想、我们得到上面的结论,那么如何证明结论呢?
问题11.观察点C 在移动过程中,圆心O 与∠ACB 有哪些位置关系?
结论:有三种情况,
圆心在圆周角的一边上时;圆心在圆周角的内部时;圆心在圆周角的外部
圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半
证明定理。
圆周角定义及定理

圆周角的定义是:顶点在圆上,角的两边都与圆相交的角。
其特点可归纳为:①顶点在圆上,②两边都和圆相交。
这两个条件缺一不可。
圆周角定理为:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。
具体来说,定理有三方面的意义:
圆心角和圆周角在同一个圆或等圆中;
它们对着同一条弧或者对的两条弧是等弧;
具备a、b两个条件的圆周角都是相等的,且等于圆心角的一半。
此外,还有以下推论:
在同圆或等圆中,相等的圆周角所对的弧相等。
直径(半圆)所对的圆周角是直角;90°的圆周角所对的弦为直径。
如果三角形一边的中线等于这边的一半,那么这个三角形是直角三角形。
圆心角圆周角定理推论笔记

圆心角圆周角定理推论笔记一、圆心角定理圆心角的度数等于它所对的弧的度数。
理解:(定义)(1)等弧对等圆心角(2)把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角.(3)因为在同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份,这时,把每一份这样得到的弧叫做1°的弧.(4)圆心角的度数和它们对的弧的度数相等.推论:在同圆或等圆中,如果(1)两个圆心角,(2)两条弧,(3)两条弦(4)两条弦上的弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等二、圆周角定理推论:圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角都等于这条弧所对的圆心角的一半。
①圆周角度数定理:圆周角的度数等于它所对的弧的度数的一半。
②同圆或等圆中,圆周角等于它所对的弧上的圆心角的一半。
③同圆或等圆中,同弧或等弧所对的圆周角相等,相等圆周角所对的弧也相等。
(不在同圆或等圆中其实也相等的。
注:仅限这一条。
)④半圆(或直径)所对圆周角是直角,90°的圆周角所对的弦是直径。
⑤圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
⑥在同圆或等圆中,圆周角相等<=>弧相等<=>弦相等。
三、圆的定义:在同一平面内,到定点的距离等于定长的点的集合叫做圆。
这个定点叫做圆的圆心。
图形一周的长度,就是圆的周长。
圆心角:顶点在圆心的角叫做圆心角。
圆周角:顶点在圆上,并且两边都和圆相交的角叫做圆周角。
圆周角的顶点在圆上,它的两边为圆的两条弦。
1、弦:连接圆上任意两点的线段。
2、弧:圆上任意两点间的部分叫做圆弧,简称弧。
弧用符号“⌒”表示以A,B为端点的弧记作“ ”,读作“圆弧AB”或“弧AB”。
优弧:大于半圆的弧(多用三个字母表示);劣弧:小于半圆的弧(多用两个字母表示)圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆。
3、圆心角:顶点在圆心的角叫做圆心角。
圆周角的概念和圆周角定理

24.1圆的有关性质(第四课时)一、内容和内容解析1.内容圆周角概念,圆周角定理及其推论.2.内容解析与圆心角一样,圆周角也是研究圆时重点研究的一类角.顶点在圆上并且两边都与圆相交的角叫做圆周角.圆周角定理(即一条弧所对的圆周角等于它所对的圆心角的一半)揭示了一条弧所对的圆周角与圆心角之间的数量关系.从而把圆周角与相对应的弧、弦联系起来.圆周角定理及其推论为与圆有关的角的计算,证明角相等,弧、弦相等等数学问题提供了十分便捷的方法和思路,即是圆心角、弦、弧之间关系的继续,又是后续研究圆与其他平面图形的桥梁和纽带.圆周角定理得证明,采用完全归纳法,通过分类讨论,把一般问题转化为特殊情况来证明,渗透了分类讨论和化一般为特殊的化归思想.基于以上分析,确定本节课的教学重点是:圆周角定理.二、目标和目标解析1.目标(1)了解圆周角的概念,会证明圆周角定理及其推论.(2)结合圆周角定理的探索与证明的过程,进一步体会分类讨论、化归的思想方法.2.目标解析达成目标(1)的标志是:能在具体的图形中正确识别一条弧所对的圆周角;知道一条弧所对的圆周角等于这条弧所对的圆心角的一半,知道同弧或等弧所对的圆周角相等,能够正确识别直径所对的圆周角,并会结合具体问题构造直径所对的圆周角;能够应用定理和推论解决简单问题.达成目标(2)的标志是:能通过画图、观察、度量、归纳等方式发现一条弧所对圆周角与圆心角之间的关系;能根据圆心与圆周角的位置关系对同弧所对的圆周角进行分类,理解证明圆周角定理需要分三种情况的必要性;理解证明圆周角定理时,可以把圆心在圆周角的内部和外部两种情况转化成特殊情况,从而证明定理.三、教学问题诊断分析圆心与圆周角具有三种不同的位置关系:圆心在圆周角的一边上,圆心在圆周角的内部,圆心在圆周角的外部.所以,圆周角定理的证明要采用完全归纳法,分情况证明.学习本节课内容时,学生已经具备一定的逻辑推理能力,但对于一个几何命题要分情况证明的经验还很缺乏.因此,教学的关键是:①在学生明确圆周角的概念后,让学生动手画圆周角,一方面让学生深入了解圆周角,另一方面,让学生在动手操作中体会圆心与圆周角具有三种不同的位置关系,为后面证明中的分类讨论做好铺垫.②学生合作交流,通过度量事先画的一条弧所对的圆周角与圆心角的度数,探究并猜想他们之间的数量关系,然后教师在利用计算机软件来验证,让学生进一步明确他们之间的关系,从而得到命题:一条弧所对的圆周角等于它所对的圆心角的一半.③从特殊的位置关系——圆心在圆周角一边上的情形入手,先证明猜想,再将其他两种情形转化为圆心在圆周角一边上的情形.基于以上分析,本节课的教学难点是:分情况证明圆周角定理.四、教学过程设计1.了解圆周角的概念问题1 如图1,∠ACB 的顶点和边有哪些特点?师生活动:学生观察图形,教师引导学生结合图形认识到:∠ACB 的顶点在O Θ上,角的两边分别交O Θ于点A,B 两点.教师进而指出:顶点在圆上,并且两边都和圆相交的角叫做圆周角.圆周角与圆心角都是圆有关的角.设计意图:结合图形,获得圆周角定义,理解圆周角的概念.练习 教科书第88页练习第一题.师生活动:学生思考并回答问题.设计意图:同时呈现有关圆周角的正例和反例,有利于学生对圆周角概念的本质属性与非本质属性进行比较,巩固对概念的理解.2.探索圆周角定理问题2 在图2中,∠ACB 是圆周角,作出弧AB所对的圆心角∠AOB.分别测量∠ACB 和∠AOB 的度数.他们之间有什么关系?师生活动:学生画图,连接OA,OB 得到圆心角∠AOB.跳时指出∠ACB 和∠AOB 都对着弧AB 提出以下问题.教师追问1:图2中,∠ACB 和∠AOB 有怎样的关系?师生活动:学生通过观察,度量,猜想AOB ACB ∠=∠21.即一条弧所对的圆周角等于它所对的圆心角的一半.教师追问2:在O Θ上任取一条弧,做出这条弧所对的圆周角和圆心角,测量它们的度数,你能得出同样的结论吗?师生活动:除学生动手画图度量,并验证猜想外,教师也可以利用《几何画板》软件的动态功能和度量功能进行演示,从更广泛的角度验证猜想:①拖动圆周角的顶点在优弧AB 上运动;②改变弧的大小;③改变圆的大小后分别进行①和②的掩演示.引导学生发现,在演示过程中,∠ACB 和∠AOB 度数的比值保持不变.设计意图:引导学生经历观察猜想、操作、分析、验证、交流等基本数学活动,探索圆周角的性质:一条弧所对的圆周角等于它所对的圆心角的一半.教师使用《几何画板》做进一步演示与验证,在动态环境中研究圆周角与圆心角的关系,即在某些量变化的过程中让学生观察不变的数量关系,帮助学生更好地理解一条弧所对的圆周角与圆心角的数量关系.3.证明圆周角定理问题 3 如何证明一条弧所对的圆周角等于它所对的圆心角的一半?教师追问1:在圆上任取弧BC ,画出圆心角∠BAC 和圆周角∠BOC,圆心与圆周角有几种位置关系?师生活动:学生动手画图、交流、思考,得到圆心与圆周角的三种位置关系(图3):①圆心在圆周角的一边上;②圆心在圆周角的内部;③圆心在圆周角的外部.设计意图:把直观操作与逻辑推理有机结合,使得推理论证成为学生观察、实验、探究得出结论的自然延续.同时进一步明确证明的必要性和证明的方法.教师追问2:第①种情况下,如何证明一条弧所对的圆周角等于它所对的圆心角的一半?师生活动:学生结合三种位置的图形,认识到第①种情况属于特殊情况,另外两种情况比第①种情况复杂.研究数学问题一般从特殊情况开始,再考虑其他情况能否转化成特殊情况.师生结合图3(1),分析第①种情况,得到BOC A C A BOC C A OC OA ∠=∠⇒⎭⎬⎫∠+∠=∠∠=∠⇒=21教师指出:符号”B A “⇒表示由条件A 推出B ,可以用”“⇒方式给出推理过程.设计意图:从特殊情况入手,证明猜想G 便于学生的学习又为其他两种情况的证明提供了转化的方向.教师追问3: 在第②③种情况下,如何证明一条弧所对的圆周角等于它所对的圆心角的一半?师生活动:学生思考,尝试解决.如果学生有困难,教师可提示学生:将第②③种情况转化成第①种情况.根据学生的情况,师生共同研究完成第②种情况的证明.证明:如图4,连接AO 并延长交ΘO 于点D.BOD BAD B BAD BOD B BAD OB OA ∠=∠⇒⎭⎬⎫∠+∠=∠∠=∠⇒=21. 同理,COD CAD ∠=∠21. BOC COD BOD CAD BAD BAC ∠=∠+∠=∠+∠=∠∴212121. 学生独立完成第③种情况的证明.从而得到定理:一条弧所对的圆周角等于它所对的圆心角的一半.设计意图:将一般情况化为特殊情况,体现了化归的数学思想.学生通过证明三种情况,感受分类证明的必要性,有利于逻辑推理能力的提升.4.探究特殊情况,获得推论问题4 我们知道,一条弧,可以对着不同的圆周角,这些圆周角之间有什么关系?也就是说,同弧或等弧所对的圆周角之间有什么关系?师生活动:学生画出弧BC 所对的几个圆周角和圆心角(图5),先观察、猜想,根据定理得到结论:一条弧所对的圆周角相等.再思考同弧或等弧的情况.如果学生遇到困难,教师可根据情况提示学生:考虑圆周角与圆心角之间的关系、弧与圆心角之间的关系,通过弧相等得到结论.设计意图:让学生经历观察、猜想、证明得出推论的探索过程,得到圆周角定理的推论,进一步认识与圆有关的角和弧之间的关系.问题5 半圆或直径所对的圆周角有什么特殊性?师生活动:学生画出弧AB 所对的几个圆周角和圆心角(图6),通过观察、猜想,根据定理得到结论:半圆(或直径)所对的圆周角是直角.教师进一步引导学生得出:90°的圆周角所对的弦是直径.设计意图:由一般到特殊进一步认识定理,加深对定理的理解,获得推论.5.应用圆周角定理与推论例如图7,OΘ的直径AB的长为10cm.弦AC长为6cm,∠ACB的平分线交OΘ于点D, 求BC,AD,BD的长.师生活动:师生共同分析已知条件、所求和解题思路.如图8,欲求BC的长,由BC所在的△ABC中AB为OΘ的直径,可知∠ACB=90°.又AB和AC已知,在Rt△ABC中,由勾股定理可求BC的长.由CD平分∠ACB得∠ACD=∠BCD,连接OD,可得∠AOD=∠BOD=90°,进而由勾股定理可求AD,BD的长.学生解答,一名学生板书,教师组织学生交流.设计意图:应用圆周角定理及其推论解决问题,巩固所学的内容.6.小结教师与学生一起回顾本节课的主要内容,并请学生回答以下问题:(1)本节课学习了哪些主要内容?(2)我们是如何证明圆周角定理的?在证明过程中用到了哪些思想方法?设计意图:通过小结使学生归纳梳理总结本节的知识、技能、方法,将本节课所学的知识与以前所学的知识进行紧密联系,有利于学生认知数学思想、教学方法,积累数学活动的经验.7.布置作业教科书第88页练习题第2,3,4题.。
圆周角定理的定理证明

圆周角定理的定理证明圆周角定理是平面几何中的一个重要定理,它给出了圆内任意一对弧所对应的圆周角相等的条件。
本文将通过推理和证明,解释圆周角定理的原理和应用。
我们来回顾一下圆周角的概念。
圆周角是由两条弧所夹的角,其中一条弧是圆上的一段弧,另一条弧是连接该圆上两个端点的弦。
我们将这两条弧所夹的角称为圆周角。
下面,我们来证明圆周角定理。
假设在一个圆上有两条弧AB和CD,它们所对应的圆周角分别为∠AOB和∠COD。
我们要证明的是∠AOB = ∠COD。
我们连接线段AC和BD,将圆分成了两个扇形OAC和OBD。
由于扇形是圆的一部分,所以扇形OAC的圆心角等于∠AOB,扇形OBD的圆心角等于∠COD。
我们要证明的是∠AOB = ∠COD,即证明扇形OAC的圆心角等于扇形OBD的圆心角。
接下来,我们来证明线段AC和BD所夹的角等于圆心角。
首先,我们连接线段AO和BO,线段OC和OD,得到了两个三角形AOB和COD。
由于AO = BO,OC = OD,而且∠AOB和∠COD都是直角,所以三角形AOB和COD是等腰直角三角形。
根据等腰直角三角形的性质,我们知道∠BAO = ∠ABO,∠CDO = ∠COD。
而且,三角形AOB和COD的两个直角边分别是AO和BO,OC和OD,它们的长度相等。
根据等腰直角三角形的性质,我们知道∠BOA = ∠DOA,∠AOC = ∠COA。
现在,我们来看看扇形OAC和OBD的圆心角。
根据扇形的定义,圆心角等于弧所对应的圆周角的两倍。
所以扇形OAC的圆心角等于∠BOA,扇形OBD的圆心角等于∠DOA。
由于∠BOA = ∠DOA,所以扇形OAC的圆心角等于扇形OBD的圆心角。
根据我们之前的推理,我们已经证明了扇形OAC和OBD的圆心角相等。
由于圆周角是由扇形的圆心角所对应的,所以我们可以得出结论:圆周角∠AOB = ∠COD。
通过上述的推理和证明,我们证明了圆周角定理的正确性。
圆周角定理的应用非常广泛,特别是在解决与圆相关的角度问题时,它可以帮助我们简化计算和推导的过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学时间课题24.1.4 圆周角课型新授课
教学目标知识和能力
1.了解圆周角与圆心角的关系.
2.探索圆周角的性质和直径所对圆周角的特征.
3.能运用圆周角的性质解决问题.
过程和方法
1.通过观察、比较,分析圆周角与圆心角的关系,发展学生合情推理能力和演绎推理能力.
2.通过观察图形,提高学生的识图能力.
3.通过引导学生添加合理的辅助线,培养学生的创造力.
4.学生在探索圆周角与圆心角的关系的过程中,学会运用分类讨论的数学思想、转化的数学思想解决问题.
情感态度
价值观引导学生对图形的观察发现,激发学生的好奇心和求知欲,并在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心.
教学重点探索圆周角与圆心角的关系,发现圆周角的性质和直径所对圆周角的特征.
教学难点发现并论证圆周角定理.
教学准备教师多媒体课件
问题与情境师生行为设计意图
[活动1 ]
演示课件或图片:
问题1
如图:同学甲站在圆心O的位置,同学乙站在正对着玻璃窗的靠墙的位置C,他们的视角( 和)有什么关系?
问题2
如果同学丙、丁分别站在其他靠墙的位置D和E,他们的视角( 和)和同学乙的视角相同吗?
教师演示课件或图片:展示一个圆柱形的海洋馆.
教师解释:在这个海洋馆里,人们可以通过其中的圆弧形玻璃窗观看窗内的海洋动物.
教师出示海洋馆的横截面示意图,提出问题.
教师结合示意图,给出圆周角的定义.利用几何画板演示,让学生辨析圆周角,并引导学生将问题1、问题2中的实际问题转化成数学问题:即研究同弧( )所对的圆心角( )与圆周角( )、同弧所对的圆周角( 、、等)之间的大小关系.教师引导学生进行探究.
教师关注:
1.问题的提出是否引起了学生的兴趣;
2.学生是否理解了示意图;
3.学生是否理解了圆周角的定义;
4.学生是否清楚了要研究的数学问题.
从生活中的实际问题入手,使学生认识到数学总是与现实问题密不可分,人们的需要产生了数学.
将实际问题数学化,让学生从一些简单的实例中,不断体会从现实世界中寻找数学模型、建立数学关系的方法.
引导学生对图形的观察,发现,激发学生的好奇心和求知欲,并在运用数学知识解答问题的活动中获取成功的体验,建立学习的自信心.
[活动2]
问题1同弧(弧AB)所对的圆心角∠AOB 与圆周角∠ACB的大小关系是怎样的?
问题2
同弧(弧AB )所对的圆周角∠ACB 与圆周角∠ADB 的大小关系是怎样的?
教师提出问题,引导学生利用度量工具(量角器)动手实验,进行度量,发现结论.
在活动中,教师应关注:
1.学生是否积极参与活动;
2.学生是否度量准确,观察、发现的结论是否正确.
由学生总结发现的规律:同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的一半.
教师利用几何画板课件“圆周角定理”,从动态的角度进行演示,验证学生的发现.教师可从以下几个方面演示,让学生观察圆周角的度数是否发生改变,同弧所对的圆周角与圆心角的关系有无变化.
1.拖动圆周角的顶点使其在圆周上运动;
2.改变圆心角的度数;
3.改变圆的半径大小.
活动2的设计是为引导学生发现.让学生亲自动手,利用度量工具(如半圆仪、)进行实验、探究,得出结论.激发学生的求知欲望,调动学生学习的积极性.教师利用几何画板从动态的角度进行演示,目的是用运动变化的观点来研究问题,从运动变化的过程中寻找不变的关系.
[活动3]
问题1
在圆上任取一个圆周角,观察圆心与圆周角的位置关系有几种情况? (课件:折痕与圆周角的关系)
问题2
当圆心在圆周角的一边上时,如何证明活动2中所发现的结论?
问题3
另外两种情况如何证明,可否转化成第一种情况呢?
教师引导学生,采取小组合作的学习方式,前后四人一组,分组讨论.
教师关注:
1.学生是否会与人合作,并能与他人交流思维的过程和结果;
2.学生能否发现圆心与圆周角的三种位置关系.
教师巡视,请学生回答问题.回答不全面时,请其他同学给予补充.
教师演示圆心与圆周角的三种位置关系.
教师引导学生从特殊情况入手证明所发现的结论.
学生写出已知、求证,完成证明.
教师关注:
1.学生能否用准确的数学符号语言表述已知和求证,并准确地画出图形来;
2.学生能否证明出结论.
学生采取小组合作的学习方式进行探索发现,教师观察指导小组活动.启发并引导学生,通过添加辅助线,将问题进行转化.
教师关注:
1.学生是否会想到添加辅助线,将另外两种情况进行转化;
2.学生添加辅助线的合理性;
3.学生是否会利用问题2的结论进行证明.
教师讲评学生的证明,板书圆周角定理.数学教学是在教师的引导下,进行的再创造、再发现的教学.通过数学活动,教给学生一种科学研究的方法,学会发现问题、提出问题、分析问题,并能解决问题.活动3的安排是让学生对所发现的结论进行证明.培养学生严谨的治学态度.
问题1的设计是让学生通过合作探索,学会运用分类讨论的数学思想研究问题.培养学生思维的深刻性.
问题2、3的提出是让学生学会一种分析问题、解决问题的方式方法:从特殊到一般.学会运用化归思想将问题转化.并启发培养学生创造性的解决问题.
[活动4]
问题1
半圆(或直径)所对的圆周角是多少度?(课件:圆周角定理推论)
问题2
90°的圆周角所对的弦是什么?
问题3
在半径不等的圆中,相等的两个圆周角所对的弧相等吗?
∠ABC=30°
∠A’B’C’=30°
问题4
在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等吗?为什么?
问题5
如图,点、、、在同一个圆上,四边形的对角线把4个内角分成8个角,这些角中哪些是相等的角? 问题6
如图,⊙O的直径AB 为10 cm,弦AC 为6 cm,∠ACB 的平分线交⊙O于D,求BC、AD、BD的长.
学生独立思考,回答问题,教师讲评.
问题1提出后,教师关注:
学生是否能由半圆(或直径)所对的圆心角的度数得出圆周角的度数.
问题2提出后,教师关注:
学生是否能由90°的圆周角推出同弧所对的圆心角度数是180°,从而得出所对的弦是直径.
问题3提出后,教师关注:
学生能否得出正确的结论,并能说明理由.
教师提醒学生:在使用圆周角定理时一定要注意定理的条件.
问题4提出后,教师关注:
学生能否利用定理得出与圆周角对同弧的圆心角相等,再由圆心角相等得到它们所对的弧相等.
问题5提出后,教师关注:
学生是否准确找出同弧所对的圆周角.
问题6提出后,教师关注:
1.学生是否能由已知条件得出直角三角形ABC、ABD;
2.学生能否将要求的线段放到三角形里求解;
活动4的设计是圆周角定理的应用.通过4个问题层层深入,考察学生对定理的理解和应用.
问题1、2是定理的推论,也是定理在特殊条件下得出的结论.问题3的设计目的是通过举反例,让学生明确定理使用的条件.问题4是定理的引申,将本节课的内容与所学过的知识紧密结合起来,使学生很好地进行知识的迁移.问题5、6是定理的应用.即时反馈有助于记忆,让学生在练习中加深对本节知识的理解.教师通过学生练习,及时发现问题,评价教学效果.
[活动5]
问题
通过本节课的学习你有哪些收获?
教师带领学生从知识、方法、数学思想等方面小结本节课所学内容.
教师关注不同层次的学生对所学内容的理解和掌握.
教师布置作业.
通过小结,使学生归纳、梳理总结本节的知识、技能、方法,将本课所学的知识与以前所学的知识进行紧密联系,有利于培养学生数学思想、数学方法、数学能力和对数学的积极情感.
增加阅读作业的目的是让学生养成看书的习惯,并通过看书加深对所学内容的理解.
课后巩固作业是对课堂所学知识的检验,让学生巩固、提高、发展.
作业
设计必做教科书P87:选做教科书P89
教学反思。
