算法流程图
算法流程图举例_课件
S←1,i←12
i←i-1
N
输出S
S←S×i
Y
结束
12.以下给出的是计算1/2+1/4+1/6+…+1/20的值的一个流程图, 判断框内应填入的条件为___.
开始 S←0,n←2,i←1
i←i+1 n←n+2 S←S+1/n
N Y 输出S 结束
13.下图流程图是计算1+1/3+1/5+…+1/99的流程图,请你补充完整. 开始
开始 x ← 1,S ← 0
x≤5 Nቤተ መጻሕፍቲ ባይዱ输出S
x←x+1 S←S+x2 Y
结束
5.如图所示的流程图输出的第2013个数为_1_0__0_7___.
开始 A←1,N←1
输出A N←N+1
N≤5000 N 结束
A←A+1/2 Y
6.下图所示流程图输入n=7,输出的结果为 13 .
开始 输入n A←1,B←1,K←3
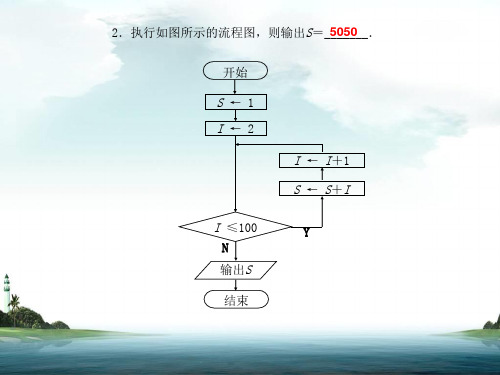
2.执行如图所示的流程图,则输出S=_5_0__5_0__.
开始 S←1 I←2
I ← I+1 S ← S+I
I ≤100
Y
N
输出S
结束
3.下图所示的流程图的输出结果为2_5__6_. 开始 p←0
i←1
p ← p+i
i ← i+2
i>31
N
Y
输出p
结束
4.下图所示的流程图的输出结果为_5_5__.
开始 i←1,m←0,T←0
输入x x>80 N
Y 输出x
T←T+x m←m+1
i←i+1
N
i>15
Y
P←T/m
输出P 结束
9.如下流程图,循环体执行的次数为 ( )
开始
算法流程图(循环结构)

i) 顺序结构
三种基本算法结构
ii) 选择结构
Y A B A
p
N B
循环结构
算法2流程图:
算法2:
开始 T←1
S1
S2
T←1;
S←2;
S←2
T←T×S S←S+1 S>5 Y 输出T 结束 N
S3
S4 S5
T←T×S;
S←S+1; 如果S不大于5,返 回 S3,否则输出T。
开始
开始
i ← 0,Sum ← 0
2010辽宁文数如果执行下图左的程序框图输入那么输出的等于a720b360c240d12010aa1b2b1输出b结束缚目录点击添加标题点击添加标题点击添加标题点击添加标题添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本点击添加文本01020304添加标添加文本点击添加文本点击添加文本点击添加文本点击添加文本会议基调年会视频
开始 Sum←0,i←1 Sum←Sum+1 i←i+1 否 i>100 是 输出Sum 结束
1.【2010· 浙江理数】 某程序框图如左图所 示,若输出的S=57, 则判断框内位( ) A. k>4? B.k>5? C. k>6? D.k>7?
2.【2010· 辽宁文数】 如果执行下图(左)的 程序框图,输入 n 6 , m 4那么输出的 等于( ) A.720 B.360 C.240 D.120
算法与程序框图(算法流程图)

程序框图的发展趋势
可视化编程
随着可视化技术的发展,程序框 图成为一种直观的编程方式。通 过图形化的方式描述程序逻辑, 降低了编程难度,提高了开发效 率。
交互式编程
交互式编程让用户在编程过程中 能够实时查看程序运行结果,及 时调整代码。这种编程方式提高 了开发效率和程序质量。
智能生成与自动优
化
基于机器学习和人工智能技术, 程序框图可以自动生成和优化程 序代码。这大大减少了编程工作 量,提高了开发效率。
算法的复杂度分析
随着计算机科学的发展,算法的复杂度分析越来越受到重 视。人们不断探索更高效的算法,以提高计算效率和准确 性。
机器学习与人工智能算法
随着人工智能的兴起,机器学习与人工智能算法成为研究 热点。这些算法能够从大量数据中自动提取有用的信息, 为决策提供支持。
并行计算与分布式算法
为了处理大规模数据和复杂问题,并行计算和分布式算法 成为研究重点。这些算法能够充分利用多核处理器和分布 式系统的优势,提高计算性能。
算法的表示方法
01
自然语言描述
用简洁明了的文字描述算法的步骤。
流程图
用图形符号表示算法的步骤和流程。
03
02
伪代码
用类似于编程语言的简化和结构化 形式描述算法。
程序代码
用编程语言实现算法的具体代码。
04
算法的复杂度分析
时间复杂度
评估算法执行时间随输入规 模增长的情况,表示为 O(f(n))。
空间复杂度
选择结构是根据条件判断选择不同的执行路径的程序框图 结构。它使用判断框来表示条件判断,根据条件的结果选 择不同的执行路径。选择结构可以有效地处理具有多个分 支的情况,提高程序的灵活性和适应性。
算法流程图的定义

算法流程图的定义An algorithm flowchart is a visual representation of the step-by-step process involved in solving a problem or completing a task. In computer science, these flowcharts help programmers and designers plan and organize their code in a clear and structured manner. By breaking down complex algorithms into simple, sequential steps, flowcharts make it easier to understand and optimize the logic behind the solution.算法流程图是解决问题或完成任务所涉及的逐步过程的视觉表示。
在计算机科学中,这些流程图帮助程序员和设计者以清晰和结构化的方式规划和组织他们的代码。
通过将复杂算法分解为简单的顺序步骤,流程图使得更容易理解和优化解决方案的逻辑。
When creating an algorithm flowchart, it is important to start with a clear understanding of the problem at hand. This involves breaking down the problem into smaller, more manageable components and identifying the specific inputs, processes, and outputs involved. By clearly defining these elements, you can create a roadmap for howthe algorithm will function and the steps needed to achieve the desired outcome.在创建算法流程图时,重要的是要先清楚地了解手头问题。
算法流程图

简介
计算机语言只是一种工具。光学习语言的规则还不够,最重要的是学会针对各种类型的问题,拟定出有效的 解决方法和步骤即算法。有了正确而有效的算法,可以利用任何一种计算机高级语言编写程序,使计算机进行工 作。因此,设计算法是程序设计的核心。为了表示一个算法,可以用不同的方法。常用的有自然语言,流程图, 伪代码,PAD图等。这其中以特定的图形符号加上说明,表示算法的图,称为算法流程图。
传统的流程图用流程线指出各框的执行顺序,对流程线的使用没有严格限制。因此,使用者可以毫不受限制 地使流程随意地转来转去,使流程图变得毫无规律,阅读者要花很大精力去追踪流程,使人难以理解算法的逻辑。 如果我们写出的算法能限制流程的无规律任意转向,而像一本书那样,由各章各节顺序组成,那样,阅读起来就 很方便,不会有任何困难,只需从头到尾顺序地看下去即可。
为了提高算法的质量,使算法的设计和阅读方便,必须限制箭头的滥用,即不允许无规律地使流程乱转向, 只能按顺序地进行下去。但是,算法上难免会包含一些分支和循环,而不可能全部由一个一个框顺序组成。如上 例不是由各框顺序进行的,包含一些流程的向前或向后的非顺序转移。为了解决这个问题,人们设想,如果规定 出几种基本结构,然后由这些基本结构按一定规律组成一个算法结构,整个算法的结构是由上而下地将各个基本 结构顺序排列起来的。1966年,Bohra和Jacoplni提出了以下三种基本结构,用这三种基本结构作为表示一个良 好算法的基本单元。
1、顺序结构:如图2所示的虚线框内,A和B两个框是顺序执行的。顺序结构是最简单的一种基本结构。
图2
2、选择结构:如图3所示的虚线框中包含一个判断框。
结构流程图
1973年美国学者提出了一种新的流程图形式。在这种流程图6中,完全去掉了带箭头的流程线。全部算法写 在一个矩形框内。在该框内还可以包含其它的从属于它的框,即可由一些基本的框组成一个大的框。这种适于结 构化程序设计的流程图称N-S结构化流程图,它用以下的流程图符号:
算法流程图
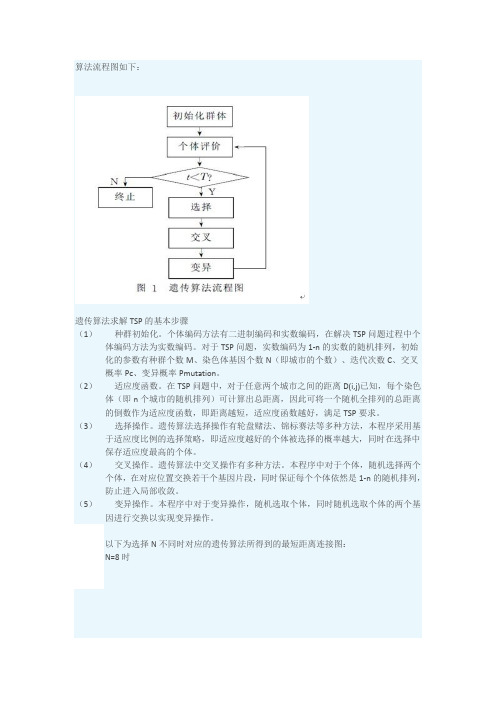
算法流程图如下:遗传算法求解TSP的基本步骤(1)种群初始化。
个体编码方法有二进制编码和实数编码,在解决TSP问题过程中个体编码方法为实数编码。
对于TSP问题,实数编码为1-n的实数的随机排列,初始化的参数有种群个数M、染色体基因个数N(即城市的个数)、迭代次数C、交叉概率Pc、变异概率Pmutation。
(2)适应度函数。
在TSP问题中,对于任意两个城市之间的距离D(i,j)已知,每个染色体(即n个城市的随机排列)可计算出总距离,因此可将一个随机全排列的总距离的倒数作为适应度函数,即距离越短,适应度函数越好,满足TSP要求。
(3)选择操作。
遗传算法选择操作有轮盘赌法、锦标赛法等多种方法,本程序采用基于适应度比例的选择策略,即适应度越好的个体被选择的概率越大,同时在选择中保存适应度最高的个体。
(4)交叉操作。
遗传算法中交叉操作有多种方法。
本程序中对于个体,随机选择两个个体,在对应位置交换若干个基因片段,同时保证每个个体依然是1-n的随机排列,防止进入局部收敛。
(5)变异操作。
本程序中对于变异操作,随机选取个体,同时随机选取个体的两个基因进行交换以实现变异操作。
以下为选择N不同时对应的遗传算法所得到的最短距离连接图:N=8时MATLAB实现程序如下:初始化的参数有种群个数M、染色体基因个数N(即城市的个数)、迭代次数C、交叉概率Pc、变异概率Pmutation。
(1)适应度函数fit.mfunction fitness=fit(len,m,maxlen,minlen)fitness=len;for i=1:length(len)fitness(i,1)=(1-(len(i,1)-minlen)/(maxlen-minlen+0.0001)).^m;end(2)个体距离计算函数 mylength.mfunction len=myLength(D,p)[N,NN]=size(D);len=D(p(1,N),p(1,1));for i=1:(N-1)len=len+D(p(1,i),p(1,i+1));endend(3)交叉操作函数 cross.mfunction [A,B]=cross(A,B)L=length(A);if L<10W=L;else if ((L/10)-floor(L/10))>=rand&&L>10%%%Matlab取整函数有: fix, floor, ceil, round.具体应用方法如下:fix朝零方向取整,如fix(-1.3)=-1; fix(1.3)=1;floor,顾名思义,就是地板,所以是取比它小的整数,即朝负无穷方向取整,如floor(-1.3)=-2; floor(1.3)=1;floor(-1.8)=-2,floor(1.8)=1ceil,与floor相反,它的意思是天花板,也就是取比它大的最小整数,即朝正无穷方向取整,如ceil(-1.3)=-1; ceil(1.3)=2;ceil(-1.8)=-1,ceil(1.8)=2round四舍五入到最近的整数,如round(-1.3)=-1;round(-1.52)=-2;round(1.3)=1;round(1.52)=2。
算法流程图的三种基本结构

算法流程图的三种基本结构
算法流程图是软件开发中非常重要的一部分,它能够清晰地展现出程序的执行
流程,帮助开发人员更好地理解和调试代码。
在算法流程图中,有三种基本的结构,它们分别是顺序结构、选择结构和循环结构。
首先,顺序结构是最简单的一种结构,它表示程序按照从上到下的顺序依次执
行各个操作。
在算法流程图中,顺序结构通常用矩形框表示,框内包含了具体的操作步骤,每个步骤都按照一定的顺序执行。
这种结构清晰明了,直观易懂,能够很好地展现出程序的执行流程。
其次,选择结构是根据某个条件的成立与否,决定程序的执行路径。
在算法流
程图中,选择结构通常用菱形框表示,菱形框内包含了条件判断的具体内容,根据条件的成立与否,程序会选择不同的执行路径。
这种结构能够很好地展现出程序的分支逻辑,帮助开发人员理清程序的执行流程。
最后,循环结构是根据某个条件的成立与否,重复执行某段代码。
在算法流程
图中,循环结构通常用圆角矩形框表示,圆角矩形框内包含了需要重复执行的代码段,同时也包含了条件判断的具体内容。
这种结构能够很好地展现出程序的循环执行逻辑,帮助开发人员理清程序的重复执行流程。
综上所述,算法流程图的三种基本结构分别是顺序结构、选择结构和循环结构。
它们分别代表了程序按照顺序执行、根据条件选择执行路径以及重复执行某段代码的逻辑。
这三种结构在算法流程图中起着非常重要的作用,能够很好地帮助开发人员理清程序的执行流程,从而更好地理解和调试代码。
在实际的软件开发中,合理运用这三种结构,能够编写出结构清晰、逻辑严谨的程序,提高代码的可读性和可维护性。
算法流程图

【范例8-4】 求区间[100, 200]内10 个随机整数中的最大数、最小数。
输出max,min 结束
用传统流程图表示三种基本结构
1、顺序结构
A
2、选择结构
不成立 条件? A B 成立
B
用传统流程图表示三种基本结构
3、循环结构
A
不成立 条件? 成立
A条件?成立不成立当型循环
直到型循环
开始 输入n的值
流程图的基础
流程图的绘制
流程图中的元素及含义
流程图主要用两种:传统流程图和N-S流程图。 1.传统流程图
起止框
输入/输出框
处理框
判断框
流程线
连接符
2、N-S流程图
P成立? A A B A B 是 否 当P成立 A A 当P成立
处理
顺序结构元素
选择结构元素
当型循环结构元素
直到型循环结构元素
流程图的绘制
2. 将1到100之间 能用3或5整 除的数打印 出来。
开始
i赋初值为1 N
i<=100?
Y
i赋初值为1 i<=100?
N
i能被3或5整 除? Y
i能被3或5整 除? T 打印i i++
用N-S图表示
F
打印i
i++ 结束 用流程图表示
1.使用word自带的流程图绘图工具 2、使用Visio绘制工具
如何表示一个算法
用自然语言表示算法 用流程图表示算法 用传统流程图表示三种基本结构 用N-S图表示算法
用伪代码表示算法
用计算机语言表示算法
用流程图表示算法
流程图相对于自然语言来说更直观形象,易于理解简洁 直观。 一个流程图包括以下几部分:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 输人一个数到变量 a ,输出它的绝对值。
(要求用单分支和双分支结构分别设计算法) 单分支结构算法:
(1) 输入任意数并赋值给变量 a ;
(2) 判断a 是否小于0,如果a 小于0 ,取a 的相反数; (3) 输出a 。
双分支结构算法:
(1) 输人任意数并赋值给变量 a ;
(2) 判断a 是否小于0,如果a 小于0则输出a 的相反数,否则输出 a 。
2. 最值问题:
max-x, i —1
i -i+1
/输出乜/
/ 输出
a /
单分支结构算法流程图
双分支结构算法流程医
(1 )求输人的两个数中的最大值。
(开始T
(3)求输入的十个数中的最大值。
「开始
J x 7 /输応
'」/输出b /
■ /输躬
]
(2 )求输人的三个数中的最大值。
3.循环求和(不同的控制循环方法)
1.求输人20个数的和。
(知道循环次数,可以采用循环变量i来控制循环次数)
计数法
3.对输入的数据求和,当所求的和超过100则停止输入并
输出求和结果(设此题中输人的
数皆为正数)。
(没有指出输人数据的具体个
数,且不能依据对输入数据的值
来控制循环,控制循环的关键就
在于对循环体中变量s
的判断)
2.求输入的若干个学生成绩
的和,输入-1表示结束。
(不能确定次数,可以用
输入的数据的值来进行控
标志法
输出a / / 输呼〃箱単b / / 輸匹
输出如下图形:
**********
**********
**********
**********
**********
A,o・o・o・o・
o・ o«o»o»oeo> o»o»o«o»o> o・o・o・o・o・ o ・o・o・o・o・B•o«o»o»c»o •©•o«oeo»o •o ・o・o・o・o •o ・o・o・o・o •o ・o・o・o・o c.・o・o・o・o・o o・o・o・o・o・•o・o・o・o ・o o*o»o«o»o«•oeoooeoeo a o ・o・o・o・o・•o・o・o・o・o
•o»o«o*o»o
o«o*oeo>o«。
