第四章最小拍及纯滞后补偿控制
纯滞后控制技术

1 e T / T 1 e T / T z 1
2、振铃现象及其消除 所谓振铃(Ringing)现象,是指数字控制器的输出u(k) 以1/2采样频率(2T采样周期) 大幅度上下摆动。振铃 现象对系统的输出几乎无影响,但会增加执行机构的磨 损,并影响多参数系统的稳定性。 例:被控对象传递函数为: G p ( s )
常规及复杂控制技术(三)
纯滞后控制技术
主要内容
1、施密斯(Smith)预估控制 2、达林(Dahin)算法
5.3.1 史密斯(Smith)预估控制
在实际生产过程中,大多数工业对象具有较大的纯滞后 时间。对象的纯滞后时间τ对控制系统的控制性能极为不利。 当对象的纯滞后时间τ与对象的时间常数Tc之比, 即τ/ Tc≥0.5时,采用常规的PID控制来克服大纯滞后是很难适应的, 而且还会使控制过程严重超调,稳定性变差。 长期以来,人们对纯滞后对象的控制作了大量的研究。 但在工程实践上有效的方法还是不多。比较有代表性的方法 有大林算法和史密斯预估算法。
给定(蓝)与系统响应(黑)
1.4
1.2
1
0.6 0.4 0.2 0
0.8
0.6
0.4
-0.2 -0.4 -0.6
0.2
0
2
4
6
8
10
12
14
16
18
20
0
0
2
4
6
8
10
12
14
16
18
20
(1)振铃现象的分析
系统的输出Y(z)和数字控制器的输出U(z)间有下列关系: Y(z)=U(z)G(z) 系统的输出Y(z)和输入函数的R(z)之间有下列关系: Y(z)=Ф(z)R(z) 则数字控制器的输出U(z)与输入函数的R(z)之间的关系:
13最少拍无差系统设计

1
2
Tz ( 2 z z ) C ( z ) ( z ) R( z ) 1 2 (1 z )
2
Tz 1 ( 2 z 1 z 2 ) C ( z ) ( z ) R( z ) 1 2 (1 z )
C ( z ) 2Tz 3Tz 4Tz
Φ (z)
R(z) r(t) + e*(t) u*(t) G(z) C(z) c(t)
D(z)
E(z) U(z)
H(s)
GC(s)
D( z )G( z ) C(z) ( z ) 系统的误差传递函数Фe(z) R( z ) 1 D( z )G( z )
为:
E ( z ) R( z ) C ( z ) C(z) e (z) 1 1 ( z ) R( z ) R( z ) R( z )
1 z 1
0
e( ) lim 1 z
z 1
1
1 ( z )R( z ) 0
典型输入Z变换的一般形式为:
A( z ) R( z ) (1 z 1 )q
A( z ) 1 ( z ) 0 e( ) lim1 z 1 q z 1 (1 z )
制时,很难满足要求。 此时,往往从被控对象的特性出发,
直接根据采样系统理论设计控制器,
这种方法称为直接设计法。
直接设计法
假定对象本身是离散化模型或者用 离散化模型表示的连续对象,以采 样理论为基础,以Z变换为工具,在 Z域中直接设计出数字调节器D(z)。
数学工具:差分方程、Z变换
由于D(z)是依照稳定性、准确性和快
E( z) e (z) 1 ( z ) R( z )
计算机控制系统 第四章 最小拍控制与纯滞后补偿

Z
根据题意,输入信号为单位速度输入,即r (t ) = t ,则有:
Φ e ( z ) = (1 − z −1 ) 2
代入式(4-12)求出最小拍控制器为
5.435(1 − 0.5 z −1 )(1 − 0.368z −1 ) D( z ) = (1 − z −1 )(1 + 0.718z −1 )
s ( 0 .5 s + 1)
位速度输入时的最小拍控制器。 解:根据图4-1可求出系统广义被控对象脉冲传递函数
1 − e −Ts 2 ] G( z) = Z[ ⋅ s s (0.5s + 1) 4 = Z [(1 − e −Ts ) 2 ] s ( s + 2) 4 4e −Ts = Z[ 2 ] − Z[ 2 ] s ( s + 2) s ( s + 2) 2 1 1 2 1 1 = Z[ 2 − + ] − Z [e −Ts ( 2 − + )] s s s+2 s s s+2 e − 2T z −1 (1 − z −1 + e 2T z −1 ) = (1 − z −1 )(1 − e − 2T z −1 )
对最小拍控制系统设计的要求是: (1)调节时间最短,即系统跟踪输入信号所需的采样周期数 最少; (2)在采样点处无静差,即对特定的参考输入信号,在达到 稳态后,系统在采样点能精确实现对输入信号的跟踪; (3)设计出来的数字控制器必须是物理上可以实现的; (4)闭环系统必须是稳定的。
一、最小拍闭环脉冲传递函数的确定 首先根据对控制系统性能指标的要求和其他约束条件, Φ (z 构造系统的闭环脉冲传递函数 。) 最小拍控制系统的设计要求是对特定的参考输入信号, 在系统达到稳态后,系统在采样点处静差为零。根据此约束条 件可以构造出系统的误差脉冲传递函数 Φ e (z )。典型计算机控制 系统结构图如图4-1所示。
纯滞后控制技术

史密斯预估控制原理
r(t)
+ -
e(t)
u(t)
y(t)
D(s)
G p ( s )e s
图5.3.1 带纯滞后环节的控制系统 D(s) 表示调节器(控制器)的传递函数; Gp(s) e-τs 表示被控对象的传递函数; Gp(s) 为被控对象中不包含纯滞后部分的传递函数; e -τs 为被控对象纯滞后部分的传递函数。
其中:C
1
1
1 1 (T1e T / T2 T2 e 1 / T1 ) (T1e T / T1 T2 e T / T2 ) C 2 e T (1 / T1 1 / T2 ) T2 T1 T2 T1
N 1
( z) z
可以得到达林算法的数字控制器为:
(4)计算控制器的输出 u(k) 当控制器采用 PID 控制算法时,则
u(k ) u(k 1) u(k )
其中
u(k ) K P [e2 (k ) e2 (k 1)] K I e2 (k ) K D [e2 (k ) 2e2 (k 1) e2 (k 2)]
1 e T / T 1 e T / T z 1
2、振铃现象及其消除 所谓振铃(Ringing)现象,是指数字控制器的输出u(k) 以1/2采样频率(2T采样周期) 大幅度上下摆动。振铃 现象对系统的输出几乎无影响,但会增加执行机构的磨 损,并影响多参数系统的稳定性。 例:被控对象传递函数为: G p ( s )
(2)二阶惯性环节的达林算法 当被控对象为带纯滞后的二阶惯性环节时
Ke s G p (s) (1 T1 s )(1 T2 s )
1 e Ts Ke s Kz N 1 (C1 C 2 z 1 ) G( z) Z s (1 T1 s )(1 T2 s ) (1 e T / T1 z 1 )(1 e T / T2 z 1 )
纯滞后控制实验报告

一、实验目的1. 理解纯滞后控制系统的概念及其在工业控制系统中的应用。
2. 掌握大林算法在纯滞后控制系统中的应用原理。
3. 通过实验验证大林算法在纯滞后控制系统中的控制效果。
二、实验原理1. 纯滞后控制系统:纯滞后控制系统是指被控对象具有纯滞后特性,即输入信号到输出信号的传递过程中存在一定的时间延迟。
这种时间延迟会使得控制作用不及时,从而影响系统的稳定性和动态性能。
2. 大林算法:大林算法是一种针对纯滞后控制系统的控制策略,其基本思想是在设计闭环控制系统时,采用一阶惯性环节代替最少拍多项式,并在闭环控制系统中引入与被控对象相同的纯滞后环节,以补偿系统的滞后特性。
三、实验设备1. MATLAB 6.5软件一套2. 个人PC机一台四、实验步骤1. 设计实验模型:根据实验要求,设计一个具有纯滞后特性的被控对象模型,并确定其参数。
2. 构建大林算法控制器:根据大林算法的原理,设计一个大林算法控制器,并确定其参数。
3. 进行仿真实验:在MATLAB软件中搭建实验平台,将设计的被控对象模型和大林算法控制器进行联接,进行仿真实验。
4. 分析实验结果:观察实验过程中系统的动态性能,分析大林算法在纯滞后控制系统中的应用效果。
五、实验结果与分析1. 实验结果(1)无控制策略:在无控制策略的情况下,被控对象的输出信号存在较大的超调和振荡,系统稳定性较差。
(2)大林算法控制:在采用大林算法控制的情况下,被控对象的输出信号超调量明显减小,振荡幅度减小,系统稳定性得到提高。
2. 分析(1)无控制策略:由于被控对象具有纯滞后特性,系统动态性能较差,导致输出信号存在较大超调和振荡。
(2)大林算法控制:大林算法通过引入与被控对象相同的纯滞后环节,有效补偿了系统的滞后特性,使得控制作用更加及时,从而提高了系统的动态性能和稳定性。
六、实验结论1. 纯滞后控制系统在实际工业生产中普遍存在,对系统的稳定性、动态性能和抗干扰能力具有较大影响。
计算机控制技术清华出版社第四章纯滞后控制

(2)施密斯预估控制原理是:与D(s)并接一补偿环节,用来
补偿被控制对象中的纯滞后部分。这个补偿环节称为预估器,
其传递函数为
G P ( s,)(τ1为 纯e 滞s )后时间。
图4-23 带施密斯预估器的控制系统
由施密斯预估器和调节器D(s)组成的补偿回路称为纯滞后补
偿器,其传递函数为
D
'
(s)
1
D
0.221z 3
G(z) Z
s
4s 1 1 e1/4 z1 1 0.779z1
(z)
Z
1 eTs
s
e s T s
1
z2 (1 e1/ 2τ )z1 1 e1/ 2 z1
1
0.393z 3 0.607z1
D(z)
(1
e1
(1 e1 2 )(1 e1 4 z1) 4 ) 1 e1 2 z1 (1 e1
u(k ) u(k 1) u(k )
u(k 1) K P e2 (k ) e2 (k 1) K I e2 (k ) K D e2 (k ) 2e2 (k 1) e2 (k 2)
4.4.2 达林(Dahlin)算法
对于具有纯滞后的控制系统,比如热工或化工 过程,由于滞后的存在,容易引起系统超调和持续 震荡。对这些系统的调节,快速性是次要的,而对 稳定性、不产生超调的要求却是主要的。本节介绍 能满足这些性能指标的一种直接设计数字控制器的 方法—达林算法。
U(z) 中含有单位圆内靠近 z = -1 处的极点(称 为振铃极点),且该极点越靠近 z=-1 ,振幅就越 大。
U(z) (z) R(z) G(z)
U (z) u(z)R(z)
u(z)
(z) G(z)
最小拍控制详解

例3 对于一阶对象(T=1)
0.5z 1 G(z) 1 0.5z1
讨论按速度输入设计的最少拍系统对不同输入的响应。 解 若选择单位速度输入的最少拍控制器,得数字控制器为
经采样(T=l)和零阶保持,试求其对于单位阶跃输入的最
少拍控制器。
解:(1)广义被控对象 G(z)
G(z)
1 eTs
Z
s
2.1
s
2
(
s
1.252)
0.265z1(1 2.78z1 )(1 0.2z1 ) (1 z1 )2 (1 0.286z 1 )
广义被控对象零极点的分布:
圆外极点 无 ,
2020/12/31
6
取 M p ,则一定能保证
e
lim(
z1
z
1)e
(
z
)
R(
z
)
lim(1 z1
z1 )(1
z1 )M
F ( z ) A( z )
(1
z1 ) p
0
其中:F(z) a0 a1z1 a2z2 aqzq
✓ 系统的快速性 要求系统的误差函数应在最短时间内趋近于零。
(z)
z (r1) (b1z 1 b2z 2 bp z e (z) (1 z1 ) p F2 (z)
p
)F1 ( z )
•对不稳定的广义被控对象 G(z)
(z)
z(r1) (b1z1 b2z2 bp z p )(1 1 )(1 2 )(1 e (z) (1 z1 ) p (1 1 )(1 2 )(1 i )F2(z)
统闭环脉冲传递函数(或误差脉冲传递函数)的结构。
2020/12/31
3
1.闭环脉冲传递函数的结构设计
计算机控制系统作业参考答案
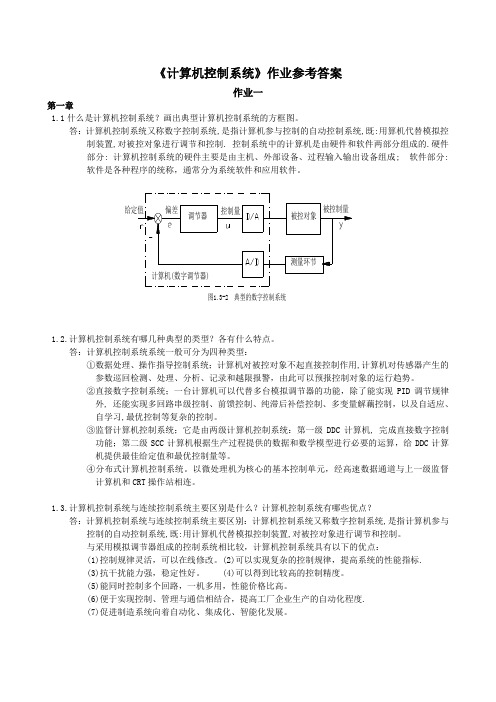
《计算机控制系统》作业参考答案作业一第一章1.1什么是计算机控制系统?画出典型计算机控制系统的方框图。
答:计算机控制系统又称数字控制系统,是指计算机参与控制的自动控制系统,既:用算机代替模拟控制装置,对被控对象进行调节和控制. 控制系统中的计算机是由硬件和软件两部分组成的.硬件部分: 计算机控制系统的硬件主要是由主机、外部设备、过程输入输出设备组成; 软件部分: 软件是各种程序的统称,通常分为系统软件和应用软件。
图1.3-2 典型的数字控制系统1.2.计算机控制系统有哪几种典型的类型?各有什么特点。
答:计算机控制系统系统一般可分为四种类型:①数据处理、操作指导控制系统;计算机对被控对象不起直接控制作用,计算机对传感器产生的参数巡回检测、处理、分析、记录和越限报警,由此可以预报控制对象的运行趋势。
②直接数字控制系统;一台计算机可以代替多台模拟调节器的功能,除了能实现PID调节规律外, 还能实现多回路串级控制、前馈控制、纯滞后补偿控制、多变量解藕控制,以及自适应、自学习,最优控制等复杂的控制。
③监督计算机控制系统;它是由两级计算机控制系统:第一级DDC计算机, 完成直接数字控制功能;第二级SCC计算机根据生产过程提供的数据和数学模型进行必要的运算,给DDC计算机提供最佳给定值和最优控制量等。
④分布式计算机控制系统。
以微处理机为核心的基本控制单元,经高速数据通道与上一级监督计算机和CRT操作站相连。
1.3.计算机控制系统与连续控制系统主要区别是什么?计算机控制系统有哪些优点?答:计算机控制系统与连续控制系统主要区别:计算机控制系统又称数字控制系统,是指计算机参与控制的自动控制系统,既:用计算机代替模拟控制装置,对被控对象进行调节和控制。
与采用模拟调节器组成的控制系统相比较,计算机控制系统具有以下的优点:(1)控制规律灵活,可以在线修改。
(2)可以实现复杂的控制规律,提高系统的性能指标.(3)抗干扰能力强,稳定性好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最小拍控制器设计
Smith纯滞后补偿控制算法 Dahlin算法 本章小结
第4章 计算机控制系统的常规控制策略
4.1
数字控制器的直接设计方法
最小拍控制系统设计的要求是:
1.最小拍控制系统设计
1)调节时间最短,即系统跟随输入信号所需的采样周期数最少; 2)在采样点处无静差,即特定的参考输入信号,在达到稳态后,
e
D( s)
u * (t )
T U ( z)
E( z)
1 e Ts s
最少拍控制系统的误差脉冲传递函数 ( z)为
e( z )
图4-11 典型计算机控制系统结构图
E ( z ) R( z ) Y ( z ) 1 1 ( z ) R( z ) R( z ) 1 D( z )G( z )
(4-17)
1 q 由于A(z)不包含的 (1 z 1 ) 因子,因此稳态误差为零的条件是 e ( z)含有 (1 z ) 则 e ( z) 可为下列形式: e ( z) (1 z 1 )q F ( z) (4-18)
第4章 计算机控制系统的常规控制策略 这里 F ( z )为 z 1的有限多项式,系数待定,即
( z ) D( z )G ( z ) 1 D( z )G ( z )
(4-22)
由此可以得到最少拍数字控制器为
D( z ) ( z ) G ( z )[1 ( z )]
(4-23) (4-24)
或
D( z )
1 e ( z) G ( z ) e ( z )
将 G ( z ) 、 e ( z) 和 ( z ) 代入式(4-23)或式(4-24)中即可求出 最小拍控制器 D ( z ) 。对于三种典型输入信号,最小拍控制系统的 ( z) e 和最小拍控制器D ( z )汇总于表4-3中。
第4章 计算机控制系统的常规控制策略
采样周期 T 0.5s ,试设计在单位速度输入时的最小拍控制器 D ( z ) 解:根据图4-11可求出系统的广义被控对象脉冲传递函数
1 eTs 2 2 G( z) Z [ ] (1 z 1 ) Z [ 2 ] s s(0.5s 1) s (0.5s 1) e2T z 1 (1 z 1 e2T z 1 ) 0.368 z 1 (1 0.718z 1 ) 1 2T 1 (1 z )(1 e z ) (1 z 1 )(1 0.368 z 1 )
第4章 计算机控制系统的常规控制策略
它们都可以表示为
R( z )
A( z ) (1 z 1 )q
(4-15)
式中, A( z )是不包括 (1 z 1 ) 的 z 1 多项式; q 为正整数 ,对于不同的输入函数,只是 q 不同而已,一般只讨论 q 1, 2,3 的情况。 将式(4-15)代入式(4-14),得
,
根据题意,输入信号为单位速度输入,即
r (t ) t
,则有 e ( z) (1 z 1 )2
e ( z) (1 z 1 )q
那么期望的闭环脉冲传递函数 ( z ) 为
(4-20)
( z) 1 e ( z) 1 (1 z 1 )q
(4-21)
第4章 计算机控制系统的常规控制策略
2) 最小拍控制器的确定
由式(4-13)求出图4-11所示的计算机控制系统的闭环脉冲传递函数为
第4章 计算机控制系统的常规控制策略
表4-3 三种典型输入信号的最小拍控制器
输入信号
单位阶跃
单位速度
单位加速度
r (k )
偏差脉冲传递函数
e ( z )
闭环脉冲传递函数
1 z 1
2 ( 1 z 1 )
3 ( 1 z 1 )
( z )
最小拍控制器
z 1
2 z 1 z 2
(4-13)
系统输出的偏差为
E( z) e ( z) R( z)
(4-14)
对于一般控制系统的三种典型输入函数:
1 T 2 z 1 (1 z 1 ) 单位阶跃输入: r (t ) t 2, R( z ) 2 2(1 z 1 )3 1 单位速度输入: r (t ) 1, R( z ) 1 z 1 1 Tz 单位加速度输入: r (t ) t , R( z ) (1 z 1 )2
A( z ) E ( z) e ( z) (1 z 1 ) q
根据z变换的终值定理,可以求出系统的稳态误差为
(4-16)
e() lim e(k ) lim(1 z 1 ) E ( z ) lim(1 z 1 ) e ( z)
z 1 z 1 z 1
A( z ) (1 z 1 )q
系统在采样点能精确地实现对输入信号的跟踪;
3)设计出来的数字控制器必须是物理可实现的; 4)闭环系统必须是稳定的。
第4章 计算机控制系统的常规控制策略
1.最小拍控制系统设计
r (t )
( z) G( z) R( z ) e* (t )
T
Y (z) G p ( s)
T y (t )
1) 最小拍闭环脉冲传递函数
3z 1 3z 2 z 3
D( z )
1 2 3 1 2 z 1 3 z 3 z z 2z z (1 z 1 )G( z ) (1 z 1 ) 2 G ( z ) (1 z 1 )3 G( z )
2 G ( s ) 【例4-1】 设最小拍控制系统如图4-11所示,被控对象的传递函数 s (0.5s 1)
F ( z) 1 f1z 1 f2 z 2
f n z n
(4-19)
由最小拍控制系统的时间最短约束条件来确定F ( z )的形式。 当取 F ( z ) 1 时,不仅可以简化数字控制器,降低控制器阶数,而 且还可以使 E ( z )的项数最少,调节时间最短。 因此,由式(4-18)和式(4-19)得 e ( z) 为
