衡水中学期中考试
2024届衡水市重点中学物理高三第一学期期中考试试题含解析

2024届衡水市重点中学物理高三第一学期期中考试试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.一、单项选择题:本题共6小题,每小题4分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、将一质量为m的小球靠近墙面整直向上抛出,图甲是向上运动小球的频闪照片,图乙是下降时的频闪照片,O是运动的最高点,甲乙两次闪光频率相同,重力加速度为g,假设小球所受的阻力大小不变,则可估算小球受到的阻力大小约为()A.mg B.13mg C.110mg D.12mg2、如图,静电场中的一条电场线上有M、N两点,箭头代表电场的方向,则()A.M点的电势比N点的低B.M点的场强大小一定比N点的大C.电子在M点的电势能比在N点的低D.电子在M点受到的电场力大小一定比在N点的大3、物体做匀加速直线运动,相继经过两段距离为36m的路程,第一段用时4s,第二段用时2s,则物体的加速度是()A.1.5m/s2B.2m/s2C.3m/s2D.4m/s24、水平传送带被广泛地应用于机场和火车站,用于对旅客的行李进行安全检查。
如图所示为一水平传送带装置示意图,紧绷的传送带AB始终保持恒定速率2m/sv=运行。
旅客把行李无初速度地放在A处,设行李与传送带之间的动摩擦因数0.1μ=,AB间的距离为2m,g取10m/2s.若旅客把行李放到传送带的同时以1m/sv 的恒定速度平行于传送带运动到B处取行李,则A.乘客与行李同时到达B处B.乘客提前0.5s到达B处C.行李提前0.5s到达B处D.若传送带速度再增大,行李能更快到达B处5、某星体可视为均匀球体,半径为R,自转周期为T,其同步卫星的轨道半径为9R。
2023-2024学年河北省衡水市冀州中学高三(上)期中数学试卷【答案版】
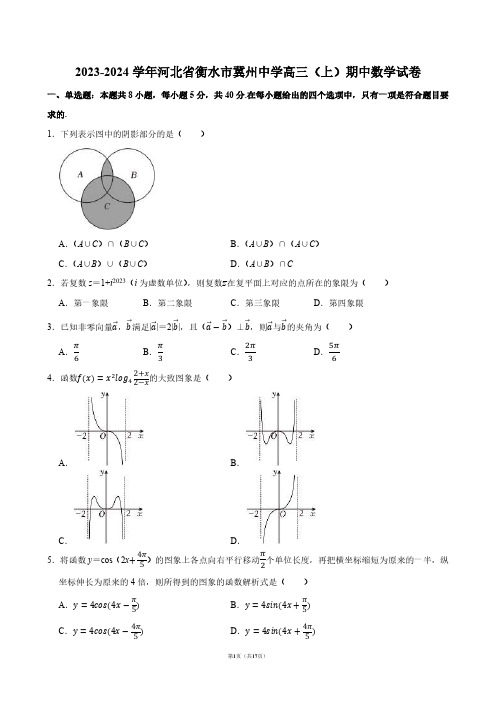
2023-2024学年河北省衡水市冀州中学高三(上)期中数学试卷一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列表示图中的阴影部分的是( )A .(A ∪C )∩(B ∪C ) B .(A ∪B )∩(A ∪C ) C .(A ∪B )∪(B ∪C )D .(A ∪B )∩C2.若复数z =1+i 2023(i 为虚数单位),则复数z 在复平面上对应的点所在的象限为( ) A .第一象限B .第二象限C .第三象限D .第四象限3.已知非零向量a →,b →满足|a →|=2|b →|,且(a →−b →)⊥b →,则a →与b →的夹角为( ) A .π6B .π3C .2π3D .5π64.函数f(x)=x 2log 42+x2−x的大致图象是( )A .B .C .D .5.将函数y =cos (2x +4π5)的图象上各点向右平行移动π2个单位长度,再把横坐标缩短为原来的一半,纵坐标伸长为原来的4倍,则所得到的图象的函数解析式是( ) A .y =4cos(4x −π5)B .y =4sin(4x +π5)C .y =4cos(4x −4π5) D .y =4sin(4x +4π5)6.已知数列{a n }的首项为1,D 是△ABC 边BC 所在直线上一点,且AC →=3(a n +1)AD →−(a n+1−2)AB →,则数列{a n }的通项公式为( ) A .3n ﹣2 B .3n +1﹣2 C .5×(−3)n−1−14D .5×(−3)n −147.已知正方形ABCD 的边长为2,将△ACD 沿AC 翻折到△ACD ′的位置,得到四面体D ′﹣ABC ,在翻折过程中,点D ′始终位于△ABC 所在平面的同一侧,且BD ′的最小值为√2,则点D 的运动轨迹的长度为( ) A .πB .2πC .2√2π3D .4√2π38.已知三角形ABC 中,BC =3,角A 的平分线交BC 于点D ,若BDDC =12,则三角形ABC 面积的最大值为( ) A .1B .2C .3D .4二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分. 9.下列命题中正确的是( )A .若a >0,b >0,a +b =1,则a 2+b 2≥12B .命题:“∀x ≥0,x 2≥0”的否定是“∃x <0,x 2<0”C .已知函数f (2x +1)的定义域为[﹣1,1],则函数f (x )的定义域为[﹣1,3]D .若函数f(√x −1)=x −3√x ,则f (x )=x 2﹣x ﹣2(x ≥﹣1)10.已知A ,B 是函数f(x)=tan(3x +π6)的图象与直线y =3的两个交点,则下列结论正确的是( )A .|AB|min =π3B .f (x )的定义域为{x ∈R|x ≠3kπ+3π2,k ∈Z} C .f (x )在区间(0,π6)单调递增D .f (x )的图象的对称中心为点(kπ6−π18,0),k ∈Z 11.已知数列{a n }的前n 项的和为S n ,S 1=4,S 2=8,4S n =S n +1+4S n ﹣1(n ≥2),则下列说法正确的是( ) A .S 4=32B .{a n +1﹣2a n }是等比数列C .a n ={4,n =12n+1−4,n ≥2D .a n ={4,n =12n,n ≥212.设函数f (x )的定义域为R ,且满足f (x )=f (2﹣x ),f (x )=﹣f (x +2),当x ∈(0,1]时,f (x )=e x ﹣2x ﹣1,则( ) A .f (x )是奇函数 B .f (2023)=e ﹣3C .f (x )的值域是[1﹣2ln 2,2ln 2﹣1]D .方程f (x )=3﹣e 在区间[0,2024]内恰有1518个实数解 三、填空题:本题共4小题,每小题5分,共20分.13.已知等差数列{a n }满足a 1=4,a 3+a 5=a 42+1,则a 7= .14.已知函数f (x )的定义域为(﹣∞,+∞),y =f (x )+e x 为偶函数,y =f (x )﹣2e x 为奇函数,则f (x )的最小值为 .15.在三棱锥A ﹣BCD 中,∠ABD =∠ABC =60°,BC =BD =2,AB =4,则三棱锥A ﹣BCD 外接球的表面积为 .16.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知c =4,C =60°,BD →=DC →2+DA →,则DA →⋅DB→的最大值为 .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知数列{a n }为等比数列,在数列{b n }中,b 1=2,b 2=4,且a n +1=a n (b n +1﹣b n ). (1)求数列{b n }的通项公式;(2)若a 1=1,c n =a n +b n ,求数列{c n }的前n 项和S n . 18.(12分)已知α∈(0,π),sinα+cosα=√62,且cos α<sin α.(1)求角α的大小;(2)已知函数f (x )=sin2x +2sin 2(x +α),若f (x )在区间(0,m )上有极大值,无极小值,求m 的取值范围.19.(12分)已知函数f(x)=−2a 2lnx +12x 2+ax(a ∈R).(1)当a =1时,求曲线y =f (x )在(1,f (1))处的切线方程; (2)讨论函数f (x )的单调性.20.(12分)已知数列{a n }的前n 项和为S n ,a 1=√2,a n >0,a n +1•(S n +1+S n )=2. (1)求S n ;(2)求1S 1+S 2+1S 2+S 3+⋯+1S n +S n+1.21.(12分)如图,有一景区的平面图是一个半圆形,其中O 为圆心,直径AB 的长为2km ,C ,D 两点在半圆弧上,且BC =CD ,设∠COB =θ. (1)当θ=π6时,求四边形ABCD 的面积;(2)若要在景区内铺设一条由线段AB ,BC ,CD 和DA 组成的观光道路,则当θ为何值时,观光道路的总长l 最长,并求出l 的最大值.22.(12分)已知函数f (x )=sin 3x cos x ,f ′(x )为f (x )的导函数. (1)求f (x )在(0,2π)上的极值;(2)设n ∈N *,求证:sin 2x •sin 22x •sin 24x …sin 22nx ≤3n4n .2023-2024学年河北省衡水市冀州中学高三(上)期中数学试卷参考答案与试题解析一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列表示图中的阴影部分的是( )A .(A ∪C )∩(B ∪C ) B .(A ∪B )∩(A ∪C ) C .(A ∪B )∪(B ∪C )D .(A ∪B )∩C解:图中阴影部分表示元素满足:是C 中的元素,或者是A 与B 的公共元素, 故可以表示为C ∪(A ∩B ), 也可以表示为:(A ∪C )∩(B ∪C ), 结合选项可知应为:(A ∪C )∩(B ∪C ). 故选:A .2.若复数z =1+i 2023(i 为虚数单位),则复数z 在复平面上对应的点所在的象限为( ) A .第一象限B .第二象限C .第三象限D .第四象限解:因为z =1+i 2023=1﹣i ,所以z =1+i 在复平面上对应的点为(1,1),该点在第一象限. 故选:A .3.已知非零向量a →,b →满足|a →|=2|b →|,且(a →−b →)⊥b →,则a →与b →的夹角为( ) A .π6B .π3C .2π3D .5π6解:∵(a →−b →)⊥b →,∴(a →−b →)⋅b →=a →⋅b →−b →2=|a|→|b|→cos <a →,b →>−b →2=0, ∴cos <a →,b →>=|b|→2|a|→|b|→=|b|→22|b|→2=12,∵<a →,b →>∈[0,π],∴<a →,b →>=π3.故选:B . 4.函数f(x)=x 2log 42+x2−x的大致图象是( )A .B .C .D . 解:方法一:因为2+x2−x >0,即(x +2)•(x ﹣2)<0,所以﹣2<x <2,所以函数f(x)=x 2log 42+x2−x的定义域为(﹣2,2),关于原点对称, 又f(−x)=(−x)2log 42−x2+x=−f(x),所以函数f (x )是奇函数,其图象关于原点对称, 故排除B ,C ; 当x ∈(0,2)时,2+x 2−x>1,即log 42+x2−x >0,因此f (x )>0,故排除A .故选:D .方法二:由方法一,知函数f (x )是奇函数,其图象关于原点对称,故排除B ,C ; 又f(1)=12log 23>0,所以排除A .故选:D . 5.将函数y =cos (2x +4π5)的图象上各点向右平行移动π2个单位长度,再把横坐标缩短为原来的一半,纵坐标伸长为原来的4倍,则所得到的图象的函数解析式是( ) A .y =4cos(4x −π5)B .y =4sin(4x +π5)C .y =4cos(4x −4π5) D .y =4sin(4x +4π5) 解:由题意函数y =cos(2x +4π5)的图象上各点向右平移π2个单位长度,得到y =cos(2x −π+4π5)=cos(2x −π5),再把横坐标缩短为原来的一半,得到y =cos(4x −π5),再把纵坐标伸长为原来的4倍,得到y =4cos(4x −π5),考察四个选项知,A 是正确的 故选:A .6.已知数列{a n }的首项为1,D 是△ABC 边BC 所在直线上一点,且AC →=3(a n +1)AD →−(a n+1−2)AB →,则数列{a n }的通项公式为( ) A .3n ﹣2 B .3n +1﹣2 C .5×(−3)n−1−14D .5×(−3)n −14解:依题意,由B ,C ,D 三点共线,可得3(a n +1)﹣(a n +1﹣2)=1,化简整理,可得a n +1=3a n +4, 两边同时加2,可得a n +1+2=3a n +4+2=3(a n +2), ∵a 1+2=3,∴数列{a n +2}是以3为首项,3为公比的等比数列, ∴a n +2=3×3n−1=3n , ∴a n =3n −2,n ∈N *. 故选:A .7.已知正方形ABCD 的边长为2,将△ACD 沿AC 翻折到△ACD ′的位置,得到四面体D ′﹣ABC ,在翻折过程中,点D ′始终位于△ABC 所在平面的同一侧,且BD ′的最小值为√2,则点D 的运动轨迹的长度为( ) A .πB .2πC .2√2π3D .4√2π3解:设方形ABCD 对角线AC 与BD 交于O ,由题意,翻折后BD ′=√2时,△OD ′B 为边长为√2的等边三角形,此时∠D ′OB =π3,若继续翻折BD ′<√2,如下图示BD ′=√2,所以点D 的运动轨迹是以O 为圆心,√2为半径的圆心角为2π3的圆弧,所以点D的运动轨迹的长度为2π3×√2=2√2π3.故选:C.8.已知三角形ABC中,BC=3,角A的平分线交BC于点D,若BDDC=12,则三角形ABC面积的最大值为()A.1B.2C.3D.4解:因为角A的平分线交BC于点D,若BDDC=12,由角平分线的性质可得ABAC=BDDC=12,设AB=x,则AC=2x,BC=3,由余弦定理可得cos A=AB2+AC2−BC22AB⋅AC=5x2−94x2,所以sin A=√(4x2)2−(5x2−9)24x2=√−9x4+90x2−814x2=3√−x4+10x2−94x2,所以S△ABC=12AB•AC•sin A=12•2x2•3√−x4+10x2−94x2=34•√−x4+10x2−9=34•√−(x2−5)2+16≤34•√16=3,当x2=5时,即x=√5时取等号.所以三角形ABC面积的最大值为3.故选:C.二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列命题中正确的是()A.若a>0,b>0,a+b=1,则a2+b2≥12B.命题:“∀x≥0,x2≥0”的否定是“∃x<0,x2<0”C.已知函数f(2x+1)的定义域为[﹣1,1],则函数f(x)的定义域为[﹣1,3]D.若函数f(√x−1)=x−3√x,则f(x)=x2﹣x﹣2(x≥﹣1)解:对于A,由a>0,b>0,a+b=1,得b=1﹣a,且0<a<1,则a2+b2=a2+(1−a)2=2a2−2a+1=2(a−12)2+12,0<a<1,所以当a=12时,a2+b2取到最小值12,所以a2+b2≥12,故A正确;对于B,“∀x≥0,x2≥0”的否定是“∃x≥0,x2<0”,故B错误;对于C,f(2x+1)的定义域为[﹣1,1],设t=2x+1,当x∈[﹣1,1]时,t∈[﹣1,3],故f(x)的定义域为[﹣1,3],C正确;对于D ,令t =√x −1,则√x =t +1,t ≥﹣1,由f(√x −1)=x −3√x ,得f (t )=(t +1)2﹣3(t +1)=t 2﹣t ﹣2,t ≥﹣1, 所以函数f (x )的表达式为f (x )=x 2﹣x ﹣2,x ≥﹣1,D 正确. 故选:ACD .10.已知A ,B 是函数f(x)=tan(3x +π6)的图象与直线y =3的两个交点,则下列结论正确的是( )A .|AB|min =π3B .f (x )的定义域为{x ∈R|x ≠3kπ+3π2,k ∈Z} C .f (x )在区间(0,π6)单调递增D .f (x )的图象的对称中心为点(kπ6−π18,0),k ∈Z 解:因为A ,B 是函数f(x)=tan(3x +π6)的图象与直线y =3的交点,所以|AB |的最小值为函数f (x )的最小正周期,T =π3,所以|AB|min =π3,故A 正确;令3x +π6≠π2+kπ,k ∈Z ,解得x ≠π9+kπ3,k ∈Z ,所以f (x )的定义域为{x ∈R|x ≠π9+kπ3,k ∈Z},故B 错;因为x ∈(0,π6),所以3x +π6∈(π6,2π3),因为函数y =tan x 在(π6,2π3)上不单调,所以函数f (x )在(0,π6)上不单调,故C 错;令3x +π6=kπ2,k ∈Z ,解得x =−π18+kπ6,k ∈Z ,所以f (x )的对称中心为点(−π18+kπ6,0),k ∈Z ,故D 正确. 故选:AD .11.已知数列{a n }的前n 项的和为S n ,S 1=4,S 2=8,4S n =S n +1+4S n ﹣1(n ≥2),则下列说法正确的是( ) A .S 4=32B .{a n +1﹣2a n }是等比数列C .a n ={4,n =12n+1−4,n ≥2D .a n ={4,n =12n ,n ≥2解:由题意可知S 3=4S 2﹣4S 1=16,所以S 4=4S 3﹣4S 2=32,故A 正确; 因为a 3﹣2a 2=S 3﹣S 2﹣2(S 2﹣S 1)=S 3﹣3S 2+2S 1=0, 所以{a n +1﹣2a n }不能是等比数列,故B 错误;因为4S n =S n +1+4S n ﹣1(n ≥2),即S n +1=4S n ﹣4S n ﹣1(n ≥2),所以S n+1−2S n =21(S n −2S n−1)=22(S n−1−2S n−2)=⋯=2n (S 2﹣2S 1)=0, 所以S n +1﹣2S n =0,即S n+1S n=2,又因为S 2S 1=84=2,所以{S n }是以2为首项,4为公比的等比数列,所以S n =4×2n−1=2n+1,所以a 1=S 1=4,a n =S n −S n−1=2n+1−2n =2n (n ≥2), 即a n ={4,n =12n ,n ≥2,故选项C 错误;D 正确.故选:AD .12.设函数f (x )的定义域为R ,且满足f (x )=f (2﹣x ),f (x )=﹣f (x +2),当x ∈(0,1]时,f (x )=e x ﹣2x ﹣1,则( ) A .f (x )是奇函数 B .f (2023)=e ﹣3C .f (x )的值域是[1﹣2ln 2,2ln 2﹣1]D .方程f (x )=3﹣e 在区间[0,2024]内恰有1518个实数解解:函数f (x )的定义域为R ,关于原点对称,因为f (x )=f (2﹣x ),所以f (﹣x )=f (x +2), 又因为f (x +2)=﹣f (x ),所以f (﹣x )=﹣f (x ),所以f (x )是奇函数,A 正确; 由f (x )=﹣f (x +2),得f (x +4)=﹣f (x +2)=f (x ),所以f (x )以4为周期,因为f (2023)=f (4×506﹣1)=f (﹣1)=﹣f (1)=3﹣e ,所以f (2023)=3﹣e ,故B 错误; 因为当x ∈(0,1]时,f (x )=e x ﹣2x ﹣1,所以f ′(x )=e x ﹣2, 当0<x <ln 2时,f ′(x )<0,当ln 2<x ≤1时,f ′(x )>0, 所以f (x )在(0,ln 2)上单调递减,在(ln 2,1)上单调递增,所以f (x )min =f (ln 2)=1﹣2ln 2,又f (1)=e ﹣3<0,所以f (x )∈[1﹣2ln 2,0). 因为f (x )为奇函数,所以当x ∈[﹣1,0]时,f (x )∈[0,2ln 2﹣1],因为f (x )的图象关于直线x =1对称,所以当x ∈[﹣1,3]时,f (x )∈[1﹣2ln 2,2ln 2﹣1], 因为f (x )的周期为4,所以当x ∈R 时,f (x )∈[1﹣2ln 2,2ln 2﹣1],故C 正确; 方程f (x )=3﹣e 的解的个数,即y =f (x )的图象与y =3﹣e 的图象交点个数. 因为y =f (x )的周期为4,且当x ∈[0,4]时,y =f (x )与y =3﹣e 有3个交点, 所以当x ∈[0,2024]时,y =f (x )与y =3﹣e 有20244×3=1518个交点,故D 正确.故选:ACD.三、填空题:本题共4小题,每小题5分,共20分.13.已知等差数列{a n}满足a1=4,a3+a5=a42+1,则a7=﹣2.解:在等差数列{a n}中,∵等差数列{a n}满足a1=4,a3+a5=a42+1,又a3+a5=2a4,∴a42−2a4+1=0,解得a4=1,又a1=4,而a1+a7=2a4,解得a7=﹣2.故答案为:﹣2.14.已知函数f(x)的定义域为(﹣∞,+∞),y=f(x)+e x为偶函数,y=f(x)﹣2e x为奇函数,则f(x)的最小值为√3.解:y=f(x)+e x是偶函数,所以f(﹣x)+e﹣x=f(x)+e x,y=f(x)﹣2e x是奇函数,所以f(﹣x)﹣2e﹣x=﹣f(x)+2e x,两式联立解得f(x)=12e x+32e−x,由基本不等式得f(x)=12e x+32e−x≥12×2√e x⋅3e−x=√3,当且仅当e x=3e﹣x,即x=ln√3时,等号成立,因此f(x)的最小值是√3.故答案为:√3.15.在三棱锥A﹣BCD中,∠ABD=∠ABC=60°,BC=BD=2,AB=4,则三棱锥A﹣BCD外接球的表面积为16 π.解:由∠ABD=∠ABC=60°,BC=BD=2,AB=4,根据余弦定理可得 AC =AD =2√3, 则 AC ⊥BC ,AD ⊥BD ,取AB 中点O ,则OA =OB =OC =OD , 则三棱锥A ﹣BCD 外接球的直径为AB =4, 故三棱锥A ﹣BCD 外接球的表面积为4π⋅(AB 2)2=16π. 故答案为:16π.16.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知c =4,C =60°,BD →=DC→2+DA →,则DA →⋅DB→的最大值为 −8825. 解:由题意,BD →=DC →2+DA →=32DC →+CA →=−32CD →+CA →,BD →=BC →+CD →,消去BD →得:CD →=25(CA →+CB →),因为DA →⋅DB →=(DC →+CA →)⋅(DC →+CB →)=(35CA →−25CB →)⋅(35CB →−25CA →)=−625(a 2+b 2)+1325abcos60°,由cos60°=a 2+b 2−162ab,得a 2+b 2=ab +16≥2ab ,当且仅当a =b 时等号成立,所以0<ab ≤16, 所以原式=−625(16+ab)+1350ab =150ab −9625≤−8825. 故答案为:−8825.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知数列{a n }为等比数列,在数列{b n }中,b 1=2,b 2=4,且a n +1=a n (b n +1﹣b n ). (1)求数列{b n }的通项公式;(2)若a 1=1,c n =a n +b n ,求数列{c n }的前n 项和S n . 解:(1)设数列{a n }的公比为q , 由a n +1=a n (b n +1﹣b n ),知b n +1﹣b n =a n+1a n=q ,为常数,所以数列{b n }是等差数列,设其公差为d , 由b 1=2,b 2=4,知d =2,所以b n =2+(n ﹣1)×2=2n ,且q =2, 故数列{b n }的通项公式为b n =2n . (2)由(1)知a n+1a n=2,若a 1=1,则a n =2•2n ﹣1=2n , 所以c n =a n +b n =2n +2n ,所以S n =(21+2)+(22+4)+(23+6)+…+(2n+2n )=(21+22+23+ (2))+(2+4+6+…+2n )=2−2n⋅21−2+n(2+2n)2=2n +1﹣2+n 2+n . 18.(12分)已知α∈(0,π),sinα+cosα=√62,且cos α<sin α.(1)求角α的大小;(2)已知函数f (x )=sin2x +2sin 2(x +α),若f (x )在区间(0,m )上有极大值,无极小值,求m 的取值范围.解:(1)因为sinα+cosα=√62,所以(sinα+cosα)2=1+sin2α=32,则sin2α=12,因为α∈(0,π), 所以2α∈(0,2π), 则2α=π6或2α=5π6,解得α=π12或α=5π12, 因为cos α<sin α, 所以α=5π12; (2)由(1)知f(x)=sin2x +2sin 2(x +5π12)=sin2x +1−cos(2x +5π6) =32sin2x +√32cos2x +1=√3sin(2x +π6)+1, 当x ∈(0,m )时,2x +π6∈(π6,2m +π6),因为f(x)在区间(0,m)上有极大(最大)值,无极小(最小)值,所以π2<2m+π6≤3π2,解得π6<m≤2π3,则m的取值范围为(π6,2π3].19.(12分)已知函数f(x)=−2a2lnx+12x2+ax(a∈R).(1)当a=1时,求曲线y=f(x)在(1,f(1))处的切线方程;(2)讨论函数f(x)的单调性.解:(1)当a=1时,f(x)=−2lnx+12x2+x,f′(x)=−2x+x+1,f′(1)=−2+1+1=0,f(1)=32,所以曲线y=f(x)在(1,f(1))处的切线方程为y=3 2.(2)f′(x)=x2+ax−2a2x=(x+2a)(x−a)x,①当a=0时,f′(x)=x>0,所以函数在(0,+∞)上单调递增;②当a>0时,令f′(x)=0,则x1=﹣2a(舍)或x2=a,f′(x)<0,0<x<a,当x∈(0,a)时,函数f(x)单调递减;f′(x)>0,x>a,当x∈(a,+∞)时,函数f(x)单调递增.③当a<0时,令f′(x)=0,则x1=﹣2a或x2=a(舍),f′(x)<0,0<x<﹣2a,当x∈(0,﹣2a)时,函数f(x)单调递减;f′(x)>0,x>﹣2a,当x∈(﹣2a,+∞)时,函数f(x)单调递增.综上所述:当a=0时,函数在(0,+∞)上单调递增;当a>0时,函数f(x)在(0,a)上单调递减,函数f(x)在(a,+∞)上单调递增;当a<0时,函数f(x)在(0,﹣2a)上单调递减,函数f(x)在(﹣2a,+∞)上单调递增.20.(12分)已知数列{a n}的前n项和为S n,a1=√2,a n>0,a n+1•(S n+1+S n)=2.(1)求S n;(2)求1S1+S2+1S2+S3+⋯+1S n+S n+1.解:(1)a1=√2,a n>0,a n+1•(S n+1+S n)=2,可得(S n+1﹣S n)(S n+1+S n)=2,可得S n+12﹣S n2=2,即数列{S n2}为首项为2,公差为2的等差数列,可得S n2=2+2(n﹣1)=2n,由a n>0,可得S n=√2n;(2)1S n+S n+1=√2n+√2(n+1)=√22(√n+√n+1)=√22(√n+1−√n),即有1S1+S2+1S2+S3+⋯+1S n+S n+1=√22(√2−1+√3−√2+2−√3+⋯+√n+1−√n)=√22(√n+1−1).21.(12分)如图,有一景区的平面图是一个半圆形,其中O为圆心,直径AB的长为2km,C,D两点在半圆弧上,且BC=CD,设∠COB=θ.(1)当θ=π6时,求四边形ABCD的面积;(2)若要在景区内铺设一条由线段AB,BC,CD和DA组成的观光道路,则当θ为何值时,观光道路的总长l最长,并求出l的最大值.解:(1)连结OD,则∠COD=π6,∠AOD=2π3,所以四边形ABCD的面积为S四边形ABCD=S四边形OBCD+S△AOB=2×12×1×1×sinπ6+12×1×1×sin2π3=2+√34(km2);(2)由题意,在△BOC中,∠OBC=π−θ2,由正弦定理得BCsinθ=OBsinπ−θ2=1cosθ2,所以BC=CD=sinθcosθ2=2sinθ2,同理在△AOD中,∠OAD=θ,∠DOA=π﹣2θ,由正弦定理得DAsin(π−2θ)=ODsinθ,所以DA=sin2θsinθ=2cosθ,所以l=2+4sin θ2+2cosθ=2+4sinθ2+2(1−2sin2θ2),0<θ<π2;令t =sin θ2(0<t <√22),所以l =2+4t +2(1−2t 2)=4+4t −4t 2=−4(t −12)2+5,当t =12时,即θ=π3,l 的最大值为5.22.(12分)已知函数f (x )=sin 3x cos x ,f ′(x )为f (x )的导函数. (1)求f (x )在(0,2π)上的极值;(2)设n ∈N *,求证:sin 2x •sin 22x •sin 24x …sin 22nx ≤3n4n .解:(1)已知函数f (x )=sin 3x cos x ,因为f (x +π)=sin 3(x +π)cos (x +π)=sin 3x cos x =f (x ) 所以π是函数f (x )的周期,可得f ′(x )=3sin 2x cos 2x ﹣sin 4x =sin 2x (4cos 2x ﹣1), 当0<x <π3时,f ′(x )>0,f (x )单调递增;当π3<x <2π3时,f ′(x )<0,f (x )单调递减;当2π3<x <π时,f ′(x )>0,f (x )单调递增,所以f (x )在(0,π)上的极小值为−3√316,极大值为3√316, 由周期性可知函数f (x )在(π,2π)上的极小值为−3√316,极大值为3√316, 且函数f (x )在(2π3,π)上单调递增,(π,4π3)上单调递增, 因为f (x )是基本初等函数,一定连续, 所以x =π不是f (x )的极值点, 故f (x )在(0,2π)上的极小值为−3√316,极大值为3√316; (2)证明:易知f (0)=0,由(1)知f(x)=sin 3xcosx =12sin 2xsin2x ∈[−3√316,3√316],所以0≤|sin 2xsin2x|≤3√38,则|sin2x⋅sin22x⋅sin24x⋯sin22n x|=|(sin3x⋅sin32x⋅sin34x⋯sin32n x)2 3|=[|sinx||sin2xsin2x|⋯|sin22n x|]23≤(|sinx|×3√38×⋯×|sin22n x|)23≤[(3√38)n]23=(34)n=3n4n,故sin2x⋅sin22x⋅sin24x⋯⋯sin22n x≤3n4n成立.。
2024届河北衡水中学高一物理第一学期期中复习检测模拟试题含解析

2024届河北衡水中学高一物理第一学期期中复习检测模拟试题注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,有的只有一项符合题目要求,有的有多项符合题目要求。
全部选对的得5分,选对但不全的得3分,有选错的得0分。
1、物体做直线运动,它的加速度随时间变化图象如图所示,已知在t=0s时,物体的速度为零,下列说法正确的是A.t=2s时,物体恰好回到出发点B.t=4s时,物体恰好回到出发点C.t=2s时,物体速度大小为零D.物体做往复运动2、钓鱼岛自古就是我国固有的领土,它到温州的距离为356 km.若某天我国海监船为维护我国对钓鱼岛的主权,早上8:00从温州出发去钓鱼岛巡航,航行了480 km,历时8时20分到达钓鱼岛.下列说法中正确的是( )A.8:00是指时间间隔。
B.8时20分是指时刻。
C.该海监船位移大小为480 km,路程为356 km。
D.尽管海监船比较大,但在研究从温州出发去钓鱼岛巡航的位移时,可以将它看成质点。
3、如图所示为甲、乙两车在平直公路上运动的s—t图象.由图象可知,在t1到t2时间内()A .甲车的速度始终大于乙车的速度B .甲车运动方向有发生变化,而乙车没有C .甲车的平均速度大于乙车的平均速度D .甲乙两车所经过的路程相等4、如图,在水平面上有质量为2kg 的物体,正在向右运动,在运动过程中还受到一水平向左、大小为10N 的拉力F 的作用,则物体所受的合力为(已知物体与地面间的动摩擦因数为,):A .0NB .20N ,向右C .20N ,向左D .10N ,向右5、一质点由静止做匀加速直线运动,加速度大小为1α,经过时间一段后,加速度方向反向、大小变为2α,经过相同时间,恰好回到出发点,则两次的加速度大小之比12:αα为( )A .1:2B .1:3C .1:4D .1:56、如图所示为一物体作匀变速直线运动的速度图象,物体在前2s 内向东运动,则根据图线作出以下判断,正确的是( )A .物体在前2s 内向东运动,后两秒内向西运动B .物体在4s 内的加速度大小为5m/s 2,方向始终向西C .物体在4s 内的加速度大小不变,方向先向西,后向东D .物体在第2s 末距出发点最近7、对于自由落体运动,g =9.8m/s 2,下列说法正确的是( )A .在1s 末、2s 末、3s 末的速度之比是1:3:5B .在第1s 内、第2s 内、第3s 内的位移之比是1:3:5C .在第1s 内、第2s 内、第3s 内的平均速度比是1:4:9D.每经过1s,速度增加9.8m/s8、下列说法正确的是( )A.两个大小不变的共点力,其合力大小随着两力夹角的增大而增大B.合力一定大于任一个分力C.合力有可能小于任一个分力D.物体受5N、8N和12N三个共点力作用有可能作匀速直线运动9、如图所示,有一质量不计的杆AO,长为R,可绕A自由转动.用绳在O点悬挂一个重为G的物体,另一根绳一端系在O点,另一端系在以O点为圆心的圆弧形墙壁上的C点.当点C由图示位置逐渐向上沿圆弧CB移动过程中(保持OA与地面夹角θ不变),下列说法正确的是()A.OC绳所受拉力逐渐变小B.OC绳所受拉力先减小后增大C.OA杆所受弹力逐渐减小D.OA杆所受弹力逐渐先增大后减小10、如下图所示,光滑半球形容器固定在水平面上,O为球心,一质量为m的小滑块,在水平力F的作用下从半球形容器最低点缓慢移近最高点.设滑块所受支持力为F N,则下列判断正确的是()A.F缓慢增大B.F缓慢减小C.F N缓慢增大D.F N缓慢减小二、实验题11、(4分)根据打点记时器打出的纸带,我们可以从纸带上直接测量而得到的物理量是(____)A.时间间隔B.位移C.瞬时速度D.平均速度12、(10分)在做研究匀变速直线运动的实验时,某同学得到一条用打点计时器打下的纸带,并在其上取的a、b、c、d、e、f、g7个记数点,每一箱里两个技术点间还有4个打点计时器打出的点没有画出来,b、c、d、e、f、g到a点的距离依次是d1,d2,d3,d4,d5,d6,打点计时器每打两个点间的时间间隔t=0.02s,他把一把毫米刻度尺放在纸带上。
河北省衡水市第十五中学2024-2025学年九年级上学期期中考试物理试题(含答案)

2024-2025学年九年级上学期期中物理试题总分:60分时间:60分钟一、选择题(共20分每小题2分,共20分)1.下列关于内能、热量、温度的说法中正确的是( )A.热量总是从内能大的物体向内能小的物体传递。
B.两杯水温度相同,内能也一定相同。
C.由于水的比热容大,工厂里的冷却塔常用水作为冷却介质。
D.质量、初温相同的水和煤油放出相同的热量后,水的温度低于煤油的温度。
2.古代人们常用钻木取火,下列情况改变内能方式与其不同的是( )A.甲图:冬天搓手取暖B.乙图:小朋友溜滑梯臀部发热C.丙图:热鸡蛋放在冷水中冷却D.丁图:压缩空气使其内能增大3.对于欧姆定律的公式的理解,以下说法正确的是( )A.导体两端电压越大,通过导体电流越大B.导体电阻越大,通过导体电流越小C.由可知,可知导体电阻与电压成正比,与电流成反比D.导体中的电流是由加在它两端的电压和它的电阻来决定的4.如图所示的电路中,R 是滑动变阻器,L 是小灯泡,闭合开关S ,在确保各元件安全的前提下,把滑动变阻器的滑片P 自左向右移动,下列选项正确的是( )A.电流表示数变大B.电路总电阻变大C.小灯泡L 变亮D.滑动变阻器有分压的作用5.如图所示,电源电压保持不变,电阻R 1∶R 2=3∶8,S 闭合时,甲、乙两处接入电压表;S 断开时,甲、乙两处接入电流表。
则S 闭合时,甲、乙两电压表示数之比U 甲∶U 乙与断开时甲、乙两电流表示数之比I 甲∶I 乙分别是()U I R =U I R =U R I=A.3∶8,1∶1B.3∶8,3∶8C.3∶8,8∶3D,1∶9,8∶36.小灯泡L和定值电阻R接在如图甲所示的电路中,其两者的I-U关系图象如图乙所示,下列说法中正确的是()A.图乙中曲线A表示电阻R的I-U关系图象B.当电源电压为4V时,电流表示数为0.5AC.当电源电压为4V时,小灯泡的电流为0.4AD.当电流表示数为0.25A时,电源电压为2V7.如图所示,电源电压不变,R1是定值电阻,R2是滑动变阻器。
河北衡水中学2023-2024学年高一下学期第二次综合素养评级考试(期中)物理试卷

河北衡水中学2023-2024学年高一下学期第二次综合素养评级考试(期中)物理试卷一、单选题1.火车转弯时,如果铁路弯道的内、外轨一样高,则外轨对轮缘(如左图所示)挤压的弹力F提供了火车转弯的向心力(如图中所示),但是靠这种办法得到向心力,铁轨和车轮极易受损。
在修筑铁路时,弯道处的外轨会略高于内轨(如右图所示),当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的侧向挤压,设此时的速度大小为v,重力加速度为g,以下说法中正确的是()A.该弯道的半径2v Rg =B.当火车质量改变时,规定的行驶速度也将改变C.当火车速率大于v时,外轨将受到轮缘的挤压D.按规定速度行驶时,支持力小于重力2.如图所示,a、b两个小球均从一个倾角为45︒的斜面顶端以不同的初速度向右水平抛出,斜面与一个14圆弧对接,斜面高度与圆弧半径相等,斜面的底端在圆心O的正下方。
则下列说法正确的是()A.a、b两个小球在空中运动时间一定不相同B.a、b两个小球平抛运动末速度方向一定不相同C.若a、b两个小球分别落到斜面和圆弧面等高位置时,速度大小一定不相等D.若小球落到圆弧面上时,其速度方向可能与该处圆的切线垂直3.在我国古代,人们曾经用一种叫“唧筒”的装置进行灭火,这种灭火装置的特点是:简是长筒,下开窍,以絮囊水杆,自窍唧水,既能汲水,又能排水。
简单来说,就是一种特制的水枪。
设灭火时保持水喷出时的速率不变,唧筒与水平面夹角为锐角,则下列说法正确的是()A.灭火时应将“唧筒”的轴线指向着火点B.想要使水达到更远的着火点,必须调小“唧筒”与水平面间的夹角C.想要使水达到更远的着火点,必须调大“唧筒”与水平面间的夹角D.想要使水达到更高的着火点,可以调大“唧筒”与水平面间的夹角4.北斗定位系统中的两颗卫星P、Q绕地球做匀速圆周运动的周期之比为1∶8,则它们运行的线速度之比为()A.2∶1B.1∶2C D.5.2023年11月1日,我国在太原卫星发射中心成功将“天绘五号”卫星发射升空,并顺利进入预定轨道。
2023-2024学年河北省衡水志华实验中学高一(上)期中数学试卷【答案版】

2023-2024学年河北省衡水志华实验中学高一(上)期中数学试卷一、单选题(每小题5分,共40分)1.已知集合A ={x ∈N |﹣3<x <3},B ={﹣5,﹣2,0,2,5},则A ∩B =( ) A .{﹣2,0,2}B .{0,2}C .{0}D .{2}2.下列函数中,与函数y =x +2是同一个函数的是( ) A .y =(√x +2)2B .y =√x 33+2C .y =x 2x+2D .y =√x 2+23.化简二次根式√−8a 3的结果为( ) A .−2a √−2aB .2a √2aC .2a √−2aD .−2a √2a4.已知函数y ={x 2+1(x ≤0)2x(x >0),若f (a )=10,则a 的值是( )A .3或﹣3B .﹣3或5C .﹣3D .3或﹣3或55.已知函数f (x )=x 2+(k ﹣2)x 是[1,+∞)上的增函数,则k 的取值范围为( ) A .(﹣∞,0]B .[0,+∞)C .(﹣∞,1]D .[1,+∞)6.中国清朝数学家李善兰在859年翻译《代数学》中首次将“function ”译做“函数”,沿用至今.为什么这么翻译,书中解释说“凡此变数中函彼变数者,则此为彼之函数.”这个解释说明了函数的内涵:只要有一个法则,使得取值范围中的每一个值x ,有一个确定的y 和它对应就行了,不管这个对应的法则是公式、图象、表格还是其它形式.已知函数f (x )由如下表给出,则f (f (﹣2)+1)的值为( )A .1B .2C .3D .47.已知幂函数f (x )=x α(α∈R )的图象经过点(12,4),且f (a +1)<f (3),则a 的取值范围为( ) A .(﹣∞,2)B .(2,+∞)C .(﹣∞,﹣4)∪(2,+∞)D .(﹣4,2)8.若两个正实数x ,y 满足4x +y =2xy ,且不等式x +y4<m 2+m 有解,则实数m 的取值范围是( ) A .(﹣1,2) B .(﹣∞,﹣1)∪(2,+∞)C .(﹣2,1)D .(﹣∞,﹣2)∪(1,+∞)二、多选题(每小题5分,多选或错选得0分,少选得2分,共20分) 9.下列各命题中为假命题的是( ) A .∀x ∈R ,x ≥0B .如果x <5,则x <2C .∃x ∈R ,x 2≤﹣1D .∀x ∈R ,x 2+1≠010.已知幂函数f(x)=(2a −1)x m2−3m+2,其中a ,m ∈R ,则下列说法正确的是( )A .a =1B .f (x )恒过定点(1,1)C .若m =3时,y =f (x )关于y 轴对称D .若12<m <1时,f (2)<f (1) 11.下列命题是真命题的是( )A .已知函数f (2x +1)的定义域为[﹣1,1],则函数f (x )的定义域为[﹣1,3]B .若y =f (x )是一次函数,满足f (f (x ))=16x +5,则f (x )=4x ﹣1C .函数y =f (x )的图象与y 轴最多有一个交点D .函数y =1x+1在(﹣∞,﹣1)∪(﹣1,+∞)上是单调递减函数 12.定义在R 上的函数f (x ),对任意的x 1,x 2∈(﹣∞,2],都有f(x 2)−f(x 1)x 2−x 1>0,且函数y =f (x +2)为偶函数,则下列说法正确的是( ) A .y =f (x ﹣2)关于直线x =4对称 B .y =f (x )在x ∈(2,+∞)上单调递增 C .f (1)>f (π)D .若f (0)=0,则(x ﹣1)f (x )>0的解集为(﹣∞,0)∪(1,4) 三、填空题(每题5分,共20分)13.已知实数a >0,b >0,化简:a 32b 52√ab= .14.已知函数f (x )=ax 2+bx +c ,x ∈[﹣2a ﹣5,1]是偶函数,则a +2b = .15.如果关于x 的不等式﹣x 2+6ax ﹣3a 2≥0的解集为[x 1,x 2],其中常数a >0,则x 1+x 2+3ax 1x 2的最小值是 .16.已知函数f (x )={ax −x 2,x ≥0−2x ,x <0,①若对任意x 1,x 2∈R ,且x 1≠x 2都有f(x 2)−f(x 1)x 2−x 1<0,则实数a 的取值范围为 ;②若f (x )在[﹣1,t )上的值域为[0,4],则实数t 的取值范围为 . 四、解答题(17题10分,18-22每题12分,共70分) 17.(10分)已知关于x 的不等式2kx 2+kx ﹣1<0. (1)若不等式的解集为(−32,1),求实数k 的值;(2)若不等式的解集为R,求实数k的取值范围.18.(12分)已知集合P={x|3a﹣10≤x<2a+1},Q={x||2x﹣3|≤7}.(1)当a=2时,求P∩(∁R Q);(2)若“x∈P”是“x∈Q”必要不充分条件,求实数a的取值范围.19.(12分)已知函数f(x)=x+mx,且f(1)=5.(Ⅰ)求m;(Ⅱ)判断并证明f(x)的奇偶性;(Ⅲ)判断函数f(x)在(2,+∞),上是单调递增还是单调递减?并证明.20.(12分)经市场调查,某种商品在过去50天的销售量和价格均为销售时间t(天)的函数,且销售量近似地满足f(t)=﹣2t+200(1≤t≤50,t∈N).前30天价格为g(t)=12t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).(1)写出该种商品的日销售额S与时间t的函数关系;(2)求日销售额S的最大值.21.(12分)已知函数f(x)是定义在R上的奇函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象如图所示.(Ⅰ)请画出函数f(x)在y轴右侧的图象,并写出函数f(x)在R上的单调减区间;(Ⅱ)写出函数f(x),x∈R的解析式;(Ⅲ)若函数g(x)=f(x)﹣2ax+2,x∈[1,2],求函数g(x)的最大值h(a)的解析式.22.(12分)已知函数f(x)的定义域为R,对任意x,y都有f(xy)=f(x)•f(y)+f(x)+f(y),且f (﹣1)=0.(1)求证:f(1)=0;(2)判断f(x)奇偶性,并证明;(3)若f(2)=3,且f(x)在(0,+∞)上单调递增,解关于x的不等式f(x﹣1)<15.2023-2024学年河北省衡水志华实验中学高一(上)期中数学试卷参考答案与试题解析一、单选题(每小题5分,共40分)1.已知集合A ={x ∈N |﹣3<x <3},B ={﹣5,﹣2,0,2,5},则A ∩B =( ) A .{﹣2,0,2}B .{0,2}C .{0}D .{2}解:因为A ={x ∈N |﹣3<x <3}={0,1,2},所以A ∩B ={0,2}. 故选:B .2.下列函数中,与函数y =x +2是同一个函数的是( ) A .y =(√x +2)2B .y =√x 33+2C .y =x 2x +2D .y =√x 2+2解:y =x +2的定义域为R ,值域为R ,对于A ,y =(√x +2)2定义域为[﹣2,+∞),与y =x +2定义域不同,不是同一函数,A 错误; 对于B ,y =√x 33+2=x +2,与y =x +2定义域相同,解析式相同,是同一函数,B 正确; 对于C ,y =x 2x+2定义域为{x |x ≠0},与y =x +2定义域不同,不是同一函数,C 错误; 对于D ,y =√x 2+2值域为[2,+∞),与y =x +2值域不同,不是同一函数,D 错误. 故选:B .3.化简二次根式√−8a 3的结果为( ) A .−2a √−2aB .2a √2aC .2a √−2aD .−2a √2a解:因为﹣8a 3≥0,所以a ≤0,所以√−8a 3=2|a|√−2a =−2a √−2a . 故选:A .4.已知函数y ={x 2+1(x ≤0)2x(x >0),若f (a )=10,则a 的值是( )A .3或﹣3B .﹣3或5C .﹣3D .3或﹣3或5解:若a ≤0,则f (a )=a 2+1=10,∴a =﹣3(a =3舍去) 若a >0,则f (a )=2a =10,∴a =5 综上可得,a =5或a =﹣3 故选:B .5.已知函数f (x )=x 2+(k ﹣2)x 是[1,+∞)上的增函数,则k 的取值范围为( ) A .(﹣∞,0]B .[0,+∞)C .(﹣∞,1]D .[1,+∞)解:根据题意,函数f (x )=x 2+(k ﹣2)x 为开口向上的二次函数,其对称轴为x =−k−22,若函数f(x)=x2+(k﹣2)x是[1,+∞)上的增函数,则必有−k−22≤1⇒k≥0,即k的取值范围为[0,+∞);故选:B.6.中国清朝数学家李善兰在859年翻译《代数学》中首次将“function”译做“函数”,沿用至今.为什么这么翻译,书中解释说“凡此变数中函彼变数者,则此为彼之函数.”这个解释说明了函数的内涵:只要有一个法则,使得取值范围中的每一个值x,有一个确定的y和它对应就行了,不管这个对应的法则是公式、图象、表格还是其它形式.已知函数f(x)由如下表给出,则f(f(﹣2)+1)的值为()A.1B.2C.3D.4解:根据题意,f(x)={1,x≤02,0<x<23,x≥2,则f(﹣2)=1,f(f(﹣2)+1)=f(2)=3,故选:C.7.已知幂函数f(x)=xα(α∈R)的图象经过点(12,4),且f(a+1)<f(3),则a的取值范围为()A.(﹣∞,2)B.(2,+∞)C.(﹣∞,﹣4)∪(2,+∞)D.(﹣4,2)解:∵幂函数f(x)=xα(α∈R)的图象经过点(12,4),∴4=(12)α,∴α=﹣2,∴f(x)=x﹣2=1x2,∴函数f(x)是偶函数,在(0,+∞)上单调递减,在(﹣∞,0)上单调递增,∵f(a+1)<f(3),∴|a+1|>3,解得:a<﹣4或a>2,即a的取值范围为(﹣∞,﹣4)∪(2,+∞).故选:C.8.若两个正实数x,y满足4x+y=2xy,且不等式x+y4<m2+m有解,则实数m的取值范围是()A.(﹣1,2)B.(﹣∞,﹣1)∪(2,+∞)C.(﹣2,1)D.(﹣∞,﹣2)∪(1,+∞)解:若两个正实数x,y满足4x+y=2xy,即4y +1x=2,所以x +y 4=(x +y 4)(1x +4y)×12=12(2+y 4x +4x y )≥12(2+2√y 4x ⋅4xy )=2,当且仅当y =4x 且4y +1x=2,即x =1,y =4时取等号,故x +y4的最小值为2,因为不等式x +y4<m 2+m 有解,所以2<m 2+m ,解得m >1或m <﹣2. 故选:D .二、多选题(每小题5分,多选或错选得0分,少选得2分,共20分) 9.下列各命题中为假命题的是( ) A .∀x ∈R ,x ≥0 B .如果x <5,则x <2 C .∃x ∈R ,x 2≤﹣1D .∀x ∈R ,x 2+1≠0解:对于A 选项:当x =﹣2∈R 时,x <0,所以命题“∀x ∈R ,x ≥0”为假命题; 对于B 选项:当x =4时,则2<x <5,所以命题“如果x <5,则x <2”为假命题; 对于C 选项:当x ∈R 时,x 2≥0,所以命题“∃x ∈R ,x 2≤﹣1”为假命题; 对于D 选项,∀x ∈R ,x 2≥0,则x 2+1≥1,所以命题“∀x ∈R ,x 2+1≠0”为真命题. 故选:ABC .10.已知幂函数f(x)=(2a −1)x m2−3m+2,其中a ,m ∈R ,则下列说法正确的是( )A .a =1B .f (x )恒过定点(1,1)C .若m =3时,y =f (x )关于y 轴对称D .若12<m <1时,f (2)<f (1) 解:∵函数f(x)=(2a −1)x m 2−3m+2为幂函数,∴2a ﹣1=1,解得a =1,故A 正确;∵f (x )=x m2−3m+2,∴f (x )恒过定点(1,1),故B 正确;又当m =3时,f (x )=x 2,为偶函数,故y =f (x )关于y 轴对称,即C 正确; ∵m 2﹣3m +2=(m ﹣2)(m ﹣1), ∴当12<m <1时,m 2﹣3m +2>0,∴f (x )=x m2−3m+2在(0,+∞)上单调递增,∴f (2)>f (1),故D 错误; 故选:ABC .11.下列命题是真命题的是( )A .已知函数f (2x +1)的定义域为[﹣1,1],则函数f (x )的定义域为[﹣1,3]B .若y =f (x )是一次函数,满足f (f (x ))=16x +5,则f (x )=4x ﹣1C .函数y =f (x )的图象与y 轴最多有一个交点D .函数y =1x+1在(﹣∞,﹣1)∪(﹣1,+∞)上是单调递减函数 解:对于A ,因为函数f (2x +1)的定义域为[﹣1,1],则2x +1∈[﹣1,3], 所以函数f (x )的定义域为[﹣1,3],故A 正确. 对于B ,设f (x )=kx +b (k ≠0),则f (f (x ))=k (kx +b )+b =k 2x +kb +b =16x +5,所以{k 2=16kb +b =5,解得{k =4b =1或{k =−4b =−53,所以f (x )=4x +1或f(x)=−4x −53,故B 错误.对于C ,根据函数的定义可得函数y =f (x )的图象与y 轴最多有一个交点,故C 正确. 对于D ,函数y =1x+1在(﹣∞,﹣1),(﹣1,+∞)上是单调递减函数,故D 错误. 故选:AC .12.定义在R 上的函数f (x ),对任意的x 1,x 2∈(﹣∞,2],都有f(x 2)−f(x 1)x 2−x 1>0,且函数y =f (x +2)为偶函数,则下列说法正确的是( ) A .y =f (x ﹣2)关于直线x =4对称 B .y =f (x )在x ∈(2,+∞)上单调递增 C .f (1)>f (π)D .若f (0)=0,则(x ﹣1)f (x )>0的解集为(﹣∞,0)∪(1,4) 解:因为对任意的x 1,x 2∈(﹣∞,2],都有(x 1﹣x 2)[f (x 1)﹣f (x 2)]>0, 所以函数f (x )在(﹣∞,2]上单调递增,又因为函数y =f (x +2)为偶函数,所以函数f (x )关于直线x =2对称,所以函数y =f (x ﹣2)关于直线x =4对称,A 正确; 根据函数f (x )在(﹣∞,2]上单调递增,且关于直线x =2对称, 可得函数y =f (x )在x ∈(2,+∞)上单调递减,B 错误; 因为函数y =f (x )在x ∈(2,+∞)上单调递减,所以f (π)<f (3),且f (3)=f (1),所以f (1)>f (π),C 正确; 由f (0)=0可得,f (4)=0,则结合函数的单调性和对称性可得,x ∈(﹣∞,0)时,f (x )<0,x ∈(0,4)时,f (x )>0,x ∈(4,+∞)时,f (x )<0, 所以由(x ﹣1)f (x )>0,可得{x −1>0f(x)>0或{x −1<0f(x)<0,解得1<x <4或x <0,D 正确.故选:ACD .三、填空题(每题5分,共20分)13.已知实数a >0,b >0,化简:a 32b 52√ab= ab 2 .解:实数a >0,b >0,则a 32b 52√ab=a 32b 52a 12b 12=a 32−12b 52−12=ab 2.故答案为:ab 2.14.已知函数f (x )=ax 2+bx +c ,x ∈[﹣2a ﹣5,1]是偶函数,则a +2b = ﹣2 . 解:根据题意,函数f (x )=ax 2+bx +c ,x ∈[﹣2a ﹣5,1]是偶函数, 则有﹣2a ﹣5+1=0,解可得a =﹣2,则函数f (x )是开口向下的二次函数,必有b =0,故a +2b =﹣2. 故答案为:﹣2.15.如果关于x 的不等式﹣x 2+6ax ﹣3a 2≥0的解集为[x 1,x 2],其中常数a >0,则x 1+x 2+3ax 1x 2的最小值是 2√6 .解:不等式﹣x 2+6ax ﹣3a 2≥0的解集为[x 1,x 2],其中常数a >0, 所以x 1,x 2是方程x 2﹣6ax +3a 2=0的实数根, a >0时,Δ=(﹣6a )2﹣4×3a 2=24a 2>0, 所以{x 1+x 2=6a x 1x 2=3a 2,所以x 1+x 2+3a x 1x 2=6a +1a ≥2√6a ⋅1a =2√6,当且仅当6a =1a ,即a =√66时取等号, 故x 1+x 2+3ax 1x 2的最小值是2√6.故答案为:2√6.16.已知函数f (x )={ax −x 2,x ≥0−2x ,x <0,①若对任意x 1,x 2∈R ,且x 1≠x 2都有f(x 2)−f(x 1)x 2−x 1<0,则实数a 的取值范围为 (﹣∞,0] ;②若f (x )在[﹣1,t )上的值域为[0,4],则实数t 的取值范围为 (2,4] . 解:①若对任意x 1,x 2∈R ,且x 1≠x 2都有f(x 2)−f(x 1)x 2−x 1<0,则f (x )在(﹣∞,+∞)上单调递减,则a 2≤0,即a ≤0.∴实数a 的取值范围为(﹣∞,0]; ②当a >0时,若f (x )在[﹣1,t )上的值域为[0,4],可得f (a2)=a 22−a 24=4,解得a =4或a =﹣4(舍去),又f (﹣1)=2,f (0)=f (4)=0,∴2<t ≤4; 当a ≤0时,由①可知,f (x )在[﹣1,t )上单调递减, 则f (x )在[﹣1,t )上的最大值为f (﹣1)=2,不合题意. ∴实数t 的取值范围为(2,4]. 故答案为:①(﹣∞,0];②(2,4].四、解答题(17题10分,18-22每题12分,共70分) 17.(10分)已知关于x 的不等式2kx 2+kx ﹣1<0. (1)若不等式的解集为(−32,1),求实数k 的值; (2)若不等式的解集为R ,求实数k 的取值范围.解:(1)关于x 的不等式2kx 2+kx ﹣1<0的解集为(−32,1), 所以−32和1是方程2kx 2+kx ﹣1=0的两个实数根, 代入x =1得2k +k ﹣1=0,解得k =13; (2)若不等式2kx 2+kx ﹣1<0的解集为R , 则k =0时,不等式为﹣1<0,满足题意; k ≠0时,应满足{k <0△=k 2+8k <0,解得﹣8<k <0;综上知,实数k 的取值范围是﹣8<k ≤0.18.(12分)已知集合P ={x |3a ﹣10≤x <2a +1},Q ={x ||2x ﹣3|≤7}. (1)当a =2时,求P ∩(∁R Q );(2)若“x ∈P ”是“x ∈Q ”必要不充分条件,求实数a 的取值范围.解:(1)根据题意,得Q ={x ||2x ﹣3|≤7}={x |﹣2≤x ≤5},可得∁R Q =x |x <﹣2或x >5}, 因为a =2时,P ={x |﹣4≤x <5},所以P ∩(∁R Q )={x |﹣4≤x <﹣2}; (2)因为“x ∈P ”是“x ∈Q ”的必要不充分条件,所以Q ⫋P ,P 不是空集,故当3a ﹣10<2a +1,解得a <11.根据包含关系,可得{3a −10≤−22a +1>5,解得2<a ≤83,所以实数a 的取值范围是(2,83].19.(12分)已知函数f (x )=x +m x,且f (1)=5. (Ⅰ)求m ;(Ⅱ)判断并证明f (x )的奇偶性;(Ⅲ)判断函数f (x )在(2,+∞),上是单调递增还是单调递减?并证明. 解:(1)根据题意,函数f (x )=x +m x ,且f (1)=5, 则f (1)=1+m =5,解得m =4;(2)由(1)可知f (x )=x +4x,其定义域为{x |x ≠0},关于原点对称, 又由f (﹣x )=﹣x −4x =−(x +4x )=﹣f (x ), 所以f (x )是奇函数;(3)f (x )在(2,+∞)上是单调递增函数. 证明如下:设2<x 1<x 2, f (x 1)﹣f (x 2)=(x 1+4x 1)﹣(x 2+4x 2)=(x 1﹣x 2)x 1x 2−4x 1x 2, 因为2<x 1<x 2,所以x 1x 2>4,x 1﹣x 2<0, 则f (x 1)﹣f (x 2)<0,即f (x 1)<f (x 2), 所以f (x )在(2,+∞)上是单调递增函数.20.(12分)经市场调查,某种商品在过去50天的销售量和价格均为销售时间t (天)的函数,且销售量近似地满足f (t )=﹣2t +200(1≤t ≤50,t ∈N ).前30天价格为g(t)=12t +30(1≤t ≤30,t ∈N),后20天价格为g (t )=45(31≤t ≤50,t ∈N ). (1)写出该种商品的日销售额S 与时间t 的函数关系; (2)求日销售额S 的最大值.解:(1)当1≤t ≤30时,由题知f (t )•g (t )=(﹣2t +200)•(12t +30)=﹣t 2+40t +6000, 当31≤t ≤50时,由题知f (t )•g (t )=45(﹣2t +200)=﹣90t +9000, 所以日销售额S 与时间t 的函数关系为S ={−t 2+40t +6000,1≤t ≤30−90t +9000,31≤t ≤50;(2)当1≤t ≤30,t ∈N 时,S =﹣(t ﹣20)2+6400,当t =20时,S max =6400元;当31≤t≤50,t∈N时,S=﹣90t+9000是减函数,当t=31时,S max=6210元.∵6210<6400,则S的最大值为6400元.21.(12分)已知函数f(x)是定义在R上的奇函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象如图所示.(Ⅰ)请画出函数f(x)在y轴右侧的图象,并写出函数f(x)在R上的单调减区间;(Ⅱ)写出函数f(x),x∈R的解析式;(Ⅲ)若函数g(x)=f(x)﹣2ax+2,x∈[1,2],求函数g(x)的最大值h(a)的解析式.解:(Ⅰ)图象如图所示:单调减区间是(﹣∞,﹣1),(1,+∞).(Ⅱ)∵函数f(x)是定义在R上的奇函数,∴f(﹣x)=﹣f(x),当x≤0时,f(x)=x2+2x,∴当x>0时,﹣x<0,f(x)=﹣f(﹣x)=﹣[(﹣x)2+2×(﹣x)]=﹣x2+2x,∴f(x)={x2+2x,x≤0−x2+2x,x>0.(Ⅲ)∵函数g(x)=f(x)﹣2ax+2,x∈[1,2],∴g(x)=﹣x2+(2﹣2a)x+2,x∈[1,2],①当1﹣a≤1时,即a≥0,h(a)=[g(x)]max=g(1)=3﹣2a;②当1<1﹣a≤2时,即﹣1≤a<0,h(a)=[g(x)]max=g(1﹣a)=a2﹣2a+3;③当1﹣a>2时,即a≥0,h(a)=[g(x)]max=g(2)=2﹣4a,∴h(a)={3−2a,a≥0a2−2a+3,−1≤a<0 2−4a,a<−1.22.(12分)已知函数f(x)的定义域为R,对任意x,y都有f(xy)=f(x)•f(y)+f(x)+f(y),且f (﹣1)=0.(1)求证:f(1)=0;(2)判断f(x)奇偶性,并证明;(3)若f(2)=3,且f(x)在(0,+∞)上单调递增,解关于x的不等式f(x﹣1)<15.解:(1)证明:函数f(x)的定义域为R,对任意x,y都有f(xy)=f(x)•f(y)+f(x)+f(y),令x=y=﹣1,则f(1)=f(﹣1)•f(﹣1)+f(﹣1)+f(﹣1)=0,得证;(2)f(x)为偶函数,证明:令y=﹣1,则f(﹣x)=f(x)•f(﹣1)+f(x)+f(﹣1)=f(x),因为f(x)定义域为R,所以函数f(x)为偶函数;(3)由题设,令x=y=2得f(4)=f(2×2)=f(2)•f(2)+f(2)+f(2)=3×3+3+3=15,由(2)得:函数f(x)为偶函数,且f(x)在(0,+∞)上递增,则在(﹣∞,0)上递减,所以f(x﹣1)<15=f(4),则|x﹣1|<4,解得﹣3<x<5,所以不等式的解集为{x|﹣3<x<5}.。
河北省衡水市衡水中学2024届高一物理第一学期期中综合测试试题含解析

河北省衡水市衡水中学2024届高一物理第一学期期中综合测试试题注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确.全部选对的得5分,选不全的得3分,有选错的或不答的得0分)1、有四位同学把斜面对重物的支持力,分别画成如图的四种情况,其中画正确的是( )A .B .C .D .2、宇航员乘坐宇宙飞船环绕地球做匀速圆周运动时,下列说法正确的是( )A .宇航员处于完全失重状态B .宇航员处于超重状态C .宇航员的加速度等于零D .地球对宇航员没有引力3、一物体做匀加速直线运动,第4s 内的位移是14m ,第5s 内的位移是18m ,下列说法中正确的是() A .第4秒内的平均速度是32/m s B .第5s 初的瞬时速度是16/m sC .物体的初速度不为零D .物体运动的加速度是23/m s4、关于摩擦力说法错误的是( )A .摩擦力的方向不一定与物体的运动方向相同B .静摩擦力的方向不一定与运动方向共线C .受静摩擦力或滑动摩擦力的物体不一定静止或运动D .静摩擦力不一定是阻力,滑动摩擦力一定是阻力5、下列关于瞬时速度和平均速度的说法中,正确的是( )A .若物体在某段时间内每时刻的瞬时速度都等于零,则它在这段时间内的平均速度一定为零B .若物体在某段时间内的平均速度等于零,则它在这段时间内任一时刻的瞬时速度一定为零D.变速直线运动中任意一段时间内的平均速度一定不等于某一时刻的瞬时速度6、关于摩擦力的下列说法正确的是( )A.相互挤压的粗糙物体间一定产生摩擦力B.摩擦力可以是阻力也可以是动力C.一个物体在另一个物体表面滑动时,一定受到摩擦力的作用D.只有静止的物体才能受到静摩擦力,只有运动的物体才有可能受到滑动摩擦力7、一物体做匀变速直线运动,某时刻速度大小为2m/s, 1 s后的速度大小变为12 m/s,在这1 s内物体的加速度大小可能为:A.可能等于10 m/s2B.可能小于10 m/s2C.一定等于10 m/s2D.可能等于14m/s28、如图所示,以8 m/s匀速行驶的汽车即将通过路口,绿灯还有2 s将熄灭,此时汽车距离停车线18 m.。
河北省衡水中学2025届高三地理上学期期中试题

河北省衡水中学2025届高三地理上学期期中试题本试卷满分100分,考试时间90分钟。
留意事项∶1.答卷Ⅰ前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.答卷Ⅰ时,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
3.答卷Ⅱ时,答案肯定要答在答案纸上,不能答在试卷上第Ⅰ卷(选择题共60分)一、选择题(60 分)下图为2024年1月3日夜间至4日江苏省最大积雪深度分布图,据此完成1—3题。
1.形成此次降雪的天气系统的中心位置可能位于()A.盐城旁边B.连云港旁边C.苏州旁边D.南通旁边2.此次降雪期间,南京市()A.白昼变短B.空气质量下降C.日出东北D.气压升3。
为防止路面积雪及结冰,江苏省各降雪城市可实行的有效措施是()A.重物碾压促进溶化B.喷酒热水加速融雪C.人工堆放在绿化带D.利用城市热岛效应融雪2024年有网友爆出的一张照片呈现出如下美景∶山路的一边是暖黄色的水杉林,一边是墨绿色的柳杉林。
水杉属落叶乔木,喜暖和潮湿,适生土壤为酸性山地土壤或冲积土,多生于山谷或山麓旁边,地势平缓、潮湿或稍有积水的地方。
柳杉是常绿乔木,喜爱暖和潮湿、云雾充满、夏季较凉快的山区气候,喜深厚肥沃的沙质土壤,忌积水。
据此完成 4-6 题。
4.导致马路两侧植被差异的主要自然因素是(A.光照B.气温C.降水D.土壤5.欣赏此美景的最佳季节是()A.春B.夏C.秋D.冬6.该美景最可能出现在()A.重庆B.上海C.北京D.乌鲁木齐读"大气受热过程图",回答第7 题。
7.若图中区域()A.晴朗天气,a大部分为大气汲取 B.为湖泊湿地,b能和缓地加热大气C. CO.增多,c补偿地面失热较少D. 冰雪地面,a→b 的转化率增加据报道,某年8月21日,我国科考队员在中国南极昆仑站(下图)观看了极夜后的首次日出。
据此完成8-9 题。
8.这一天,科考队员在昆仑站看到日出时,国际标准时间及日出方位是()A.7时北方B. 10时东方C.13时西方D.15时南方9.据此推算,昆仑站此次极夜起先的时间约在前一年的()A. 3月 21日~30日B.4月1日~10日D.4月 21日~30日C. 4月11日~20日冻土是指温度在 0℃或 0℃以下,含有冰的土层或岩层,分为季节冻土和多年冻土。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• • • • • • • • •
纵笔三首 苏轼 寂寂东坡一病翁,白须萧散满霜风。 小儿误喜朱颜在,一笑那知是酒红。 父老争看乌角巾,应缘曾现宰官身。 溪边古路三叉口,独立斜阳数过人。 北船不到米如珠,醉饱萧条半月无。 明日东家知祀灶,只鸡斗酒定膰吾。
• 白话译文 • 其一 • 孤苦寂然的东坡老翁我在病中,须发萧然,就像一世 不散的霜风。 • 小儿欣喜地夸我脸色泛红,我木然一笑露出了真相, 原来是酒后的醉容。 • 其二 • 父老们争着看我这黑色的头巾,是因为我这个平民, 曾有过官职在身。 • 而如今,溪边路口人独立,看夕阳西沉,数过路行人。 • 其三 • 北来的粮船未到,近来米贵如珍珠,半月不知饱和醉, 这肚子好萧条好清苦。 • 好在明天是祭灶日,难得这年末岁尾,东家宰鸡,烤 肉,备酒,定会饷我祭肉醉一回。
古同“淡”,清淡
•
贞元二年,河北蝗旱,米斗一千五百文。复大 兵之后,民无蓄积,饿殍相枕。孝忠所食,豆 瓣而已,其下皆甘粗粝,人皆服其勤俭,孝忠 为一时之贤将也。三年,加检校司空,仍以其 子茂宗尚义章公主。孝忠遣其妻邓国夫人昧谷 氏入朝,执亲迎之礼。上嘉之,赏赉隆厚。七 年三月卒,时年六十二,废朝三日,追封上谷 郡王,赠太傅,再赠魏州大都督,册赠太师, 谥曰贞武。
•
宣德五年,河南旱荒,民多转徙。帝以源廉 正有为,命为左布政使,俾驰驿之任。时侍 郎许廓往抚辑,廷议又起丁忧布政使李昌祺原 官。源与廓、昌祺发仓廪,免逋赋杂役,流民 渐归。雨亦旋降,岁大丰。居三年,召还,授 刑部左侍郎。明年,永丰民夏九旭等据大盘山 为乱。帝以源江西人,命抚之,都督任礼帅兵 随其后。未至,官军擒九旭,因命二人采木四 川,兼饬边务。
• (3)皇帝认为魏源有功劳,搁置不予追究, 事情办完后回到朝廷,魏源与都御史陈智在 值班房相互责骂,陈智把这件事报告给皇帝, 皇帝下发诏书,责备了他们俩。
•
岁旱,录上疑狱,且请推行于天下,报可。 旋坐决狱不当,与侍郎何文渊俱下狱。得宥, 复以上辽王贵烚罪状,不言其内乱事,与三司 官皆系诏狱。累月,释还职。源在刑部久,议 狱多平恕。陕西佥事计资言,武臣杂犯等罪, 予半俸,谪极边。源以所言深刻,奏寝之。 六年以足疾命朝朔望。八年致仕,卒。
• 许便宜行事:允许他根据情况自行决断 处理事情 • 按行:巡查
• 墩堠:瞭望敌情的堡垒,烽堠 • 悉括归伍:收编
•
寻以宣、大军务久弛,请召还巡抚佥都御 史卢睿,而荐兵部侍郎于谦为镇守参赞。于 是言官以临边擅易置大臣为源罪,合疏劾之。
帝以源有劳,置不问。事竣还朝,与都 御史陈智相詈于直庐①。智以闻,诏两 责之。
超旷闲逸
• 其一:以一笑否定小儿误喜自己容颜未老,诗 人能用达观的态度、风趣的笔墨去对待和描写 引人感伤之事,有过人的胸襟和笔力,体现超 旷闲逸 • 其二以恬淡的笔触,不露痕迹地来反映悲凉情 境,将身世的不幸和社会的不平蕴藏在父老相 迎的热闹与过人的寂寞中,不显沉痛,却又超 旷闲逸。 • 其三以直截之笔写真率之怀。它直写诗人的渴 酒思肉,直写对邻人送酒肉的期待,毫不掩饰, 毫不做作,超旷闲逸
• 甫冠:刚刚二十岁
• 校艺:考试
• 恩例:帝王为宣示恩德而颁布条例 • 增秩:增加俸禄 • 治剧:处理繁重难办的事物
•
伯思好古文奇字,洛下公卿家商、周、秦、汉彝器 款识,研究字画体制,悉能辨正是非,道其本末,遂 以古文名家,凡字书讨论备尽。初,淳化中博求古法 书,命待诏王著续正法帖,伯思病其乖伪庞杂,考引 载籍,咸有依据,作《刊误》二卷。由是篆、隶、正、 行、草、章草、飞白皆至妙绝,得其尺牍者,多 藏弆。 又二年,除详定《九域图志》所编修官兼《六典》检阅 文字,改京秩。
• 宽裕:宽容、宽大 • 偏将:副将 • 先登:1、先于众人而登 2、比喻出众 的人才3、先锋 • 先登陷阵:作为先锋冲锋陷阵
• 上元中,李宝臣奏授左领军郎将。宝臣以孝 忠谨重骁勇,甚委信之,以妻妹昧谷氏妻 焉,仍悉以易州诸镇兵马令其统制。前后居 城镇十余年,甚著威惠。
• 以孝忠谨重骁勇: • 认为孝忠谨慎稳重、英勇善战
衡水中学期中考试
•
踏莎行①
• 张孝祥 • 万里扁舟,五年三至。故人相见忧堪 喜。山阴乘兴②不须回,毗耶问疾难 为对③。 • 不药身轻,高谈心会。匆匆我又成归 计。它时江海肯相寻,绿蓑青蒻④。 看清贵。 • 15.这首词表达了词人哪些情感?请 简要分析。(6分)
15.这首词表达了词人哪些情感? 请简要分析。(6分)
• ①与友人相聚时的喜悦之情。访问友人乘兴而 去,流连忘返。故人相会一处,虽生病但不用 服药也身心轻松,愉快地进行者高深而高尚的 文流。 • ②对友人深切的眷恋之情。美好的相聚时光对 词人来说总是那么短暂,不禁感叹每次匆匆聚 首又匆匆告别。 • ③意欲归隐之情。词的结尾词人写自己内心已 厌倦了世俗生活,有一天将会披着蓑衣,戴着 斗笠,从尘世中隐退,以一种蔑视权贵的心态 立于世间
• (3)皇帝认为魏源有功劳,搁置不予追究, 事情办完后回到朝廷,魏源与都御史陈智在值 班房相互责骂,陈智把这件事报告给皇帝,皇 帝下发诏书,责备了他们俩。
张孝忠
•
张孝忠,本奚之种类。开元中以众归国 授鸿胪卿同正以孝忠贵赠户部尚书孝忠以勇 闻于燕赵形体魁伟长六尺余性宽裕事亲恭孝。 天宝末,以善射授内供奉。后为偏将,破九 姓突厥,先登陷阵,以功授果毅折冲。
• 如不胜衣:像是不能支撑衣服的样子 • 弄:戏耍 • 觉:觉悟、发觉,表明,高大、正直 • 睡醒,通“较”,相差
• 甫冠,入太学,校艺屡占上游。履将以恩例 奏增秩,伯思固辞,履益奇之。元符三年,
进士高等,调磁州司法参军,久不任,改通州 司户。丁内艰,服除,除河南府户曹参军, 治剧不劳而办。秩满,留守邓洵武辟知右军 巡院。
• 录:记载、记录,簿籍,采纳,收集、收 藏,没收、录用,审查、衡量,次第,总 领,逮捕 • 平恕:持平宽仁 • 深刻:苛刻
• 慕:依恋、想念,羡慕、企求,敬仰, 趋附,效法
魏源
•
魏源,字文渊,建昌县人。永乐四年进士, 除监察御史,辨松江知府黄子威诬。奏减浙 东濒海渔课。巡按陕西,西安大疫,疗活甚 众。奏言:“诸府仓粟积一千九十余万石, 足支十年。今民疫妨农,请输钞代两税之 半。”从之。两遭丧,俱起复。
• 课:考核,督促,教授学习,工作功课, 征税、赋税,占卜 • 输钞:上交纸币
• 笺奏:1.同“牋奏”。古代文书的一种,属章 奏一类。2.牋奏:书札、奏章。 • 精诣:精到。谓学养精粹 • 羸瘵: [léi zhài]病困。
•
伯思颇好道家自号云林子别字霄宾及至京 梦人告曰子非久人间上帝有命典司文翰觉而书 之。不逾月,以政和八年卒,年四十。伯思学 问慕扬雄,诗慕李白,文慕柳宗元。有文集 五十卷、《翼骚》一卷。
• 俾驰驿之任:让他骑驿站的马快速赴任 • 抚辑:安抚
• 仓廪:储藏谷米的仓库
• 饬:整顿
• 英宗即位,进尚书。正统二年五月命整饬大 同、宣府诸边,许便宜行事。源遣都督佥 事李谦守独石,按行天城、朔州诸险要,令 将吏分守。设威远卫,增修开平、龙门城, 自独石抵宣府,增置墩堠。免屯军租一年, 储火器为边备,诸依权贵避役者悉括归伍。
•
无几,宝臣死,其子惟岳阻兵不受命,朝 廷诏幽州节度使讨之。滔以孝忠宿将善战,有 精兵八千在易州,虑军兴则挠其后,乃使判 官蔡雄说孝忠曰:“惟岳小子骄贵,不达人事, 辄拒朝命。使君诚能去逆效顺,必受重任,
有先归国之功矣!”孝忠然之,乃遣衙官随雄 报滔,又遣易州录事参军董稹入朝。德宗嘉之, 授孝忠检校工部尚书,仍赐实封二百户。 • 阻兵:仗恃军队、手握兵权 • 宿将:指久经战争的将领 • 挠:.扰乱,阻止
• 去逆效顺:脱离叛逆者,效法忠于国家的 人
• 及朱滔、王武俊谋叛,将救田悦于魏州,虑 孝忠踵后,滔军将发,复遣蔡雄往说之。孝 忠曰:“李惟岳背国作逆,孝忠归国,今为 忠臣。孝忠性直,业已效忠,不复助逆矣。” 滔又啖以金帛,终拒而不从。易定居二凶之 间,四面受敌,孝忠修峻沟垒,感励将士,
竟不受二凶之荧惑,议者多之。 • 踵:1.脚后跟 2 行、走 、到3.追随,继承 • 啖:1、.吃或给人吃:2.拿利益引诱人:3.
• 委信:委任信赖Fra bibliotek• 甚著威惠:声威、惠政都十分闻名
• 田承嗣之寇冀州也,宝臣俾孝忠以精骑数千 御之。承嗣见其整肃,叹曰:“孝忠在
焉,冀州未易图也!”乃焚营宵遁。 • 俾:1、使2、通“比”、顺从3、通 “裨”裨益、益处4、通“睥睨” • (1)田承嗣看到张孝忠的军队阵容整 齐严肃,感叹道:“张孝忠在这里,冀 州不容易谋取了。”于是烧毁营寨连夜 逃跑了
• 博求:广泛搜求 • 病:疲倦,苦、困乏,饥饿,缺点,损害,失败, 为难,怨恨、不满,耻辱,忧虑 • 法书,也叫法帖,学习书法可以作为楷模的范本 • 乖伪:谬误 • 载籍:典籍、书籍 • 弆jǔ收藏;保藏 • 京秩:指京官。
•
寻监护崇恩太后园陵使司,掌管笺奏。以修 书恩,升朝列,擢秘书省校书郎。未几,迁秘 书郎。纵观册府藏书,至忘寝食,自《六经》 及历代史书、诸子百家、天官地理、律历卜筮 之说无不精诣。凡诏讲明前世典章文物、集古 器考定真赝,以素学与闻,议论发明居多,馆 阁诸公自以为不及也。逾再考,丁外艰,宿抱 羸瘵,因丧尤甚。服除,复旧职。
• (1)孝忠修峻沟垒,感励将士,竟不受二凶之荧惑,议者多之。
• (1)张孝忠深挖战壕、髙筑堡垒,感召激励将士, 最终没有受到两个叛徒的诱惑,受到时论的赞 美。
(2)源与廓、昌祺发仓廪,免逋赋杂役,流民渐归 (2)魏源与许廓、李昌祺打开粮仓救济,免除
拖欠的赋税和各种杂役,流亡的百姓逐渐回归 家园
• (3)帝以源有劳,置不问,事竣还朝,与都御史陈 智相詈于直庐。智以闻,诏两责之。(5分)
• 尚:娶公主为妻、侍奉公主 • 增添、超过、凌驾、时间久远、喜好、主 管、帮助、仍然
黄伯思
• 黄伯思,字长睿,其远祖自光州固始徙闽,为 邵武人。祖履,资政殿大学士。父应求,饶州 司录。伯思体弱,如不胜衣,风韵洒落,飘 飘有凌云意。自幼警敏,不好弄,日诵书千余 言。每听履讲经史,退与他儿言,无遗误者。 尝梦孔雀集于庭,觉而赋之,词采甚丽。以 履任为假承务郎。
