数电习题解答_杨志忠_第四章练习题_部分
数电第四章习题答案
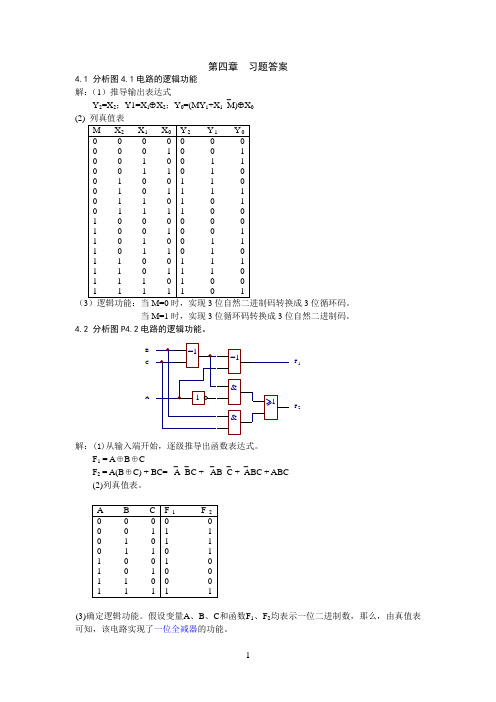
第四章习题答案4.1 分析图4.1电路的逻辑功能解:(1)推导输出表达式Y2=X2;Y1=X1⊕X2;Y0=(MY1+X1⎺M)⊕X0A 、B 、C 、F 1、F 2分别表示被减数、减数、来自低位的借位、本位差、本位向高位的借位。
A BCF 1F 2-被减数减 数借 位差4.3分析图4.3电路的逻辑功能 解:(1)F 1=A ⊕B ⊕C ;F 2=(A ⊕B)C+AB (2)(3)4.4 设ABCD 是一个8421BCD 码,试用最少与非门设计一个能判断该8421BCD 码是否大于等于5的电路,该数大于等于5,F= 1;否则为0。
解:(1)列真值表10 1 1 010 1 0 100 1 0 000 0 1 110 1 1 100 0 1 000 0 0 100 0 0 0F A B C D Ø1 1 1 0Ø1 1 0 1Ø1 1 0 0Ø1 0 1 1Ø1 1 1 1Ø1 0 1 011 0 0 111 0 0 0F A B C D(2)写最简表达式F = A + BD + BC=⎺A · BD · BC&&&DBC AF&4.6 试设计一个将8421BCD码转换成余3码的电路。
(F2=⎺C⎺D+CD F1=⎺D 电路图略。
4.7 在双轨输入条件下用最少与非门设计下列组合电路:(1)F(ABC)=∑m(1,3,4,6,7)(2) F(ABCD)=∑m(0,2,6,7,8,10,12,14,15)解:F=⎺B⎺D+A⎺D+BC∑+∑m)3(φ(DCFAB,,,7,4,0(10=) ,)12),9,8,6,5,2(解:函数的卡诺图如下所示:4.10 电话室对3种电话编码控制,按紧急次序排列优先权高低是:火警电话、急救电话、普通电话,分别编码为11,10,01。
试设计该编码电路。
F 1=A+BF 2=BA +4.11 试将2/4译码器扩展成4/16译码器 解:A 3A 2A 1 A 0⎺Y 0⎺Y 1⎺Y 2⎺Y 3 ⎺Y 4 ⎺Y 5⎺Y 6⎺Y 7 ⎺Y 8⎺Y 9⎺Y 10⎺Y 11 ⎺ Y 12⎺Y 13⎺Y 14⎺Y 154.12 试用74138设计一个多输出组合网络,它的输入是4位二进制码ABCD ,输出为: F 1 :ABCD 是4的倍数。
数字电路_第四章答案
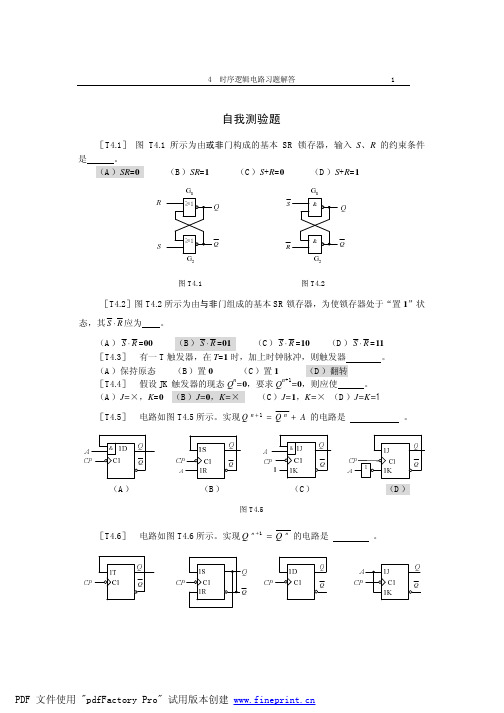
解:
Q (a)
图 P4.4
(b)
[P4.5] 有一简单时序逻辑电路如图 P4.5 所示,试写出当 C=0 和 C=1 时,电路的状 态方程 Qn+1,并说出各自实现的功能。
PDF 文件使用 "pdfFactory Pro" 试用版本创建
4 时序逻辑电路习题解答
5
图 P4. 5
4 时序逻辑电路习题解答
13
Q2 Q1 Q0
(6)逻辑功能 同步六进制加法计数器
(7)自启动校验 可以自启动 [P4.18]同步时序电路如图 P4.18 所示。 (1)试分析图中虚线框电路,画出 Q0、Q1、Q2 波形,并说明虚线框内电路的逻辑功
能。
(2)若把电路中的 Y 输出和置零端 RD 连接在一起,试说明当 X0X1X2 为 110 时,整个
J1 = Q2nQ0n
K1 = Q0 n
J 2 = Q2 nQ0 n
K 2 = Q0 n
Y = Q2 nQ0 n
(2)写出状态方程
(4)列出状态转换真值表
Q n+1 0
=
Q0 n
Q n+1 1
=
Q2 n
Q1nQ0 n
+ Q1n Q0 n
Q n+1 2
=
Q2 n
Q1nQ0 n
+ Q2 n Q0 n
Q2 n
(3)列出状态转换真值表
Q2 n
Q1 n
Q0 n
Q2 n+1 Q1n+1 Q0 n+1 Q2 n
Q1 n
Q0 n
Q2 n+1 Q1n+1 Q0 n+1
0
数字电子技术第4章组合逻辑电路习题解答

习题4.1写出图所示电路的逻辑表达式,并说明电路实现哪种逻辑门的功能。
习题4.1图解:B A B A B A B A B A F ⊕=+=+= 该电路实现异或门的功能4.2分析图所示电路,写出输出函数F 。
习题4.2图解:[]B A B BB A F ⊕=⊕⊕⊕=)(4.3已知图示电路及输入A 、B 的波形,试画出相应的输出波形F ,不计门的延迟.图解:B A B A B A AB B AB A AB B AB A F ⊕=•=•••=•••=4.4由与非门构成的某表决电路如图所示。
其中A 、B 、C 、D 表示4个人,L=1时表示决议通过。
(1) 试分析电路,说明决议通过的情况有几种。
(2) 分析A 、B 、C 、D 四个人中,谁的权利最大。
习题4.4图解:(1)ABD BC CD ABD BC CD L ++=••=B AC & && & D L B A =1 =1=1FF A B & &&& & F B A(3)4.5分析图所示逻辑电路,已知S 1﹑S 0为功能控制输入,A ﹑B 为输入信号,L 为输出,求电路所具有的功能。
习题4.5图解:(1)011011)(S S B S A S S B S A L ⊕⊕+⊕=⊕⊕•⊕= (2)4.6试分析图所示电路的逻辑功能。
习题4.6图解:(1)ABC C B A F )(++=10电路逻辑功能为:“判输入ABC 是否相同”电路。
4.7已知某组合电路的输入A 、B 、C 和输出F 的波形如下图所示,试写出F 的最简与或表达式。
习题4.7图解:(1)根据波形图得到真值表:C AB BC A C B A F ++=4.8、设∑=)14,12,10,9,8,4,2(),,,(m D C B A F ,要求用最简单的方法,实现的电路最简单。
1)用与非门实现。
2)用或非门实现。
3) 用与或非门实现。
电子教案《数字电子技术(第5版_杨志忠)》教学资源第4章练习题参考答案
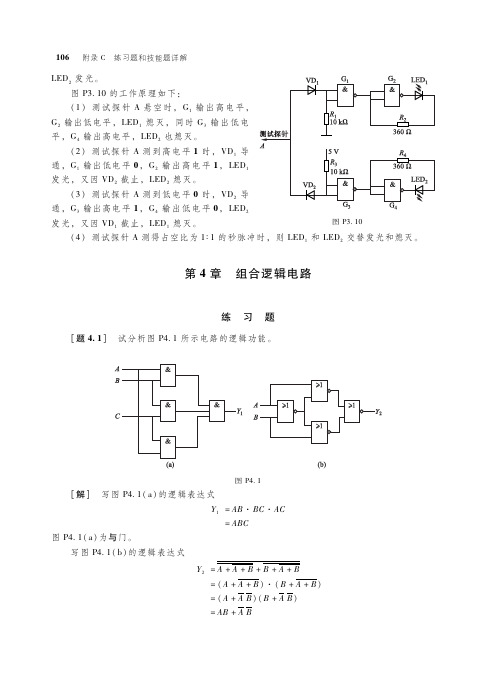
意提案时用 1 表示,不同意时用 0 表示。表决结果为 Y,提案通过时,用 1 表示,被否决时,
用 0 表示,由此,根据题意可列出[题 4 8]的真值表。
[题 4 8]的真值表
输 入
输出
输 入
输出
A
B
C
D
Y
A
B
C
D
Y
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
1
0
0
1
1
0
0
1
0
0
1
0
1
0
1
0
0
1
1
0
1
图 P4 2(b)的真值表
输 出
输 入
YA
YB
A
B
C
0
0
1
0
0
1
0
1
0
1
1
0
1
1
0
0
1
1
1
1
输 出
YA
YB
1
0
0
1
0
1
1
1
将输入 A、B、C 的各种取值组合代入 YA 和 YB 式中进行计算,由此可列出真值表。 (3)由图 P4 2(b)的真值表可知,如 A 为加数,B 为被加数,C 为相邻低位来的进位数; YA为本位和,YB 为进位数时,则图 P4 2(b)所示电路为一位全加器。 [题 4 3] 试分析图 P4 3 所示电路在 M = 0 时实现何种功能?而在 M = 1 时又能实现什 么功能? [解] (1)写输出逻辑表达式
数字电子技术基础教材第四章答案

习题44-1 分析图P4-1所示得各组合电路,写出输出函数表达式,列出真值表,说明电路得逻辑功能。
解:图(a):;;真值表如下表所示:其功能为一位比较器。
A>B时,;A=B时,;A<B时,图(b):真值表如下表所示:功能:一位半加器,为本位与,为进位。
图(c):真值表如下表所示:功能:一位全加器,为本位与,为本位向高位得进位。
图(d):;;功能:为一位比较器,A<B时,=1;A=B时,=1;A>B时,=14-2 分析图P4-2所示得组合电路,写出输出函数表达式,列出真值表,指出该电路完成得逻辑功能。
解:该电路得输出逻辑函数表达式为:因此该电路就是一个四选一数据选择器,其真值表如下表所示:,当M=1时,完成4为二进制码至格雷码得转换;当M=0时,完成4为格雷码至二进制得转换。
试分别写出,,,得逻辑函数得表达式,并列出真值表,说明该电路得工作原理。
解:该电路得输入为,输出为。
真值表如下:由此可得:完成二进制至格雷码得转换。
完成格雷码至二进制得转换。
4-4 图P4-4就是一个多功能逻辑运算电路,图中,,,为控制输入端。
试列表说明电路在,,,得各种取值组合下F与A,B得逻辑关系。
解:,功能如下表所示,两个变量有四个最小项,最多可构造种不同得组合,因此该电路就是一个能产生十六种函数得多功能逻辑运算器电路。
4-5 已知某组合电路得输出波形如图P4-5所示,试用最少得或非门实现之。
解:电路图如下:4-6 用逻辑门设计一个受光,声与触摸控制得电灯开关逻辑电路,分别用A,B,C表示光,声与触摸信号,用F表示电灯。
灯亮得条件就是:无论有无光,声信号,只要有人触摸开关,灯就亮;当无人触摸开关时,只有当无关,有声音时灯才亮。
试列出真值表,写出输出函数表达式,并画出最简逻辑电路图。
解:根据题意,列出真值表如下:由真值表可以作出卡诺图,如下图:C AB 00 10 11 100 1由卡诺图得到它得逻辑表达式为: 由此得到逻辑电路为:4-7 用逻辑门设计一个多输出逻辑电路,输入为8421BCD 码,输出为3个检测信号。
数字电子技术基础(第四版)课后习题答案_第四章

第4章触发器[题4.1]画出图P4.1所示由与非门组成的根本RS触发器输出端Q、Q的电压波形,输入端S、R的电压波形如图中所示。
图P4.1[解]见图A4.1图A4.1[题4.2]画出图P4.2由或非门组成的根本R-S触发器输出端Q、Q的电压波形,输出入端S D,R D的电压波形如图中所示。
图P4.2[解]见图A4.2[题4.3]试分析图P4.3所示电路的逻辑功能,列出真值表写出逻辑函数式。
图P4.3 [解]:图P4.3所示电路的真值表S R Q n Q n+1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 0* 1 110*由真值表得逻辑函数式 01=+=+SR Q R S Q nn[题4.4] 图P4.4所示为一个防抖动输出的开关电路。
当拨动开关S 时,由于开关触点接触瞬间发生振颤,D S 和D R 的电压波形如图中所示,试画出Q 、Q 端对应的电压波形。
图P4.4[解] 见图A4.4图A4.4[题4.5] 在图P4.5电路中,假设CP 、S 、R 的电压波形如图中所示,试画出Q 和Q 端与之对应的电压波形。
假定触发器的初始状态为Q =0。
图P4.5[解]见图A4.5图A4.5[题4.6]假设将同步RS触发器的Q与R、Q与S相连如图P4.6所示,试画出在CP 信号作用下Q和Q端的电压波形。
己知CP信号的宽度t w = 4 t Pd 。
t Pd为门电路的平均传输延迟时间,假定t Pd≈t PHL≈t PLH,设触发器的初始状态为Q=0。
图P4.6图A4.6[解]见图A4.6[题4.7]假设主从结构RS触发器各输入端的电压波形如图P4.7中所给出,试画Q、Q端对应的电压波形。
设触发器的初始状态为Q=0。
图P4.7[解] 见图A4.7图A4.7[题4.8]假设主从结构RS触发器的CP、S、R、DR各输入端的电压波形如图P4.8所示,1DS。
数电第四章习题答案

4.11图P4.11(a)所示各电路中,FF1~FF2均为边沿触发器:
1)写出各个触发器次态输出的函数表达式;
图P4.2
解答:见图A4.2
图A4.2
4.3一种特殊的RS触发器如图P4.3所示。
1)试列出状态转换真值表;
2)写出次态方程;
3)R与S是否需要约束条件?
图P4.3
解答:1)
①CP=0时,SS=1,RR=1,期间 ,状态保持。
2CP=1时,
即在CP=1的情况下:若R=0,S=0。则RR=1,SS=1,有 ,状态保持。
图P4.13
解答:根据电路图可知 ,而该电路中的触发器是CP上升沿触发的D触发器,其新态方程为: 。据已知的CP信号波形,可以画出A、B端的输出波形如图A4.13所示。
图A4.13
4.14什么是触发器的空翻现象?造成空翻的原因是什么?
解答:所谓触发器的“空翻”是指在同一个时钟脉冲作用期间触发器状态发生两次或两次以
图A4.17
4.18图P4.18一个扭环计数器,如果电路的初始状态为 ,试画出在一系列CP作用下的 、 、 、 波形(CP数目多于8)。
图P4.18
解答:从电路图可知, (CP上升沿时成立)
如果电路的初始状态为 ,可以画出在一系列CP作用下 、 、 、 的波形如图A4.18所示。
图A4.18
4.19据如图P4.19示的电路,试画出在8个CP作用下 、 、 的波形,假设电路的初始状态为 。
为使主从JK触发器按其特性表正常工作,在CP = 1期间,必须使JK端的状态保持
数字电子技术第四章习题答案

4.8 用4片8线-3线优先编码器组成 线-5线优先编码器。 线优先编码器组成32线 线优先编码器 线优先编码器。 片 线 线优先编码器组成
YS'
1 0 1 0
Y’2(4) 0 1 1 1 1
' YEX
状态 不工作 工作, 工作,但无输入 工作, 工作,且有输入 不可能出现
1 1 0 0
Y’2(3) 1 0 1 1 1
C 0 1 0 1 0 1 0 1
MS 0 1 × 0 × × × 1
ML 0 0 × 1 × × × 1
MS
BC 00 A 0 1 0 x BC 00 0 x
01 1 x
11 0 1
10 x x
ML A 0 1
01 0 x
11 1 1
10 x x
MS=A+B’C ML=B
B ML
《数字电子技术基础》第五版 数字电子技术基础》
《数字电子技术基础》第五版 数字电子技术基础》
4.3
解:输入变量——水位检测结果 输入变量 水位检测结果 来表示, 用A,B,C来表示, , , 来表示 高于检测元件时为“ , 高于检测元件时为“0”, 低于检测元件时为“1”; 低于检测元件时为“ ; 输出变量——水泵工作状态 输出变量 水泵工作状态 用ML,MS分别代表两个水泵 工作为“ ,不工作为“ 。 工作为“1”,不工作为“0”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教材:数字电子技术基础(“十五”国家级规划教材) 杨志忠 卫桦林 郭顺华 编著高等教育出版社2009年7月第2版; 2010年1月 北京 第2次印刷;第四章 组合逻辑电路(部分练习题答案)练习题P172【4.1】、试分析图P4.1所示电路的逻辑功能。
解题思路:根据逻辑图依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
(b )、Y AB AB A B =+=:;(同或功能) 真值表略; 【4.2】、试分析图P4.2所示电路的逻辑功能。
解题思路:根据逻辑图依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
(a )、Y AB AB AB AB A B =⋅=+=⊕;(异或功能) 真值表略; 【4.3】、试分析图P4.3所示电路的逻辑功能。
解题思路:根据逻辑图从输入到输出逐级依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
(a )、()Y ABC A ABC B ABC C ABC A B C ABC ABC =⋅+⋅+⋅=⋅++=+; 真值表略; 【4.4】、试分析图P4.4所示电路的逻辑功能。
解题思路:根据逻辑图从输入到输出逐级依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
解:12 Y A B C Y AB A B C AB A B C =⊕⊕=⋅⊕⋅=+⊕⋅;该逻辑电路实现一位全加运算。
Y1表示本位和数,Y2是进位输出。
mi A B C Y1 Y2 0 0 0 0 0 0 1 0 0 1 1 02 0 1 0 1 03 0 1 1 0 14 1 0 0 1 05 1 0 1 0 16 1 1 0 0 17 1 1 1 1 1【4.6】、写出图P4.6所示电路的逻辑函数表达式,并且把它化成最简与或表达式。
解题思路:变量译码器实现逻辑函数是把逻辑变量输入译码器地址码,译码器输出i i m Y =,再用与非门(输出低电平有效)变换就可以得到所需的逻辑函数,输出函数具有下列的表达形式:(,,)0356m(0,3,5,6)A B C F Y Y Y Y ==∑。
解:(,,)0346(,,)2567m(0,3,4,6) m(2,5,6,7)A A B C B A B C Y Y Y Y Y YY Y Y Y ====∑∑采用卡诺图化简:(,,)A A B C Y B C A C ABC =⋅+⋅+;(,,)B A B C Y AC BC =+;【4.10】、用与非门设计一个数值范围判别电路。
设电路输入A 、B 、C 、D 为表示1位十进制数X 的BCD 码,当X 符合下列条件时,输出Y 为1,否则输出Y=0。
(1)、4≦X ≦8; (2)、X ≦4或X ≥8;解题思路:组合逻辑电路设计题目,按设计步骤完成,本题可以利用X 不大于9的条件(大于9的输入项看作无关项)进一步简化电路。
解:1、逻辑抽象:A 、B 、C 、D 分别表示输入X 的4位二进制代码,Y 2,Y 1表示两种情况的输出。
2、真值表:3、逻辑函数表达式:,,(4,5,6,7,8)d(10,11,12,13,14,15)B C D m +,,(0,1,2,3,4,8,9)d(10,11,12,13,14,15)B C m ∑、函数化简与变换:(利用无关项化简)(卡诺图化简法,化简结果如下)AD CD =mi A B C D Y 2 0 0 0 0 0 0 1 1 0 0 0 1 0 1 2 0 0 1 0 0 1 3 0 0 1 1 0 1 4 0 1 0 0 1 1 5 0 1 0 1 1 06 07 08 19 1 10 1 11 1 12 1 13 1 14 1 15 15、根据表达式画出逻辑电路图:1Y B AD B AD =+=⋅ 2Y B CD B CD =+=⋅【4.13】、用最少的门电路设计一个代码转换电路。
输入为4位格雷码,输出为四位二进制码。
解题思路:组合逻辑电路设计题目,按设计步骤完成,同时考虑多输出函数的硬件复用设计问题,让整个电路实现最低硬件代价。
解:1、逻辑抽象:A 、B 、C 、D 分别表示输入的4位格雷码,Y 3,Y 2,Y 1,Y 0表示输出Y 的4位二进制代码。
2、真值表:(下页) 3、逻辑函数表达式:3(,,,)(8,9,10,11,12,13,14,15)A B C D Y m =∑ 2(,,,)(4,5,6,7,8,9,10,11)A B C D Y m =∑;1(,,,)(2,3,4,5,8,9,14,15)A B C D Y m =∑0(,,,)(1,2,4,7,8,11,13,14)A B C D Y m =∑4、函数化简与变换:(多输出函数化简); (卡诺图化简法,化简结果如下)3Y A =;2Y AB AB A B =+=⊕;1()Y ABC ABC ABC ABC A B C A B C A B C =+++=⊕+⊕⋅=⊕⊕;0 ()()()()Y ABCD ABCD ABCD ABCD ABCD ABCD ABCD ABCDAB C D ABC D ABC D AB C D A B C D A B C D A B C D=+++++++=⊕+⊕+⊕+⊕=⊕⊕+⊕⊕=⊕⊕⊕5、根据表达式画出逻辑电路图:【4.16】、试用输出高电平有效的3线—8线译码器和门电路设计下列组合逻辑电路,其输出逻辑函数为:(2)、Y AB AC BC =⋅⋅;mi A B C D Y 3 Y 2 Y 1 Y 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 3 0 0 1 1 0 0 1 0 2 0 0 1 0 0 0 1 1 6 0 1 1 0 0 1 0 07 0 1 1 1 0 1 0 1 5 0 1 0 1 0 1 1 0 4 0 1 0 0 0 1 1 1 12 1 1 0 0 1 0 0 013 1 1 0 1 1 0 0 1 15 1 1 1 1 1 0 1 014 1 1 1 0 1 0 1 1 10 1 0 1 0 1 1 0 011 1 0 1 1 1 1 0 1 9 1 0 0 1 1 1 1 0 8 1 0 0 0 1 1 1 1解题思路:译码器实现逻辑函数时,输入变量接在地址码端;输出的函数的形式为:01i Y Y Y Y mi =⋅⋅⋅⋅=∑(输出低电平有效);01...i Y Y Y Y mi =+++=∑(输出高电平有效)。
解:3567(3,5,6,7)Y AB AC BC AB AC BC m YY Y Y =⋅⋅=++==+++∑;【4.17】、试用3线—8线译码器CT74LS138和门电路设计多输出组合逻辑电路,其输出逻辑函数为:A B C Y AB ABC Y A B C Y AC BC =+=⊕⊕=+解题思路:译码器实现逻辑函数时,输入变量接在地址码端;输出的函数的形式为:01i Y Y Y Y mi =⋅⋅⋅⋅=∑(输出低电平有效);01...i Y Y Y Y mi =+++=∑(输出高电平有效)。
解:把逻辑函数整理成最小项表达式:(0,6,7)A Y AB ABC m =+=∑;()()(1,2,4,7)B Y A B C AB AB C AB AB C AB AB C m =⊕⊕=+⊕=+++⋅=∑;(1,5,7)C Y AC BC ABC ABC ABC m =+=++=∑;按照01i Y Y Y Y mi =⋅⋅⋅⋅=∑形式和与非门组成电路:74LS1381 2G212076543211(0,6,7)A Y m =∑(1,2,4,7)B Y m =∑(1,5,7)C Y m =∑【4.18】、试用4选1数据选择器和门电路设计下列组合逻辑电路,其输出逻辑函数为:(1)+ (2)Y ABC AC BC Y A B C =+=⊕⊕解题思路:数据选择器实现逻辑函数分三种情况,2n 选一数据选择器实现(1)、n 变量逻辑函数;(2)、n+1变量逻辑函数;(3)、n+2变量逻辑函数;可以采用代数法和卡诺图法求出Di 的值。
关键是求解Di 余函数的值。
01231,,0,1D D A D D ====+Y ABC AC BC=+B C0123,,,D A D A D A D A====Y A B C=⊕⊕A【4.20】、试用8选1数据选择器CT74LS151/CCHCT151和门电路设计下列组合逻辑电路,其输出逻辑函数为:(2) Y A B C =⊕⊕解题思路:数据选择器实现逻辑函数分三种情况,2n 选一数据选择器实现(1)、n 变量逻辑函数;(2)、n+1变量逻辑函数;(3)、n+2变量逻辑函数;可以采用代数法和卡诺图法求出Di 的值。
关键是求解Di 余函数的值。
解:(1,2,4,7)Y A B C m =⊕⊕=∑;(,,)(1,2,4,7)A B C Y A B C m =⊕⊕=∑012345670,1,1,01,0,0,1D D D D D D D D ========【4.21】、试用8选1数据选择器74LS151/CCHCT151和门电路设计下列组合逻辑电路,其输出逻辑函数为:(3)、(,,,)(0,1,2,5,8,10,11,12,13)A B C D Y m =∑解题思路:数据选择器实现逻辑函数分三种情况,2n 选一数据选择器实现(1)、n 变量逻辑函数;(2)、n+1变量逻辑函数;(3)、n+2变量逻辑函数;可以采用代数法和卡诺图法求出Di 的值。
关键是求解Di 余函数的值。
解:(,,,)(0,1,2,5,8,10,11,12,13)A B C D Y m =∑,012345671,1,,10,0D D A D D A D A D D D ========(,,,)(0,1,2,5,8,10,11,12,13)A B C D Y m =∑【4.25】、试判别下列逻辑函数是否存在冒险现象:(2)、()()Y A C B C =++; (3)、Y AB AC BC =++解题思路:用卡诺图法判断是否存在冒险;把逻辑函数用卡诺图表示,如果卡诺圈相切就存在冒险;增加多余项就会消除冒险产生。
()()Y A C B C =++Y AB AC BC=++(2)、A=0,B=0时,C 变量存在冒险; (3)、B=1,C=0时,A 变量存在冒险;A=1,C=0时,B 变量存在冒险;END。
