第二章 结构图的等效变换求系统的传递函数
自动控制原理胡寿松主编课后习题答案详解-胡寿松第六版自控答案

20 db(t) + 5b(t) = 10c(t) dt
且初始条件均为零,试求传递函数 C(s) / R(s) 及 E(s) / R(s)
解:系统结构图及微分方程得:
G(s) = 20
H (s) = 10
6s + 10
20s + 5
20
C(s) = 10G(s) =
方程。 解:
设正常工作点为 A,这时 Q0 = K P0
在该点附近用泰勒级数展开近似为:
y
=
f
(
x0
)
+
df (x) dx
x0
(
x
−
x0
)
即 Q − Q0 = K1 (P − P0 )
其中 K1
= dQ dP P=P0
=
1K 2
1 P0
2-7 设弹簧特性由下式描述:
F = 12.65 y1.1
2-3 试证明图2-58(a)的电网络与(b)的机械系统有相同的数学模型。
2
胡寿松自动控制原理习题解答第二章
图 2-58 电网络与机械系统
1
解:(a):利用运算阻抗法得: Z1
=
R1
//
1 C1s
=
R1 C1s
R1
+
1 C1s
=
R1 = R1 R1C1s + 1 T1s + 1
Z2=Βιβλιοθήκη R2+1 C2s
运动模态 e −0.5t
−1t
所以: x(t) = t − 2(1 − e 2 )
(2) &x&(t) + x&(t) + x(t) = δ (t)。
第二章传递函数案例

解:
系统的结构图为
3. 结构图化简 (结构图的等效变换)
化简目的:
将结构图化简为一个方块,即传递函数。
化简原则:
保证化简前后的代数等价关系不变
等效变换法则
环节串联
环节并联
反馈回路化简
负反馈
正反馈
相加点移动
分支点移动
前移
后移
信号的分支点与相加点不可以互换
例:化简结构图,求取传递函数
阶跃响应曲线
七、比例积分环节 (P-I)
定义:环节输出正比于输入信号和它对时间的积分。
微分方程
1 c( t ) K r t Ti
0 r t dt
t
传递函数
1 G( s) K 1 T s i
阶跃响应曲线
八 、延迟环节
四、惯性环节
定义:环节的输出不能立即复现输入,而是经过 一定时间后才能复现输入的变化。
微分方程 传递函数
dc( t ) T c( t ) Kr ( t ) dt
K G( s) Ts 1
运算放大器
1 1 Rf Rf Cf s Cf s U 2 ( s) U1 ( s ) R1 Rf R1 K Rf Cf s 1 Ts 1
dr ( t ) c( t ) K r ( t ) TD d t
微分方程
传递函数
G( s)
c s r s
K 1 TD s
在放大器上加以 RC 网 络 反 馈 , 当 增益K足够大时
U 2 ( s) U1 ( s ) K 1 1 K RCs 1 K RCs 1 RCs 1 K RCs 1 RC 1 s 1 K K RCs 1 s1
第二章习题解答

第二章2-3 设系统传递函数为342)(2++=s s s G 初始条件0/)0(,1)0(=-=dt dc c 。
求单位阶跃输入r (t)=1(t)时,系统的输出响应c (t)。
【解】系统传递函数与微分方程是一一对应的,故通过传递函数先求出微分方程,然后通过拉氏变换的方法求解微分方程。
系统对应的微分方程为 4()3()2()c c t c t r t ++= 在给定的非零初始条件下,进行拉氏变换22(43)()(0)(0)4(0)s s C s sc c c s++---=整理后2221()(43)(43)s C s s s s s s +=-++++部分分式展开后,拉氏反变换111223242/35/25/6()[()][][](43)(43)13255326t t s c t L C s L L s s s s s s s s e e -----+==-=-+++++++=-+2-4 在图2-48中,已知G (s) 和H (s)两方框对应的微分方程分别为()2()5()4()3()6()c t c t e t b t b t c t +=+=图2-48 习题2-4系统结构框图且初始条件为零,试求传递函数C (s)/R (s)。
【解】求出每个方框的传递函数,利用反馈等效的方法求C(s)/R(s)。
根据定义可得 5()2G s s =+,6()43H s s =+ 255()5()25(43)10075(2)56()1()()(2)(43)30411361(2)(43)C s G s s s s R s G s H s s s s s s s +++====+++++++++2-5 图2-49是由电阻、电容和运算法放大器组成的无源网络和有源网络,试列写以V in (t)为输入量,V out (t)为输出量的传递函数。
(a) (b )(c) (d)图2-49 习题2-5电路图【解】(a) 1211211,1RZ R Z C s RC s C s===+ 22112121211()1()11Z C s RC s G s R Z Z R C C s RC s C s +===+++++(b ) 21122211R Z R Z R Cs R Cs ===+ 2222111211()1R Z R Cs R G s Z R R R Cs +=-==-+ (c) 32321123232321()(1)1()1()1R R R R Cs Cs Z R Z R R Cs R R Cs R R Cs++==+==++++ 323232211132(1)()11()()1R R Cs R R Cs R Z R Cs G s Z R R R R Cs ++++=-=-=-++ (d)本题和(b)、(c)做法图通,因为反馈通路有接地的部分。
第二章习题解题过程和参考答案

第二章习题解题过程和参考答案第二章习题解题过程和参考答案2-1 试建立题2-1图所示各系统的微分方程 [其中外力)(t f ,位移)(t x 和电压)(t u r为输入量;位移)(t y 和电压)(t u c为输出量;k (弹性系数),μ(阻尼系数),R (电阻),C (电容)和m (质量)均为常数]。
解:2-1(a) 取质量m 为受力对象,如图,取向下为力和位移的正方向。
作用在质量块m 上的力有外力f(t),重力mg ,这两个力向下,为正。
有弹簧恢复力[]0)(y t y k +和阻尼力()dy t dtμ,这两个力向上,为负。
其中,0y 为0)(=t f 、物体处于静平衡位置时弹簧的预伸长量。
根据牛顿第二定理F ma ∑=,有[]22()()()()dy t d y t f t mg k y t y m dt dtμ+-+-= 其中:0ky mg =代入上式得22)()()()(dt t y d mdt t dy t ky t f =--μ整理成标准式:22()()()()d y t dy t m ky t f t dt dtμ++=μμ()f t[()k y t +()dy t dt或也可写成:22()()1()()d y t dy t k y t f t dt m dt m mμ++=它是一个二阶线性定常微分方程。
2-1(b) 如图,取A 点为辅助质点,设该点位移为()Ax t ,方向如图。
再取B 点也为辅助质点,则该点位移即为输出量()y t ,方向如图A 点力平衡方程:1()()[()()][]AAdx t dy t k x t x t dt dtμ-=- ① B 点力平衡方程:2()()()[]Adx t dy t k y t dt dtμ=- ②由①和②:12[()()]()A k x t x t k y t -= 得:21()()()Akx t x t y t k=-二边微分:21()()()Adx t k dx t dy t dt dt k dt=-③将③代入②:221()()()()[]k dx t dy t dy t k y t dt k dt dtμ=--整理成标准式:1221()()()k k k dy t dx t y t k dt dtμ++=或也可写成:()A t AB1211212()()()()k k k dy t dx t y t dt k k k k dtμ+=++它是一个一阶线性定常微分方程。
第二章 传递函数-梅逊公式
2.3 传递函数与系统动态结构图
2.3.1 传递函数的定义
设系统的标准微分方程为
an
dnc(t) dt n
a n1
dn1c(t) dt n 1
……
a1
dc(t) dt
a0c(t)
bm
dmr(t) dt m
bm1
d m 1r ( t ) dt m1
……
b1
dr(t) dt
点
上图所示的是
G(s)
(s
(s 1)(s 2) 3)(s 2 2s
2)
的零、极点分布图。
2.2 传递函数
比
比例环节(无惯性环节): c(t)=kr(t)
例
传递函数:G(S)=C(S)/R(S)=k
c(t)
环
阶跃响应:R(S)=1/S
r(t)
节
C(S)=kR(S)=k/S C(t)=k
0
方框图: R(S) k/s C(S)
3
传
递
积分调节器:
C
在A点列方程可得:
函 数
Ur(t)
R
i2
i1
A
Uc(t) i2=i1, i1=Uc(t)/R Uc(t)=1/C∫i2(t)dt=1/(RC)∫Uc(t)dt
设RC=T(积分时间常数),则有:Uc(t)=1/T∫Uc(t)dt
拉氏变换后为:Uc(S)=1/(TS)Uc(S)
5)传递函数具有正、负号(输入量和输出量的变化方向)。
6)传递函数的单位是输出量的单位与输入量的单位之比。
m
(s z j )
7)传递函数可以写成
G(s)
Kg
j1 n
第二章-系统的传递函数方框图及其简化.

系统闭环传递函数
GB (s)
X o (s) Xi (s)
由图可知
X i (s) E(s) G(s)
B(s)
H (s)
X o (s)
E(s) Xi (s) B(s) Xi (s) Xo(s)H (s) Xo(s) G(s)E(s) G(s)[Xi (s) Xo(s)H (s)]
G(s)Xi (s) G(s)Xo(s)H (s) 由此可得:
GK (s) G(s)H (s) E(s)
无量纲.
系统闭环传递函数
GB (s)
X o (s) Xi (s)
注意:我们所指的前向通道的传递函数、反馈回路的
传递函数和开环传递函数都是针对一个闭环系统而
言的。它们都是闭环系统的一部分。系统闭环传递
函数是闭环系统的传递函数。看一个传递函数是什
么具体类型,要从定义出发,而不能只看其符号。
8.分支点和相加点之间等效规则
X1(s)
X1(s) X2(s)
X 2 (s)
X1(s) X2(s)
X1(s)
X 2 (s)
X1(s) X2(s)
X1(s) X2(s)
X 2 (s)
一般应避免分支点和相加点之间的相互移动
三、方框图简化的一般方法 (法1)
1.确定系统的输入量和输出量.若作用在系统上的输 入量或输出量有多个,则必须分别对每一输入量,逐个 进行方框图的简化,以求得各自的传递函数. 2.若方框图中有交叉连接,则利用分支点或相加点的 移动规则,将交叉消除,简化成无交叉的多回路方框图 的形式.(大回路套小回路) 3.对多回路方框图,按照先里后外的顺序依次对各个 回路进行简化. 4.写出系统的传递函数.
Ua (s) 0
黄家英自动控制原理第二版第二章习题答案

6 s
部分分式展开 5 1 −4 Y(s) = + + s+3 s+2 s
∴ y (t ) = −4e −3 t + 5e −2t + 1 , t ≥ 0
已知控制系统的微分方程(或微分方程组) B2.9 已知控制系统的微分方程(或微分方程组)为
式中r(t)为输入量,y(t)为输出量, (t)、 (t)和 式中r(t)为输入量,y(t)为输出量,z1(t)、z2(t)和z3(t) r(t)为输入量 为输出量 为中间变量, 均为常数。 为中间变量,τ、β、K1和K2均为常数。 试求: a)各系统的传递函数Y(s)/R(s);(b)各系统含 各系统的传递函数Y(s)/R(s) 试求:(a)各系统的传递函数Y(s)/R(s);(b)各系统含 有哪些典型环节? 有哪些典型环节?
在图B2.4所示的电路中电压u (t)为输入量 B2.4所示的电路中电压 为输入量, B2.4 在图B2.4所示的电路中电压u1(t)为输入量,试以电 (t)或 (t)作为输出量 分别列写该系统的微分方程。 作为输出量, 压u2(t)或uC2(t)作为输出量,分别列写该系统的微分方程。
B 2.4解: u 2作为输出,应用网络的 复阻抗法: 作为输出, 复阻抗法: Q U 2 (s ) = U 1 (s ) 1 R1 1 C1s + R2 + 1 C 2s R1 + C1s 1 (R 2 + ) C 2s
B2.8 设系统的微分方程为
试用拉氏变换法进行求解。 试用拉氏变换法进行求解。
B 2.8解: 进行拉氏变换 & s 2 Y(s) - (sy(0) + y(0)) + 5sY(s) - 5y(0) + 6Y(s) =
《自动控制原理》第二章传递函数
G2 ( s ) N ( s) 1 + G1 ( s)G 2 ( s) H ( s)
∑ C ( s ) = Φ ( s) R( s) + Φ ( s) N ( s) =
G2 ( s )[G1 ( s) R ( s) + N ( s )] 1 + G1 ( s)G 2 ( s ) H ( s)
20
N ( s)
14
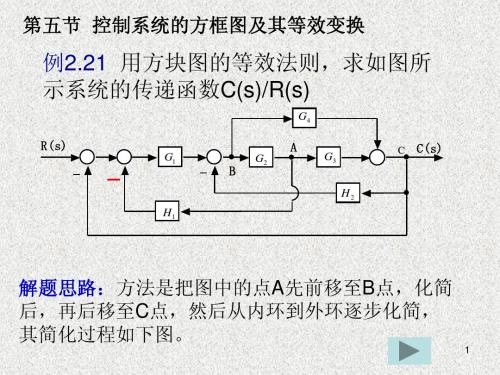
例2.23
R(s)
G4 G1 A G3 H2 H1
C
p1 = G1G2G3
_
-
B
G2
C (s)
∆1 = 1
L1 = −G1 G 2 H 1
p2 = G1G4
∆2 = 1
L2 = − G 2 G 3 H 2 L3 = −G 1 G 2 G3
L4 = − G 4 H 2
注意:回路 注意: 找不全是最 大的问题
5
1 R 1 G1 -1 1 G2 -1 1 G3 -1 K C
1
-1
•前向通路:开始于输入节点,沿支路箭头方向,每个节点 前向通路:开始于输入节点,沿支路箭头方向, 前向通路 只经过一次,最终到达输出节点的通路称之前向通路。 只经过一次,最终到达输出节点的通路称之前向通路。 •回路:起点和终点在同一节点,并与其它节点相遇仅一次的通路。 回路:起点和终点在同一节点,并与其它节点相遇仅一次的通路。 回路 •回路中所有支路的乘积称为回路增益。 回路中所有支路的乘积称为回路增益。 回路中所有支路的乘积称为回路增益 •不接触回路:回路之间没有公共节点时, 不接触回路:回路之间没有公共节点时, 不接触回路 不接触回路。 这种回路叫做 不接触回路。 •在信号流图中,可以有两个或两个以上不接触回路。 在信号流图中, 在信号流图中 可以有两个或两个以上不接触回路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
向同无类用移功动
G2
错!
G2
H1
G3
G1
G2
G1 H1
G4
G1
G2
H1
G4
G1
G2
H1 H1
作用分解
G3 H3
G3 H3 H3
R(s)
A
G1 C
D G2
C(s)
B
当综合点和引出点出现相交叉的情况时,如上 图所示系统,综合点A因为取出点C、D的存在, 取出点因为综合点A、B的存在不能前后移动, 不能用方框图化简的方法来求传递函数,
CCC(s(()ss))
HHH2(22s(()ss)) H3(s)
HHH3(33s(()ss))
C(s)
R(s)
E(S) P1=H–P1G(s1)2=H13 △△1=11=+G1 2HH2 2(s)P1△1= ?
E(s)= R(s)[ (1+G2H2) +(- G3G2H3)] +(–G2H3)N(s)
G3(s)
梅逊公式求E(s)
R(s)
E(SG)GG3(33s(()ss))
RRR(s(()ss)) EEE(S((S)S))
P2= - G3G2H3
GGG1(11s(()ss))
△2= 1 P2△2=?
HHH1(11s(()ss))
G1(s)
NNN((s(ss)))
G2(s)
GGG2(22s(()ss))
由系统结构图绘制 信号流图
R(s) x2E(s)
x1
G1
G4 x3 G2
H1 x6
G4
x4 G3 x5 C(s) H2
1
1
G1 x3 G2
G3
1
R
x1
x2 1
-H1 1
x4 -H2 x5
C
-H2
E
x6
由系统结构图绘制 信号流图
1、支路增益为1的相邻节点,可以合并为一 个节点,但源节点和阱节点不能合并
g H3(s)
△1=1
△2=1+G1H1
G4(s) GCR1((s(s)s))=? G2试(s着) 写出2= G4G3
L1= –G1 H1 L2= – G3 H3 L3= – G1G2G3H3H1 L4= – G4G3
L5 = – G1G2G3 L1L2= (–G1H1) (–G3H3) = G1G3H1H3 L1L4=(–G1H1)(–G4G3)=G1G3G4H1
重要的名词术语
1
d g
a
b
c
x1
x2 e x3 f
x4
x5 1 x5
回路:起点和终点是同一节点,信号通过每一节点 不多于一次的闭合通路,回路增益 La表示
(1)x2、x3、x2,L1=ae
(2)x3、x4、x3,L2=bf
(3)x5、x5,L3=g
不接触回路:回路间没有公共节点
(1)x2、x3、x2和x5、x5 (2)x3、x4、x3和x5、x5
引出点移动
G1(s) H1(s)
H3(s) G1+2(Gs)2GG3H2G213++GG4G3G(G3s(4)3sHG()sG)34 (4s()sH) G3(s4()s)
H2(s)
1 G4 (s)
G1G 2G 3G 4 1+G1G2G3G4H1 +G2G3H2 +G3G4H3
综合点移动 G3 G1
而必须借助梅森(Mason)增益公式。
梅逊公式介绍 R-C : △称为系统特征式
C(s) R(s)
=
∑Pk△k △
△= 1 - ∑La + ∑LbLc -∑LdLeLf+…
其中:
— ∑La 所有单独回路增益之和
∑LbLc—所有两两互不接触回路增益乘积之和
∑LdLeLf—所有三个互不接触回路增益乘积之和
Pk—从R(s)到C(s)的第k条前向通路传递函数
△k称为第k条前向通路的余子式
△k求法: 去掉第k条前向通路后所求的△
△k=1-∑LA+ ∑LBLC- ∑LDLELF+…
梅逊公式例R-C
R(s)
a
c b
G4(s)
GG11((ss)) d
f
GG22((ss) )
GG33((ss)) h C(s)
H1(s) e
x4
x5 1 x5
源节点(输入节点):只有输出没有输入 x1
阱节点(输出节点):只有输入没有输出 x5 混合节点:既有输入也有输出 x2、x3、x4、x5 前向通路:从输入到输出,每个节点只通过一次, 前向通路增益:通路上各支路增益之乘积, pk
(1)x1、x2、x3、x4、x5、x6,前向通路增益p1=abc (2)x1、x2、x5,前向通路增益p2 =d
2、在结构图比较点之前没有引出点,只需要 在比较点后设置一个节点便可
3、在比较点之前有引出点,就需在引出点和 比较点各设置一个节点,分别标志两个变 量,它们之间的支路增益是1
本章小结
数学模型:微分方程、传递函数、结构图、 信号流图及其相互间的关系
用解析法建立系统输入输出的数学模型— 微分方程
由结构图等效变换求传递函数 由梅森(Mason)增益公式求传递函数
1 - G1H1 + G2H2 + G1G2H3 -G1H1G2 H2
信号流图
信号流图起源于梅森利用图示法来描述一 个或一组线性代数方程式,它是由节点和 支路组成的一种信号传递网络。
节点,表示信号,等于输入信号的代数和 K 支路,表示增益和信号的流动方向
重要的名词术语
1
d g
a
b
c
x1
x2 e x3 f
