2017年中考总复习—关于圆的经典题型汇总(含答案)
2017中考复习-圆综合题
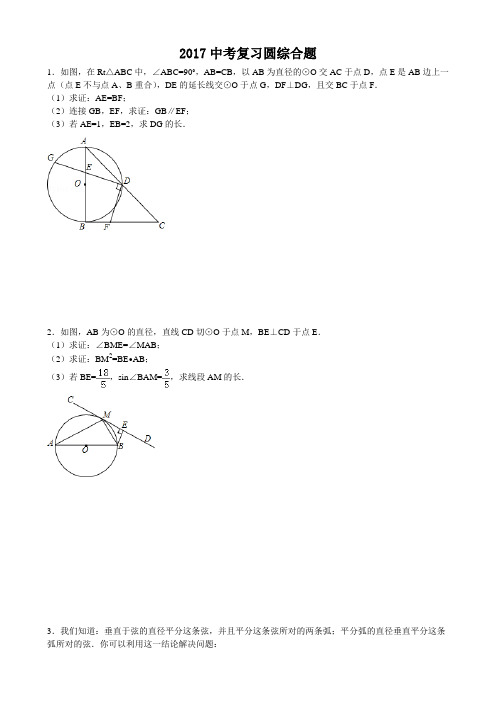
2017中考复习圆综合题1.如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.(1)求证:AE=BF;(2)连接GB,EF,求证:GB∥EF;(3)若AE=1,EB=2,求DG的长.2.如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.(1)求证:∠BME=∠MAB;(2)求证:BM2=BE•AB;(3)若BE=,sin∠BAM=,求线段AM的长.3.我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:如图,点P在以MN(南北方向)为直径的⊙O上,MN=8,PQ⊥MN交⊙O于点Q,垂足为H,PQ≠MN,弦PC、PD分别交MN于点E、F,且PE=PF.(1)比较与的大小;(2)若OH=2,求证:OP∥CD;(3)设直线MN、CD相交所成的锐角为α,试确定cosα=时,点P的位置.4.如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.(1)求证:BE是⊙O的切线;(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BG•BA=48,FG=,DF=2BF,求AH 的值.5.如图,在平面直角坐标系中,O(0,0),A(0,﹣6),B(8,0)三点在⊙P上.(1)求圆的半径及圆心P的坐标;(2)M为劣弧的中点,求证:AM是∠OAB的平分线;(3)连接BM并延长交y轴于点N,求N,M点的坐标.6.如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG,已知DE=4,AE=8.(1)求证:DF是⊙O的切线;(2)求证:OC2=OE•OP;(3)求线段EG的长.7.如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.(1)求证:AB是⊙O的切线.(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=,求的值.(3)在(2)的条件下,设⊙O的半径为3,求AB的长.8.如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.(1)判断直线l与⊙O的位置关系,并说明理由;(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;(3)在(2)的条件下,若DE=4,DF=3,求AF的长.9.如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH.(1)求证:MH为⊙O的切线.(2)若MH=,tan∠ABC=,求⊙O的半径.(3)在(2)的条件下分别过点A、B作⊙O的切线,两切线交于点D,AD与⊙O相切于N点,过N点作NQ⊥BC,垂足为E,且交⊙O于Q点,求线段NQ的长度.10.已知:△ABC内接于⊙O,D是上一点,OD⊥BC,垂足为H.(1)如图1,当圆心O在AB边上时,求证:AC=2OH;(2)如图2,当圆心O在△ABC外部时,连接AD、CD,AD与BC交于点P,求证:∠ACD=∠APB;(3)在(2)的条件下,如图3,连接BD,E为⊙O上一点,连接DE交BC于点Q、交AB于点N,连接OE,BF为⊙O的弦,BF⊥OE于点R交DE于点G,若∠ACD﹣∠ABD=2∠BDN,AC=5,BN=3,tan∠ABC=,求BF的长.11.如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.(1)求证:AE为⊙O的切线.(2)当BC=8,AC=12时,求⊙O的半径.(3)在(2)的条件下,求线段BG的长.12.已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.(1)求证:BD是⊙O的切线;(2)求证:CE2=EH•EA;(3)若⊙O的半径为5,sinA=,求BH的长.13.已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.①判断OQ与AC的位置关系,并说明理由;②求线段PQ的长.14.已知:⊙O上两个定点A,B和两个动点C,D,AC与BD交于点E.(1)如图1,求证:EA•EC=EB•ED;(2)如图2,若=,AD是⊙O的直径,求证:AD•AC=2BD•BC;(3)如图3,若AC⊥BD,点O到AD的距离为2,求BC的长.15.如图,在直角坐标系中,⊙M经过原点O(0,0),点A(,0)与点B(0,﹣),点D在劣弧上,连接BD交x轴于点C,且∠COD=∠CBO.(1)求⊙M的半径;(2)求证:BD平分∠ABO;(3)在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.16.如图,AB是⊙O的直径,C、G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA 的延长线于点E,连接BC,交OD于点F.(1)求证:CD是⊙O的切线.(2)若,求∠E的度数.(3)连接AD,在(2)的条件下,若CD=,求AD的长.17.如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.(1)用关于x的代数式表示BQ,DF.(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.(3)在点P的整个运动过程中,①当AP为何值时,矩形DEGF是正方形?②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案).18.如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O 于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.(1)求证:AC平分∠BAD;(2)探究线段PB,AB之间的数量关系,并说明理由;(3)若AD=3,求△ABC的面积.19.如图,AB是⊙O的直径,AB=6,过点O作OH⊥AB交圆于点H,点C是弧AH上异于A、H的动点,过点C作CD⊥OA,CE⊥OH,垂足分别为D、E,过点C的直线交OA的延长线于点G,且∠GCD=∠CED.(1)求证:GC是⊙O的切线;(2)求DE的长;(3)过点C作CF⊥DE于点F,若∠CED=30°,求CF的长.20.如图1,水平放置一个三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,AB=BC=6cm,OD=3cm,开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动.(1)当B与O重合的时候,求三角板运动的时间;(2)如图2,当AC与半圆相切时,求AD;(3)如图3,当AB和DE重合时,求证:CF2=CG•CE.21.⊙O是△ABC的外接圆,AB是直径,过的中点P作⊙O的直径PG交弦BC于点D,连接AG、CP、PB.(1)如图1,若D是线段OP的中点,求∠BAC的度数;(2)如图2,在DG上取一点K,使DK=DP,连接CK,求证:四边形AGKC是平行四边形;(3)如图3,取CP的中点E,连接ED并延长ED交AB于点H,连接PH,求证:PH⊥AB.22.如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.(1)试说明CE是⊙O的切线;(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;(3)设点D是线段AC上任意一点(不含端点),连接OD,当CD+OD的最小值为6时,求⊙O的直径AB的长.23.AB,CD是⊙O的两条弦,直线AB,CD互相垂直,垂足为点E,连接AD,过点B作BF⊥AD,垂足为点F,直线BF交直线CD于点G.(1)如图1,当点E在⊙O外时,连接BC,求证:BE平分∠GBC;(2)如图2,当点E在⊙O内时,连接AC,AG,求证:AC=AG;(3)如图3,在(2)条件下,连接BO并延长交AD于点H,若BH平分∠ABF,AG=4,tan∠D=,求线段AH的长.24.已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD,BD交AC于点F.(1)求证:BD平分∠ABC;(2)延长AC到点P,使PF=PB,求证:PB是⊙O的切线;(3)如果AB=10,cos∠ABC=,求AD.25.如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别于EF,GF交于I,H两点.(1)求∠FDE的度数;(2)试判断四边形FACD的形状,并证明你的结论;(3)当G为线段DC的中点时,①求证:FD=FI;②设AC=2m,BD=2n,求⊙O的面积与菱形ABCD的面积之比.26.已知,如图,AB是半圆O的直径,弦CD∥AB,动点P,Q分别在线段OC,CD上,且DQ=OP,AP的延长线与射线OQ相交于点E,与弦CD相交于点F(点F与点C,D不重合),AB=20,cos∠AOC=,设OP=x,△CPF的面积为y.(1)求证:AP=OQ;(2)求y关于x的函数关系式,并写出它的定义域;(3)当△OPE是直角三角形时,求线段OP的长.27.已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O于点E.(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.①若CF=CD时,求sin∠CAB的值;②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)28.如图1,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2.过点D作DF∥BC,交AB的延长线于点F.(1)求证:DF为⊙O的切线;(2)若∠BAC=60°,DE=,求图中阴影部分的面积;(3)若=,DF+BF=8,如图2,求BF的长.29.在△ABC的外接圆⊙O中,△ABC的外角平分线CD交⊙O于点D,F为上﹣点,且=连接DF,并延长DF交BA的延长线于点E.(1)判断DB与DA的数量关系,并说明理由;(2)求证:△BCD≌△AFD;(3)若∠ACM=120°,⊙O的半径为5,DC=6,求DE的长.30.如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.(1)如图1,求⊙O的半径;(2)如图1,若点E是BC的中点,连接PE,求PE的长度;(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.答案1.(2016•包头)如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E 是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.(1)求证:AE=BF;(2)连接GB,EF,求证:GB∥EF;【分析】(1)连接BD,由三角形ABC为等腰直角三角形,求出∠A与∠C的度数,根据AB为圆的直径,利用圆周角定理得到∠ADB为直角,即BD垂直于AC,利用直角三角形斜边上的中线等于斜边的一半,得到AD=DC=BD=AC,进而确定出∠A=∠FBD,再利用同角的余角相等得到一对角相等,利用ASA得到三角形AED与三角形BFD全等,利用全等三角形对应边相等即可得证;(2)连接EF,BG,由三角形AED与三角形BFD全等,得到ED=FD,进而得到三角形DEF为等腰直角三角形,利用圆周角定理及等腰直角三角形性质得到一对同位角相等,利用同位角相等两直线平行即可得证;(3)由全等三角形对应边相等得到AE=BF=1,在直角三角形BEF中,利用勾股定理求出EF的长,利用锐角三角形函数定义求出DE的长,利用两对角相等的三角形相似得到三角形AED与三角形GEB相似,由相似得比例,求出GE的长,由GE+ED求出GD的长即可.【解答】(1)证明:连接BD,在Rt△ABC中,∠ABC=90°,AB=BC,∴∠A=∠C=45°,∵AB为圆O的直径,∴∠ADB=90°,即BD⊥AC,∴AD=DC=BD=AC,∠CBD=∠C=45°,∴∠A=∠FBD,∵DF⊥DG,∴∠FDG=90°,∴∠FDB+∠BDG=90°,∵∠EDA+∠BDG=90°,∴∠EDA=∠FDB,在△AED和△BFD中,,∴△AED≌△BFD(ASA),∴AE=BF;(2)证明:连接EF,BG,∵△AED≌△BFD,∴DE=DF,∵∠EDF=90°,∴△EDF是等腰直角三角形,∴∠DEF=45°,∵∠G=∠A=45°,∴∠G=∠DEF,(3)∵AE=BF,AE=1,∴BF=1,在Rt△EBF中,∠EBF=90°,∴根据勾股定理得:EF2=EB2+BF2,∵EB=2,BF=1,∴EF==,∵△DEF为等腰直角三角形,∠EDF=90°,∴cos∠DEF=,∵EF=,∴DE=×=,∵∠G=∠A,∠GEB=∠AED,∴△GEB∽△AED,∴=,即GE•ED=AE•EB,∴•GE=2,即GE=,则GD=GE+ED=.【点评】此题属于圆综合题,涉及的知识有:全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,圆周角定理,以及平行线的判定与性质,熟练掌握判定与性质是解本题的关键.2.(2016•青海)如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.(1)求证:∠BME=∠MAB;(2)求证:BM2=BE•AB;(3)若BE=,sin∠BAM=,求线段AM的长.【分析】(1)由切线的性质得出∠BME+∠OMB=90°,再由直径得出∠AMB=90°,利用同角的余角相等判断出结论;(3)先在Rt△BEM中,用三角函数求出BM,再在Rt△ABM中,用三角函数和勾股定理计算即可.【解答】解:(1)如图,连接OM,∵直线CD切⊙O于点M,∴∠OMD=90°,∴∠BME+∠OMB=90°,∵AB为⊙O的直径,∴∠AMB=90°.∴∠AMO+∠OMB=90°,∴∠BME=∠AMO,∵OA=OM,∴∠MAB=∠AMO,∴∠BME=∠MAB;(2)由(1)有,∠BME=∠MAB,∵BE⊥CD,∴∠BEM=∠AMB=90°,∴△BME∽△BAM,∴,∴BM2=BE•AB;(3)由(1)有,∠BME=∠MAB,∵sin∠BAM=,∴sin∠BME=,在Rt△BEM中,BE=,∴sin∠BME==,∴BM=6,在Rt△ABM中,sin∠BAM=,∴sin∠BAM==,∴AB=BM=10,根据勾股定理得,AM=8.【点评】此题是圆的综合题,主要考查了切线的性质,直径所对的圆周角是直径,相似三角形的性质和判定,三角函数,解本题的关键是判断出,△BME∽△BAM.3.(2016•泉州)我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:如图,点P在以MN(南北方向)为直径的⊙O上,MN=8,PQ⊥MN交⊙O于点Q,垂足为H,PQ≠MN,弦PC、PD分别交MN于点E、F,且PE=PF.(1)比较与的大小;(2)若OH=2,求证:OP∥CD;(3)设直线MN、CD相交所成的锐角为α,试确定cosα=时,点P的位置.【分析】(1)根据等腰三角形的性质,由PE=PF,PH⊥EF可判断PH平分∠FPE,然后根据圆周角定理得到=;(2)连结CD、OP、OQ,OQ交CD于B,如图,先计算出PH=2,则可判断△OPH为等腰直角三角形得到∠OPQ=45°,再判断△OPQ为等腰直角三角形得到∠POQ=90°,然后根据垂径的推理由=得到OQ⊥CD,则根据平行线的判定方法得OP∥CD;(3)直线CD交MN于A,如图,由特殊角的三角函数值得∠α=30°,即直线MN、CD相交所成的锐角为30°,利用OB⊥CD得到∠AOB=60°,则∠POH=60°,然后在Rt△POH中利用正弦的定义计算出PH即可.【解答】(1)解:∵PE=PF,PH⊥EF,∴PH平分∠FPE,∴∠DPQ=∠CPQ,∴=;(2)证明:连结CD、OP、OQ,OQ交CD于B,如图,∵OH=2,OP=4,∴PH==2,∴△OPH为等腰直角三角形,∴∠OPQ=45°,而OP=OQ,∴△OPQ为等腰直角三角形,∴∠POQ=90°,∴OP⊥OQ,∵=,∴OQ⊥CD,(3)解:直线CD交MN于A,如图,∵cosα=,∴∠α=30°,即直线MN、CD相交所成的锐角为30°,而OB⊥CD,∴∠AOB=60°,∵OH⊥PQ,∴∠POH=60°,在Rt△POH中,∵sin∠POH=,∴PH=4sin60°=2,即点P到MN的距离为2.【点评】本题考查了圆的综合题:熟练掌握垂径定理及其推理、圆周角定理;能够灵活应用等腰直角三角形的性质和三角函数进行几何计算.4.(2016•泸州)如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.(1)求证:BE是⊙O的切线;(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BG•BA=48,FG=,DF=2BF,求AH 的值.【分析】(1)欲证明BE是⊙O的切线,只要证明∠EBD=90°.(2)由△ABC∽△CBG,得=求出BC,再由△BFC∽△BCD,得BC2=BF•BD求出BF,CF,CG,GB,再通过计算发现CG=AG,进而可以证明CH=CB,求出AC即可解决问题.【解答】(1)证明:连接CD,∵BD是直径,∴∠BCD=90°,即∠D+∠CBD=90°,∵∠A=∠D,∠A=∠EBC,∴∠CBD+∠EBC=90°,∴BE是⊙O切线.(2)解:∵CG∥EB,∴∠BCG=∠EBC,∴∠A=∠BCG,∵∠CBG=∠ABC∴△ABC∽△CBG,∴=,即BC2=BG•BA=48,∴BC=4,∵CG∥EB,∴CF⊥BD,∴△BFC∽△BCD,∴BC2=BF•BD,∵DF=2BF,∴BF=4,在RT△BCF中,CF==4,∴CG=CF+FG=5,在RT△BFG中,BG==3,∵BG•BA=48,∴即AG=5,∴CG=AG,∴∠A=∠ACG=∠BCG,∠CFH=∠CFB=90°,∴∠CHF=∠CBF,∴CH=CB=4,∵△ABC∽△CBG,∴=,∴AC==,∴AH=AC﹣CH=.【点评】本题考查切线的判定、圆的有关知识、相似三角形的判定和性质、勾股定理.等腰三角形的判定和性质等知识,解题的关键是巧妙利用相似三角形的性质解决问题,属于中考压轴题.5.(2016•赤峰)如图,在平面直角坐标系中,O(0,0),A(0,﹣6),B(8,0)三点在⊙P上.(1)求圆的半径及圆心P的坐标;(2)M为劣弧的中点,求证:AM是∠OAB的平分线;(3)连接BM并延长交y轴于点N,求N,M点的坐标.【分析】(1)先利用勾股定理计算出AB=10,再利用圆周角定理的推理可判断AB为⊙P的直径,则得到⊙P的半径是5,然后利用线段的中点坐标公式得到P点坐标;(2)根据圆周角定理由=,∠OAM=∠MAB,于是可判断AM为∠OAB的平分线;(3)连接PM交OB于点Q,如图,先利用垂径定理的推论得到PM⊥OB,BQ=OQ=OB=4,再利用勾股定理计算出PQ=3,则MQ=2,于是可写出M点坐标,接着证明MQ为△BON的中位线得到ON=2MQ=4,然后写出N点的坐标.【解答】解:(1)∵O(0,0),A(0,﹣6),B(8,0),∴OA=6,OB=8,∴AB==10,∵∠AOB=90°,∴AB为⊙P的直径,∴⊙P的半径是5∵点P为AB的中点,∴P(4,﹣3);(2)∵M点是劣弧OB的中点,∴=,∴∠OAM=∠MAB,∴AM为∠OAB的平分线;(3)连接PM交OB于点Q,如图,∵=,∴PM⊥OB,BQ=OQ=OB=4,在Rt△PBQ中,PQ===3,∴MQ=2,∴M点的坐标为(4,2);∵MQ∥ON,而OQ=BQ,∴MQ为△BON的中位线,∴ON=2MQ=4,∴N点的坐标为(0,4).【点评】本题考查了圆的综合题:熟练掌握垂径定理和圆周角定理;理解坐标与图形的性质,记住线段的中点坐标公式,会利用勾股定理计算线段的长.此类题目通常解由半径、弦心距和弦的一半所组成的直角三角形.6.(2016•恩施州)如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF 的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG,已知DE=4,AE=8.(1)求证:DF是⊙O的切线;(2)求证:OC2=OE•OP;(3)求线段EG的长.【分析】(1)连接OD,由等腰三角形的性质得出∠DAB=∠ADO,再由已知条件得出∠ADO=∠DAF,证出OD∥AF,由已知DF⊥AF,得出DF⊥OD,即可得出结论;(2)由射影定理得出OD2=OE•OP,由OC=OD,即可得出OC2=OE•OP;(3)由垂径定理得出DE=CE=4,∠OEC=90°,由相交弦定理得出DE2=AE×BE,求出BE=2,得出直径CG=AB=AE+BE=10,半径OC=CG=5,由三角函数的定义得出cosC==,在△CEG中,由余弦定理求出EG2,即可得出EG的长.【解答】(1)证明:连接OD,如图所示:∵OA=OD,∴∠DAB=∠ADO,∵∠DAF=∠DAB,∴∠ADO=∠DAF,∴OD∥AF,又∵DF⊥AF,∴DF⊥OD,∴DF是⊙O的切线;(2)证明:由(1)得:DF⊥OD,∴∠ODF=90°,∵AB⊥CD,∴由射影定理得:OD2=OE•OP,∵OC=OD,∴OC2=OE•OP;(3)解:∵AB⊥CD,∴DE=CE=4,∠OEC=90°,由相交弦定理得:DE2=AE×BE,即42=8×BE,解得:BE=2,∴CG=AB=AE+BE=8+2=10,∴OC=CG=5,∴cosC==,在△CEG中,由余弦定理得:EG2=CG2+CE2﹣2×CG×CE×cosC=102+42﹣2×10×4×=52,∴EG==2.【点评】本题是圆的综合题目,考查了切线的判定、等腰三角形的性质、平行线的判定、射影定理、相交弦定理、余弦定理、三角函数等知识;本题综合性强,有一定难度,特别是(3)中,需要运用相交弦定理、三角函数和余弦定理采才能得出结果.7.(2016•鄂州)如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.(1)求证:AB是⊙O的切线.(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=,求的值.(3)在(2)的条件下,设⊙O的半径为3,求AB的长.【分析】(1)由于题目没有说明直线AB与⊙O有交点,所以过点O作OF⊥AB于点F,然后证明OC=OF 即可;(2)连接CE,先求证∠ACE=∠ODC,然后可知△ACE∽△ADC,所以,而tan∠D==;(3)由(2)可知,AC2=AE•AD,所以可求出AE和AC的长度,由(1)可知,△OFB∽△ABC,所以,然后利用勾股定理即可求得AB的长度.【解答】(1)如图,过点O作OF⊥AB于点F,∵AO平分∠CAB,OC⊥AC,OF⊥AB,∴OC=OF,∴AB是⊙O的切线;(2)如图,连接CE,∵ED是⊙O的直径,∴∠ECD=90°,∴∠ECO+∠OCD=90°,∵∠ACB=90°,∴∠ACE+∠ECO=90°,∴∠ACE=∠OCD,∵OC=OD,∴∠OCD=∠ODC,∴∠ACE=∠ODC,∵∠CAE=∠CAE,∴△ACE∽△ADC,∴,∵tan∠D=,∴=,∴=;(3)由(2)可知:=,∴设AE=x,AC=2x,∵△ACE∽△ADC,∴,∴AC2=AE•AD,∴(2x)2=x(x+6),解得:x=2或x=0(不合题意,舍去),∴AE=2,AC=4,由(1)可知:AC=AF=4,∠OFB=∠ACB=90°,∵∠B=∠B,∴△OFB∽△ACB,∴=,设BF=a,∴BC=,∴BO=BC﹣OC=﹣3,在Rt△BOF中,BO2=OF2+BF2,∴(﹣3)2=32+a2,∴解得:a=或a=0(不合题意,舍去),∴AB=AF+BF=.【点评】本题考查圆的综合问题,解题的关键是证明△ACE∽△ADC.本题涉及勾股定理,解方程,圆的切线判定知识,内容比较综合,需要学生构造辅助线才能解决问题,对学生综合能力要求较高.8.(2016•德州)如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E 做直线l∥BC.(1)判断直线l与⊙O的位置关系,并说明理由;(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;(3)在(2)的条件下,若DE=4,DF=3,求AF的长.【分析】(1)连接OE、OB、OC.由题意可证明,于是得到∠BOE=∠COE,由等腰三角形三线合一的性质可证明OE⊥BC,于是可证明OE⊥l,故此可证明直线l与⊙O相切;(2)先由角平分线的定义可知∠ABF=∠CBF,然后再证明∠CBE=∠BAF,于是可得到∠EBF=∠EFB,最后依据等角对等边证明BE=EF即可;(3)先求得BE的长,然后证明△BED∽△AEB,由相似三角形的性质可求得AE的长,于是可得到AF 的长.【解答】解:(1)直线l与⊙O相切.理由:如图1所示:连接OE、OB、OC.∵AE平分∠BAC,∴∠BAE=∠CAE.∴.∴∠BOE=∠COE.又∵OB=OC,∴OE⊥BC.∵l∥BC,∴OE⊥l.∴直线l与⊙O相切.(2)∵BF平分∠ABC,∴∠ABF=∠CBF.又∵∠CBE=∠CAE=∠BAE,∴∠CBE+∠CBF=∠BAE+∠ABF.又∵∠EFB=∠BAE+∠ABF,∴∠EBF=∠EFB.∴BE=EF.(3)由(2)得BE=EF=DE+DF=7.∵∠DBE=∠BAE,∠DEB=∠BEA,∴△BED∽△AEB.∴,即,解得;AE=.∴AF=AE﹣EF=﹣7=.【点评】本题主要考查的是圆的性质、相似三角形的性质和判定、等腰三角形的性质、三角形外角的性质、切线的判定,证得∠EBF=∠EFB是解题的关键.9.(2016•大庆)如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC 的中点,连接MH.(1)求证:MH为⊙O的切线.(2)若MH=,tan∠ABC=,求⊙O的半径.(3)在(2)的条件下分别过点A、B作⊙O的切线,两切线交于点D,AD与⊙O相切于N点,过N点作NQ⊥BC,垂足为E,且交⊙O于Q点,求线段NQ的长度.【分析】(1)连接OH、OM,易证OH是△ABC的中位线,利用中位线的性质可证明△COH≌△MOH,所以∠HCO=∠HMO=90°,从而可知MH是⊙O的切线;(2)由切线长定理可知:MH=HC,再由点M是AC的中点可知AC=3,由tan∠ABC=,所以BC=4,从而可知⊙O的半径为2;(3)连接CN,AO,CN与AO相交于I,由AC、AN是⊙O的切线可知AO⊥CN,利用等面积可求出可求得CI的长度,设CE为x,然后利用勾股定理可求得CE的长度,利用垂径定理即可求得NQ.【解答】解:(1)连接OH、OM,∵H是AC的中点,O是BC的中点,∴OH是△ABC的中位线,∴OH∥AB,∴∠COH=∠ABC,∠MOH=∠OMB,又∵OB=OM,∴∠OMB=∠MBO,∴∠COH=∠MOH,在△COH与△MOH中,,∴△COH≌△MOH(SAS),∴∠HCO=∠HMO=90°,∴MH是⊙O的切线;(2)∵MH、AC是⊙O的切线,∴HC=MH=,∴AC=2HC=3,∵tan∠ABC=,∴=,∴BC=4,∴⊙O的半径为2;(3)连接OA、CN、ON,OA与CN相交于点I,∵AC与AN都是⊙O的切线,∴AC=AN,AO平分∠CAD,∴AO⊥CN,∵AC=3,OC=2,∴由勾股定理可求得:AO=,∵AC•OC=AO•CI,∴CI=,∴由垂径定理可求得:CN=,设OE=x,由勾股定理可得:CN2﹣CE2=ON2﹣OE2,∴﹣(2+x)2=4﹣x2,∴x=,∴OE=,由勾股定理可求得:EN=,∴由垂径定理可知:NQ=2EN=.【点评】本题考查圆的综合问题,涉及垂径定理,勾股定理,全等三角形的判定与性质,切线的判定等知识内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.10.(2016•哈尔滨)已知:△ABC内接于⊙O,D是上一点,OD⊥BC,垂足为H.(1)如图1,当圆心O在AB边上时,求证:AC=2OH;(2)如图2,当圆心O在△ABC外部时,连接AD、CD,AD与BC交于点P,求证:∠ACD=∠APB;(3)在(2)的条件下,如图3,连接BD,E为⊙O上一点,连接DE交BC于点Q、交AB于点N,连接OE,BF为⊙O的弦,BF⊥OE于点R交DE于点G,若∠ACD﹣∠ABD=2∠BDN,AC=5,BN=3,tan∠ABC=,求BF的长.【分析】(1)OD⊥BC可知点H是BC的中点,又中位线的性质可得AC=2OH;(2)由垂径定理可知:,所以∠BAD=∠CAD,由因为∠ABC=∠ADC,所以∠ACD=∠APB;(3)由∠ACD﹣∠ABD=2∠BDN可知∠AND=90°,由tan∠ABC=可知NQ和BQ的长度,再由BF⊥OE和OD⊥BC可知∠GBN=∠ABC,所以BG=BQ,连接AO并延长交⊙O于点I,连接IC后利用圆周角定理可求得IC和AI的长度,设QH=x,利用勾股定理可求出QH和HD的长度,利用垂径定理可求得ED的长度,最后利用tan∠OED=即可求得RG的长度,最后由垂径定理可求得BF的长度.【解答】解:(1)∵OD⊥BC,∴由垂径定理可知:点H是BC的中点,∵点O是AB的中点,∴OH是△ABC的中位线,∴AC=2OH;(2)∵OD⊥BC,∴由垂径定理可知:,∴∠BAD=∠CAD,∵,∴∠ABC=∠ADC,∴180°﹣∠BAD﹣∠ABC=180°﹣∠CAD﹣∠ADC,∴∠ACD=∠APB,(3)连接AO延长交于⊙O于点I,连接IC,AB与OD相交于点M,∵∠ACD﹣∠ABD=2∠BDN,∴∠ACD﹣∠BDN=∠ABD+∠BDN,∵∠ABD+∠BDN=∠AND,∴∠ACD﹣∠BDN=∠AND,∵∠ACD+∠ABD=180°,∴∠ABD+∠BDN=180°﹣∠AND,∴∠AND=180°﹣∠AND,∴∠AND=90°,∵tan∠ABC=,BN=3,∴NQ=,∴由勾股定理可求得:BQ=,∵∠BNQ=∠QHD=90°,∴∠ABC=∠QDH,∵OE=OD,∴∠OED=∠QDH,∵∠ERG=90°,∴∠OED=∠GBN,∴∠GBN=∠ABC,∵AB⊥ED,∴BG=BQ=,GN=NQ=,∵AI是⊙O直径,∴∠ACI=90°,∵tan∠AIC=tan∠ABC=,∴=,∴IC=10,∴由勾股定理可求得:AI=25,连接OB,设QH=x,∵tan∠ABC=tan∠ODE=,∴,∴HD=2x,∴OH=OD﹣HD=﹣2x,BH=BQ+QH=+x,由勾股定理可得:OB2=BH2+OH2,∴()2=(+x)2+(﹣2x)2,解得:x=或x=,当QH=时,∴QD=QH=,∴ND=QD+NQ=6,∴MN=3,MD=15∵MD>,∴QH=不符合题意,舍去,当QH=时,∴QD=QH=∴ND=NQ+QD=4,由垂径定理可求得:ED=10,∴GD=GN+ND=∴EG=ED﹣GD=,∵tan∠OED=,∴,∴EG=RG,∴RG=,∴BR=RG+BG=12∴由垂径定理可知:BF=2BR=24.【点评】本题考查圆的综合问题,涉及圆周角定理,中位线的性质,锐角三角函数,勾股定理等知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.11.(2015•鄂州)如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.(1)求证:AE为⊙O的切线.(2)当BC=8,AC=12时,求⊙O的半径.(3)在(2)的条件下,求线段BG的长.【分析】(1)连接OM.利用角平分线的性质和平行线的性质得到AE⊥OM后即可证得AE是⊙O的切线;(2)设⊙O的半径为R,根据OM∥BE,得到△OMA∽△BEA,利用平行线的性质得到=,即可解得R=3,从而求得⊙O的半径为3;(3)过点O作OH⊥BG于点H,则BG=2BH,根据∠OME=∠MEH=∠EHO=90°,得到四边形OMEH是矩形,从而得到HE=OM=3和BH=1,证得结论BG=2BH=2.【解答】(1)证明:连接OM.∵AC=AB,AE平分∠BAC,∴AE⊥BC,CE=BE=BC=4,∵OB=OM,∴∠OBM=∠OMB,∵BM平分∠ABC,∴∠OBM=∠CBM,∴∠OMB=∠CBM,∴OM∥BC又∵AE⊥BC,∴AE⊥OM,∴AE是⊙O的切线;(2)设⊙O的半径为R,∵OM∥BE,∴△OMA∽△BEA,∴=即=,解得R=3,∴⊙O的半径为3;(3)过点O作OH⊥BG于点H,则BG=2BH,∵∠OME=∠MEH=∠EHO=90°,∴四边形OMEH是矩形,∴HE=OM=3,∴BH=1,∴BG=2BH=2.【点评】本题考查了圆的综合知识,题目中还运用到了切线的判定与性质、相似三角形的判定与性质,综合性较强,难度较大.12.(2015•荆门)已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.(1)求证:BD是⊙O的切线;(2)求证:CE2=EH•EA;(3)若⊙O的半径为5,sinA=,求BH的长.【分析】(1)由圆周角定理和已知条件证出∠ODB=∠ABC,再证出∠ABC+∠DBF=90°,即∠OBD=90°,即可得出BD是⊙O的切线;(2)连接AC,由垂径定理得出,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例,即可得出结论;(3)连接BE,由圆周角定理得出∠AEB=90°,由三角函数求出BE,再根据勾股定理求出EA,得出BE=CE=6,由(2)的结论求出EH,然后根据勾股定理求出BH即可.【解答】(1)证明:∵∠ODB=∠AEC,∠AEC=∠ABC,∴∠ODB=∠ABC,∵OF⊥BC,∴∠BFD=90°,∴∠ODB+∠DBF=90°,∴∠ABC+∠DBF=90°,即∠OBD=90°,∴BD⊥OB,∴BD是⊙O的切线;(2)证明:连接AC,如图1所示:∵OF⊥BC,∴,∴∠CAE=∠ECB,∵∠CEA=∠HEC,∴△CEH∽△AEC,∴,∴CE2=EH•EA;(3)解:连接BE,如图2所示:∵AB是⊙O的直径,∴∠AEB=90°,∵⊙O的半径为5,sin∠BAE=,∴AB=10,BE=AB•sin∠BAE=10×=6,∴EA===8,∵,∴BE=CE=6,∵CE2=EH•EA,∴EH==,在Rt△BEH中,BH===.【点评】本题是圆的综合题目,考查了切线的判定、圆周角定理、圆心角、弧、弦之间的关系定理、勾股定理、三角函数、相似三角形的判定与性质等知识;本题难度较大,综合性强,特别是(2)(3)中,需要通过作辅助线证明三角形相似和运用三角函数、勾股定理才能得出结果.13.(2015•福建)已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.①判断OQ与AC的位置关系,并说明理由;②求线段PQ的长.【分析】(1)如图①,连接OQ.利用切线的性质和勾股定理来求PQ的长度.(2)如图②,连接BC.利用三角形中位线的判定与性质得到BC∥OQ.根据圆周角定理推知BC⊥AC,所以,OQ⊥AC.(3)利用割线定理来求PQ的长度即可.【解答】解:(1)如图①,连接OQ.∵线段PQ所在的直线与⊙O相切,点Q在⊙O上,∴OQ⊥OP.又∵BP=OB=OQ=2,∴PQ===2,即PQ=2;(2)OQ⊥AC.理由如下:如图②,连接BC.∵BP=OB,∴点B是OP的中点,又∵PC=CQ,∴点C是PQ的中点,∴BC是△PQO的中位线,∴BC∥OQ.又∵AB是直径,∴∠ACB=90°,即BC⊥AC,∴OQ⊥AC.(3)如图②,PC•PQ=PB•PA,即PQ2=2×6,解得PQ=2.【点评】本题考查了圆的综合题.掌握圆周角定理,三角形中位线定理,平行线的性质,熟练利用割线定理进行几何计算.14.(2015•宿迁)已知:⊙O上两个定点A,B和两个动点C,D,AC与BD交于点E.(1)如图1,求证:EA•EC=EB•ED;(2)如图2,若=,AD是⊙O的直径,求证:AD•AC=2BD•BC;(3)如图3,若AC⊥BD,点O到AD的距离为2,求BC的长.【分析】(1)根据同弧所对的圆周角相等得到角相等,从而证得三角形相似,于是得到结论;(2)如图2,连接CD,OB交AC于点F由B是弧AC的中点得到∠BAC=∠ADB=∠ACB,且AF=CF=0.5AC.证得△CBF∽△ABD.即可得到结论;(3)如图3,连接AO并延长交⊙O于F,连接DF得到AF为⊙O的直径于是得到∠ADF=90°,过O作OH⊥AD于H,根据三角形的中位线定理得到DF=2OH=4,通过△ABE∽△ADF,得到1=∠2,于是结论可得.【解答】(1)证明:∵∠EAD=∠EBC,∠BCE=∠ADE,∴△AED∽△BEC,∴,∴EA•EC=EB•ED;(2)证明:如图2,连接CD,OB交AC于点F∵B是弧AC的中点,∴∠BAC=∠ADB=∠ACB,且AF=CF=0.5AC.又∵AD为⊙O直径,∴∠ABD=90°,又∠CFB=90°.∴△CBF∽△ABD.∴,故CF•AD=BD•BC.∴AC•AD=2BD•BC;(3)解:如图3,连接AO并延长交⊙O于F,连接DF,∴AF为⊙O的直径,∴∠ADF=90°,过O作OH⊥AD于H,∴AH=DH,OH∥DF,∵AO=OF,∴DF=2OH=4,∵AC⊥BD,∴∠AEB=∠ADF=90°,∵∠ABD=∠F,∴△ABE∽△ADF,∴∠1=∠2,∴,∴BC=DF=4.【点评】本题考查了圆周角定理,垂径定理,相似三角形的判定和性质,三角形的中位线的性质,正确作出辅助线是解题的关键.15.(2015•长沙)如图,在直角坐标系中,⊙M经过原点O(0,0),点A(,0)与点B(0,﹣),点D在劣弧上,连接BD交x轴于点C,且∠COD=∠CBO.(1)求⊙M的半径;(2)求证:BD平分∠ABO;(3)在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.【分析】(1)由点A(,0)与点B(0,﹣),可求得线段AB的长,然后由∠AOB=90°,可得AB 是直径,继而求得⊙M的半径;(2)由圆周角定理可得:∠COD=∠ABC,又由∠COD=∠CBO,即可得BD平分∠ABO;(3)首先过点A作AE⊥AB,垂足为A,交BD的延长线于点E,过点E作EF⊥OA于点F,易得△AEC 是等边三角形,继而求得EF与AF的长,则可求得点E的坐标.【解答】解:(1)∵点A(,0)与点B(0,﹣),∴OA=,OB=,∴AB==2,。
2017年全国中考数学真题分类 圆的基本性质2017(填空题)

2017年全国中考数学真题分类圆的基本性质填空题二、填空题1. (2017重庆,15,4分)如图,BC 是⊙O 的直径,点A 在圆上,连接AO ,AC ,∠AOB =64゜,则∠ACB = 度.答案:32 解析:从图形中可以看出,∠AOB 、∠C 分别是⊙O 中弧AB 所对的圆心角、圆周角,利用圆周角定理可得∠AOB =2∠C ,代入∠AOB 的度数即可得∠C 的度数.解:∵∠AOB 、∠C 分别是⊙O 中弧AB 所对的圆心角、圆周角,∴∠AOB =2∠C .∵∠AOB =64°,∴∠C =32°.2. (2017四川自贡,17,3分)如图,等腰△ABC 内接于⊙O ,已知AB =AC , ∠ABC =30°,BD 是⊙O 的直径,如果CD =33,则AD = .D OABC答案:4,解析:∵AB =AC , ∴弧AB =弧AC ,∵∠ABC =30°,∴∠ADB =∠ADC =30°,∴∠BDC=60°.在Rt △BDC 中,∵BD 是⊙O 的直径,∴∠BAD =∠BCD =90°,∠DBC =180°-90°-60°-30°,∴∠ADB =∠DBC ,∴AB =CD =433.在Rt △ABD 中,∵ADB =30°,∴AD =433tan 303AB=︒ 4.3. (2017江苏盐城,14,3分)如图,将⊙O 沿弦AB 折叠,点C 在AmB 上,点D 在AB 上,若∠ACB =70°,则∠ADB =________°.答案:110°,解析:如图,设点D ′是点D 折叠前的位置,连接AD ′、BD ′,则∠ADB =∠AD ′B .在圆内接四边形ACBD ′中,∠ACB +∠D ′=180°,所以∠D ′=180°-70°=110°,所以∠ADB =110°.4. 14.(2017江苏连云港,14,4分)如图,线段AB 与O ⊙相切于点B ,线段AO 与O ⊙相交于点C ,12AB ,8AC ,则O ⊙的半径长为 .答案:5,解析:连接OB ,根据切线的性质可知OB ⊥AB ,设圆的半径为r ,然后根据勾股定理可得222()r AB r AC +=+,即22212(8)r r +=+,解得r =5.5. (2017四川达州16,3分)如图,矩形ABCD 中,E 是BC 上一点,连接AE ,将矩形沿AE 翻折,使点B 落在CD 边F 处,连接AF ,在AF 上取点O ,以O 为圆心,OF 长为半径作O 与AD 相切于点P .若633AB BC ==,F 是CD 的中点;②O 的半径是2;③92AE CE =;④3S =阴影.其中正确结论的序号是 . CDABOmCDABOmD 'E P答案:①②④,解析:由折叠可知AF =AB =6,在Rt △ADF 中,DF=3==,∴DF =12CD ,即F 是CD 的中点,所以①是正确的;连接OP ,则OP ⊥AD ,∵DF =3,AF =6,∴∠DAF =30°,∴AO =2OA ,而OP =PF ,∴AF =2OA +OF =6,∴OP =OF =2,∴⊙O 的半径为2,∴②是正确的;∵∠DAF =30°,∴∠AFD =60°,∵∠AFE =90°,∴∠EFC =30°,∴EF =2EC ,又∵∠FAE =∠BAE =30°,∴AE =2EF =4EC ,所以③是错误的;设⊙O 与CD 的另一个交点为I ,∵OI =OF ,∠OFI =60°,∴△OIF 为等边三角形,∴∠IOF =60°,∴∠POI =60°,∴OPDF =S OIF OPI S S S ∆--梯形扇形+OIF OIF S S ∆-扇形 =22360242360+π⨯+26024360π⨯=23π+23π,所以④是正确折,故本题填:①②④ E P6. 17.(2017四川眉山,17,3分)如图,AB 是⊙O 的弦,半径OC ⊥AB 于点D ,且AB =8cm ,DC=2cm ,则OC =______cm .答案:5,解析:连接OA ,因为半径OC ⊥AB 于点D ,所以AD =12AB =12×8=4(cm),设⊙O 的半径为x cm ,在Rt △OAD 中,OA 2=OD 2+AD 2,即x 2=(x -2)2+42,解得x =5,所以OC =5cm .7. (2017江苏淮安,16,3分)如图,在圆内接四边形ABCD 中,若∠A 、∠B 、∠C 的度数之比为4∶3∶5,则∠D 的度数是________︒.答案:120,解析:因为四边形ABCD 是⊙O 的内接四边形,所以∠A +∠C =∠B +∠D =180°.因为∠A 、∠B 、∠C 的度数之比为4∶3∶5,所以∠A 、∠B 、∠C 、∠D 的度数之比为4∶3∶5∶6,所以∠D =636+×180°=120°.8. 16.(2017湖南岳阳,16,4分)如右图,O 为等腰△ABC 的外接圆,直径AB =12,P为弧BC 上任意一点(不与B ,C 重合),直线CP 交AB 延长线于点Q,O 在点P 处切线PD 交BQ 于点D ,下列结论正确的是 .(写出所有正确结论得序号) ①若∠PAB =30°,则弧BP 的长为π; ②若PD ∥BC ,则AP 平分∠CAB ;③若PB =BD ,则PD=; ④无论点P 在弧BC 上的位置如何变化,CP ·CQ 为定值.AACA答案:③④,解析:直径AB =12,则半径长6. ∠APB =90°;等腰△ABC ,则CO ⊥AB . AC =BC =①因为∠PAB =30°,则弧BP 的圆心角为60°,弧BP 长为606180π⨯⨯=2π,故①错误. ②PD ∥BC ,DP 为切线,则∠QPD =∠BCP =∠PAB ,得不到AP 平分∠CAB ,故②错误. ③ PB =BD ,DP 为切线,则∠BPD =∠BDP =∠PAB ,因为△APQ 内角和180°,∠APB =90°,所以∠BPD =∠BDP =∠PAB =30°.因为第16题图AB =12,所以PB =BD =6.过B 作BE ⊥PD 于E 点,则BE =3,PE =DE =33,PD =63.故③正确. ④过O 作OF ⊥CP 于F 点,则∠COP =2∠COF =2∠CAP ,∠COF =∠CAP ;因为∠COF +∠OCF =∠Q +∠OCF ,所以∠Q =∠COF =∠CAP ,则△CAP ∽△CQA ,CP ·CQ =AC 2=(62)2=72,故④正确.9. 15.(2017江苏扬州,,3分)如图,已知⊙O 是△ABC 的外接圆,连接AO ,若∠B =40°,则∠OAC= ▲ °. 【答案】50【解析】根据“同弧所对的圆周角等于它所对圆心角的一半”,连接OC ,便有2AOC B ∠=∠=080再由OA=OC,根据“等边对等角”及“三角形内角和定理”可以求得050OAC ∠=10. 14.(2017甘肃酒泉,14,3分)如图,ABC △内接于O ⊙,若32OAB ∠°,则C ∠ .答案:58°,解析:连接OB .在△OAB 中,OA =OB (⊙O 的半径),∴∠OAB =∠OBA ;又∵∠OAB =28°,∴∠OBA =28°;∴∠AOB =180°﹣2×28°=124°; 而∠C =∠AOB (同弧所对的圆周角是所对的圆心角的一半),∴∠C =62°; 故答案是:62°.第14题图.ABC第15题图O11. 15.(2017江苏泰州,15,3分)如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0),(2,5),(4,2),若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为.答案:(7,4),(6,5),解析:如图,以点P为圆心,PA为半径作圆,⊙P在第一项限经过的符合条件的点有两个,分别是(7,4)和(6,5).故答案为(7,4),(6,5).12.12.(2017浙江义乌,12,5分)如图,一块含45°角的直角三角形,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠EOD的度数为.答案:90°,解析:根据一条弧所对的圆周角是它所对的圆心角的一半,得到∠EOD=2∠A=2×45°=90°.13.(2017湖北十堰,14,5分)如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的角平分线交⊙O于D ,若AC =6,BD =52,则BC 的长为 .答案:8,解析:连接DA ,因为∠ACB =90°,所以AB 为直径,所以∠ADB =90°,因为CD 平分∠ACB ,所以BD =AD ,在△ABD 中AB =22AD BD +=22(52)(52)+=10,在△ABC 中BC =22AB AC -=22106-=8.14. (2017湖北随州,13,3分)如图,已知AB 是⊙O 的弦,半径OC 垂直AB ,点D 是⊙O 上一点,且点D 与点C 位于弦AB 两侧,连接AD 、CD 、OB ,若∠BOC =70°,则∠ADC =________度.ABOCD答案:35,解析:∵半径OC 垂直AB ,∴⌒AC =⌒BC ,∴∠ADC =12∠BOC =12×70°=35°.15. (2017江苏南京,15,2分)如图,四边形ABCD 是菱形,⊙O 经过点A ,C ,D 与BC 相交于点E ,连接AC ,AE ,若∠D =78°,则∠EAC =____.[来源∶Z &xx &k .Com ]答案∶27°,解析∶∵四边形ABCD 是菱形,∴AD =DC ,AD ∥BC ,∴∠DAC =∠DCA ,.∵∠D =78°,∴∠DAC =51°,∴∠ACE =51°.∵,∴,∴∠DAE =∠D =78°,∴∠EAC =78°-51°=27°.16.(2017甘肃庆阳,14,4分)如图,ABC △内接于O ⊙,若32OAB ∠°,则C ∠ .答案:58°,解析:连接OB .在△OAB 中,OA =OB (⊙O 的半径),∴∠OAB =∠OBA ;又∵∠OAB =28°,∴∠OBA =28°;∴∠AOB =180°﹣2×28°=124°; 而∠C =∠AOB (同弧所对的圆周角是所对的圆心角的一半),∴∠C =62°; 故答案是:62°.17. (2017·湖南株洲,15,3分)如图,已知AM 是圆O 的直径,直线BC 经过点M ,且AB =AC ,∠BAM =∠CAM ,线段AB 和AC 分别交圆于点D ,E .∠BMD =40°,则∠EOM = 度.答案:80,解析:由于AB =AC ,∠BAM =∠CAM ,所以M 是等腰△ABC 的顶角平分线,所以AM⊥B C .因为AM 是圆O 的直径,所以BC 是圆O 的切线,所以∠BMD =∠BAM =40°,即∠CAM =40°,所以∠EOM =2∠CAM =80°,故答案为80.18. 15.(2017宁夏,3分)如图,点A ,B ,C 均在6×6的正方形网格格点上,过A ,B ,C 三点的外接圆除经过A ,B ,C 三点外还能经过的格点数为 .A第15题图MBCEOD 第14题图CB A答案:5,解析:如图,根据“不在同一条直线上的三个点确定一个圆”,画出⊙O .根据几何直观即可得到⊙O 除经过A ,B ,C 三点外还能经过的格点数是5.OAB C19. 12.(2017浙江绍兴,5分)如图,一块含45°角的直角三角板,它的一个锐角顶点A 在⊙O 上,边AB 、AC 分别与⊙O 交于点D 、E ,则∠DOE 的度数为 .【答案】90°.【解析】根据圆周角定理得到,∠DOE =2∠A =90°,故答案为:90°.20. (2017湖北襄阳,15,3分)在半径为1的⊙O 中,弦AB,AC 的长分别为12BAC 的度数为 .答案:105°或15°,解析:如图1,当点O 在∠BAC 的内部时,连接OA ,过点O 作OM ⊥AB ,ON ⊥AC ,垂足分别为M ,N ,则AM=21,AN=22.在Rt △AOM 中,cos ∠MAO=AO AM =21,∴∠MAO=60°.在Rt △AON 中,cos ∠NAO=AO AN =22,∴∠NAO=45°,∴∠BAC=60°+45°=105°;如图2,当点O 在∠BAC ′的外部时,∠BAC ′=60°+45°=105°.图1 图221. 16.(2017湖南永州,4分)如图,四边形ABCD 是⊙O 的内接四边形,点D 是AC ⌒的中点,点E是BC ⌒上的一点,若∠CED =40°,则∠ADC =________度.答案:100,解析:连接AE ,∵点D 是AC ⌒的中点,∴∠AED =∠CED =40°,∴∠AEC =80°.∵∠AEC +∠ADC =180°,∴∠ADC =180°-∠AEC =180°-80°=100°.22. (2017·辽宁大连,12,3分)如图,在⊙O 中,弦AB =8cm ,OC ⊥AB ,垂足为C ,OC =3cm ,则⊙O 的半径为 cm .答案:5 解析:由于在⊙O 中,弦AB =8cm ,OC ⊥AB ,所以BC =21=4cm ,设圆的半径为R ,第12题AB C O则R =22BC OC +=2243+=5cm ,故答案为:5.23. (2017山东东营,14,3分)如图,AB 是半圆直径,半径OC ⊥AB 于点O ,D 为半圆上一点,AC ∥OD ,AD 与OC 交于点E ,连结CD 、BD ,给出以下三个结论:①OD 平分∠COB ;②BD =CD ;③CD 2= CE ·CO .其中正确结论的序号是________________.【答案】①②③【解析】由AC ∥OD ,可得∠CAD =∠ADO ,由OA =OD 可得∠DAO =∠ADO ,∴∠CAD =∠DAB ,根据圆周角定理可得∠BOD =2∠DAB ,∠COD =2∠CAD ,∴∠BOD =∠COD ,即OD 平分∠COB ,①正确;由∠BOD =∠COD ,根据“在同圆或等圆中,相等的 圆心角所对的弦相等”可得BD =CD ,②正确;∵AB 是半圆直径, OC ⊥AB ,∴AC =BC ,易得∠ CDA =∠COD ,又∵∠DCE =∠OCD ∴△CDE ∽△COD ,∴ CD 2= CE ·CO ,③正确24. (2017年湖南长沙,15,3分)如图,AB 为圆O 的直径,弦CD ⊥AB 于点E ,已知CD=6,EB=1,则圆O 的半径为答案:5,解析:连接OC ,因为弦CD ⊥AB ,所以CE=21CD=3,设OC=x ,则OE=x-1,由勾股定理得(x-1)2+32=x 2,所以x=5 E O DC A25. 13.(2017江苏省南通市,13,3分) 四边形ABCD 内接于圆,若∠A =110°,则∠C =______度.答案:70 解析:∵四边形ABCD 内接于圆,∴∠A +∠C =180°,因为∠A =110°,所以∠C =70°26. (2017青海西宁,17,2分)如图4,四边形ABCD 内接于⊙O ,点E 在BC 的延长线上,若∠BOD =120°,则∠DCE = .答案:60°,解析:∵∠BOD =120°∴∠BAD =60°,又∠BAD +∠BCD =180°.∠DCE +∠BCD =180°,∴∠DCE =∠BAD =60°27. (2017黑龙江大庆,14,3分)ABC ∆中,C ∠为直角,2=AB ,则这个三角形的外接圆半径为 .答案:1,解析:直角三角形外接圆圆心在斜边中点,或90°所对的弦为直径可知,半径为1.28. 17.(2017贵州遵义)如图,AB 是⊙O 的直径,AB =4,点M 是OA 的中点,过点M 的直线与⊙O交于C 、D 两点.若∠CMA=45°,则弦CD 的长为 .答案:14,解析:过点O 作ON ⊥CD 于N ,连接OC ,∵∠CMA=45°,∠ONC=90°,∴△MON 是等腰直角三角形,∵AB=4,点M 是OA 的中点,∴OM=1,根据勾股定理解得ON=22,在Rt △CON 中,CN=222222()2OC ON -=-=142,∴CD=2CN=14.29. (2017内蒙古包头)如图,点A B C 、、为O 上的三个点,02,40BOC AOB BAC ∠=∠∠=,则ACB ∠=________度.(第17题)CB AO答案:20,解析:考点圆周角定理的应用,圆周角定理是指圆周角的度数等于它所对弧上的圆心角度数的一半.∵040BAC ∠=∴由圆周角定理可知0=280BOC BAC ∠∠=又∵2BOC AOB ∠=∠∴=40AOB ∠︒再次利用圆周角定理得到0=240AOB ACB ∠∠=,得020ACB ∠=.30. (2017湖北荆州,16,3分)如图,A 、B 、C 是⊙O 上的三点,且四边形OABC 是菱形.若点D 是圆上异于A 、B 、C 的另一点,则∠ADC 的度数是___________________.答案:60°或120°,解析:连接OB,∵四边形OABC是菱形,∴AB=OA=OB=BC,∴△AOB是等边三角形,∴∠ADC=60°,∠AD′C=120°.。
2017年中考数学试题分项版解析汇编(第01期)专题11 圆(含解析)

专题11 圆一、选择题1.(2017浙江衢州第10题)运用图形变化的方法研究下列问题:如图,AB 是⊙O 的直径,CD ,EF 是⊙O 的弦,且AB ∥CD ∥EF ,AB=10,CD=6,EF=8。
则图中阴影部分的面积是( )A. π225B. π10C. π424+D. π524+【答案】A.【解析】试题解析:作直径CG ,连接OD 、OE 、OF 、DG .∵CG 是圆的直径,∴∠CDG=90°,则2222106CG CD -=-=8,又∵EF=8,∴DG=EF ,∴DG EF =,∴S 扇形ODG =S 扇形OEF ,∵AB ∥CD ∥EF ,∴S △OCD =S △ACD ,S △OEF =S △AEF ,∴S 阴影=S 扇形OCD +S 扇形OEF =S 扇形OCD +S 扇形ODG =S 半圆=12π×52=252π.2考点:1.圆周角定理;2.扇形面积的计算.2.(2017浙江宁波第9题)如图,在Rt ABC △中,90A =∠°,22BC =以BC 的中点O 为圆心分别与AB ,AC 相切于D ,E 两点,则DE 的长为( )A.4pB.2pC.pD.2p 【答案】B.【解析】试题解析:如图,连接OD ,OE∵AC ,AB 是圆O 的切线∴OE ⊥AC ,OD ⊥AB∵O 是BC 的中点∴点E ,点D 分别是AC ,AB 的中点∴OE=12AB ,OD= 12AC∵OE=OD∴AC=AB∵2由勾股定理得AB=2∴OE=1DE 的弧长=901180π⨯⨯=2π.考点:1.三角形的中位线;2.弧长的计算.3.(2017重庆A 卷第9题)如图,矩形ABCD 的边AB=1,BE 平分∠ABC ,交AD 于点E ,若点E 是AD 的中点,以点B 为圆心,BE 为半径画弧,交BC 于点F ,则图中阴影部分的面积是( )A .24π- B .324π- C .28π- D .328π- 【答案】B.∴图中阴影部分的面积=S 矩形ABCD ﹣S △ABE ﹣S 扇形EBF=1×2﹣12×1×1﹣245360π⨯ =324π-. 故选B .考点:1.矩形的性质;2.扇形的面积计算.4.(2017广西贵港第9题)如图,,,,A B C D 是O 上的四个点,B 是AC 的中点,M 是半径OD 上任意一点,若40BDC ∠= ,则AMB ∠的度数不可能是( )A.45 B.60 C. 75 D.85【答案】D【解析】试题解析:∵B是AC的中点,∴∠AOB=2∠BDC=80°,又∵M是OD上一点,∴∠AMB≤∠AOB=80°.则不符合条件的只有85°.故选D.考点:圆周角定理;圆心角、弧、弦的关系.5.(2017贵州如故经9题)如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为()A.65B.85C.75D.35【答案】B4【解析】试题解析:连接BD.∵AB是直径,∴∠ADB=90°.∵OC∥AD,∴∠A=∠BOC,∴cos∠A=cos∠BOC.∵BC切⊙O于点B,∴OB⊥BC,∴cos∠BOC=25 OBOC,∴cos∠A=cos∠BOC=25.又∵cos∠A=ADAB,AB=4,∴AD=85.故选B.考点:解直角三角形;平行线的性质;圆周角定理.6.(2017湖北武汉第9题)已知一个三角形的三边长分别为5,7,8.则其内切圆的半径为()A.32C..【答案】C【解析】试题解析:如图,AB=7,BC=5,AC=8过A作AD⊥BC于D,设BD=x,则CD=5-x由勾腰定理得:72-x2=82-(5-x)2解得:x=1∴3设ΔABC的内切圆的半径为r,则有:1 2(5r+7r+8r)=12×5×3解得:3故选C.考点:三角形的内切圆.7.(2017江苏无锡第9题)如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于()A.5 B.6 C.D.6【答案】C.【解析】试题解析:如图作DH⊥AB于H,连接BD,延长AO交BD于E.∵菱形ABCD的边AB=20,面积为320,∴AB•DH=32O,∴DH=16,在Rt△ADH中,,∴HB=AB﹣AH=8,在Rt△BDH中,=设⊙O与AB相切于F,连接AF.∵AD=AB,OA平分∠DAB,∴AE⊥BD,∵∠OAF+∠ABE=90°,∠ABE+∠BDH=90°,∴∠OAF=∠BDH,∵∠AFO=∠DHB=90°,∴△AOF∽△DBH,∴OA OFBD BH=,108OF=,∴.故选C.考点:1.切线的性质;2.菱形的性质.8.(2017甘肃兰州第4题)如图,在O⊙中,AB BC=,点D在O⊙上,25CDB=∠°,则AOB=∠( )A.45°B.50°C.55°D.60°【答案】B考点:圆周角定理.9.(2017甘肃兰州第2题)如图,正方形ABCD内接于半径为2的O⊙,则图中阴影部分的面积为( ) A.1p+ B.2p+ C.1p- D.2p-【答案】D.【解析】试题解析:连接AO,DO,∵ABCD是正方形,∴∠AOD=90°,2222OA OD+=,圆内接正方形的边长为=14[4π﹣(2]=(π﹣2)cm2.故选D.8考点:1正多边形和圆;2.扇形面积的计算.10.(2017贵州黔东南州第5题)如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为()A.2 B.﹣1 C D.4【答案】A.【解析】试题解析:∵⊙O的直径AB垂直于弦CD,∴CE=DE,∠CEO=90°,∵∠A=15°,∴∠COE=30°,∵OC=2,∴CE=12OC=1,∴CD=2OE=2,故选A.考点:圆周角定理;勾股定理;垂径定理.11. (2017贵州黔东南州第8题)如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为()A.60° B.67.5°C.75° D.54°【答案】A.【解析】10 试题解析:如图,连接DF 、BF .∵FE ⊥AB ,AE=EB ,∴FA=FB ,∵AF=2AE ,∴AF=AB=FB ,∴△AFB 是等边三角形,∵AF=AD=AB ,∴点A 是△DBF 的外接圆的圆心,∴∠FDB=12∠FAB=30°, ∵四边形ABCD 是正方形,∴AD=BC ,∠DAB=∠ABC=90°,∠ADB=∠DBC=45°,∴∠FAD=∠FBC ,∴△FAD ≌△FBC ,∴∠ADF=∠FCB=15°,∴∠DOC=∠OBC+∠OCB=60°.故选A .考点:正方形的性质.12.(2017山东烟台第9题)如图,□ABCD 中,070=∠B ,6=BC ,以AD 为直径的⊙O 交CD 于点E ,则弧DE 的长为( )A .π31B .π32 C. π67 D .π34【答案】B .∴DE 的长=40321803ππ⨯=.故选:B .考点:弧长的计算;平行四边形的性质;圆周角定理.13.(2017四川泸州第6题)如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E .若AB=8,AE=1,则弦CD 的长是().6 D .8【答案】B .12考点:1.垂径定理;2.勾股定理.14.(2017四川自贡第10题)AB 是⊙O 的直径,PA 切⊙O 于点A ,PO 交⊙O 于点C ;连接BC ,若∠P=40°,则∠B 等于( )A .20°B .25°C .30°D .40°【答案】B.【解析】试题解析:∵PA 切⊙O 于点A ,∴∠PAB=90°,∵∠P=40°,∴∠POA=90°﹣40°=50°,∵OC=OB ,∴∠B=∠BCO=25°,故选B .考点:切线的性质.15.(2017新疆建设兵团第9题)如图,⊙O 的半径OD 垂直于弦AB ,垂足为点C ,连接AO 并延长交⊙O 于点E ,连接BE ,CE .若AB=8,CD=2,则△BCE 的面积为( )A .12B .15C .16D .18【答案】A.【解析】考点:圆周角定理;垂径定理.16.(2017江苏徐州第6题)如图,点,,A B C ,在⊙O 上,72AOB ∠=,则ACB ∠=()A .28B .54 C.18 D .36【答案】D .14【解析】试题解析:根据圆周角定理可知,∠AOB=2∠ACB=72°,即∠ACB=36°,故选D .考点:圆周角定理.二、填空题1.(2017浙江衢州第15题)如图,在直角坐标系中,⊙A 的圆心A 的坐标为(-1,0),半径为1,点P 为直线343+-=x y 上的动点,过点P 作⊙A 的切线,切点为Q ,则切线长PQ 的最小值是__________ 【答案】22【解析】试题解析:连接AP ,PQ ,当AP 最小时,PQ 最小,∴当AP ⊥直线y=﹣34x+3时,PQ 最小, ∵A 的坐标为(﹣1,0),y=﹣34x+3可化为3x+4y ﹣12=0,∴|3(1)4012|=3,∴.考点:1.切线的性质;2.一次函数的性质.2.(2017山东德州第17题)某景区修建一栋复古建筑,其窗户设计如图所示.圆O 的圆心与矩形ABCD 对角线的交点重合,且圆与矩形上下两边相切(E 为上切点),与左右两边相交(,F G 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m ,根据设计要求,若45EOF ∠= ,则此窗户的透光率(透光区域与矩形窗面的面枳的比值)为 .【解析】试题解析:如图,过F 作FG ⊥OF ,连接OG,OM,ON△OFH 是等腰直角三角形, ∴FH=OFsin45°=22,AB=2,BC=2OF=2 ∴矩形ABCD 面积=22∴S 空白=2S 扇形FOM+2S ΔAOG =290112+2113602π⨯⨯⨯⨯⨯⨯16 =+12π∴窗户的透光率=(+2)28π 考点:扇形的面积及概率3.(2017重庆A 卷第15题)如图,BC 是⊙O 的直径,点A 在圆上,连接AO ,AC ,∠AOB=64°,则∠ACB= .【答案】32°.【解析】试题解析:∵AO=OC ,∴∠ACB=∠OAC ,∵∠AOB=64°,∴∠ACB+∠OAC=64°,∴∠AC B=64°÷2=32°.考点:圆周角定理.4.(2017甘肃庆阳第14题)如图,△ABC 内接于⊙O ,若∠OAB=32°,则∠C= °.【答案】58°.【解析】试题解析:如图,连接OB ,∵OA=OB ,∴△AOB 是等腰三角形,∴∠OAB=∠OBA ,∵∠OAB=32°,∴∠OAB=∠OAB=32°,∴∠AOB=116°,∴∠C=58°.考点:圆周角定理.5. (2017甘肃庆阳第17题)如图,在△ABC 中,∠ACB=90°,AC=1,AB=2,以点A 为圆心、AC 的长为半径画弧,交AB 边于点D ,则弧CD 的长等于 .(结果保留π)【答案】3π. 【解析】考点:弧长的计算;含30度角的直角三角形.6.(2017广西贵港第17题)如图,在扇形OAB 中,C 是OA 的中点,,CD OA CD ⊥ 与AB 交于点D ,以O 为圆心,OC 的长为半径作CE 交OB 于点E ,若4,120OA AOB =∠=,则图中阴影部分的面积为 .(结果保留π)18【答案】4233π+ 【解析】试题解析:连接OD 、AD ,∵点C 为OA 的中点,∴∠CDO=30°,∠DOC=60°,∴△ADO 为等边三角形,∴S 扇形AOD =260483603ππ⨯=, ∴S 阴影=S 扇形AOB ﹣S 扇形COE ﹣(S 扇形AOD ﹣S △COD ) =221204120281(223)36036032πππ⨯⨯---⨯⨯ =164823333πππ--+=4233π+ 考点:扇形面积的计算;线段垂直平分线的性质.7.(2017湖南怀化第14题)如图,O ⊙的半径为2,点A ,B 在O ⊙上,90AOB =∠°,则阴影部分的面积为 .【答案】π﹣2.考点:扇形面积的计算.8. (2017湖南怀化第16题)如图,在菱形ABCD中,120∠°,10cmAB=,点P是这个菱形内部ABC=或边上的一点,若以,,P B C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为cm.【答案】10(cm).【解析】试题解析:连接BD,在菱形ABCD中,∵∠ABC=120°,AB=BC=AD=CD=10,∴∠A=∠C=60°,∴△ABD,△BCD都是等边三角形,①若以边BC为底,则BC垂直平分线上(在菱形的边及其内部)的点满足题意,此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短”,即当点P与点D重合时,PA最小,最小值PA=10;②若以边PB为底,∠PCB为顶角时,以点C为圆心,BC长为半径作圆,与AC相交于一点,则弧BD(除点B外)上的所有点都满足△PBC是等腰三角形,当点P在AC上时,AP最小,最小值为10;③若以边PC为底,∠PBC为顶角,以点B为圆心,BC为半径作圆,则弧AC上的点A与点D均满足△PBC为等腰三角形,当点P与点A重合时,PA最小,显然不满足题意,故此种情况不存在;综上所述,PD的最小值为10(cm).2考点:菱形的性质;等腰三角形的性质.9.(2017江苏无锡第17题)如图,已知矩形ABCD 中,AB=3,AD=2,分别以边AD ,BC 为直径在矩形ABCD 的内部作半圆O 1和半圆O 2,一平行于AB 的直线EF 与这两个半圆分别交于点E 、点F ,且EF=2(EF 与AB 在圆心O 1和O 2的同侧),则由AE ,EF ,FB ,AB 所围成图形(图中阴影部分)的面积等于 .53﹣6π. 【解析】试题解析:连接O 1O 2,O 1E ,O 2F ,则四边形O 1O 2FE 是等腰梯形,过E 作EG ⊥O 1O 2,过F ⊥O 1O 2,∴四边形EGHF 是矩形,∴GH=EF=2,∴O 1G=12, ∵O 1E=1,∴3 ∴1112O G O E =;∴∠O 1EG=30°,∴∠AO 1E=30°,同理∠BO 2F=30°,∴阴影部分的面积=S 矩形ABO2O1﹣2S 扇形AO1E ﹣S 梯形EFO2O1=3×1﹣2×2301360π⨯⨯=12(2+3=36π. 考点:1.扇形面积的计算;2.矩形的性质.10.(2017江苏盐城第14题)如图,将⊙O 沿弦AB 折叠,点C 在AmB 上,点D 在AB 上,若∠ACB=70°,则∠ADB= °.【答案】110°【解析】试题解析:∵点C 在AmB 上,点D 在AB 上,若∠ACB=70°,∴∠ADB+∠ACB=180°,∴∠ADB=110°考点:圆周角定理.11.(2017山东烟台第18题)如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB .已知6=OA ,取OA 的中点C ,过点C 作OA CD ⊥交弧AB 于点D ,点F 是弧AB 上一点,若将扇形BOD 沿OD 翻折,点B 恰好与点F 重合.用剪刀沿着线段FA DF BD ,,依次剪下,则剪下的纸片(形状同阴影图形)面积之和为 .22【答案】36π﹣108【解析】试题解析:如图,∵CD ⊥OA ,∴∠DCO=∠AOB=90°,∵OA=OD=OB=6,OC=12OA=12OD , ∴∠ODC=∠BOD=30°,作DE ⊥OB 于点E ,则DE=12OD=3, ∴S 弓形BD =S 扇形BOD ﹣S △BOD =2306360π⨯﹣12×6×3=3π﹣9, 则剪下的纸片面积之和为12×(3π﹣9)=36π﹣108考点:扇形面积的计算12.(2017四川宜宾第15题)如图,⊙O 的内接正五边形ABCDE 的对角线AD 与BE 相交于点G ,AE=2,则EG 的长是 .1【解析】考点:正多边形和圆.13.(2017四川宜宾第17题)如图,等腰△ABC内接于⊙O,已知AB=AC,∠ABC=30°,BD是⊙O的直径,,则AD= .如果CD=3【答案】4.【解析】试题解析:∵AB=AC,∴∠ABC=∠ACB=∠ADB=30°,∵BD是直径,∴∠BAD=90°,∠ABD=60°,∴∠CBD=∠ABD﹣∠ABC=30°,∴∠ABC=∠CBD,∴AC CD AB==,∴CB AD=,∴AD=CB,∵∠BCD=90°,433,∴AD=BC=4.考点:1.圆周角定理;2.等腰三角形的性质;3.含30°角的直角三角形.14.(2017江苏徐州第15题)正六边形的每个内角等于.【答案】120°.【解析】试题解析:六边形的内角和为:(6-2)×180°=720°,∴正六边形的每个内角为:7206︒=120°.考点:多边形的内角与外角.15. (2017江苏徐州第16题)如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为,2D AB BC==,则AOB∠=.【答案】60°.【解析】24考点:切线的性质.ABm=︒,16.(2017浙江嘉兴第13题)如图,小明自制一块乒乓球拍,正面是半径为8cm的O,90弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为.【答案】(32+48π)cm2【解析】试题解析:连接OA、OB,∵AB=90°,∴∠AOB=90°,∴S△AOB=12×8×8=32,扇形ACB(阴影部分)=22036078π⨯⨯=48π,则弓形ACB胶皮面积为(32+48π)cm2考点:1.垂径定理的应用;2.扇形面积的计算.三、解答题1.(2017浙江衢州第19题)如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。
(最新整理)2017年中考数学试卷汇编——圆(带答案)

2017年中考数学试卷汇编——圆(带答案)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017年中考数学试卷汇编——圆(带答案))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017年中考数学试卷汇编——圆(带答案)的全部内容。
圆的有关性质一、选择题1.(2016·山东省滨州市·3分)如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD 分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )A.②④⑤⑥B.①③⑤⑥C.②③④⑥D.①③④⑤【考点】圆的综合题.【分析】①由直径所对圆周角是直角,②由于∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角角,③由平行线得到∠OCB=∠DBC,再由圆的性质得到结论判断出∠OBC=∠DBC;④用半径垂直于不是直径的弦,必平分弦;⑤用三角形的中位线得到结论;⑥得不到△CEF和△BED中对应相等的边,所以不一定全等.【解答】解:①、∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥BD,②、∵∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角角,∴∠AOC≠∠AEC,③、∵OC∥BD,∴∠OCB=∠DBC,∵OC=OB,∴∠OCB=∠OBC,∴∠OBC=∠DBC,∴CB平分∠ABD,④、∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥BD,∵OC∥BD,∴∠AFO=90°,∵点O为圆心,∴AF=DF,⑤、由④有,AF=DF,∵点O为AB中点,∴OF是△ABD的中位线,∴BD=2OF,⑥∵△CEF和△BED中,没有相等的边,∴△CEF与△BED不全等,故选D【点评】此题是圆综合题,主要考查了圆的性质,平行线的性质,角平分线的性质,解本题的关键是熟练掌握圆的性质.2.(2016·山东省德州市·3分)《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”( )A.3步B.5步C.6步D.8步【考点】三角形的内切圆与内心.【专题】圆的有关概念及性质.【分析】根据勾股定理求出直角三角形的斜边,即可确定出内切圆半径.【解答】解:根据勾股定理得:斜边为=17,则该直角三角形能容纳的圆形(内切圆)半径r==3(步),即直径为6步,故选C【点评】此题考查了三角形的内切圆与内心,Rt△ABC,三边长为a,b,c(斜边),其内切圆半径r=.3.(2016·山东省济宁市·3分)如图,在⊙O中, =,∠AOB=40°,则∠ADC的度数是( )A.40°B.30°C.20°D.15°【考点】圆心角、弧、弦的关系.【分析】先由圆心角、弧、弦的关系求出∠AOC=∠AOB=50°,再由圆周角定理即可得出结论.【解答】解:∵在⊙O中, =,∴∠AOC=∠AOB,∵∠AOB=40°,∴∠AOC=40°,∴∠ADC=∠AOC=20°,故选C.4。
2017中考真题分类汇编—圆(解答题部分)(1)(含解析)

2017中考真题分类汇编—圆20.〔10分〕〔2017•〕如图,在四边形ABCD 中,AD=BC ,∠B=∠D ,AD 不平行于BC ,过点C 作CE ∥AD 交△ABC 的外接圆O 于点E ,连接AE . 〔1〕求证:四边形AECD 为平行四边形;〔2〕连接CO ,求证:CO 平分∠BCE .2.〔2017·〕如图,四边形ABCD 接于O ,AB 是O 的直径,点P 在CA 的延长线上,45CAD ∠=.〔Ⅰ〕假设4AB =,求弧CD 的长;〔Ⅱ〕假设弧BC =弧AD ,AD AP =,求证:PD 是O 的切线.3. 〔2017·〕如图,ABC △接于O ⊙,BC 是O ⊙的直径,弦AF 交BC 于点E ,延长BC 到点D ,连接OA ,AD ,使得FAC AOD ∠∠,D BAF ∠∠.(1)求证:AD 是O ⊙的切线; (2)假设O ⊙的半径为5,2CE ,求EF 的长.4.〔2017·〕如图,△ABD 是⊙O 的接三角形,E 是弦BD 的中点,点C 是⊙O 外一点且∠DBC=∠A ,连接OE 延长与圆相交于点F ,与BC 相交于点C .〔1〕求证:BC 是⊙O 的切线;〔2〕假设⊙O 的半径为6,BC=8,求弦BD 的长.5.〔2017·〕如图,AN 是M 的直径,//NB x 轴,AB 交M 于点C .(1)假设点(0,6),(0,2),30A N ABN ∠=,求点B 的坐标; (2)假设D 为线段NB 的中点,求证:直线CD 是M 的切线.6.〔2017·〕如图,⊙O 的半径为2,AB 为直径,CD 为弦.AB 与CD 交于点M ,将沿CD 翻折后,点A 与圆心O 重合,延长OA 至P ,使AP=OA ,连接PC〔1〕求CD 的长;〔2〕求证:PC 是⊙O 的切线;〔3〕点G 为的中点,在PC 延长线上有一动点Q ,连接QG 交AB 于点E .交于点F 〔F 与B 、C 不重合〕.问GE •GF 是否为定值?如果是,求出该定值;如果不是,请说明理由.7.〔2017·〕如图,AB 是⊙O 的直径,AB=4,点E 为线段OB 上一点〔不与O ,B 重合〕,作CE ⊥OB ,交⊙O 于点C ,垂足为点E ,作直径CD ,过点C 的切线交DB 的延长线于点P ,AF ⊥PC 于点F ,连接CB .〔1〕求证:CB 是∠ECP 的平分线;〔2〕求证:CF=CE ;〔3〕当=时,求劣弧的长度〔结果保存π〕25. 如图, 是 的直径,,,连接 .〔1〕求证:; 〔2〕假设直线 为的切线, 是切点,在直线 上取一点 ,使 , 所在的直线与所在的直线相交于点 ,连接 . ①试探究与 之间的数量关系,并证明你的结论; ②是否为定值?假设是,请求出这个定值;假设不是,请说明理由.16. 〔2017·黄冈〕:如图,MN 为O 的直径,ME 是O 的弦,MD 垂直于过点的直线DE ,垂足为点D ,且ME 平分DMN ∠.求证:〔1〕DE 是O 的切线; 〔2〕2ME MD MN =.9. 〔2017·六盘水〕如图,MN 是O ⊙的直径,4MN,点A 在O ⊙上,30AMN ∠°,B为AN 的中点,P 是直径MN 上一动点. (1)利用尺规作图,确定当PA PB 最小时P 点的位置(不写作法,但要保存作图痕迹).(2)求PA PB 的最小值.10. 〔2017·〕如图,16AB =,O 为AB 中点,点C 在线段OB 上(不与点O ,B 重合),将OC 绕点O 逆时针旋转270︒后得到扇形COD ,AP ,BQ 分别切优弧CD 于点P ,Q ,且点P ,Q 在AB 异侧,连接OP .(1)求证:AP BQ =;(2)当43BQ =时,求QD 的长(结果保存π);(3)假设APO ∆的外心在扇形COD 的部,求OC 的取值围.11. 〔2017·〕如图,AB 是⊙O 的直径,PB 与⊙O 相切于点B ,连接PA 交⊙O 于点C .连接BC .〔1〕求证:CBP BAC ∠=∠; 〔2〕求证:PA PC PB ⋅=2;〔3〕当3,6==CP AC 时,求PAB ∠sin 的值.12.〔2017·〕如图,BC 是⊙O 的直径,点D 为BC 延长线上的一点,点A 为圆上一点,且AB=AD ,AC=CD .〔1〕求证:△ACD ∽△BAD ;〔2〕求证:AD 是⊙O 的切线.13.〔2017·随州〕如图,在Rt △ABC 中,∠C=90°,AC=BC ,点O 在AB 上,经过点A 的⊙O 与BC 相切于点D ,交AB 于点E .〔1〕求证:AD 平分∠BAC ;〔2〕假设CD=1,求图中阴影局部的面积〔结果保存π〕.21.〔2017·〕如图,ABC ∆接于O ,,AB AC CO =的延长线交AB 于点D .〔1〕求证AO 平分BAC ∠;〔2〕假设36,sin 5BC BAC =∠=,求AC 和CD 的长.14.〔2017·〕在等腰△ABC 中,AC=BC ,以BC 为直径的⊙O 分别与AB ,AC 相交于点D ,E ,过点D 作DF ⊥AC ,垂足为点F .〔1〕求证:DF 是⊙O 的切线;〔2〕分别延长CB ,FD ,相交于点G ,∠A=60°,⊙O 的半径为6,求阴影局部的面积.17. 〔2017·〕如图,⊙O 的直径AB =12,弦AC =10,D 是BC 的中点,过点D 作DE ⊥AC 交AC 的延长线于点E .〔1〕求证:DE 是⊙O 的切线; 〔2〕求AE 的长.18. 〔2017·〕如图1,O 的直径12,AB P =是弦BC 上一动点〔与点,B C 不重合〕,030ABC ∠=,过点P 作PD OP ⊥交O 于点D .〔1〕如图2,当//PD AB 时,求PD 的长;〔2〕如图3,当DC AC =时,延长AB 至点E ,使12BE AB =,连接DE . ①求证:DE 是O 的切线;②求PC 的长.19.有两个角分别是它们对角的一半的四边形叫做半对角四边形.(1)如图1,在半对角四边形ABCD 中,12BD ∠∠,12C A ∠∠,求B ∠与C ∠的度数之和; (2)如图2,锐角ABC △接于O ⊙,假设边AB 上存在一点D ,使得BD BO ,OBA ∠的平分线交OA 于点E ,连结DE 并延长交AC 于点F ,2AFE EAF ∠∠.求证:四边形DBCF 是半对角四边形;(3)如图3,在(2)的条件下,过点D 作DGOB 于点H ,交BC 于点G ,当DH BG 时,求BGH △与ABC △的面积之比.20.〔2017·黔东南〕如图,直线PT 与⊙O 相切于点T ,直线PO 与⊙O 相交于A ,B 两点.〔1〕求证:PT 2=PA•PB ;〔2〕假设PT=TB=,求图中阴影局部的面积.21. 〔2017·〕如图,,90,Rt ABC C D ︒∆∠=为BC 的中点.以AC 为直径的圆O 交AB 于点E .〔1〕求证:DE 是圆O 的切线.(2)假设:1:2,6AE EB BC ==,求AE 的长.23.〔10分〕如图,在⊙O 中,直径AB 经过弦CD 的中点E ,点M 在OD 上,AM的延长线交⊙O于点G,交过D的直线于F,∠1=∠2,连结BD与CG交于点N.〔1〕求证:DF是⊙O的切线;〔2〕假设点M是OD的中点,⊙O的半径为3,tan∠BOD=2,求BN的长.20.如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,〔1〕交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.求证:DH是圆O的切线;〔2〕假设A为EH的中点,求的值;〔3〕假设EA=EF=1,求圆O的半径.25.〔10分〕如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.〔1〕求证:AF⊥EF;〔2〕假设AC=6,CF=2,求⊙O的半径.22.〔8分〕如图,△ABC中,以BC为直径的⊙O交AB于点D,AE平分∠BAC 交BC 于点E ,交CD 于点F .且CE=CF .〔1〕求证:直线CA 是⊙O 的切线;〔2〕假设BD=DC ,求的值.24.〔12分〕如图,在Rt △ABC 中,∠ABC=90°,以AB 为直径的⊙O 与AC 交于点D ,点E 是BC 的中点,连接BD ,DE .〔1〕假设=,求sinC ;〔2〕求证:DE 是⊙O 的切线.23.〔9分〕如图,AB 是⊙O 的直径,AC 是上半圆的弦,过点C 作⊙O 的切线DE 交AB 的延长线于点E ,过点A 作切线DE 的垂线,垂足为D ,且与⊙O 交于点F ,设∠DAC ,∠CEA 的度数分别是α,β.〔1〕用含α的代数式表示β,并直接写出α的取值围;〔2〕连接OF 与AC 交于点O′,当点O′是AC 的中点时,求α,β的值.18. 如图,在ABC ∆中,AB AC =,以AB 为直径的⊙O 交AC 边于点D ,过点C 作//CF AB ,与过点B 的切线交于点F ,连接BD .〔1〕求证:BD BF =; 〔2〕假设10AB =,4CD =,求BC 的长.23.〔2017省德阳市,第23题,11分〕如图,AB 、CD 为⊙O的两条直线,DF 为切线,过AO 上一点N 作NM ⊥DF 于M ,连结DN 并延长交⊙O 于点E,连结CE .〔1〕求证:ΔDMN ≌ΔCED ;〔2〕设G 为点E关于AB 对称点,连结GD .GN ,如果∠DNO =45°,⊙O 的半径为3,求22DN GN +的值.22.如图,△ABC 中,以BC 为直径的⊙O 交AB 于点D ,AE 平分∠BAC 交BC 于点E ,交CD 于点F .且CE=CF .〔1〕求证:直线CA 是⊙O 的切线; 〔2〕假设BD=43DC ,求DF CF的值.24.〔2017省市,第24题,10分〕如图,CD 是⊙O 的直径,点B 在⊙O 上,连接BC 、. . . .11 / 11 BD ,直线AB 与CD 的延长线相交于点A ,2AB AD AC ,OE ∥BD 交直线AB 于点E ,OE 与BC 相交于点F .〔1〕求证:直线AE 是⊙O 的切线; 〔2〕假设⊙O 的半径为3,cosA=45,求OF 的长.23.〔本小题总分值10分〕如图,AB 是⊙O 的直径,点D ,E 在⊙O 上,∠A=2∠BDE ,点C 在AB 的延长线上,∠C=∠ABD .〔1〕求证:CE 是⊙O 的切线; 〔2〕假设BF=2,EF=13,求⊙O 的半径长.21.〔8分〕〔2017•〕如图,⊙O 是△ABC 的外接圆,BC 为⊙O 的直径,点E 为△ABC 的心,连接AE 并延长交⊙O 于D 点,连接BD 并延长至F ,使得BD=DF ,连接CF 、BE . 〔1〕求证:DB=DE ;〔2〕求证:直线CF 为⊙O 的切线.。
2017中考数学全国试题汇编------圆(含详细解析)

FhseFhee2017中考数学全国试题汇编-■■■■■圆24 (2017.北京)如图,AB是LI O的一条弦,LI O的切线交CE的延长线于点D .(1)求证:DB 二DE ;(2)若AB =12, BD =5,求LI O 的半径.【解析】E是AB的中点,过点E作EC_OA于点C ,过点B作试题分析:(1)由切线性质及等量代换推出/ 4=7 5,再利用等角对等边可得出结论;(2)由已知条件得出sin7 DEF和sin7 AOE的值,禾用对应角的三角函数值相等推出结论.试题解析:(1)证明:T DC 丄OA, A / 1 + 7 3=90°, v BD 为切线,二OB 丄BD, /-Z 2+7 5=90°, v OA=OB, •••7 1=7 2,v/ 3=7 4,A/ 4=7 5,在厶DEB中, 7 4=7 5,A DE=DB.⑵作DF丄AB 于F,连接OE, ・,.EF^-EE=3/在RTADEF中,EA3, DE=BD=5J EQ3 , J.f~nj jQ-F* 4Y彗一3 =斗——=-3「.在irrAAOE 中rDE5TAEh,二曲二二■ ■考点:圆的性质,切线定理,三角形相似,三角函数27 (2017甘肃白银)•如图,AN是L M的直径,NB//X轴, ~A OAB交L M于点C .(1)若点A 0,6 , N 0,2厂ABN =30°,求点B的坐标;(2)若D为线段NB的中点,求证:直线CD是L M的切线.解:(1)v A 的坐标为(0, 6), N (0, 2)••• AN=4, .............................................................................................................. 1 分vZ ABN=30°, / ANB=90°,••• AB=2AN=8, ...................................................................................................... 2分•••由勾股定理可知:NB=4..3 ,••• B ( 4 3 , 2) ....................................................... 3 分(2)连接MC , NC ........................................................................................... 4 分v AN是O M的直径,•••Z ACN=90°°•••Z NCB=90° ° ................................................................................................... 5 分在Rt A NCB中,D为NB的中点,1•CD= = N B=ND ,2•Z CND=Z NCD, .............................. 6 分v MC=MN ,•Z MCN=Z MNC.vZ MNC+Z CND=90°°• Z MCN+Z NCD=90° ° ...................... 7 分即MC I CD.•直线CD是。
2017年中考数学真题汇编:圆(带答案)

2017年浙江中考真题分类汇编(数学):专题11 圆一、单选题1、(2017·金华)如图,在半径为13的圆形铁片上切下一块高为8的弓形铁片,则弓形弦的长为()A、10B、16C、24D、262、(2017•宁波)如图,在△中,∠A=90°,=.以的中点O为圆心的圆分别与、相切于D、E两点,则的长为()A、B、C、D、3、(2017·丽水)如图,点C是以为直径的半圆O的三等分点,2,则图中阴影部分的面积是()A、B、C、D、4、(2017·衢州)运用图形变化的方法研究下列问题:如图,是⊙O的直径,,是⊙O的弦,且∥∥,10,6,8。
则图中阴影部分的面积是()A、B、C、D、二、填空题5、(2017•杭州)如图,切⊙O于点A,是⊙O的直径.若∠40°,则∠.6、(2017•湖州)如图,已知在中,.以为直径作半圆,交于点.若,则的度数是度.7、(2017·台州)如图,扇形纸扇完全打开后,外侧两竹条,的夹角为120°,长为30,则弧的长为(结果保留)8、(2017•绍兴)如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边,分别与⊙O交于点D,E.则∠的度数为.9、(2017·嘉兴)如图,小明自制一块乒乓球拍,正面是半径为的,,弓形(阴影部分)粘贴胶皮,则胶皮面积为.10、(2017•湖州)如图,已知,在射线上取点,以为圆心的圆与相切;在射线上取点,以为圆心,为半径的圆与相切;在射线上取点,以为圆心,为半径的圆与相切;;在射线上取点,以为圆心,为半径的圆与相切.若的半径为,则的半径长是.11、(2017·衢州)如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线上的动点,过点P作⊙A的切线,切点为Q,则切线长的最小值是三、解答题12、(2017•湖州)如图,为的直角边上一点,以为半径的与斜边相切于点,交于点.已知,.(1)求的长;(2)求图中阴影部分的面积.13、(2017·台州)如图,已知等腰直角△,点P是斜边上一点(不与B,C重合),是△的外接圆⊙O的直径(1)求证:△是等腰直角三角形;(2)若⊙O的直径为2,求的值14、(2017·衢州)如图,为半圆O的直径,C为延长线上一点,切半圆O 于点D。
2017年中考总复习—关于圆的经典题型汇总(含答案)
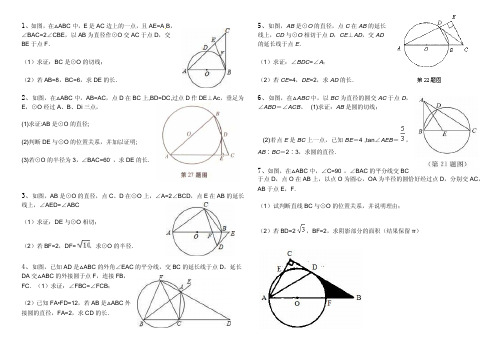
30、如图,AB 是⊙0 的直径,C 是⊙0 上的一点,直线 MN 经过点 C,过点 A 作直线
MN 的垂线,垂足为点 D,且∠BAC=∠DAC.
(1)猜想直线 MN 与⊙0 的位置关系,并 说明理由;
(2)如果⊙0 的半径为 5,sin∠ADE= ,求 BF 的长.
(1)求证:PA 是⊙O 的切线;
39、如图,点 D 是等边△ABC 中 BC 边的延长线上一点,且 AC=CD,以 AB 为直径
作⊙O,分别交边 AC、BC 于点 E、点 F
(1)求证:AD 是⊙O 的切线;
(2)连接 OC,交⊙O 于点 G,若
(2)若 = ,且 OC=4,求 PA 的长和 tanD 的值.
(3) 若 AC= DE,求 tan∠ABD 的值.
21、如图,在平面直角坐标系 xOy 中,以点 O 为圆心的
圆分别交 x 轴的正半轴于点 M,交 y 轴的正半轴于点 N.劣
弧 的长为 π,直线 y=﹣ x+4 与 x 轴、y 轴分别交于 点 A、B.
(1)求证:直线 AB 与⊙O 相切;
(2)求图中所示的阴影部分的面积(结果用 π 表示)
(2)已知 FA•FD=12,若 AB 是△ABC 外 接圆的直径,FA=2,求 CD 的长.
8、如图, AB 为⊙O 的直径,
C 是⊙O 上一点,过点 C 的直 线交 AB 的延长线于点 D, AE⊥DC,垂足为 E,F 是 AE 与⊙O 的交点,AC 平分∠BAE. (1)求证 :DE 是 ⊙O 的切线; (2)若 AE=6,∠D=30°,求图 中阴影部分的面积.
1、如图,在△ABC 中,E 是 AC 边上的一点,且 AE=A B,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、如图,在△ABC中,E是AC边上的一点,且AE=A B,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点
D,交BE 于点 F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
2、如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥Ac,垂足为
E,⊙O 经过 A、B、Di 三点,
(1)求证:AB 是⊙O 的直径;
(2)判断 DE 与⊙O 的位置关系,并加以证明;
(3)若⊙O 的半径为 3,∠BAC=60。
,求 DE 的长.
3、如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB 的延长线上,∠AED=∠ABC
(1)求证:DE与⊙O相切;
(2)若BF=2,DF= ,求⊙O的半径.
4、如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA 交△ABC 的外接圆于点 F,连接 FB,FC.(1)求证:∠FBC=∠FCB;
(2)已知FA•FD=12,若AB是△ABC外
接圆的直径,FA=2,求CD的长.5、如图,AB是⊙O的直径,点C在AB
的延长线上,CD与⊙O相切于点D,
CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
6、如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB。
(1)求证:AB是圆的切
线;
(2)若点E是BC上一点,已知BE=4 ,tan∠AEB =,
AB∶BC=2∶3,求圆的直径.
7、如图,在△ABC中,∠C=90°,∠BAC的平分线交BC
于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB 于点 E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2,BF=2,求阴影部分的面积(结果保留π)
8、如图,AB为⊙O的直径,
C 是⊙O 上一点,过点 C 的直线
交AB的延长线于点D,
AE⊥DC,垂足为 E,F 是 AE
与⊙O的交点,AC平分
∠BAE.(1)求证:DE是⊙O
的切线;(2)若AE=6,
∠D=30°,求图中阴影部分的面
积.
9、如图,AB是⊙O的直径,C是⊙O上的一
点,直线MN经过点C,过点A作直线MN的
垂线,垂足为点D,且∠BAC=∠CAD.
(1)求证:直线MN是⊙O的切线;
(2)若CD=3,∠CAD= 30°,求⊙O的半径.
10、如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.(1)求证:BE是⊙O的切线;
(2)若BC= ,AC=5,求圆的直径AD及切线
BE 的长.
11、如图,在Rt△ABC中,∠ACB=90º,AO是△ABC
的角平分线。
以O为圆心,OC为半径作⊙O。
(1)求证:AB是⊙O的切线。
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD =,求的值。
(3)在(2)的条件下,设⊙O的半径为3,求AB的长。
12、如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结 BD.
(1)求证:∠A=∠BDC;
(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.
13、如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.
14、如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
15、如图,点D在⊙O的直径AB的延长线上,点C在
⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
16、如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC 相交于点 E,连接 EF,过 F 作 FG⊥BC 于点 G,其中∠OFE= ∠A.
(1)求证:BC是⊙O的切线;
(2)若sinB= ,⊙O的半径为r,求△EHG的面积
(用含r的代数式表示).17、如图,在△BCE中,点A时边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点 F 为 OC 与⊙O 的交点,连接 AF.(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的
面积.
18、如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切
线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD.
(1)求证:BD平分∠PBC;
(2)若⊙O的半径为1,PD=3DE,求OE及AB的长.
19、如图,以△ABC的BC边上一点O为圆心,经过A, C 两点且与 BC 边交于点 E,点 D 为 CE 的下半圆弧的中点,连接 AD 交线段 EO 于点F,若 AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF= ,求⊙O的半径r及sinB.
20、如图,已知AB为半圆O的直径,C为半圆
O 上一点,连接 AC,BC,过点 O 作 OD⊥AC 于
点 D,过点 A 作半圆 O 的切线交 OD 的延长线于
点 E,连接 BD 并延长交 AE 于点 F.
(1)求证:AE•BC=AD•AB;
(2)若半圆O的直径为10,sin∠BAC= ,
求AF 的长.
21、如图,在平面直角坐标系xOy中,以点O为圆心的圆
分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣
弧的长为π,直线 y=﹣x+4 与 x 轴、y 轴分别交于
点 A、B.
(1)求证:直线AB与⊙O相切;
(2)求图中所示的阴影部分的面积(结果用π表示)
22、如图,在Rt ABC中,∠ACB=90°,∠BAC的角平分线交BC于点O,OC=1,以点O为圆心OC为半径作圆.
(1)求证:AB为⊙O的切线;
(2)如果tan∠CAO =,求cosB的值. 23、图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交 AD 的延长线于点 E,点 F 为 CE 的中点,连接 DB、DC、DF
(1) 求∠CDE的度数;
(2) 求证:DF是⊙O的切线;
(3) 若AC=DE,求 tan∠ABD 的值.
24、如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC 的延长线相交于点 E.
(1)求证:AD是半圆O的切线;
(2)连结CD.求证:∠A=2∠CDE;
(3)若∠CDE=27°,OB=2,求弧BD的长.
:
25、如图13,在中,,以边
为直径作⊙交边于点,过点作
于点,、的延长线交于点.
(1)求证:是⊙的切线;
(2)若,且,求⊙的半径与线段的长.
26、如图,点B、C、D 都在上,过点C 作交OB延长线于点A,连接CD ,且°,DB=cm.
(1)求证:AC 是的切线;
(2)求由弦CD、BD与弧BC所围成的阴
影部分的面积.(结果保留)27、如图,D为上一点,点C在直径BA的延长线上,且. (1)求证:;
(2)求证:是的切线;
(3)过点B 作的切线交CD的延长线于点E,
若BC=12,,求BE的长.
28、如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA 的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.
(1)求证:AP是⊙O的切线;
(2)OC=CP,AB=6,求CD的长.。
