梯形中位线定理 ppt课件
合集下载
梯形中位线

试一试: 如图所示的三角架,各横木之间互相平 行,且PA=AE=BE,PD=DF=FC.若EF=40cm,则 AD= 20 cm. P 想一想:你会求BC的长吗? A D E B F C
梯形的中位线定义:
连结梯形两腰中点的线段叫做梯形 的中位线。 D A
E B
F C
做一做: 1.画一个梯形ABCD,使AD∥BC; 2.分别取AB、CD的中点E、F,连接EF; 3.沿AF将梯形分成两部分,并画出将△AFD 绕点F旋转1800后的图形.
A E· B D
C
探究发现: 如图,△ABC中,边BC=a, 若 D1、E1分别是 1 AB、AC的中点,则D1E1= 2 a ; 若D2、E2分别是D1B、E1C的中点, A 则D 2E 2= 1 ( 1 a a ) 3 a ;
2 2 4
D1 若D3、E3分别是D2B、E2C的中点, 则 D 3 E 3 = 1 ( 3 a a ) 7 a ; D2 D 3 2 4 8 B 若Dn、En分别是Dn-1B、En-1C的中点, 则D nE n= .
E1 E2 E C3
课堂小结
梯形的中位线定义,定理及证明
课后作业
; https:/// 东京房价
jor593fhl
它了”。我一瞬间觉得天旋地转,这都是什么跟什么,我先是在来的路上遇到了啥不知名的东西,问我像不像,然后住进了诡 异的房子,遇到了白虎,还有山神,我不是在做梦吧,我觉得我应该是做梦吧,我希望闭上眼睛睁开后还是在原来的家里,可 我睁开眼睛看到的确实一位穿着古代衣服的绝色美男,我最近是怎么了,遇到山神,想想就不可能,我是疯了吗,精神分裂了, 然后出现了幻觉,那男的拍了拍我的肩膀说:“你不是吓傻了吧”我呆呆的望着眼前这是陌生的男子,顿时有种想哭的感觉, 仰天长叹:“天哪,你是跟我开玩笑吗,难道以前的生活就回不去了吗”。刚说完,一道闪电划过天际,雷声响起,看来天要 灭我啊,我摇摇头,还是无法接受这个事实。我突然想到他是山神那应该就知道那栋房子的事情吧,我问:“你知道那栋房子, 就是我住那栋以前是谁的吗?”这时我们已经走到房子的大门口了,这还是我来到这里第一次仔细地看看这栋古老的建筑,这 是一栋很大的古宅,在外面一眼就可以认出来,大门上雕刻着精美的花鸟虽因古老而被腐蚀,但却有种沧桑的美感,进去后是 石子铺成的小路,两旁是些破败的杂草和不知名的花再往前就是房屋了是中国传统的建筑。山神看着这栋房子若有所思地说: “这是我的一个老朋友的”我说:“你认识我的母亲?”“你母亲”他疑惑地看着我说。我从背包里拿出了我母亲的照片给他 看,他摇摇头说:“我不认识”。“那为什么我母亲死后告诉我这栋房子是她的”“这个我不知道”他露出无奈的表情。我心 想怎么会这样,我问:“那你的老朋友是谁”他说:“是一个男的,告诉你,你也不认识啊”,我很不爽的白了他一眼还想再 问他这房子怎么回事,他就不耐烦地摆摆手说:“行了,今天就到这,你就先回去吧,还有你应该不可以离开这里,应为这栋 房子不让你离开,否自你也不会遇上白虎了,我也不知道他们为什么一定要让你在这里”我惊奇到:“什么叫这栋房子不让我 离开,它会不会杀了我啊,你可是山神啊,你救救我吧,让我离开这里,我感觉这里妖气冲天啊”“我怎么没看出来这里有妖 气啊,我觉得他们不会杀你的,不然早就动手了,这也不是我管的事情,虽然我是这里的山神,可唯独这栋房子不归我管,我 也不知道为什么,我们就是这样规定的,你好好保重吧,我会来看你的”山神一脸贱贱的表情说完就不见了。独留我一人还在 神游,什么叫这栋房子不让我离开,哼我偏要走,我转身刚走,耳边就响起山神的声音说:“你还是省省吧,再出去,说不定 遇到的就是狰这种凶神了,而且还有可能是一群啊,别白费心急了”我想想也是,我手无缚鸡之力的,还是别找死了。我回到 客厅里看看还是来时的样子,回到卧室里想想这些天发生的事情
23梯形中位线
∠DBC=30°,求证:AC=MN.
A
D
O
M
N
E
B
C
思考
有一个木匠想制作一个木梯,共需5根横木共 200cm,其中最上端的横木长20cm,求其他 四根横木的长度?(每两根横木的距离相等)
①求证:梯形ABCD是等腰梯形;
②当AB与AC具有什么位置关系时,四边形AECD是菱形? 请说明理由,并求出此时菱形AECD的面积.
例3.如图,在梯形ABCD中,AD∥BC,AB=DC,对角线 AC、BD交于点O,AC⊥BD,E、F、G、H分别是 AB、BC、CD、DA的中点. ①求证:四边形EFGH是正方形. ②若AD=2,BC=4.求四边形EFGH的面积.
A
D
F
E
A
D
E
F
B
C
B
C
中位线性质定理的推论:经过梯形一腰的中点与底 平行的直线必平分另一腰.
思考: 梯形面积公式
S梯形
1(a 2
b)h
中位线x高
lh
①一个梯形的上底长4 cm,下底长6 cm,则其中位线长为
____5__cm;
②一个梯形的上底长10 cm,中位线长16 cm,则其下底长为
____2_2__cm;
∴BG=2,
设AB=x,则CD=x-2,
G
∵EF为中位线,
∴AB+CD=2EF,即x+x-2=8,解得x=5,
课堂小结
1、梯形中位线的定义
2、梯形中位线定理及推论
3、梯形中位线与三角形中位线的 区别与联系 4、梯形面积公式
拓展提升
如图所示的梯形ABCD中,AD∥BC,对角线
AC 与 BD 垂 直 相 交 于 O , MN 是 中 位 线 ,
苏科版八年级数学梯形的中位线课件

1 EF= (AD+BC) 2
B E
梯形
中位线定理
梯形的中位线平行于两底,并且等 于两底和的一半
A D F G C
已知:梯形ABCD中,AD∥BC,
AE=EB,DF=FC 求证:EF∥BC 且
1 EF= (AD+BC) 2
B
H
E
梯形
中位线定理
梯形的中位线平行于两底,并且等 于两底和的一半
A E D F C
①准备好梯形硬纸片,折出梯形的中位线. A D F
②用剪刀对梯形剪下一块 , 再拼成一 个三角形 , 并且使梯形的中位线成为 E 三角形的中位线.
B
C
演示2
梯形
中位线定理
梯形的中位线平行于两底,并且等 于两底和的一半
A D
F C G
已知:梯形ABCD中,AD∥BC,
AE=EB,DF=FC 求证:EF∥BC 且
C )
D.300cm2
三、问答:
更上一层楼
1、梯形的中位线长能不能与它的一条 底边相等?为什么?
2 、梯形的中位线一定平分梯形的对角 线吗?为什么?
四、计算:
智力大冲浪
如图,梯形ABCD中,AD∥BC,中位线分别交 对角线 BD 、 AC 于点 M 、 N ,若 AD=4cm,BC=8cm, 求:MN的长
EF∥BC, EF AD BC
D
E
F
B
1 EF∥BC, EF ( BC AD) 1 2 EF∥BC, EF ( AD BC ) 2
B
C
C
★ 知道了梯形的中位线的定义
★ 会用转化的思想来证明梯形中位线定理 ★ 梯形的第二种面积公式 ★ 利用梯形中位线定理来解决一些数学问题
B E
梯形
中位线定理
梯形的中位线平行于两底,并且等 于两底和的一半
A D F G C
已知:梯形ABCD中,AD∥BC,
AE=EB,DF=FC 求证:EF∥BC 且
1 EF= (AD+BC) 2
B
H
E
梯形
中位线定理
梯形的中位线平行于两底,并且等 于两底和的一半
A E D F C
①准备好梯形硬纸片,折出梯形的中位线. A D F
②用剪刀对梯形剪下一块 , 再拼成一 个三角形 , 并且使梯形的中位线成为 E 三角形的中位线.
B
C
演示2
梯形
中位线定理
梯形的中位线平行于两底,并且等 于两底和的一半
A D
F C G
已知:梯形ABCD中,AD∥BC,
AE=EB,DF=FC 求证:EF∥BC 且
C )
D.300cm2
三、问答:
更上一层楼
1、梯形的中位线长能不能与它的一条 底边相等?为什么?
2 、梯形的中位线一定平分梯形的对角 线吗?为什么?
四、计算:
智力大冲浪
如图,梯形ABCD中,AD∥BC,中位线分别交 对角线 BD 、 AC 于点 M 、 N ,若 AD=4cm,BC=8cm, 求:MN的长
EF∥BC, EF AD BC
D
E
F
B
1 EF∥BC, EF ( BC AD) 1 2 EF∥BC, EF ( AD BC ) 2
B
C
C
★ 知道了梯形的中位线的定义
★ 会用转化的思想来证明梯形中位线定理 ★ 梯形的第二种面积公式 ★ 利用梯形中位线定理来解决一些数学问题
梯形中位线定理

①一个梯形的上底长4 cm,下底长6 cm,则 其中位线长为 5 cm;
②一个梯形的上底长10 cm,中位线长16 cm, 则其下底长为 22 cm; ③已知梯形的中位线长为6 cm,高为8 cm, 48 则该梯形的面积为________ cm2 ; ④已知等腰梯形的周长为80 cm,中位线与腰 长相等,则它的中位线长 20 cm;
如图所示的梯形梯子, AA/∥EE/, AB=BC=CD=DE, A/B/=B/C/=C/D/=D/E/ , /=0.5 m,EE/=0.8 m. (第 3 题) AA 求BB/、CC/、DD/的长.
举例应用4
如图梯形ABCD中,AB∥CD,且 AB>CD,EF分别是AC和BD的中点, 1 求证:EF= 2 (AB – CD)
A 如图,点E、F分 别是AB、CD的中 点,则线段EF是 E 梯形ABCD的中位 线 B
D F C
三、议一议
E B
A
D
F C
如图,EF是梯形ABCD的中位线,连接 AF并延长,与BC的延长线相交于点G.
G
⑶通过刚才的探究你能得 ⑴∆ADF与∆GCF全等吗?为什么? ⑵梯形的中位线EF与两底AD,BC有怎样 出怎样的结论? 的位置关系?有怎样的数量关系?
六、举例应用1
如图,在梯形ABCD中,AD∥BC, CD⊥BC, ∠B=45 °,AD=CD=a。 求梯形ABCD的中位线EF长.
A E B
G
ቤተ መጻሕፍቲ ባይዱ
D F C
举例应用2 如 图 , 在 梯 形 ABCD 中 , AD∥BC, AB=AD+BC,E为CD的中点. 求证:AE⊥BE.
A
D
F
B
E
C
举例应用3
②一个梯形的上底长10 cm,中位线长16 cm, 则其下底长为 22 cm; ③已知梯形的中位线长为6 cm,高为8 cm, 48 则该梯形的面积为________ cm2 ; ④已知等腰梯形的周长为80 cm,中位线与腰 长相等,则它的中位线长 20 cm;
如图所示的梯形梯子, AA/∥EE/, AB=BC=CD=DE, A/B/=B/C/=C/D/=D/E/ , /=0.5 m,EE/=0.8 m. (第 3 题) AA 求BB/、CC/、DD/的长.
举例应用4
如图梯形ABCD中,AB∥CD,且 AB>CD,EF分别是AC和BD的中点, 1 求证:EF= 2 (AB – CD)
A 如图,点E、F分 别是AB、CD的中 点,则线段EF是 E 梯形ABCD的中位 线 B
D F C
三、议一议
E B
A
D
F C
如图,EF是梯形ABCD的中位线,连接 AF并延长,与BC的延长线相交于点G.
G
⑶通过刚才的探究你能得 ⑴∆ADF与∆GCF全等吗?为什么? ⑵梯形的中位线EF与两底AD,BC有怎样 出怎样的结论? 的位置关系?有怎样的数量关系?
六、举例应用1
如图,在梯形ABCD中,AD∥BC, CD⊥BC, ∠B=45 °,AD=CD=a。 求梯形ABCD的中位线EF长.
A E B
G
ቤተ መጻሕፍቲ ባይዱ
D F C
举例应用2 如 图 , 在 梯 形 ABCD 中 , AD∥BC, AB=AD+BC,E为CD的中点. 求证:AE⊥BE.
A
D
F
B
E
C
举例应用3
梯形的中位线

有祖母懂得那些落叶,也只有那些落叶懂得祖母,她们惺惺相惜,彼此嘘寒问暖。 怀念祖母,是从一片叶子开始的,
• 在梯形ABCD中,AD∥BC,EF是中 位线.1)若AD=8cm,EF= 12cm,则BC=___cm.
2)若EF=10cm,高AH=6c m,则AD+BC=___cm.
3)若一个等腰梯形的中位线长是6cm, 腰长是5cm,则这个等腰梯形的周 长是___cm.
• 求底AB与DC的长
D
C
A
EB
;代办资质 代办资质 ;
一转身,我已找不到他,只看见攒动的人头,闪动的各色衣服…… ④还记得那年春天,我一人在秦岭深处行走,山路两旁开满野花:灯芯花、野草莓花、苜蓿花、蒲公英花……路下面的小河,清澈如镜,温柔如绸,淙淙的水声像母亲轻唤谁的乳名。四周的群山,一律被松树、柏树、桦树和茂密
中年乞丐。我急忙赶回家,拿上我去年穿过的那件防寒服给他。可是来到南大街,已看不见他,于是我在东大街找他,又在北大街找他,都没有找到。最后我来到丁字路口,还是没有找到他,却遇到了一个老年乞丐。一转身,苦难转换了方向,交换了背影,但苦难的身份没有改变,都是苦难。
于是我把防寒的衣服披在了这位贫苦的老人身上,希望他下降的体温能稍稍回升,希望降温的人性能稍稍回升。我由此想到,亚洲的穷人,非洲的穷人,全世界的穷人,想到徘徊在文明大街上的那些孤苦身影,一转身,他们到那里去了?而文明,你能否追上去,轻轻拉起那褴褛的衣襟,或者握
。我想在记忆里逼真地收藏一个像野花一样纯真的秦岭女孩。这也许是她一生里最生动的瞬间,我记起了泰戈尔的诗句:“你不知道你是多么美丽,你像花一样盲目。”我情不自禁地转过身来,沿着小女孩走的方向走着,走到山路转弯的地方,出现了个三岔路口。我已经无法知道小女孩走进了
15 1.6中位线定理(第二课时梯形中位线)

(2)分别取AB、CD的中点M、N,连接MN;
(3)沿AN将梯形剪成两部分,并将△ADN绕点N按顺时针方向旋转180°到△ECN的位置,得△ABE,如右图。
思考并讨论:在上图中,MN与BE有怎样的位置关系和数量关系?为什么?
师生总结
1.梯形中位线定义:连接梯形两腰中点的线段
2.梯形中位线的性质:梯形中位线平行于两底且等于两底和的一半。
【定理的证明师生分析后由学生自己写出】
定理符号语言表达:
在梯形ABCD中,AD∥BC
∵;
∴。
巩固提升:
1、一个梯形的上底长4 cm,下底长6 cm,则其中位线长为cm;
2、一个梯形的上底长10 cm,中位线长16 cm,则其下底长为cm;
3、已知梯形的中位线长为6 cm,高为8 cm,则该梯形的面积为________ cm2;
3.若梯形的周长为80cm,中位线长于腰长相等,高为12cm,则它的面积为。
4.一个等腰梯形的对角线互相垂直,梯形的高为2cm,,则梯形的面积为。
5.有一个木匠想制作一个木梯,共需5根横木共200cm,其中最上端的横木长20cm,求其他四根横木的长度(每两根横木的距离相等)。
课
后
延
伸
(分析辅助线的添加)已知:如图在梯形ABCD中,AD∥BC,AB=AD+BC,P为CD的中点,求证:AP⊥BP
教(学)后反思
4、已知等腰梯形的周长为80 cm,中位线与腰长相等,则它的中位线长cm;
课堂小结:
通过今天的学习你有哪些收获?
还存在哪些困惑和疑虑?
达标检测:
1.已知梯形的中位线长为24厘米,上、下底的比为1:3,则梯形的上、下底之差是( )
A.24厘米B.12厘米; C.36厘米D.48厘米
(3)沿AN将梯形剪成两部分,并将△ADN绕点N按顺时针方向旋转180°到△ECN的位置,得△ABE,如右图。
思考并讨论:在上图中,MN与BE有怎样的位置关系和数量关系?为什么?
师生总结
1.梯形中位线定义:连接梯形两腰中点的线段
2.梯形中位线的性质:梯形中位线平行于两底且等于两底和的一半。
【定理的证明师生分析后由学生自己写出】
定理符号语言表达:
在梯形ABCD中,AD∥BC
∵;
∴。
巩固提升:
1、一个梯形的上底长4 cm,下底长6 cm,则其中位线长为cm;
2、一个梯形的上底长10 cm,中位线长16 cm,则其下底长为cm;
3、已知梯形的中位线长为6 cm,高为8 cm,则该梯形的面积为________ cm2;
3.若梯形的周长为80cm,中位线长于腰长相等,高为12cm,则它的面积为。
4.一个等腰梯形的对角线互相垂直,梯形的高为2cm,,则梯形的面积为。
5.有一个木匠想制作一个木梯,共需5根横木共200cm,其中最上端的横木长20cm,求其他四根横木的长度(每两根横木的距离相等)。
课
后
延
伸
(分析辅助线的添加)已知:如图在梯形ABCD中,AD∥BC,AB=AD+BC,P为CD的中点,求证:AP⊥BP
教(学)后反思
4、已知等腰梯形的周长为80 cm,中位线与腰长相等,则它的中位线长cm;
课堂小结:
通过今天的学习你有哪些收获?
还存在哪些困惑和疑虑?
达标检测:
1.已知梯形的中位线长为24厘米,上、下底的比为1:3,则梯形的上、下底之差是( )
A.24厘米B.12厘米; C.36厘米D.48厘米
梯形中位线的证明

连结af并延长交bc的延长线于点madfmcf40知识巩固已知等腰梯形中位线长6cm它的腰长5cm则这个梯形的周长为cm一个等腰梯形周长80如果它的中位线与腰长相等它的中位线长122220梯形的中位线长9cm一条对角线把中位线分成1
1
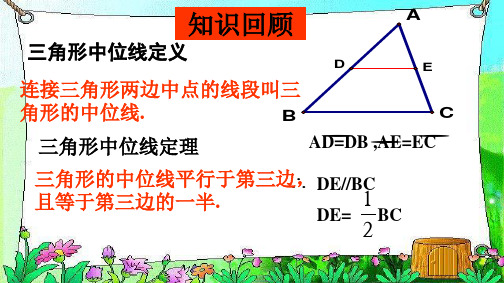
三角形中位线定理
A
三角形的中位线平行于第三边,
并且等于它的一半
E
D
M
F
C N
D F
C
38
A E B
D
M
F
C N
A E B
G A E B
D
M
F
C N
D F
C
39
知识巩固
1 梯形的上底长8,下底长10,则这个梯形的中位线长_9_ 2 梯形的上底长8,中位线长10,则下底长是_1_2 3 已知等腰梯形中位线长6cm,它的腰长5cm,则这个梯形 的周长为_22__cm 4 一个等腰梯形周长80,如果它的中位线与腰长相等,它的 中位线长_20_ 5 梯形的中位线长9cm,一条对角线把中位线分成1:2两部 分,则该梯形的下底长_12__cm
即EF//BC ,EF= ½BC
B
F
C
2
梯形中位线定理
梯形的中位线平行于两底,并且等于两底和的一半
已知:梯形ABCD中,
A
AD//BC,AE=EB,DF=FC
E
求证:EF//BC,EF=½ (BC+AD)
B
证明:连结AF并延长,交BC的延长线于点M
D 1F
23
C
M
∵ DF=FC,∠1=∠2,∠D=∠3,
A E B
D
M
F
C N
G A E B
D F
1
三角形中位线定理
A
三角形的中位线平行于第三边,
并且等于它的一半
E
D
M
F
C N
D F
C
38
A E B
D
M
F
C N
A E B
G A E B
D
M
F
C N
D F
C
39
知识巩固
1 梯形的上底长8,下底长10,则这个梯形的中位线长_9_ 2 梯形的上底长8,中位线长10,则下底长是_1_2 3 已知等腰梯形中位线长6cm,它的腰长5cm,则这个梯形 的周长为_22__cm 4 一个等腰梯形周长80,如果它的中位线与腰长相等,它的 中位线长_20_ 5 梯形的中位线长9cm,一条对角线把中位线分成1:2两部 分,则该梯形的下底长_12__cm
即EF//BC ,EF= ½BC
B
F
C
2
梯形中位线定理
梯形的中位线平行于两底,并且等于两底和的一半
已知:梯形ABCD中,
A
AD//BC,AE=EB,DF=FC
E
求证:EF//BC,EF=½ (BC+AD)
B
证明:连结AF并延长,交BC的延长线于点M
D 1F
23
C
M
∵ DF=FC,∠1=∠2,∠D=∠3,
A E B
D
M
F
C N
G A E B
D F
七年级数学上册 梯形中位线定理 课件 青岛版

例1、如图,等腰梯形ABCD,AD ∥BC,EF是中位线,且 EF=15cm, ∠ABC =60°,BD平分∠ABC. ⑴图中能分别解出几个“三角形中位线”A 和“梯形中位线” 这两个基本图形? E 还有别的基本图形吗? G D F C
⑵ 求梯形的周长.
分析与略解:
B
梯形的周长,就转化为求其中一腰或一底就可以了。 ⑴显然可证 G为BD的中点,所以可分解出两个“三角形中 设AD=AB=DC=x,则BC=2x. 位线”这个基本图形和一个“梯形中位线”这个基本图形。 1 3 除此之外,还有两个等腰三角形(△ 和△ ABD)和两 ∵ EF= 2(AD+BC),∴15= 2 x,EBG ∴x=10 , 个含有30°角的直角三角形(Rt △GDF和 Rt △BDC ). ∴梯形周长为50㎝.
2.梯形的中位线一定平分梯形的对角线吗?为什么?
答:一定平分梯形的对角线.因为梯形的中位线平行于两 底,根据平行线等分线段定理,中位线一定平分对角线.
3.梯形的中位线长能不能与它的一条底边长相等?为什么? 答:不能.如果和一条底边长相等,那么和另一条底边长 也相等,这时四边形的对边平行且相等,这是平行四边形 而不是梯形.
∴ AF=GF,AD=GC 又∵AE=EB
E
B
F
C G
∴EF是△ABG的中位线.
∴EF ∥BG ,EF= 1 BG(三角形的中位线定理 ) ∵BG=BC+CG=BC+AD
2
∴EF= 1 (BC+AD)
2
在小学我们学过梯形面积的计算公 1 式S= 2 (a+b)h,根据梯形中位线定理,如 1 果中位线长为L,那么L= 2 (a+b),因此梯 形还有下面的面积计算公式: S=L· h.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求证:MN∥BC,MN = 1(BC+AD) 2
A
D
M
N
B
C
E
A 40cm D
E 45cm F
OK
M 50cm N
G 55cm H
B
60cm
C
思考
梯形面积公式
S梯形12(ab)h
中位线 × 高 lh
试一试
① 一个梯形的上底长 4 cm,下底长 6 cm, 则其中位线长为 5 cm;
② 一个梯形的上底长10cm,中位线长16cm, 则其下底长为 22 cm;
D
两腰AB、DC中点,
E
F
则EF叫做
。 B
C
定义:联结梯形两腰中点的线段叫做
梯形的中位线。
观察猜想
A
D
E
F
动手量一量
B
C
在梯形ABCD中,中位线EF和AD、BC什么关系?
命题:梯形的中位线平行于两底,并且 等于两底和的一半.
已知:在梯形ABCD中,AD∥BC,AE=EB,
DF=FC。
求证:EF∥BC,
AD=4,BC=8,
求: EF= 。
A
D
M
N
EF
B
C
已知:直角梯形的一条对角线把梯形分成两个 三角形,其中一个边长为50cm的等边三角形, 则梯形的中位线长为 。
A
D
B
C
EF= 1 (BC+AD) 2
A
D
E
F
B
C
梯形的中位线的性质
梯形中位线定理: 梯形的中位线平行
于两底,并且等于两底之和的一半
用符号语言表示
A
D
∵ EF是梯形ABCD的中位线
E
∴ EF∥BC( EF∥AD ),
F
EF= 1 (AD+BC) 2
B
C
已知:在梯形ABCD中,AD∥BC,AM=MB,DN=NC,
1 2
B
C△ ABC
F
C
(4)S△ DEF=
1 4
S△ ABC
已知:正方形ABCD中,P为CD的中点,
PQ∥AD,求证:PQ= 1 AB 2
A
D形”一定是平行四边形, 它是不是特殊的平行四边形取决于它的对角 线是否垂直或者是否相等.
原四边形两条对角线 互相垂直 相等
互相垂直且相等 既不互相垂直也不相等
中点四边形
矩形 菱形 正方形 平行四边形
在△ABC中,AD=BD,AE=EC,
则 DE —∥— BC(位置关系), D DE —= —12 BC(数量关系)。 B
在梯形ABCD中,AD∥BC,AE=BE, A
若EF∥AD,则 DF —=— FC
E
(数量关系)。
B
A E C D F C
如图:E、F为梯形ABCD A
③ 已知梯形的中位线长为6 cm,高为8 cm, 则该梯形的面积为___4_8__ cm2 ;
④ 已知等腰梯形的周长为80 cm,中位线与 腰长相等,则它的中位线长 20 cm;
已知:如图,在梯形ABCD中,AD∥BC,
AB=AD+BC,E为CD的中点.
求证:AE⊥BE.
A
D
F
E
B
C
已知:在梯形ABCD中,MN为中位线,
一个木匠要修补一个木梯,共需 3 根横木, 其中上端的横木长40cm,下端的横木长60cm, 求这 3 根横木的长度?(每两根横木的距离相等)
40cm
60cm
如图:D、E、F为AB、AC、BC中点,
(1)若AC=8,则DF= 4 ;
A
(2)若∠ADE=60°,
D
E
则∠B= 60 度,
(3)C△ DEF=
A
D
M
N
B
C
E
A 40cm D
E 45cm F
OK
M 50cm N
G 55cm H
B
60cm
C
思考
梯形面积公式
S梯形12(ab)h
中位线 × 高 lh
试一试
① 一个梯形的上底长 4 cm,下底长 6 cm, 则其中位线长为 5 cm;
② 一个梯形的上底长10cm,中位线长16cm, 则其下底长为 22 cm;
D
两腰AB、DC中点,
E
F
则EF叫做
。 B
C
定义:联结梯形两腰中点的线段叫做
梯形的中位线。
观察猜想
A
D
E
F
动手量一量
B
C
在梯形ABCD中,中位线EF和AD、BC什么关系?
命题:梯形的中位线平行于两底,并且 等于两底和的一半.
已知:在梯形ABCD中,AD∥BC,AE=EB,
DF=FC。
求证:EF∥BC,
AD=4,BC=8,
求: EF= 。
A
D
M
N
EF
B
C
已知:直角梯形的一条对角线把梯形分成两个 三角形,其中一个边长为50cm的等边三角形, 则梯形的中位线长为 。
A
D
B
C
EF= 1 (BC+AD) 2
A
D
E
F
B
C
梯形的中位线的性质
梯形中位线定理: 梯形的中位线平行
于两底,并且等于两底之和的一半
用符号语言表示
A
D
∵ EF是梯形ABCD的中位线
E
∴ EF∥BC( EF∥AD ),
F
EF= 1 (AD+BC) 2
B
C
已知:在梯形ABCD中,AD∥BC,AM=MB,DN=NC,
1 2
B
C△ ABC
F
C
(4)S△ DEF=
1 4
S△ ABC
已知:正方形ABCD中,P为CD的中点,
PQ∥AD,求证:PQ= 1 AB 2
A
D形”一定是平行四边形, 它是不是特殊的平行四边形取决于它的对角 线是否垂直或者是否相等.
原四边形两条对角线 互相垂直 相等
互相垂直且相等 既不互相垂直也不相等
中点四边形
矩形 菱形 正方形 平行四边形
在△ABC中,AD=BD,AE=EC,
则 DE —∥— BC(位置关系), D DE —= —12 BC(数量关系)。 B
在梯形ABCD中,AD∥BC,AE=BE, A
若EF∥AD,则 DF —=— FC
E
(数量关系)。
B
A E C D F C
如图:E、F为梯形ABCD A
③ 已知梯形的中位线长为6 cm,高为8 cm, 则该梯形的面积为___4_8__ cm2 ;
④ 已知等腰梯形的周长为80 cm,中位线与 腰长相等,则它的中位线长 20 cm;
已知:如图,在梯形ABCD中,AD∥BC,
AB=AD+BC,E为CD的中点.
求证:AE⊥BE.
A
D
F
E
B
C
已知:在梯形ABCD中,MN为中位线,
一个木匠要修补一个木梯,共需 3 根横木, 其中上端的横木长40cm,下端的横木长60cm, 求这 3 根横木的长度?(每两根横木的距离相等)
40cm
60cm
如图:D、E、F为AB、AC、BC中点,
(1)若AC=8,则DF= 4 ;
A
(2)若∠ADE=60°,
D
E
则∠B= 60 度,
(3)C△ DEF=
