实验报告-主应力测定
实验五 弯扭组合主应力电测实验 - 山东理工大学

实验五弯扭组合主应力电测实验 - 山东理工大学一、实验目的1. 掌握压电晶体主应力测量原理及应用;2. 了解弯扭组合应力的数学模型和电测电路设计;3. 实现不同应力状态下的主应力测量和数据记录。
二、实验原理1. 压电晶体的应变与电量的关系杨氏模量 E:表示晶体单位应变对应的应力,即E=σ/ε压电系数 d33:表示晶片沿极化方向(3)的压电效应,σ = d33×ε2. 弯扭组合应力在构件中,因为同时作用有多个正应力和剪应力,使得它们所产生的同方向主应力不再与构件体坐标系保持一致,不是单向的,这种情况称为“主应力变向”。
3. 电测电路设计放大器是一个直流差动放大器。
它主要由四个放大器管和一个差分负载组成。
通常使用皮卡德电阻电桥作为应力传感器,测出的电势差信号被放大器扩大,即可得到相应的应力信号。
实验器材:压电晶体、动力学实验台、电源、斜坡波发生器、示波器、放大器、连接线等。
实验步骤1. 产生不同应力状态通过动力学实验台的加工模块产生不同的弯矩和扭矩,以这些载荷对标准试件(如钢棒、铜柱等)施加不同的应力状态。
2. 测量压电晶体电势将压电晶体片紧贴标准试件表面,并从标准试件表面传递应力。
此时,晶片上的应变将导致电场强度的变化,从而在晶片上出现电势差。
将示波器和放大器连接上后,即可获得相应的电位和电流信号。
3. 记录实验数据测量各数据点的电位和电流数值,经过放大处理后,得到应力和应变大小。
根据弯扭组合应力的数学模型,得到各状态下的主应力大小。
根据测得的数据,用图形显示出主应力大小和各个轴向应力的方向。
实验注意事项1. 实验前需要对实验器材进行检查。
2. 实验中需要注意操作安全,避免造成人员伤害和财物损失。
实验结论通过本次实验,我们掌握了压电晶体主应力测量原理和应用,了解了弯扭组合应力的数学模型和电测电路设计,并实现了不同应力状态下的主应力测量和数据记录。
在实验过程中,我们需要注意操作安全,避免造成人员伤害和财物损失,同时还要对实验器材进行清理和维护。
主应力实验报告

主应力实验报告主应力实验报告引言:主应力是材料力学中的重要参数,它对材料的强度、变形和断裂行为有着重要影响。
为了研究主应力对材料力学性能的影响,我们进行了一系列的主应力实验。
本报告将对实验过程、结果和分析进行详细描述。
实验目的:1. 研究主应力对材料的强度和变形行为的影响;2. 探究主应力对材料断裂行为的影响;3. 验证主应力理论在材料力学中的适用性。
实验装置和方法:本次实验采用了一台电子万能试验机和标准的主应力试样。
试样材料为金属材料,通过电子万能试验机施加不同的轴向拉伸力和侧向压力,从而产生主应力场。
实验过程中,通过传感器测量试样的应变和力,得到应力-应变曲线。
实验过程:1. 准备试样:根据实验要求,选择合适的试样尺寸,并进行表面处理以消除表面缺陷。
2. 安装试样:将试样固定在电子万能试验机上,保证试样与试验机夹具之间的接触良好。
3. 施加轴向拉伸力:根据实验设计,逐渐增加轴向拉伸力,同时记录试样的应变和力值。
4. 施加侧向压力:在轴向拉伸力的作用下,逐渐增加侧向压力,同时记录试样的应变和力值。
5. 停止加载:当试样出现明显的塑性变形或断裂时,停止加载,并记录相应的应变和力值。
实验结果与分析:根据实验数据,我们绘制了应力-应变曲线,并进行了如下分析:1. 强度和变形行为:通过应力-应变曲线可以观察到试样的屈服点、最大应力点和断裂点。
随着轴向拉伸力的增加,试样的应力逐渐增大,直至达到屈服点。
在屈服点之后,试样的应力逐渐下降,但仍然保持一定的强度。
当试样达到最大应力点时,开始出现明显的塑性变形。
最终,在达到断裂点时,试样发生破裂。
2. 断裂行为:通过观察断裂面形貌,我们可以推测试样的断裂模式。
根据实验结果,试样的断裂面呈现出典型的韧性断裂特征,即具有一定的延展性。
这表明试样在受到主应力作用时,会发生塑性变形,而不是立即断裂。
3. 主应力理论验证:通过实验数据和分析,我们验证了主应力理论在材料力学中的适用性。
应变花测定主应力实验(弯扭组合)
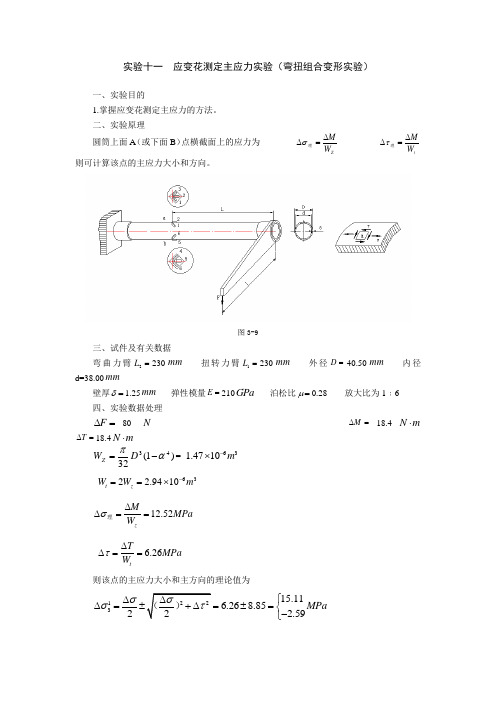
实验十一 应变花测定主应力实验(弯扭组合变形实验)一、实验目的1.掌握应变花测定主应力的方法。
二、实验原理圆筒上面A (或下面B )点横截面上的应力为 Z W M ∆=∆理σ tW M∆=∆理τ 则可计算该点的主应力大小和方向。
图3-9三、试件及有关数据弯曲力臂=2L 230mm 扭转力臂=1L 230mm 外径=D 40.50mm 内径 d=38.00mm壁厚=δ 1.25mm 弹性模量=E 210GPa 泊松比=μ0.28 放大比为1﹕6四、实验数据处理F ∆=80 N=∆M 18.4N m ⋅=∆T18.4N m ⋅)1(3243απ-=D W Z = 631.4710m -⨯632 2.9410t z W W m -==⨯12.52zMMPa W σ∆∆==理 6.26tTMPa W τ∆∆== 则该点的主应力大小和主方向的理论值为1315.116.268.85 2.592MPa σσ⎧∆∆=±=±=⎨-⎩2tan 2τασ-∆=-=∆12.52112.52= 0022.5α=注:该点应变花的三片应变片为451-=εε,02εε=,453εε=或456-=εε,05εε=,454εε=或接成半桥互为补偿时,︒-45、︒0、︒45三个方向分别对应为1和4,2和5,3和6的三个接桥的线应变方向。
的则其主应力和主方向的测试值为=-+-+±-+=∆--20452045454513)()()1(22)1(2)(εεεεμμεεσEE {15.72210(61.516.5) 6.569.16 2.62(10.28)-=±=-- 04545045452262.561.516.5tan 2 1.02561.516.5εεεαεε----⨯-+===-+ 0022.9α=相对误差 =1η =2η =3η。
实验四 薄壁圆筒在弯扭组合变形下主应力测定

实验四薄壁圆筒在弯扭组合变形下主应力测定实验内容:构件在弯扭组合作用下,根据强度理论,其强度条件就是。
计算当量应力,首先要确定主应力,而主应力得方向就是未知得,所以不能直接测量主应力.通过测定三个不同方向得应变,计算主应变,最后计算出主应力得大小与方向.本实验测定应变得三个方向分别就是-45°、0°与45°.实验目得与要求:1、用电法测定平面应力状态下一点得主应力得大小与方向2、进一步熟悉电阻应变仪得使用,学会1/4桥法测应变得实验方法设计思路:为了测量圆管得应力大小与方向,在圆管某一截面得管顶B点、管底D点各粘贴一个45°应变花,测得圆管顶B点得-45°、0°与45°三个方向得线应变、、.应变花得粘贴示意图实验装置示意图关键技术分析:由材料力学公式:得从以上三式解得主应变根据广义胡克定律1、实验得主应力大小__________________ 122 4545450450 2()2()() 2(1)2(1)E Eσεεεεεεσμμ--+⎫=±-+-⎬-+⎭实实方向2、理论计算主应力3、误差实验过程1、测量试件尺寸、力臂长度与测点距力臂得距离,确定试件有关参数.附表1 2、拟定加载方案。
先选取适当得初载荷P 0(一般取P o=lO %P max 左右)。
估算P max (该实验载荷范围P max 〈400N),分4~6级加载。
3。
根据加载方案,调整好实验加载装置。
4.加载.均匀缓慢加载至初载荷P o ,记下各点应变得初始读数;然后分级等增量加载,每增加一级载荷,依次记录各点电阻应变片得应变值,直到最终载荷。
实验至少重复两次。
5.作完试验后,卸掉载荷,关闭电源,整理好所用仪器设备,清理实验现场,将所用仪器设备复原,实验资料交指导教师检查签字。
6、实验装置中,圆筒得管壁很薄,为避免损坏装置,注意切勿超载,不能用力扳动圆筒得自由端与力臂。
弯扭组合变形的主应力测试实验

弯扭组合变形的主应力测试实验一、实验目的1.用电测法测定平面应力状态下主应力的大小及方向;2.测定薄壁圆管在弯扭组合变形作用下,分别由弯矩、剪力和扭矩所引起的应力。
二、实验仪器和设备1. 弯扭组合实验装置;2. 应变&力综合测试仪三、实验原理和方法弯扭组合实验装置如图1所示。
它由薄壁圆管1(已粘好应变片),扇臂2,钢索3,传感器4,加载手轮5,座体6,数字测力仪7等组成。
试验时,逆时针转动加载手轮,传感器受力,将信号传给数字测力仪,此时,数字测力仪显示的数字即为作用在扇臂顶端的载荷值,扇臂顶端作用力传递至薄壁圆管上,薄壁圆管产生弯图1扭组合变形。
薄壁圆管材料为铝合金,其弹性模量E为722GN, 泊松比μ为m0.33。
薄壁圆管截面尺寸、受力简图如图2所示,Ⅰ-Ⅰ截面为被测试截面,由材料力学可知,该截面上的内力有弯矩、剪力和扭矩。
取Ⅰ-Ⅰ截面的A、B、C、D四个被测点,其应力状态如图3所示。
每点处按–450、00、+450方向粘贴一枚三轴450应变花,如图4所示。
图2图3 图4 图51. 指定点的主应力大小和方向的测定受弯扭组合变形作用的薄壁圆管其表面各点处于平面应力状态,用应变花测出三个方向的线应变, 然后运用应变-应力换算关系求出主应力的大小和方向。
本实验用的是450应变花,若测得应变ε-45、ε0、ε45,则主应力大小的计算公式为()()()⎥⎦⎤⎢⎣⎡-+--±++-=--24502045454523121211εεεεμεεμμσσE 主应力方向计算公式为 ()()04545045452εεεεεεα----=--tg2. 弯矩、剪力、扭矩所分别引起的应力的测定a. 弯矩M 引起的正应力的测定用B 、D 两被测点00方向的应变片组成图5(a )所示半桥线路,可测得弯矩M 引起的正应变 2Md M εε=由虎克定律可求得弯矩M 引起的正应力 2MdM M E E εεσ==b. 扭矩M n 引起的剪应力的测定用A 、C 两被测点-450、450方向的应变片组成图5(b )所示全桥线路,可测得扭矩M n在450方向所引起的应变为 4nd n εε=由广义虎克定律可求得剪力M n 引起的剪应力 ()214nd nd n G E εμετ=+=c. 剪力Q 引起的剪应力的测定用A 、C 两被测点-450、450方向的应变片组成图5(c )所示全桥线路,可测得剪力Q 在450方向所引起的应变为 4QdQ εε=由广义虎克定律可求得剪力Q 引起的剪应力 ()214Qd Qd Q G E εμετ=+=四、实验步骤1.将传感器与测力仪连接,接通测力仪电源,将测力仪开关置开。
薄壁圆筒弯扭组合主应力测定

实验三薄壁圆筒弯扭组合主应力测定一、试验目的1.测定薄壁圆筒弯扭组合变形时指定点的主应力和主方向,并与理论计算值比较。
2.学习用应变花测定构件某点主应力和主方向的方法。
二、设备和仪器1、多功能力学实验台2、YE2538A 程控静态应变仪三、试样薄壁圆筒(见图)左端固定,籍固定在圆筒右端的水平杆加载。
在截面I-I 处粘贴有应变片m、n、a、b、c、d、e 和f,在截面II-II 处粘贴有应变片g 和h,其中应变片m 和n 粘贴于圆筒最高点和最低点,其方位均沿圆柱面母线。
其余各应变片粘贴的位置如图11-1a 和图11-1b 所示,它们的方位均与圆周线成45°或-45°角,展开图如图(11-1c)所示。
圆筒用不锈钢1Cr18Ni9Ti 制造,材料弹性模量E = 202 Gpa ,泊松比μ=0.28 ,圆筒外径D=40mm,内径d=36.40mm。
在图中的k 是三轴应变花,它的三个敏感栅与圆筒母线的夹角分别是0°、60°和120°(见图)。
四、实验原理据平面应变分析理论知,若某点任意三个方向的线应变已知,就能计算出该点的主应变和主方向,从而计算出主应力。
因此测量某点的主应力和主方向时,必须在测点布置三枚应变片。
通常将三个敏感栅粘贴在同一基底上,称为应变花。
常用的应变花有两种:一种是三敏感栅轴线互成120°角(如图13-1 所示),称等角应变花。
另一种是两敏感栅轴线互相垂直,另一敏感栅轴线在它们的分角线上,称直角应变花。
我们采用的是前者。
由应变分析和应力分析理论知,测得ε0 o、ε60 o 和ε120 o 后,可按下列公式计算主应力和主方向:五、实验步骤1.将弯扭组合实验装置旋转到位(有锥销定位)并固定,将加载用附件安装好。
2.力传感器接线、设置参数。
载荷限值设置350N3.将应变花的三个敏感栅分别接入所选通道(通常0°、60°、120°三敏感栅依次选1、2、3 通道),按多点1/4 桥公共补偿法接线。
主应力的测量

b
γ xy εx −εy
(3-2)
a
对于各向同性材料,主应变 ε 1 、 ε 3 和主应力
p
a = 250
D=55
d D
σ 1 、 σ 3 方向一致。应用广义胡克定律,即可确定主应力为:
b = 260
d=51
σ1 =
E (ε 1 + µε 3 ) 1− µ 2
σ3 =
E (ε 3 + µε 1 ) (3-3) 1− µ 2
0 0 0 0 0
0
(3-5)
将式(3-25)代入式(3-2) ,可得主应变和主方向为:
ε 1 ε − 45 + ε 45 2 (ε − 45 − ε 0 ) 2 + (ε 45 − ε 0 ) 2 ± = ε3 2 2
0 0 0 0 0 0
tan 2a o =
ε 45 − ε − 45 2ε 0 − ε − 45 − ε 45
弯扭组合变形的主应力测定
一、实验目的 (1)测定薄壁圆筒表面上一点的主应力。 (2)测定薄壁圆筒所受的弯矩和扭矩。 (3)掌握通过桥路的不同连接方案消扭测弯、消弯测扭的方法。 二、实验设备 (1)多功能组合实验台 (2)静态数字电阻应变仪 (3)游标卡尺和钢尺 三、实验原理和方法 1.测定主应力大小和方向 薄壁圆筒弯扭组合变形受力简图,截面为被测位置,由应力状态理论分析可知,薄壁圆筒表 面上的 A 、B 点处于平面应力状态。 若再被测位置 x 、y 平面内, 沿 x 、y 方向的线应变 ε x 、
T=
Eε n π ( D 4 − d 4 ) (1 + µ ) 16 D
(1)测量试件尺寸、加力臂的长度和测点距力臂的距离。 (2)将薄壁圆筒上的应变片按不同测试要求接入电阻应变仪组成不同的测量电桥,并调整 好所用仪器设备。完成以下两项参数的测定: ①主应力大小、方向测定:将 A 、 B 两点的应变片按半桥接线,并按公共温度补偿法组成 测量线路,进行半桥测量。 ②测定弯矩 M 、扭矩 T :根据上述接法组桥,或自行设计组桥方案。 (3)实验加载。用均匀慢速加载至初荷载 Fo ,记录各点应变仪的初读数,然后分级等增量 加载,每增加一级荷载,依次记录各点应变片的应变读数,直至最终荷载。每项实验至少重 复两次。 (4)完成一项测试后,重新组桥测试,重复步骤(2)和(3) 。 (5)完成全部实验后,卸除载荷,关闭电源,拆线整理仪器设备,清理现场。 注意: 注意:实验装置中, 实验装置中,圆筒的管壁很薄, 圆筒的管壁很薄,为避免损坏装置, 为避免损坏装置,注意切勿超载, 注意切勿超载,不能用力扳动圆 筒的自由端和力臂。 筒的自由端和力臂 。 五、实 验 结 果 处 理 (1)根据所测应变值计算主应力 σ 1 和 σ 3 及主应力方向 a o ,并与理论值进行比较,计算 相对误差。 (2)根据各种组桥方式测出的应变,计算出弯矩和扭矩。并与理论值比较,计算相对误差 值。 (3)分析误差产生的主要原因。 (4)按规定写出实验报告。
薄壁圆管在弯曲和扭转组合变形下的主应力测定

、进一步2、掌握接多通点电测测力法。仪与应变仪电源 125、0小KN型,3圆、点管击接弯静扭线态组电合阻装应置变仪“手动”铵钮,依次记录各点数据。
一3、、进理一论4步、值掌的调握计多零算点:电如测上法图。,当P 点的载荷为100N时,A、B、C、D的主应力与主方向的理论值可以用解析法或图解法计算。
21、 、接测通量5测纯、力弯逐仪曲与梁级应有加变关仪 尺载电寸,源 记录数据
第五讲 薄壁圆管在弯曲和扭转组合 变形下的主应力测定
一、实验目的#2. 幻灯片 2 二、实验设备#3. 幻灯片 3 三、实验原理#4. 幻灯片 4 四、实验步骤#5. 四、实验步骤 五、实验数据处理 六、实验报告 七、实验思考题(P71:2)
一、实验目的
1、测定圆管在弯扭组合变形下的四点处 主应力及主方向。
三、实验原理
二、 实 验 值 的 测 定
四、实验步骤
测量仪器为YJ-22型静态测量处理仪
1、测量纯弯曲梁有关尺寸 2、接通测力仪与应变仪电源 3、接线 4、调零 5、逐级加载,记录数据 6、重复三次 7、拆。
9、逆时针旋转手轮预加初 始载荷0.05KN,按住静 态电阻应变仪“调零” 铵钮,待指示灯熄灭后 松手,仪器逐点将电桥 预调平衡。
返回 七、实验思考题(P71:2)
返回
9、逆时针旋转手轮预加初始载荷0.
四、实验步骤#5.
1、测定圆管在弯扭组合变形下的四点处 主应力及主方向。
8、分别如图3a、b所示 接线。
9、逆时针旋转手轮预 加初始载荷0.05KN, 逐点“调零”。
10、逐级加载。 F1=0.150KN,点击 静态电阻应变仪 “手动”铵钮,依 次记录各点数据。
095、K逆N,时6按针、住旋重静转态手复电轮三阻预应加次变初仪始“载调荷零0. ”铵钮,待指示灯熄灭后松手,仪器逐点将电桥预调平衡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空心圆管主应力的测定
实验日期实验地点报告成绩
实验者班组编号环境条件℃、%RH 一、实验目的:
二、使用仪器:
三、实验原理:
四、实验数据记录:
1、标画出测点位置及贴片方位的示意图:
2、试样尺寸及材料常数:
试样编号N O∶应变仪灵敏系数K y = 应变计灵敏系数K=
3、各方向应变值的测定:单位:×10- 6
实验指导教师(签名):
五、实验数据处理:
六、实验结果:
七、思考题:
*1、如果将本实验中所使用的应变花逆时针方向旋转45°,主应力的实测值是否与实验中的相同?为什么?试推出旋转后的主应力和主方向的计算公式。
*2、如果换用60°的应变花应如何贴片?其主应力和主方向的计算公式又如何?
批阅报告教师(签名):
八、问题讨论:。
