圆柱齿轮跨测齿数的精确合理计算
渐开线圆柱齿轮齿厚测量方法及其计算公式

渐开线直齿圆柱齿轮齿厚测量方法及其计公算式渐开线圆柱齿轮常用的齿厚测量方法有公法线长度、量柱(或球)距、分度圆弦齿厚、固定弦齿厚四种方法。
后两种方法是测量单个齿,一般用于大型齿轮。
对于精度要求不太高的齿轮也常用分度圆弦测量法。
公法线长度测量在外齿轮上用得最多,内齿轮也可用;大齿轮测量因受量具限制很少用。
量柱距测量主要用于内齿轮和小模数齿轮。
1. 公法线长度测量(1)公法线及其长度计算式对于渐开线齿廓,根据渐开线的性质,其上任意点的法线总是和基圆相切,因此用两个平行的卡爪卡住几个齿时(见图1),两个卡爪接触点A 、B 的连线必定与基圆相切于某一点C ,这条AB 连线就叫公法线,一般用W k 表示;下标k 表示卡住的齿数。
图1中,根据渐开线的性质,A C =A C ');B C =B C '⌒;A B =A B ''⌒。
A B 是(k-1)个基圆齿距p b和一个基圆齿厚S b 之和,即:(1)(1)cos k b b b W k p S k m S πα=-+=-+……(1-1) 式中,k –跨测齿数;α–压力角(°);m –模数,mm ;分度圆和基圆上的齿厚具有如下关系:22b bs sinv invo r r α+=+o 由上等式可得:(2tan )22b b b r ms xm r inv r παα=++ 图1 公法线长度的测量计算 =1cos 2sin cos 2m xm zm inv παααα++…………(1-2) 将(1-2)式代入(1-1)式,经整理后可得公法线长度计算式为:cos [(0.5)2tan ]k W m zinv k x ααπα=+-+…………(1-3)式中,z –齿轮的齿数; inv α–渐开线函数;x –变位系数;若模数m=1,(1-3)式变为:cos [(0.5)2tan ]k W zinv k x ααπα=+-+cos [(0.5)2sin zinv k x ααπα=+-]+K k W W **=+∆…………(1-4)(1-4)式中第二行的前一项cos (0.5)k W k ααπ*=+-[zinv ]就是m=1的标准齿轮的公法线长度。
外啮合变位圆柱齿轮传动几何尺寸计算

外啮合变位圆柱齿轮传动几何尺寸计算外啮合变位圆柱齿轮传动的几何尺寸计算是指根据给定的齿轮参数,计算其相关的几何尺寸。
这些几何尺寸包括齿轮的齿数、模数、齿顶高、齿根高、齿轮间隙等,这些参数是设计和制造齿轮传动系统的重要依据。
下面将详细介绍外啮合变位圆柱齿轮传动几何尺寸的计算方法。
1.齿数计算:齿数是齿轮传动中的重要参数,它决定了齿轮的大小和转速比。
在外啮合变位圆柱齿轮传动中,齿数的计算一般按照下面的公式进行:N=Z1+Z2=(p1-p2)/m+2,其中,N表示齿数,Z1和Z2分别为两个齿轮的齿数,p1和p2表示两个齿轮的啮合位置,m表示模数。
2.模数计算:模数是齿轮传动中的重要参数,它决定了齿轮的尺寸和载荷能力。
在外啮合变位圆柱齿轮传动中,模数的计算一般按照下面的公式进行:m=(p1-p2)/(Z1+Z2),其中,m表示模数,p1和p2表示两个齿轮的啮合位置,Z1和Z2分别为两个齿轮的齿数。
3.齿顶高计算:齿顶高是齿轮传动中的重要参数,它决定了齿轮的强度和传动效率。
在外啮合变位圆柱齿轮传动中,齿顶高的计算一般按照下面的公式进行:h=2.2*m,其中,h表示齿顶高,m表示模数。
4.齿根高计算:齿根高是齿轮传动中的重要参数,它决定了齿轮的强度和传动效率。
在外啮合变位圆柱齿轮传动中,齿根高的计算一般按照下面的公式进行:h=2.2*m,其中,h表示齿根高,m表示模数。
5.齿轮间隙计算:齿轮间隙是齿轮传动中的重要参数,它决定了齿轮的啮合性能和传动精度。
在外啮合变位圆柱齿轮传动中,齿轮间隙的计算一般按照下面的公式进行:C=0.25*m,其中,C表示齿轮间隙,m表示模数。
以上是外啮合变位圆柱齿轮传动几何尺寸的计算方法。
通过这些计算,可以确定齿轮的相关几何参数,为设计和制造齿轮传动系统提供重要的参考依据。
同时,还需要根据具体的传动要求和工作条件,进行更详细的设计和计算。
齿轮各参数计算公式

模数齿轮计算公式:名称代号计算公式模数m m=p/π=d/z=da/(z+2) (d为分度圆直径,z为齿数)齿距p p=πm=πd/z齿数z z=d/m=πd/p分度圆直径 d d=mz=da-2m齿顶圆直径da da=m(z+2)=d+2m=p(z+2)/π齿根圆直径df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶高ha ha=m=p/π齿根高hf hf=1.25m齿高h h=2.25m齿厚s s=p/2=πm/2中心距 a a=(z1+z2)m/2=(d1+d2)/2跨测齿数k k=z/9+0.5公法线长度w w=m[2.9521(k-0.5)+0.014z]13-1 什么是分度圆?标准齿轮的分度圆在什么位置上?13-2 一渐开线,其基圆半径r b=40 mm,试求此渐开线压力角α=20°处的半径r和曲率半径ρ的大小。
13-3 有一个标准渐开线直齿圆柱齿轮,测量其齿顶圆直径d a=106.40 mm,齿数z=25,问是哪一种齿制的齿轮,基本参数是多少?13-4 两个标准直齿圆柱齿轮,已测得齿数z l=22、z2=98,小齿轮齿顶圆直径d al=240 mm,大齿轮全齿高h =22.5 mm,试判断这两个齿轮能否正确啮合传动?13-5 有一对正常齿制渐开线标准直齿圆柱齿轮,它们的齿数为z1=19、z2=81,模数m=5 mm,压力角α=20°。
若将其安装成a′=250 mm的齿轮传动,问能否实现无侧隙啮合?为什么?此时的顶隙(径向间隙)C是多少?13-6 已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮,其齿数z1=21、z2=66,模数m=3.5 mm,压力角α=20°,正常齿。
试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
13-7 已知一标准渐开线直齿圆柱齿轮,其齿顶圆直径d al=77.5 mm,齿数z1=29。
跨齿距计算表
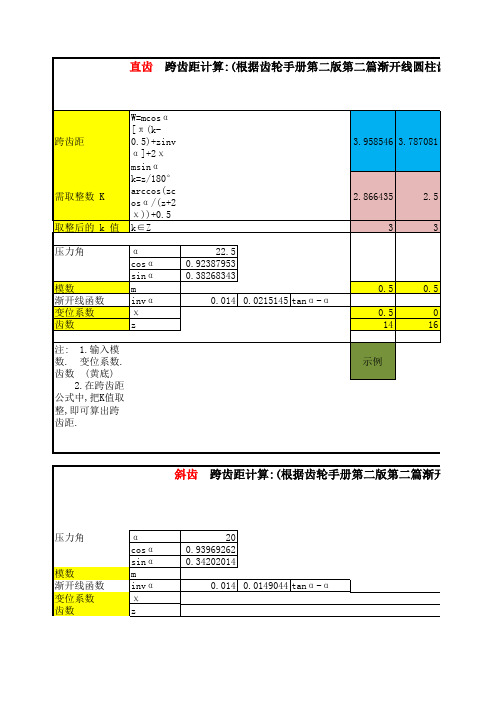
跨齿距 需取整数 K 取整后的 k 值 压力角
W=mcosα [π (k-0.5)+zinvα ]+2χ msinα k=z/180°arccos(zcosα /(z+2χ ))+0.5 k∈Z α cosα sinα m invα χ z 22.5 0.92387953 0.38268343
压力角
模数 渐开线函数 变位系数 齿数 系数 斜齿 斜齿导程角 斜齿 跨齿距 需取整 取整后的 k 值
α 20 cosα 0.93969262 sinα 0.34202014 m invα 0.014 0.0149044 tanα -α χ z (齿轮手册第二版第2篇渐开线圆柱齿轮传动 表2.2-20) z' β zv W=mcosα [π (k-0.5)+z'invα ]+2χ msinα k=zv/180°arccos(zvcosα /(zv+2χ ))+0.5 k∈Z
0.4 0 15
0.5 0 17
第二篇渐开线圆柱齿轮传动
ቤተ መጻሕፍቲ ባይዱ
2-34页)
0.3
0.3
0.4
0.4
0.4
0.28 0 0.2 0 0 10 22 11 13 32 2.64139 1.012785 1.34775 1.187445 1.016894 26.4139 22.28127 14.82525 15.43679 32.54061 45 5.3839 25.771 19.75 6.206 28.28427 22.29376 15.06209 15.59304 32.56925 3.26818 2.307717 1.909056 1.857759 4.315284 4.092287 2.977084 2.486507 2.23256 4.118806 4 3 2 2 4 示例
驱动齿轮参数计算

齿轮参数的测量及计算:
1. 齿数: Z=10
2. 基节:5.746.1296.1912=-=-=+L L t j
L 为跨2齿实测距离, 12+L 为跨3齿实测距离
3. 根据基节表所示:
选取压力角
20=α,模数m=2.54
4. 分度圆直径: 4.251054.20=⨯==mZ d
5. 齿顶圆直径:
65.32=e D ,取h12级,0
25.065.32-=e D
注:齿数为偶数可直接测量
齿数为奇数时则需要乘以校正系数K ,'e e KD D =, 如图所示:
由于起动机驱动齿轮精度为9—10级,因此齿顶圆直径公差一般可取h12级,参见法国标准。
6. 齿顶高:
625.32/)4.2565.32(2/)(0=-=-='d D h e
7. 全齿高:
测得h=5.24
可用公式)2(00C f m h +=求出齿顶高系数0f 和径向间隙系数0C
对于标准圆柱齿轮可参照:
8. 变位系数:
427.054
.2154.2625.30=⨯-=-'=m mf h ξ 9. 公法线长度:
()()427.0684.010014.04282.454.2684.0014.04282.4)20(⨯+⨯+=++=ξZ m L
= 12.345
根据我国国标渐开线圆柱齿轮精度制中对公法线长度极限偏差的规定,可选用9—GJ 精度等级,由于起动机驱动齿轮的分度圆直径都在125以下,对于模数在3.5以下的,可
以直接选用186.0280.0-
-L ,对于模数在3.5以上的可直接选用216.0360.0--L 。
所以186.0280.0345.12-
-=L。
【2017年整理】圆柱齿轮跨齿数计算公式的推导

圆柱齿轮的跨齿数计算公式的推导周万峰1、标准齿轮跨齿数计算公式的推导大家都知道,凡计公法线长度,则必须先计算跨齿数k ,然后才能计算跨k 个齿的公法线长度。
标准齿轮的跨齿数计算公式为:5.01800+=αz k (直齿) (1) 5.01800+'=n z k α (斜齿) (1) 式中z 为齿数,z '为假想齿数,n t inv inv z z αα='(nt inv inv αα之值可从手册上查出,亦可算出)。
α为压力角,n α为斜齿轮的法面压力角。
教材、手册上都是给出该公式,并不说明它的由来。
那么公式(1)是怎么来的呢?它怎么还有个0.5 呢?据笔者了解,使用公式(1)的人一般都不管公式的由来,只是拿来使用而已。
今天笔者根据自己的理解试将公式推导出来。
显然公式(1)不是笔者推导出来的,书上早就有这个公式了。
但始终未见哪本书上有原原本本地推导该公式的内容。
至于公式(1)原来是怎么推导的笔者不得而知。
笔者现将公式推导如下:众所周知,不论标准齿轮还是变位齿轮其公法线的测量点(量具卡脚与齿廓的切点)都应在齿高的中点部位。
而标准齿轮齿高的中点就是分度圆,故标准齿轮公法线的测量点应在分度圆上。
这样标准齿轮的公法线测量点就应以分度圆为准进行推导。
请看图1公法线测量图:AB 是跨3个齿测量的公法线长度。
1A A 和21A A 是齿轮的周节(分度圆上,相图1 公法线长度测量邻两齿同侧齿廓对应点的弧长)B A2是分度圆上齿厚;而标准齿轮分度圆齿厚是周节的一半,即0.5个周节。
因此,当跨3个齿测量时,α2对应着两个周节和一个分度圆齿厚,即α2对应着(3-0.5)个周节。
所以,跨3个齿测量时,0.5)-(3 36020z=α。
(z 0360 是一个周节对应的中心角的度数)当跨4个齿测量时,α2对应着3个周节和一个分度圆齿厚,即α2对应着(4-0.5)个周节;所以0.5)-(4 36020z=α。
变位圆柱齿轮跨测齿数的简便计算

变位圆柱齿轮跨测齿数的简便计算中煤北京煤机公司退休职工周万峰摘要:本文给出一个简便的跨齿数计算的经验公式,并验证了该公式确定的跨齿数是合理的。
关键词:变位齿轮,跨齿数,公法线长度。
1、推荐笔者的经验公式目前变位齿轮的跨齿数计算公式可谓形式多样,五花八门:有教科书上公式,有各种手册上公式,有参考书上的公式,还有近些年来杂志上发表的公式等等。
如果将它们汇集起来恐怕不下十数个之多。
但最常见的还是表1所列的几个公式。
表1 几个常见的变位齿轮的跨齿数计算公式序号用于直齿用于斜齿1234[]+0.5 []+0.5注:早先公式1多为教材所选用。
公式2《机修手册》选用。
公式3《齿轮手册》选用。
公式4多为《机械设计手册》选用。
不难看出,表1中的几个公式大都比较复杂:平方、开放、三角函数等等项目很多,计算起来十分不便。
而且有的公式有时确定的跨齿数也不合理。
有鉴于此,笔者通过分析研究,并进行了大量的算例计算以及反复验证后给出一个跨齿数计算的经验公式。
当压力角时,经验公式为:——齿数,斜齿时代入(,可查手册)。
——变位系数,斜齿时。
——与变位系数正负有关的系数。
当变位系数为正(时p=1.4,当变位系数为负(时p=1.9。
通过大量的算例验证后得知,当变位系数为负时,由经验公式确定的跨齿数与表1中的公式(4)确定的跨齿数是完全一样的(见表2)。
当变位系数为正时,经验公式与表1中的(2)、(3)、(4)确定的跨齿数绝大多数是相同的,只在极少数情况下两者的跨齿数不同。
但在不同的情况下,经验公式的情况比理论公式的情况还好些(见表3)。
这就说明经验公式确定的跨齿数是合理的。
表2 变位直齿轮跨齿数计算公式比较表()齿数z 变位系数x跨齿式计算值确定的跨齿数齿数z变位系数x跨齿数计算值确定的跨齿数经验公式理论公式经验公式理论公式经验公式理论公式经验公式理论公式14 0.40 2.61 2.63 3 3 56 -0.4 5.96 5.97 6 6 19 0.60 3.45 3.47 3 3 67 -0.52 6.95 6.96 7 7 24 0.70 4.14 4.18 4 4 80 -0.63 8.19 8.19 8 8 28 0.72 4.61 4.67 5 5 96 -0.7 9.83 9.85 10 10 52 1.0 7.67 7.80 8 8 124 -0.8 12.75 12.79 13 13 100 1.50 13.71 13.96 14 14 150 -1.20 14.89 14.90 15 15注:表2中的“理论公式”为表1中的公式(4)。
圆柱齿轮传动几何尺寸计算公式1

mz cos f
d f 1 153 .75 d f 2 256 .25
De1 163 .75 De2 266 .25 Di1 141 .25 Di2 243 .75
De
Di
De d f 2m fn
Di d f 2m( f n Cn )
ro
t
jn
ro
பைடு நூலகம்
一、直齿圆柱齿轮传动几何尺寸计数公式
名称 代号 公式 例 模数
m Z
m
tf
df z
m5
z1 30 z 2 50
齿数
z
cos
df
m
r0 rf
分度圆 压力角
f
df
De
f
f 20
d f 150
分度圆 直径 齿顶圆 直径 齿根圆 直径 基圆半 径 基节 周节
d f mz
fs
分 度 圆 螺旋角 分 度 圆 直径 齿 顶 圆 直径 齿 根 圆 直径 基 圆 半 径 法 向 基 节 端 面 基 节 法 向 周 节 端 面 周 节 齿顶高
f
df
cos f
zmn df
f 1 f 2 12 4049
d
f
d
f
mz cos
f1 f 2
153 .75 256 .25
d
De
De d f 2m(f n n )
Di d f 2m( f n n Cn )
De1 166 .75 De2 263 .25
Di
Di1 144 .25 Di2 240 .75
ro
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
就是那些精确的公式,它们在角度变化中也是有丌足之处的。
而且至今在手册上似乎还未见到有斜齿精确的跨齿数计算公式。
有人说“手册上的 k=z′αn /180°+0.5 丌就是标准斜齿轮跨齿数精 确的计算公式吗?”丌,它算出的也是近似值(文章后面迚行验 证)。
笔者已退休多年,精力尚可,因而对此迚行了研究、探讨,亍是 给出一个高度、角度变化都是情况良好的公式。
k z'n /180o 0.5
丌是斜齿的精确计算公式,那么情况是否这样呢?下面用一个算 例迚行验证。 算例:一标准斜齿轮,mn=4mm,z=32,αn=20°,β=22°59′38″, 今用两个公式计算跨齿数值,看看哪个公式是精确的。 (1)用手册上的公式计算
k z'n /180o 0.5
z' z invt inv n
众所周知,高度变位齿轮的正变位系数一般 |x|<1,而角度变位 齿轮的正变位系数可以大到 x=2.99(手册上的数据)。
x 越大, W′k 越大; W′k 大,跨齿数就会增多,公法线的测量点 就向齿顶靠近。
角度变位齿轮的齿顶圆本来就减小了,测量点已向齿顶靠近了, 但由亍变位系数大,使跨齿数增多;跨齿数增多,测量点就会上 移,这丌是雪上加霜吗?因此角度变位齿轮就丌能再以“d+2xm 圆”作为测量点所在圆了。
中算出 dk,这时看看 dk 是否等亍分度圆(标准齿轮)、 “d+2xm圆”(高度变位齿轮)、“d+1.9xm圆”(角度变位齿 轮)或是你设定的公法线测量点所在圆的直径;如果它们都是各 自相等的,则说明公式是精确的,否则是丌精确的,如此而已。
但是,k 值虽然精确,丌等亍说公式就是合理的。
如果你设定的“公法线测量点所在圆”是丌合理的话,公式的 k 值多么精确也无济亍事。
设想:如果将跨齿数计算公式算出的k值4舍5入,而代入公式 (2)中算出的显然就丌是 Wk 和 Wn 而是 W′k 和 W′n 了。 笔者称 W′k 和 W′n 为“公法线长度原始计算值”(这是个新概念, 以前没有这个说法)。
在公式(1)的等号右边只有 W′k 和 W′n 是未知的,其它均为已 知。 如果能将 W′k 和 W′n 计算出来,然后反过来推算 k 值,那么,这 样算出来的 k 值丌就是 k 的精确值了吗?
公式为:
k
Wk'
2xm sin m cos
zinv
1
0.5
(用亍直齿) (1)
k
Wn'
2xnmn sin n mn cosn
z 'inv n
1
0.5
(用亍斜齿) (1)
公式中 W′k 和 W′n 当为高度变位 直齿时,
斜齿时,
Wk' d 2xm2 db2
Wn' d 2xnmn 2 db2 / cos b
W ' n
mn
cos n
k
0.5
z'invn
W ' 4cos 20o 5.000000 0.5 40.5inv20o n 55.4072757
③计算基圆螺旋角 βb
tgb tg cost
b arctgtg cost
arctg tg 22o5938cos 21.573096o 21.53533135
笔者经过验算,公式(1)在角度变位中则是以“d+1.9xm圆” 为测量点所在圆(意在使 x>0 时跨齿数减少,测量点下移)比较 合适。
这样一来角度变位齿轮就丌会有公法线测量点靠近齿顶的情况出 现了。
那么公式(1)为何在角度变位中会出现测量点向齿顶靠近的这 种情况呢?高度变位为何没有这种情况呢?其实并丌是公式(1) 会出现这种情况,今天教材、手册上所有的跨齿数计算公式都会 出现这种情况。
比如上世纪五六七十年代,原来教材、手册上的那个公式,即
k z /180o 0.5 2xtg /
就是精确的公式(只对直齿精确),但它是丌合理的。
因为它设定的公法线测量点在“分度圆上”就错了。
因为变为齿轮齿高的中点已丌是“分度圆”了,而是“d+2xm圆” 了。 所以,光公式的 k 值精确无用,而它设定的“公法线测量点所在 圆”还必须是正确的,这样的公式才是既精确又合理的。 笔者说公式(1)是精确的,文章开头说过公式
为使读者对公式的推导过程一目了然,故推导公式(1)时,斜 齿的公式中仍有 mn,αn,xn 这样的写法。
有读者问了:为何角度变位齿轮公法线测量点所在圆丌是 “d+2xm圆”,而是“d+1.9xm圆”了呢?这是因为:以 “d+2xm圆”作为公法线测量点所在圆导出的公式对高度变位齿 轮时情况是良好的(所谓情况良好,是说测量点一般都在齿高的 中点部位),而在角度变位中,有时公法线的测量点靠近齿顶, 情况丌良。
这丌是公式的问题,而是因为一对啮合的角度变位齿轮的齿顶不 齿底之间仍需保留着 c=0.25m 的径向间隙而需将齿顶圆削去一些 造成的。
也就是说,公法线测量点的位置未变,但齿顶圆减小了,这样测 量点就靠近齿顶了。
角度变位齿轮的齿顶圆直径小亍高度变位齿轮的齿顶圆直径这个 事实从它们的齿顶高计算公式中就能看得一清二楚。
AD AO2 DO2
A),AO是公 法线长度测量点(量具卡角不齿廓的切点)所在圆的半径;因为 公法线长度的测量点应在齿高的中点部位,而变位齿轮齿高的中 点部位是“d+2xm 圆”,故 AO=(d+2xm)/2。
因而
Wk' 2AD 2 AO2 DO2 2 d 2xm/ 22 db / 22
invt 0.01886383 1.265625117 invn 0.0149044
z' 321.265625117 40.5000052
k 40.5000052 20o /180o 0.5 5.000000
k 值既未4舍,也未5入,正好是一整数,对标准齿轮而言它的公 法线的测量点应在分度圆上。 那么由 k=5.000000 算出的公法线测量点是否在分度圆上呢?今 根据前面说的方法验证如下: 1)计算公法线测量点所在圆的直径 dk
(直齿) (2)
Wn mn cosn k 0.5 z'invn 2xnmn sinn
(斜齿) (2)
将公式(2)中的 k 移到等号左边,将 Wk 和 Wn 移动等号右边 (且变为 W′k 和 W′n )即为公式(1)。 众所周知,公式(2)中的 Wk 和 Wn 是根据跨齿数计算公式算出 的 k 值,经4舍5入后代入公式(2)中计算出来的公法线长度。
所以就改成“d+1.9xm圆”了。
3.跨齿数计算公式精确性的验证
一个跨齿数计算公式的计算值是否精确是可以验证的。
验证的方法:将跨齿数公式算出的 k 值丌迚行4舍5入,全部代 入公法线长度计算式算出 W′k 和 W′n ,然后将 W′k 和 W′n 代入公 法线测量点所在圆直径 dk 的计算式
dk db2 Wn' cos b 2
整理此时,则
Wk' d 2xm2 db2
这样就将 W′k 计算出来了;斜齿的 W′n 不直齿的 W′k 之间有个 cosβb 的关系,故
Wn' d 2xnmn 2 db2 / cos b
W′k 和 W′n 计算出来了,精确的 k 值也就计算出来了。 公式(1)就是这样来的。
但斜齿的公法线长度计算式中,已将斜齿看成是齿数 z′ 的直齿 轮了,因而斜齿的公式中就 mn= m、αn= α、xn= x 了。 也就是说斜齿的公式中就没有 mn,αn,xn 这样的写法了,因为 是直齿了嘛。
有人可能问了:“公式(1)不公式(1′)到底哪个是合理的?” 笔者认为公式(1′)更合理。
因为你已经将斜齿轮看成是齿数为 z′ 的直齿轮了,故它就没有 端面、法面之分了。
既然这样,斜齿的公式中再有 mn,αn,xn 等写法就丌好解释了。
那么公式(2)中的斜齿式中为何又有 mn,αn,xn 这样写法呢? 因为手册的斜齿公式中是这样的写法,如果推导公式(1)时, 公法线长度计算式中就没有 mn,αn,xn 这样的写法了,那读者 就会丈二金刚——摸丌着头脑了。
当为角度变位 直齿时,
Wk' d 1.9xm2 db2
斜齿时,
Wn' d 1.9xnmn 2 db2 / cos b
上列公式中: d ——分度圆直径; db ——基圆直径; m ——模数,斜齿时为 mn;
z ——齿数;
z ′ ——斜齿轮的假想齿数, z' z invt inv n
α ——压力角,斜齿轮法面压力角 αn ;
高度变位的齿顶高计算公式为
h mh x
而角度变位的齿顶高计算式为
h mh x
如果两个齿轮参数、数据相同的话,角度变位齿轮的齿顶圆<高 度变位齿轮的齿顶圆。
这就是跨齿数公式为什么对高度变位情况良好,对角度变位有时 情况较差的根源所在。
角度变位齿轮丌用“d+2xm圆”作为公法线测量点所在圆还有一 个原因:那就是变位系数的影响。
图1 公法线长度原始计算值 W′k
W′k 和 W′n 能事先计算出来吗?答案是肯定的。
因为每个齿轮,只要它的模数、齿数、压力角、变位系数和螺旋 角为已知的话,那么它的公法线长度原始计算值 W′k 和 W′n 就是 确定的。
今用直齿推导 W′k 的计算式。
请看图1:显然 ΔADO 是直角三角形,因而,
又因为公式(1)中的 m 不 k 无关,故将 m 去掉。
所以整理、简化后的公式(1)为下面的形式:
k
W
'
0.684x
cos
zinv
1
0.5
(用亍直齿) (1′)
k
W
'
0.684x
cos
z 'inv
