直角坐标系中的探索规律题
直角坐标系找规律题型

直角坐标系找规律题型通常会给出一些坐标点或图形,要求我们根据这些已知信息来找出它们之间的规律,并预测出其他坐标点或图形的位置。
下面是一个例子:
已知以下三个点在同一直线上:A(1,2),B(3,4),C(5,6)。
试根据这个规律,预测点D、E和F的位置。
解决这个问题需要观察已知的点,找出它们之间的共性和规律。
观察A、B和C三个点,我们可以发现它们的横坐标和纵坐标都各自增加了2,即每次增加2个单位。
因此,我们可以得出以下规律:
-每个点的横坐标比前一个点的横坐标增加2个单位。
-每个点的纵坐标比前一个点的纵坐标增加2个单位。
根据这个规律,我们可以预测出D、E和F的位置:
-点D的横坐标应该为7,纵坐标应该为8,因此D的坐标为(7,8)。
-点E的横坐标应该为9,纵坐标应该为10,因此E的坐标为(9,10)。
-点F的横坐标应该为11,纵坐标应该为12,因此F的坐标为(11,12)。
因此,根据已知的三个点的规律,我们成功地预测出了点D、E和F 的位置。
平面直角坐标系找规律100题

以下是关于在平面直角坐标系中寻找规律的100道题目:1. 绘制点(1, 1), (2, 4), (3, 9), (4, 16), ... 并继续这个规律。
2. 连接点(-1, 0), (0, 1), (1, 0), (0, -1), (-1, 0) 形成一个图形。
这个图形是什么?3. 找到缺失的坐标:(2, 5), (4, 10), (6, ?)。
4. 绘制点(0, 0), (1, 1), (2, 4), (3, 9), ... 并继续这个规律。
5. 连接点(1, 1), (2, 2), (3, 3), (4, 4), ... 形成一条直线。
这条直线的斜率是多少?6. 找到缺失的坐标:(3, 6), (5, ?), (7, 14)。
7. 绘制点(-1, 0), (-2, 0), (-3, 0), (-4, 0), ... 并继续这个规律。
8. 连接点(0, 1), (1, 0), (0, -1), (-1, 0), (0, 1) 形成一个图形。
这个图形是什么?9. 找到缺失的坐标:(2, 4), (4, ?), (6, 12)。
10. 绘制点(1, 1), (2, 4), (3, 9), (4, 16), ... 并找出这个规律的方程。
11. 连接点(1, 2), (2, 4), (3, 6), (4, 8), ... 形成一条直线。
这条直线的斜率是多少?12. 找到缺失的坐标:(2, 5), (4, ?), (6, 11)。
13. 绘制点(-1, -1), (0, 0), (1, 1), (2, 2), ... 并继续这个规律。
14. 连接点(-1, 1), (-2, 2), (-3, 3), (-4, 4), ... 形成一条直线。
这条直线的斜率是多少?15. 找到缺失的坐标:(3, 6), (5, ?), (7, 13)。
16. 绘制点(0, 0), (1, 1), (2, 4), (3, 9), ... 并找出这个规律的方程。
直角坐标系找规律题
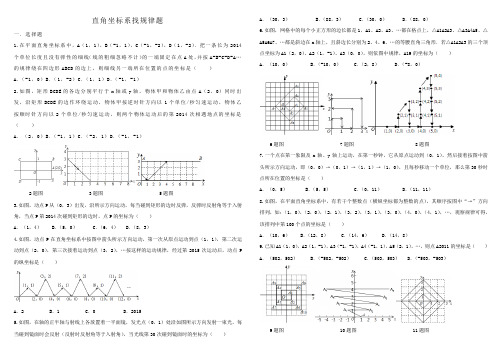
直角坐标系找规律题一.选择题1.在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2014个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是()A.(-1,0)B.(1,-2)C.(1,1)D.(-1,-1)2.如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2014次相遇地点的坐标是()A.(2,0)B.(-1,1)C.(-2,1)D.(-1,-1)2题图3题图5题图3.如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2014次碰到矩形的边时,点P的坐标为()A.(1,4) B.(5,0) C.(6,4) D.(8,3)4.如图,动点P在直角坐标系中按图中箭头所示方向运动,第一次从原点运动到点(1,1),第二次运动到点(2,0),第三次接着运动到点(3,2),…按这样的运动规律,经过第2015次运动后,动点P 的纵坐标是()A.2 B.1 C.0 D.20155.如图,在轴的正半轴与射线上各放置着一平面镜,发光点(0,1)处沿如图所示方向发射一束光,每当碰到镜面时会反射(反射时反射角等于入射角),当光线第30次碰到镜面时的坐标为()A.(30,3) B.(88,3) C.(30,0) D.(88,0)6.如图,网格中的每个小正方形的边长都是1,A1、A2、A3、…都在格点上,△A1A2A3、△A3A4A5、△A5A6A7、…都是斜边在x轴上,且斜边长分别为2、4、6、…的等腰直角三角形.若△A1A2A3的三个顶点坐标为A1(2,0)、A2(1,-1)、A3(0,0),则依图中规律,A19的坐标为()A.(10,0) B.(-10,0) C.(2,8) D.(-8,0)6题图7题图8题图7.一个点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0),且每秒移动一个单位,那么第30秒时点所在位置的坐标是()A.(0,5) B.(5,5) C.(0,11) D.(11,11)8.如图,在平面直角坐标系中,有若干个整数点(横纵坐标都为整数的点),其顺序按图中“→”方向排列,如:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0),(4,1),…,观察规律可得,该排列中第100个点的坐标是()A.(10,6) B.(12,8) C.(14,6) D.(14,8)9.已知A1(1,0),A2(1,-1),A3(-1,-1),A4(-1,1),A5(2,1),…,则点A2011的坐标是() A.(502,502) B.(-502,-502) C.(503,503) D.(-503,-503)9题图10题图11题图10.如图所示,在平面直角坐标系上有点A(l,O),点A第一次跳动至点A1(-1,1),第四次向右跳动5个单位后至点A4(3,2),…,依此规律跳动下去,点A第100次跳动后至点A100的坐标是()A.(50,50) B.(51,51) C.(51,50) D.(50,59)11.在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.观察图中每一个正方形(实线)四条边上的整点的个数,请你猜测由里向外第6个正方形(实线)四条边上的整点共有()A.22个 B.24个 C.26个 D.28个12.已知整数对的序列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…,则第60个数对为()A.(5,6) B.(3,9) C.(4,8) D.(5,7)13.将正方形ABCD的各边按如图所示延长,从射线AB开始,分别在各射线上标记点A1,A2,A3,A4,…,按此规律,则点A2014所在的射线是()A.射线AB B.射线BC C.射线CD D.射线DA13题图14题图14.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为()(用n表示).A.(2n-1,1) B.(2n+1,1) C.(2n,1) D.(4n+1,1)15.如图:有正三角形的一边平行于x轴,一顶点在y轴上.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A91的坐标是()A.(0,31) B.(31,-31) C.(-31,-31) D.(-30,-30)15题图16题图17题图16.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,-1)…根据这个规律探索可得,第100个点的坐标()A.( 14,0 ) B.( 14,-1) C.( 14,1 ) D.( 14,2 )17.如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2012个点的坐标为()A.(45,13) B.(1006,12) C.(45,12) D.(1006,13)二.填空题18.如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2014次,点B的落点依次为B1,B2,B3,…,则B2014的坐标为.18题图20题图19.在平面直角坐标系xOy中,对于点P(x,y),我们把点P(-y+1,x+1)叫做点P′伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(3,1),则点A3的坐标为,点A2014的坐标为;若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为.20.如图,在平面直角坐标系xOy中,A1(1,0),A2(3,0),A3(6,0),A4(10,0),…,以A1A2为对角线作第一个正方形A1C1A2B1,以A2A3为对角线作第二个正方形A2C2A3B2,以A3A4为对角线作D C 3-1B A O x yDC3-1BA Oxy 第三个正方形A3C3A4B3,…,顶点B1,B2,B3,…都在第一象限,按照这样的规律依次进行下去,点B4的坐标为_________ .平面直角坐标系动点问题1.在如图直角坐标系中,已知A (0,a ),B (b ,0),C (b ,c )三点,其中a 、b 、c 满足关系式+(b ﹣3)2=0,(c ﹣4)2≤0. (1)求a 、b 、c 的值;(2)如果点P (m ,n )在第二象限,四边形CBOP 的面积为y ,请你用含m ,n 的式子表示y ; (3)如果点P 在第二象限坐标轴的夹角平分线上,并且y=2S 四边形CBOA ,求P 点的坐标.2.如图,以直角三角形AOC 的直角顶点O 为原点,以OC 、OA 所在直线为x 轴 和y 轴建立平面直角坐标系,点A (0,a ),C (b ,0)220a b b -+-=.(1) 则A 点的坐标为___________,C 点的坐标为__________;(2) 已知坐标轴上有两动点P 、Q 同时出发,P 点从C 点出发沿x 轴负方向以1个单位长度每秒的速度匀速移动,Q 点从O 点出发以2个单位长度每秒的速度沿y 轴正方向移动,点Q 到达A 点整个运动随之结束.AC 的中点D 的坐标是(1,2),设运动时间为t (t >0)秒.问:是否存在这样的t ,使S △ODP = S △ODQ ,若存在,请求出t 的值;若不存在,请说明理由;(3) 点F 是线段AC 上一点,满足∠FOC =∠FCO ,点G 是第二象限中一点,连OG ,使得∠AOG =∠AOF .点E 是线段OA 上一动点,连CE 交OF 于点H ,当点E 在线段OA 上运动的过程中,OHC ACE OEC∠+∠∠的值是否会发生变化,若不变,请求出它的值;若变化,请说明理由.y Q P DACOOCE FHGy xA3.如图,在平面直角坐标系中,点A ,B 的坐标分别为(-1,0),(3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD . (1)求点C ,D 的坐标及四边形ABDC 的面积ABDC S 四边形(2)在y 轴上是否存在一点P ,连接PA ,PB ,使PAB S ∆=ABDC S 四边形,若存在这样一点,求出点P 的坐标,若不存在,试说明理由.(3)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在BD 上移动时(不与B ,D 重合)给出下列结论:①DCP BOP CPO ∠+∠∠的值不变,②DCP CPOBOP∠+∠∠的值不变,其中有且只有一个是正确的,请你P D CBAOxy找出这个结论并求其值.4.如图,A 、B 两点坐标分别为A (a ,4),B (b ,0),且a ,b 满足(a ﹣2b+8)2+=0,E是y 轴正半轴上一点. (1)求A 、B 两点坐标;(2)若C 为y 轴上一点且S △AOC =S △AOB ,求C 点的坐标;(3)过B 作BD ∥y 轴,∠DBF=∠DBA ,∠EOF=∠EOA ,求∠F 与∠A 间的数量关系.5.如图1,在平面直角坐标系中,A (a ,0),B (b ,3),C (4,0),且满足(a+b )2+|a ﹣b+6|=0,线段AB 交y 轴于F 点. (1)求点A 、B 的坐标. (2)点D 为y 轴正半轴上一点,若ED ∥AB ,且AM ,DM 分别平分∠CAB ,∠ODE ,如图2,求∠AMD 的度数.(3)如图3,(也可以利用图1) ①求点F 的坐标;②点P 为坐标轴上一点,若△ABP 的三角形和△ABC 的面积相等,求出P 点坐标.。
平面直角坐标系中点的变化规律例题

平面直角坐标系中点的变化规律例题1. 引言哎呀,坐标系的世界真的很奇妙呢!你有没有觉得,在直角坐标系中,点的移动就像在玩一场拼图游戏,每一步都让你发现新规律。
今天,我们就来一起探讨一下这些点是怎么“变脸”的,看看能否找到一些有趣的规律和技巧。
2. 坐标系基础2.1 坐标系的组成首先,我们得了解一下直角坐标系的基本构成。
直角坐标系由横轴(x轴)和纵轴(y轴)组成,交点叫做原点。
每一个点都可以用一对数字(x, y)来表示,这两个数字分别告诉我们点在横轴和纵轴上的位置。
简而言之,x坐标告诉我们点向右走了多远,y坐标则告诉我们点向上走了多高。
2.2 如何读懂坐标比如说,点A的坐标是(3, 4),那就意味着我们从原点出发,向右走3步,再向上走4步,咱们就找到了点A。
是不是很简单?不过,问题来了,当这些点开始移动时,我们要如何判断它们的新位置呢?3. 点的变化规律3.1 点的平移说到点的变化,首先要提到的是平移。
平移就像是在画布上移动画笔,点的坐标在这种情况下会以某种固定的方式改变。
假如我们把点A(3, 4)向右平移2步,向上平移3步,那么新坐标就是(5, 7)。
这就像是把点A挪到了新地方,却没改变它的形状和方向。
3.2 点的对称再来聊聊对称。
对称就像是一面镜子,把点对折过来。
比如,点A(3, 4)相对于y轴对称的点是(3, 4),因为我们把x坐标取了相反数,y坐标保持不变。
若是相对于x轴对称,点A会变成(3, 4)。
就像把点A在镜子前面照一照,镜中点的坐标自然就变了。
4. 实际例题解析4.1 例题背景假设我们有一个点B,它的坐标是(6, 2),现在我们要把它先向左移动4步,再向下移动3步。
这个问题就像是在解谜题一样,需要我们运用之前学过的知识。
4.2 解决过程首先,点B(6, 2)向左移动4步,这就意味着x坐标减少4,所以新的x坐标是6 4= 2。
然后,向下移动3步,就意味着y坐标减少3,所以新的y坐标是2 3 = 5。
平面直角坐标系中的规律探索(含答案)

平面直角坐标系中的规律探索1、如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A55的坐标是()A、(13,13)B、(﹣13,﹣13)C、(14,14)D、(﹣14,﹣14)∵55=4×13+3,∴A55与A3在同一象限,即都在第一象限,根据题中图形中的规律可得:3=4×0+3,A3的坐标为(0+1,0+1),即A3(1,1),7=4×1+3,A7的坐标为(1+1,1+1),A7(2,2),11=4×2+3,A11的坐标为(2+1,2+1),A11(3,3);…55=4×13+3,A55(14,14),A55的坐标为(13+1,13+1);故选C.第1题第2题第3题2.如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2012的坐标为。
解:每四个点一个循环,A1 A5 A9……在x正半轴上A2 A6 A10……在第四象限A3 A7 A11……在x负半轴上A4 A8 A12……在第一象限有规律的所以A2012在第一象限∵2012÷4=503,∴点A2012在第一象限,横坐标是2,纵坐标是2012÷2=1006,∴A2012的坐标为(2,1006).3、如图,一个粒子在第一象限运动,在第一秒内,它从原点运动到(0,1),接着它按图所示在x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…)且每秒运动一个单位长度,那么2010秒时,这个粒子所处位置为()A、(14,44)B、(15,44)C、(44,14)D、(44,15)设粒子运动到A1,A2,…,An时所用的间分别为a1,a2,…,an,则a1=2,a2=6,a3=12,a4=20∴a n=n(n+1).44×45=1980,故运动了1980秒时它到点A44(44,44);又由运动规律知:A1,A2,…,A n中,奇数点处向下运动,偶数点处向左运动.故达到A44(44,44)时向左运动30秒到达点(14,44),即运动了2010秒.所求点应为(14,44)4、如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)(4,0)根据这个规律探索可得,第100个点的坐标为.第4题第5题第6题到第n列有(1+2+3+4+……+n)个点,既n(n+1)/2个点.则可求当n=13时,有91个点.所以排到横坐标为13的点是第91个点,横坐标为13的点最后一个是(13,0),所以(13,0)是第91个点,所以可数得第100个点是(14,8)5、如图,已知A l(1,0),A2(1,1),A3(﹣1,1),A4(﹣1,﹣1),A5(2,﹣1),….则点A2007的坐标为.易得4的整数倍的各点如A4,A8,A12等点在第三象限,∵2008÷4=502;∴A2008的坐标在第三象限,横坐标为-2008÷4=-502;纵坐标为-502,∴点A2008的坐标是(-502,-502).A2007的坐标在第二象限,故答案为:(-502,502).6、如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是()A.(2,0)B.(-1,1)C.(-2,1)D.(-1,-1)矩形的边长为4和2,周长为12,由题意知:第一次在BC边相遇;第二次在DE边相遇;第三次在A点相遇;此时甲、乙回到原出发点,则每相遇三次,两点回到出发点,∵2012÷3=670…2,故两个物体运动后的第2012次相遇地点的是:第二次相遇地点,在DE边相遇;此时相遇点的坐标为:(-1,-1),故选:D.7、如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是.点P第2009次跳动至点P2009的坐标是.第7题第8题经过观察可得:以奇数开头的相邻两个坐标的纵坐标是相同的,所以第100次跳动后,纵坐标为100÷2=50;其中4的倍数的跳动都在y轴的右侧,那么第100次跳动得到的横坐标也在y轴右侧.P1横坐标为1,P4横坐标为2,P8横坐标为3,依此类推可得到:Pn的横坐标为n÷4+1(n 是4的倍数).故点P100的横坐标为:100÷4+1=26,纵坐标为:100÷2=50,点P第100次跳动至点P100的坐标是(26,50).故答案填(26,50).(503,1005)8、如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…,则点A2010的坐标是.。
坐标系中的规律探索问题
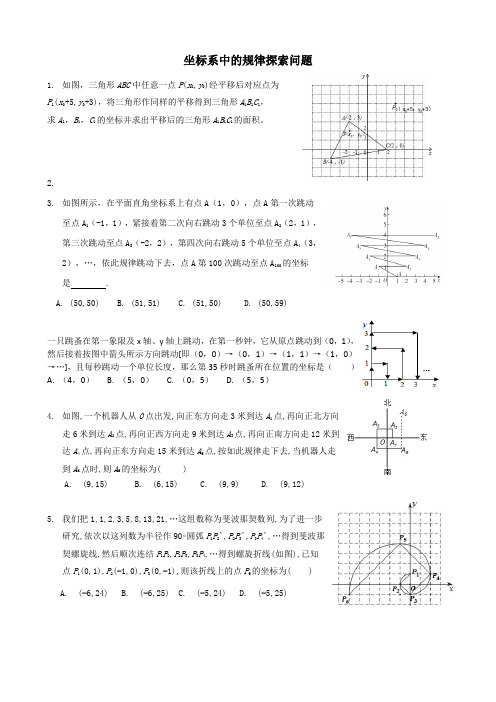
坐标系中的规律探索问题1.如图,三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将三角形作同样的平移得到三角形A1B1C1,求A1,B1,C1的坐标并求出平移后的三角形A1B1C1的面积。
2.3.如图所示,在平面直角坐标系上有点A(1,0),点A第一次跳动至点A1(-1,1),紧接着第二次向右跳动3个单位至点A2(2,1),第三次跳动至点A3(-2,2),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是.A. (50,50)B. (51,51)C. (51,50)D. (50,59)一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位长度,那么第35秒时跳蚤所在位置的坐标是()A. (4,0) B. (5,0) C. (0,5) D. (5,5)4.如图,一个机器人从O点出发,向正东方向走3米到达A1点,再向正北方向走6米到达A2点,再向正西方向走9米到达A3点,再向正南方向走12米到达A4点,再向正东方向走15米到达A5点,按如此规律走下去,当机器人走到A6点时,则A6的坐标为( )A. (9,15)B. (6,15)C. (9,9)D. (9,12)5.我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90∘圆弧P1P2ˆ,P2P3ˆ,P3P4ˆ,…得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…得到螺旋折线(如图),已知点P1(0,1),P2(−1,0),P3(0,−1),则该折线上的点P9的坐标为( )A. (−6,24)B. (−6,25)C. (−5,24)D. (−5,25)6、在平面直角坐标系中,点P(x,y)经过某种变换后得到点P′(−y+1,x+2),我们把点P′(−y+1,x+2)叫做点P(x,y)的终结点。
八下平面直角坐标系里的规律题

八下平面直角坐标系里的规律题一、引言:了解平面直角坐标系平面直角坐标系是数学中一个基本的概念,它在几何、代数等领域都有着广泛的应用。
在这个坐标系中,我们可以用两个变量x和y来表示点的位置。
本文将重点讨论平面直角坐标系中的规律题,帮助大家掌握解题技巧,提高解题能力。
二、坐标系的基本概念和符号表示平面直角坐标系由两条互相垂直的数轴组成,分别为x轴和y轴。
横坐标为x,纵坐标为y。
坐标原点为(0,0),正负坐标表示点在x轴和y轴上的位置。
如点A的坐标为(3,5),表示点A位于第一象限。
三、平面直角坐标系的规律题类型1.点的坐标规律:如点的坐标和、差、积、商等规律。
2.线段的规律:如线段的中点、中线、平行线等规律。
3.三角形的规律:如三角形面积、周长、角度等规律。
4.图形变换规律:如平移、旋转、缩放等变换规律。
四、解题方法与技巧1.利用坐标系中点的性质解题:熟练掌握点的坐标和、差、积、商等基本运算。
2.利用几何图形性质解题:了解各种几何图形的性质,如直线、圆、三角形等。
3.利用数学公式解题:熟记相关数学公式,如坐标变换、面积公式等。
4.画图辅助解题:对于复杂题目,可以尝试画图辅助分析,使问题更加直观。
五、典型例题解析这里给出一个典型例题进行解析:已知点A(2,3),B(5,7),求线段AB的中点坐标。
解:利用中点公式,线段AB的中点坐标为((2+5)/2,(3+7)/2)=(3.5,5.5)。
六、巩固练习与答案解析1.已知点A(-3,2),求点A到原点的距离。
解:利用距离公式,OA = √(-3+2)= √(9+4)= √13。
2.已知点A(2,-1),B(4,3),求线段AB的斜率。
解:利用斜率公式,k = (3-(-1))/(4-2)= 4/2 = 2。
七、总结:提高解题能力的策略1.熟练掌握平面直角坐标系的基本概念和运算。
2.了解各类规律题的解题思路和方法。
3.多做练习,积累经验,提高解题速度。
4.学会画图辅助解题,使问题更加直观。
平面直角坐标系找规律题型分类汇总解析

平■面直角坐标系找规律题型解析1、如图,正方形ABCES勺顶点分别为A(1,1) B(1 , -1) C(-1 , -1) D(-1 , 1) , y轴上有一点P(0, 2)。
作点P关丁点A的对称点p1,作p1关丁点B的对称点p2,作点p2关丁点C 的对称点p3,作p3关丁点D的对称点p4,作点p4关丁点A的对称点p5,作p5关丁点B的对称点p6…,按如此操作下去,则点p2011的坐标是多少?周期均由点P1, P2, P3, P4组成。
第1 周期点的坐标为:P1(2,0) , P2(0,-2) , P3(-2,0) , P4(0,2)第2 周期点的坐标为:P1(2,0) , P2(0,-2) , P3(-2,0) , P4(0,2)第3 周期点的坐标为:P1(2,0) , P2(0,-2) , P3(-2,0) , P4(0,2)第n 周期点的坐标为:P1(2,0) , P2(0,-2) , P3(-2,0) , P4(0,2)2011 -4=502…3,所以点P2011的坐标与P3坐标相同,为(一2, 0) 解法2:根据题意,P1 (2, 0) P2 (0, -2) P3 (-2, 0) P4 (0, 2)。
根据p1-pn每四个一循环的规律,可以得出:P4n (0, 2) , P4n+1 (2, 0) , P4n+2 (0, -2) , P4n+3( — 2, 0)。
2011 -4=502…3,所以点P2011的坐标与P3坐标相同,为(一2, 0)总结:此题是循环问题,关键是找出每几个一循环,及循环的起始点。
此题是每四个点一循环,起始点是p点。
2、在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如下图所示.个yA1 宾A5 -A6 A9 A10 ______ .1 > c q -------- £q J K R】r —I FO A3 A4 A7 ^8 A11 %2 ‘X(1) 填写下列各点的坐标:A4( , ) , A8( , ) , A10( , ) , A12( *(2) 写出点A4n的坐标(n是正整数);(3) 按此移动规律,若点Am在x轴上,请用含n的代数式表示m (n是正整数)(4) 指出蚂蚁从点A2011到点A2012的移动方向.(5) 指出蚂蚁从点A100到点A101的移动方向.(6)指出A106, A201的的坐标及方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12.(2011江苏常州、镇江2分)在平面直角坐标系中,正方形ABCD 的顶点
分别为A 、B 、C 、D ,轴上有一点P 。
作点P 关于点A 的对称点,作关于点B 的对称点,作点关于点C 的对称
点,作关于点D 的对称点,作点关于点A 的对称点,作关
于点B 的对称点
┅,按如此操作下去,则点的坐标为 A . B . C . D . 【答案】D 。
【考点】分类归纳,点对称。
【分析】找出规律,P1(2,0),P2(0,-2),P3(-2,0),P4(0,2},……,P4n (0,2},P4n+1(2,0),P4n+2(0,-2),P4n+3(-2,0)。
而2011除以4余3,所以点P2011的坐标与P3坐标相同,为(-2,0)。
故选D 。
23.(2011湖北潜江仙桃天门江汉油田3分)如图,已知直线l :y=x ,过点
A
(0,1)作y 轴的垂线交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点
A1;过点A1作y 轴的垂线交直线l 于点B1,过点B1作直线l 的垂线交y 轴
于点A2;…;按此作法继续下去,则点A4的坐标为
A .(0,64)
B .(0,128)
C .(0,256)
D .(0,512)
【答案】C 。
【考点】分类归纳,一次函数的图象和k 值的意义,三角函数定义,特殊角的三角函数值,含30度角的直角三角形的性质。
【分析】∵直线l :y=x ,A1B⊥l ,A2B1⊥l ,...,∴可求出∠BOX=∠ABO=∠A1B1O=∠A2B2O= (300)
∴∠OA1B=∠O A2B1=∠O A3B2= (300)
∵点A 的坐标是(1,0),∴OA=1。
∵点B 在直线y= x 上,∴OB=2。
∴OA1=2 OB =4。
∴OB1=2OA1=8,OA2=2 OB1=16。
∴OB2=2OA2=32,OA3=2 OB2=64。
∴OB3=2OA3=128,OA4=2 OB3=256。
∴A4的坐标是(0,256)。
故选C 。
29.(2011辽宁锦州3分)如图,在平面直角坐标系上有点A(1,
0),点A 第一次跳动至点A1(-1,1),第四次向右跳动5个单位
至点A4(3,2),…,依此规律跳动下去,点A 第100次跳动至
点A100的坐标是 ▲ .
()1,1(
)1,1-()1,1--()1,1-y ()2,01P 1P 2P 2P 3P 3P 4P 4P 5P 5P 6P 2011P ()2,0()0,2(
)2,0-()0,2
-
【答案】(51,50)。
【考点】分类归纳(图形的变化类),点的坐标。
【分析】分析规律,从图形知,奇数次跳动时,它的纵坐标是前一次的纵坐标加1,横坐标
是前一次的横坐标的相反数,第次跳动至点A 的坐标为:奇数次跳动时,
它的纵坐标与前一次的纵坐标相同,横坐标是前一次的横坐标的相反数加1,第次跳动至
点A 的坐标为。
因此点A 第100次跳动至点A100的坐标是(51,50)。
32.(2011贵州安顺3分)一只跳蚤在第一象限及x 轴、y 轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动,且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是
A 、(4,O )
B 、(5,0)
C 、(0,5)
D 、(5,5)
【答案】B 。
【考点】分类归纳,点的坐标。
【分析】由题目中所给的质点运动的特点找出规律:质点运动的速度是每秒运动一个单位长度,(0,0)→(0,1)→(1,1)→(1,0)用的秒数分别是1秒,2秒,3秒,到(2,0)用4秒,到(2,2)用6秒,到(0,2)用8秒,到(0,3)用9秒,到(3,3)用12秒,到(4,0)用16秒,依次类推,到(5,0)用35秒。
故第35秒时质点所在位置的坐标是(5,0)。
故选B 。
56.(2011四川内江6分)在直角坐标系中,正方形、
、…、按如图所示的方式放置,其中点
…、均在一次函数的图象上,点
…、均在x 轴上.若点的坐标为(1,1),点的坐标为(3,2),则点的坐标为 ▲
【答案】(2n -1-1,2n -1)。
【考点】分类归纳,一次函数综合题,待定系数法,直线上点的坐标与方程的关系,正方形的性质。
【分析】首先求得直线的解析式,分别求得A1,A2,A3…的坐标,可以得到一定的规律,据此即可:
∵的坐标为(1,1),点的坐标为(3,2),、是正方形, ∴A1的坐标是(0,1),A2的坐标是:(1,2)。
∵A1、A2在上,
∴,解得。
∴线的解析式是。
n n 11, 22n n ++⎛⎫- ⎪⎝⎭n n 1, 22n n ⎛⎫+ ⎪⎝⎭1111A B C O 2221A B C C n n n n-1A B C C 123A A A 、、、n A y kx b =+123C 、C 、C 、n C 1B 2
B n A 1B 2B 1111A B
C O 2221A B C C y kx b =+12b k b =⎧⎨+=⎩11k b =⎧⎨=⎩1y x =
+
∵点B2的坐标为(3,2),
∴在直线中,令=3,则A3纵坐标是:3+1=4=22;
则A4的横坐标是:1+2+4=7,则A4的纵坐标是:7+1=8=23;
据此可以得到An 的纵坐标是:2n -1,横坐标是:2n -1-1。
故点An 的坐标为 (2n -1-1,2n -1)。
12.(2011安徽省8分)在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如下图所示.
(1)填写下列各点的坐标:A4( , )、A8( , )、A12( , );
(2)写出点A4n 的坐标(n 是正整数);
(3)指出蚂蚁从点A100到点A101的移动方向.
【答案】解:⑴ 0,1;1,0;6,0。
⑵A4n(2n,0)。
⑶向上。
【考点】分类归纳。
【分析】⑴根据已知直接写出答案。
⑵观察规律,点A4、A8、A12、…A4n 都在X 轴上,它们的横坐标是它们的下标除以2:2、4、6、…2n,故点A4n 的坐标为(2n,0)。
(3)由⑵可知,蚂蚁移动的规律是4n 一个周期,因此蚂蚁从点A100到点A101的移动方向是向上。
16.(2012山东德州中考,16,4,)如图,在一单位为1的方格
纸上,△,△,△,……,都是斜边在x 轴上、斜边长分别为2,4,6,……的等腰直角三角形.若△的顶点坐标分别为 (2,0), (1,-1),
(0,0),则依图中所示规律,的坐标为 . 16.【解析】画出图像可找到规律,下标为4n(n 为非负整数)的A 点横坐标为2,纵坐标为2n,则的坐标为(2,1006).
【答案】(2,1006)
【点评】这类问题要善于总结,正确分析出题中所隐含的规律.
1y x =+x 123A A A 345A A A 567A A A 123A A A 1A 2A 3A 2012A 2012
A。
