蔡氏电路matlab仿真报告
电路matlab模拟实验报告
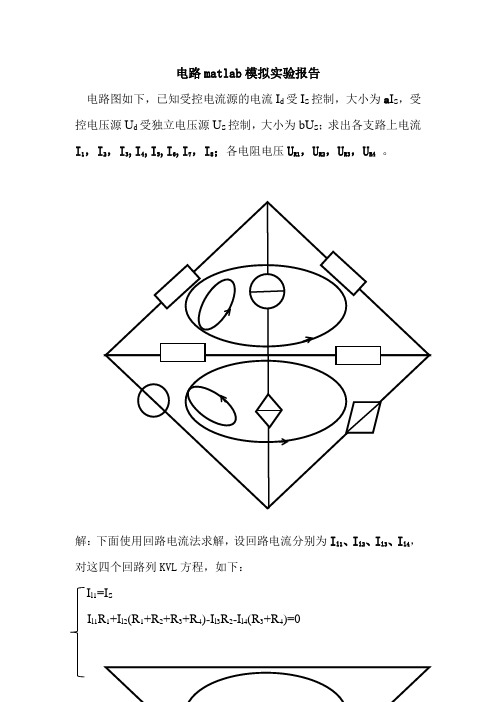
电路matlab模拟实验报告电路图如下,已知受控电流源的电流I d受I S控制,大小为a I S,受控电压源U d受独立电压源U S控制,大小为bU S;求出各支路上电流I1,I2,I3,I4,I5,I6,I7,I8;各电阻电压U R1,U R2,U R3,U R4。
解:下面使用回路电流法求解,设回路电流分别为I l1、I l2、I l3、I l4,对这四个回路列KVL方程,如下:I l1=I SI l1R1+I l2(R1+R2+R3+R4)-I l3R2-I l4(R3+R4)=0I l3= -I d-I l1R2-I l2(R2+R4)+I l3R2+I l4(R2+R4)=U d+Us补充方程:I d=aI SU d=bU S将补充方程代入上述方程组中得:I l1=I SI l1R1+I l2(R1+R2+R3+R4)-I l3R2-I l4(R3+R4)=0I l3= - aI S-I l1R2-I l2(R2+R4)+I l3R2+I l4(R2+R4)= bU S+Us将上述方程组的左端的系数、未知数,右端常数转化成矩阵,用矩阵的运算方式来表达方程组,即:1 0 0 0 I l1 I SR1 R1+R2+R3+R4 -R2 R3+R4 I l2 00 0 1 0 I l3 = -a I S- R2 -(R2+R4) R2 R2+R4 I l4 bU S+Us由电路图可知,各待求量为:I1= I l1+ I l2 U R1= I1*R1I2= I l1- I l3 U R2= I2*R2I3= I l2 U R3= I3* R3I4=I l2- I l4 U R4= I4 *R4I5= I SI6=-( I l3 +I l4)I7= a I SI8= I l4下面通过matlab编写相关程序,求此方程组:建立m文件,代码如下:%此部分为提醒操作者给各变量R1、R2、R3、R4、I S、Us、a、b %赋值R1=input('请输入电阻R1的值(单位:欧姆)');R2=input('请输入电阻R2的值(单位:欧姆)');R3=input('请输入电阻R3的值(单位:欧姆)');R4=input('请输入电阻R4的值(单位:欧姆)');Is=input('请输入独立电流源的大小(单位:安培)');Us=input('请输入独立电压源的大小(单位:伏特)');a=input('请输入受控电流源的控制系数a:');b=input('请输入受控电压源的控制系数b:');A=[1 0 0 0;R1 R1+R2+R3+R4 -R2 R3+R4;0 0 1 0;-R2 -(R2+R4) R2 R2+R4]; %此为系数矩阵B=[Is 0 -a*Is b*Us+Us]' ;Il=inv(A)*B; %此为计算出环路电流矩阵的步骤%下面为得到各待求量I1=Il(1)+Il(2)I2=Il(1)-Il(3)I3=Il(2)I4=Il(2)-Il(4)I5=IsI6=-(Il(3)+Il(4))I7=a*IsI8=Il(4)U1=I1*R1U2=I2*R2U3=I3*R3U4=I4*R4下面我们通过一组确切的值来求出各待解量取R1=8欧姆;R2=6欧姆;R3=20欧姆;R4=12欧姆;Is=4A,Us=15V;a=0.4;b=0.9;解得为。
基于蔡氏电路的MATLAB仿真

1、引 言 作为一种普遍存在的非线性现象, 混沌的发现对科学的发
展 具 有 深 远 的 影 响[1 ,2 ].混 沌 行 为 是 确 定 性 因 素 导 致 的 类 似 随 机 运动的行为,即:一个可由确定性方程描述的 非 线 性 系 统,其 长 期 行为表现为明显的随机性和不可预测性, 我们就认为该系统存 在 混 沌 现 象.混 沌 具 有 三 个 特 点[1-3 ]:随 机 性;遍 历 性;规 律 性.混 沌 有 一 个 很 重 要 的 性 质:系 统 行 为 对 初 始 条 件 非 常 敏 感.近 年 来 许 多学者通过非线性电路对混沌行为进行了广泛地研究, 其中最 典型的是蔡氏电路[4-7],它是能产生混沌行为的最 小 、最 简 单 的 三 阶自治电路. 2、蔡 氏 电 路 模 型
a0 = 0.8, a1 = 0.1
初始值为:[0.1,0.1,0.1],其仿真如图 3 所示. 在 2005 年,W ei Lin 等 提 出 一 种 新 型 的 蔡 氏 电 路 简 化 后 无
量 纲 的 标 准 型 [8]:
(2)
其中,
g ( x )
=
m0 x
+
1 2
(m1
- m0 )(
x +1
参考文献: 1.盛昭瀚,马军海.非线性动力系统分析引论[M ].科学出版社,2001 2.胡岗,萧井华,郑志刚.混沌控制[M ].上海科技教育出版社,2000. 3.曹建 福 ,韩 崇 昭 ,方 洋 旺.非 线 性 系 统 理 论 及 应 用[M ].西 安 交 通 大 学 出 版 社 ,2001 4.J C Sprott. C om plex B ehavior of Sim ple System [C ].InternationalC onfer- ence on com plex System s,2000. 5.M T Y assen.A daptive control and synchronization of a m odified C hua's circuit system [J].A pplied M athem atics and C om putation,2001,(11):1- 9. 6.T zuyin W u,M in - Shin C hen.C haos control of m odified C hua's circuit system [J].Physics D ,2002,(2867):1- 6. 7.A S Elw akil,M P K ennedy.C hua's circuit decom position:a system atic de- sign approach for chaotic oscillators [J].Journal of the Franklin Institute, 2000,(337):251- 265. 8.W ei Lin and Y angbo H e. C om plete synchronization of the noise- per- turbed C hua's circuits C haos 15,023705 (2005)
matlab电路仿真报告

matlab电路仿真报告一. 仿真背景和目的在电路设计和验证过程中,电路仿真技术是非常重要的。
Matlab这一强大的仿真软件,可快速有效地在仿真环境中进行电路设计验证,确保电路设计在实际应用中的可靠性和稳定性。
二. 仿真内容介绍本次仿真实验主要涉及四个方面的内容:交流电路、直流电路、半导体器件、功率放大器。
1. 交流电路仿真交流电路仿真是电路设计的基础。
本次仿真实验中,我们构建了简单的交流电路,通过仿真计算得到了交流电流、交流电压以及电路功率等参数。
2. 直流电路仿真直流电路仿真实验中,我们建立了稳定的直流电源和直流电路,在仿真环境中模拟了直流电路的工作状态,包括电流、电压、功率等参数。
通过仿真结果可以得到直流电路的性能评估。
3. 半导体器件仿真半导体器件在现代电子电路中广泛应用。
本次仿真中,我们针对开关电路的应用设计了半导体管,通过仿真计算得到了开关电路在不同工作状态下的输出特性,包括开关电压、开通电流等。
4. 功率放大器仿真功率放大器是实际应用中常见的一种电路结构。
仿真实验中,我们设计了基本的功率放大器电路,在仿真环境中计算得到了频率响应、增益、输出功率等参数,用于评估该功率放大器的性能和稳定性。
三. 仿真结果分析通过仿真计算和实验结果分析,可以得出以下几点结论:1. 交流电路仿真结果表明,输入交流电源的电流和电压随时间变化而变化,同时可以计算得到电路的功率和电阻等参数。
2. 直流电路仿真结果表明,直流电路的电流和电压稳定,可以计算得到直流电路的电流、电压和功率等参数。
3. 半导体器件仿真结果表明,半导体器件可以有效地用于开关电路应用,可以计算得到器件的开通电流、开关电压等参数。
4. 功率放大器仿真结果表明,功率放大器可以在一定的频率范围内实现较大的增益和输出功率。
同时,该电路还具有一定的稳定性和可靠性。
四. 总结和展望通过对电路仿真实验的分析和总结,我们可以发现,电路仿真技术在电路设计和验证过程中具有不可替代的作用。
matlab仿真实验报告

matlab仿真实验报告Matlab仿真实验报告引言:Matlab是一种广泛应用于科学和工程领域的数值计算软件,它提供了强大的数学和图形处理功能,可用于解决各种实际问题。
本文将通过一个具体的Matlab 仿真实验来展示其在工程领域中的应用。
实验背景:本次实验的目标是通过Matlab仿真分析一个电路的性能。
该电路是一个简单的放大器电路,由一个输入电阻、一个输出电阻和一个放大倍数组成。
我们将通过Matlab对该电路进行仿真,以了解其放大性能。
实验步骤:1. 定义电路参数:首先,我们需要定义电路的各个参数,包括输入电阻、输出电阻和放大倍数。
这些参数将作为Matlab仿真的输入。
2. 构建电路模型:接下来,我们需要在Matlab中构建电路模型。
可以使用电路元件的模型来表示电路的行为,并使用Matlab的电路分析工具进行仿真。
3. 仿真分析:在电路模型构建完成后,我们可以通过Matlab进行仿真分析。
可以通过输入不同的信号波形,观察电路的输出响应,并计算放大倍数。
4. 结果可视化:为了更直观地观察仿真结果,我们可以使用Matlab的图形处理功能将仿真结果可视化。
可以绘制输入信号波形、输出信号波形和放大倍数的变化曲线图。
实验结果:通过仿真分析,我们得到了以下实验结果:1. 输入信号波形与输出信号波形的对比图:通过绘制输入信号波形和输出信号波形的变化曲线,我们可以观察到电路的放大效果。
可以看到输出信号的幅度大于输入信号,说明电路具有放大功能。
2. 放大倍数的计算结果:通过对输出信号和输入信号的幅度进行计算,我们可以得到电路的放大倍数。
通过比较不同输入信号幅度下的输出信号幅度,可以得到放大倍数的变化情况。
讨论与分析:通过对实验结果的讨论和分析,我们可以得出以下结论:1. 电路的放大性能:根据实验结果,我们可以评估电路的放大性能。
通过观察输出信号的幅度和输入信号的幅度之间的比值,可以判断电路的放大效果是否符合设计要求。
四阶蔡氏电路的建模与仿真

四阶蔡氏电路的建模与仿真摘要:混沌现象是一种确定性的非线性运动,在非线性控制领域,混沌控制的研究受到人们越来越多的关注。
典型蔡氏电路结构简单,但有复杂的混沌动力学特征,因而在混沌控制领域中成为研究的重要对象。
本次设计简单介绍了混沌学基本理论,从理论分析和仿真实验两个角度分别研究Chua's Circuit 的混沌行为,用Multisim 软件对电路进行仿真实验,通过改变参数,得到了系统各周期的相轨图,并对实验中遇到的现象进行简单的讨论。
在三阶蔡氏电路的基础上添加一个电感,可以建立四阶蔡氏电路,在此四阶蔡氏电路的基础上,进行了简单的数值分析与仿真分析。
由于普通蔡氏电路在产生混沌现象时, 其元件参数可调围很小,且对初始条件极为敏感,不易于搭建实验电路。
所以引入了电感等效电路,在本文中将蔡氏电路中的电感用等效电路替代,从而实现了无感蔡氏电路。
关键词:混沌;蔡氏电路;Multisim ;等效电感Experimental Study of Chua's circuit chaoticAbstract :Chaos is a deterministic non-linear movement, in the field of nonlinear control, chaotic control get more and more attention by people. Typical Chua's circuit is simple, but complex and chaotic dynamics characteristics, so become an important research object in the field of chaos control . The design simple introduced the basic theory of chaos, study the chaotic behavior of Chua'sCircuit from two angles of the theoretical analysis and experimental with Multisim circuit simulation software, by changing the parameters, get each cycle tracks phase diagram of the system, simple discuss the experimental phenomena encountered, couple the second-order Chua's circuit with a linear circuit ("oscillation absorber"), get even more chaotic behavior of the rich. As the general chaos in Chua's circuit in the production, its range of component parameters adjustable is very small, and extremely sensitive to initial conditions, hard to set up experimental circuit. Therefore introduce the inductor equivalent circuit, in this final, change the inductor of Chua's circuit with the equivalent circuit, thus achieving non- inductor of Chua's circuit.Key words :chaos; Chua's circuit; Multisim; vibration absorber; equivalent inductance目录第一章混沌学基本理论. (5)1.1 混沌的简单介绍 (5)1.1.1 混沌的定义. (5)1.1.2 混沌的主要特征. (6)1.1.3 混沌的现实意义和应用. (7)1.1.4 混沌的前景展望. (8)1.2 蔡氏电路简介 (9)1.3 蔡氏电路的研究 (10)1.4 软件介绍 (10)1.4.1 数值仿真软件. (10)1.4.2 电路仿真软件. (11)第二章三阶蔡氏电路分析. (12)2.1 电路原理与数学建模 (12)2.2 数值仿真分析 (13)2.3 蔡氏二极管等效电路设计 (15)2.4 三阶蔡氏电路制作和电路仿真 (17)2.5 蔡氏电路的平衡点及稳定性 (19)第三章四阶蔡氏电路分析. (22)3.1 四阶蔡氏电路数学建模 (22)3.2 四阶蔡氏电路数值仿真分析 (24)3.3 四阶蔡氏电路电路仿真分析. (25)3.4 三阶蔡氏电路等效电感分析 (27)第四章总结与分析. (30)参考文献. (31)致. (32)附录Matlab 程序 (33)第一章混沌学基本理论1.1 混沌的简单介绍1.1.1 混沌的定义混沌是非线性动力学系统所特有的一种运动形式,是自然界及社会中的一种普遍现象,它是一种在确定性系统中所出现的类似随机而无规则运动的动力学行为。
蔡氏电路混沌现象的仿真

目录引言 (1)1 混沌学概述 (2) (2)1.2 混沌的含义 (3)2 混沌理论 (4) (4)2.2奇怪吸引子与分形 (5)2.3研究混沌的主要方法 (7)——分岔 (8)3蔡氏电路模型及MALAB仿真 (9)3.1 电路模型 (9)3.2 蔡氏电路数学模型及其分析 (12)3.3蔡氏电路仿真研究 (13)3.4 实验结论 (18)结束语 (19)致谢 (20)附录A 英文文献原文 (21)附录B 英文文献翻译 (27)附录C 仿真源代码 (30)蔡氏电路混沌现象的仿真[摘要]本文从理论分析与Matlab仿真两个角度分别研究非线性电路中的混沌现象。
简要介绍了混沌及其特征,混沌产生的机理和条件,以及非线性电路分析仿真的算法。
在分析与仿真蔡氏电路的基础上,构造一个变形蔡氏电路模型,对其电路的非线性元件利用分段线性化方法处理,用MATLAB编程语言对该非线性微分方程进行分析与仿真该变形蔡氏电路通向混沌的道路。
结果表明该变形蔡氏电路也和蔡氏电路一样,在不同的参数下存在有丰富的分岔和混沌现象,并在特定参数下存在所谓的“双涡卷”混沌吸引子。
混沌理论运用于各种学科,如通信的保密通信;利用分形研究物质结构及性能;经济混沌和经济波动的非线性动力学理论等。
[关键字]:混沌;MATLAB仿真分析;蔡氏电路模型;Simulation of Chaos in Chua’s Curcuit[Abstract]: The chaos phenomenon in nonlinear circuit is studied by MATLAB simulation and theoretical analysis in the paper. This paper introduces simply chaos and its characteristic, the chaos output mechanism and condition, and the calculable method of analytic simulation of nonlinear circuit. In the foundation of the analysis and simulation of Chua’s circuit, a modified Chua’s circuit model is constructed. Its nonlinear component is processed using the way of the segment lining. Then the language of MATLAB are used to analyze the nonlinear differential equation and to si mulate the way of this modified Chua’s circuit to the chaos. The result is that the modified Chua’s circuit exists abundantly bifurcation and chaos phenomenon under the different parameter, and exists so-called" double scroll" chaos attractor under the par ticular parameter as soon as Chua’s one.[Key words]: Chaos ; Analysis of MATLAB simulation.;Chua’s circuit model ;引言混沌研究最先起源于Lorenz研究天气预报时用到的三个动力学方程.后来的研究表明,无论是复杂系统,如气象系统、太阳系,还是简单系统,如钟摆、滴水龙头等,皆因存在着内在随机性而出现类似无轨,但实际是非周期有序运动,即混沌现象.现在混沌研究涉及的领域包括数学、物理学、生物学、化学、天文学、经济学及工程技术的众多学科,并对这些学科的发展产生了深远影响.随着计算机和计算科学的快速发展,混沌现象及其应用研究已成为自然科学技术和社会科学研究领域的一个热点。
蔡氏电路仿真报告

非线性电路理论及应用课程作业XXXXXXXXX蔡氏对偶混沌电路仿真报告一、蔡氏对偶混沌电路分析应用一个三阶自治电路进行仿真,电路如图1所示,其中包含一个电流控制型的非线性电阻元件,其伏安特性关系如图2所示。
L 2L 2i 1CR 2u r u c+-+-i 2i-2-1120.20.1-0.1-0.2O u r /Vi 1/A图1 蔡氏对偶电路 图2 流控型非线性电阻伏安特性对于图1中所示的电路,其状态方程推导如下:2c c 21022112011d d )(d d )()(d d i t uC u i i R t iL i r i i R t i L -=+-=--= 整理上述各式得2c c 22120211121011d d 1)(d d )(1)(d d i Ct u u L i i L R t i i r L i i L R t i -=+-=--=为分析方便,对方程进行归一化处理 令20()L t R τ=,t L Rd d 20=τ 且令 120,,c x i y i z u R ===则上述各方程变为y CR L t z z y x t yx r x y L L t x 0212d d d d )]([d d -=+-=--=上述方程中,将时间τ任记为t ,则方程变为标准蔡氏方程,即为:y tzz y x t yx f y t xβα-=+-=-=d d d d )]([d d 其中21L a L =,220L b CR = 001()()0.5()(11)r x f x m x m m x x ==+-+--二、计算机仿真1、参数设置上述蔡氏对偶电路的微分方程描述的动态系统关于原点对称,对应于分段线性电流控制型电阻的特性,若将f (x )特性分为三段考虑,即为⎪⎩⎪⎨⎧-≤--≤≥-+=1)(1||1)()(1010101x m m x m x x m x m m x m x f为了进行计算机仿真计算分析,我们令 8001.0008.012===L L α,5.121104.6008.0402=⨯⨯==-CR L β 而取2.0510-=-=m ,4.0521==m取初始值为(0.025,-0.022,0.8)应用MATLAB 进行仿真。
三阶蔡氏电路matlab仿真代码

一、背景介绍三阶蔡氏电路是一种经典的电路结构,在信号处理、滤波等领域有着重要的应用。
利用MATLAB对三阶蔡氏电路进行仿真分析,可以帮助工程师和研究人员更好地理解电路的特性和行为,对于电路设计和优化具有重要意义。
二、三阶蔡氏电路的基本原理三阶蔡氏电路由三个积分器和两个比例放大器组成,是一种具有强大信号处理能力的电路结构。
它可以用于实现各种滤波器,包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器等。
在电子电路和通信系统中有广泛的应用。
三、MATLAB仿真环境的搭建1. 安装MATLAB软件,并确保其正常运行。
2. 新建一个MATLAB脚本文件,用于编写三阶蔡氏电路的仿真代码。
3. 导入必要的工具箱和函数库,确保能够进行电路仿真分析所需的基本操作和函数调用。
四、三阶蔡氏电路的参数设置1. 根据具体的电路结构和设计要求,设置电路的参数,包括电阻值、电容值、放大倍数等。
2. 考虑电路中可能存在的噪声以及非线性元件的影响,进行适当的参数修正和补偿。
五、三阶蔡氏电路的MATLAB仿真代码实现1. 编写三阶蔡氏电路的节点方程,建立电路的数学模型。
2. 利用MATLAB的数值计算工具,如ode45函数等,对电路进行仿真计算。
3. 对仿真结果进行分析和后处理,得到电路的频率响应、相位特性等重要信息。
六、仿真结果与分析1. 利用MATLAB绘制三阶蔡氏电路的幅频特性曲线和相频特性曲线,观察电路的频率响应特性。
2. 对比不同参数设置下的仿真结果,分析电路性能随参数变化的规律和特点。
3. 考虑电路可能存在的非线性特性,对其进行深入分析和讨论,为实际应用提供参考依据。
七、结论与展望通过MATLAB对三阶蔡氏电路的仿真分析,我们深入了解了电路的特性和行为。
这对于电路的设计和优化具有重要意义。
在未来的研究中,可以进一步探究电路在实际应用中的性能表现,以及对其进行更加精细的仿真和分析。
也可以考虑将仿真结果与实际测试数据进行对比,验证仿真模型的准确性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
蔡氏电路仿真分析
学院:电气工程学院
班级:硕6036
姓名:***
学号:**********
目录
1.基本分析 (2)
2.MATLAB仿真 (5)
蔡氏电路
蔡氏电路是著名的非线性混沌电路,结构简单,但却出现双涡卷奇怪吸引子和及其丰富的混沌动力学行为。
1.基本分析
蔡氏电路是一个典型的混沌电路,最早由著名华裔科学家、美国加州大学蔡少堂教授设计。
他证明了在满足以下条件时能够产生混沌现象。
(1) 非线性元件不少于1 个;
(2) 线性有效电阻不少于1 个;
(3) 储能元件不少于3 个。
根据以上条件,在图1.1中给出蔡氏电路方框图。
图中R 为线性有效电阻,L 、C 1、C 2为储能元件,R N 为非线性元件。
图2.2给出非线性电阻伏安特性曲线。
图1.1 蔡氏电路方框图
图1.2 非线性电阻伏安特性曲线
对于图2.1提出的蔡氏电路,其状态方程推导如下
12112122121()()1()(1)C C C C C C C L L C du C u u g u dt R du C u u i dt R di L u dt ⎧=--⎪⎪⎪=-+⎨⎪⎪=-⎪⎩
其中函数1()C g u 是分段线性函数,其形式为:
11111()()()2
C b C a b C C g u G u G G u E u E =+-⨯+-- 作变量代换:
12
22
221,,,,1
C C L
u u i x y z E E EG
C C tG C C LG G R ταβ===
==== 式(1)可以写为如下形式
[]
()(2)dx y x f x d dy x y z
d dz y d αττ
βτ⎧=--⎪⎪⎪=--⎨⎪⎪=-⎪⎩
式(2)即是蔡氏电路的标准方程形式。
其中()f x 可表示为如下形式
10101
01(),1(),1(),1m x m m x f x m x x m x m m x +-≥⎧⎪=≤⎨⎪--≤-⎩
其中
01,a b m G E m G E ==
蔡氏电路的三个状态方程式在状态空间的三个子空间为
101={(,,)| 1}
={(,,)| 1}={(,,)| 1}
D x y z x D x y z x D x y z x -≥≤≤-
在状态空间的三个子空间内分别具有唯一平衡点如下
1011(,0,),
(0,0,0),
(,0,).P k k D Q D P k k D +--=-∈=∈=-∈
其中,
1011
m m k m -=+ 在P +、1P -和Q 处的雅可比矩阵分别为:
1(1)011100P P m J J ααβ+--+⎛⎫ ⎪==- ⎪ ⎪-⎝⎭,0(1)011100Q m J ααβ-+⎛⎫ ⎪=- ⎪ ⎪-⎝⎭
取10α=,15β=,0 1.2m =-,10.6m =-,则在P +、1P -处的特征值为
一个实数值和一对共轭复数值。
其中的一个实数值为
-5.3938P λ=
而一对共轭复数值为
j 0.1969 j 3.3294P P σω+=±
可见0P λ<,而0P σ>。
在Q 处的特征值也为一个实数值和一对共轭复数值。
其中的一个实数值为
3.1201P λ=
而一对共轭复数值为
j -1.0601 j2.9140P P σω+=±
可见0P λ>,而0P σ<。
因此,所有的平衡点P +、1P -和Q 均为鞍焦点。
2.MATLAB 仿真
在对蔡氏电路进行建模过程中,要用到加法器、积分器、增益模块、常数模块等单元,这些可以方便地从 Simulink 标准库模块中直接提取。
除此之外,还需用到显示 x 和 y 信号相图的平面图形显示器(XY Graph )模块和示波器模块;最后,把模型顺序连接起来,得到用基本模块元素建立的数学仿真模型,如下图所示。
取0.1,0.1,0.1x y z ===为初值,作为系统的初始值,在t=[0,300]的时
间范围内求解系统的运动轨迹,其投影相图及时域波形如下:
图2.1 x-y-z 立体相图
图2.2 x时域波形图 2.3 y时域波形
图 2.4 z时域波形图图 2.7 x-y平面相图
图 2.6 y-z平面相图
图 2.5 x-z平面相图
从仿真结果图可以,蔡氏电路的正规化状态方程描述了一个连续时间系统,这个系统在所给参数和初值的条件下可以产生双涡卷吸引子的混沌现象。
改变参数和初值,还可以产生其它很多有趣的混沌现象。
利用系统平衡点处的线性化矩阵,可以定性分析系统的动力学行为,以便寻找能使系统产生混沌的参数。
