中考数学一轮复习分式及其运算课件浙教版
合集下载
2014年浙江中考数学第一轮复习课件_第一章数与式第3讲分式(共36张PPT)

浙江三年中考
基础知识梳理
考题类型展示
浙江名师预测
跟踪训练
首页
与分母都乘以(或除以)同一个不等于 0 的整式,分式的值不变. a· m a a÷ m a (1) = , = (m≠0); b· m b b÷ m b (2)约分的关键是确定分式的分子与分母中的最大公因式.确定最大公因式的一般步骤 是:当分子、分母是多项式时, 先因式分解,取系数的最大公约数,相同字母(因式)的最低次幂的积为最大公因式. (3)通分的关键是确定 n 个分式的最简公分母.确定最简公分母的一般步骤是:当分母 是多项式时,先因式分解,再取系数的最小公倍数,所有不同字母(因式)的最高次幂的积为 最简公分母.
2014年浙江中考第一轮复习
数 学
第3讲
分式
按ESC退出
浙江三年中考
基础知识梳理
考题类型展示
浙江名师预测
跟踪训练
首页
按ESC退出
1 1.(2012· 湖州)要使分式 有意义,x的取值满足( x A.x=0 B.x≠0 C.x>0 D.x<0
答案:B
)
1 a 2.(2011· 金华)计算 - 的结果为( a-1 a-1 1+a a A. B.- a-1 a-1 C.-1 D.1-a
a2-4 7.(2012· 宁波)计算: +a+2. a+2 a+2a-2 解:原式= +a+2=a-2+a+2=2a. a+2
x2 1 8.(2012· 衢州)先化简 + ,再选取一个你喜欢的数代入求值. x-1 1-x
x2-1 x2 1 解: + = =x+1,代入求值(除x=1外的任何实数都可以),如代入x=2,得 x-1 1-x x-1 原式=2+1=3.
答案:C
浙教版初中数学中考复习分式及其运算(39张)

分式及其运算
命题趋势:
• 1.分式的有关概念,主要是分式的判定以及分式有(无)意义、值为0 的条件. • 2.分式基本性质的应用,如约分、通分、分式符号变化、分式的各项系数化成整数等. • 3.分式的运算是分式考查中的重点,分式的化简与求值问题,一是常规的分式化简求 值, • 二是在已知条件下进行分式的化简求值,包括一些条件开放性求值问题. • 4.主要体现的思想方法:类比的思想、转化的思想等.
37
考点四:分式的创新应用
38
解析:
39
•
(3)利用分式的基本性质,经过通分求解.
• 【答案】A
DC
浙教版初中数学中考复习:分式及其 运算 (39页)-PPT执教课件【推荐】
15
浙教版初中数学中考复习:分式及其 运算 (39页)-PPT执教课件【推荐】
考点二:分式性质的运用
浙教版初中数学中考复习:分式及其 运算 (39页)-PPT执教课件【推荐】
2
考点一:分式的有关概念
B≠0 B=0 A=0,B≠0
3
考点一:分式的有关概念
4
浙教版初中数学中考复习:分式及其 运算 (39页)-PPT执教课件【推荐】
解析:
浙教版初中数学中考复习:分式及其 运算 (39页)-PPT执教课件【推荐】
5
浙教版初中数学中考复习:分式及其 运算 (39页)-PPT执教课件【推荐】
24
解析:
25
思维提升:
• 分式的混合运算顺序与实数的混合运算顺序相同,此外,实数的运算律对分式 运算同样适用,注意灵活运用,提高解题的质量和速度;分子或分母的系数是负数 时,要把“-”号提到分式本身的前边;分式运算的最终结果若是分式,一定要化为 最简分式.
命题趋势:
• 1.分式的有关概念,主要是分式的判定以及分式有(无)意义、值为0 的条件. • 2.分式基本性质的应用,如约分、通分、分式符号变化、分式的各项系数化成整数等. • 3.分式的运算是分式考查中的重点,分式的化简与求值问题,一是常规的分式化简求 值, • 二是在已知条件下进行分式的化简求值,包括一些条件开放性求值问题. • 4.主要体现的思想方法:类比的思想、转化的思想等.
37
考点四:分式的创新应用
38
解析:
39
•
(3)利用分式的基本性质,经过通分求解.
• 【答案】A
DC
浙教版初中数学中考复习:分式及其 运算 (39页)-PPT执教课件【推荐】
15
浙教版初中数学中考复习:分式及其 运算 (39页)-PPT执教课件【推荐】
考点二:分式性质的运用
浙教版初中数学中考复习:分式及其 运算 (39页)-PPT执教课件【推荐】
2
考点一:分式的有关概念
B≠0 B=0 A=0,B≠0
3
考点一:分式的有关概念
4
浙教版初中数学中考复习:分式及其 运算 (39页)-PPT执教课件【推荐】
解析:
浙教版初中数学中考复习:分式及其 运算 (39页)-PPT执教课件【推荐】
5
浙教版初中数学中考复习:分式及其 运算 (39页)-PPT执教课件【推荐】
24
解析:
25
思维提升:
• 分式的混合运算顺序与实数的混合运算顺序相同,此外,实数的运算律对分式 运算同样适用,注意灵活运用,提高解题的质量和速度;分子或分母的系数是负数 时,要把“-”号提到分式本身的前边;分式运算的最终结果若是分式,一定要化为 最简分式.
分式ppt5 浙教版
约分的依据是什么?
分式的基本性质
在化简结果中,分子和分母已没有公因 式,这样的分式成为最简分式
化简分式时,通常 要使结果成为最简 分式或者整式
随堂练习
随堂练习
P158 1.2.3
接纠错练习
本节课小结
1.分式的基本性质。
2.分式的约分。
3.你在这节课的学习中体会最深刻的问 题是什么?
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
b by ax a (xy0 ) (xb0) 2x 2xy bx b
分式性质应用2
• 填空
2xy 2 (_____) 3 x 15 x ( x y ) 2 2 , 5(x+y)2 xy x y x y (______
1 x y (_____) 2 2 x y x y
3 x x4
x3 2 x 1
x 4 ( x 2)(x 3)
2
2 3
10 与 15
16 8 ; 与 42 21
是否相等?依据是什么?
分数的基本性质
分数的分子与分母都乘以或除以 同一个不等于零的数,分数的值 不变。
1 你认为分式 与 相等吗? 2x 2 b ab 与 2 呢? a a
第七章分式
第一节:分式(2)
温故知新
回顾 & 思考 ☞
整式A除以整式B,可以表示成 A 的形式。 B 如果除式 B 中含有字母,那么称 A 为分 B 式,其中 A 称为分式的分子, B 为分式的分 母。
对于任意一个分式,分母都不能为零。
练一练
当x取什么值时,下列分式有意义: 当x取什么值时,下列分式值为零:
浙江中考数学课件PPT 第3课时 分 式

典型考题展示
考点一 确定分式有意义的条件 要使分式xx- +12有意义,则 x 的取值范围是( C )
A.x<-2 B.x>-2 C.x≠-2 D.x≠1 【思路点拨】分式有意义的条件是分母不等于零,即 x+2≠0. 【自主解答】
要使分式5-1 x有意义,则 x 的取值范围是 x≠5 .
考点二 确定分式的值为 0 的条件
没有公因式的分式叫做 最简分式 .
约分的关键是确定分式的分子与分母中的 最大公因式 .确 定最大公因式的一般步骤:当分子、分母是多项式时,先 分解因 式 ,取系数的 最大公因数 ,相同字母(因式)的 最低次幂 的积 为最大公因式.
3.通分:把分母不相同的几个分式化成 分母相同 的分式, 叫做通分.通分的关键是确定几个分式的 最简公分母 .确定最 简公分母的一般步骤:当分母是多项式时,先 分解因式 ,再取 系数的 最小公倍数 ,所有不同字母(因式)的 最高次幂 的积为最 简公分母.
A.x=1
B.x=-6
C.x≠1
D.x≠-6
2.要使分式x-x 11有意义,则 x 的取值应满足( C )
A.x≠0
B.x>0
C.x≠11
D.x>11
(x+y)2-(x-y)2
3.计算
4xy
的结果为( A )
A.1
B.12
C.14
D.0
【解析】原式=x2+2xy+y24-xyx2+2xy-y2=44xxyy=1.故选 A.
C.x+x 1÷x-1 1
D.x2+x+2x1+1
D.xx2--11
5.下列计算正确的是( B )
A.3xy÷3xy=x2
B.3xy2 ·3xy=1x
浙江省2020届中考一轮复习浙教版数学课件:第1讲 实数及其运算(共39张PPT)

点拨
解
答案
(2)在一列数:a1,a2,a3,…,an中,a1=3,a2=7,从第三个数开始, 每一个数都等于它前两个数之积的个位数字,则这一列数中的第2017 个数是( B )
A.1
B.3
C.7
D.9
解 依题意得:a1=3,a2=7,a3=1,a4=7,a5=7,a6=9,a7=3, a8=7;周期为6; ∵2017÷6=336…1, ∴a2017=a1=3.
3. 零指数幂,负整数指数幂
(1)任何不等于零的数的零次幂都等于1,即a0=_1__(a≠0).
(2)任何不等于零的数的-p次幂,等于这个数p次幂的倒数,即a-p
=
1 ap
(a≠0,p为正整数).
4. 实数的大小比较 (1)代数比较法:正数大于零,负数小于零,正数大于一切负数;两个 正数,绝对值大的数大;两个负数,绝对值大的数反而小. (2)数轴比较法:将两个实数分别表示在数轴上,右边的数总比左边的 数大. (3)差值比较法:设a,b是任意两个实数,则a-b>0⇔a>b;a-b< 0(4⇔)商a<值b比;较a-法b:=设0⇔a,a=b b是. 两个正数,则:ab>1⇔a>b;ab=1⇔a=b;ab< 1⇔a<b. 在具体解题时,视题目的情况灵活选择最优方法.
解
题型四 科学计数法
自主演练
1.据报道,目前我国“天河二号”超级计算机的运算速度位居全球第
一,其运算速度达到了每秒338 600 000亿次,数字338 600 000用科学
记数法可简洁表示为( A )
A.3.386×108
B.0.3386×109
C.33.86×107
D.3.386×109
答案
2.近似数5.0×102精确到( C )
浙江省中考数学一轮复习 第4课 分式及其运算课件

_整__式__,分式的值不变,用式子表示为:_BA_=__AB_××__MM_,_AB_=__AB_÷÷__MM(M 是 _(_M__是_不__等__于__零__的__整__式__)___.
要点梳理
3.分式的运算法则: (1)符号法则:分子、分母与分式本身的符号,改变其中任何
两个,分式的值不变. 用式子表示为:ab=--ab=--ba=--ba,-ba=-ab=-ba. (2)分式的加减法:
基础自测
5.(2011·芜湖) 分式方程2xx--25=2-3 x的解是
A.x=-2
B.x=2
C.x=1
D.x=1 或 x=2
( C)
解析 当 x=1 时,方程左边=2×1-1-2 5=--31=3, 右边=2-3 1=3,∴x=1 是方程的解.
题型分类 题型一 分式的概念,求字母的取值范围
【例 1】 (1)(2012·宁夏)当 a __≠__-__2__时,分式a+1 2有意义. 解析 当 a+2≠0,a≠-2 时,分式a+1 2有意义. (2)(2011·泉州) 当 x=____2____时,分式xx-+22的值为 0. 解析 当 x-2=0,x=2 时,分母 x+2=4,分式的值为 0.
(2)(2011·贵阳) 在三个整式 x2-1,x2+2x+1,x2+x 中, 请你从中任意选择两个,将其中一个作为分子,另一个 作为分母组成一个分式,并将这个分式进行化简,再求 当 x=2 时分式的值.
解 答案不唯一.如,选择 x2-1 为分子,x2+2x+1 为分母,
x2-1 组成分式x2+2x+1.
探究提高
(1)首先求出使分母等于0的字母的值,然后让未知数 不等于这些值,便可使分式有意义; (2)首先求出使分子为0的字母的值,再检验这个字母 的值是否使分母的值为0,当它使分母的值不为0时, 型一 分式的概念,求字母的取值范围
要点梳理
3.分式的运算法则: (1)符号法则:分子、分母与分式本身的符号,改变其中任何
两个,分式的值不变. 用式子表示为:ab=--ab=--ba=--ba,-ba=-ab=-ba. (2)分式的加减法:
基础自测
5.(2011·芜湖) 分式方程2xx--25=2-3 x的解是
A.x=-2
B.x=2
C.x=1
D.x=1 或 x=2
( C)
解析 当 x=1 时,方程左边=2×1-1-2 5=--31=3, 右边=2-3 1=3,∴x=1 是方程的解.
题型分类 题型一 分式的概念,求字母的取值范围
【例 1】 (1)(2012·宁夏)当 a __≠__-__2__时,分式a+1 2有意义. 解析 当 a+2≠0,a≠-2 时,分式a+1 2有意义. (2)(2011·泉州) 当 x=____2____时,分式xx-+22的值为 0. 解析 当 x-2=0,x=2 时,分母 x+2=4,分式的值为 0.
(2)(2011·贵阳) 在三个整式 x2-1,x2+2x+1,x2+x 中, 请你从中任意选择两个,将其中一个作为分子,另一个 作为分母组成一个分式,并将这个分式进行化简,再求 当 x=2 时分式的值.
解 答案不唯一.如,选择 x2-1 为分子,x2+2x+1 为分母,
x2-1 组成分式x2+2x+1.
探究提高
(1)首先求出使分母等于0的字母的值,然后让未知数 不等于这些值,便可使分式有意义; (2)首先求出使分子为0的字母的值,再检验这个字母 的值是否使分母的值为0,当它使分母的值不为0时, 型一 分式的概念,求字母的取值范围
中考数学 第一单元 数与式 第03课时 分式课件浙教浙教级数学课件
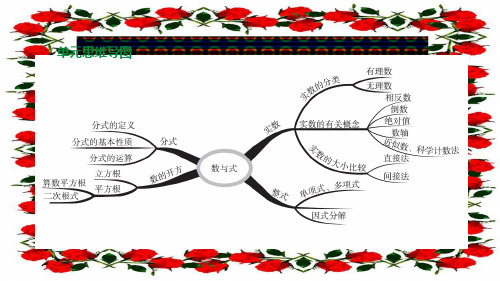
(-1)2
-1-(-1)(+1)
÷
(+1)(-1)
+1
=
-1 -1-( 2 -1)
-1 - 2
+1
+1 +1
÷
+1
=
∵满足- 5<x< 5的整数有-2,-1,0,1,2,且当 x=±1 或 x=0 时,分母的值为 0,
∴x 只能取-2 或 2.
1
当 x=-2 时,原式= ,
=x+1,
课前双基巩固
3.[2018·包头] 化简:
2 -4+4
2 +2
÷(
4
+2
2-
-1)=
.
[解析]
2 -4+4
2 +2
=
(-2)2
(+2)
÷(
4
+2
-1)
c
+2 2-
×
2-
=
.
课前双基巩固
知识梳理
分式
的加减
分式
的乘除
分式的
混合运算
±
-
+
5.[2018·滨州] 若分式
C.-1
没有意义,则 m= -2
2 -9
-3
D.-5
.
的值为 0,则 x 的值为
-3
.
当堂效果检测
2 -2+1
6.[2017·威海] 先化简
2 -2+1
解:原式=
2 -1
-1
2 -1
÷(
-1
+1
÷ +1 -(-1) =
2013中考数学复习课件因式分解+分式(浙教版)

法或其他方法继续分解下去,直到不能分解为止.
类型之四 因式分解中的开放性问题 [2010·龙岩]给出三个单项式:a2,b2,2ab. (1)在上面三个单项式中任选两个相减,并进行因式分解; (2)当a=2010,b=2009时,求代数式a2+b2-2ab的值. 【解析】由乘法公式和提取公因式进行分解. 解:(1)a2-b2=(a+b)(a-b);
②④.
【点悟】把一个多项式化为几个整式的积的形式,叫做把这个多项式
因式分解.应用因式分解的概念时一定要注意:①因式分解专指多项
式的恒等变形;②因式分解的结果必须是几个整式的积的形式;③因
式分解与整式的乘法互为逆变形.
类型之二 利用提公因式法因式分解
因式分解:(x+y)2-3(x+y)=
.
【解析】把x+y看作一个整体,原式=(x+y)(x+y-3).
类型之三利用公式法因式分解
[2010·济宁]把代数式3x3-6x2y+3xy2分解因式,3y)
B.3x(x2-2xy+y2)
C.x(3x-y)2
D.3x(x-y)2
【【解点析悟】】原分式解=时3,x有(x公2-因2x式y的+y要2先)=提3x取(公x-因y)式2.,再考虑能否应D用公式
(2)异分母的分式相加减,先通分,化为同分母的分式,然后按照同 分母的分式加减法进行计算.
ab±cd=adbd±bcbd=ad±bcbd.
分式的乘法:两个分式相乘,把分子相乘的积作为积的分子,把分母 相乘的积作为积的分母.
ab·cd=acbd. 分式的除法:两个分式相除,把除式的分子和分母颠倒位置后再与被 除式相乘.
ab÷cd=ab·dc=adbc.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.正确理解分式的概念及分式有意义 判断某一个代数式属于不属于分式,不能看化简后的结果, 而应看到它的本来面目,分式的概念是以形式上规定的. 解有关分式是否有意义的问题时,常用到“或”与“且”来 表达,正确使用“或”与“且”也是解题的关键.“或” 表示一种选择关系,含有“你行,他也行”的意思;“且” 表示递进关系,也有“同时”的意思.
第4课 分式及其运算
要点梳理
1.分式的基本概念:
(1)形如
A(A,B是整式,且B中含有字母,B≠0) B
的式子
叫分式;
(2)当 B≠0 时,分式 A 有意义;当 B=0 时,分式无意 B
义;当 A=0且B≠0 时,分式的值为零.
2.分式的基本性质:
分式的分子与分母都乘以(或除以) 同一个不等于零的整式 ,
老师忠告 (1)分式中的分母不能为零,这是同学们熟知的,但在解题时, 往往忽视题目中的这一隐含条件,从而导致解题错误; (2)利用分式的基本性质进行恒等变形时,应注意分子与分母同 乘或同除的整式的值不能是零; (3)解分式方程为什么要检验?因为用各分母的最简公分母去乘 方程的两边时,不能肯定所得方程与原方程同解.如果最后x取 值使这个最简公分母不为零,则这个步骤符合方程同解原理, 这个取值就是方程的解;否则,不保证新方程与原方程同解. 从另一角度看,既然使各分母的最简公分母为零,则必使某个 分母为零,该分式则无意义,原方程不可能成立,这个取值就 不是原方程的解.
m 2-x
无解,则m=____1____.
解析: = ,
去分母,x-3=-m,m=3-x. 当x=2时,m=3-2=1.
答题规范
1.勿忘分母不能为零
考题再现 当a取什么值时,方程 的解是负数?
x-1-x-2= 2x+a x-2 x+1 x-2x+1
学生作答 解:原方程两边同乘以(x-2)(x+1),得 x2-1-x2+4x-4=2x+a,2x=a+5,
[3分] [5分]
探究提高 准确、灵活、简便地运用法则进行化简,注意在取a的 值时,不能取使分式无意义的±2.
知=-2. x-1 x2-1
解:原式=
=
==
=-1.
(2)计算:( 3a - a )·a2-9
a-3 a+3
a
解:原式= · - ·
解析: =- .
题型三 分式的四则混合运算
【例3】 先化简代数式( a + 2 )÷ 1 ,然后选取一个 a+2 a-2 a2-4
合适的a值,代入求值.
解题示范——规范步骤,该得的分,一分不丢!
解:原式=( + )·(a+2)(a-2)
[2分]
=a(a-2)+2(a+2)=a2-2a+2a+4 =a2+4 取a=1,得原式=12+4=5
知能迁移2 (1)(2011·聊城)化简: a2-b2 ÷ 2a-2b = . a2+2ab+b2 a+b
解析:
÷
=
·
=.
(2)下列运算中,错误的是( D )
A. a = ac (c≠0)
b bc
C.
0.5a+b 0.2a-0.3b
=
5a+10b 2a-3b
B.-a+a-bb =-1 D. xx-+yy=yy-+xx
(2)分式的加减法:
同分母加减法:
a ±b =a±b cc c
;
异分母加减法:
b±d= bc±ad a c ac
.
(3)分式的乘除法: a·c = ac , b d bd a÷ c = ad . b d bc
(4)分式的乘方:
a b
n=
abnn(n为正整数)
.
4.分式的约分、通分: 把分式中分子与分母的公因式约去,这种变形叫做约分, 其根据是分式的基本性质. 把几个异分母分式化为与原分式的值相等的同分母分式, 这种变形叫做分式的通分,通分的根据是分式的基本性 质.通分的关键是确定几个分式的最简公分母.
=3(a+3)-(a-3) =2a+12.
(3)(2011·贵阳)在三个整式x2-1,x2+2x+1,x2+x中,请你 从中任意选择两个,将其中一个作为分子,另一个作为分母 组成一个分式,并将这个分式进行化简,再求当x=2时分式 的值.
解:答案不唯一. 如,选择x2-1为分子,x2+2x+1为分母,
2 无意义; x-1
解析:当x-1=0,x=1时,分式无意义.
(2)(2011·泉州)当x=___2____时,分式xx- +22的值为0. 解析:当x-2=0,x=2时,分母x+2=4,分式的值是0.
探究提高 1.首先求出使分母等于0的字母的值,然后让未知数不等于 这些值,便可使分式有意义. 2.首先求出使分子为0的字母的值,再检验这个字母的值是 否使分母的值为0,当它使分母的值不为0时,这就是所要求 的字母的值.
思想方法 感悟提高
方法与技巧 1.分式运算过程较长,运算中错一个符号,往往会使原来能够
化简的趋势改观,使算式越来越繁,形成对分式运算厌烦 甚至惧怕的心理.为了避免这种现象,一定要养成分类分 级逐步演算的习惯,每次添、去括号时,要注意每一个符 号的正确处理. 2.在加深对方法的原理理解的前提下,清楚地归纳运算步骤, 宜分步式,不宜跳步,不宜一个符号下完成数个步骤.
xx2B--.21-的1值为0C,.则±x的1 值为D(.D2
)
解析:当x-2=0,x=2时,x2-1≠0,故选D.
题型二 分式的性质
【例2】
(1)(2011·湛江)化简 a2 - b2 的结果是( a-b a-b
A
)
A.a+b B.a-b C.a2-b2 D.1
解析: - =
=
=a+b.
(2)已知 1 - 1=3,求分式2x-14xy-2y的值.
∴x=
.
由
<0,得a<-5.
故当a<-5时,原方程的解是负数.
规范解答 解:当x≠-1且x≠2时,原方程两边都乘以(x-2)(x+1), 得x2-1-x2+4x-4=2x+a, 2x=a+5,
∴x=
.
由 <0,得a<-5.
又由
≠2,得a≠-1; ≠-1,得a≠-7,
故当a<-5且a≠-7时,原方程的解是负数.
xy
x-2xy-y
解法一:∵ - =3,
∴ =3,y-x=3xy,x-y=-3xy.
原式=
=
=
=
=4.
解法二:∵ - =3,∴xy≠0, ∴原式=
=
=
=
=
=4.
探究提高 1.分式的基本性质是分式变形的理论依据,所有分式变形 都不得与此相违背,否则分式的值改变. 2.将分式化简,即约分,要先找出分子、分母的公因式, 如果分子、分母是多项式,要先将它们分别分解因式,然 后再约分,约分应彻底. 3.巧用分式的性质,可以解决某些较复杂的计算题,可应 用逆向思维,将要求的算式向已知条件“凑”而求得结 果.
基础自测
1.(2011·江津)下列式子是分式的是( B )
A. x 2
B.x+x 1
C. x+y 2
D.x 3
解析:根据分式的定义,分母中必含字母的代数式叫分式.
2.(2011·南充)当分式xx-+12的值为0时,x的值是( B )
A.0
B.1
C.-1
D.-2
解析:当x=1时,分子x-1=0,而分母x+2=3≠0, 所以分式的值为0.
5.分式的混合运算: 在分式的混合运算中,应先算乘方,再将除法化为乘法, 进行约分化简,最后进行加减运算.遇有括号,先算括号 里面的.灵活运用运算律,运算结果必须是最简分式或整 式.
6.解分式方程,其思路是去分母转化为整式方程,要特别注 意验根,使分母为0的未知数的值,是增根,需舍去.
[难点正本 疑点清源]
知能迁移4
(1)(2011·潼南)解分式方程:x+x 1
- 1 =1. x-1
解:方程两边同乘(x+1)(x-1),得
x(x-1)-(x+1)=(x+1)(x-1),
化简,得-2x-1=-1,
解得 x=0.
检验:当x=0时,(x+1)(x-1)≠0,
所以x=0是原分式方程的解.
(2)若方程
x-3= x-2
失误与防范 1.分式的分母不为零,分式才有意义,这又是分式的值为0的前
提.讨论分式的值为0,即要求分母不为0,又要求分子为0, 二者缺一不可.
2.当分式的分子或分母为多项式时,在运算顺序上,相当于使
分子或分母的外面有一个括号,从而把它们分别当成一个整体 看,例如:5· x-,2 应得 5x-2, 而不是 5x-.2 3.分式加减法中的x通+分3 是等值变x+形3,不要在学了x解+分3 式方程后, 两者混淆,把通分变形成去分母了.
组成分式
.
=
=.
将x=2代入 ,得原式= = .
题型四 分式方程的解法
【例4】
解分式方程:x2+5 3x
-
1 x2-x
=0.
解题示范——规范步骤,该得的分,一分不丢!
解:原式=
-
=0,
去分母,5(x-1)-(x+3)=0,
去括号,5x-5-x-3=0, 4x-8=0, 4x=8,x=2. 经检验,x=2是原方程的根. ∴原方程的根是x=2.
3.(2A0.111a·+-金a1华)计算a-B1.1 --aa--aa 11 的结果为( C )
C.-1
D.2
解析: 1 - a = 1-a = a-1 a-1 a-1
=-1.
4.(2011·潜江)化简(
m2 m-2
+4 2-m
)÷(m+2)的结果是(
B
)
A.0
B.1
C.-1
D.(m+2)2
解析:原式=
第4课 分式及其运算
要点梳理
1.分式的基本概念:
(1)形如
A(A,B是整式,且B中含有字母,B≠0) B
的式子
叫分式;
(2)当 B≠0 时,分式 A 有意义;当 B=0 时,分式无意 B
义;当 A=0且B≠0 时,分式的值为零.
2.分式的基本性质:
分式的分子与分母都乘以(或除以) 同一个不等于零的整式 ,
老师忠告 (1)分式中的分母不能为零,这是同学们熟知的,但在解题时, 往往忽视题目中的这一隐含条件,从而导致解题错误; (2)利用分式的基本性质进行恒等变形时,应注意分子与分母同 乘或同除的整式的值不能是零; (3)解分式方程为什么要检验?因为用各分母的最简公分母去乘 方程的两边时,不能肯定所得方程与原方程同解.如果最后x取 值使这个最简公分母不为零,则这个步骤符合方程同解原理, 这个取值就是方程的解;否则,不保证新方程与原方程同解. 从另一角度看,既然使各分母的最简公分母为零,则必使某个 分母为零,该分式则无意义,原方程不可能成立,这个取值就 不是原方程的解.
m 2-x
无解,则m=____1____.
解析: = ,
去分母,x-3=-m,m=3-x. 当x=2时,m=3-2=1.
答题规范
1.勿忘分母不能为零
考题再现 当a取什么值时,方程 的解是负数?
x-1-x-2= 2x+a x-2 x+1 x-2x+1
学生作答 解:原方程两边同乘以(x-2)(x+1),得 x2-1-x2+4x-4=2x+a,2x=a+5,
[3分] [5分]
探究提高 准确、灵活、简便地运用法则进行化简,注意在取a的 值时,不能取使分式无意义的±2.
知=-2. x-1 x2-1
解:原式=
=
==
=-1.
(2)计算:( 3a - a )·a2-9
a-3 a+3
a
解:原式= · - ·
解析: =- .
题型三 分式的四则混合运算
【例3】 先化简代数式( a + 2 )÷ 1 ,然后选取一个 a+2 a-2 a2-4
合适的a值,代入求值.
解题示范——规范步骤,该得的分,一分不丢!
解:原式=( + )·(a+2)(a-2)
[2分]
=a(a-2)+2(a+2)=a2-2a+2a+4 =a2+4 取a=1,得原式=12+4=5
知能迁移2 (1)(2011·聊城)化简: a2-b2 ÷ 2a-2b = . a2+2ab+b2 a+b
解析:
÷
=
·
=.
(2)下列运算中,错误的是( D )
A. a = ac (c≠0)
b bc
C.
0.5a+b 0.2a-0.3b
=
5a+10b 2a-3b
B.-a+a-bb =-1 D. xx-+yy=yy-+xx
(2)分式的加减法:
同分母加减法:
a ±b =a±b cc c
;
异分母加减法:
b±d= bc±ad a c ac
.
(3)分式的乘除法: a·c = ac , b d bd a÷ c = ad . b d bc
(4)分式的乘方:
a b
n=
abnn(n为正整数)
.
4.分式的约分、通分: 把分式中分子与分母的公因式约去,这种变形叫做约分, 其根据是分式的基本性质. 把几个异分母分式化为与原分式的值相等的同分母分式, 这种变形叫做分式的通分,通分的根据是分式的基本性 质.通分的关键是确定几个分式的最简公分母.
=3(a+3)-(a-3) =2a+12.
(3)(2011·贵阳)在三个整式x2-1,x2+2x+1,x2+x中,请你 从中任意选择两个,将其中一个作为分子,另一个作为分母 组成一个分式,并将这个分式进行化简,再求当x=2时分式 的值.
解:答案不唯一. 如,选择x2-1为分子,x2+2x+1为分母,
2 无意义; x-1
解析:当x-1=0,x=1时,分式无意义.
(2)(2011·泉州)当x=___2____时,分式xx- +22的值为0. 解析:当x-2=0,x=2时,分母x+2=4,分式的值是0.
探究提高 1.首先求出使分母等于0的字母的值,然后让未知数不等于 这些值,便可使分式有意义. 2.首先求出使分子为0的字母的值,再检验这个字母的值是 否使分母的值为0,当它使分母的值不为0时,这就是所要求 的字母的值.
思想方法 感悟提高
方法与技巧 1.分式运算过程较长,运算中错一个符号,往往会使原来能够
化简的趋势改观,使算式越来越繁,形成对分式运算厌烦 甚至惧怕的心理.为了避免这种现象,一定要养成分类分 级逐步演算的习惯,每次添、去括号时,要注意每一个符 号的正确处理. 2.在加深对方法的原理理解的前提下,清楚地归纳运算步骤, 宜分步式,不宜跳步,不宜一个符号下完成数个步骤.
xx2B--.21-的1值为0C,.则±x的1 值为D(.D2
)
解析:当x-2=0,x=2时,x2-1≠0,故选D.
题型二 分式的性质
【例2】
(1)(2011·湛江)化简 a2 - b2 的结果是( a-b a-b
A
)
A.a+b B.a-b C.a2-b2 D.1
解析: - =
=
=a+b.
(2)已知 1 - 1=3,求分式2x-14xy-2y的值.
∴x=
.
由
<0,得a<-5.
故当a<-5时,原方程的解是负数.
规范解答 解:当x≠-1且x≠2时,原方程两边都乘以(x-2)(x+1), 得x2-1-x2+4x-4=2x+a, 2x=a+5,
∴x=
.
由 <0,得a<-5.
又由
≠2,得a≠-1; ≠-1,得a≠-7,
故当a<-5且a≠-7时,原方程的解是负数.
xy
x-2xy-y
解法一:∵ - =3,
∴ =3,y-x=3xy,x-y=-3xy.
原式=
=
=
=
=4.
解法二:∵ - =3,∴xy≠0, ∴原式=
=
=
=
=
=4.
探究提高 1.分式的基本性质是分式变形的理论依据,所有分式变形 都不得与此相违背,否则分式的值改变. 2.将分式化简,即约分,要先找出分子、分母的公因式, 如果分子、分母是多项式,要先将它们分别分解因式,然 后再约分,约分应彻底. 3.巧用分式的性质,可以解决某些较复杂的计算题,可应 用逆向思维,将要求的算式向已知条件“凑”而求得结 果.
基础自测
1.(2011·江津)下列式子是分式的是( B )
A. x 2
B.x+x 1
C. x+y 2
D.x 3
解析:根据分式的定义,分母中必含字母的代数式叫分式.
2.(2011·南充)当分式xx-+12的值为0时,x的值是( B )
A.0
B.1
C.-1
D.-2
解析:当x=1时,分子x-1=0,而分母x+2=3≠0, 所以分式的值为0.
5.分式的混合运算: 在分式的混合运算中,应先算乘方,再将除法化为乘法, 进行约分化简,最后进行加减运算.遇有括号,先算括号 里面的.灵活运用运算律,运算结果必须是最简分式或整 式.
6.解分式方程,其思路是去分母转化为整式方程,要特别注 意验根,使分母为0的未知数的值,是增根,需舍去.
[难点正本 疑点清源]
知能迁移4
(1)(2011·潼南)解分式方程:x+x 1
- 1 =1. x-1
解:方程两边同乘(x+1)(x-1),得
x(x-1)-(x+1)=(x+1)(x-1),
化简,得-2x-1=-1,
解得 x=0.
检验:当x=0时,(x+1)(x-1)≠0,
所以x=0是原分式方程的解.
(2)若方程
x-3= x-2
失误与防范 1.分式的分母不为零,分式才有意义,这又是分式的值为0的前
提.讨论分式的值为0,即要求分母不为0,又要求分子为0, 二者缺一不可.
2.当分式的分子或分母为多项式时,在运算顺序上,相当于使
分子或分母的外面有一个括号,从而把它们分别当成一个整体 看,例如:5· x-,2 应得 5x-2, 而不是 5x-.2 3.分式加减法中的x通+分3 是等值变x+形3,不要在学了x解+分3 式方程后, 两者混淆,把通分变形成去分母了.
组成分式
.
=
=.
将x=2代入 ,得原式= = .
题型四 分式方程的解法
【例4】
解分式方程:x2+5 3x
-
1 x2-x
=0.
解题示范——规范步骤,该得的分,一分不丢!
解:原式=
-
=0,
去分母,5(x-1)-(x+3)=0,
去括号,5x-5-x-3=0, 4x-8=0, 4x=8,x=2. 经检验,x=2是原方程的根. ∴原方程的根是x=2.
3.(2A0.111a·+-金a1华)计算a-B1.1 --aa--aa 11 的结果为( C )
C.-1
D.2
解析: 1 - a = 1-a = a-1 a-1 a-1
=-1.
4.(2011·潜江)化简(
m2 m-2
+4 2-m
)÷(m+2)的结果是(
B
)
A.0
B.1
C.-1
D.(m+2)2
解析:原式=
