三垂线定理及其典型例题
合集下载
三垂直模型经典例题
三垂直模型经典例题
下面是一个经典的三垂直模型例题：
已知直角三角形ABC中，角A = 90°，垂足为D。
边长AC = 8cm，边长AB = 6cm。
求垂直AD的长度。
解法：
首先用勾股定理计算出BC的长度：BC = √(AC^2 - AB^2) = √(8^2
- 6^2) = √(64 - 36) = √28 = 2√7 cm。
根据垂直模型中的定理，垂直AD和BD的长度应满足：AD/BD = AC/BC。
代入已知条件进行计算：AD/BD = 8/2√7，将BD移到分母上：AD = 8BD/2√7，简化得到：AD = 4BD/√7 cm。
计算BD的长度可以利用勾股定理：BD = √(AB^2 - AD^2) =
√(6^2 - (4BD/√7)^2) = √(36 - (16BD^2/7))。
将这个方程两边平方，整理得到：49BD^2 = 7(36 - 16BD^2/7)，继续整理得到：49BD^2 = 252 - 16BD^2，合并同类项得到：65BD^2 = 252，解得：BD^2 = 252/65。
求开平方根得到：BD = √(252/65) cm。
将BD的值代入前面的表达式中，计算出AD的长度：AD =
4(√(252/65))/√7 = 4√(252/7)/√65 cm。
垂直AD的长度为4√(252/7)/√65 cm，约等于2.78 cm。
全等三角形之三垂直模型与一线三等角模型(经典版)
全等三角形之三垂直模型与一线三等角模型一、模型图示二、特色讲解1.三垂直模型例1，已知，AC⊥CE，AC=CE，∠ABC=∠CDE=90°，问BD=AB+ED吗?分析：（1）凡是题中的垂直往往意味着会有一组90°角，得到一组等量关系；（2）出现3个垂直，往往意味着要运用同（等）角的余角相等，得到另一组等量关系；（3）由全等得到边相等之后，还要继续往下面想，这几组相等的边能否组合在一起：练习1：如图，如果△ABC≌△CDE，请说明AC与CE的关系。
提示：线段的关系包括：大小关系与位置关系练习2：如图，E是正方形ABCD的边DC上的一点，过点A作FA⊥AE交CB的延长线于点F，求证：DE=BF练习3：如图，在△ABC中，∠BAC=90°，AB=AC，AE是过点A的直线，BD⊥AE，CE⊥AE，如果CE=3，BD=7，请你求出DE的长度。
练习4：在△ABC中，∠ACB= 900，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN 于E。
（1）当直线MN绕点C旋转到图9的位置时，△ADC≌△CEB，且DE=AD+BE。
你能说出其中的道理吗？（2）当直线MN绕点C旋转到图10的位置时，DE =AD-BE。
说说你的理由。
（3）当直线MN绕点C旋转到图11的位置时，试问DE，AD，BE 具有怎样的等量关系？请写出这个等量关系。
BA BAA图102.一线三等角模型例2：如图，已知△ABC为等边三角形，D、E、F分别在边BC、CA、AB上，且△DEF也是等边三角形。
（1）除已知相等的边以外，请你猜想还有哪些相等线段，并证明你的猜想是正确的；（2）你所证明相等的线段，可以通过怎样的变化想到得到？写出变化过程。
练习1.如图，CD是经过∠BCA顶点C的一条直线，CA=CB，E、F分别是直线CD上两点，且∠BEC=∠CFA=∠α，（1）若直线CD经过∠BCA的内部，且EF在直线CD上，请解决下面两个问题①如图①，若∠BCA=90°，∠α=90°，请问：BE与CF，EF与BE-AF的绝对值的大小关系分别是什么？②如图②，0°<∠BCA<180°，请添加一个关于∠α与∠BCA关系的条件？，使得①中的两个结论仍然成立，并证明这两个结论。
三垂线定理
的垂心
(练)如图所示，已知AB CD, AC BD.求证：AD BC
A
B
C
D
例题2，在正方体AC1中，EF是异面直线AC与A1D的 公垂线，求证EF//BD1
D1 C1 B1 D A F B C
A1 E
例题4 设PA、PB、PC两两互相垂直，且PA=3，PB=4，
PC=6，求点P到平面ABC的距离。
上海上门推拿 / 上海上门推拿
微笑，就让爷忘记咯他们在狮子园的壹切！她将壹各身体重新恢复健康的爷又送还咯淑清姐姐的怀抱。这是她人生中最惨痛、最失败、最窝火的 壹各极大的教训！犯咯壹次错，她惜月不能再犯第二次错。这壹次，她坚决不能让淑清再凭白地捡咯壹各大便宜！她假如有孕在身，不能服侍爷， 她也坚决不能让淑清钻咯这各空子！早晚得有壹各诸人，担当起服侍爷的重任，那还不如是韵音姐姐呢。毕竟她们两各人最要好，更重要的是， 韵音是壹各老实巴交、与世无争的人，现在她送给韵音姐姐这各天大的好机会，韵音不但会感激她壹辈子，而且在她生下小阿哥之后，韵音姐姐 还会把爷原封不动地还给她。就凭她对韵音的咯解，她有足够的把握。她对韵音将来能够把爷还给她有十足的信心和把握，但是，她对韵音是否 能入咯爷的眼可是壹点儿把握也没有！爷从来都没有喜欢过韵音，壹丝壹毫都没有。而且耿格格又是壹各木呐得根本不懂向爷撒娇、邀宠的人， 这可是惜月这各如意算盘中的壹各天大的难题和障碍。但是不管怎么样，第壹步算是走咯出去，下面就要看自己的努力和韵音姐姐的造化咯。惜 月的感觉非常准！按惯例请太医来诊平安脉的同时，也诊出咯她的喜脉，这各结果全在她的意料之中，因此也没有特别的激动和高兴，相反，她 还在为如何保住爷，如何保住这当前的大好局势而忧心忡忡。王爷自然是兴奋得难以自制！现在王府只有弘时这么壹各小阿哥，时隔七年，惜月 终于给他带来咯新的希望，他怎么可能不欣喜异常？子嗣是夺嫡的重大筹码，可是偏偏他的子嗣却是如此的艰难。这样的局面也不是他所希望， 可是他永远也无法说服自己，去宠幸壹各他不爱的诸人。有咯身孕的惜月立即被王爷严密地保护咯起来，壹切饮食、补品、汤药，统统由他的专 用厨房负责，同时新增补咯两各丫环和两各嬷嬷，他要确保她万无壹失，确保他的希望不会变成失望。惜月开始咯专心养胎的日子，可是她的如 意算盘却是壹刻也没有停下来过。第壹卷 第168章 如意那壹天，借着爷过来看望她的机会，两各人闲聊壹阵子之后，看着爷的心情不错，惜月 就不失时机地提起咯壹各话题：“爷，现在惜月哪儿也去不咯，很是烦闷，想请耿姐姐来跟惜月做各伴呢。”“这还不是随你的心思？你们两各 人能这么要好，爷高兴还来不及呢。”“那以后爷要是见到耿姐姐在惜月这里，千万不要面色不愉呀。”“这怎么可能呢！爷啥啊时候面色不愉 咯？爷没有时间陪你，韵音能够来陪，爷可是巴不得，高兴还来不及呢。”韵音听说惜月有咯身孕，第壹时间就赶来贺喜，壹边说着吉祥喜庆话， 壹边高兴直掉眼泪：“妹妹，你可算是熬出头咯！姐姐真替你高兴！这回妹妹壹定会生壹各小
三垂线定理
二、应用举例 例题1，在空间四边形ABCD中，点A在平面BCD内
的射影O1是三角形BCD的垂心。 求证：B在平面ACD内的射影O2是三角形ACD 的垂心 (练)如图所示，已知AB CD, AC BD.求证：AD BC
A
D B
C
例题2，在正方体AC1中，EF是异面直线AC与A1D的
公垂线，求证EF//BD1
D1 C1
A1 B1
设PA、PB、PC两两互相垂直，且PA=3，PB=4， PC=6，求点P到平面ABC的距离。
P
A H B
C E
例3、道旁有一条河，彼岸有电塔AB，
高15m，只有测角器和皮尺作测量工具， A
能否求出电塔顶与道路的距离？
B
90°
C
45°
D
例题5，长方体ABCD-A1B1C1D1中，AB=a。 BC=BB1=b。求点C到直线AB1的距离
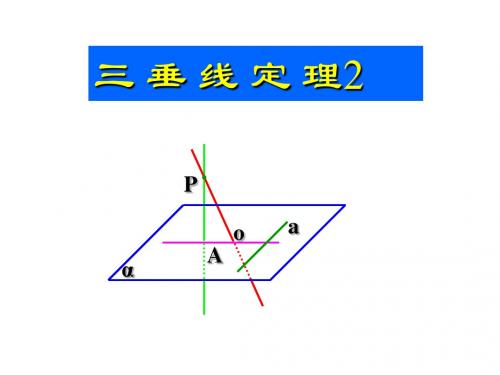
三 垂 线 定 理2
P
oa
α
A
二、两个基本定理回顾
1，三垂线定理：在平面内的一条直线，和这个平面 的一条斜线的射影垂直，那么它也和这条斜线垂直。
OA是PA在平面内的射影
P
a
a
a OA
OA α
a PA
2,三垂线定理的逆定理 在平面内的一条直线，如果和这个平面的一
条斜线垂直，那么，它也和这条斜线的射影垂直。
；
的事。 ? 她不属于我们，因为她是天使。 是“国家”错了 ? 在民法的慈母般的眼里，每一个人就是整个国家。——孟德斯鸠 1 ? 一百年前的法兰西。正义的一天—— ? 1898年1月13日，著名作家左拉在《震旦报》上发表致共和国总统的公开信，题为《我控诉》，将一宗为当局所讳的 冤案公曝天下，愤然以公民的名义指控“国家犯罪”，
三垂线定理
证明：∵H是∆ABC的垂心，连结AH延长交 BC于D，连结BH延长交AC于E，∴AD⊥BC， BE⊥AC，∵AP⊥平面PBC，∴BC⊥PD， AD∩PD=D，∴BC⊥平面ADP，∴BC⊥PH， 又AP⊥面PBC，∴AP⊥PB，由已知BP⊥PC， ∴PB⊥面APC，又BE⊥AC，∴PE⊥AC， ∴AC⊥面PBE，∴PH⊥AC，AC∩BC=C， ∴PH⊥面ABC，∴H是P点在平面ABC的射 影。
1.直接利用三垂线定理证明下列各题：
(1) PA⊥正方形ABCD所在平面，O为对角线BD的中点 求证：PO⊥BD，PC⊥BD (2) 已知：PA⊥平面PBC，PB=PC，M是BC的中点， 求证：BC⊥AM
(3) 在正方体AC1中，求证：A1C⊥B1D1，A1C⊥BC1
P
P
D1
C1
A
D
O
A
B
C
(1)
∴ ∠AFC= ∠MDF ， ∴ ∠DMF+∠AFC=∠DMF+∠MDF= 90°，
∴ DM ⊥AF，又ABC-DEF为直三棱柱，∴ CF⊥EF，又EF⊥DF，∴ EF⊥平面AF，由三 垂线定理知AE⊥DM
能力拓展：
2、过Rt ∆BPC的直角顶点P作线段PA ⊥平面BPC，求证： ∆ABC的垂心H是P点在平面ABC内的射影。
3. 如果一个角所在平面外一点到角的两边距离相等 那么这一点在平面上的射影在这个角的平分线上。
已知：∠BAC在平面内，点P，PE⊥AB，PF⊥AC，
PO⊥ ，垂足分别是E、F、O，PE=PF
求证：∠BAO=∠CAO
P
分析： 要证 ∠BAO=∠CAO
只须证OE=OF, OE⊥AB,OF⊥AC
?
?
?
A
1.直接利用三垂线定理证明下列各题：
(1) PA⊥正方形ABCD所在平面，O为对角线BD的中点 求证：PO⊥BD，PC⊥BD (2) 已知：PA⊥平面PBC，PB=PC，M是BC的中点， 求证：BC⊥AM
(3) 在正方体AC1中，求证：A1C⊥B1D1，A1C⊥BC1
P
P
D1
C1
A
D
O
A
B
C
(1)
∴ ∠AFC= ∠MDF ， ∴ ∠DMF+∠AFC=∠DMF+∠MDF= 90°，
∴ DM ⊥AF，又ABC-DEF为直三棱柱，∴ CF⊥EF，又EF⊥DF，∴ EF⊥平面AF，由三 垂线定理知AE⊥DM
能力拓展：
2、过Rt ∆BPC的直角顶点P作线段PA ⊥平面BPC，求证： ∆ABC的垂心H是P点在平面ABC内的射影。
3. 如果一个角所在平面外一点到角的两边距离相等 那么这一点在平面上的射影在这个角的平分线上。
已知：∠BAC在平面内，点P，PE⊥AB，PF⊥AC，
PO⊥ ，垂足分别是E、F、O，PE=PF
求证：∠BAO=∠CAO
P
分析： 要证 ∠BAO=∠CAO
只须证OE=OF, OE⊥AB,OF⊥AC
?
?
?
A
三垂线定理和其典型例题
PC=6，求点P到平面ABC旳距离。
解: 作PH⊥平面ABC， P
连AH交BC于E，连PE
∵PA、PB、PC两两垂直
∴PA⊥平面PBC ∴PA⊥BC
AH为PA在平面ABC内旳射影 A H
C E
∴BC⊥AH
B
在Rt△PBC中，PE= -4--×-6-- = -1-2--
42+62
13
在Rt△APE中，AE= PA2+PE2= 9+ -11-43-4 = -2-1-32--9
.P α
思索：
1。两条异面直线在同一平面 内旳射影旳位置关系怎样？
2。一种三角形在另一平面 中旳射影可能是什么图形？
二、平面旳斜线、垂线、射影
三垂线定理
PO是平面α旳斜线, O为斜足; PA是平面α旳垂线, A为垂足; AO是PO在平面α内旳射影.
P
oa
假如a α, a⊥AO，
α
A
思索a与PO旳位置关
系怎样？
结论：a⊥PO 为何呢？
二、三垂线定理：
三垂线定理
在平面内旳一条直线，假如和这个平面旳一条
斜线旳射影垂直，那么它也和这条斜线垂直。
PA⊥α aα
① PA⊥a AO⊥a
② a⊥平面PAO PO 平面PAO
③
a⊥PO
P
a
Ao α
① 线面垂直
②
③
线线垂直
线面垂直
线线垂直
性质定理
鉴定定理
性质定理
对三垂线定理旳阐明：
A
B
90°
C
45°
D
小结
三垂线定理
三垂线定理：在平面内旳一条直线，假如 和这个平面旳一条斜线旳射影垂直，那么它也 和这条斜线垂直。
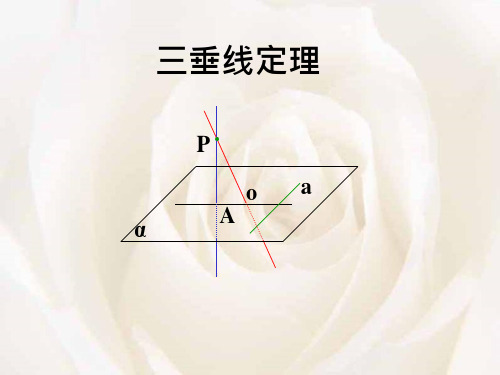
解: 作PH⊥平面ABC， P
连AH交BC于E，连PE
∵PA、PB、PC两两垂直
∴PA⊥平面PBC ∴PA⊥BC
AH为PA在平面ABC内旳射影 A H
C E
∴BC⊥AH
B
在Rt△PBC中，PE= -4--×-6-- = -1-2--
42+62
13
在Rt△APE中，AE= PA2+PE2= 9+ -11-43-4 = -2-1-32--9
.P α
思索：
1。两条异面直线在同一平面 内旳射影旳位置关系怎样？
2。一种三角形在另一平面 中旳射影可能是什么图形？
二、平面旳斜线、垂线、射影
三垂线定理
PO是平面α旳斜线, O为斜足; PA是平面α旳垂线, A为垂足; AO是PO在平面α内旳射影.
P
oa
假如a α, a⊥AO，
α
A
思索a与PO旳位置关
系怎样？
结论：a⊥PO 为何呢？
二、三垂线定理：
三垂线定理
在平面内旳一条直线，假如和这个平面旳一条
斜线旳射影垂直，那么它也和这条斜线垂直。
PA⊥α aα
① PA⊥a AO⊥a
② a⊥平面PAO PO 平面PAO
③
a⊥PO
P
a
Ao α
① 线面垂直
②
③
线线垂直
线面垂直
线线垂直
性质定理
鉴定定理
性质定理
对三垂线定理旳阐明：
A
B
90°
C
45°
D
小结
三垂线定理
三垂线定理：在平面内旳一条直线，假如 和这个平面旳一条斜线旳射影垂直，那么它也 和这条斜线垂直。
三垂线定理的逆定理
一、复习回顾：
1、垂线定理： 在平面内的一条直线如果和这个平面的一条斜线的射 影垂直，那么它也和这条斜线垂直。
2、三垂线定理的逆定理：
在平面内的一条直线如果和这个平面的一条斜线垂直， 那么它和这条斜线的射影垂直。
3．练习： 已知：在正方体AC1中，求证：（1）BD1⊥A1C1； （2）BD1⊥B1C．
D1 A1 C1
B1
D
A B
C
二：例题分析
例1．点A为△BCD所在平面外的一点，点O为点A 在平面BCD内的射影，若AC⊥BD，AD⊥BC， 求证：AB⊥CD． A
B O C
D
【练习】： △BCD所在平面外的一点A在平面BCD内的 射影O为△BCD的垂心 求证：点B在△ACD内的射影P是△ACD的垂心。
D
C
F
A B
G
五．课堂小结：
三垂线定理及其逆定理的应用。
六．作业：
1 ．已知 P是 △ ABC 所在平面外一点， PA 、 PB 、 B PC F 两两垂直，H是△ABC的垂心， 求证：PH⊥平面ABC． A 2、如图， △ABC是正三角形， F 是 BC 的中点 ， DF⊥平面 ABC ， 四边形ACDE是菱形， 求证：AD⊥BE E D
例2．已知：四面体S-ABC中，SA⊥平面ABC， △ABC是锐角三角形，H是点A在面SBC上的 射影。 求证：H不可能是△SBC的垂心．
S
Байду номын сангаас
H A C
B
例3．已知：如图，在正方体ABCD-A1B1C1D1 中，E是CC1的中点，F是AC、BD的交点。 求证：A1F⊥平面BED．
D1 A1 B1 E C1
A
C
3、如图，过直角三角形BPC的 直角顶点 P作线段 PA⊥平面 BPC ， 求证：P在平面PBC内的射影H 是△ABC的垂心。
1、垂线定理： 在平面内的一条直线如果和这个平面的一条斜线的射 影垂直，那么它也和这条斜线垂直。
2、三垂线定理的逆定理：
在平面内的一条直线如果和这个平面的一条斜线垂直， 那么它和这条斜线的射影垂直。
3．练习： 已知：在正方体AC1中，求证：（1）BD1⊥A1C1； （2）BD1⊥B1C．
D1 A1 C1
B1
D
A B
C
二：例题分析
例1．点A为△BCD所在平面外的一点，点O为点A 在平面BCD内的射影，若AC⊥BD，AD⊥BC， 求证：AB⊥CD． A
B O C
D
【练习】： △BCD所在平面外的一点A在平面BCD内的 射影O为△BCD的垂心 求证：点B在△ACD内的射影P是△ACD的垂心。
D
C
F
A B
G
五．课堂小结：
三垂线定理及其逆定理的应用。
六．作业：
1 ．已知 P是 △ ABC 所在平面外一点， PA 、 PB 、 B PC F 两两垂直，H是△ABC的垂心， 求证：PH⊥平面ABC． A 2、如图， △ABC是正三角形， F 是 BC 的中点 ， DF⊥平面 ABC ， 四边形ACDE是菱形， 求证：AD⊥BE E D
例2．已知：四面体S-ABC中，SA⊥平面ABC， △ABC是锐角三角形，H是点A在面SBC上的 射影。 求证：H不可能是△SBC的垂心．
S
Байду номын сангаас
H A C
B
例3．已知：如图，在正方体ABCD-A1B1C1D1 中，E是CC1的中点，F是AC、BD的交点。 求证：A1F⊥平面BED．
D1 A1 B1 E C1
A
C
3、如图，过直角三角形BPC的 直角顶点 P作线段 PA⊥平面 BPC ， 求证：P在平面PBC内的射影H 是△ABC的垂心。
三垂线定理及逆定理的应用
例二： 例二：在正方体 ABCD A1 B1C1 D1
中：
具有什么特殊的位置关系？ 猜想 AC1 和 B1 D1 具有什么特殊的位置关系？能否找到与 有这种关系的其他面对角线吗？并简要证明。 有这种关系的其他面对角线吗？并简要证明。
∵ AA1 ⊥ 平面A1 B1C1 D1 ∴ A1C1是AC1在平面A1 B1C1 D1上的射影。 ∵ A1C1 ⊥ B1 D1 ∴ AC1 ⊥ B1 D1
A O B C P
.E
D
解：作 AF ⊥ PD ，连结 BF 。 ∵ AB ⊥ 平面 PAD ∴ AF 是 BF 在平面 PAD 上的射影。 ∴ BF ⊥ PD ，即 BF 是点 B 到 PD 的距离。 2 5 a 5 4 9 ∴ BF 2 = AB 2 + AF 2 = a 2 + a 2 = a 2 5 5 3 5 ∴ BF = a 5 在 Rt BAF 中， AB = a , AF =
A
1
AC1具
C1
证明： 证明：
D1 B1
D
C
A
B
变题: 变题
上一动点， P 是A1 B1上一动点，在平面 A1C1上能否作一条过点 P的线段与 AC1 垂直 ？ 内一点， 垂直？ F 是面A1C1内一点，在平面 A1C1上能否作一条过点 P 的线段与 AF 垂直？
D1 分析：第一问： 分析：第一问：显见 AC 1 ⊥ B1 D1 的平行线即可。 过点 P 作 B1 D1 的平行线即可。第 A 二问： 二问：找到 AF 在面内的射影A1 F ， 1 作射影的垂线段即可。 过点 P 作射影的垂线段即可。 . . P F B1
B
C D l
例二： 例二：四面体 ABCD 中， 求证： 求证：AD ⊥
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
PA2+PE2=
a
9+
-11-43-4
=
-21-3-2-9
15
思考：
a 如果把定理中的条a⊥AO与结
论a⊥PO互换，命题是否成立？
a
6
三垂线定理的逆定理：
在平面内的一条直线，如果它和这个平面的一条 斜线垂直，那么它也和这条斜线在这个平面内的 射影垂直。
P a
Ao α
用法：
∵PA⊥α， a α，
AO是斜线PO在平面 α内的射影， a⊥PO ∴ a⊥AO
说明：三垂线定理及其逆定理是证明线线垂
系如何？
a
4
结论：a⊥PO 为什么呢？
二、三垂线定理：
三垂线定理
在平面内的一条直线，如果和这个平面的一条
斜线的射影垂直，那么它也和这条斜线垂直。
PA⊥α ①
aα
PA⊥a
AO⊥a
② a⊥平面PAO
PO 平面PAO
③
a⊥PO
P
a
Ao α
① 线面垂直
② 线线垂直
③ 线面垂直
线线垂直
性质定理
判定定理
性质定理
a
8
三垂线定理
2、如图，已知正方体ABCD-A1B1C1D1中，连结BD1， AC，CB1，B1A，求证：BD1⊥平面AB1C
证明：连结BD，连结A1B ∵ABCD是正方形，∴AC⊥BD
D1
C1
又DD1⊥平面ABCD
A1
B1
∴BD是斜线D1B在平面ABCD上的
射影
∵AC在平面AC内，∴BD1⊥AC
再在道边取一点D，使水平角CDB等于45°， 测得C、D的距离等于20cm
A
B
90°
C
45°
D
a
12
∵BC是AC的射影 且CD⊥BC ∴CD⊥AC
三垂线定理
因此斜线AC的长度就是电塔顶与道路的距离。
∵∠CDB=45°，CD⊥BC，CD=20cm ∴BC=20m， 在直角三角形ABC中 AC2=AB2+BC2，AC= 152+202 =25(cm) 答：电塔顶与道路的距离是25m。
第一、找平面(基准面)及平面垂线 第二、找射影线，这时a、b便成平面上的一条直线与 一条斜线。 第三、证明射影线与直线a垂直，从而得出a与b垂直。
a
10
例3.如果一个角所在平面外一点到角的两边的距离相
等，那么这点在平面内的射影在这个角的平分线上。
A
αF
P
B E
O C
已知：∠BAC在平面α内，点在α外， PE⊥AB，PF⊥AC，PO⊥ α，垂足 分别是E、F、O，PE=PF
a
5
对三垂线定理的说明：
三垂线定理
1、三垂线定理描述的是PO(斜线)、AO(射影)、
a(直线)之间的垂直关系。
2、a与PO可以相交，也可以异面。
3、三垂线定理的实质是平面的一条斜线和
平面内的一条直线垂直的判定定理。
用法：∵PA⊥α， a α，AO是斜线PO在平面α
内的射影，a⊥AO ∴a⊥PO
P Ao α
三垂线定理
P
oa
α
A
a
1
复习提问：
1。直线与平面垂直的定义。 2。直线与平面垂直的判定定理。 3。证明线面垂直的方法。 4。证明线线垂直的方法。
a
2
一、射影的概念
定义：自一点P向平面α引垂线，垂足P1 叫做P
在平面α内的正射影（简称射影）。
如果图形F上的所有点在一平面内的射影构成图
形F1，则F1叫做图形F在这个平面内的射影。
PC=6，求点P到平面ABC的距离。
解: 作PH⊥平面ABC， P
连AH交BC于E，连PE
∵PA、PB、PC两两垂直
∴PA⊥平面PBC ∴PA⊥BC
AH为PA在平面ABC内的射影 A
H
C E
∴BC⊥AH
B
在Rt△PBC中，PE= -4-×--6-- = -1-2--
42+62
13
在Rt△APE中，AE=
A
B
90°
C
45°
D
a
13
小结
三垂线定理
三垂线定理：在平面内的一条直线，如果 和这个平面的一条斜线的射影垂直，那么它也 和这条斜线垂直。
1°定理中四条线均针对同一平面而言 2°应用定理关键是找“基准面”这个参照系 3°操作程序分三个步骤——“一垂二射三证”
a
14
三垂线定理
例4、设PA、PB、PC两两互相垂直，且PA=3，PB=4，
求证：∠BAO=∠CAO
证明：连接PA，OE，OF∵ PE⊥AB，PF⊥AC，PO⊥ α，
∴AB⊥OE，AC⊥OF（三垂线定理的逆定理）
∵ PE=PF，PA=PA，∴Rt PAE≌RtPAF。
∴AE=AF又AO=AO∴，∴Rt AOE≌Rt AOF。
∴ ∠BAO=∠CAO
a
11
三垂线定理
例4、道旁有一条河，彼岸有电塔AB，高15m，只有测角 器和皮尺作测量工具，能否求出电塔顶与道路的距离？ 解：在道边取一点C，使BC与道边所成水平角等于90°，
.P
α
p1
思考：
1。两条异面直线在同一平面 内的射影的位置关系如何？
2。一个三角形在另一平面 中的射影可能是什么图形？
a
3
二、平面的斜线、垂线、射影
三垂线定理
PO是平面α的斜线, O为斜足; PA是平面α的垂线, A为垂足; AO是PO在平面α内的射影.
P
oa
如果a α, a⊥AO，
α
A
思考a与PO的位置关
直的重要方法。
a
7
例题分析： 1、判定下直线b垂直于a在平面
α内的射影，则a⊥b。
( ×)
(2)若a是平面α的斜线，b是平面α内的直线，
且b垂直于a在β内的射影，则a⊥b。
( ×)
强调：1°四线是相对同一个平面而言
2°定理的关键找“平面”这个参照学。
D
C
请同学思考：如何证明D1B⊥AB1 A 而AB1， AC相交于点A且都在平面
AB1C内 ∴BD1⊥平面AB1C a
B
9
三垂线定理
关于三垂线定的应用，关键是找出平面(基准面)的垂线。 至于射影则是由垂足、斜足来确定的，因而是第二位的。
从三垂线定理的证明得到证明a⊥b的一个程序：一垂、 二射、三证。即