回归分析的人工神经网络算法模型研究
人工神经网络的研究进展与应用

人工神经网络的研究进展与应用人工神经网络是一种基于神经元模型的计算机模型,它能够通过学习和适应提高自己的性能,从而解决各种复杂的问题。
近年来,随着科学技术的不断进步,人工神经网络的研究和应用也越来越广泛,本文将以此为主题,探讨其研究进展和应用。
一、人工神经网络的发展历程人工神经网络的概念最早可以追溯到1943年,当时生物学家麦卡洛克和数学家皮茨在研究海马的神经元模型时,提出了“神经元网络”的概念。
然而,由于当时计算机技术的不发达,研究进展缓慢,直到20世纪80年代,人工神经网络才开始进入蓬勃发展期。
在接下来的几十年里,人工神经网络不断得到完善和改进。
1986年,加利福尼亚大学教授里夫金首次提出了反向传播算法,从理论上提高了神经网络的学习能力;1998年,Yan LeCun等人在训练卷积神经网络上取得了突破性的进展,为语音识别、图像识别等领域的应用奠定了基础;2006年,西谷和众人提出了深层神经网络,在语音识别、自然语言处理、图像处理等领域取得了重大突破。
二、人工神经网络的应用领域1. 图像识别人工神经网络在图像识别领域的应用非常广泛。
以2012年ImageNet大规模视觉识别挑战赛为例,该比赛采用卷积神经网络进行图像识别,识别准确率达到了85.4%,远高于传统算法。
2. 语音识别人工神经网络在语音识别领域也有广泛的应用。
在过去的十年里,深度神经网络被广泛用于语音识别,取得了显著的进展。
例如,微软研究院的DeepSpeech就是一种深度神经网络模型,能够通过学习进行语音识别并生成相应的文本。
3. 金融分析人工神经网络在金融领域也有广泛的应用。
例如,在股票交易中,人工神经网络能够通过学习历史股价数据,预测未来的股票价格走势。
此外,人工神经网络还可以用于信用评估、风险管理等方面,为金融决策提供有力的辅助。
4. 医学诊断人工神经网络在医学诊断领域也有广泛的应用。
例如,在疾病诊断方面,人工神经网络能够通过学习医学数据,对病情进行准确的判断和诊断。
研究不同变量之间影响关系的算法

研究不同变量之间影响关系的算法
研究不同变量之间影响关系的算法有很多种,以下是一些常用的算法:
1. 相关分析:通过计算变量之间的相关系数来衡量它们之间的线性关系。
常用的相关系数包括Pearson相关系数、Spearman相关系数和Kendall相关系数。
2. 回归分析:通过建立一个数学模型来描述变量之间的关系。
常用的回归分析方法包括线性回归、多元线性回归和逻辑回归。
3. 因子分析:将一组相关的变量转化为几个无关的因子,以减少变量的数量并揭示变量之间的潜在关系。
4. 聚类分析:将样本或变量分成互相相似的组,以揭示变量之间的相似性和差异性。
5. 结构方程模型:通过建立一个结构模型来描述变量之间的关系,并进行模型拟合和参数估计。
6. 神经网络:通过建立一个多层的人工神经网络模型,学习变量之间的复杂关系。
7. 决策树:通过构建一棵树形结构来描述变量之间的条件关系,用于分类和预测。
这些算法可以根据具体的研究问题和数据特点选择和应用。
同时,还可以结合统计方法和机器学习方法进行分析,以获取更准确和全面的结果。
神经网络在回归问题上的应用研究

神经网络在回归问题上的应用研究神经网络是一种模仿人脑神经网络结构和功能而设计的数学模型,用于处理复杂的输入输出关系,近年来在计算机科学领域得到了广泛的应用。
其中,神经网络在回归问题上的应用研究是一个非常重要的方向。
回归问题是指一类针对回归分析的问题,即寻找输入与输出之间的函数关系,通常是一个连续变量做因变量的问题。
为了解决回归问题,传统的方法包括线性回归、多项式回归、岭回归等,并且这些方法在实际应用中得到了广泛的应用。
不过,这些方法存在的限制是需要人为地选择特征和参数,并且不能发现非线性关系。
相比之下,神经网络的优势就在于它可以用于任何形式的输入输出,自动学习关系并发现非线性特征。
现在,神经网络在回归问题上的应用非常广泛。
首先,神经网络可以用于解决多变量的回归问题。
多变量回归是一种更复杂的回归问题,其中存在多个输入变量和一个输出变量。
这种问题通常需要对每个输入变量的影响进行分析,并找到它们与输出变量之间的最佳关系。
神经网络的多层结构可以很好地表示这种关系,并利用反向传播算法进行参数优化。
其次,神经网络也可以用于时间序列预测。
时间序列预测是预测一个连续变量在未来时间段内的走势。
这种问题通常与数据的趋势、周期和季节性有关,因此需要寻找隐藏在数据中的模式。
传统的统计方法往往过于简单,不能充分挖掘数据的信息,而神经网络可以通过窗口滑动来识别这些模式并进行预测。
此外,神经网络也可以用于非参数回归问题。
非参数回归是在没有假定一个具体形式的基函数或先验概率下,对样本空间的连续数据建立回归函数的一种方法。
一个典型的例子是核回归,其中一个核函数(如高斯核)用于评估每个样本与目标之间的距离。
神经网络可以用于非参数回归,通过运用自适应阶段和反向传播算法,可以发现数据中的非线性特征。
最后,神经网络也可以用于局部回归问题。
局部回归是一种回归方法,其中与查询点相邻的训练数据被用来生成局部线性模型,查询点的输出变量是根据这些局部模型的加权平均值生成的。
基于人工神经网络的预测算法研究

基于人工神经网络的预测算法研究人工神经网络(Artificial Neural Network)是一种模拟人脑神经系统工作原理的计算模型,它通过大量的神经元单元之间的连接和相应的加权值,模拟人脑神经元之间的信息传递和处理过程。
基于人工神经网络的预测算法利用这一模型,通过对已有数据进行学习和训练,来预测未来的数据走势和趋势。
本文将围绕基于人工神经网络的预测算法进行研究,讨论其原理、应用、优势和局限性。
首先,我们来介绍基于人工神经网络的预测算法的原理。
人工神经网络由输入层、隐藏层和输出层组成,其中隐藏层可以包含多层。
每个神经元接收来自上一层的输入,并通过加权值和激活函数对输入进行处理,然后将结果传递给下一层。
在预测问题中,输入层通常表示历史数据特征,而输出层表示预测结果。
通过在训练过程中调整神经网络的连接权重,以及选择合适的激活函数和网络结构,使网络能够对输入与输出之间的关系进行建模和预测。
基于人工神经网络的预测算法在多个领域都有广泛的应用。
例如,它可以应用于金融市场预测,通过学习历史行情数据,来预测未来股票价格的走势;它也可以应用于气象预测,通过学习气象观测数据,来预测未来天气的变化;此外,它还可以应用于交通流量预测、销售预测、疾病预测等领域。
基于人工神经网络的预测算法可以为决策提供参考和辅助,帮助人们做出更准确的预测和计划。
相比于传统的统计分析方法,基于人工神经网络的预测算法具有一些优势。
首先,它可以处理非线性关系,而传统方法通常只能处理线性关系;其次,它可以自动学习和提取特征,无需过多人工干预;此外,它对于噪声和缺失数据具有一定的容错性,能够处理部分数据缺失的情况。
因此,基于人工神经网络的预测算法在处理复杂、非线性的预测问题时表现出色。
然而,基于人工神经网络的预测算法也存在一些局限性。
首先,神经网络的训练过程较为耗时,特别是在大规模数据集上进行训练时;其次,网络结构和参数的选择对预测结果的影响较大,需要进行一定的调试和优化;此外,神经网络的黑盒特性使得其内部的判断过程难以解释和理解,缺乏可解释性。
《人工神经网络:模型、算法及应用》习题参考答案

习题2.1什么是感知机?感知机的基本结构是什么样的?解答:感知机是Frank Rosenblatt在1957年就职于Cornell航空实验室时发明的一种人工神经网络。
它可以被视为一种最简单形式的前馈人工神经网络,是一种二元线性分类器。
感知机结构:2.2单层感知机与多层感知机之间的差异是什么?请举例说明。
解答:单层感知机与多层感知机的区别:1. 单层感知机只有输入层和输出层,多层感知机在输入与输出层之间还有若干隐藏层;2. 单层感知机只能解决线性可分问题,多层感知机还可以解决非线性可分问题。
2.3证明定理:样本集线性可分的充分必要条件是正实例点集所构成的凸壳与负实例点集构成的凸壳互不相交.解答:首先给出凸壳与线性可分的定义凸壳定义1:设集合S⊂R n,是由R n中的k个点所组成的集合,即S={x1,x2,⋯,x k}。
定义S的凸壳为conv(S)为:conv(S)={x=∑λi x iki=1|∑λi=1,λi≥0,i=1,2,⋯,k ki=1}线性可分定义2:给定一个数据集T={(x1,y1),(x2,y2),⋯,(x n,y n)}其中x i∈X=R n , y i∈Y={+1,−1} , i=1,2,⋯,n ,如果存在在某个超平面S:w∙x+b=0能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧,即对所有的正例点即y i=+1的实例i,有w∙x+b>0,对所有负实例点即y i=−1的实例i,有w∙x+b<0,则称数据集T为线性可分数据集;否则,称数据集T线性不可分。
必要性:线性可分→凸壳不相交设数据集T中的正例点集为S+,S+的凸壳为conv(S+),负实例点集为S−,S−的凸壳为conv(S−),若T是线性可分的,则存在一个超平面:w ∙x +b =0能够将S +和S −完全分离。
假设对于所有的正例点x i ,有:w ∙x i +b =εi易知εi >0,i =1,2,⋯,|S +|。
供应链管理中的预测算法研究

供应链管理中的预测算法研究随着全球贸易的不断增加,供应链管理越来越成为企业经营和战略规划的重要方面。
在供应链管理中,预测算法被广泛应用于预测需求、库存管理、生产计划以及供应网络优化等方面。
本文将探讨供应链管理中常用的预测算法及其应用。
一、基于时间序列的预测算法基于时间序列的预测算法是目前供应链管理中最常用的预测方法之一。
它是一种通过分析历史数据,预测未来趋势的方法。
时间序列预测算法可以分为两种类型:平稳时间序列和非平稳时间序列。
对于平稳时间序列,最常用的预测方法是ARIMA模型。
ARIMA模型是一种基于差分和自回归移动平均模型的预测方法。
它通过对历史数据进行差分,使序列变为平稳时间序列,然后使用自回归移动平均模型对未来进行预测。
对于非平稳时间序列,最常用的预测方法是趋势指数法。
趋势指数法是一种通过幂函数拟合数据并预测未来趋势的方法。
它可以反映出未来趋势的增减速度和变动幅度,并对未来数据进行预测。
二、基于回归分析的预测算法基于回归分析的预测算法是一种通过分析变量之间的关系,预测未来趋势的方法。
在供应链管理中,基于回归分析的预测算法主要应用于需求预测和价格预测。
对于需求预测,最常用的方法是多元回归分析。
多元回归分析通过分析多个变量和需求之间的线性关系,预测未来需求。
在实际应用中,需求预测模型通常包括历史需求、价格、促销活动等变量。
对于价格预测,最常用的方法是回归分析。
回归分析通过分析价格和市场变量之间的线性关系,预测未来的价格。
在实际应用中,价格预测模型通常包括市场规模、品牌影响力、竞争力度等变量。
三、基于人工神经网络的预测算法基于人工神经网络的预测算法是目前较为热门的预测方法之一。
人工神经网络模型通过模拟人脑的神经网络系统,对数据进行分析和预测。
在供应链管理中,人工神经网络模型主要应用于需求预测和库存管理。
对于需求预测,人工神经网络模型最主要的优势是可以处理非线性关系。
与传统的基于线性回归的预测方法相比,人工神经网络模型不受变量之间的线性关系限制,并且可以处理复杂的非线性关系。
多元线性回归与BP神经网络预测模型对比与运用研究

多元线性回归与BP神经网络预测模型对比与运用研究一、本文概述本文旨在探讨多元线性回归模型与BP(反向传播)神经网络预测模型在数据分析与预测任务中的对比与运用。
我们将首先概述这两种模型的基本原理和特性,然后分析它们在处理不同数据集时的性能表现。
通过实例研究,我们将详细比较这两种模型在预测准确性、稳健性、模型可解释性以及计算效率等方面的优缺点。
多元线性回归模型是一种基于最小二乘法的统计模型,通过构建自变量与因变量之间的线性关系进行预测。
它假设数据之间的关系是线性的,并且误差项独立同分布。
这种模型易于理解和解释,但其预测能力受限于线性假设的合理性。
BP神经网络预测模型则是一种基于神经网络的非线性预测模型,它通过模拟人脑神经元的连接方式构建复杂的网络结构,从而能够处理非线性关系。
BP神经网络在数据拟合和预测方面具有强大的能力,但模型的结构和参数设置通常需要更多的经验和调整。
本文将通过实际数据集的应用,展示这两种模型在不同场景下的表现,并探讨如何结合它们各自的优势来提高预测精度和模型的实用性。
我们还将讨论这两种模型在实际应用中可能遇到的挑战,包括数据预处理、模型选择、超参数调整以及模型评估等问题。
通过本文的研究,我们期望为数据分析和预测领域的实践者提供有关多元线性回归和BP神经网络预测模型选择和应用的有益参考。
二、多元线性回归模型多元线性回归模型是一种经典的统计预测方法,它通过构建自变量与因变量之间的线性关系,来预测因变量的取值。
在多元线性回归模型中,自变量通常表示为多个特征,每个特征都对因变量有一定的影响。
多元线性回归模型的基本原理是,通过最小化预测值与真实值之间的误差平方和,来求解模型中的参数。
这些参数代表了各自变量对因变量的影响程度。
在求解过程中,通常使用最小二乘法进行参数估计,这种方法可以确保预测误差的平方和最小。
多元线性回归模型的优点在于其简单易懂,参数估计方法成熟稳定,且易于实现。
多元线性回归还可以提供自变量对因变量的影响方向和大小,具有一定的解释性。
人工神经网络和随机森林在回归问题中的应用比较
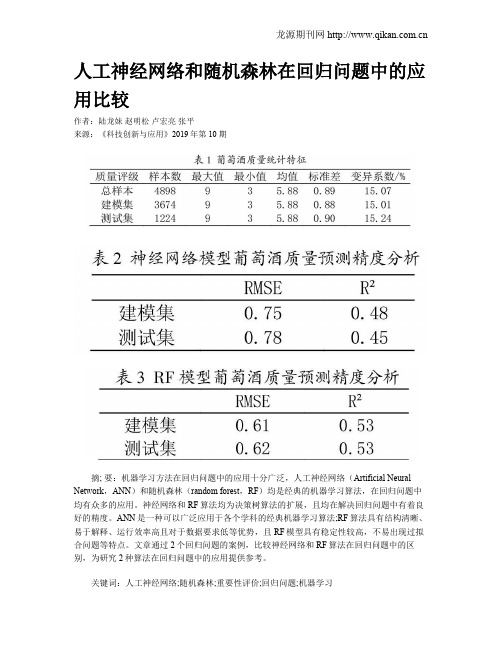
人工神经网络和随机森林在回归问题中的应用比较作者:陆龙妹赵明松卢宏亮张平来源:《科技创新与应用》2019年第10期摘; 要:机器学习方法在回归问题中的应用十分广泛,人工神经网络(Artificial Neural Network,ANN)和随机森林(random forest,RF)均是经典的机器学习算法,在回归问题中均有众多的应用。
神经网络和RF算法均为决策树算法的扩展,且均在解决回归问题中有着良好的精度。
ANN是一种可以广泛应用于各个学科的经典机器学习算法;RF算法具有结构清晰、易于解释、运行效率高且对于数据要求低等优势,且RF模型具有稳定性较高,不易出现过拟合问题等特点。
文章通过2个回归问题的案例,比较神经网络和RF算法在回归问题中的区别,为研究2种算法在回归问题中的应用提供参考。
关键词:人工神经网络;随机森林;重要性评价;回归问题;机器学习中图分类号:TP391.77; ; ; 文献标志码:A 文章编号:2095-2945(2019)10-0031-03Abstract: The machine learning method is widely used in regression. Artificial neural network (ANN) and random forest (RF) are classical machine learning algorithms widely applied in regression problems. Both neural network and RF algorithm are extensions of decision tree algorithm, and both of them have good accuracy in solving regression problems. ANN is a classical machine learning algorithm which can be widely used in various disciplines, RF algorithm has the advantages of clear structure, easy interpretation, high running efficiency and low data requirements, and the RF model has high stability. It is not easy to have the characteristics of over-fitting problem and so on. In this paper, two cases of regression problems are used to compare the difference between neural network and RF algorithm in regression problems, which provides a reference for the study of the application of the two algorithms in regression problems.Keywords: artificial neural network; stochastic forest; importance evaluation; regression problem; machine learning1 概述随着计算机和信息技术不断地发展,大数据的到来使机器学习算法成为解决实际问题的重要工具,对于机器学习算法的研究也成为了热门的研究方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∑p
j=
1
2 kj
=
1,
{f
k} 是未知“光滑”函数。
·46 ·
3. 单层神经网络模型 单层神经网络模型是一类较简单的模型, 其在医学中的应用有人曾进行探讨。 单层神经网络模型为: o= ( W X ) ( 2. 8) 这里 的定义如前, 网络结构见图 4。
图 4 单层网络示意图
这里 W 连接输入层到输出层的权重向量, X 是输入向量。
人工神经网络理论的崛起, 首先在信息学 科得到了广泛的应用, 而在统计理论及应用方 面的成果还尚少。本文就此方面的研究情况进 行了初步探讨, 对单层神经网络、BP L 神经网 络和 P PL 神经网络在回归分析中的应用情况 进行了比较分析。
神经网络模型的概念及基本组成
神经网络是一种模拟人类大脑思维方式的 数学模型, 它具有学习、记忆、纠错的功能。人的 大脑是由多达 1011 个不同的种类的神经元及神
8. J . H . Friedman. Classif icat ion and mul ti ple reg res sion t hr ou gh project ion pur suit , Depart ment of St ati st ics , St anf ord U niver sit y. 1992
在神经网络的研究历程中, Hopf iel d 将能 量函数引入对称、反馈的网络结构, 研究联想记 忆 和 最 优 化 计 算: Rumelhar t 、H int on 和 Williams 提出的反向传播算法训练多层前传网 络以逼近期望的连续函数, 是永远值得记载的 重大事件。正是这两项研究唤起了人们对神经 网络的研究热情, 促进了神经网络迅猛发展。虽 然自此以后很难评价神经网络的那一项研究标 志着新的重大突破, 但我们可以越来越清楚地 看到, 神经网络理论的研究正越来越深化, 其框 架体系日趋完善; 神经网络硬件的快速发展以 及在各个领域中应用的成功经验, 正促使它向 实用化转变; 同时, 神经网络软件和专用处理器 的出现, 也使得神经计算机不再是神话〔2〕。
2. 虽然人工神经网络技术可用于很多回 归问题, 但由于该模型在建立时其计算复杂度 比较高, 因而对于较简单的回归模型不宜采用 此方法, 如有人采 用神经 网络模 型与 log ist ic 回归模型进行对比研究; 用神经网络对多变量 自由回归模型进行探讨等等。
3. 对于非线性回归问题, 采用传统的方法 往往存在最优模型的选择问题。这时, 可考虑采 用 BPL 模型或 PPL 模型, 因为神 经网络模型 对非线性问题具有很强的逼近作用。
2. 徐 铮, 等. 神 经网络 理论与 应用. 华 南理工 大学出 版社, 1994
3. R . Hecht -N ielsen. T heory of b ack-propagat ion neural net w orks . Proc. Int ′l Joint Conf . on N eural N et w orks 1989; 2 ( 1) : 593
式中 i 为 0 或 1, 是 单 位 阶 梯 函 数 式, 即
H eaverside 函数:
(x) = 1 x 0 0 x< 0
( 1. 2)
权 w ij 代表从神经元 j 连接到神经元 i 的 突触强度, 它可以是正的, 也可以是负的, 分别 相应于兴奋性突触和抑制性突触。 i 是单元 i 的阈值。
能量函数为:
q
∑ E =
W iE( yi - y i ) 2
i= 1
q
∑ =
W iE 〔y i - E〔y i〕 -
i= 1
m
∑ ik f k(
T k
x
)
〕2
k= 1
( 3. 2)
这里 W i = 1/ V ar( y i)
以上网络的学 习算法其过程 是非常复杂
的, 目前在理论上还不太完善。即使都采用最速
算法。
1. BPL 网络算法模型〔5, 6〕
BP L 网络模型的几何结构见图 2。
这里, 网络的学习模型为两层感知器, 其数
学模型为:
m
p
∑ ∑ y i =
ikf k〔 w kj x j - w k0 〕
k= 1
j= 1
m
p
∑ ∑ =
ik 〔 w kj x j - w k0〕 ( 2. 4)
k= 1
经纤维等组成的树状网络结构。人们思考的过 程是信号从一个神经元沿着神经纤维向一个突 触上的另一神经元传输的过程, 它是一个复杂 的化学反应过程。1943 年 M cCulloch 和 Pit t s 提出将神经元看成一个二进制阈值元件的简单 模型, 简称 M -P 模型( 图 1) 〔3〕。
图 1 M -P 神经元模型 示意图
·44 ·
中国卫生统计 1998 年第 15 卷第 5 期
回归分析的人工神经网络算法模型研究
第三军医大学( 400038) 易 东 王文昌 张 蔚 许汝福
人工神经网络或神经计算机计算是近十几 年来发展极为迅速的一门边缘学科。它在信号 处理、模式识别、智能控制等领域中越来越多的 成功应用是令人鼓舞的, 即使是最初持观望态 度的人也不得不逐渐放弃对它的怀疑。神经网 络对众多学科的包容性、应用范围的广泛性以 及理论分析方法的多样性是前所未有的〔1〕。
j= 1
k = 1, 2, …m i = 1, 2…q
w k0 是 第 k 个隐含层的 神经元的偏 移项,
w kj 是连接输入层的 第j 个神经元 与隐含层的
·45 ·
图 2 BPL 神经网络算法结构示意图
第 k 个神经元的权重, ik 是连接输出层的第 i 个神经元与隐含层的第 k 个神经元的权重, f k 是非线性激励函数, 通常情况下 f k 取单调递增 的归一化函数 ( z )
5. G . Cybenko. A pproxi mat ion by superposit ion of a s igmoid f unct ion . U nivers it y of Illi nois, D ept . of Elect and Comput er E ngr. , Tech nical Report 1989: 856
(z) =
1 1 + e- z
( 2. 5)
这时, 得到{ gi( x ) , i = 1, 2, …q} 的逼近为:
m
p
∑ ∑ gi ( x ) =
ik 〔 w kj x j - w k0〕 ( 2. 6)
k= 1
j= 1
2. PP L 神经网络算法模型〔7, 8〕
图 3 P PL 神经网络算法结构示意图
回归关系的神经网络算法模型
迄今为止, 神经网络在回归分析中的应用 研究还不太深入, 其有效的方法尚少。为了从广 泛的意义上讨论神经网络算法模型, 这里, 我们 仅就一种广义的回归模型进行讨论: 即多变量 自由回归模型〔4〕。
( y l, x l) = ( y l1, yl2 , …y lq, x l1, x l2 , …x lp )
6. K . Hornik . M ult ilayer f eedf or ward net w orks are U niversal approxim at ions. N eural N et w orks , 1989; 2( 5) : 359
7. J . H. Friedman and W. S tu et zle. Projection purs uit regress ion . Journal of t he A merican St atis t ical A ssociat ion, 1981; 76( 376) : 817
l = 1, 2, …n
( 2. 1)
其中{ y l} 是所谓的 多元反应向量, { x l} 为
独立变量或“载体”
y li = gi( x l) + li
l = 1, 2, …n; i = 1, 2…q ( 2. 2)
{ gi } 为未知光滑的非参函数, li 是独立同
分布的随机变量, E〔li 〕= 0
M -P 模型推动了人们对大脑 中神经网络 建模的研究。从神经生理学的观点来看, 这些模
型过于简单, 不过他们对于认识生物“计算”的 原则仍是很有价值的。
具体地说, M -P 模型神经元计算来自其他 单元输出的加权和, 然后视该加权和是低于还
是高于一阈值而输出 0 或 1:
∑ S ( t + 1) = 〔 w ij Sj ( t) - i〕( 1. 1) j
4. J . N . Hw ang, Li D , M art in an d J. S chimert . Project ion purs uit l earning net w ork f or regression . E ngineering A ppl ic. A rt if . Int ell, N ew York : Pergamon Press Lt d 1992; 5( 3) : 193
M -P 模型神经元虽然很简单, 但却是一种
很强的计算模型。M cCulloch 和 P it t s 证明, 由 这种神经元组成的同步系统, 原则上讲能够进
行普通的计算, 只要适当地选择权 w ij , 也就是
说一般普通数字计算机能做的, M -P 模型系统 也能做到。
在实际应用中常用的神经网络模型通常包 含一个输入层、一个或几个隐含层和一个输出 层, 各层中对数据的处理单位称为处理单元, 其 信息传递过程为由一个输入层到输出层的单向 传递。
下降法, 但各种变形方法迄今仍是研究的热门,
且没有绝对好的方法。
讨 论
1. 从本质上讲, 回归分析是一种追溯历史 资料, 建立变量在数量上依赖关系的方法论。而
