lingo习题
数学建模lingo软件经典例题

客户 1
客户 2
客户 3
客户 4
客户 5
客户 6
员工 1
20
15
16
5
4
7
员工 2
17
15
33
12
8
6
员工 3
9
12
18
16
30
13
员工 4
12
8
11
27
19
14
员工 5
未服务
7
10
21
10
32
员工 6
未服务
未服务
未服务
6
11
13
5、设某企业拥有两个工厂甲和乙、四个销售超市和三个仓库。工厂产量分别为 9,8 个单位。四个顾客需求量分
别为 3,5,4,5 个单位。工厂到仓库、仓库到超市的运费单价如下表。问如何安排总运费最少的运输方案。
工厂 1
工厂 2
超市 1
超市 2
超市 3
超市 4
仓库 1
1
3
5
7
——
——
仓库 2
2
1
9
6
7
——
仓库 3
——
2
——
6
7
4
6、某公司有 6 个建筑工地要开工,每个工地的位置(用平面坐标 ( a, b)表示,距离单位为千米)及水泥的日用
量 d (用量单位为吨)由下表给出。目前有两个临时料场位于 P (5,1) 和 Q( 2, 7),日储量各有 20 吨。
1
2
3
4
5
6
a
1.25
8.75
0.5
5.75
3
lingo例题

例1.1.1某工厂有两条生产线,分别用生产M 和P 两种型号的产品,利润分别为200元/个和300元/个,生产线的最大生产能力分别为每日100和120,生产线每生产一个M 产品需要1个劳动日(1个工人工作8小时成为1个劳动日)进行调试、检测等工作,而每个P 产品需要2个劳动日,该厂工人每天共计能提供160劳动日,假如原材料等其他条件不受限制,问应如何安排生产计划,才能使获得的利润最大?解:设两种产品的生产量分别为1x 和2x ,则目标函数 12max 200300z x x =+约束条件 1212100,120,2160,0,1,2.i x x x x x i ≤⎧⎪≤⎪⎨+≤⎪⎪≥=⎩ 例1.1.2 基金的优化使用(2001年数学建模竞赛C 题)假设某校基金会得到了一笔数额为M 万元的基金,打算将其存入银行,校基金会计划在n 年末仍保留原基金数额.银行存款税后利率见表元,5n =年的情况下设计具体存款方案.解:分析:假定首次发放奖金的时间是在基金到位后一年,以后每隔一年发放一次,每年发放的时间大致相同,校基金会希望获得最佳的基金使用计划,以提高每年的奖金额,且在n 年末仍保留原基金数额M ,实际上n 年中发放的奖金额全部来自于利息。
如果全部基金都存为一年定期,每年都用到期利息发放奖金,则每年的奖金数为50000.01890⨯=万元,这是没有优化的存款方案。
显然,准备在两年后使用的款项应当存成两年定期,比存两次一年定期的收益高,以此类推。
目标是合理分配基金的存款方案,使得n 年的利息总额最多。
定义:收益比a =(本金+利息)/本金。
于是存2年的收益比为21 2.16%2 1.0432a =+⨯=。
按照银行存款税后利率表计算得到各存款年限对应的最优收益比见表(1) 一次性存成最长期,优于两个(或两个以上)比较短期的组合(中途转存)(2) 当存款年限需要组合时,收益比与组合的先后次序无关。
建立模型 把总基金M 分成5+1份,分别用123456,,,,,x x x x x x 表示,其中12345,,,,x x x x x 分别存成15 年定期,到期后本息合计用于当年发放奖金,6x 存5年定期,到期的本息合计等于原基金总数M 。
lingo模型参考习题
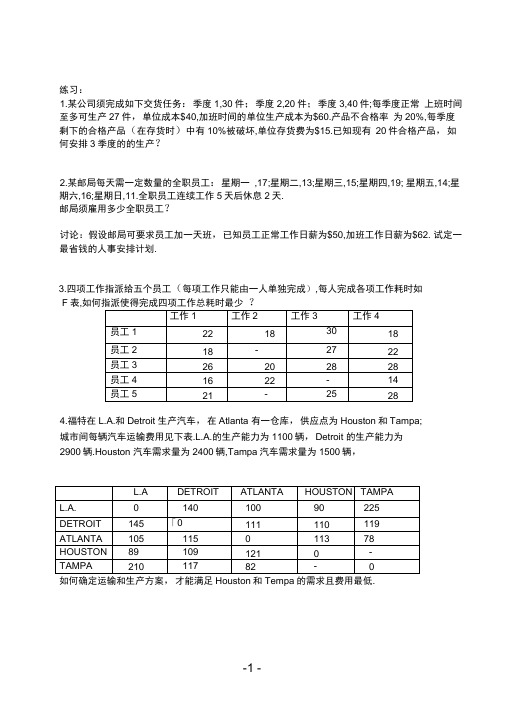
练习:1.某公司须完成如下交货任务:季度1,30件;季度2,20件;季度3,40件;每季度正常上班时间至多可生产27件,单位成本$40,加班时间的单位生产成本为$60.产品不合格率为20%,每季度剩下的合格产品(在存货时)中有10%被破坏,单位存货费为$15.已知现有20件合格产品,如何安排3季度的的生产?2.某邮局每天需一定数量的全职员工:星期一,17;星期二,13;星期三,15;星期四,19; 星期五,14;星期六,16;星期日,11.全职员工连续工作5天后休息2天.邮局须雇用多少全职员工?讨论:假设邮局可要求员工加一天班,已知员工正常工作日薪为$50,加班工作日薪为$62. 试定一最省钱的人事安排计划.3.四项工作指派给五个员工(每项工作只能由一人单独完成),每人完成各项工作耗时如F表,如何指派使得完成四项工作总耗时最少4.福特在L.A.和Detroit 生产汽车,在Atlanta 有一仓库,供应点为Houston和Tampa;城市间每辆汽车运输费用见下表.L.A.的生产能力为1100辆,Detroit 的生产能力为2900辆.Houston 汽车需求量为2400辆,Tampa汽车需求量为1500辆,如何确定运输和生产方案,才能满足Houston和Tempa的需求且费用最低.5.设有三个化肥厂供应四个地区的农用化肥.假定等量的化肥在这些地区使用效果相同.各化肥厂年产量,各地区年需要量及从各化肥厂到各地区运送单位化肥的运价(万元/6」ndianapolis 航空公司计划每天从Indianapolis 飞6个航班,计划目的地为:New试帮该公司确定航线和相应的航班次数7.某种机器可在高低两种不同的负荷下进行生产,设机器在高负荷下生产的年产量函数为:y=8x,(x:投入生产的机器台数),年完好率为0.7;机器在低负荷下生产的年产量函数为:y=5x,(x:投入生产的机器台数),年完好率为0.9;假定开始生产时完好的机器数量为1000台,试问每年如何安排机器在高,低负荷下的生产,使在五年内生产的产品总产量最咼.讨论:如果5年末完好机器数必为500台,又将如何?8.某工厂要对一种产品制定今后四个时期的生产计划,据估计在今后四个时期内,市场对于该产品的需求量如表所示,假定该厂生产每批产品的固定成本为3(千元),若不生产为0;每单位产品成本为1(千元);每个时期生产能力所允许的最大生产批量为不超过6个单位;每个时期末未售出的产品,每单位需存储费0.5(千元).还假定在第一个时期的初始储存量为0,第四个时期之末的库存量也为0.试问如何安排各个时期的生产与库存,才能在满足市场需要的条件下,使总成本最小.9. Bran east 航空公司须为每天飞行于New York和Chicago的航班配备空姐。
Lingo精选题目及参考答案

Lingo 精选题目及答案答题要求:将Lingo 程序复制到Word 文档中,并且附上最终结果。
1、简单线性规划求解(目标函数)2134maxx x z += s.t.(约束条件)⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0,781022122121x x x x x x x2、整数规划求解219040Max x x z +=⎪⎩⎪⎨⎧≥≤+≤+0,702075679212121x x x x x x 3、0-1规划求解Max 432215.18.04.0x x x x f +++=10106234321≤+++x x x x10,,,4321或=x x x x4、非线性规划求解||4||3||2||min 4321x x x x z +++=s.t. ⎪⎪⎩⎪⎪⎨⎧-=+--=-+-=+--2132130432143214321x x x x x x x x x x x x5、集合综合应用产生一个集合5052--=x x y ,(10,...,2,1=x ),求y 前6个数的和S 1,后6个数的和S 2,第2~8个数中的最小值S 3,最大值S 4。
6、综合题要求列出具体的目标函数和约束条件,然后附上Lingo 程序和最终结果。
6.1 指派问题有四个工人,要指派他们分别完成4项工作,每人做各项工作所消耗的时间如下表:问指派哪个人去完成哪项工作,可使总的消耗时间为最小?6.2 分配问题某两个煤厂A1,A2每月进煤数量分别为60t和100t,联合供应3个居民区B1,B2,B3。
3个居民区每月对煤的需求量依次分别为50t,70t,40t,煤厂A1离3个居民区B1,B2,B3的距离依次分别为10km,5km,6km,煤厂A2离3个居民区B1,B2,B3的距离分别为4km,8km,12km。
问如何分配供煤量使得运输量(即t·km)达到最小?1、model:max=4*x1+3*x2;2*x1+x2<10;x1+x2<8;x2<7;end2、model:max=40*x1+90*x2;9*x1+7*x2<56;7*x1+20*x2<70;@gin(x1);@gin(x2);end3、model:max=x1^2+0.4*x2+0.8*x3+1.5*x4;3*x1+2*x2+6*x3+10*x4<10;@bin(x1); @bin(x2);@bin(x3); @bin(x4);end4、model:max=@abs(x1)+2*@abs(x2)+3*@abs(x3)+4*@abs(x4);x1-x2-x3+x4=0;x1-x2+x3-3*x4=1;x1-x2-2*x3+3*x4=-1/2;end5、model:sets:jihe/1..10/:y;ss/1..4/:S;endsets!由于y和s中部分有负数,所以要先去掉这个约束;@for(jihe:@free(y));@for(ss(i):@free(S));!产生元素;@for (jihe(x):y(x)=x^2-5*x-50); S(1)=@sum (jihe(i)|i#le#6:y(i)); S(2)=@sum (jihe(i)|i#ge#5:y(i));S(3)=@min (jihe(i)|i#ge#2 #and# i#le#8:y(i)); S(4)=@max (jihe(i)|i#ge#2 #and# i#le#8:y(i)); end6.1、设:第i 个工人做第j 项工作用时ij t ,标志变量ij f 定义如下:⎩⎨⎧=其他件工作个工人去做第指派第01j i f ijmin∑∑==⨯4141i j ij ijt fs.t. 141=∑=i ijf()4,3,2,1=j 每份工作都有一人做∑==411j ijf()4,3,2,1=i 每人都只做一项工作model : sets :work/A B C D/;worker/jia yi bing ding/; time(worker,work):t,f; endsets!目标函数可以用[obj]标志出,也可以省略;[obj] min =@sum (time(i,j):t(i,j)*f(i,j)); data :!可以直接复制表格,但是在最后要有分号; t=; e !每份工作都有一人做;@for (work(j):@sum (time(i,j):f(i,j))=1); !每人都只做一项工作;@for (worker(i):@sum (time(i,j):f(i,j))=1); !让f 取0-1值,此条件可以省略;!@for(time(i,j):@bin(f(i,j))); end6.2设:煤厂进煤量i s ,居民区需求量为i d ,煤厂i 距居民区j 的距离为ij L ,煤厂i 供给居民区j 的煤量为ij g那么可以列出如下优化方程式∑∑==⨯=3121min j i ij ij L gs.t ()3,2,121==∑=j d gi jij()2,131=≤∑=i s gj iijmodel : sets :supply/1,2/:s; demand/1,2,3/:d;link(supply,demand):road,sd; endsets data :road=10 5 6 4 8 12; d=50 70 40; s=60 100; enddata[obj] min =@sum (link(i,j):road(i,j)*sd(i,j)); @for (demand(i):@sum (supply(j):sd(j,i))=d(i)); @for (supply(i):@sum (demand(j):sd(i,j))<s(i));end1.线性规划模型。
Lingo精选题目及答案

Lingo 精选题目及答案答题要求:将Lingo 程序复制到Word 文档中,并且附上最终结果。
1、简单线性规划求解(目标函数)2134maxx x z += s.t.(约束条件)⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0,781022122121x x x x x x x2、整数规划求解219040Max x x z +=⎪⎩⎪⎨⎧≥≤+≤+0,702075679212121x x x x x x 3、0-1规划求解Max 432215.18.04.0x x x x f +++=10106234321≤+++x x x x10,,,4321或=x x x x4、非线性规划求解||4||3||2||min 4321x x x x z +++=s.t. ⎪⎪⎩⎪⎪⎨⎧-=+--=-+-=+--2132130432143214321x x x x x x x x x x x x5、集合综合应用产生一个集合5052--=x x y ,(10,...,2,1=x ),求y 前6个数的和S 1,后6个数的和S 2,第2~8个数中的最小值S 3,最大值S 4。
6、综合题要求列出具体的目标函数和约束条件,然后附上Lingo 程序和最终结果。
6.1 指派问题6.2 分配问题某两个煤厂A1,A2每月进煤数量分别为60t和100t,联合供应3个居民区B1,B2,B3。
3个居民区每月对煤的需求量依次分别为50t,70t,40t,煤厂A1离3个居民区B1,B2,B3的距离依次分别为10km,5km,6km,煤厂A2离3个居民区B1,B2,B3的距离分别为4km,8km,12km。
问如何分配供煤量使得运输量(即t·km)达到最小?1、model:max=4*x1+3*x2;2*x1+x2<10;x1+x2<8;x2<7;end2、model:max=40*x1+90*x2;9*x1+7*x2<56;7*x1+20*x2<70;@gin(x1);@gin(x2);end3、model:max=x1^2+0.4*x2+0.8*x3+1.5*x4;3*x1+2*x2+6*x3+10*x4<10;@bin(x1); @bin(x2);@bin(x3); @bin(x4);end4、model:max=@abs(x1)+2*@abs(x2)+3*@abs(x3)+4*@abs(x4);x1-x2-x3+x4=0;x1-x2+x3-3*x4=1;x1-x2-2*x3+3*x4=-1/2;end5、model:sets:jihe/1..10/:y;ss/1..4/:S;endsets!由于y和s中部分有负数,所以要先去掉这个约束;@for(jihe:@free(y));@for(ss(i):@free(S));!产生元素;@for (jihe(x):y(x)=x^2-5*x-50); S(1)=@sum (jihe(i)|i#le#6:y(i)); S(2)=@sum (jihe(i)|i#ge#5:y(i));S(3)=@min (jihe(i)|i#ge#2 #and# i#le#8:y(i)); S(4)=@max (jihe(i)|i#ge#2 #and# i#le#8:y(i)); end6.1、设:第i 个工人做第j 项工作用时ij t ,标志变量ij f 定义如下:⎩⎨⎧=其他件工作个工人去做第指派第01j i f ijmin∑∑==⨯4141i j ij ijt fs.t. 141=∑=i ijf()4,3,2,1=j 每份工作都有一人做∑==411j ijf()4,3,2,1=i 每人都只做一项工作model : sets :work/A B C D/;worker/jia yi bing ding/; time(worker,work):t,f; endsets!目标函数可以用[obj]标志出,也可以省略;[obj] min =@sum (time(i,j):t(i,j)*f(i,j)); data :!可以直接复制表格,但是在最后要有分号; t=; e !每份工作都有一人做;@for (work(j):@sum (time(i,j):f(i,j))=1); !每人都只做一项工作;@for (worker(i):@sum (time(i,j):f(i,j))=1); !让f 取0-1值,此条件可以省略;!@for(time(i,j):@bin(f(i,j))); end6.2设:煤厂进煤量i s ,居民区需求量为i d ,煤厂i 距居民区j 的距离为ij L ,煤厂i 供给居民区j 的煤量为ij g那么可以列出如下优化方程式∑∑==⨯=3121min j i ij ij L gs.t ()3,2,121==∑=j d gi jij()2,131=≤∑=i s gj iijmodel : sets :supply/1,2/:s; demand/1,2,3/:d;link(supply,demand):road,sd; endsets data :road=10 5 6 4 8 12; d=50 70 40; s=60 100; enddata[obj] min =@sum (link(i,j):road(i,j)*sd(i,j)); @for (demand(i):@sum (supply(j):sd(j,i))=d(i)); @for (supply(i):@sum (demand(j):sd(i,j))<s(i));end1.线性规划模型。
lingo题目与答案(附程序)

Lingo软件题目与答案1.一奶产品加工厂用牛奶生产A1,A2两种奶产品,1桶牛奶可以在甲类设备上用12h加工,成3kg A1,或者在乙类设备上用8h加工成4kg A2。
根据市场需求,生产的A1,A2全部能售出,且每千克A1获利24元,每千克A2获利16元。
现在加工厂每天能得到50桶牛奶供应,每天正式工人的劳动时间为480h,并且甲类设备每天最多加工100kg A1,乙类设备的加工时间没有限制,讨论以下问题1)若35元可以买一桶牛奶,做这项投资是否值得?若投资,每天最多购买多少桶牛奶?2)若聘用临时工人以增加劳动时间,付给临时工人的工资最多是多少?3)由于市场需求变化,每千克A1的获利增加到30元,是否改变原有的生产计划?Lingo程序:model:max=72*x+64*y;x+y<50;12*x+8*y<480;3*x<100;end2.一汽车厂生产小、中、大三种类型的的汽车,已知各类型每辆车对钢材、劳动时间的需求,利润以及每月工厂钢材、劳动时间如下表。
1)制定生产计划,使工厂利润最大;2)若生产某类型车,则至少需生产80辆,求改变后的生产计划。
3.建筑工地的位置(a,b)和水泥日用量d如下表,目前有两个临时料场位于P(5,1),Q(2,7),日储量各有20t。
1)求从P,Q两料场分别向各工地运送多少吨水泥,使总的吨公里数最小;2)现打算舍弃原有料场,新建两个料场A,B,求新料场的位置,使新的吨公里数最小,此时与P,Q相比能节省多少吨公里。
4.设从4个产地Ai往3个销地Bj运送物资,产量、销量和单位运费如下表,求总运费最少的运输方案和总运费。
Lingo程序:Model:sets:warehouse/1..3/:a;customer/1..4/:b;link(warehouse,customer):c,x;endsetsdata:a=30,25,21;b=15,17,22,12;c=6,2,6,7,4,9,5,3,8,8,1,5;enddata[OBJ]min=@sum(link:c*x);@for(warehouse(i): @sum(customer(j):x(i,j))<a(i));@for(customer(j):@sum(warehouse(i):x(i,j))=b(j));end5.求下图中v1到v11的最短路Lingo程序:Model:sets:cities/1..11/;roads(cities,cities):p,w,x; endsetsdata: !半连通图和权图;p=0 1 1 1 0 0 0 0 0 0 00 0 1 0 1 0 0 0 0 0 0 0 1 0 1 1 1 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 0 1 0 1 0 0 0 0 1 1 0 1 0 0 1 1 0 0 0 0 0 1 0 0 0 1 0 10 0 0 0 1 1 1 1 0 1 10 0 0 0 0 0 1 0 1 0 10 0 0 0 0 0 0 1 1 1 0;w=0 2 8 1 0 0 0 0 0 0 02 0 6 0 1 0 0 0 0 0 08 6 0 7 5 1 2 0 0 0 01 0 7 0 0 0 9 0 0 0 00 1 5 0 0 3 0 2 9 0 00 0 1 0 3 0 4 0 6 0 00 0 2 9 0 4 0 0 3 1 00 0 0 0 2 0 0 0 7 0 90 0 0 0 9 6 3 7 0 1 20 0 0 0 0 0 1 0 1 0 40 0 0 0 0 0 0 0 9 2 4;enddatan=@size(cities);min=@sum(roads:w*x);@for(cities(i)|I # ne # 1 # and # I # ne # n: @sum(cities(j):p(i,j)*x(i,j))=@sum(cities(j):p(j,i)*x(j,i)));@sum(cities(j):p(1,j)*x(1,j))=1;end6.露天矿里有若干个爆破生成的石料堆,每堆称为一个铲位,每个铲位已预先根据铁含量将石料分成矿石和岩石。
Lingo考试
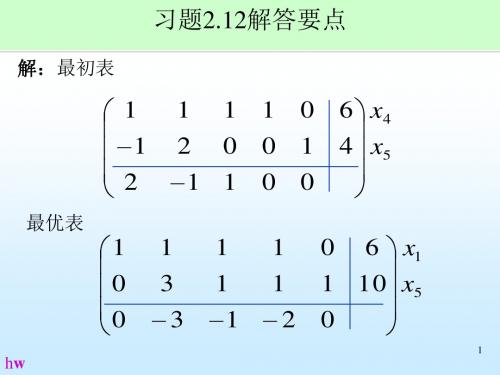
解:最初表
1 1 1 1 2 0 2 1 1
最优表
1 0 0 1
0 1 0 0
6 x4 4 x5 6 x1 1 10 x5 0
1
1 0 0
hw
1 3 3
1
1 1 1 2
习题2.12(a)
1 0 1 0 1 最优基 B 1 1 , 其逆 B 1 1 (a) 因x1是基变量,由最优表可得
5
0 2/3 0 2/3 1 1/ 3 0 5/3
*
新的最优值
z 28 / 3
习题2.16(a)
解:最初表
3 5 1 0 450 x4 6 3 4 5 0 1 300 x 5 30 10 40 0 0 最优表 1 1/ 3 0 1/ 3 1/ 3 50 x1 1 1 1/ 5 2 / 5 30 x3 0 0 20 0 2 6
1 50 b1 3 1 B b 0 30 1 b 1 5 得 150 b1 150,所以雇佣150h为宜。
hw
9
最优生产计划:A、C分别生产50、30件,不生产B 最大利润为2700元
6
hw
习题2.16(b)
因x1是基变量,由最优表可得
1 1 1 20 1 2 1 6 1 0 3 3 3
从而
6 1 18
即当 24 C1 48 时, 上述最优计划不变;
当 C3 (, 2] 时,问题的最优解不变 。
hw
2
习题2.12(b)
6 1 0 1 6 1 由 10 1 1 0 10 0 1 得 1 6
lingo习题及答案
第一题:一、摘要本文是一篇关于基金的使用计划模型。
在现实经济高速发展的背景下,人们越来越清醒地意识到:一个合理的数学应用模型对于现今生产、投资、规划等实际应用项目的重要性。
本文所建立的存款模型就是个很好的例子,此模型最终要解决的是选择最佳基金使用计划,使得学校基金会能够有充分的资金在基金会运转。
这个模型的解决是我们更清楚掌握了最优化模型的解决方法及LINGO软件求解线性规划的方法。
二、问题的提出某校基金会有一笔数额为M元的基金,打算将其存入银行或购买国库券。
当前银行存款及各期国库券的利率见下表。
假设国库券每年至少发行一次,发行时间不定。
取款政策参考银行的现行政策。
校基金会计划在n年内每年用部分本息奖励优秀师生,要求每年的奖金额大致相同,且在n年末仍保留原基金数额。
校基金会希望获得最佳的基金使用计划,以提高每年的奖金额。
请你帮助校基金会在如下情况下设计基金使用方案,并对M=5000万元,n=10年给出具体结果:1.只存款不购国库券;2.可存款也可购国库券。
3.学校在基金到位后的第3年要举行百年校庆,基金会希望这一年的奖金二、模型的假设(1)银行利息和国库券结算方式为单利;(2) 定期存款和国库券不到期均不能取款;(3)国库券每年发行一期,发行月份不定,但于发行月一号发行;(4)基金结算后马上又进行投资(存入银行或买国库券)中间间隔时间不予考虑;(5)定期存款实际收益利率为公布利率的80%(20%为利息税上交国库)国库券存款利率与同期的定期存款利率相同,但不交利息税;(6)每年年初评奖且奖金数目相同(除第三问),N年后本金仍为M;三、符号的说明x第i年所存入银行的j年期的存款;ijy第i年说购买的j年期的国库券;ij'r银行同期活期利率;r银行同期活期税后利率;'r银行同期j年期固定利率;jr银行同期j年期固定利率税后利率;jM本金=5000万元,Z=每年的奖金四、模型的建立与求解第一种情况:只存款不买国库券我们考虑到这种情况下,存款的时间是一定的,所以活期和三个月,半年的利率都太低,所以在这种情况下,我们直接考虑一年的利率,这样才能获得较多的利息,从而使得每年发放的奖金数目尽可能多——即我们要实现的目标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、某工厂要做100套钢架,每套钢架用长为2.9m,2.1m,1.5m,2.0m的圆钢各一根。
已知原料每根长为7.4m,问:应该如何下料,可使所用原料最省2、某工厂生产 A 和 B 两种产品,按计划每天生产 A、B 各不得少于 10 吨,已知生产 A 产品一吨需用煤 9 吨、电 4 度、劳动力 3 个(按工作日计算);生产 B 产品一吨需用煤 4 吨、电 5 度、劳动力 10 个.如果 A 产品每吨价值 7 万元,B 产品每吨价值 12 万元,而且每天用煤不超过 300 吨,用电不超过 200 度,劳动力最多只有 300 个.1)每天应安排生产 A、B 两种产品各多少,才能既保证完成生产计划,又能为国家创造最多的产值?2)请计算不等式右端资源影子价格,并计算保持影子价格不变的自变量的变化范围。
3)保持最优解不变的目标函数系数变化范围3.甲、乙两地生产某种产品,它们可调出的数量分别为 300t 和 750t,A、B、C 三地需要该种产品的数量分别为 200t、450t 和 400t,甲地运往 A、B、C 三地的运费分别是 6 元/吨、3 元/吨、5 元/吨,乙地运往 A、B、C 三地的运费分别是 5 远/吨、9 元/吨、6 元/吨,问怎样的调运方案才能使总运费最省?4、2)请计算不等式右端资源影子价格,并计算保持影子价格不变的自变量的变化范围。
3)保持最优解不变的目标函数系数变化范围5、2)请计算不等式右端资源影子价格,并计算保持影子价格不变的自变量的变化范围。
3)保持最优解不变的目标函数系数变化范围6、2)请计算不等式右端资源影子价格,并计算保持影子价格不变的自变量的变化范围。
3)保持最优解不变的目标函数系数变化范围7、某排球国家队需要准备从以下队员中选拔4名队员为正式队员,每个位置一名,并使平均身高尽可能高,这8名预备队员情况如下表所示预备队员号码身高 cm位置小甲1193主攻小乙2191主攻小丙3187副攻8、某货运飞机,其载重量为24t ,客运物品的重量机器运费收入如下表,其中个物品只有一件可供选择。
问如何选择物品运费收入总费用最多9、某麻辣烫店铺拟要在爱民区、向阳区、东安区建立分店,有7个点A i ,i=1…7可供选择,要求满足以下条件:1)在爱民区的三个点123,,A A A 至多选两个2)在向阳区的两个点45,A A 至多选一个3)在东安区的两个点67,A A 两个点互斥(只能选一个,必须选一个) 4)选3A 必选5A若A i 点投资b i 万元,每年可获利C i 万元,投资总额为B 万元,建立模型,是获利最大(不求解)10 、某旅行者的大包中只能装17千克的物品,等待装的有如下7件物品,其重量和价值表如下要求选5号必须选择3号物品,请问他的背包中应该携带哪些物品,才可能使物品的价值最大。
11、12、13、A1..a10=[2.5 3 2.6 4 3.2 3.1 3.4 3.2 3.6 4];C1..c10=[4 5 5.3 6 6.1 6.1 6.2 5 6 7];14、15、16、某大型公司计划开办5家酒店,为了尽早建成营业,公司决定由5家建筑公司分别承建,设建筑公司Ai (i=1,2,3,4,5)对5家酒店Bj(j=1,2,3,4,5)的建造费用的报价(万元)为cij(I,j=1,2,3,4,5)见下表,如何分配建造任务,才能A i,C ij,B j B1B2B3B4B5A14871512A279171410A3691287A46714610A5691210617、18、某卡车公司拨款800万元用于购买新的运输工具,有3种运输工具可供选择:A的载重量10吨,平均时速45千米,价格26万元;B的载重量20吨,平均时速40千米,价格36万元;C的载重量18吨,平均时速40千米,价格42万元。
其中,C是B的变种,新设了一个卧铺,所以载重降低了、价格上升了。
A需要1名司机,如果每天三班工作,每天可运行18小时. 当地法律规定B和C均需要两名司机,如果三班工作,B每天可运行18小时,C可运行21小时. 该公司目前每天有150名司机可用,短期内无法招募到其他训练有素的司机。
当地工会禁止司机每天工作超过一个班次。
此外,受维修保障能力的限制,公司最多能拥有30辆运输工具。
请你建立数学模型,确定A、B、C的数量使得公司的总运力最大。
19、某公司用两种原油(A和B)混合加工成两种汽油(甲和乙)。
甲、乙两种汽油含原油A的最低比例分别为50%和60%,每吨售价分别为4800元和5600元。
该公司现有原油A和B的库存量分别为500吨和1000吨,还可以从市场上买到不超过1500吨的原油A. 原油A的市场价为:购买量不超过500吨时的单价为10000元/吨;购买量超过500吨但不超过1000吨时,超过500吨的部分单价为8000元/吨;购买量超过1000吨时,超过1000吨的部分单价为6000元/吨。
该公司应怎样安排原油的采购和加工?(利润达到最大值5000千元.)20、某地有三个小食品厂,它供应三个大的超市,各个食品厂的产量,各个食品厂与超市之间的单位运价如下表,假定在第1,2,3食品厂制作单位食品的利润分别是12元,16元和1121、某汽车厂在L.A. 和 Detroit生产汽车,在Atlanta有一仓库,供应点为Houston 和 Tampa;城市间每辆汽车运输费用见下表. L.A.的生产能力为1100辆, Detroit的生产能力为2900辆. Houston汽车需求量为2400辆, Tampa汽22、某公司须完成如下交货任务: 季度1,30件; 季度2,20件; 季度3,40件;每季度正常上班时间至多可生产27件,单位成本$40,加班时间的单位生产成本为$60.产品不合格率为20%,每季度剩下的合格产品(在存货时)中有10%被破坏,单位存货费为$15.已知现有20件合格产品, 如何安排3季度的的生产?(用集合语言)23、Chicago教育委员会为该城市的四条学生公交线路招标.四家公司做出如下竟公司140005000--公司2-4000-4000公司33000-2000-公司4--40005000(b) 假设每位竟标者至多可分配到两条线路,问委员会将如何招标?24、已知,j=1 (20)aj=[12 3 2 1 4 2 34 3 5 2 5 2 5 6 7 8 9 3 12 11];cj=[4 6 7 5 8 6 5 4 3 7 5 8 9 6 4 7 8 6 5 10];25、要求建立集合求解26、27、28、某市有三个面粉厂,他们供给三个面食加工厂所需的面粉,各面粉厂的产量、各面食加工厂加工面粉的能力、各面食加工厂和各面粉厂之间的单位运价,均式于下表。
假定在第1,2和3面食加工厂制作单位面粉食品的利润分别为12元、16元和11元,试确定使总效益最食品厂面粉厂123面粉厂产值1 2 3348101111284203020销量15252029、某公司有资金4万元,可向A、B、C三个项目投资,已知各项目的投资回报如下,求最大回报。
项目投资额及收益01234A041486066B042506066C06468787630、某工厂生产三种产品,各种产品重量与利润关系如下表,现将此三种产品运往市场出售,运输能力总重量不超过6t,问应运输每种产品各多少件可使总利润最大。
产品重量(t/件)利润(千元/件)12802313031、已知123123123max 2422240,1,,4j Z x x x x x x x x x x j =++⎧++≤⎪-+≤⎨⎪≥=⎩L ()1) 求最优解;2)目标函数c1,c2在什么范围内变动时候,上述最优解不变; 3)当约束右端b1,b2中一个保持不变,另一个在什么范围内变化,上述最优解保持不变;4)当目标函数变为max z=4x1+x2+4x3时原始最优解怎么变化。
32、已知123132313min 41218332250z x x x x x x x x -=+++≥⎧⎪+≥⎨⎪≥⎩1) 求最优解;2)目标函数c1,c2在什么范围内变动时候,上述最优解不变; 3)当约束右端b1,b2中一个保持不变,另一个在什么范围内变化,上述最优解保持不变;4)当目标函数变为minz=4x1+8x2+18x3时原始最优解怎么变化。
(b ) 若产品乙、丙的单件利润不变,则产品的利润在什么范围变动时,上述最优解是不变的;(c ) 若有一种新产品丁,其原料消耗定额,A 为3单位,B 为2单位,单件利润为2.5单位。
问该种产品是否值得安排生产,并求新的最优计划?(d ) 若原材料A 市场紧缺,除拥有量外一时无法购进,而原料B 如数量不足可以去市场购买,单价为0.5,问该厂是否购买?购买多少为宜? 34、某厂生产Ⅰ、Ⅱ、Ⅲ三种产品,分别经过A 、B 、C 三种设备加工,已知生产单位各种产品所需要的设备台时,设备的现有加工能力以及每件产品的预期的利润如下表: (a ) 求获利最大的产品计划?(b ) 产品Ⅲ每件的利润增加到多大时才值得安排生产?如果产品Ⅲ的每件利润增加到50/6元,求最优计划的变化? (c ) 设备A 的能力如为10010θ+,确定保持最优基不变的θ的变化范围?(d ) 如有一种新产品,加工一件设备A 、B 、C 的台时为1、4、3小时,预期每件的利35、某厂准备生产A,B,C 三种产品,它们都消耗劳动力和材料,有关数据见表所示:(a ) 所确定获利最大的产品生产计划:(b ) 产品A 的利润在什么变动时,上述最优计划不变;(c ) 如设计一种新的产品D ,单件劳动力消耗为8单位,材料消耗为2单位,每件可获利3元,问该种产品是否值得生产?(d ) 如劳动力数量不变,材料不足时可以从市场上购买,每单位0.4元,问该厂要36、给出线性规划问题maxz =2x 1+3x 2+x 31/3x 1+1/3x 2+1/3x 3≤1st 1/3x 1+4/3x 2+7/3x 3≤3x j ≥0试分析下列各种条件下,最优解的变化:1) 目标函数中变量x 3的系数变为6;2) 分别确定目标函数中变量x 1和x 2的系数C 1、C 2在什么范围内变动时最优解不变;3) 约束条件的右端由 1 变为 2 ;3 337、maxz =2x 1-x 2+x 3x 1+ x 2+ x 3≤6st -x 1+2x 2 ≤4x 1,x 2,x 3≥01) 用单纯形法求最优解2) 分析当目标函数变为maxz =2x 1+3x 2+x 3时最优解的变化;3) 分析第一个约束条件右端系数变为3时最优解的变化。
4) 约束右端b1,b2中一个保持不变,另一个在什么范围内变化,上述最优解保持不变;38、已知12312312312313max 42924z x x x x x x x x x x x x x -=--+++≤⎧⎪+-≤⎪⎨-++≤⎪⎪≥⎩ 1)求最优解2)若右端列向量932244b ⎡⎤⎡⎤⎢⎥⎢⎥=−−−→⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦变为,求新问题的最优解。
