第14讲 图的遍历及应用
数据结构-图的遍历

1 ^ 4^
3
4
3 ^5^
可编辑ppt
7
复习-图的存储结构
AC
B
0A
01
1B ∧
2C
2 1∧
0 2∧∧ 2 0∧∧
可编辑ppt
8
存储结构的比较
一、应用范围
•邻接矩阵可用于DG、UDG、DN、UDN •邻接表可用于DG、UDG、DN、UDN •十字链表用于DG和DN •邻接多重链表用于UDG和UDN
可编辑ppt
11
存储结构的比较
2、插入和删除顶点 InsertVex(&G, v); //在图G中增添新顶点v。 DeleteVex(&G, v); // 删除G中顶点v及其相关的弧。
都要对存放顶点数组元素的操作 但是对邻接矩阵,还要修改邻接矩阵
可编辑ppt
12
存储结构的比较
3、插入和删除弧 InsertArc(&G, v, w); DeleteArc(&G, v, w);
EnQueue(Q, v);
// v入队列
while (!QueueEmpty(Q)) {
DeQueue(Q, u);
// 队头元素出队并置为u
for(w=FirstAdjVex(G, u); w;
w=NextAdjVex(G,u,w))
if ( ! visited[w]) {
visited[w]=TRUE; Visit(w); EnQueue(Q, w); // 访问的顶点w入队列
4、邻接边 •邻接矩阵:第v行 •邻接表:第v个链表 •十字链表:第v个链表 •多重邻接表:第v个链表
可编辑ppt
17
邻接点函数的实现
图的遍历和搜索

INPUT.TXT 123456789 3 OUTPUT.TXT 192 384 576 219 438 657 273 546 819 327 654 981
用数组B[0..9]来存储N个数字 存储规则: B[0]存储N个数字中0的个数 B[1]存储N个数字中1的个数 B[2]存储N个数字中2的个数 ………… ………… B[8]存储N个数字中8的个数 B[9]存储N个数字中9的个数
2 1
1 2
设置8个方向变化 初始化board Board[1,1] try(1,1,2,q) q 1
Y
N
输出结果
输出无解信息
K Try(x,y,i,q)
表示对(x,y)位置 作为第i步向前试探 的过程.若试探成 功,逻辑变量q的值 为true,否则为false
0 k←k+1 q1←false u←x+a[1,k] v←y+a[2,k] 合格 Y N Board=0 N Y Board[u,v] ←i i<n*n N
1 3 7 9 0 8 2 6 4 5
For I:=1 to 3 For j:=4 to 9 For k:=11 to 31 For p:=32 to 99
求I*i ,分离各位数字 求j*j ,分离各位数字 求k*k, 分离各位数字 求p*p , 分离各位数字
Y Try(u,v,i+1,q1) Q1:=true Not (q1) N Y Board[u,v]:=0 Q1 OR (K=8) Q:=Q1
试编程将1至N(N≤10)的自然数序列1,2,…, N重新排列,使任意相邻两数之和为素数.例如N =3时有两种排列方案123,321满足要求. 输入要求:N从键盘输入. 输出要求:每行输出一种排列方案(相邻数字之间 用空格分隔). 最后一行输出排列方案总数. 例如输入 3 输出 1 2 3 3 2 1 2
数据结构课程设计--图的遍历

1.引言数据结构是计算机科学与技术专业的一门核心专业基础课程,是一门理论性强、思维抽象、难度较大的课程。
在软件工程专业的课程体系中起着承上启下的作用,学好数据结构对于提高理论认知水平和实践能力有着极为重要的作用。
通过本门课程的学习,我们应该能透彻地理解各种数据对象的特点,学会数据的组织方法和实现方法,并进一步培养良好的程序设计能力和解决实际问题的能力。
我认为学习数据结构的最终目的是为了获得求解问题的能力。
对于现实世界中的问题,我们应该能从中抽象出一个适当的数学模型,该数学模型在计算机内部用相应的数据结构来表示,然后设计一个解此数学模型的算法,再进行编程调试,最后获得问题的解答。
图是一种非常重要的数据结构,在《数据结构》中也占着相当大的比重。
这个学期的数据结构课程中,我们学习了很多图的存储结构,有邻接矩阵、邻接表、十字链表等。
其中邻接矩阵和邻接表为图的主要存储结构。
图的邻接矩阵存储结构的主要特点是把图的边信息存储在一个矩阵中,是一种静态存储方法。
图的邻接表存储结构是一种顺序存储与链式存储相结合的存储方法。
从空间性能上说,图越稀疏邻接表的空间效率相应的越高。
从时间性能上来说,邻接表在图的算法中时间代价较邻接矩阵要低。
本课程设计主要是实现使用邻接表存储结构存储一个图,并在所存储的图中实现深度优先和广度优先遍历以及其链表结构的输出。
2.需求分析2.1 原理当图比较稀疏时,邻接表存储是最佳的选择。
并且在存储图的时候邻接表要比邻接矩阵节省时间。
在图存储在系统中后,我们有时还需要对图进行一些操作,如需要添加一个顶点,修改一个顶点,或者删除一个顶点,而这些操作都需要一图的深度优先及广度优先遍历为基础。
本系统将构建一个图,图的结点存储的是int型数据。
运行本系统可对该图进行链式结构输出、深度优先及广度优先遍历。
控制方法如下:表2-1 控制键的功能2.2 要求(1)建立基于邻接表的图;(2)对图进行遍历;(3)输出遍历结果;2.3 运行环境(1)WINDOWS 7系统(2)C++ 编译环境2.4 开发工具C++语言3.数据结构分析本课程设计是针对于图的,程序中采用邻接表进行数据存储。
图的遍历

6
8 4 2 1
3.1 深度优先搜索遍历
1 2 4 5 8
1
栈
3 6 7
非递归
2
4
3
5
8
6
6 8 4 2 1
3.1 深度优先搜索遍历
1 2 4 5 8
1
栈
3 6 7
非递归
2
4
3
5
8
6
7
3 6 8 4 2 1
3.1 深度优先搜索遍历
1 2 4 5 8
1
栈
3 6 7
非递归
2
4
3
5
8
6
7
7的邻接 表空, 逐一退 栈
问过为止。
1 2 4 5 8 3 6 7
深度优先
1
2
4
3
所有都访 问完毕了
5
8
6
7
2已经访问返 回8
3.1 深度优先搜索遍历
下面以下图为例来讨论dfs算法的执行过程:调用dfs(1)
此箭头表示是从遍历运 算 dfs(1) 中调用 dfs(2) , 即从顶点1直接转到2
此虚箭头表示是在 dfs(3) 执行完毕后返回到遍历 运算 dfs(2) 中,即从顶点 3返回到2
1
2 3
以3为起点根本 不能遍历整个图
1
2
4
2
1 3
4 7 9 8
24
10
3
5
6
5
6
3.1 深度优先搜索遍历
3. 深度遍历算法的应用
问题: (1)如何设计算法以判断给定的无向图是否是连通的? (2)如何设计算法以求解给定的无向图中的边数? (3)设计算法以判断给定的无向图是树。 (4)设计算法以判断给定的有向图是以v0为根的有向树。 (5)设计算法以判断图中的一个节点是否为关节点。
图的遍历
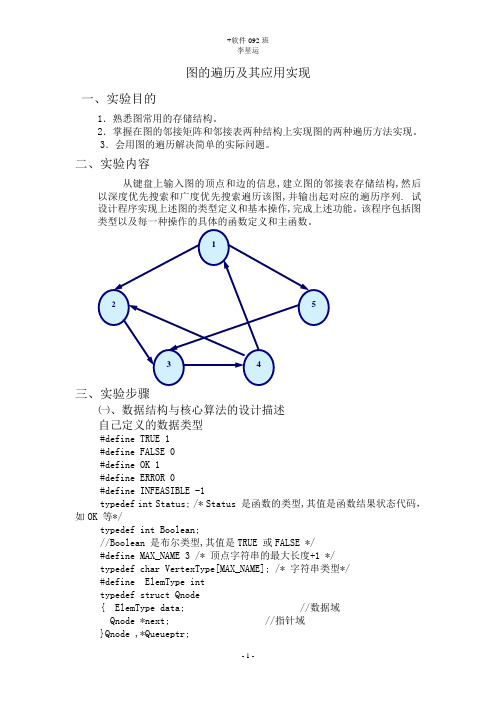
图的遍历及其应用实现一、实验目的1.熟悉图常用的存储结构。
2.掌握在图的邻接矩阵和邻接表两种结构上实现图的两种遍历方法实现。
3.会用图的遍历解决简单的实际问题。
二、实验内容从键盘上输入图的顶点和边的信息,建立图的邻接表存储结构,然后以深度优先搜索和广度优先搜索遍历该图,并输出起对应的遍历序列. 试设计程序实现上述图的类型定义和基本操作,完成上述功能。
该程序包括图类型以及每一种操作的具体的函数定义和主函数。
12534三、实验步骤㈠、数据结构与核心算法的设计描述自己定义的数据类型#define TRUE 1#define FALSE 0#define OK 1#define ERROR 0#define INFEASIBLE -1typedef int Status; /* Status 是函数的类型,其值是函数结果状态代码,如OK 等*/typedef int Boolean;//Boolean 是布尔类型,其值是TRUE 或FALSE */#define MAX_NAME 3 /* 顶点字符串的最大长度+1 */typedef char VertexType[MAX_NAME]; /* 字符串类型*/#define ElemType inttypedef struct Qnode{ ElemType data; //数据域Qnode *next; //指针域}Qnode ,*Queueptr;typedef struct{Queueptr front; //头指针Queueptr rear; //尾指针}LinkQueue;在广度遍历中需要需要用到队列,下面就是对队列的基本应用v oid InitQueue(LinkQueue & Q)//初始化队列void EnQueue(LinkQueue & Q,ElemType x)//插入值为X的结点到队列中ElemType DeQueue (LinkQueue & Q,int &x)int QueueEmpty(LinkQueue & Q)int LocateVex(ALGraph G,VertexType u){ /* 初始条件: 图G 存在,u 和G 中顶点有相同特征*//* 操作结果: 若G 中存在顶点u,则返回该顶点在图中位置;否则返回-1 */}Status CreateGraph(ALGraph &G){ /* 采用邻接表存储结构,构造没有相关信息的图G}void DestroyGraph(ALGraph &G){ /* 初始条件: 图G 存在。
图的遍历(深度优先遍历和广度优先遍历)

遍历规则 从图中某结点v0出发,深度优先遍历(DFS: Depth First Search)图的规则为: 访问v0; 对v0的各个出点v01,v02,…,v0m,每次从它们中按一定方式(也可任选)选取一个未被访问过的结点,从该结点出发按深度优先遍历方式遍历。 然,因为我们没有规定对出点的遍历次序,所以,图的深度优先遍历结果一般不唯一。
20.2 深度优先遍历
例如,对图 20‑1给出的有向图与无向图,一些遍历结果(结点访问次序)为: 左图:从1出发:1,2,4,5;或1,5,2,4 从2出发:2,1,5,4;或2,4,1,5 右图:从a出发:a,b,c,d;或a,b,d,c; … …
A 如果不想让visited或top做为函数参数,也可以在函数中将其定义为static型量。但是,这样的程序是不可再入的,即函数再次被调用时,static型的量也不重新初始化,造成错误!
上面函数中的参数visited和top实质上是中间变量,只是为了避免在递归调用时重新初始化而放在参数表中,造成使用的不方便,为此,做个包装程序: long DFS1(int g[][CNST_NumNodes], long n, long v0, long *resu ) { char *visited; long top=0; visited = new char[n]; for (long i=0; i<n; i++) visited[i]=0; long num=DFS1( g, n, v0, visited, resu, top ); delete visited; return num; }
深度优先遍历非递归算法的一般性描述。
long DFS_NR(图g,结点v0)
单击此处可添加副标题
图的遍历演示

2.广度优先搜索(遍历)步骤: 广度优先搜索(遍历)步骤: 广度优先搜索
简单归纳: 简单归纳:
• • • 在访问了起始点v之后, 的邻接点; 在访问了起始点 之后,依次访问 v的邻接点; 之后 的邻接点 然后再依次访问这些顶点中未被访问过的邻接点; 然后再依次访问这些顶点中未被访问过的邻接点; 直到所有顶点都被访问过为止。 直到所有顶点都被访问过为止。 广度优先搜索是一种分层的搜索过程, 广度优先搜索是一种分层的搜索过程,每向前走一 步可能访问一批顶点, 步可能访问一批顶点,不像深度优先搜索那样有回 退的情况。因此, 退的情况。因此,广度优先搜索不是一个递归的过 其算法也不是递归的。 程,其算法也不是递归的。
可以用递归算法! 可以用递归算法 讨论2 讨论2: DFS算法如何编程? ——可以用递归算法! DFS算法如何编程? 算法如何编程
void ExtMGraph <T>::DFS (int v, void *visit()) , //设A[n][n]为邻接矩阵,v为起始顶点(编号) //设A[n][n]为邻接矩阵, 为起始顶点(编号) 为邻接矩阵 { visit(v); ( ) //访问 例如打印)顶点v 访问( //访问(例如打印)顶点v visited[v]=1; //访问后立即修改辅助数组标志 //访问后立即修改辅助数组标志 //从v所在行从头搜索邻接点 //从 所在行从头搜索邻接点 从头 for( j=0; j<n; j++) if ( A[v, j] && ! visited[j] ) DFS (j, visit); , return; 深度优先 visited [j ]=0 A[v,j] =1 } // DFS
借助于队列实现
《离散数学》课件第14章图的基本概念

定义14.5(图同构)设两个无向图G1=<V1,E1>, G2=<V2,E2>,如果存在双射函数f:V1→V2,使得对 于 任 意 的 e=(vi,vj)∈E1 当 且 仅 当 e’=(f(vi), f(vj))∈E2,并且e与e’的重数相同,则称G1和G2是 同构的,记作G1≌G2。
若vi=vj,则称ek与vi的关联次 数为2;
若vi不是ek的端点,则称ek与vi 的关联次数为0。
无边关联的顶点称为孤立点 (isolated vertex) 。
19
定义(相邻) 设无向图G=<V,E>, 若∃et∈E且et=(vi,vj),则称vi和vj是相邻的 若ek,el∈E且有公共端点,则称ek与el是相邻的。
素称为有向边,简称边。 由定义,有向图的边ek是有序对<vi,vj>,称vi,
vj是ek的端点,其中vi为ek的始点(origin),vj为ek 的终点(terminus)。
当vi=vj时,称ek为环,它是vi到自身的有向边。
11
每条边都是无向边的图称为无向图(undirected graph)。
定义(邻接与相邻) 设有向图D=<V,E>, 若∃et∈E且et=<vi,vj>,则称vi邻接到vj,vj邻接 于vi。 若ek,el∈E且ek的终点为el的始点,则称ek与el是相 邻的。
20
定义14.4(度) 设G=<V,E>为一无向图,∀v∈V,称 v作为边的端点的次数之和为v的度数,简称为度 (degree),记为d(v)。
定理14.2 (有向图握手定理)设D=<V,E>为任 意的有向图,V={v1,v2,…,vn},|E|=m,则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
顶点表示课程
有向弧表示先决条件
若课程i是课程j的先决条件
则图中有弧<i,j>
拓扑排序
应怎样学习这些课程,才能顺 把AOV网络中各顶点
利完成学业?
按照它们之间的先后
关系排列成一个线性
序列的过程
拓扑序列
广东石油化工学院 理学院
23
拓扑排序的过程
C0
C1
C2
C3
C4
C5
有向无环图
在邻接表的表头结点增加存放顶点入度的域
栈存放入度为零的顶点
v1
0
v2
2
v3
1
v4
2
v5
3
v6
0
4
3
2
5
2
5
5
4
拓扑序列:1 6 4 3 2 5
广东石油化工学院 理学院
27 27
AOV网 顶点表示活动的网 顶点表示活动,弧表示活动间的先后关系 AOV网中不允许有回路,这意味着某项活动以 自己为先决条件
广东石油化工学院 理学院
21
C4
C5
C2
C1
C3
C7
C12 C8
C9
C10
C6
C11
死锁?
课程代号 C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 C11 C12
V2
V3
V4 V5 V6 V7
V8
V1
V2
V3
V4 V5 V6 V7
V8 广度优先生成树
广东石油化工学院 理学院
11
非连通图的生成森林
非连通图,每个连通分量中的顶点集和遍历时走
过的边一起构成若干棵生成树
这些连通分量的生成树组成非连通图的生成森林
A
CD
F
G
I J
L
B E H K
M
A
D
LCF
E
15
最小生成树(Prim)算法
方法 设N=(V,E)是连通网,T=(U,E‘)是正在构造中的生成树 初始时,生成树只有一个结点,没有边
U={u0},E’={ },u0是任意选定的顶点, 从初始状态开始重复执行下列的操作
在所有u∈U,v∈V-U的边(u,v),(u,v)∈E中找一条 代价最小的边(u‘,v’)并入集合E‘,同时V’并入集合U, 直到V=U为止。
visited[v]=1;
queue.clear();
queue.add(v);
while(!queue.isEmpty()){
v=queue.poll();//队头元素v出队列
Arcnode p=graph[v].getFirstArc();
while(p!=null){
w=p.getAdjvex();
if(visited[w]==0){
System.out.print("访问顶点"+w+" ");
visited[w]=1;
queue.add(w);//顶点w进队列Q
}
p=p.getNextArc();
}
}
}
队列
V1
V2
V3
V4 V5 V6 V7
V8
广东石油化工学院 理学院
88
图的连通性
怎样求图的连通分量?
在带权无向完全图中,访问每个顶点恰好一次、并且返 回出发点、总权数最小的回路
适合稠密图
广东石油化工学院 理学院
14
普里姆(Prim)算法最小生成树的过程
28
01
10 14 16
562
25 24 18 12
4 22 3
01
10 14 16
562
25 4
12
3
22
原图
(a)
广东石油化工学院 理学院
如此重复,直到所有顶点均被访问过为止 V1
public static void dfs(Vexnode[] graph,int v,int[] visited){
Arcnode p;
System.out.print(“访问顶点”+v+“ ”);
V2
visited[v]=1;//表示被访问
p=graph[v].getFirstArc();
广东石油化工学院 理学院
25
拓扑排序的方法
从有向图中任选一个入度为0的顶点,并访问 删除该顶点和所有以它为尾的弧
重复上述两步,直至全部顶点均已访问,或当
图中不存在度为0的顶点为止 不存在度为0的顶点: 存在环
弧头顶点的入度减1
广东石油化工学院 理学院
26
构造拓扑排序的存储结构
AOV网用邻接表存储
广东石油化工学院 理学院
18
练习题
615
2
1
5
5
4
3 36
5
2
(Prim)算法
1
2
1
4
5
3 3
5
2
广东石油化工学院 理学院
19
克鲁斯卡尔(Kruskal)算法
A 6
B 14 12
D 14
15 F
8
C 17
E 5
6A8
B 14
C
12
D
E
F5
广东石油化工学院 理学院
20
有向无环图有关概念
无环图(DAG) 一个无环(回路)的有向图叫做有向无环图 directed acycline graph
算法 时间复杂度为o(n2),其中n为网中顶点的个数 Prim算法适用于求边稠密的网的最小生成树
广东石油化工学院 理学院
16
克鲁斯卡尔算法构造最小生成树的过程
适合简单图
28
01
01
10 14 16
5 6 25 6 2
25 24
18 12
43
43
22
原图
(a)
广东石油化工学院 理学院
01
C0
C1
C2
C4 C0 C3 C2 C1 C5
C3
C4
C5
广东石油化工学院 理学院
24
拓扑排序举例
一个AOV网的拓
扑序列不是唯一的
C4 C2 C1 C12
C9 C10
C5
C3
C7
C8 C6
C11
拓扑序列: C1-C2-C3-C4-C5-C7-C9-C10-C11-C6-C12-C8 或: C9-C10-C11-C6-C1-C12-C4-C2-C3-C5-C7-C8
第14讲 图的遍历及应用 ----(最小生成树和拓扑排序)
广东石油化工学院 理学院
1
图的遍历
从图中某顶点出发,沿一些边访问图中顶点,使每个 顶点都被访问到,且仅被访问一次,叫做图的遍历
无重复,无遗漏 关键点
图中可能存在回路
图的顶点可能与其它顶点相通,在访问完某顶点后,可能沿 着某些边回到曾经访问过的顶点
while(p!=null) {
V4 V5
if(visited[p.getAdjvex()]==0)//没有访问过
dfs(graph,p.getAdjvex(),visited);
p=p.getNextArc();
V8
}
}
visited
v1
v2
v3
v4
v5
v6
v7
0
0
0
0
0
00Βιβλιοθήκη V3V6V7
v8 0
广东石油化工学院 理学院
广东石油化工学院 理学院
课程名称 程序设计基础
离散数学 数据结构 汇编语言 算法分析与设计 计算机原理 编译原理 操作系统 高等数学 线性代数 普通物理 数值分析
先修课 无 C1
C1,C2 C1
C3,C4 C11
C3,C5 C3,C6
无 C9 C9 C1,C9,C10
22
拓扑排序
问题提出
选修课程问题
为避免重复访问,可设辅助数组visited[]
将其初始化为0 遍历时,如果某顶点 i 被访问,将 visited [i]置 为1 以此防止顶点i被多次访问
广东石油化工学院 理学院
2
图的深度优先搜索(DFS)
广东石油化工学院 理学院
3
图的深度优先搜索(DFS)
DFS:V1 V2 V4 V8 V5 V3 V6 V7
广东石油化工学院 理学院
10
V1
V2
V3
深度遍历: V1 V2 V4 V8 V5 V3 V6 V7
广度遍历: V1 V2 V3 V4 V5 V6 V7 V8
V4 V5 V6 V7
V1
V8
V1
V2
V3
V1
V2
V3
V4
V6
V4 V5 V6 V7 V8
V7
V8
V5
深度优先生成树
M JB
深度优先生成森林
G
K
I
H
广东石油化工学院 理学院
12 12
最小生成树
问题提出 在n个城市间建立通信网络
顶点—表示城市 权—城市间建立通信线路所需
花费代价
1
7
2
13
7 9
5
5 6
24
17
10 12
3
18
4
希望找到一条路径,使建立该 通信网所需花费的总代价最小
路径上各边权值的和最小
图的广度优先搜索算法
