赵凯华电磁学第三版磁介质
合集下载
赵凯华陈煕谋《电磁学》第三版思考题及习题答案(完整版)
ห้องสมุดไป่ตู้
1、 在地球表面上某处电子受到的电场力与它本身的重量相等， 求该处的电场强度 （已知电 子质量 m=9.1×10-31kg,电荷为-e=-1.610-19C）. 解： 2、 电子所带的电荷量（基本电荷-e）最先是由密立根通过油滴实验测出的。密立根设计的 实验装置如图所示。一个很小的带电油滴在电场 E 内。调节 E，使作用在油滴上的电场力与 油滴的重量平衡。如果油滴的半径为 1.64×10-4cm,在平衡时，E=1.92×105N/C。求油滴上 的电荷（已知油的密度为 0.851g/cm3） 解： 3、 在早期（1911 年）的一连串实验中，密立根在不同时刻观察单个油滴上呈现的电荷， 其测量结果（绝对值）如下： 6.568×10-19 库仑 13.13×10-19 库仑 19.71×10-19 库仑 8.204×10-19 库仑 16.48×10-19 库仑 22.89×10-19 库仑 11.50×10-19 库仑 18.08×10-19 库仑 26.13×10-19 库仑 根据这些数据，可以推得基本电荷 e 的数值为多少？ 解：油滴所带电荷为基本电荷的整数倍。则各实验数据可表示为 kie。取各项之差点儿 4、 根据经典理论，在正常状态下，氢原子中电子绕核作圆周运动，其轨道半径为 5.29× 10-11 米。已知质子电荷为 e=1.60×10-19 库,求电子所在处原子核（即质子）的电场强度。 解： 5、 两个点电荷，q1=+8 微库仑，q2=-16 微库仑（1 微库仑=10-6 库仑） ，相距 20 厘米。求 离它们都是 20 厘米处的电场强度。 解： 与两电荷相距 20cm 的点在一个圆周上，各点 E 大小相等，方向在圆锥在上。 6、 如图所示， 一电偶极子的电偶极矩 P=ql.P 点到偶极子中心 O 的距离为 r ,r 与 l 的夹角为。 在 r>>l 时，求 P 点的电场强度 E 在 r=OP 方向的分量 Er 和垂直于 r 方向上的分量 Eθ。 解：
1、 在地球表面上某处电子受到的电场力与它本身的重量相等， 求该处的电场强度 （已知电 子质量 m=9.1×10-31kg,电荷为-e=-1.610-19C）. 解： 2、 电子所带的电荷量（基本电荷-e）最先是由密立根通过油滴实验测出的。密立根设计的 实验装置如图所示。一个很小的带电油滴在电场 E 内。调节 E，使作用在油滴上的电场力与 油滴的重量平衡。如果油滴的半径为 1.64×10-4cm,在平衡时，E=1.92×105N/C。求油滴上 的电荷（已知油的密度为 0.851g/cm3） 解： 3、 在早期（1911 年）的一连串实验中，密立根在不同时刻观察单个油滴上呈现的电荷， 其测量结果（绝对值）如下： 6.568×10-19 库仑 13.13×10-19 库仑 19.71×10-19 库仑 8.204×10-19 库仑 16.48×10-19 库仑 22.89×10-19 库仑 11.50×10-19 库仑 18.08×10-19 库仑 26.13×10-19 库仑 根据这些数据，可以推得基本电荷 e 的数值为多少？ 解：油滴所带电荷为基本电荷的整数倍。则各实验数据可表示为 kie。取各项之差点儿 4、 根据经典理论，在正常状态下，氢原子中电子绕核作圆周运动，其轨道半径为 5.29× 10-11 米。已知质子电荷为 e=1.60×10-19 库,求电子所在处原子核（即质子）的电场强度。 解： 5、 两个点电荷，q1=+8 微库仑，q2=-16 微库仑（1 微库仑=10-6 库仑） ，相距 20 厘米。求 离它们都是 20 厘米处的电场强度。 解： 与两电荷相距 20cm 的点在一个圆周上，各点 E 大小相等，方向在圆锥在上。 6、 如图所示， 一电偶极子的电偶极矩 P=ql.P 点到偶极子中心 O 的距离为 r ,r 与 l 的夹角为。 在 r>>l 时，求 P 点的电场强度 E 在 r=OP 方向的分量 Er 和垂直于 r 方向上的分量 Eθ。 解：
赵凯华-电磁学-第三版-第二章-静电场中的导体和电介质
R2 R1 R0
解： 1)导体电荷只分布在表面上 球A的电荷只可能在球的表面
B
Q
Aq
o
壳电B荷有可两能个分表布面在内、外两个表面R（2具体R1分布？）R0
由于A、B同心放置
带电体系具有球对称性
电量在表面上均匀分布（满足E内＝0要求）
电量在表面上均匀分布 Q q
电量q在球A表面上均匀分
R 1
4 0
9109 m 103 RE 1F
106 F
法拉单位过大, 常用单位: 1nF 109 F
1pF 1012 F
二.导体组的电容
由静电屏蔽:导体壳内部的电场只由腔内的电 量和几何条件及介质决定电位差仅与电荷 Q，几何尺寸有关，不受外部电场的影响，可
以定义电容。
UB
E dr
R2
4 0r R2 4 0 R2
例3 如图所示，接地导体球附近有一点电荷 。
求:导体上感应电荷的电量
解: 接地，即 U 0
设:感应电量为 Q
R
由于导体是个等势体
O
l
q
O点的电势也为零 ，则
Q q 0 40 R 40l
Q Rq l
腔内无电场，E腔内＝0 腔内电势处处相等
S
证明: 在导体壳内紧贴内表面作高斯面S
E ds 0 高斯定理 S
Qi 内表面 0
1.处处没有电荷
与等位矛盾 证明了上述 两个结论
2.内表面有一部分是正 则 会 从 正 电 荷 向 负 电荷，一部分是负电荷 电荷发出电力线
这就是物质对静电场的响应---第二章的研究内容：电场中的导体感应、 电解质极化， 并且分析感应、极化电荷对静电场的影响---静电场与物质的 相互作用(影响)
电磁学(赵凯华,陈熙谋第三版)第三章 习题解答
习题 ! ! "
" ’ , # ) !* ) !* ! (! （ ) +*） () "% ’ , # & !% $! % ・ ・ ・ $ ・ ・( & (& ! ) +* （ ) !*） (&! %&
" ! . ’% !( . ’%%% . $ " % . % " &% . % " ’% . ! " % ) $ ! " % . ’% !! ) $ ! " % #) " & ! . % " ’% . % " &%
(
!
!
)
习题 ! ! ""
新概念物理教程・电磁学$ 第三章 电磁感应 电磁场的相对论变换$ 习题解答
$ $ ! ! "# " 如本题图，一金属棒长为 % " &% ! 水平放置，以长度的 " # & 处为轴， 在水平面内 旋转， 每秒转两转。 已知该处地磁场在竖直方 向上的分量 $ " % % " &% "#， 求 &、 ’ 两端的电势 差。 解：在图中棒上轴的右边取一点 &(，使 它到轴的距离等于 & 点到轴的距离。 这两段导 相互抵消， 因此 ) & ’ %! ! &(’ %! （ ! * "） ・$# %! " " ! $ ( +,’ # ! +,&($# ) # # " !& !’ # %! * # ! * # * % " &% * "% * ( % " ’% ! % " "% # ) % %!’ " ( * "% % " #
" ’ , # ) !* ) !* ! (! （ ) +*） () "% ’ , # & !% $! % ・ ・ ・ $ ・ ・( & (& ! ) +* （ ) !*） (&! %&
" ! . ’% !( . ’%%% . $ " % . % " &% . % " ’% . ! " % ) $ ! " % . ’% !! ) $ ! " % #) " & ! . % " ’% . % " &%
(
!
!
)
习题 ! ! ""
新概念物理教程・电磁学$ 第三章 电磁感应 电磁场的相对论变换$ 习题解答
$ $ ! ! "# " 如本题图，一金属棒长为 % " &% ! 水平放置，以长度的 " # & 处为轴， 在水平面内 旋转， 每秒转两转。 已知该处地磁场在竖直方 向上的分量 $ " % % " &% "#， 求 &、 ’ 两端的电势 差。 解：在图中棒上轴的右边取一点 &(，使 它到轴的距离等于 & 点到轴的距离。 这两段导 相互抵消， 因此 ) & ’ %! ! &(’ %! （ ! * "） ・$# %! " " ! $ ( +,’ # ! +,&($# ) # # " !& !’ # %! * # ! * # * % " &% * "% * ( % " ’% ! % " "% # ) % %!’ " ( * "% % " #
电磁学第三版赵凯华答案
2. 真空中两个点电荷q与Q，相距5.0毫米，吸引力为40达 因。已知q=1.2 10-6 库仑，求Q。
解： 依库仑定律：F
4 0r 2
Q F • 4 0r 2
q
4.0104
4 3.14 8.85 1012 1.2 10 6
5.0 10 3
2
9.310（13 库仑）
3. 为了得到一库仑电量大小的概念，试计算两个都是一库 仑的点电荷在真空中相距一米时的相互作用力和相距一千 米时的相互作用力。
解：若此处的电场为E，则
E
mg q
9.110 31 9.8 1.6 10 19
5.6 10 11
伏/米
2. 电子说带的电荷量（基本电荷 -e ）最先是由密立根通过油
滴试验测的。密立根设计的试验装置如附图所示。一个很小的 带电油滴在电场E内。调节E，使作用在油滴上的电场力与油滴 的总量平衡。如果油滴的半径为1.64 10－4厘米，在平衡时， E＝1.92 105牛顿/库仑。求油滴上的电荷（已知油的密度为 0.851克/厘米3）。
5.141011伏 / 米或牛顿/ 库仑
5. 两个点电荷，q1 ＝＋8.0微库仑，q2= - 16.0微库仑（1微 库仑＝10－6库仑），相距20厘米。求离它们都是20厘米处的 电场强度E。
解：依题意，作如图所示：
E1
q1
4 0r12
E2
q2
4 0r22
E y E1y E2 E1 cos 600 E2 cos 600
电荷重合在一起。证明：在它们的延长线上离中心（即负电荷）
为r处，
E
3Q
4 0r 4
(r
l ),
+q -2q +q
赵凯华_电磁学_第三版_第一章_静电场_129_pages
dq
dV
q
P
（点电荷！！）组成，然后利用场强叠加 原理
r
dE
E
q
dE
q
dq 4 0 r
ˆ r 2
dq dV ds dl
体电荷 密度 面电荷 密度 线电荷 密度
dq dl
dq dV
dq ds
电荷密度 一般是位 置的函数
例1
等量异号电荷的电场 电荷之间的距离为 l。
E q 4 0 r ˆ r 2
球对称！！（图示见 下页） r 从源电荷指向场点 场强方向：
两式得
正电荷受力方向
z
F q ˆ r 2 q0 4 0 r
o
j
A
y
球对称！
静电场基本 特性的原因 ！！！
x
问题 如何求 任意 带电体的场强？
方法： 电力叠加原理＋场强定义
2 0
E E E
在可视为电 偶极子时 E
ˆ r
4 r
q
2 0
ˆ r
ˆ ˆ p 3 r p r 3 4 0 r
1
推导：
E 4 r q
2 0
ˆ r
4 r
q
P
ˆ r
2 0
r
r
l
q r r E 3 3 4 0 r r
由图中
q
r
q
矢量关系
平方
2 2
l r r 2
2
l r r 2
l r r r l 4
2 2 2
l r r r l, 4
赵凯华 电磁学 第三版 第四章 稳恒磁场(2) 14 pages
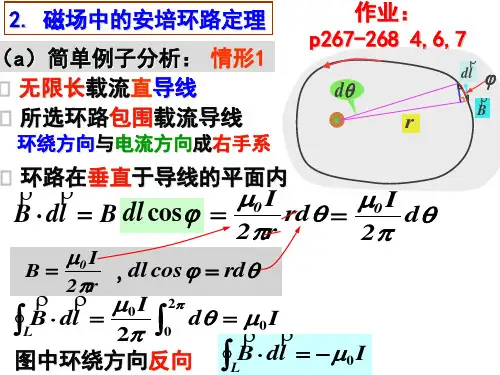
dl
L
L
dl
p
p
dl
p p dS 的立体角dω ω dS 的立体角d 立体角>0 立体角<0
分为两段积分
2
L
L p2 p1 B dl B dl B dl p p1 p2 p L p1 0 I p2 p1 d p2 B dl 4 0 I ( p2 ) ( p1 ) B dl p2 p1 4 2 0 2 0 I P1、 P2无限靠近 4 0 I 电流回路平面时 4 在如图所示的情形 B dl 0 I
?
安培环路定理证明 （任意闭合电流） 不讲授！ 说明
Your attention please !
B dl 0 I i内
L i
B由多个闭合电流回路产生，对单个电流回路 证明安培环路定理成立，多个回路由单回路 叠加即可。
单个电流回路安培环路定理证明 B dl 0 I L 0 Idl r ˆ B 4 L r 2
C
A C
ˆ 0 I dl r dl r 2 4 L
ˆ n
C h
B
A
S
B
A
S
0 I dl ( dl ) r ˆ B dl r 2 4 L ˆ ˆ r r 0 I ( dl ) ( dl )( r ) ˆ 2 4 L r
i
i
B dl B1 dl B2 dl 0 I 1
L L L
穿越安培环路的电流线必须闭合或无穷长
赵凯华电磁学第三版麦克斯韦电磁理论和电磁波232pages精品PPT课件
一些有见识的物理学家支持麦克斯韦的电磁理论，赫 兹的大学老师-----亥姆霍兹就是其中之一。
1879年冬，德国柏林科学院根据亥姆霍兹的倡议， 颁布了一项科学竞赛奖，以重金向当时科学界征求对 麦克斯韦部分理论的证明。
1887-1888年赫兹完成了电磁波证实实验。
（2）实验仪器及现象
电感、电容小，振荡频率高，且有电阻，是阻尼振荡。
赫兹的局限：由于时代的局限和未能进一步深入研究，他在电磁波的应用方面也
犯下了失误．在电磁波被证实以后，有一些工程界人士对于其实用价值极感兴趣，但遗 憾的是他本人对这一点却持怀疑、否定的态度．他说：“如果要利用电磁波进行通讯联 系，那非得有一面和欧洲大陆面积差不多大的巨型反射镜才行．”而且还要把它“悬挂 在很高很高的天上．” -------如何反射传播？
四、偶极振子发射的电磁波（一般了解）
1、电偶极振子模型
p
p0
cost
一段通有高频电流的直导线，当导线长度远小于波长，且导线直径与导线
长度之比远小于1时，可近似的认为导线上各点电流的幅值和相位相同。这样
的一段直导线称为基本振子，
由于基本振子在辐射电磁波的过程中，导线上流动的电流会在导线的两端
点形成电量相等、符号相反的电荷，与静电场中电偶极子十分相似，因此基
微 厘米波 0.1～0.01 3～30千兆赫 电视、雷达、导航
波
米
毫米波 0.01 ～ 0.001米
30～300千兆 雷达、导肮、其它专
赫
门用途
红外线
1、发现：1800年 赫谢耳 2、主要作用：热作用， 3、产生：一切物体 4、应用：红外线探测，如红外摄影
防盗报警 导弹制导 测温（Sars）
红外摄影－－高红外光部分强
电磁学_赵凯华_教学大纲
第1章电磁学教学大纲（包括讲座共60学时）第2章静电场参考学时 10§1 库仑定律•扭称实验及其它实验，电力平方反比律•库仑定律的物理内涵•库仑定律的成立条件• 电荷守恒定律，电荷的量子性§2 电场电场强度•电场，电场强度矢量•场强叠加原理§3 静电场的高斯定理•源与旋，通量与环流•静电场的高斯定理§4 静电场的环路定理电势•静电场的环路定理•关于静电场高斯定理和环路定理的几点说明•电势•场强与电势的微分关系§5静电场的基本微分方程*讲座：“电力平方反比律的理论与示零实验”；第3章静电场中的导体和电介质参考学时 8§1导体和电介质§2 静电场中的导体•导体的静电平衡条件•导体空腔与静电屏蔽•导体的静电平衡的基本性质•静电场边值问题的唯一性定理•尖端放电及其应用§3电容和电容器•孤立导体的电容•电容器及其电容•平行板电容器球形电容器同轴柱形电容器•分布电容•电容器的串并联§4 电介质极化•极化的微观机制•极化的描绘•极化强度矢量P和极化电荷q’的关系•极化强度矢量P和总电场E的关系——极化规律•各向异性电介质铁电体•例题§4有介质时的静电场•有介质时的高斯定理电位移矢量•应用例举§5静电场的边界条件•D的法向分量连续•E的切向分量连续§5带电体系的静电能•带电体系的静电势能•电容器储存的静电能•静电场的能量第4章直流电参考学时 4§1电流的连续性方程恒定条件·电流和电流密度矢量·电流的连续性方程恒定条件§2欧姆定律· 欧姆定律（积分形式）·电阻率和电导率·欧姆定律（微分形式）·焦耳定律•金属导电的经典微观解释§3 电源和电动势•电源的电动势•电源的路端电压•电源的功率•直流电路中的静电场的作用•温差电动势§4 直流电路•简单电路·复杂电路基尔霍夫定律第5章恒定磁场参考学时 10§1奥斯特实验•磁的基本现象•奥斯特实验•相关实验•研究课题§2毕奥-萨伐尔定律•毕奥-萨伐尔定律的建立•磁感应强度•载流回路的磁场§3磁场的“高斯定理”和“安培环路定律”•磁感应线•磁场的高斯定理•矢势*•磁单极* •安培环路定理§4安培定律•安培定律的建立* •安培定律=毕萨定律+安培力公式•磁场对载流线圈的作用，磁矩含讲座：“毕奥－萨筏尔定律、安培定律的示零实验”；§5 洛伦滋力•洛仑兹力•带电粒子在均匀电磁场中的运动•回旋加速器基本原理•霍耳效应•J.J.Thowmson的阴极射线实验，电子的发现•例题含讲座：“带电粒子在电磁场中的运动—磁约束、漂移、寝渐不变量”；第6章磁介质参考学时 4§1“分子电流”模型§2 顺磁质与抗磁质•顺磁质•抗磁质§3 磁化规律• 磁化的描绘•磁化强度矢量M与磁化电流I’的关系• 磁化强度矢量M与总磁感应强度B的关系§4有磁介质存在时的磁场•有磁介质存在时的磁高斯定理•有磁介质存在时的安培环路定理•磁介质的磁化规律§4 铁磁质•铁磁质的磁化规律•铁磁质磁化机制•铁磁材料的分类及其应用§5磁场的边界条件和磁路定理•B的法向分量连续•H的切向分量连续•磁路定理•磁屏蔽第7章电磁感应参考学时 10§1法拉第电磁感应定律•电磁感应现象的发现•法拉第对电磁感应的研究*•法拉第电磁感应定律•楞次定律•涡电流，电磁阻尼和电磁驱动含讲座：“法拉第电磁感应定律及其定量表达式”；§2动生电动势感生电动势涡旋电场•动生电动势•感生电动势，涡旋电场•交流发电机原理•电子感应加速器§3自感与互感•自感系数与互感系数•自感磁能与互感磁能•磁场的能量与能量密度§4暂态过程• RL电路的暂态过程•RC电路的暂态过程•RLC电路的暂态过程•灵敏电流计讲座：“超导体”；第8章交流电参考学时 8§1交流电概述• 各种形式的交流电• 简谐交流电的特征量• 几点说明§2交流电路中的基本元件•电阻元件•电感元件•电容元件•小结§3 元件的串联、并联——矢量图解法•串联电路•并联电路•多个元件的串、并联电路§4 交流电路的复数解法•交流电的复数表示法• 串、并联电路的复数解法• 串、并联电路的应用•复数形式的基尔霍夫定律•交流电桥§5 谐振电路•串联谐振电路•并联谐振电路• Q值的物理意义•谐振电路应用例举§6 交流电功率•瞬时功率、平均功率和功率因数•有功电阻与电抗•有功电流和无功电流•视在功率和无功功率•提高功率因数的意义•提高功率因数的方法§7 变压器简介•理想变压器•电压变比公式•电流变比公式•阻抗变比公式•功率传输效率§8 三相交流电•三相交流电• 相电压、线电压•负载的联接•三相电功率第9章麦克斯韦方程组——电磁波参考学时6讲座：“Maxwell电磁理论的建立”§1位移电流•电磁场的基本规律•位移电流§2麦克斯韦方程组•积分形式•微分形式•边界条件§3电磁波•电磁波的产生和传播•赫兹实验•电磁波的性质•电磁场的能量与动量•电磁波的传输与辐射•电磁理论与时空观狭义相对论的提出•麦克斯韦*。
赵凯华编《电磁学》4-6 边界条件,磁路定理
2011-3-13 12
2011-3-13 6
欧姆定律
ε = ∑ IR
= I ∑ Ri
i
磁路定理
ε m = ∑ Φ m Rmi
= Φ m ∑ Rmi
i
li = I∑ i σ i Si
= Φm ∑
i
µ 0 µ i Si
li
空气中，磁阻大，通量小 介质中，磁阻小，通量大，磁通量较多通过 介质，磁力线集中在铁芯内。
2011-3-13 7
2011-3-13
∂σ 0 n ⋅ ( j2 − j1 ) = − ∂t
n × ( E 2 − E1 ) = 0
3
电流线、电场线和磁感应线 在边界上的“折射”
j、D、B法向分量连续，切向分量不 、 、 法向分量连续 法向分量连续， 连续——三者在两种界面发生折射 三者在两种界面发生折射 连续
µ1 H1t µ1 tgθ1 B1t = = = tgθ 2 B2t µ 2 H 2t µ 2
2011-3-13 1
导体界面上的边界条件 设界面上有自由电荷积累σ0 高斯定理和电流连续性方程可得
dq d ∫∫ j ⋅ dS = 底1 j ⋅ dS＋底2 j ⋅ dS＋侧面 j ⋅ dS＝－ dt = − dt ∫∫σ 0 dS ∫∫ ∫∫ ∫∫ S S ∂σ 0 − j1 ⋅ n∆S j2 ⋅ n∆S − ∆S ∂t
电介质界面上，D法向连续，E切向连续 法向连续， 切向连续 电介质界面上， 法向连续 n ⋅ ( D2 − D1 ) = 0 n × ( E 2 − E1 ) = 0 以上设界面上没有自由电荷和无传导电流 以上设界面上没有自由电荷和无传导电流 两种导体界面上， 法向连续， 两种导体界面上，j法向连续，E切向连续
2011-3-13 6
欧姆定律
ε = ∑ IR
= I ∑ Ri
i
磁路定理
ε m = ∑ Φ m Rmi
= Φ m ∑ Rmi
i
li = I∑ i σ i Si
= Φm ∑
i
µ 0 µ i Si
li
空气中，磁阻大，通量小 介质中，磁阻小，通量大，磁通量较多通过 介质，磁力线集中在铁芯内。
2011-3-13 7
2011-3-13
∂σ 0 n ⋅ ( j2 − j1 ) = − ∂t
n × ( E 2 − E1 ) = 0
3
电流线、电场线和磁感应线 在边界上的“折射”
j、D、B法向分量连续，切向分量不 、 、 法向分量连续 法向分量连续， 连续——三者在两种界面发生折射 三者在两种界面发生折射 连续
µ1 H1t µ1 tgθ1 B1t = = = tgθ 2 B2t µ 2 H 2t µ 2
2011-3-13 1
导体界面上的边界条件 设界面上有自由电荷积累σ0 高斯定理和电流连续性方程可得
dq d ∫∫ j ⋅ dS = 底1 j ⋅ dS＋底2 j ⋅ dS＋侧面 j ⋅ dS＝－ dt = − dt ∫∫σ 0 dS ∫∫ ∫∫ ∫∫ S S ∂σ 0 − j1 ⋅ n∆S j2 ⋅ n∆S − ∆S ∂t
电介质界面上，D法向连续，E切向连续 法向连续， 切向连续 电介质界面上， 法向连续 n ⋅ ( D2 − D1 ) = 0 n × ( E 2 − E1 ) = 0 以上设界面上没有自由电荷和无传导电流 以上设界面上没有自由电荷和无传导电流 两种导体界面上， 法向连续， 两种导体界面上，j法向连续，E切向连续
电磁学赵凯华陈熙谋第三版习题及解答
从右边看，两极板间的电势差为
两电势差相等，因此有
(
-
+%
$
-
"!% !’
$，
"!" % ,! "!（" $ !%）- ! "!" $，
"
由 !、" 两式可解出
"!"
- ! $ " ’，! " ! $ !! % ,% #
!
"!%
- ! $ !! % ,% " ! $ !! % ,%
" ’， #
( ( - "!% $ - "［ ! $ !（ ! !%）%］’ $ " !’ !’ #［" ! $ !（ ! !%）%］
#
)# ’" !" !# &
# )" & +%# !$ "" # +(" ($
+&" # +%# !& +%# !%" +"" #
#
#*"
)
+%#& #"
新概念物理教程·电磁学" " 第四章" 电磁介质" 习题解答
" " ! ! !" 平行板电容器两极板相距 #" $ !"，其间放有一
层 ! # %" $ 的电介质，位置和厚度如本题图所示。已知极板 上面电荷密度为 "#$ # &" ’ $($ !(( $ % "% ，略去边缘效应，求：
电磁学(赵凯华,陈熙谋第三版)第六章 习题及解答
为氢原子内部的场强的 $ 倍有余，在太阳辐射转移区内的场强约为 氢原子内部场强的 & - ( 有余。
新概念物理教程・电磁学! 第六章 麦克斯韦电磁理论 电磁波 电磁单位制 习题解答
! ! ! ! " " 设 "## ! 的电灯泡将所有能量以电磁波的形式沿各方向均匀地 辐射出去， 求： （"） $# " 以外的地方电场强度和磁场强度的方均根值； （ $ ）在该处对理想反射面产生的光压。 解： （"） # $ "## " " $ & ’ $ %!% $ # # $
!
(
)
(
)
由于同心球形电容器中放电电流具有球对称性分布， 电流产生的磁场 分布也必定是球对称的； 然而磁场是轴矢量， 球对称的磁场只能处处为 & ， 即电容器中没有磁场。
新概念物理教程・电磁学! 第六章 麦克斯韦电磁理论 电磁波 电磁单位制 习题解答
! ! ! ! " " 太阳每分钟垂直射于地球表面上每 !"" 的能量约为 " !#$ （ # !#$" $ % " &） ， 求地面上日光中电场强度 # 和磁场强度 $ 的方均根值。 解：% & # # # $ & " % % " ! !% " "%
&
新概念物理教程・电磁学! 第六章 麦克斯韦电磁理论 电磁波 电磁单位制 习题解答
! ! ! ! "" " 利用电报方程证明： 长度为 # 的平行双线 （ 损耗可以忽略）两端 开启时电压和电流分别形成如下形式的驻波： "%$ " !"# & ! ’$%& ( $ ’ !& ( ) ， " # ! （ & % #， $， %， …） &!’ "% *" * #’( ( ) ) ) $%& ， ( ’ !& " " # &! " 指出电压、 电流的波腹和波节的位置， 以 其中谐振角频率为 ! & % #! +& ,& 及波长的大小。
新概念物理教程・电磁学! 第六章 麦克斯韦电磁理论 电磁波 电磁单位制 习题解答
! ! ! ! " " 设 "## ! 的电灯泡将所有能量以电磁波的形式沿各方向均匀地 辐射出去， 求： （"） $# " 以外的地方电场强度和磁场强度的方均根值； （ $ ）在该处对理想反射面产生的光压。 解： （"） # $ "## " " $ & ’ $ %!% $ # # $
!
(
)
(
)
由于同心球形电容器中放电电流具有球对称性分布， 电流产生的磁场 分布也必定是球对称的； 然而磁场是轴矢量， 球对称的磁场只能处处为 & ， 即电容器中没有磁场。
新概念物理教程・电磁学! 第六章 麦克斯韦电磁理论 电磁波 电磁单位制 习题解答
! ! ! ! " " 太阳每分钟垂直射于地球表面上每 !"" 的能量约为 " !#$ （ # !#$" $ % " &） ， 求地面上日光中电场强度 # 和磁场强度 $ 的方均根值。 解：% & # # # $ & " % % " ! !% " "%
&
新概念物理教程・电磁学! 第六章 麦克斯韦电磁理论 电磁波 电磁单位制 习题解答
! ! ! ! "" " 利用电报方程证明： 长度为 # 的平行双线 （ 损耗可以忽略）两端 开启时电压和电流分别形成如下形式的驻波： "%$ " !"# & ! ’$%& ( $ ’ !& ( ) ， " # ! （ & % #， $， %， …） &!’ "% *" * #’( ( ) ) ) $%& ， ( ’ !& " " # &! " 指出电压、 电流的波腹和波节的位置， 以 其中谐振角频率为 ! & % #! +& ,& 及波长的大小。
电磁学赵凯华_第三版_第四章_稳恒磁场
奥斯汀发现电流磁效应的半年后，就基本建立了电流磁场的知 识体系。电学、磁学合并成为一个新的学科：电磁学。
1.1不同的磁作用形式
（1） 磁铁 磁铁
物质成分
天然磁铁：Fe3O4
人工磁铁: 铷铁硼合金 钴镆合金等
最新进展：日本采用纳米技术 制备强磁性氮化铁
中性区 磁极
磁铁分区
条形磁铁的两端磁性强，称作磁极，中部磁性弱，称作中性 区
础－－重视实验研究；
（电流3的）本质我是运国动的科电荷学源头创新的困境思考。
电流方向变化、磁针转动方向也
运动的电荷产生磁场
变化
磁与电的关系
问题 电流对磁铁有作用，磁铁对电流是否有作用？
实验
N 极向内
结论
和磁铁一样，载流导线不仅具有磁性，也受 磁作用力
I=0
I
（3）电流 电流(应该存在作用力)
实验
结论
环向电流
产生磁场的源应该相同
安培分子 环流假说
条形磁铁 环向电流
1822安培提出：组成磁铁的最小单元(磁分子)就是环形电流，这些分子环流定向排列， 在宏观上就会显示出N、S极。
图示 N
等效宏观表面电流 S
磁铁内部分子电流相互抵消
为什么是假说？
安培提出了分子环流，但在安培时代，还没有建立 物质的分子、原子模型。因此，安培的模型为假说。
0 4
2dI1看ld2 产l1作生试探电流元，磁
I1dl1 rˆ12 r122
I2dl2 dB
(2) I产d生l 的说明dB
dB
0
4
Idl rˆ r2
dE
1
4 0
dq r2
rˆ
dB特 性：
dB
1.1不同的磁作用形式
（1） 磁铁 磁铁
物质成分
天然磁铁：Fe3O4
人工磁铁: 铷铁硼合金 钴镆合金等
最新进展：日本采用纳米技术 制备强磁性氮化铁
中性区 磁极
磁铁分区
条形磁铁的两端磁性强，称作磁极，中部磁性弱，称作中性 区
础－－重视实验研究；
（电流3的）本质我是运国动的科电荷学源头创新的困境思考。
电流方向变化、磁针转动方向也
运动的电荷产生磁场
变化
磁与电的关系
问题 电流对磁铁有作用，磁铁对电流是否有作用？
实验
N 极向内
结论
和磁铁一样，载流导线不仅具有磁性，也受 磁作用力
I=0
I
（3）电流 电流(应该存在作用力)
实验
结论
环向电流
产生磁场的源应该相同
安培分子 环流假说
条形磁铁 环向电流
1822安培提出：组成磁铁的最小单元(磁分子)就是环形电流，这些分子环流定向排列， 在宏观上就会显示出N、S极。
图示 N
等效宏观表面电流 S
磁铁内部分子电流相互抵消
为什么是假说？
安培提出了分子环流，但在安培时代，还没有建立 物质的分子、原子模型。因此，安培的模型为假说。
0 4
2dI1看ld2 产l1作生试探电流元，磁
I1dl1 rˆ12 r122
I2dl2 dB
(2) I产d生l 的说明dB
dB
0
4
Idl rˆ r2
dE
1
4 0
dq r2
rˆ
dB特 性：
dB
电磁学(赵凯华)答案[第4章 电磁介质]
![电磁学(赵凯华)答案[第4章 电磁介质]](https://img.taocdn.com/s3/m/64ee6be37c1cfad6195fa719.png)
1.如图所示，一根细长的永磁棒沿轴向均匀磁化，磁化强度为。
试求图中表示的1、2、3、4、5、6、7各点的磁感应强度和磁场强度。
解永磁体被磁化，可以认为表面出现磁化电流，由磁化电流与磁化强度的关系，可知。
并且磁化电流产生的磁感应强度可与一细长螺线管产生的磁场等效，所以由细长螺线管磁场分布可知，在细长螺线管轴线上，其端部的磁感应强度恰为其中部的一半，故表明磁感应线连续。
因为沿方向的投影式为所以表明磁场不连续。
2有一圆柱形无限长载流导体，其相对磁导率为，半径为，今有电流沿轴线方向均匀分布，试求： 导体内任一点的 ； （2）导体外任一点的 ； （3）通过长为的圆柱体的纵截面的一半的磁通量。
解 （1）在导体内过距轴线为 的任一点作一个与轴垂直，圆心在轴线上，半径为 的圆周作为积分线路，如图所示。
此圆周与磁场线重合，而且沿圆周 是常数。
故得根据含介质的安培环路定理因导体内电流均匀分布，所以电流密度为在半径为 的截面中所以 ,则（2）在导体外任一点 ，以过这一点而圆心在轴线上的圆周作为积分线路，同样得因 ，故 ，所以 ,(3)如图所示，通过长为的圆柱体纵截面的一半的磁通量为3同轴电缆由两同心导体组成，内层是半径为的导体圆柱，外层是半径分别为、的导体圆筒，如图所示。
两导体内电流等量而反向，均匀分布在横截面上，导体的相对磁导率为,两导体间充满相对磁导率为的不导电的均匀磁介质。
试求在各区域中的分布。
解:对称性分析可知，在半径相等处的磁场强度大小相等，方向与电流方向成右手螺旋关系。
可用含介质时的安培环路定理求得，再由、之间的关系求得分布。
在中，,所以在中所以在中所以在中,, 各区域的方向与内层导体圆柱中的电流方向成右手螺旋关系。
4 一铁环外均匀绕有绝缘导线，导线中通有恒定电流，今若在环上开一条狭缝。
试求：（1）开狭缝前后，铁环中的，和如何变化；（2）铁环与缝隙中的，和。
解由高斯定理可知，磁场中磁感应强度总是闭合曲线，而磁场强度线却不一定连续；的环流是由回路中的传导电流决定的，而的环流是由回路中的传导电流和磁化电流（也称束缚电流）共同决定的。
赵凯华陈煕谋《电磁学》第三版的思考题和习题答案
解：
其中--
7、 把电偶极矩 P= ql 的电偶极子放在点电荷 Q 的电场内，P 的中心 O 到 Q 的距离为 r(r>>l), 分别求：（1）P//QO 和（2）P⊥QO 时偶极子所受的力 F 和力矩 L。 解：（1）
F 的作用线过轴心 O，力矩为零 （2）
8、 附图中所示是一种电四极子，它由两个相同的电偶极子 P=ql 组成，这两偶极子在一直 线上，但方向相反，它们的负电荷重合在一起。证明：在它们的延长线上离中心为 r 处， 解： 9、附图中所示为另一种电四极子，设 q 和 l 都已知，图中 P 点到电四极子中心 O 的距离为 x.PO 与正方形的一对边平行。求 P 点的电场强度 E。当 x>>l 时，E=？ 解： 10、均匀带电细棒（1）在通过自身端点的垂直面上和（2）在自身的延长线上的场强分布， 设棒长为 2l，带电总量为 q . 解：（1）一端的垂直面上任一点 A 处
解：（1）电子的运动方程得
(2 ) -----------------------------------------------------------------------------------------------------------------§1.3 高斯定理 思考题： 1、 一般地说，电力线代表点电荷在电场中运动的轨迹吗？为什么？ 答：一般情况下，电力线不代表点电荷在电场中运动的轨迹。因为电力线一般是曲线，若电 荷沿电力线作曲线运动，应有法向力存在；但电力线上各点场强只沿切线方向，运动电荷必 定偏离弯曲的电力线。仅当电力线是直线，且不考虑重力影响时，初速度为零的点电荷才能 沿着电力线运动。若考虑重力影响时，静止的点电荷只能沿竖直方向电力线运动。 2、 空间里的电力线为什么不相交？ 答：电力线上任一点的切线方向即为该点场强方向。如果空间某点有几条电力线相交，过交 点对每条电力线都可作一条切线，则交点处的场强方向不唯一，这与电场中任一点场强有确 定方向相矛盾。 3、 一个点电荷 q 放在球形高斯面的中心处，试问在下列情况下，穿过这高斯面的电通量是 否改变？ （1） 如果第二个点电荷放在高斯球面外附近； （2） 如果第二个点电荷放在高斯球面内； （3） 如果将原来的点电荷移离了高斯球面的球心，但仍在高斯球面内。 答：由于穿过高斯面的电通量仅与其内电量的代数和有关，与面内电荷的分布及面外电荷无 关，所以 （1） ；（2） ；（3） 4、（1）如果上题中高斯球面被一个体积减小一半的立方体表面所代替，而点电荷在立方体 的中心，则穿过该高斯面的电通量如何变化？（2）通过这立方体六个表面之一的电通量是 多少？
赵凯华-电磁学-第三版-第六章----磁介质
（a）组成抗磁质 的物质分 子磁矩：
m分 mi自 旋 mi轨 道 0
i
电介质 无极分子
（b）（电简子单轨说道明磁）矩对ca外se磁1场的响//应B
外加磁场→fL （与f库伦同向）→f向心增加
B0
→轨道线速度V 增加(f向心=mv2/r）(r=c)
V
m m
[讨论]
外
部
磁
化
磁
场
B0增
加
，M
增
加
在 真 均 匀
空 中 ，M 0( 没 有 磁 磁 化 ：M （r）＝C，
介
质)；
(2)
磁化强度
M
与磁化电流 I的关系
电极化中
e，Pe的关系
比
较
磁化中
I ，M的 关 系
推导方法： 高斯定理
推导方法： 安培环路 定理（？）
3、 （定量）磁化描述：－－磁介质产生 B 大小的衡量
(1)
磁化强度
M
定义： 单位体积内磁分子的分子磁矩之矢量和，即
M
m分
V
单位：
安 米2 米3
安米
M n m分 n i分a
n：单位体积内的磁介质分子数
当 没 有 外 磁 场 时 ，M 0，B 0， 非 永 久 磁 体 ；
质
为
纯
数(
M、H同
量
纲
）
，
线
性时
与H无
关
，
各
点
的
可
m
以
不
同
电磁学(赵凯华,陈熙谋第三版)第四章 习题及解答
!%
介质的电容器并联，于是有 % & %$ ’%%
& !$ !& $$
’!% !& $% " #
习题 ! ! "
新概念物理教程·电磁学! ! 第四章! 电磁介质! 习题解答
! ! ! ! "" 如本题图所示，一平行板电容器两极板的面积都是 #，相距为 $，
今在其间平行地插入厚度为 %、介电常量为 ! 的均匀电介质，其面积为 # & "，
!" ’% (!% ’"
)#
#%*
# !% !" !# & * !" ’% (!% ’"
( ) #
$" # +"" # +(" "" # +"" # +%# !&
($ +%# !%" ($" # +&"
+"" # # +%#
!&
+%#
###
$ # )" & +%# !$ $，
$%
#（
!%
!%）!#
,%
（&）极板间电势差 *；
（!）两层介质中的电位移 +"
解：（$） 设上极板带正电，面电荷密度为 "!% ，下极板带负电，面电
荷密度为 !"!% ，则可得
#
#
+ & "!% ，#
,$
&+ !$ !%
& "!% ，# !$ !%
赵凯华电磁学第三版电磁感应与暂态过程141pages精品PPT课件
dt k为比例系数，在SI制中：k=1 ，定律表成
d
dt
2、定律讨论
（1）N 匝串联，总电动势
N
i
i 1
d dt
N
i
i 1
d
dt
N
i 为总磁通，或称为磁链。 i 1
若 1 2 N → → N
（2） 的大小
N d
dt
d ，并非 dt
（3） 的正负 （的负号说明）
第五章 电磁感应与暂态过程
§0 引言 §1 电磁感应定律 §2 动生电动势和感生电动势 §3 互感和自感 §4 暂态过程
§0 引言
电流（运动的电）产生磁场，磁场是否产生电场？
磁生电的发现、认识历程。
安培，科拉顿的认识及做法：
大电流→强磁场。一般情况下，没有观察到磁产生的电，磁场
不够强，采用大电流\强磁场产生电。
0,
B(t) / B(t) Vx / xx
例2：无限长直导线，流稳恒电流，线圈运动形式如图所
示
I
解： ① 1 0
①
v
② 在如图所示的正环绕方向下
2
xb 0I adx 0Ia ln x b
x 2x
2 x
2
d2
dt
0 Ia 2
d dx
ln
x b x
dx dt
b x(t) a ②
v
(b)相对于磁场运动的大块 金属
状，称其为涡电流， 简称涡流。
单个金属闭合回路
大块导体
2、涡流的磁场与引起涡流的磁场的相位关系 （由楞次定律分析）
B(t)
B’(t)
Hale Waihona Puke 3、涡流的物理效应(1)热效应：电流通过导体产生焦耳热。 应用：真空熔炼、熔化焊接；电磁灶。 危害：涡流损耗---变压器、电机铁芯，制成片状， 缩小涡流范围，减少损耗。
d
dt
2、定律讨论
（1）N 匝串联，总电动势
N
i
i 1
d dt
N
i
i 1
d
dt
N
i 为总磁通，或称为磁链。 i 1
若 1 2 N → → N
（2） 的大小
N d
dt
d ，并非 dt
（3） 的正负 （的负号说明）
第五章 电磁感应与暂态过程
§0 引言 §1 电磁感应定律 §2 动生电动势和感生电动势 §3 互感和自感 §4 暂态过程
§0 引言
电流（运动的电）产生磁场，磁场是否产生电场？
磁生电的发现、认识历程。
安培，科拉顿的认识及做法：
大电流→强磁场。一般情况下，没有观察到磁产生的电，磁场
不够强，采用大电流\强磁场产生电。
0,
B(t) / B(t) Vx / xx
例2：无限长直导线，流稳恒电流，线圈运动形式如图所
示
I
解： ① 1 0
①
v
② 在如图所示的正环绕方向下
2
xb 0I adx 0Ia ln x b
x 2x
2 x
2
d2
dt
0 Ia 2
d dx
ln
x b x
dx dt
b x(t) a ②
v
(b)相对于磁场运动的大块 金属
状，称其为涡电流， 简称涡流。
单个金属闭合回路
大块导体
2、涡流的磁场与引起涡流的磁场的相位关系 （由楞次定律分析）
B(t)
B’(t)
Hale Waihona Puke 3、涡流的物理效应(1)热效应：电流通过导体产生焦耳热。 应用：真空熔炼、熔化焊接；电磁灶。 危害：涡流损耗---变压器、电机铁芯，制成片状， 缩小涡流范围，减少损耗。
赵凯华 电磁学 第三版 第三章 恒定电流 38 pages
dq(t ) ∆q 电流仅在某一导体截面上有定义， 电流仅在某一导体截面上有定义，在某一点 I = ∆t → 0 I = 单位： 上没有定义，不具备定义矢量条件 单位：安培 矢量条件。 上没有定义，不具备定义矢量条件。 dt ∆t
5.电流密度 5.电流密度 current density （1）为什么引入电流密度？ 为什么引入电流密度？ 在大块导体中， 在大块导体中，各处的电荷流动速度不同
J 2 , ∆S 2
v J
J 1 , ∆ S1
性质2 稳恒时， 性质2：稳恒时，电流管中电流密度与电流 管界面成反比 同电场线性质） 反比（ 管界面成反比（同电场线性质）疏密 、大小
欧姆定律、电阻、 三 欧姆定律、电阻、电阻率 1. 欧姆定律 表述：在稳恒条件下， (1) 表述：在稳恒条件下，通过一段导体 的电流强度和导体两端的电压成正比 的电流强度和导体两端的电压成正比 U I = r v R 问题1 (2) 问题1：引入电位的条件是 ∫ E ⋅ d l = 0 静电场条件下满足， 静电场条件下满足，为什么在稳恒电 场中场中也能引入电压？ 场中也能引入电压 场中场中也能引入电压？ 电荷静止不动 电荷运动 电荷分布不变 静电场 仅有电荷产 仅有电荷产 生的静电场 生的静电场
r r 电流线终止于 终止于dq/dt>0处 处 J ⋅ d s < 0 电流线终止于
电流线终止于 电流线终止于-dq/dt<0处 终止于 处
正电荷增加处） （即dq/dt>0 --->正电荷增加处） 正电荷增加处
电力线终止于 电力线终止于q<0 终止于
处 电流线由何处发出？ 电流线由何处发出？ -dq/dt>0处 , 即dq/dt<0
2.电流线与电荷运动、增减的 2.电流线与电荷运动、增减的 电流线与电荷运动 2.关系 2.关系 图像理解
赵凯华电磁学第三版磁介质共69页文档
赵凯华电磁学第三版磁介质
1、纪律是管理关系的形式。——阿法 纳西耶 夫 2、改革如果不讲纪律，就难以成功。
3、道德行为训练，不是通过语言影响 ，而是 让儿童 练习良 好道德 行为， 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体，养 成儿童 自觉的 纪律性 ，这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
谢谢！
36、自己的鞋子，自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢，但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何，且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔，思而不学则殆。——孔子
1、纪律是管理关系的形式。——阿法 纳西耶 夫 2、改革如果不讲纪律，就难以成功。
3、道德行为训练，不是通过语言影响 ，而是 让儿童 练习良 好道德 行为， 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体，养 成儿童 自觉的 纪律性 ，这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
谢谢！
36、自己的鞋子，自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢，但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何，且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔，思而不学则殆。——孔子
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第六章 磁介质
导引概念
作业：p388 3,4,5
物质处在外磁场中，在外磁场作用下能发生变 化，并能反过来影响外磁场的媒质叫做磁介 质。
各种物质都是磁介质
在外磁场作用下磁介质出现磁性或磁性发生变化 的现象称为磁化
§1 分子电流观点
1.1、介质的磁化
1.介质与磁场的作用（与电场比较 ）
电介质电场的产生 电场对电介质的作用
1、磁介质与磁场间的相互影响
外场 B0 磁介质 磁化 磁化电流 I 激发B B0 B B
最终决定介质磁化的是总磁场
B B0 B'
2、示例
求充满磁介质的螺绕环内的总场 B 。
设螺绕环通电流 I0 ，介质均匀磁化，强度为M ，
则
B0 B
0nI0 0i
0
M
i 0
i
两者同向，总磁场为：B
B0
B
B 0 ( nI i ) 0nI 0 M
问题：M, i 仍然是未知量，如何求总磁场？
1.3 磁场强度 H， 磁介质中的场方程（比较静电场）
1. 对比 磁场
电场
B
B0
B( M
)
引入H f (B)
消去M , 省去磁
如 何 求H?
化
电
流
的
分
E
E0
E(P )
引
入
D
0
E
析消
0
P
nˆ
将I M dl 用于介质表面
M
L
Mt
I il M dl Mtl
il
i
L
Mt l
Mt
i
M 1sin
l i
M
n
不同磁介质L表面的磁化电流分析Байду номын сангаас
iL
M
n
M n : :介为质磁表介面质的磁法化向强矢度量
i 0
底面 n
i
i 0
n
侧面
1.2 磁介质内的总磁场
a
dl
nm分 子 dl M dl
● 穿越安培回路L分子环流电流强度： dI M dl
I dI M dl 穿出
L
穿入
L
L
● 均匀磁介质 (比较电介质)
均匀磁介质
均匀电介质
(b)磁表化LM 面电电流 d流面l：密i度I与 M磁 0?化强度的表 关S面 P系电dS荷 ： nqe
→本质上是对电介质电荷的作用 →物质的电结构→电偶极子
磁介质磁场的产生 磁场对磁介质的作用
→对物质电流的作用 →物质的电流（磁结构）→？
2、用分子电流观点解释磁化现象
（1）历史上首先形成的解释磁化的观点: 磁荷观点
(a)认为磁场由磁荷产生，磁介质同电介质；
(b)该观点不符合现代物质结构； (c) 但可用于计算（简单）；可解释磁化现象（如
介
质)；
(2)
磁化强度
M
与磁化电流
I
的关系
电极化中
e，Pe的关系
比
较
磁化中
I ，M的 关 系
推导方法： 高斯定理
推导方法： 安培环路 定理（？）
e SPPdnS qe
M dl I
L i M?
(a) 穿越磁介质内安培环路的磁化电流 I I M dl L
L
仅穿越回路L的C类分子对电流有贡献
去P ,
省
去
极
化电
荷
D的 求 解 ： D S q0
S
的
分
析
2. H的 定 义 及 求 解
B dl 0 I 0 I0 0 I 0 I0 0 M dl
传导电流 分子电流
( B 0 M ) dl 0 I0 ( B 0 M ) dl I0
定义：H B 0 M H dl I0
(3)极磁化化电电荷流→（产生对比E极→化总电电荷场）：
E
E0
E
磁化电流→产生 B→ 总磁场： B B0 B
问题 （1）磁化电流产生磁场遵守的定律？
（2）磁化电流总存在磁介质表面？
（3） B B0 B 仅适于介质内部？ （4）磁化电流是否有热效应？
3、 （定量）磁化描述：－－磁介质产生 B 大小的衡量
退磁）（自学）。
（2） 分子电流观点（讲授）
(2) 分子电流观点
（a）分子等效磁矩
组成磁介质分子的原子核、电子组成的复杂
带电系统。 由于电子、原子核的运动，分子有 一个等效电流i ,相应有一个分子等效磁矩
m分 i分 a
i分
a
m分
按照量子力学的观点：
m分 是各个的电子轨道磁矩、电子自旋磁矩、原子
C类分子的所在空间：分子电流环中心与
c dl
边界L的距离<分子电流环半径
dl 段上的C类分子数（下页)
三类磁分子
L cc
dl
d
l
M
a分
dl
ddl以段N上dl的n为cd类棱V分的子斜数n柱（ ：体分的a子分 d中子l心） 数在以
a
为底，
穿越 dl
dI
段上的分子环流的电流 强度： i分dN i分na dl ni分
H dl I0(自由电荷电流)
D dS q0(自由电荷)
S
3. 磁介质存在时磁场中的“高斯定理”
B dS ( B0 B ) dS B0 dS B dS 0 0 0
S
S
S
S
应用：两种不同磁介质中
连续
B连续，但 “折射”
B2
B1
问题：仅采用 H dl I0，是否可得到B？
磁介质存在时的 安培环路定理
H的 名 称 ： 磁 场 强 度
单 位 ： 安 培/ 米 H dl I0 ,常 用 单 位 ： 奥 斯 特(Oe )
1Oe
103
4
安培 米
理
解
H dl I0
L与I0成
右
手
系,
I0为
传
导
电流
。
H定 义 为 磁 场 强 度 ， 对 应静 电 学 中 的E，D？
例子
轴 对 称
2rH
I0
H
I
0
2r
H
B
0
M
B
0
(
H
M
)
I0
尚 需 条 件 ：M f ( H ) 磁化规律
下一节
§2 等效的磁荷观点（自学要点） P561-562 P580表6-2
P581最后一段
(1)
磁化强度
M
定义： 单位体积内磁分子的分子磁矩之矢量和，即
M
m分
V
单位：
安 米2 米3
安米
M
n
m分
n
i分a
n：单位体积内的磁介质分子数
当 没 有 外 磁 场 时 ，M 0，B 0， 非 永 久 磁 体 ；
[讨论]
外
部
磁
化
磁
场
B0增
加
，M
增
加
在 真 均 匀
空 中 ，M 0( 没 有 磁 磁 化 ：M（r）＝C，
核磁矩的总和。
（b）按分子等效磁矩特性进行 磁介质分类 B0 0时 ，m分 0 ,分子具有固有磁矩，称为 顺磁质
顺磁质的磁化
何谓“顺
无外场时：各分子的磁矩取向杂乱无章，宏观对外不显磁性
（无磁场）
B0 0
B0 0
有外场时：分子磁矩在外磁场的作用下，一定程度上沿 外磁场方向有序排列。 对外表现出宏观磁性 （产生磁场） 宏观磁化电流（下页）
导引概念
作业：p388 3,4,5
物质处在外磁场中，在外磁场作用下能发生变 化，并能反过来影响外磁场的媒质叫做磁介 质。
各种物质都是磁介质
在外磁场作用下磁介质出现磁性或磁性发生变化 的现象称为磁化
§1 分子电流观点
1.1、介质的磁化
1.介质与磁场的作用（与电场比较 ）
电介质电场的产生 电场对电介质的作用
1、磁介质与磁场间的相互影响
外场 B0 磁介质 磁化 磁化电流 I 激发B B0 B B
最终决定介质磁化的是总磁场
B B0 B'
2、示例
求充满磁介质的螺绕环内的总场 B 。
设螺绕环通电流 I0 ，介质均匀磁化，强度为M ，
则
B0 B
0nI0 0i
0
M
i 0
i
两者同向，总磁场为：B
B0
B
B 0 ( nI i ) 0nI 0 M
问题：M, i 仍然是未知量，如何求总磁场？
1.3 磁场强度 H， 磁介质中的场方程（比较静电场）
1. 对比 磁场
电场
B
B0
B( M
)
引入H f (B)
消去M , 省去磁
如 何 求H?
化
电
流
的
分
E
E0
E(P )
引
入
D
0
E
析消
0
P
nˆ
将I M dl 用于介质表面
M
L
Mt
I il M dl Mtl
il
i
L
Mt l
Mt
i
M 1sin
l i
M
n
不同磁介质L表面的磁化电流分析Байду номын сангаас
iL
M
n
M n : :介为质磁表介面质的磁法化向强矢度量
i 0
底面 n
i
i 0
n
侧面
1.2 磁介质内的总磁场
a
dl
nm分 子 dl M dl
● 穿越安培回路L分子环流电流强度： dI M dl
I dI M dl 穿出
L
穿入
L
L
● 均匀磁介质 (比较电介质)
均匀磁介质
均匀电介质
(b)磁表化LM 面电电流 d流面l：密i度I与 M磁 0?化强度的表 关S面 P系电dS荷 ： nqe
→本质上是对电介质电荷的作用 →物质的电结构→电偶极子
磁介质磁场的产生 磁场对磁介质的作用
→对物质电流的作用 →物质的电流（磁结构）→？
2、用分子电流观点解释磁化现象
（1）历史上首先形成的解释磁化的观点: 磁荷观点
(a)认为磁场由磁荷产生，磁介质同电介质；
(b)该观点不符合现代物质结构； (c) 但可用于计算（简单）；可解释磁化现象（如
介
质)；
(2)
磁化强度
M
与磁化电流
I
的关系
电极化中
e，Pe的关系
比
较
磁化中
I ，M的 关 系
推导方法： 高斯定理
推导方法： 安培环路 定理（？）
e SPPdnS qe
M dl I
L i M?
(a) 穿越磁介质内安培环路的磁化电流 I I M dl L
L
仅穿越回路L的C类分子对电流有贡献
去P ,
省
去
极
化电
荷
D的 求 解 ： D S q0
S
的
分
析
2. H的 定 义 及 求 解
B dl 0 I 0 I0 0 I 0 I0 0 M dl
传导电流 分子电流
( B 0 M ) dl 0 I0 ( B 0 M ) dl I0
定义：H B 0 M H dl I0
(3)极磁化化电电荷流→（产生对比E极→化总电电荷场）：
E
E0
E
磁化电流→产生 B→ 总磁场： B B0 B
问题 （1）磁化电流产生磁场遵守的定律？
（2）磁化电流总存在磁介质表面？
（3） B B0 B 仅适于介质内部？ （4）磁化电流是否有热效应？
3、 （定量）磁化描述：－－磁介质产生 B 大小的衡量
退磁）（自学）。
（2） 分子电流观点（讲授）
(2) 分子电流观点
（a）分子等效磁矩
组成磁介质分子的原子核、电子组成的复杂
带电系统。 由于电子、原子核的运动，分子有 一个等效电流i ,相应有一个分子等效磁矩
m分 i分 a
i分
a
m分
按照量子力学的观点：
m分 是各个的电子轨道磁矩、电子自旋磁矩、原子
C类分子的所在空间：分子电流环中心与
c dl
边界L的距离<分子电流环半径
dl 段上的C类分子数（下页)
三类磁分子
L cc
dl
d
l
M
a分
dl
ddl以段N上dl的n为cd类棱V分的子斜数n柱（ ：体分的a子分 d中子l心） 数在以
a
为底，
穿越 dl
dI
段上的分子环流的电流 强度： i分dN i分na dl ni分
H dl I0(自由电荷电流)
D dS q0(自由电荷)
S
3. 磁介质存在时磁场中的“高斯定理”
B dS ( B0 B ) dS B0 dS B dS 0 0 0
S
S
S
S
应用：两种不同磁介质中
连续
B连续，但 “折射”
B2
B1
问题：仅采用 H dl I0，是否可得到B？
磁介质存在时的 安培环路定理
H的 名 称 ： 磁 场 强 度
单 位 ： 安 培/ 米 H dl I0 ,常 用 单 位 ： 奥 斯 特(Oe )
1Oe
103
4
安培 米
理
解
H dl I0
L与I0成
右
手
系,
I0为
传
导
电流
。
H定 义 为 磁 场 强 度 ， 对 应静 电 学 中 的E，D？
例子
轴 对 称
2rH
I0
H
I
0
2r
H
B
0
M
B
0
(
H
M
)
I0
尚 需 条 件 ：M f ( H ) 磁化规律
下一节
§2 等效的磁荷观点（自学要点） P561-562 P580表6-2
P581最后一段
(1)
磁化强度
M
定义： 单位体积内磁分子的分子磁矩之矢量和，即
M
m分
V
单位：
安 米2 米3
安米
M
n
m分
n
i分a
n：单位体积内的磁介质分子数
当 没 有 外 磁 场 时 ，M 0，B 0， 非 永 久 磁 体 ；
[讨论]
外
部
磁
化
磁
场
B0增
加
，M
增
加
在 真 均 匀
空 中 ，M 0( 没 有 磁 磁 化 ：M（r）＝C，
核磁矩的总和。
（b）按分子等效磁矩特性进行 磁介质分类 B0 0时 ，m分 0 ,分子具有固有磁矩，称为 顺磁质
顺磁质的磁化
何谓“顺
无外场时：各分子的磁矩取向杂乱无章，宏观对外不显磁性
（无磁场）
B0 0
B0 0
有外场时：分子磁矩在外磁场的作用下，一定程度上沿 外磁场方向有序排列。 对外表现出宏观磁性 （产生磁场） 宏观磁化电流（下页）