水平荷载作用下的结构侧移计算
框架结构课程设计(1)
M bl
r Mb
Mu c
l ib M bl l r ( M cu M cl ) ib ib r ib r M b l r ( M cu M cl ) ib ib
水平荷载作用下的D值法 六、梁剪力、柱轴力等 同用分层法进行竖向荷载下内力计算,即:
取各梁为隔离体,由平衡关系 求得梁端剪力。
15.81kN 27.39kN 31.77kN 22.33kN
A2
15.81kN
B2
59.16kN
C2
22.33kN
29.01kN 20.89kN
72.36kN 33.11kN 38.67kN
35.53kN 28.83kN
A1
49.9kN
B1
144.14kN
C1
64.36kN
竖向荷载作用下的分层法
框架在竖向荷载作用下的计算简图:
双 向 板
双向板
单
向
板
用分层法进行竖向荷载作用下框架的内力计算。
框架在水平荷载(风载)作用下的计算简图:
视为均匀分布,风压高度变 化系数按框架顶部标高确定。
进一步将均布荷载简化为作 用在梁柱节点上的水平集中力。
框架在水平荷载(风载)作用下的计算简图:
用反弯点法或D值法进行水平荷载作用下框架的内力计算。
梁端截面: M max、 M max、Vmax
跨中截面: M max
M max 及相应的N和V
Nmax及相应的M和V
N min及相应的M和V
六、框架结构的结构构件设计
1、排架柱的计算长度l0(见教材表13-2) 2、框架节点的构造要求
A2 15.81
B2 59.16
C2 22.33
框架结构的内力和位移计算

框架梁跨中截面: T型截面
框架梁支座截面: 矩形截面
边框架:I=I0
注:I0为矩形截面框架梁的截面惯性矩
框架结构的内力和位移计算
10
§ 3.2 竖向荷载作用下的近似计算方法——分层法 计算假定:
➢ 多层多跨框架在一般竖向荷载作用下,侧移小, 作为无侧移框架按力矩分配法进行内力分析
➢ 多层框架简化为单层框架,分层作力矩分配计算
17
2 弯矩二次分配法
具体计算步骤: (1)根据各杆件的线刚度计算各节点的杆端弯矩
分配系数,并计算竖向荷载作用下各跨梁的固端弯矩。 (2)计算框架各节点的不平衡弯矩,并对所有节
点的不平衡弯矩同时进行第一次分配(其间不进行弯 矩传递)。
框架结构的内力和位移计算
18
(3)将所有杆端的分配弯矩同时向其远端传递(对 于刚接框架,传递系数均取1/2)。
首先,将多层框架分解成一层一层的单层框架
框架结构的内力和位移计算
12
分层法 例题:
框架结构的内力和位移计算
13
分层法
力学知识回顾
➢转动刚度——对转动的抵抗能力。杆端的转动刚度以S表示 等于杆端产生单位转角时需要施加的力矩。
➢固端弯矩 方向 +
框架结构的内力和位移计算
14
分层法
➢传递系数
➢分配系数
框架结构的内力和位移计算
2
荷载和设计要求
步骤四:内力计算 ➢ 竖向恒荷载作用下内力计算 ➢ 竖向活荷载作用下内力计算 ➢ 水平风荷载作用下内力计算 ➢ 地震作用下内力计算
步骤五:侧移验算 ➢ 侧移不满足要求回到步骤一
步骤六:控制截面及控制截面内力调整 ➢ 梁柱轴线端内力调整至构件边缘端 ➢ 竖向荷载梁端出现塑铰产生的塑性内力重分布
3框架内力与位移计算5(水平位移)

(3-22)
N是水平荷载引起的边柱内力。令水平荷载引起的总力矩为M(z),则 N=±M(z)/B (c) A为边柱截面面积。假定边柱截面沿z轴呈直线变化,令 n=A顶/A底 A(z)=[1-(1-n)z/H] A底 (d) A顶及A底分别为顶层柱及底层柱截面面积。
2 把式(b)、(c)、(d)代人式(a)得 EB2 A底
(d)
2 EB2 A底
N j
N j
Hj
( H j z)M ( z) 1 (1 n) z / H
0
dz
(e)
M(z)与外荷载有关,积分后得到的计算公式如下:
V0 H 3 Fn EB2 A底
式中,V0——基底剪力; Fn——系数。 在不同荷载形式下,V0及Fn不同。V0可根据荷载计算。
作 业 练 习
梁、柱杆件的轴向变形、弯曲变形对框架在水平荷载下的侧移变形有何影响? 框 架为什么具有剪切型侧向变形曲线?
作业题:某三层两跨框架,跨度及层高、尺寸如图,柱截面积尺寸300×350,左跨梁截面为250×500,
0.8kN 3.60m
右跨梁截面为250×400,现浇梁柱及楼面,采用C30钢筋混凝土(Ec=3.0×104MPa),试求其相对侧移δ、 绝对侧移Δ;并比较和分析ΔM 和ΔN 在Δ中所占比例 。
j层侧移 i 1 n M M 顶点侧移 n i i 1
M i
【例3—4 】 求图所示三跨 12 层框架内杆件弯曲产生的顶点侧移 Δn 及最 大层间侧移 δj,层高 h=400cm,总高 H=400×12=4800cm, 弹性模量 E=2.0×104MPa。各层梁截面尺寸相同,柱截面 尺寸有四种,7层以上柱断面尺寸减小,内柱、外柱尺寸不 同,详见图中所注。
多层框架结构的荷载、内力和侧移计算

分层法计算内力时,假定上、下柱的远端是固定的, 但实际上除底层柱外,其它各层柱均是弹性支承,有转 角产生。为了减少计算中的误差,将除底层柱以外的其 它各层柱的线刚度乘以折减系数0.9,并取它的传递系数 为1/3;底层柱不折减,传递系数取1/2。
分层法适用于节点梁柱线刚度比,结构和荷 载沿高度变化不大的规则框生单位水平位移
时柱中产生的剪力,与两端约束条件有关。根据 假定②,各柱端转角为零,柱的侧移刚度为
D 12ic / h2
式中: ic —柱的线刚度; h —柱的高度。
(7-2)
③ 同层各柱剪力。
以图7-9(b)为例,将框架沿第i层各柱的反弯点处切
开,令Vi为框架第i层的层间剪力,它等于i层以上所有水 平力之和;Vik为第i层第k根柱分配到的剪力,假定第i层 共有m根柱,由层间水平力平衡条件得
M
d ik
Vik (1/ 2)h
(7-9)
式中:M
u ik
、M
d ik
--柱子上端和下端弯矩;
h —-第 i 层柱的柱高。
⑤ 梁端弯矩。
根据节点平衡条件,梁端弯矩之和等于柱端
弯矩之和,节点左右梁端弯矩大小按其线刚度
2)弯矩分配法。
由分层法的计算可知,多层框架某节点的不 平衡弯矩仅对与其相邻的节点影响较大,对较远 节点的影响较小,因而可将各节点的不平衡弯矩 进行第一次分配,并向远端传递,再将新的不平 衡弯矩进行第二次分配,此即弯矩二次分配法。
具体计算步骤为:
① 根据各杆件的线刚度计算各节点的杆端弯矩分配 系数。
Vik
d ik
m
Vi
dik
(7-6)
k 1
由此可见,同层各柱剪力是按各柱间的侧移刚
第四章 框架结构内力计算

4、计算和确定梁、柱弯矩分配系数。 按修正后的刚度计算各结点周围杆件的杆 端分配系数。 5、按力矩分配法计算单层梁、柱弯矩。 6、将每个单层框架的计算结果按相应部分迭 加起来便得到原框架的计算结果,即柱的弯矩 取相邻两个单元中同一柱对应弯矩之和,而梁 的弯矩直接采用。
四、计算例题
作业2
3.2 水平荷载下内力的近似计算—反弯点法
d
i 1
m
V pj
ij
4、柱端弯矩的确定 M j V jY j 柱下端弯矩 柱上端弯矩 M j V j (h j Yj )
5、梁端弯矩的确定 M ml (M mt M m1b ) 对于边柱 ibl 对于中柱
M ml ( M mt M m1b ) M mr ibl ibr ibr ( M mt M m1b ) ibl ibr
第3章 框架结构的内力和位移计算
3.1 竖向荷载下内力的近似计算—分层法 3.2 水平荷载下内力的近似计算—反弯点法 3.3 水平荷载下内力的近似计算—D值法 3.4 水平荷载作用下侧移的近似计算
3.1 竖向荷载下内力近似计算—分层法
一、竖向荷载 自重、活荷、雪荷载及施工检修荷载等。 二、分层法的基本假设 1、忽略侧移的影响; 2、忽略每层梁的竖向荷载对其它各层梁 的影响。 三、分层法计算要点 1、将N层框架划分成N个单层框架,柱 端假定为固端, 用力矩分配法计算。
三、柱的侧移刚度D 12ic D 2 h
—为柱侧移刚度修正系数,表示梁柱刚 度比对柱侧移刚度的影响。
四、剪力计算 有了D值后,与反弯点法类似,计算各柱分 配的剪力 Dij Vij V pj Dij 五、确定柱反弯点高度比 影响柱反弯点高度的主要因素是柱上下端的 约束条件。
框架—侧移计算例题上课讲义

侧移验算——剪切型变形计算
对第i层柱,其层间相 对侧移为:
uiM
Vi
m
Dij
j 1
i
对第i层柱顶的侧移为:uiM uk k 1
n
顶层柱顶的侧移为: unM uk k 1
侧移验算——弯曲型变形计算
建筑高度越大,宽度越小,则在水平荷载作用下由 轴向变形引起的侧移越大。对于高度不大于50m或高宽 比小于4的钢筋混凝土框架结构,柱轴向变形引起的顶 点位移在框架梁柱弯曲变形引起的顶点侧移的5%以内, 可以忽略不计。
(0.6)
(0.9)
3.3m
74kN
C
(1.7) G
(1.0)
K
(0.7)
(0.9)
B
80.7kN
(2.4) F
(0.6)
(0.8)
A
E
2.7m
(1.2)
8.1m
(0.9) 3.3m
J
(0.8) 3.9m
I
解:由于框架同层各柱 h 相等,可直接用杆件线刚度的相对值计算各柱的
分配系数。
DH
M
(1)求各柱剪力分配系数:
侧移验算—— 侧移值要求
高度不大于150m的框架结构在正常使用条件下的变 形验算要求各层的层间侧移值与该层层高之比不宜超过 1/550的限值,即:
ui hi 1 550
详情请参阅《高规》。
用反弯点法求下图框架的弯矩图。图中括号内的数值为该杆
的线刚度比值。
37kN D
H
(1.5)
M (0.8)
(0.7)
)
1.0 1.7 1.0
30.56kN
M GC
(M GH
水平作用下框架结构侧移计算
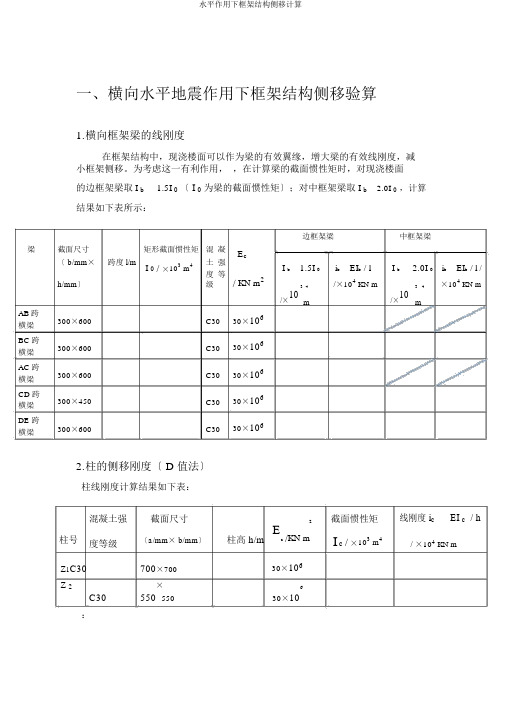
一、横向水平地震作用下框架结构侧移验算1.横向框架梁的线刚度在框架结构中,现浇楼面可以作为梁的有效翼缘,增大梁的有效线刚度,减小框架侧移。
为考虑这一有利作用, ,在计算梁的截面惯性矩时,对现浇楼面的边框架梁取 I b1.5I 0 〔 I 0 为梁的截面惯性矩〕;对中框架梁取 I b2.0I 0 ,计算结果如下表所示:边框架梁中框架梁梁截面尺寸矩形截面惯性矩 混 凝E c〔 b/mm ×跨度 l/m土 强i b EI b / li b EI b / l /I 0 / ×103 m4I b1.5I 0I b 2.0I 0h/mm 〕度 等/ KN m2/×104KN m×104KN m级3 4/×103 4/×10mmAB 跨 300×600C3030×106横梁BC 跨 300×600C3030×106横梁AC 跨 300×600C30 30×106横梁CD 跨 300×450C3030×106横梁DE 跨 300×600C3030×106横梁2.柱的侧移刚度〔 D 值法〕柱线刚度计算结果如下表:混凝土强 截面尺寸2截面惯性矩线刚度 i c EI c / h柱号度等级〔a/mm × b/mm 〕柱高 h/mEc/KN mIc / ×103 m 4/ ×104 KN mZ 1C30 700×70030×106Z 2C30 ×6550 55030×10:楼层横向框架柱侧移刚度〔 D 值〕计算如下表所示:Ki b K(一般层 )(一般层 )2i c K12柱类型Dic h 2根数i b/ 104KN / mK K(底层 )2(底层 )i c K一层其他层边框架边柱边框架中柱中框架边柱中框架中柱D边框架边柱边框架中柱中框架边柱中框架中柱DA 轴2E 轴2C 轴2D 轴2A 轴2B 轴4E 轴6B 轴2C 轴6D 轴6653520KN/mA 轴2E 轴2C 轴2D 轴2A 轴2B 轴4E 轴6B 轴2C 轴6D 轴6794540KN/m3.横向框架自振周期结构自振周期按顶点位移法计算,将各楼层面处的重力荷载代表值G i作为水平荷载作用在各楼层标高处,按弹性方法求得结构顶点的假想侧移,并考虑填充墙对框架的影响取折减系数r,计算结果如下表结构顶点的假想侧移G/KN nG i/KND i / KN m 1i / mm i / mm楼层V Gii 16999099907945405114582144879454041145832906794540311458443647945402114585582279454011241563237653520T1T T4.横向水平地震作用及楼层地震剪力计算本结构重量和刚度沿高度方向分布比拟均匀,高度不超过40m,变形以剪切变形为主,故水平地震作用采用底部剪力法计算。
水平荷载作用下结构侧移计算
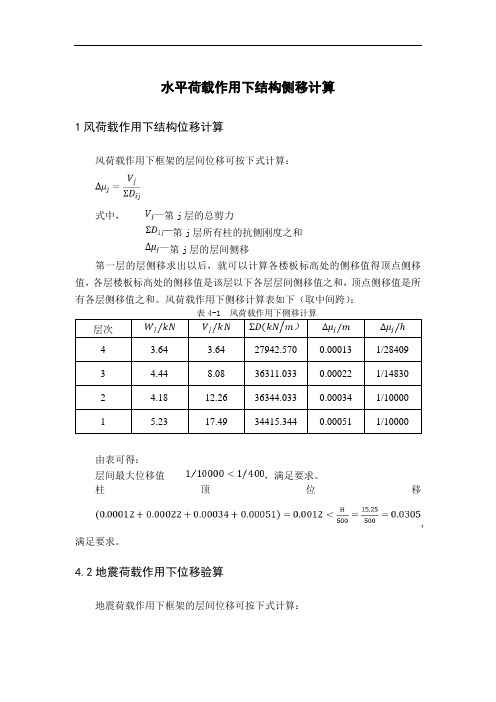
水平荷载作用下结构侧移计算
1风荷载作用下结构位移计算
风荷载作用下框架的层间位移可按下式计算:
式中,第j层的总剪力
第j层所有柱的抗侧刚度之和
第j层的层间侧移
第一层的层侧移求出以后,就可以计算各楼板标高处的侧移值得顶点侧移值,各层楼板标高处的侧移值是该层以下各层层间侧移值之和,顶点侧移值是所有各层侧移值之和。
风荷载作用下侧移计算表如下(取中间跨):
层次
4 3.64 3.64 27942.570 0.00013 1/28409
3 4.4
4 8.08 36311.033 0.00022 1/14830
2 4.18 12.26 36344.03
3 0.0003
4 1/10000
1 5.23 17.49 34415.344 0.00051 1/10000
由表可得:
层间最大位移值,满足要求。
柱顶位移
,满足要求。
4.2地震荷载作用下位移验算
地震荷载作用下框架的层间位移可按下式计算:
式中,第j层的总剪力
第j层所有柱的抗侧刚度之和
第j层的层间侧移
层次
4 127.92 127.92 27942.570 0.004
5 1/806
3 106.27 234.19 36311.033 0.0065 1/513
2 74.27 308.46 36344.03
3 0.0085 1/389
1 50.50 358.96 34415.344 0.0104 1/473
由表可知:
(1)、各层层间位移角均小于1/250,满足要求。
(2)、顶点位移
,满足要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
水平荷载作用下的结构侧移计算
5.1 风荷载作用下的位移验算
(1)侧移刚度(表5.1~表5.2所示)
(2)风荷载作用下的框架侧移计算(表5.3~表5.4所示)。
2~5层柱的D 值得计算
采用8.8级摩擦型高强度螺栓M24,摩擦系数μ=0.4,一个螺栓的预拉力P=175kN 。
单个螺栓的抗剪承载力设计值为: N v =0.9n f μp=0.9×1.0×0.4×175kN=63kN n ≥V/N v
表5.1 2-5层柱的D 值
m 21606.5K N/m /K N 7.1026724.5669D =+⨯=
∑)(
表5.2 横向底层柱D 值
构件名称 = =)()(2i /5.0i ++ D=
(kN/m)
A 轴柱 0.236 0.329 17700.54
B 轴柱
0.472
0.393
21144.54
/m 56545.62kN m /kN 54.21144254.17700D =+⨯=∑)(
构件名称 = =/(2+) D=
(kN/m) A 轴柱 0.236 0.105 5669.4 B 轴柱 0.472
0.191
10267.7
水平荷载作用下的框架的层间侧移可按下式计算 Δu j =j v /∑ij D 式中
j v ——第j 层的总剪力;
∑ij D
——
第j 层所有柱的抗侧刚度之和
Δj u ——第j 层的层间侧移
表5.3 集中风荷载标准值
第一层的层间侧移值求出以后,就可就可计算各楼板标高处的侧移值是该层以上各层层间的侧移之和,顶点侧移是所有各层层间侧移之和,框架在风荷载作用下侧移的计算见表5.4:
表5.4 风荷载作用下侧移的计算
侧移验算
层间侧移的最大值1/1739≤1/400满足要求
柱顶侧移的最大值1/10000≤1/500满足要求
5.2 地震作用下的位移验算
各层地震标准值计算结果与地震作用下各层剪力及侧移计算结果见下表5.5:
表5.5横向水平地震作用下框架侧移计算
层间位移验算:
首层Δe u/h=0.00183/5.4=0.00034≤1/250满足要求
二层Δe u/h=0.00 183/4=0.00046 ≤1/250满足要求
顶点位移验算:u/h=0.01643/21.4=0.00077≤1/350。
