第5章Turbo码,现代编码技术、曾凡鑫
Turbo码原理简介
Turbo 码原理简介1993年C.Berrou 、A.Glavieux 和P.Thitimajshiwa 首先提出了称之为Turbo 码的并行级联编译码方案。
Turbo 码性能取决于码的距离特性。
线性码的距离分布同于重量分布,如果低重量的输入序列经编码得到的还是低重量的输出序列,则距离特性变坏。
该特性对于块码来说不存在问题;然而对于卷积码,则是个非常严重的问题。
因为卷积码的距离特性是影响误码率的一个非常重要的因素。
在Turbo 码中,利用递归系统卷积码(RSC)编码器作为成员码时,低重量的输入序列经过编码后可以得到高重量的输出序列。
同时交织器的使用,也能加大码字重量。
实际上,Turbo 码的目标不是追求高的最小距离,而是设计具有尽可能少的低重量码字的码。
Turbo 码由两个递归系统卷积码(RSC)并行级联而成。
译码采用特有的迭代译码算法。
1 Turbo 码编码原理典型的Turbo 码编码器结构框图如图2所示:由两个反馈的编码器(称为成员编码器)通过一个交织器I 并行连接而成。
如果必要,由成员编码器输出的序列经过删余阵,从而可以产生一系列不同码率的码。
例如,对于生成矩阵为g=[g1,g2]的(2,1,2)卷积码通过编码后,如果进行删余,则得到码率为1/2的编码输出序列;如果不进行删余,得到的码率为1/3。
一般情况下,Turbo 码成员编码器是RSC 编码器。
原因在于递归编码器可以改善码的比特误码率性能。
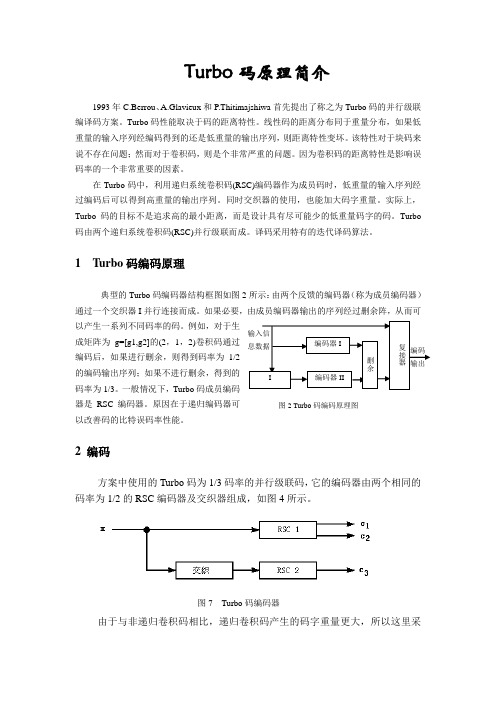
2 编码方案中使用的Turbo 码为1/3码率的并行级联码,它的编码器由两个相同的码率为1/2的RSC 编码器及交织器组成,如图4所示。
由于与非递归卷积码相比,递归卷积码产生的码字重量更大,所以这里采图7 Turbo 码编码器输入信 息数据编码器II编码器II删余复接器编码 输出图2 Turbo 码编码原理图用了两个相同的系统递归卷积码(RSC)。
信息序列分成相同的两路,第一路经过RSC 编码器1,输出系统码1c 及校验码2c 。
turbo 码原理

turbo 码原理Turbo码原理Turbo码是一种优秀的纠错编码技术,它被广泛应用于无线通信、卫星通信、光纤通信等领域。
Turbo码采用了迭代解码的方法,通过在编码和解码过程中引入反馈,从而极大地提高了通信系统的可靠性和性能。
Turbo码的核心原理是使用两个并行的卷积码编码器和迭代解码器。
在编码过程中,数据会经过两个编码器进行编码,生成两个码字序列。
这两个码字序列交替地经过交织器,并通过信道发送。
在接收端,接收到的数据经过迭代解码器进行解码,解码器通过相互交互的方式,不断迭代处理,最终得到正确的原始数据。
Turbo码的迭代解码过程是通过软判决实现的。
软判决是指通过计算接收到的数据与码字之间的距离,得到一个概率值,表示接收到的数据属于哪个码字的概率。
在迭代解码过程中,解码器会根据软判决的结果,调整自身的状态,从而提高解码的准确性。
Turbo码的优势在于其较低的误码率和较高的编码效率。
由于采用了迭代解码的方法,Turbo码能够充分利用信道的统计特性,通过多次迭代,逐渐减小误码率。
同时,Turbo码的编码效率也较高,可以在相同的误码率下传输更多的信息。
Turbo码还具有较好的抗干扰性能。
由于采用了迭代解码的方法,Turbo码能够在一定程度上抵抗信道的噪声和干扰。
在传输过程中,由于噪声和干扰的存在,接收到的数据可能会发生错误。
但是通过多次迭代解码,Turbo码能够逐渐修正这些错误,提高解码的准确性。
然而,Turbo码也有一些局限性。
首先,Turbo码的编码和解码过程相对复杂,需要较高的计算能力和存储资源。
其次,Turbo码的延迟较大,由于需要多次迭代解码,导致信号传输的延迟增加。
此外,Turbo码的设计和调试也较为困难,需要经验丰富的工程师进行系统设计和参数调优。
总体而言,Turbo码作为一种高效可靠的纠错编码技术,已经被广泛应用于通信领域。
它通过迭代解码的方法,充分利用信道的统计特性,提高了通信系统的可靠性和性能。
turbo code 计算方法

turbo code 计算方法摘要:1.引言2.Turbo码的原理3.Turbo码的计算方法4.计算实例5.结论正文:【引言】在数字通信和数据存储领域,纠错码的应用至关重要。
Turbo码作为一种可靠的信道编码技术,凭借其优异的性能在诸多领域得到了广泛应用。
本文将详细介绍Turbo码的计算方法,以期帮助读者更好地理解和应用这一技术。
【Turbo码的原理】Turbo码,又称为递归卷积码,是由Berrou等人于1993年提出的一种信道编码技术。
其基本原理是通过两个或多个简单的卷积码相互交织,构成一个复杂的编码器,从而在信道中实现高效的数据传输。
Turbo码的性能接近香农极限,且具有较好的误码率特性。
【Turbo码的计算方法】Turbo码的计算方法主要包括以下几个步骤:1.初始化:根据输入数据比特,初始化编码器的状态。
2.编码:将输入数据比特序列依次输入到编码器的各个级联卷积码中,计算出编码器的输出比特序列。
3.交织:将编码器的输出比特序列进行交织,得到交织后的比特序列。
4.校验:对交织后的比特序列进行校验,判断是否满足特定的校验条件。
若满足,则继续下一步;否则,进行反馈调整。
5.解交织:将校验后的比特序列进行解交织,得到原始输入数据比特序列。
6.反馈调整:根据解交织后的比特序列,调整编码器的状态,以实现更好的编码效果。
【计算实例】以一个简单的3级Turbo码为例,设编码器的初始状态为0,输入数据比特序列为1011。
根据Turbo码的计算方法,我们可以得到以下结果:1.初始化:状态为02.编码:输入比特1,编码器输出比特为10103.交织:交织后的比特序列为01014.校验:满足校验条件,继续下一步5.解交织:解交织后的比特序列为10106.反馈调整:状态调整为1017.重复步骤2-6,直至输入比特序列结束【结论】Turbo码作为一种高效、可靠的信道编码技术,在数字通信和数据存储等领域具有重要应用价值。
turbo码的原理

turbo码的原理Turbo码的原理引言:Turbo码是一种在无线通信和数字通信领域广泛应用的编码技术。
它被广泛应用于4G和5G移动通信标准中,以提高系统的可靠性和传输速率。
本文将介绍Turbo码的原理及其在通信系统中的应用。
一、Turbo码的基本原理Turbo码是一种迭代卷积码编码技术,由Claude Berrou于1993年提出。
它采用了并行级联的结构,在编码和解码过程中引入了迭代操作,从而大大提高了系统的纠错性能。
Turbo码的编码器由两个相同的卷积码编码器构成,这两个编码器之间通过一个交织器相连,形成了并行级联结构。
在编码过程中,Turbo码将待发送的数据分为多个数据块,并对每个数据块进行并行编码。
首先,数据块通过编码器1进行编码,然后通过交织器进行交织操作,再经过编码器2进行第二次编码。
最后,两个编码器的输出通过一个交织器再次交织,形成最终的编码输出。
二、Turbo码的解码原理Turbo码的解码过程是通过迭代解码算法实现的。
解码器采用迭代信道估计和软判决的方法,通过多次迭代来逐步提高解码的准确性。
在每一次迭代中,解码器利用已解码的信息反馈给信道估计器,用于估计信道的状态信息,并根据此信息对接收到的信号进行修正。
然后,解码器利用修正后的信号进行下一次迭代解码,直到达到设定的迭代次数或满足一定的停止准则为止。
三、Turbo码的应用Turbo码在无线通信和数字通信领域有着广泛的应用。
在4G和5G 移动通信标准中,Turbo码被用于物理层的信道编码,以提高系统在高速移动环境下的可靠性和传输速率。
此外,Turbo码还被应用于卫星通信、光纤通信和深空通信等领域。
Turbo码的优点是能够在相同的误码率下,显著提高系统的传输速率。
它具有较好的纠错性能,在相同的码率下,其误码率性能要优于其他传统的编码技术。
此外,Turbo码还具有较低的复杂度和较低的延迟,适用于实时通信系统。
结论:Turbo码作为一种高效可靠的编码技术,被广泛应用于无线通信和数字通信领域。
turbo码的名词解释

turbo码的名词解释在现代通信领域中,Turbo码是一种强大的编码技术,被广泛应用于无线通信、卫星通信、移动通信等各种通信系统。
Turbo码采用了一种特殊的编码结构,能够极大地提高数据传输的可靠性和效率。
1. Turbo码的起源和发展Turbo码最早由法国电信研究中心(Centre national d'études desTélécommunications,简称France Telecom-CNET)的Claude Berrou等人于1993年提出。
这项技术通过添加纠错码,可以在传输数据时对其进行重建和修复,提高了信道的容错能力。
Turbo码的创新性和高性能引起了全球通信界的高度关注,迅速被应用于各种通信系统中。
2. Turbo码的基本原理Turbo码的编码原理可以简单概括为“迭代编码+迭代译码”。
它通过将输入数据分成几个数据块,每个数据块经过不同的编码器编码后,并按照一定规则交叉混合,形成最终的编码序列。
在接收端,采用迭代解码算法对接收到的编码序列进行译码和解码,利用编码过程中得到的相互参考信息,反复迭代译码直至最终输出恢复的数据。
3. Turbo码的特点和优势3.1 容错性能卓越:Turbo码具有出色的误码性能,可以在信道质量差的环境下实现高可靠的数据传输。
通过反复迭代译码的方式,Turbo码可以充分利用相互参考的信息,提高了纠错能力,有效降低了传输错误率。
3.2 较低的时延:Turbo码在传输过程中的冗余码率相对较低,所以可以较好地满足实时传输的需求,减小了信号传输的时延。
3.3 适应性强:Turbo码可以根据不同的通信系统需求进行灵活配置和设计,可以应用于不同信道性质、不同码率和不同调制方式的通信系统中。
4. Turbo码的应用领域4.1 无线通信:Turbo码广泛应用于各种无线通信标准中,包括3G、4G、5G等移动通信系统。
在高速移动环境下,Turbo码通过改善信道传输质量,提高了数据的传输速率和可靠性。
turbo码编码增益

Turbo码编码增益1. 引言Turbo码是一种强大的错误纠正编码技术,广泛应用于无线通信、卫星通信和数字广播等领域。
它具有良好的纠错性能和较低的译码复杂度,被认为是一种接近香农极限的编码方案。
在Turbo码中,编码增益是一个重要的性能指标,表示通过编码后与未编码信号之间的信噪比(SNR)差异。
本文将从以下几个方面详细介绍Turbo码编码增益:•Turbo码基本原理•编码增益定义•影响编码增益的因素•编码增益优化方法2. Turbo码基本原理Turbo码是一种迭代卷积编码技术,由两个卷积编码器和一个交织器组成。
它利用了迭代解调和译码算法来提高纠错性能。
2.1 卷积编码器Turbo码使用两个相同的卷积编码器,并行地对输入数据进行编码。
每个卷积编码器都有一个生成多项式和一个移位寄存器。
输入数据经过移位寄存器后与生成多项式进行异或操作,生成编码输出。
2.2 交织器Turbo码的交织器用于打乱编码输出,以减小连续错误的概率。
交织器可以是一个简单的块交织器或者是更复杂的分组交织器。
2.3 迭代译码Turbo码的迭代译码是Turbo码性能优于其他编码方案的关键所在。
迭代译码使用了迭代解调和译码算法,其中包括软输出Viterbi算法(SOVA)和逐比特MAP算法。
在迭代译码过程中,解调器首先对接收到的信号进行初步解调,并生成一个软信息序列。
然后,这个软信息序列经过反交织器后输入到另一个卷积编码器,并与之前迭代得到的硬判决值进行异或操作。
最后,经过一系列迭代后得到最终的硬判决值。
3. 编码增益定义编码增益是指通过Turbo码编码后与未编码信号之间的信噪比(SNR)差异。
它可以用来衡量Turbo码对信号质量的改善程度。
通常情况下,信道传输中会受到噪声干扰,导致接收端收到畸变的信号。
编码增益就是通过编码技术提高信号质量,减小噪声对信号的影响。
编码增益越大,说明Turbo码在纠错方面的性能越好。
4. 影响编码增益的因素编码增益受到多个因素的影响,包括信道条件、编码方式和译码算法等。
Turbo码的编码

Turbo码的编码基本原理1..Turbo 码最先是由C. Beηou等提出的。
它实际上是一种并行级联卷积码(Parallel Concatenated Convolutional Codes)。
Turbo 码编码器是由两个反馈的系统卷积编码器通过一个交织器并行连接而成,编码后的校验位经过删余阵,从而产生不同的码率的码字。
如图所示:信息序列u={u1,u2,……,uN}经过交织器形成一个新序列u'={u1',u2',……,uN'}(长度与内容没变,但比特位经过重新排列),u 和u'分别传送到两个分量编码器(RSC1与RSC2) ,一般情况下,这两个分量编码器结构相同,生成序列X和X,为了提高码率,序列X和X需要经过删余器,采用删余(puncturing)技术从这两个校验序列中周期的删除一些校验位,形成校验序列X,X,与未编码序列X'经过复用调制后,生成了Turbo码序列X.2.....Turbo码由2个循环系统卷积码并行级联而成:译码采用迭代的串行译码交织器是Turbo 码所特有的,它可以使得信息序列随机化,增加各码字间的重量,从而提高码的保护能力基本结构Turbo码的典型编码器如图2-1所示,Turbo码编码器主要由分量删余矩阵、交织器、编码器以及复接器组成。
分量码一般选择为递归系统卷积(RSC,Recursive Systematic Convolutional)码,当然也可以是分组码(BC, Block Code)、非递归卷积(NRC,Non-Recursive Convolutional)码以及非系统卷积(NSC,Non-Systematic Convolutional)码,但从后面的分析将看到,分量码的最佳选择是递归系统卷积码。
通常两个分量码采用相同的生成矩阵,当然分量码也可以是不同的。
编码器结构图分量编码器分量编码器是Turbo码编码器中的一个重要组成部分。
turbo码结构和编码方法

摘要:Turbo码,由于性能接近Shannon理论限,在低信噪比的应用环境下比其他编码好。
因而第三代移动通信系统多种方案中,考虑将Turbo码作为无线信道的编码标准之一。
本文介绍了Turbo码的结构和编解码方法,及其在第三代移动通信系统中的应用。
关键词:信道编码;Turbo码;RSC编码器;交织器;迭代译码;第三代移动通信Abstract: Turbo codes,because of it’s outstanding performance in channel coding,has been considered by IMT-2000 as a plan of application. This paper introduces the principle of basic structure of Turbo codes.Also,the paper introduces the mainly application in 3G(3ird Generation) mobile telecomminucation systems.Key words: channel coding; Turbo codes; RSC; interleaver; recursive algorithm; 3G(the 3ird generation)mobile telecommunication systems一、引言信息论诞生50多年以来,人们一直努力寻找更加接近Shannon限、误差概率小的的编码方法。
在1993年ICC国际会议上,C.Berrou,A.Glavieux和P.Thitimajshiwa提出了一种称之为Turbo Code的编、译码方案,并在交织器大小为:情况下,迭代18次,对它进行了计算机仿真。
仿真结果表明,当归一化信噪比时,。
其编码增益比Shannon信道容量的差距小于1dB。
[1] 从第三代移动通信系统候选方案来看,普遍要求提供中速或者高速的数据业务,一般的数据业务信道为64kbps,144kbps,384kbps。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(5.1.3)
其中(M,K)=1,N=MK。
第5章 Turbo码
顺便指出,根据实际需要,Turbo码的分量编码器可以
不止两个,当然,交织器也随之增加。Turbo码的一般PCCC 结构见图5.4。
图 5.4 Turbo码的一般PCCC结构
第5章 Turbo码
2. SCCC编码结构
SCCC结构的Turbo码由两个编码器和一个交织器组成, 一个编码器对输入信息码进行编码,称为外码编码器,外码 编码器的输出经交织器随机置换后送给另一个编码器进行编 码,称为内码编码器,内码编码器的输出作为Turbo码的码 字。SCCC结构如图5.5所示。第5章 NhomakorabeaTurbo码
图 5.9 输入序列(11011001)和输出序列(01011110)的位置关系
第5章 Turbo码
设计交织器应当遵循以下原则:
(1) 尽可能用长的交织器; (2) 尽可能地提高交织器输出序列的随机性能; (3) 尽可能地避免产生使后面的编码器输出低重量码字 的序列。 交织器大致可以分为规则交织器和伪随机交织器两类。 规则交织器按一定的规则将输出序列每一个坐标上的元素映 射到输出序列的某一个坐标上,规则一旦给定,实现起来就 比较容易。伪随机交织器是把输入序列进行随机置换,因为 不存在真正意义的随机置换,所以把这种交织器称为伪随机 交织器。大多数情况下,伪随机交织器的随机性能优于规则
表5.1
例5.1.1中矢量x1p的产生过程
第5章 Turbo码
(3) 随机交织器输出为
v=(0101011) (4) 编码器RSC2的输出矢量x2p。 假设编码器RSC2已清零,x2p的产生过程见表5.2,可得 x2p=(0111100)
第5章 Turbo码
表5.2
例5.1.1中矢量x2p的产生过程
(6) 截断复接器输出码字c。截断复接器将矢量xs和xp串 接起来形成Turbo码的输出码字c,即 s s p c x1s x1p , x2 x2p ,, xis xip , , xN xN 11,11, 01,11, 00,10, 01 实际上,要实现编码器RSC1和RSC2编码后清零,信息码后 必须添加一定数量的码元,RSC1和RSC2在输出N个码元后 仍有输出,这些多余的码元都由截断复接器来去掉。
第5章 Turbo码
5.1.2 Turbo码的典型交织器
交织器并不是一种新的概念,它实际上是一种置换器, 把输入矢量进行置换,因此,交织器输出的矢量元素与其输 入的矢量元素是相同的,只是元素的位置被改变。例如, (11011001)经交织器后变为(01011110),交织器输入序列与 输出序列各分量的位置对应关系见图5.9。
第5章 Turbo码
图 5.6 一个码率为1/2的SCCC结构Turbo码的编码电路
第5章 Turbo码 表5.3 例5.1.2的外码编码器的编码过程
第5章 Turbo码
(3) 交织器输出。根据题目假设,交织器输出序列为
c(3)=(1010011) (4) 内码编码器输出c(4)。仍然假设编码前内码编码器已 清零,编码后c(4)=(1001010),内码编码器编码过程见表5.4。 (5) 输出码字c。截断复接器将各路输出串接起来形成 SCCC的输出码字c,即
(5.1.2)
第5章 Turbo码
然后,按列的顺序读出矩阵中的每一个元素,第一列读完
后读第二列,第二列读完后读第三列,以此类推,读出的元素 顺序串连起来就是交织器的输出序列。例如,将输入序列 (11001011100011111010011011101100)排成下列矩阵:
1 1 1 1
电路如图5.3所示,RSC1和RSC2的生成多项式
,即采用(37,21)系统递 1 D4 G D 1 , 1 D D 2 D3 D 4
归卷积码。取删余矩阵 P 1 0 ,交织器对输入x=(x1,
0 1
x2,x3,…,xN)产生输出v=(xN,xN-1,…,x2,x1), 即将输 入x的码元按倒序排列。求输入为x=(1101010)时,Turbo码 输出的码字。
交织器。
第5章 Turbo码
1. 规则交织器
1) 分组交织器 设输入序列为u=(u1,u2,u3,…,uN),交织器只改变 输入序列的分量的位置,不改变其内容,因此,可以用序列 分量的位置对应关系来描述交织器的规则。输入序列第i个 坐标上的元素是ui,将ui安排到一个矩阵的第t行第s列的位 置,即矩阵的第t行第s列的元素a(s,t)为 a(t,s)=ui 式中,
第5章 Turbo码
1. PCCC编码结构
PCCC结构的Turbo码有两个分量编码器,这两个分量编 码器通过一个交织器并行连接起来,编码后检验位通过删余 矩阵的删余来实现不同码率。PCCC结构见图5.2。
第5章 Turbo码
图 5.2 Turbo码的PCCC结构框图
第5章 Turbo码
例5.1.1 设一个码率为1/2的PCCC结构Turbo码的编码
第5章 Turbo码
图 5.7 HCCC的Ⅰ型结构框图
第5章 Turbo码
2) Ⅱ型结构
Ⅱ型结构相似于PCCC结构,只不过这里的PCCC结构 的编码器RSCi(i=1,2,…,M)被SCCC结构所取代。图5.8 给出了HCCC的Ⅱ型结构框图。
第5章 Turbo码
图 5.8 HCCC的Ⅱ型结构框图
a00 a 10 a20 a30 a01 a11 a21 a31 a02 a12 a22 a32
(5.1.5)
第5章 Turbo码
交织器输出序列与矩阵式(5.1.5)的元素的对应关系如表
5.5所示。 表5.5 N=12 时分组螺旋交织器的交织过程
第5章 Turbo码
c c0 c0 c0 c0 , c1 c1 c1 c1 , c2 c2 c2 c2 , 1011,0100,1110,0001,1000,0011,1110
1 2 3 4
1 2 3 4
1 2 3 4
第5章 Turbo码
表5.4 例5.1.2的内码编码器的编码过程
第5章 Turbo码
3. HCCC编码结构
HCCC编码结构不是一种新型的独立编码结构,它是一 种将PCCC和SCCC两种结构混合在一起的编码方案。常见 的HCCC编码结构有以下两种。 1) Ⅰ型结构 Ⅰ型结构非常相似于SCCC结构,只不过这里的SCCC 结构的内码编码器由一个PCCC 结构来取代。图5.7给出了 HCCC的Ⅰ型结构框图。
图 5.5 Turbo码的SCCC结构框图
第5章 Turbo码
例5.1.2 一个码率为1/2的SCCC结构Turbo码的编码电
路如图5.6所示,输入信息码x=(10011100100011)。假设交织 器输出为(1010011),求Turbo码输出的码字c。 解 (1) 信息码为 x(1)=(1010101),x(2)=(0110001) 因为是系统码,所以 c(1)=x(1)=(1010101),c(2)=x(2)=(0110001) (2) 外码编码器输出u。假设外码编码器编码前已清零, 编码后输出序列u=(0001111),编码过程见表5.3。
第5章 Turbo码
设交织器输出序列的第 i(i=0,1,2,…,N-1)个元素
为vi,交织器的读取规则如下:
vi asi ,ti
(5.1.4)
式中:si=(si-1+1)(modM),ti=(ti-1+1)(modK)。其中,令s-1 =t-1=-1。 例如,有M=4,K=3,输入序列矩阵为
第5章 Turbo码
(5) 删余矩阵删余。从删余矩阵P的结构不难看出,删
余矩阵将删除矢量x1p中偶数位置上的元素,保留奇数位置 上的元素;对x2p则相反,保留偶数位置上的元素,删掉奇 数位置上的元素。于是,删余矩阵输出矢量xp为
1 2 1 2 1 2 x p x1 p , x2 p , x3 p , x4 p , x5 p , x6 p , x1 p 1,1,1,1, 0, 0, 0 7
第5章 Turbo码
第5章 Turbo码
5.1 Turbo码的编码原理
5.2 习题 Turbo码的译码原理与性能
第5章 Turbo码
在1993年的通信国际学术会议(ICC’93)上,Berrou、
Glavieux和Thitimajshima三人联合提出了一种新的纠错编 码——Turbo码,他们给出了在加性高斯白噪声(AWGN)信 道上,信噪比≥0.7 dB时以1/2的码率进行传输,比特误码率 ≤10-5的编码性能。Turbo码这一优秀的编码性能已非常接近 香农理论界限,也正是因为如此,Turbo码刚开始时受到学 术界的怀疑,认为是一次实践的巧合,但随后越来越多的学 者不断独立重复实现这一性能,Turbo码最终得到世界公认, 成为人类构造性能接近香农理论界限好码的标志。图5.1是 由Ardakani给出的对Turbo码、卷积码和香农理论界限的仿 真性能比较结果。
交织器输出序列为
(a00a11a22a30a01a12a20a31a02a10a21a32) 这种交织方式的过程如下:
第5章 Turbo码
3) 一次剩余交织器
设交织器输入序列u=(u0,u1,u2,…,uN-1),输出序 列v=(v0,v1,v2,…,vN-1),一次剩余交织器按下列规则进 行交织,即 vi=uI(i) N)=1。 例如,N=32,a=7,r=0交织器的交织过程如表5.6所示。 (5.1.6) 式中:I(i)=(a· i+r)(modN),r<N,a称为步长,并且a<N,(a,
