平面力系平衡问题课堂练习题
理论力学 平面任意力系例题

60
l
l
F
B
F
D
60
l
l D M
M
B
3l
G
F1
l MA
G FAy
x A FAx
17
A
q
例题
平面任意力系
2. 按图示坐标,列写平衡方程。
F
60
例 题 5
y l l D M
F F
x
0,
B
FAx F1 F sin 60 0
y
0,
FAy G F cos 60 0
M作用,梁的跨度为l,求固定端的约束力。
F
45
q
A l
M
B
14
例题
平面任意力系
q
A y
例 题 4
2. 列平衡方程
M
45
F
解: 1. 取梁为研究对象,受力分析如图
B
l
Fx 0,
Fy 0,
FAx F cos 45 0
FAy ql F sin 45 0
q FAx
力系对O点的主矩为
MO
O
主矢FR在第四象限内,与x轴的夹角为 –70.84o。M
O
M F
O
FRx
70.84
A
F1 3 m G1 1.5 m G2 3.9 m 2 355 kN m
FRy
FR
7
例题
平面任意力系
2. 求合力与基线OA的交点到O点的距离 x。 合力FR的大小和方向与主矢FR相同。 合力作用线位置由合力矩定理求得。
平面任意力系习题及答案

平面任意力系习题及答案平面任意力系习题及答案力学是物理学的一个重要分支,研究物体受力的作用和运动规律。
平面任意力系是力学中的一个重要概念,它涉及到多个力在平面内的作用和平衡问题。
在本文中,我们将探讨一些关于平面任意力系的习题,并提供相应的答案。
1. 问题描述:一个物体受到三个力的作用,力的大小和方向分别为F1=10N,θ1=30°;F2=15N,θ2=120°;F3=8N,θ3=210°。
求物体所受合力的大小和方向。
解答:首先,我们需要将力的分量计算出来。
根据三角函数的定义,我们可以得到F1x=F1*cosθ1=10*cos30°=8.66N,F1y=F1*sinθ1=10*sin30°=5N;F2x=F2*cosθ2=15*cos120°=-7.5N,F2y=F2*sinθ2=15*sin120°=12.99N;F3x=F3*cosθ3=8*cos210°=-6.93N,F3y=F3*sinθ3=8*sin210°=-4N。
然后,我们将分量相加,得到合力的分量。
Fx=F1x+F2x+F3x=8.66N-7.5N-6.93N=-5.77N,Fy=F1y+F2y+F3y=5N+12.99N-4N=13.99N。
最后,我们可以利用勾股定理计算合力的大小和方向。
合力的大小为F=sqrt(Fx^2+Fy^2)=sqrt((-5.77N)^2+(13.99N)^2)=15.16N,合力的方向为θ=arctan(Fy/Fx)=arctan(13.99N/-5.77N)=-68.6°。
因此,物体所受合力的大小为15.16N,方向为-68.6°。
2. 问题描述:一个物体受到四个力的作用,力的大小和方向分别为F1=8N,θ1=30°;F2=12N,θ2=120°;F3=10N,θ3=210°;F4=6N,θ4=300°。
平面汇交力系习题

作业A一、填空题1。
平面汇交力系是指力作用线__________,且_________一点的力系。
2。
平面汇交力系平衡的必要和充分条件是_______,此时力多边形_______。
3.沿力矢量的两端向坐标轴作____,两垂足在坐标轴上截下的这段长度称为力在坐标轴上的投影,力的投影是____量,有正负之分。
4.力沿直角坐标轴方向分解,通常,过力F 矢量的两端向坐标轴作平行线构成矩形,力F 是矩形的___,矩形的____是力F 矢量的两个正交分力y x F F 、。
5。
已知一个力F 沿直角坐标轴的两个投影为y x F F 、,那么这个力的大小=F ____,方向角=α____。
(角α为F 力作用线与x 轴所夹的锐角。
) 6。
平面汇交力系的力多边形如图(a),(b ),(c )则图(a )中四个力关系的矢量表达式__________________; 图(b )中四个力关系的矢量表达式__________________; 图(c)中四个力关系的矢量表达式__________________。
7。
如图所示,不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接,若结构受力F 作用,则支座C 处的约束力大小______,方向______。
(7题图) (8题图)8.如图所示,力F 在y x 、轴上投影x F =_____、y F =_____.9.平面刚架在B 处受一水平力F 作用,如图所示,刚架自重不计,设F =20kN ,L =8m ,h =4m ,则求A 、D 处的约束反力,可以按以下步骤进行:(1)以刚架为研究对象,进行受力分析:请画出刚架的受力分析图(2)作用在刚架上的力(主动力和约束力)构成的力系属_____力系 (3)列出刚架的平衡方程(坐标如图)∑=0xF :_____________________; ∑=0yF:_____________________.(4)解方程计算D A 、处的约束反力A F =______;D F =_______。
平面任意力系的平衡方程及应用——高职教学中一道典型的例题

学生应理 解 并熟练 掌握 。本 文举一 典型 例题 来说 明平 面任 意力 系的平衡 方程 的 三种形 式 的具体运 用 。
关键 词 : 平 面任 意力 系; 平衡 方程 ; 典 型例 题
中图分 类号 : 0 3 1 2 - - 4
文 献标 识码 : B
d o i : 1 0 . 3 9 6 9 6 . i s s n . 1 6 7 3 — 0 9 6 8 . 2 0 1 3 . 0 3 . 0 3 5
0 前 言
平 面任 意 力系 的平 衡 问题是 静力 学 的主 要 内 容, 也 是理论 力学 的一项 重 要 内容 , 它是 解决 物体
系统 平衡 问题 的基 础 , 是 教 学 的重点 和难 点 , 因此 学 生应 理解并 熟 练掌握 应 用平 面任 意力 系 的平衡 c 班 …
Th e Eq u i l i b r i u m E qu a t i o n s an d Ap p l i c a t i o n o f Cop l a n ar Ar b i t r a r y F o r c e s
— —
A T y pi c l a Ex a mp l e i n Hi g h e r Vo c a t i o n a l Ed uc a t i o n
2 0 1 3年第 3舰 ( 总第 1 9 3期 )
山 东 纺 织 经 济
平面任意力系的平衡方程及应用
— —
高职教学 中一道典 型的例题
金 晓。 孟翠玉 山东烟 台 2 6 5 7 1 3 )
( 烟台南山学院
摘
要: 平 面任 意力 系的平衡 方程 及应 用是教 学的重 点和 难点 , 它是 解 决物体 系统 平衡 问题 的基 础 ,
平面汇交力系习题
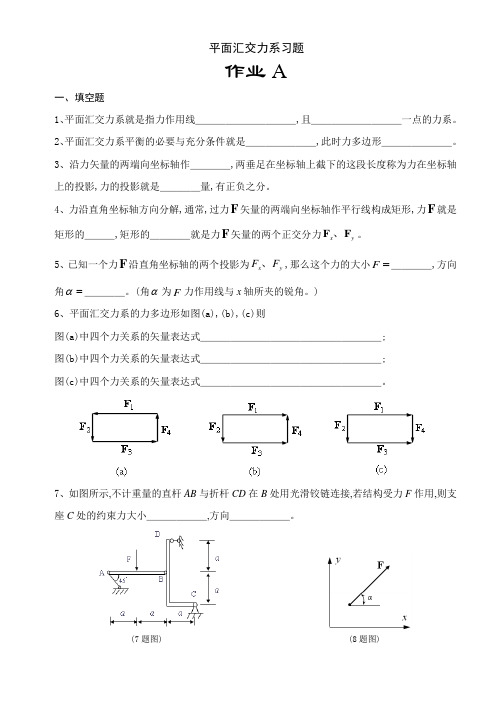
作业A一、填空题1、平面汇交力系就是指力作用线__________,且_________一点的力系。
2、平面汇交力系平衡的必要与充分条件就是_______,此时力多边形_______。
3、沿力矢量的两端向坐标轴作____,两垂足在坐标轴上截下的这段长度称为力在坐标轴上的投影,力的投影就是____量,有正负之分。
4、力沿直角坐标轴方向分解,通常,过力F 矢量的两端向坐标轴作平行线构成矩形,力F 就是矩形的___,矩形的____就是力F 矢量的两个正交分力y x F F 、。
5、已知一个力F 沿直角坐标轴的两个投影为y x F F 、,那么这个力的大小=F ____,方向角=α____。
(角α为F 力作用线与x 轴所夹的锐角。
)6、平面汇交力系的力多边形如图(a),(b),(c)则图(a)中四个力关系的矢量表达式__________________;图(b)中四个力关系的矢量表达式__________________;图(c)中四个力关系的矢量表达式__________________。
7、如图所示,不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接,若结构受力F 作用,则支座C 处的约束力大小______,方向______。
(7题图) (8题图)8、如图所示,力F 在y x 、轴上投影x F =_____、y F =_____。
9、平面刚架在B 处受一水平力F 作用,如图所示,刚架自重不计,设F =20kN ,L =8m ,h =4m ,则求A 、D 处的约束反力,可以按以下步骤进行:(1)以刚架为研究对象,进行受力分析:请画出刚架的受力分析图(2)作用在刚架上的力(主动力与约束力)构成的力系属_____力系(3)列出刚架的平衡方程(坐标如图)∑=0x F:_____________________; ∑=0yF :_____________________。
(4)解方程计算D A 、处的约束反力A F =______;D F =_______。
《理论力学》第四章-力系平衡试题及答案
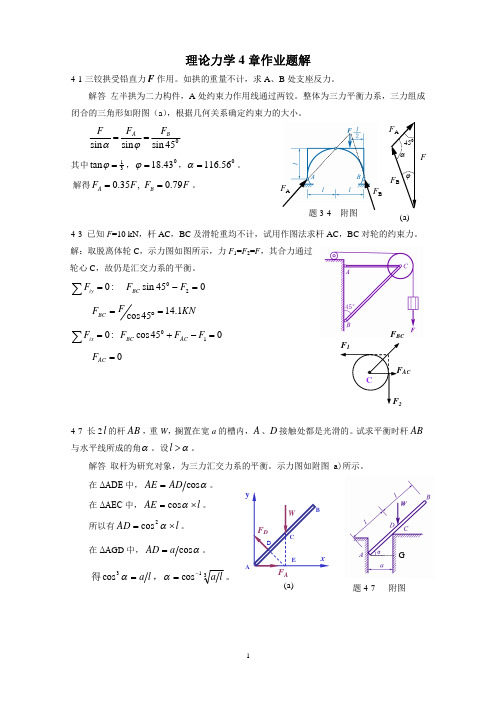
理论力学4章作业题解4-1三铰拱受铅直力F 作用。
如拱的重量不计,求A 、B 处支座反力。
解答 左半拱为二力构件,A 处约束力作用线通过两铰。
整体为三力平衡力系,三力组成闭合的三角形如附图(a ),根据几何关系确定约束力的大小。
45sin sin sin B A F F F ==j a其中31tan =j ,043.18=j ,056.116=a 。
解得F F F F B A 79.0 ,35.0==。
4-3 已知F =10 kN ,杆AC ,BC 及滑轮重均不计,试用作图法求杆AC ,BC 对轮的约束力。
解:取脱离体轮C ,示力图如图所示,力F 1=F 2=F ,其合力通过轮心C ,故仍是汇交力系的平衡。
:0=åiyF 045sin 20=-F F BCKN FF BC 1.1445cos =°=045cos :010=-+=åF F F FAC BC ix0=AC F4-7 长2l 的杆AB ,重W ,搁置在宽a 的槽内,A 、D 接触处都是光滑的。
试求平衡时杆AB 与水平线所成的角a 。
设a >l 。
解答 取杆为研究对象,为三力汇交力系的平衡。
示力图如附图(a)所示。
在ΔADE 中,a cos AD AE =。
在ΔAEC 中,l AE ´=a cos 。
所以有l AD ´=a 2cos 。
在ΔA GD 中,a cos a AD =。
得a =a 3cos ,31cosl a -=a 。
F BCAC题3-4 附图F BF AF BF AFa45j(a)A (a)题4-7 附图G4-9 AB ,AC ,AD 三连杆支撑一重物,如图所示。
已知W=10kN ,AB =4m ,AC =3 m ,且ABEC 在同一水平面内,试求三连杆所受的力。
解:取铰A 研究,示力图如图示,为汇交力系的平衡。
0=åix F : 05430sin =´°+AD AB F F 0=åiy F : 05330sin =´°+AD AC F F 0=åiZF: 030cos =-°W F AD联立求解KNF KNF KN F AD AC AB 5.115.36.4=-=-=4-8 图示结构上作用一水平力F 。
平面力系的平衡方程

题问衡平与化简系力
第5章
例3
半径为 R的半球形碗内搁一均匀的筷子 AB。 筷子长2l, 设 2R ? l ? ? R, 且为光滑接触。求
?
筷子平衡时的倾角 a。
B
l
a
A
例3
解法一
第5章 解:确定筷子为对象,作受力分析。
题问衡平与化简系力
因为? ADE是直角,所以 E一定在圆周上,
A E? 2R
? ? OAD ? ? OD ? l cosa ? AF ? 2R cos 2a
a1
?
? 4
a2
?
1 2
arcsin
9 16
a3
?
?
2
?
1 2
arcsin
9 16
题问衡平与化简系力
第5章
例4
解法二: 两矩式
y
NA
a
CA
a
P
O
NB
x aB
D
a
P
aa a a a mA ? NBacos ? P(l ? asin )sin ? P[(l ? acos )cos ? a]? 0 a a a a a [ mB ? ? NAa sin ? P (l ? a sin ) sin ? a]? P(l ? a cos ) cos ? 0
题问衡平与化简系力
第5章
刚体平衡问题的解题步骤
? 正确选取研究对象,取分离体,画受力图 ? 作直角坐标系,建立力系平衡方程。 力矩
轴应和尽量多的未知力相交或平行 ? 对于平面一般力系的刚体平衡问题,除了
一矩式外,应学会灵活应用其它两种形式。 对于空间一般力系的刚体平衡问题,一般 应用三个力的投影式及三个力矩式。 ? 解平衡方程式,最好先用文字符号表示求 解结果,并用量纲校核后,再代入数据求 出数值解。
平面任意力系平衡方程的基本形式例题分析

《工程力学》课程习题-例题分析学习项目二(平面任意力系的合成与平衡)平面任意力系平衡方程的基本形式1、起重设备重G1=10kN,可绕铅直轴AB转动;起重机的挂钩上挂一重为G2=40k N的重物,如图所示。
起重机的重心C到转动轴的距离为,其它尺寸如图所示。
求在止推轴承A和轴承B处的反作用力。
解:以起重机为研究对象,它所受的主动力有G1和G2。
由于对称性,约束反力和主动力都在同一平面内。
止推轴承A处有两个约束反力F Ax、F Ay,轴承B处只有一个与转轴垂直的约束反力F B,约束反力方向如图所示。
上述力形成平面一般力系,取坐标系如图所示,列平衡方程,即∑F x=0 F Ax+F B =0∑F y=0 F Ay-G1-G2=0∑M A(F i)=0 -F B×5-G1×-G2×=0联立以上方程,得F Ay=G1+G2=50 kNF B =--=-31kNF Ax =-F B =31kNF B 为负值,说明其方向与假设的方向相反,即应指向左。
2、防洪用弧形闸门有对称的两个支架和铰链支座。
已知闸门重G =1100kN ,静水总压力2P 2G B V A (F i )=0 B V ×2G×=0得 V B = kN 取x 、y 轴方向如图b ,列投影方程由∑F x =0 05531sin 25531sin 21='︒-'︒+-G V R P B得 R 1=由∑F y =0 05531c 25531cos 2='︒-'︒+os G V R B得R2=反力的方向如图b所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例2-19 已知: PE 10kN, PG 7kN, 各杆长度均为1m;
求: 1,2,3杆受力.
解: 取整体,求支座约束力.
Fx 0
FAx 0
M B 0 2PE PG 3FAy 0
Fy 0 FAy FBy PE PG 0
FAy 9kN
FBy 8kN
38
用截面法,取桁架左边部分.
2m
2m
解方程可得 F4 10kN
节点C在y方向的平衡方程可用来校核
C
F1
F4
F’3
当计算出杆的受力的代数值为正时,表明 该杆受力的方向符合假设的方向,即该杆受拉。 反之,当计算出该杆受力的代数值为负时,表 明该杆受压。
34
平面桁架如图所示。设两主动力大小F =10 kN , 作用在节点A和节点B上,a =1.5 m,h =3 m。求1, 2,3和4各杆受的内力。
19
例2- 已知:P , a ,各杆重不计; 24求:B 铰处约束力.
解:取整体,画受力图
MC 0 FBy 2a 0
FBy 0
取DEF杆,画受力图
M D 0 FE sin 45 a F 2a 0
Fx 0 FE cos 45 FD' x 0 ME 0 FDy 'a F 2a 0
取AB杆(不含销钉B),画受力图.
Fx 0
FAx
1 2
q
3a
FABx
0
FAx qa
Fy 0 FAy FABy 0
MA 0
FAy P qa
1 M A 2 q 3a a FABx 3a FABy a 0
M A (P qa)a
26
组合梁AC和CE用铰链C相连,A端为固定端,E端为活动 铰链支座。受力如图所示。已知: l =8 m,F=5 kN,均布载 荷集度q=2.5 kN/m,力偶矩的大小M= 5 kN•m,试求固端A, 铰链C和支座E的约束力。
4
FAy FAx
FCx FCy
解: 1.取整体为研究对象。
2.受力分析如图。
3.列平衡方程。
G
MC F 0,
5r G 2r FAx 0
解得 FAx 2.5G
5
FAy FAx
4.取杆AB为研究对象,受力分析如图。 列平衡方程
FCx FCy
Fx 0, FAx FBx FE 0
FAx 20kN
Fx 0 FAx FCx 0
FCx 20kN Fy 0 FAy FCy FT P 0
18
取BDC杆(带着轮)
MB 0 4aFCy FT 3a FT1 a FCx 4a 0
FCy 15kN FAy 10kN
取BDC 杆(不带着轮) 取ABE(带着轮) 取ABE杆(不带着轮)
例210 D
A
K
C
E
BⅠ Ⅱ G
如图所示,已知重力G, DC=CE=AC=CB=2l;定滑轮 半径为R,动滑轮半径为r,且
R=2r=l, θ=45° 。试求:A,E
支座的约束力及BD杆所受的 力。
1
D
FA
K
A
C
BⅠ
解: 1. 选取整体研究对象,受力
分析如图所示。
列平衡方程
M E F 0,
FA
C
FAy 1
4
3
A
30 2
5
D
Fx 0,
F5 F2 0
F
Fy 0,
2m
F3 F 0
2m
解方程可得
F3 10 kN F5 8.66 kN
F3
D
F2
F5
F
FBy
B
FBx
33
4. 取节点C为研究对象 ,受力分析如图。
C
1
4
列平衡方程
3
A
30 2
5
B
Fx 0
D
F
F4 cos 30 F1cos 30 0
31
2. 取节点A为研究对象,受力分析如图。
F1
A
F2 FAy
列平衡方程
Fx 0, F2 F1 cos 30 0
C
FAy 1
4 3
A
30 2
5
DF2m源自2mFy 0, FAy F1 sin 30 0
解方程可得
F1 10 kN F2 8.66 kN
FBy
B
FBx
32
3. 取节点D为研究对象。 列平衡方程
解题思路:
先分析整体 再分析BC 总结:
FBx FAx FBy FAy
一般先分析整体; 一般不拆滑轮; 矩心尽量取在较多未知力的交点上; 投影轴尽量与较多未知力相垂直。
7
例2-16 已知:如图所示结构,a,M Fa ,F1 F2 F .
求:A,D处约束力.
8
解: 以BC为研究对象,受力如图所示.
Fx 0 FBCx FC'x 0
MC 0 M FBCya 0
FBCx
1 2
qa
取销钉B,画受力图.
FBCy qa
Fx 0
F' ABx
F' BCx
0
Fy 0
F' ABy
F' BCy
P
0
F' ABx
1 2
qa
F' ABy
P qa
FABx
1 2
qa
FABy (P qa)
25
sin
18 kN
F2 F1 cos 15 kN
36
2. 选取节点B为研究对象,受力分 析如图。
h
列平衡方程
1
α 3Bα
A
Fx 0, F2 F4 0
4
2
a
a
a
F
F
Fy 0, F3 F 0
y F3
B
x
F4
F F'2
解方程得
F4 F2 15 kN F3 F 10 kN
37
1 2
F
FAy F
9
再分析BC.
Fx 0
FCx FBx 0
FCx
1 2
F
以AB为研究对象,受力如图所示.
Fx 0
FDx FCx ' 0
Fy 0
FDy FCy ' 0
MD 0 M D FCy '2a FCx '2a 0
FDx
1 2
F
FDy F M D Fa
10
11
12
2 2l G 5 l 0 2
Fx 0, FA cos 45 FEx 0
FEy
E
FEx
Fy 0, FA sin 45 FEy G 0
Ⅱ 解平衡方程
FA
5 8
2
G,
FEx
5 8
G
G
FEy G FA sin
45 13G 8
2
D
A
K
C
E D
FDB
K
FK
FCx C FCy
FEy
h
1
α 3Bα
A
4
2
a
a
a
F
F
35
解: 1. 选取节点A为研究对象,
受力分析如图所示。
h
列平衡方程
1
α 3Bα
4
2
a
a
a
F
y
F1
A
x
F2 F
Fx 0, F1 cos F2 0
A
Fy 0, F F1 sin 0
F
其中 arctan 3 33.7
解方程得
3 1.5
F1
F
ME 0 F1 1 cos300 FAy 1 0
Fy 0
Fx 0
FAy F2 sin 600 PE 0 F1 F3 F2 cos 600 0
F1 10.4kN(压) F2 1.15kN(拉)
F3 9.81kN(拉)
39
说明 : 节点法:用于设计,计算全部杆内力 截面法:用于校核,计算部分杆内力
FE sin 45 2F FD' x FE cos 45 2F
FD' y 2F
20
对ADB杆受力图
MA 0
FBx 2a FDx a 0
FBx F
21
例2-25 已知: a ,b ,P,各杆重不计, C,E处光滑;
求证: AB杆始终受压,且大小为P.
解: 取整体,画受力图.
Fx 0
F
q
AHB
C
M E
D
l/8 l/8 l/4 l/4 l/4
27
28
LOREM IPSUM DOLOR
LOREM IPSUM DOLOR
例2-18
平面桁架的尺寸和支座如图所示。在节点D处受一集中 载荷F=10 kN的作用。试求桁架各杆件所受的内力。
C
1
4
3
A
30 2
5
B
D
F
2m
2m
30
节点法
C
FAy 1
4 3
A
30 2
5
D
F
2m
2m
解: 1. 求支座约束力。
以整体为研究对象,受力分析如图所示。
列平衡方程
FBy
B
FBx
Fx 0, FBx 0
M A F 0, FBy 4 F 2 0
M B F 0, F 2 FAy 4 0
解方程可得 FBx 0
FAy FBy 5 kN
F' ADCy
b 2
FC
b 2
