江西省兴国县将军中学2013-2014学年高二下学期第一次考试数学(理)试卷
江西省赣州市兴国县将军中学2013-2014学年高二数学上学期第一次月考x试题

----------------------------精品word 文档 值得下载 值得拥有---------------------------------------------- 江西省赣州市兴国县将军中学2013-2014学年高二数学上学期第一次月考x 试题(无答案)新人教版一、选择题(在每小题给出的四个选项中,第1—7小题只有一个选项符合题目要求,第8--10小题有多个选项符合题目要求,全部选对的得4分,选不全的得2分,有选错或不答的得0分,共40分)1.根据电容的定义式UQC 可知( )A 、电容器的电容越大,则电容器所带电荷量就越多B 、电容器两极间电势差越大,电容器的电容就越小C 、电容器的电容与其电荷量成正比,与两极间的电势差成反比D 、电容器的电容不随电荷量以及两极间电势差的变化而变化2.关于电势和电势能下列说法中正确的是( ) A 、在电场中,电势高的地方,电荷在该点具有的电势能就大;B 、在电场中,电势高的地方,放在该点的电荷的电量越大,它所具有的电势能也越大;C 、在电场中的任何一点上,正电荷所具有的电势能一定大于负电荷具有的电势能;D 、在负的点电荷所产生的电场中任何一点上,正电荷所具有的电势能一定小于负电荷所具有的电势能。
3.如图所示,两平行金属板间的距离是d ,两板间的电压是U ,今有一电子从两板间的O 点沿着垂直于板的方向射出,到达A 点后即返回。
若OA 距离为h ,则此电子具有的初动能是( ) A .edh /U B .edhU C .eU /dh D .ehU /d 4.如图所示的直线是真空中某电场的一条电场线,A 、B 是这条直线上的两点。
一电子以速度v A 经过A 点向B 点运动,经过一段时间后,电子以速度v B 经过B 点,且v B 与v A 方向相反,则( )A .A 点的场强一定大于B 点的场强B .A 点的电势一定低于B 点的电势C .电子在A 点的动能一定小于它在B 点的动能D .电子在A 点的电势能一定小于它在B 点的电势能5.a 、b 、c 、d 是匀强电场中的四个点,它们正好是一个矩形的四个顶点.电场线与矩形所在平面平行。
江西省赣州市兴国县将军中学高二数学下学期第一次月考

江西省赣州市兴国县将军中学2012-2013学年高二数学下学期第一次月考试题理(无答案)北师大版一、选择题(本大题共10小题,每小题5分,共50分。
在每小题所给出的四个备选项中,只有一项是符合题目要求的。
) 1、复数21i i--(i 为虚数单位)等于( ) A .1 B .i C .2+i D .2-2i2、用反证法证明命题 “三角形的内角中至少有一个不大于60°”时假设正确的是( )A .假设三内角都不大于60°B .假设三内角至少有一个大于60°C .假设三内角都大于60°D .假设三内角至多有两个大于60° 3、函数32()g x x mx nx m 2=+++在1x =处有极值10,则m ,n 的值是( )A.3,3m n =-=B.4,11m n ==-C.4,11m n =-=D.3,3m n ==-4、已知函数()y f x =的图象如图所示,则`()y f x =的大致图象可以是图中的( )A B C D 5、已知函数32()f x ax bx c =++其导数()f x '的图象如图所示,则函数()f x 的极小值是( ) A .a b c ++ B. 32a b + C .34a b c ++ D .c6、如图,在一个长为π,宽为2的矩形OABC 内,曲线y =sin x (0≤x ≤π)与x 轴围成如图所示的阴影部分,向矩形OABC 内随机投一点(该点落在矩形OABC 内任何一点是等可能的),则所投的点落在阴影部分的概率是( ) A.1π B.2π C.π4D.3π7、一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种数为 ( )A .3×3!B .3×(3!)3C .(3!)4D .9!8、将4名新来的同学分配到A 、B 、C 三个班级中,每个班级至少安排1名学生,其中甲同学不能分配到A班,那么不同的分配方案有 ( )A .18种B .24种C .54种D .60种9、甲、乙两人从4门课程中各选修2门。
江西省兴国县将军中学2013-2014学年高二下学期第一次考试数学(理)试题 Word版含答案

江西省兴国县将军中学2013-2014学年高二下学期第一次考试数学(理)试题满分:150分 考试时间:120分钟一、选择题(在每小题给出的四个选项中,只有一个正确.每小题5分,共50分) 1.复数34343izi+=+-,则z 等于 ( ) A .3i + B .3i - C .4i + D .4i -2.已知命题p :∀x ∈R,2x <3x ;命题q :∃x ∈R ,x 3=1-x 2,则下列命题中为真命题的是 ( )A .p ∧qB .p ∧⌝qC .⌝p ∧qD .⌝p ∧⌝q 3.若函数2()2ln f x x x =-在其定义域内的一个子区间(k -1,k +1)内不是单调函数,则实数k 的取值范围是 ( )A .[1,+∞)B .[1,32)C .[1,2)D .[32,2)4. 下列四个几何体中,几何体只有正视图和侧视图相同的是 ( )A .①②B .①③C .①④D .②④5.已知a 、b 是异面直线,a ⊥平面α,b ⊥平面β,则α、β的位置关系是 ( ) A .相交 B .平行 C .重合 D .不能确定6.设椭圆的两个焦点分别为F 1,F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1F 2P 为等腰直角三角形,则椭圆的离心率为 ( ) A .22B .212-C .22-D .21-7.如图所示,正方形O′A′B′C′的边长为1,它是水平放置的一个平面图形的直观图,则原图形的周长是 ( ) A .6 B .8 C .2+3 2 D .2+2 38.已知a =(2,-1,3),b =(-1,4,-2),c =(7,5,λ),若a ,b ,c三向量共面,则实数λ等于 ( ) A.627 B.637 C.607 D.6579.设离心率为e 的双曲线C :22221(0,0)x y a b a b-=>>的右焦点为F ,直线l 过焦点F ,且斜率为k ,则直线l 与双曲线C 的左、右两支都相交的充要条件是( )A .221k e ->B .221k e -<C .221e k ->D .221e k -< 10.已知正三棱锥P —ABC 的高PO 的长为h ,点D 为侧棱PC 的中点,PO 与BD 所成角的余弦值为23,则正三棱锥P —ABC 的体积为 ( )A .3338hB .3238hC .338hD .3334h二、填空题(本大题共4小题,每小题5分,共20分.请把答案填在题中横线上) 11.计算定积分1(2)x e x dx +⎰的值为 。
江西省兴国县将军中学高二数学下学期期中考试试题 文【会员独享】

江西省兴国县将军中学2011-2012学年高二下学期期中考试数学(文)试题 本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,第I 卷1至2页,第Ⅱ卷2至4页.考试结束后,只收答题卷.全卷满分为150分,完成时间为120钟.第I 卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分1.设集合A={4,5,7,9},B={3,4,7,8,9},全集U=AB ,则集合()UC A B ⋂中的元素共有 ( ) A.3个 B.4个 C.5个 D.6个2.命题“存在04,2<-+∈a ax x R x 使”为假命题是命题“016≤≤-a ”的( )A .充要条件B .必要不充分条件C .充分不必要条件D .既不充分也不必要条件3.函数)12lg(13)(-+-=x x xx f 的定义域为 ( )A .)1,(-∞B .]1,0(C .)1,0(D . ),0(+∞4.下列有关命题的说法中错误的是( )A .若p q 或为假命题,则p 、q 均为假命题.B .“1x =”是“2320x x -+=”的充分不必要条件.C .命题“若2320,x x -+=则1x =”的逆否命题为:“若1,x ≠则2320x x -+≠”.D .对于命题:p x R 存在∈使得21x x ++<0,则:p x R 非存在∈,使210x x ++≥.5. 若:,sin 1,p x x ∀∈≤R 则( )A .:,sin 1p x x ⌝∃∈>RB . :,sin 1p x x ⌝∀∈>RC .:,sin 1p x x ⌝∃∈≥RD . :,sin 1p x x ⌝∀∈≥R6.已知集合 },61|{Z m m x x M ∈+==,},312|{Z n n x x N ∈-==,=P x x |{+=2p },61Z p ∈,则P N M ,,的关系( )A .N M=P B .M P N = C .MN P D.NP M7.下列函数中,既是奇函数又是增函数的是( )A.3y x =B.1y x =C.3log y x =D.1()2xy =8.若函数()log (01)a f x x a a =>≠,满足231()()(1)1f f f a a x>->,则的解集是( ) A .10x a << B .101x a <<- C .11x a << D .111x a<<-9.函数)(x f y =的图象如图所示,则)(x f 的解析式可能是 ( )A .x x x f cos )(--= B .x x x f sin )(--= C .x x x f sin )(= D .x x x f cos )(=10.若R x ∈、+∈N n ,定义:)2)(1(++=x x x M n x )1(-+n x ,例如:55-M =(-5)(-4)(-3)(-2)(-1)=-120,则函数199)(-=x xM x f 的奇偶性为( )A.是偶函数而不是奇函数B. 是奇函数而不是偶函数C.既是奇函数又是偶函数D.既不是奇函数又不是偶函数第Ⅱ卷(非选择题,共100分)二、填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卷的相应位置.11.设集合}23|{2x y y M -==,}1|{2-==x y y N ,则=⋂N M .12.设函数()()[)22,,1,,1,.x x f x x x -⎧∈-∞⎪=⎨∈+∞⎪⎩ 若()4f x >,则x 的取值范围是 . 13.函数()()2ln 1f x ax ax =-+的定义域为R,则实数a 的范围 . 14.含有三个实数的集合既可表示成}1,,{ab a ,又可表示成}0,,{2b a a +,则=+20122012b a . 15.若存在实数x 满足不等式2|3||5|x x m m -+-<-,则实数m 的取值范围为 . 三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.16.(本题满分12分)已知集合{}|||2A x x a =-<,26|12x B x x +⎧⎫=>⎨⎬+⎩⎭. (Ⅰ)求集合A 和集合B ;(Ⅱ)若AB R =,求a 的取值范围.17. (本小题满分12分)设函数)1ln()(2++=ax x x f 的定义域为A .(Ⅰ)若1A ∈,3A -∉,求实数a 的范围;(Ⅱ)若函数=y ()f x 的定义域为R ,求实数a 的取值范围.18.(本小题满分12分)己知集合}2|1||{<-=x x A ,}1232|{2≥+-+=x x x x B ,}012|{2<-+=mx x x C (1)求B A B A ,;(2) 若B A C ⊆,求m 的取值范围.20. (本小题满分13分)如图,某单位准备修建一个面积为600平方米和矩形场地(图中ABCD )的围墙,且要求中间用围墙EF 隔开,使得ABEF 为矩形,EFCD 为正方形,设AB x =米,已知围墙(包括EF )的修建费用均为800元每平方米,设围墙(包括EF )的修建总费用为y 元。
江西省兴国县将军中学2013-2014学年高二数学下学期第一次考试试题 文 新人教A版

江西省兴国县将军中学2013-2014学年高二下学期第一次考试数学〔文〕试题总分为:150分 考试时间:120分钟一、选择题〔在每一小题给出的四个选项中,只有一个正确.每一小题5分,共50分〕 1.设1z i =-〔i 是虚数单位〕,如此=z1〔 〕 A.i 2121- B. i 2121+ C. i 2321+D.i 2321- 2.集合A ={1,2,3,4},B ={x |x =n 2,x ∈A },如此A ∩B =( ) A .{1,4} B .{2,3}C .{9,16} D .{1,2}3.集合A ={1,a },B ={1,2,3},如此“a =3〞是“A ⊆B 〞的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件4.如下各组函数中,()f x 与()g x 是否表示同一函数为 〔 〕 ①21()ln ,()ln 2f x xg x x ==②(),()f x x g x == ③ln ()ln ,()xxf x eg x e==④1221()log ,()log f x x g x x== A .①④B .③④C .④D .③ 5.函数y =的定义域是 〔 〕A .[1,)+∞B .2(,)3+∞C .2[,1]3D .2(,1]36.函数()f x 使得3(1)(1)21f x f x x ---=-成立,如此()f x = 〔 〕 A .()2f x x = B .1()2f x x =C .11()22f x x =+D .11()22f x x =- 7.命题0125n >++∈∀=∈∃x x R x q x R x p 都有命题使R ,.01,:;25s i n ,:2>++∈∀=∈∃x x R x q x R x p 都有命题使.01,:;25s i n ,:2>++∈∀=∈∃x x R x q x R x p 都有命题使R ,.01,:;25si n ,:2>++∈∀=∈∃x x R x q x R x p 都有命题使给出如下结论:①命题“q p ∧〞是真命题 ②命题“q p ⌝∧〞是假命题③命题“q p ∨⌝〞是真命题 ④命题“q p ⌝∨⌝〞是假命题,其中正确的答案是( )A.②④B.②③C.③④D.①②③8.命题“(,),,,2330x y x y R x y ∃∈++<〞的否认是 〔 〕 A.(,),,,2330x y x y R x y ∃∈++< B.(,),,,2330x y x y RR x y ∃∈++≥C.(,),,,2330x y x R y R x y ∀∈∈++≥D.(,),,,2330x y x R y R x y ∀∈∈++>9.函数213()log (215)f x x x =-++的单调递增区间为〔 〕A .(,1]-∞B .[1,)+∞C .[1,5]D .[1,5)10.f (x )是定义在R 上的奇函数,对任意x ∈R 总有f (x +32)=-f (x ),如此f (-92)的值为( )A .0B .3 C.32D .-92二、填空题〔本大题共4小题,每一小题5分,共20分.请把答案填在题中横线上〕 11.f(2x-1)的定义域为〔-1,5],求函数f(x)的定义域。
江西省兴国县将军-高二数学第一次月考(无答案)新人教A版
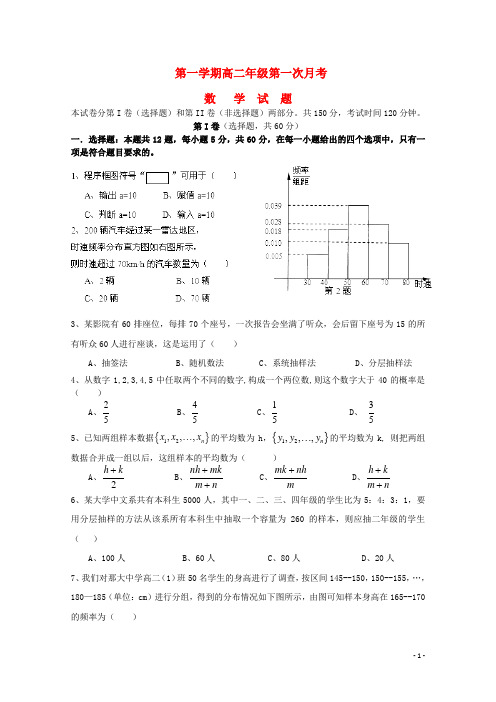
第一学期高二年级第一次月考数 学 试 题本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
共150分,考试时间120分钟。
第I 卷(选择题,共60分)一.选择题:本题共12题,每小题5分,共60分,在每一小题给出的四个选项中,只有一项是符合题目要求的。
3、某影院有60排座位,每排70个座号,一次报告会坐满了听众,会后留下座号为15的所有听众60人进行座谈,这是运用了( )A 、抽签法B 、随机数法C 、系统抽样法D 、分层抽样法4、从数字1,2,3,4,5中任取两个不同的数字,构成一个两位数,则这个数字大于40的概率是( )A 、25B 、45C 、15D 、 35 5、已知两组样本数据{}12,,,n x x x ⋯的平均数为h ,{}12,,,n y y y ⋯的平均数为k, 则把两组数据合并成一组以后,这组样本的平均数为( )A 、2k h +B 、n m mk nh ++C 、mk nh m +D 、nm k h ++ 6、某大学中文系共有本科生5000人,其中一、二、三、四年级的学生比为5:4:3:1,要用分层抽样的方法从该系所有本科生中抽取一个容量为260的样本,则应抽二年级的学生( )A 、100人B 、60人C 、80人D 、20人7、我们对那大中学高二(1)班50名学生的身高进行了调查,按区间145--150,150--155,…,180—185(单位:cm )进行分组,得到的分布情况如下图所示,由图可知样本身高在165--170的频率为( )A 、0.24B 、0.16C 、0.12D 、0.208、一个射手进行一次射击,则事件“命中环数小于6环”的对立事件是( )A 、命中环数为7、8、9、10环B 、命中环数为1、2、3、4、5、6环C 、命中环数至少为6环D 、命中环数至多为6环9、从一箱产品中随机地抽取一件,设事件A=“抽到一等品”,事件B = “抽到二等品”,事件C =“抽到三等品”,且已知 P (A )= 0.65 ,P(B)=0.2 ,P(C)=0.1。
江西省兴国县将军中学2011至2012学年高二下学期第一次月考数学理科试题
一、选择题:(本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.复数131i Z i-=+的实部是( ) A . 2 B .1- C . 1 D .4-.2.421dx x⎰等于( ) A 、2ln2- B 、2ln 2 C 、ln 2- D 、ln 23 . 由1,2,3,4组成没有重复数字的三位数的个数为( )A. 36B. 24C. 12D.64.44(1)(1)x x -+的展开式2x 的系数是( ) A .-4 B .-6 C .6 D .45.某射击选手每次射击击中目标的概率是0.8,如果他连续射击5次,则这名射手恰有4次击中目标的概率是A. 40.80.2⨯B.445C 0.8⨯ C. 445C 0.80.2⨯⨯ D. 45C 0.80.2⨯⨯ 6.已知某离散型随机变量X 服从的分布列如图,则随机变量X 的方差()D X 等于( )A. 19B.29C. 13D. 23 7.若423401234(21)x a a x a x a x a x -=++++, 则1234234a a a a +++等于( )A .4-B .8C .8-D .48.某校在高二年级开设选修课,其中数学选修课开设三个班.选课结束后,有5名同学要求选修数学,但每班至多可接受2名同学,那么不同的分配方案有( )A .45种B .90种C .150种D .180种9.如图,一环形花坛分成A B C D ,,,四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为( )。
江西省兴国县将军中学高二数学下学期期中试题 文(无答
江西省兴国县将军中学2013-2014学年高二数学(无答案)下学期期中试题 文一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合的取值范围是则若a P M P a M x x P ,}.{},1|{2==≤=υ( )A .),(1-∞- B.),∞+1[ C.]11[,- D.),(+∞-∞-[]1υ 2.已知集合的集合有则满足且=}2,1,0{},02,|{2=≤-∈B A x x N x x A υ( )个。
A .3 B.4 C.7 D.83.用反证法证明命题“如果33b b b a <>,那么”时假设的内容是( ) A .33b a =B. 33b a <C. 33b a =且33b a <D. 33b a =或33b a <4.下面四个条件中,使b a >成立的充分不必要条件的是( )A.1+>b aB.1->b aC. 22b a >D.33b a > 5.如图所示,程序框图(算法流程图)的输出结果是( )A.4B.3C.5D.86.如图,一个空间几何体的正视图、侧视图都是面积为23且一个内角为60°的菱形,俯视图为正方形,那么这个几何体的表面积为( )A .34 B.3C.43D.4 7.已知取何值取得最大值时,当x x x x )29(,5.402-<<( )A .1 B.2 C.3 D.278.已知函数等于则,若a f x a x x f ,0)1('1)(2=++=( )A .3 B.-3 C.2 D.-29.若函数x x x x f -+=||)1()(0的定义域是( )A .)1,(--∞ B.)0,1(- C.)1,1(- D.)0,1()1,(---∞υ10.设函数2)2(),0()4()0(2)0()(2-=-=-⎩⎨⎧>≤++=f f f x x c bx x x f 若,则关于x 的方程x x f =)(的解有( )个。
江西省兴国县将军中学高一数学下学期期中试题 理(无答案)
江西省兴国县将军中学2013-2014学年高一数学(无答案)下学期期中试题 理一、选择题1. 在等差数列{a n }中,已知a 1=2,a 2+a 3=13,则a 4+a 5+a 6等于( )A .40B .42C .43D .452. 已知集合A={x |2x +x -2<0},集合B={x |(2)(3)0x x +->},则(C R A)∩B=( )A .{x |2≤x <3}B .{x |1≤x <3}C .{x |-2<x <1}D .{x |-2<x ≤-1或2≤x <3}3. 若2x ,2x+1,3x+3是钝角三角形的三边,则实数x 的取值范围是( )A .24x <<B .2x >C .425x x -->或< D . 4x > 4. 已知数列}{n a 为等差数列,若11101a a <-,且它们的前n 项和n S 有最大值,则使0n S >的n 的最大值为( )A .19B .11C .20D .215. 设x ,y ∈R ,a>1,b>1,若3x y a b ==,11x y+的最大值为( ) A .2 B. 32 C .1 D. 126. 已知a 与b 均为单位向量,其中夹角为θ,有下列四个命题 1p :||1+>a b ⇔θ∈[0,23π) 2p :||1+>a b ⇔θ∈(23π,π] 3p : ||1->a b ⇔θ∈[0,3π) 4p :||1->a b ⇔θ∈(3π,π] 其中真命题是( )A .1p ,4pB .1p ,3pC .2p ,3pD .3p ,4p7. 已知向量()11,y x a =,()22,y x b =,6,32-=⋅==,则2211y x y x ++的值为( ) A.32 B.32- C.65 D.65- 8. 数列{a n }的通项公式n n a n -+=1(*N n ∈),若前n 项的和10=n S ,则项数n 为( )A .10B .11C .120D .121 9. 在Rt △ABC 中,090C ∠=,53AB CA ==,,P 为线段AB 上的点,,||||CACB CP x y xy CA CB =⋅+⋅则的最大值为( ) A .1 B .2C .3D .4 10. 在ABC ∆中,E 、F 分别为AB 、AC 中点.P 为EF 的中点,实数x 、y 满足PA xPB +0yPC +=.则2x y +的值为( )A.1-B.1C.32-D.32二、填空题11. 不等式02≤+-a x x 的解集是空集,则a 的取值范围是12. 对于使M x x ≥-22成立的所有常数M 中,我们把M 的最大值-1,称为函数x x 22-的“下确界”,若xz y z y x R z y x 2,02,,,=+-∈+的“下确界”为 13. 在ABC ∆中,3BC BD =,AD AB ⊥,1AD =,则AC AD ⋅= .14. 数列{a n }的前n 项和为S n ,若a 1=1,a n+1=3S n (n ≥1),则S 100等于________.15. 若两个等差数列{}n a 、{}n b 的前n 项和分别为n A 、n B ,且满足5524-+=n n B A n n ,则135135b b a a ++的值为 ________.三、解答题16.已知不等式ax 2-3x+6>4的解集为{x|x<1或x>2}。
江西省兴国县将军中学2013-2014学年高二上学期第二次月考(兴国
江西省兴国县将军中学2013-2014学年高二上学期第二次月考(兴国精品文档江西省兴国县将军中学2013-2014学年高二上学期第二次月考(兴国试卷说明: 命题人:一、选择题(本题包括25小题,每小题2分,共50分)1(2008年5月8日上午9时17分,北京奥运火炬祥云首次成功点亮在世界最高峰——珠峰,将奥运火送上珠峰,是一项艰巨和复杂的事情,对技术要求很高,充分体现了北京奥运会的“绿色奥运、科技奥运和人文奥运”的理念。
北京奥运火炬的外壳主要采用高品质的铝合金材料制造,燃烧系统内装环保型燃料——丙烷。
其下列对丙烷有关说法中不正确的是( )A(分子中碳原子不在一条直线上B(光照下能够发生取代反应C(比丁烷更易液化D(是石油分馏的一种产品2(在?丙烯 ?氯乙烯 ?苯 ?甲苯四种有机化合物中,分子内所有原子均在同一平面的是( )A(?? B(?? C(?? D(??3.下列物质属于有机物的是 ( )A.Na2CO3 B. CaC2 C.CO(NH2)2 D. CO4(有4种碳架如下的烃,则下列判断正确的是( )A(a和d是同分异构体B(b和c不是同系物C(a和d都能发生加成反应D(只有b和c能发生取代反应5(有八种物质:?甲烷 ?苯 ?聚乙烯 ?聚异戊二烯 ?2,丁炔 ?环己烷 ?邻二甲苯 ?环己烯,既能使KMnO41 / 7精品文档酸性溶液褪色,又能与溴水反应使之褪色的是( )A(???? B(????C(???D(?????6 .某烯烃与H2加成后得到2,2,二甲基丁烷,该烯烃的名称是( ),.2,2,二甲基,3,丁烯 ,.2,2,二甲基,2,丁烯,.2,2,二甲基,1,丁烯 ,.3,3,二甲基,1,丁烯7(设NA为阿伏加德罗常数的值,下列有关叙述不正确的是( )A(标准状况下,1L 庚烷所含有的分子数为NA/22.4B(1mol甲基(—CH3)所含电子数为9NAC(标准状况下,B2H6和C2H4的混合气体22.4L,所含的电子数约为16NAD(26g C2H2和苯蒸气的混合气体中所含的C原子数为2NA8(25?和101kPa时,乙烷、乙炔和丙烯组成的混合烃32mL与过量氧气混合并完全燃烧,除去水蒸气,恢复到原来的温度和压强,气体总体积缩小了72mL,原混合烃中乙炔的体积分数为( )A(12.5% B(25%C(50% D(75%9(加拿大天文学家观察到星际空间存在有链分子HC9N,其结构简式为,这是人类迄今发现的最重的星际分子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
满分:150分 考试时间:120分钟一、选择题(在每小题给出的四个选项中,只有一个正确.每小题5分,共50分)1.复数34343i zi +=+-,则z 等于 ( ) A .3i + B .3i - C .4i + D .4i - 2.已知命题p :∀x ∈R,2x <3x ;命题q :∃x ∈R ,x 3=1-x 2,则下列命题中为真命题的是( )A .p ∧qB .p ∧⌝qC .⌝p ∧qD .⌝p ∧⌝q3.若函数2()2ln f x x x =-在其定义域内的一个子区间(k -1,k +1)内不是单调函数,则实数k 的取值范围是 ( )A .[1,+∞)B .[1,32)C .[1,2)D .[32,2) 4. 下列四个几何体中,几何体只有正视图和侧视图相同的是 ( )A .①②B .①③C .①④D .②④5.已知a 、b 是异面直线,a ⊥平面α,b ⊥平面β,则α、β的位置关系是 ( )A .相交B .平行C .重合D .不能确定6.设椭圆的两个焦点分别为F 1,F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1F 2P为等腰直角三角形,则椭圆的离心率为 ( )A B C .2- D 1-7.如图所示,正方形O′A′B′C′的边长为1,它是水平放置的一个平面图形的直观图,则原图形的周长是 ( ) A .6 B .8 C .2+3 2 D .2+2 38.已知a =(2,-1,3),b =(-1,4,-2),c =(7,5,λ),若a ,b ,c三向量共面,则实数λ等于 ( )A.627B.637C.607D.6579.设离心率为e 的双曲线C :22221(0,0)x y a b a b-=>>的右焦点为F ,直线l 过焦点F , 且斜率为k ,则直线l 与双曲线C 的左、右两支都相交的充要条件是( )A .221k e ->B .221k e -<C .221e k ->D .221e k -<10.已知正三棱锥P —ABC 的高PO 的长为h ,点D 为侧棱PC 的中点,PO 与BD 所成,则正三棱锥P —ABC 的体积为 ( )A 3B 3C 3D 3 二、填空题(本大题共4小题,每小题5分,共20分.请把答案填在题中横线上) 11.计算定积分10(2)x e x dx +⎰的值为 。
12.如图:长方体ABCD —A 1B 1C 1D 1中,AB=3,AD=AA 1=2,E 为AB 上一点,且AE=2EB ,F为CC 1的中点,P 为C 1D 1上动点,当E F ⊥CP 时,PC 1= .13.已知过球面上,,A B C 三点的截面和球心的距离为球半径的一半,且2AB BC CA ===,则球的表面积为 .14.已知,,a b l 表示三条不同的直线,,,αβγ表示三个不同的平面,有下列四个命题:①若a αβ=,b βγ=,且//a b ,则//αγ;②若,a b 相交,且都在,αβ外,//,//,//,//a a b b αβαβ,则//αβ;③若,,,a b a b αβαββ⊥=⊂⊥,则b α⊥;④若,,,a b l a l b αα⊂⊂⊥⊥,则l α⊥。
其中正确命题的序号是 。
三、选做题:请在下列两题中任选一题作答,若两题都做,则按第一题评阅计分,本题5分15.(1)在平面直角坐标系xoy 中,直线l 的参数方程为22x t y t =+⎧⎨=-⎩(参数t R ∈),圆C 的参数方程为2cos 2sin 2x y θθ=⎧⎨=+⎩(参数[0,2)θπ∈),直线l 交圆C 于A 、B 两点,则||AB = .(2)不等式2|1||2|,(1)x x a a a -++≤+>的解集不是空集,则实数a 的最小值为四、解答题(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步 骤)16.(本小题满分12分)已知向量2(cos ,1),(3sin ,cos )222x x x m n =-=,设函数()f x m n =∙+1(Ⅰ)若[0,]2x π∈, 11()10f x =,求cos x 的值;(Ⅱ)在△ABC 中,角A ,B ,C 的对边分别是,,a b c ,且满足2cos 2b A c ≤,求()f B的取值范围.17.(本小题满分12分)如图四棱锥P —ABCD ,底面ABCD 为矩形,侧棱PA ⊥底面ABCD ,其中BC=2AB=2PA=6,M 、N 为侧棱PC 上的三等分点。
(Ⅰ)证明:AN ∥平面MBD ;(Ⅱ)求三棱锥N —MBD 的体积。
18(本小题满分12分)斜三棱柱ABC —A 1B 1C1的各棱长为a ,侧棱与底面所成的角为60o ,且侧面ABB 1A 1垂直于底面。
(Ⅰ)判断B 1C 与AC 1是否垂直,并证明你的结论;(Ⅱ)求三棱柱的全面积。
19(本小题满分12分)如下图,在直棱柱ABCD -A 1B 1C 1D 1中,AD ∥BC ,∠BAD =90°,AC ⊥BD ,BC =1,AD =AA 1=3.(Ⅰ)求异面直线AD 1与BD 所成的角的余弦值;(Ⅱ)求直线B 1C 1与平面ACD 1所成角的正弦值.A B B 1 C A 1 C 120(本小题满分13分)设椭圆C :x 2a 2+y 2b 2=1(a >b >0)的一个顶点与抛物线:x 2=4 2y 的焦点重合,F 1、F 2分别是椭圆的左、右焦点,离心率e =33,过椭圆右焦点F 2的直线l 与椭圆C 交于M 、N 两点.(Ⅰ)求椭圆C 的方程;(Ⅱ)是否存在直线l ,使得OM →·ON →=-1,若存在,求出直线l 的方程;若不存在,说明理由.21.(本小题满分14分)已知函数2ln )(bx x a x f +=在点))1(,1(f 处的切线方程为01=--y x .(Ⅰ)求)(x f 的表达式;(Ⅱ)若)(x f 满足)()(x g x f ≥恒成立,则称)(x f 是)(x g 的一个“上界函数”,如果函数)(x f 为x xt x g ln )(-=(∈t R )的一个“上界函数”,求t 的取值范围; (Ⅲ)当0>m 时,讨论x mm x x f x F 12)()(22+-+=在区间(0,2)上极值点的个数.高二数学(理)参考答案一.选择题:BCBDA DBDCC二.填空题11.e ; 12.2; 13.649π; 14.②③三.选做题:(1); (2)2。
四.解答题16.解:(1)211()cos cos 1cos 22222x x x f x x x =-+=-+ 1sin()62x π=-+,∵11()10f x =,∴3sin()65x π-=; 又∵[0,]2x π∈,∴[,]663x πππ-∈-,即4cos()65x π-=3cos cos[()]cos()cos sin()sin 66666610x x x x ππππππ∴=-+=---=(2)由2cos 2b A c ≤得2sin cos 2sin B A C A ≤可得2sin cos 2sin()B A A B A ≤+-2sin cos cos (0,]6A B A B B π≥⇒≥⇒∈ ∴1sin()(,0]62B π-∈-,即11()sin()()(0,]622f B B f B π=-+⇒∈∴2222S S 2S =+=+=侧全底 19.解:(1)易知,AB ,AD ,AA 1两两垂直.如图2,以A 为坐标原点,AB ,AD ,AA 1所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系.设AB =t ,则相关各点的坐标为:A (0,0,0),B (t,0,0),B 1(t,0,3),C (t,1,0),C 1(t,1,3),D (0,3,0),D 1(0,3,3).从而1B D =(-t,3,-3),AC =(t,1,0),BD =(-t,3,0).因为AC ⊥BD ,所以AC ·BD =-t 2+3+0=0.解得t =3或=-3(舍去). ∴BD ,而1(0,3,3)AD = 111cos ,||||BD AD BD AD BD AD= 332==⨯于是1B D =(-3,3,-3),AC =(3,1,0).(2)由(1)知,1AD =(0,3,3),AC =(3,1,0),11B C =(0,1,0).设n =(x ,y ,z )是平面ACD 1的一个法向量,则⎩⎪⎨⎪⎧ n ·AC →=0,n ·AD 1→=0,即⎩⎨⎧3x +y =0,3y +3z =0.令x =1,则n =(1,-3,3). 设直线B 1C 1与平面ACD 1所成角为θ,则sin θ=|cos 〈n ,11B C 〉|=|n ·B 1C 1→|n |·|B 1C 1→||=37=217. 即直线B 1C 1与平面ACD 1所成角的正弦值为217. 20.解 (1)椭圆的顶点为(0,2),即b = 2.e =c a = 1-b 2a 2=33,解得a =3, ∴椭圆的标准方程为x 23+y 22=1. (2)由题可知,直线l 与椭圆必相交.①当直线斜率不存在时,经检验不合题意.②设存在直线l 为y =k (x -1),且M (x 1,y 1),N (x 2,y 2), 由⎩⎪⎨⎪⎧ x 23+y 22=1,y =k x -得(2+3k 2)x 2-6k 2x +3k 2-6=0. x 1+x 2=6k 22+3k 2,x 1·x 2=3k 2-62+3k 2, OM →·ON →=x 1x 2+y 1y 2=x 1x 2+k 2[x 1x 2-(x 1+x 2)+1]=3k 2-62+3k 2+k 2⎝ ⎛⎭⎪⎫3k 2-62+3k 2-6k 22+3k 2+1=-k 2-62+3k 2=-1. 所以k =±2,故直线l 的方程为y =2(x -1)或y =-2(x -1).21、(1)a=1 b=0 3分(2)∵x xt xln ln -≥恒成立 ∴x x t ln 2≤恒成立,()2ln ,h x x x =令()22ln h x x '=+则,e x x h 1,0)(≥≥'则令, ∴当0)(,10<'<<x h ex 时, ∴)(x h 的最小值为e e h 2)1(-=,∴et 2-≤ 8分 (3)mx mx m x m m x x x F )1)((11)(2--=+-+=',令)(x F =0,得mx m x 1==或 当 210≤<m 时,21≥m,m x =为)(x F 在区间(0,2)上的极大值点 当121<<m 时,211<<m ,mx m x 1==和为)(x F 在区间(0,2)上的极值点 当1=m 时,)(x F 在区间(0,2)上无极值点当21<<m 时,1121<<m ,mx m x 1==和为)(x F 在区间(0,2)上的极值点 当2=m 时,211=m ,mx 1=为)(x F 在区间(0,2)上的极大值点 当2>m 时,2110<<m ,mx 1=为)(x F 在区间(0,2)上的极大值点 由以上可知:当121<<m 或21<<m 时,)(x F 在区间(0,2)上有两个极值点 当210≤<m 或2≥m 时,)(x F 在区间(0,2)上有一个极值点; 当1=m 时,)(x F 在区间(0,2)上无极值点 14分。
