安徽省阜南县王店亲情学校13—14学年下学期高二第二次月考数学(文)(附答案)
安徽省阜南县王店亲情学校高二物理下学期第二次月考试题新人教版

1亲情学校2013—2014下学期第二次月考高二物理试题一、单项选择题:(每小题4分,共计40分) 1.饮水机是一种常见的家用电器,其工作电路可简化为如图所示的电路,其中S 是一温度控制开关,当水温升高到一定温度时,它会自动切换,使饮水机处于保温状态;R 0是饮水机加热管的电阻,R 是与加热管串联的电阻。
下表是从其说明书中摘录的一些技术数据。
(不考虑R 0、R 的电阻受温度变化的影响,表中的功率均指加热管的功率........) ,当开关S 闭合时,饮水机处于何工作状态及R 0的阻值为A .加热,220ΩB .加热,88ΩC .保温,88ΩD .保温,220Ω2.矩形导线框abcd 固定在匀强磁场中,磁感线的方向与导线框所在平面垂直,规定磁场的正方向垂直纸面向里,磁感应强度B 随时间变化的规律如图所示。
若规定顺时针方向为感应电流的正方向,(纵轴表电流,横轴表时间)下列各图中正确的是3.家用电子调光灯的调光原理是用电子线路将输入的正弦交流电压的波形截去一部分来实现的,由截去部分的多少来调节电压,从而实现灯光的可调,比过去用变压器调压方便且体积较小。
某电子调光灯经调整后的电压波形如图所示,若用多用电表测灯泡的两端的电压,多用电表示数为A.22U mB.24UC.12U mD.14U m 4.如图所示,AB 为固定的通电直导线,闭合导线框P 与AB 在同一平面内。
当P远离AB 匀速运动时,它受到AB 的作用力为 A .零B .引力,且逐步变小C .引力,且大小不变D .斥力,且逐步变小 5.一质量为m 的带电小球,在竖直方向的匀强电场中以初速度v 0水平抛出,小球的加速度大小为2g/3,则小球在下落h 高度过程中,以下说法错误..的是 A .动能增加了23 mgh B .电势能增加了13mghC .重力势能减少了mghD .机械能增加了23mgh6.每时每刻都有大量宇宙射线向地球射来,地磁场可以改变射线中大多数带电粒子的运动方向,使它们不能到达地面,这对地球上的生命有十分重要的意义。
安徽省阜阳市阜南县王店孜乡亲情学校2022-2023学年高一下学期第一次月考语文试题(含答案)

王店孜乡亲情学校2022-2023学年高一下学期第一次月考语文本试卷共8页。
全卷满分150分,考试时间150分钟。
注意事项:1.答卷前,先将自己的姓名、准考证号填写在答题卡,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用合乎要求的2B铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选题的作答:用合乎要求的签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,19分)阅读下面的文字,完成1~5题。
材料一:近年来,博物馆成为公众喜爱的文化“打卡”地,一些精品大展现场经常出现排长队的景象。
但是线上展览的观展热度似乎远远不及线下。
是什么阻挡了观展热情?首先,在电脑或手机屏幕上欣赏文物、浏览展厅,与身临其境面对实物所带来的审美体验、艺术震撼是不一样的。
线上展览受到观展设备、展示程序、网络环境等因素影响,操作不便捷、画面不清晰、切换不流畅,都会让观展体验大打折扣。
其次,线上展消弭了空间感,也隐去了观展同伴,参观者难以直观地感受展厅布置的精美、展线设计的巧妙,在观展过程中也没有伙伴可以交流,相应地减少了一些乐趣。
线上展览存在不少局限,但它也有自己的优势。
它在云端持续开放,没有闭展时间,让亿万观众可以随时随地自由参观。
借助先进的数字技术,文物图像可以多角度清晰显示,让观众看到一些现场看不到的细节。
独自观展省去了排队、拥挤的烦恼,能让人更专注地欣赏文物。
线上展和线下展在很多方面都有显著差别,因此,线上展不应是简单地把线下展览搬到网上,而是要对展览进行延伸、拓展,甚至“再创作”。
从三维到二维,少了空间的束缚,线上展览可以打破原有展线设置,为观众提供多样化的观展线路和更丰富的展示内容。
线下展览无法实现的检索、细读等功能,在网络平台都可以实现,以更好地满足文博“发烧友”(线上观展核心人群)的需求。
江苏省阜宁中学2013至2014高二下学期第二次学情调研数学试题
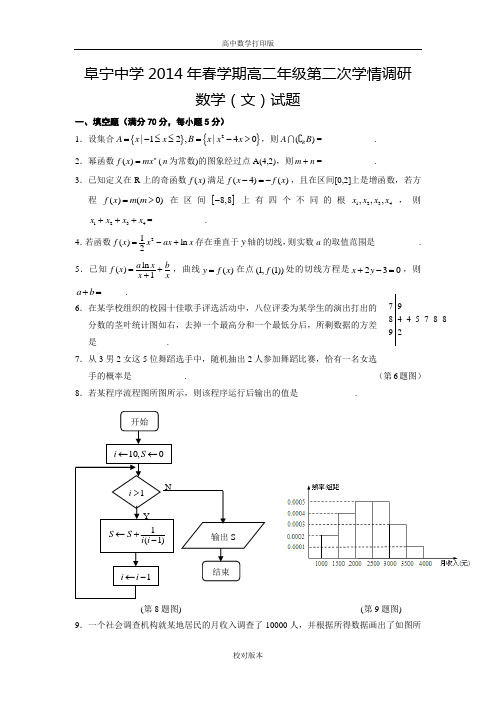
阜宁中学2014年春学期高二年级第二次学情调研数学(文)试题一、填空题(满分70分,每小题5分)1.设集合{}{}2|12,|40A x x B x x x =-≤≤=->,则()R AB =____________.2.幂函数()n f x mx =(n 为常数)的图象经过点A(4,2),则m n +=____________.3.已知定义在R 上的奇函数()f x 满足(4)()f x f x -=-,且在区间[0,2]上是增函数,若方程()(0)f x m m =>在区间[]8,8-上有四个不同的根1234,,,x x x x ,则1234x x x x +++=____________.4.若函数21()ln 2f x x ax x =-+存在垂直于y 轴的切线,则实数a 的取值范围是__________.5.已知ln ()1a x b f x x x=++,曲线()y f x =在点(1,(1))f 处的切线方程是230x y +-=,则a b +=_____.6.在某学校组织的校园十佳歌手评选活动中,八位评委为某学生的演出打出的 分数的茎叶统计图如右,去掉一个最高分和一个最低分后,所剩数据的方差 是________________.7.从3男2女这5位舞蹈选手中,随机抽出2人参加舞蹈比赛,恰有一名女选手的概率是____________. (第6题图) 8.若某程序流程图所图所示,则该程序运行后输出的值是_____________.(第8题图) (第9题图) 9.一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画出了如图所7 98 4 4 5 7 8 8 9 2开始10,0i S ←←1i >1(1)S S i i ←+- 1i i ←-输出S结束NY示频率分布直方图,现要从这10000人中再用分层抽样的方法抽出100人作进一步调查,则月收入在[)2500,3000 内应抽出___________人.10.在△ABC 中,60ACB ∠=,sin :sin 8:5A B =,则以A 、B 为焦点且过点C 的椭圆的离心率为______________.11.根据如图所示的伪代码,当输入x 为60时,输出的y 的值___________. 12.设2(),()(1)x f x xe g x x a ==-++,若12,x x R ∀∈,使得21()()g x f x ≤成立,则实数a 的取值范围是______________.13.已知函数(13)10(7)()log (6)(7)aa x a x f x x x -+≤⎧=⎨->⎩ 是定义域上的减函数,则a 的取范围是____________.14.在平面直角坐标系中,已知P 是函数()(0)x f x e x =>的图象上的动点,该图象在点P 处的切线l 交y 轴于M 点,过P 作l 的垂线交y 轴于N 点.设线段MN 的中点的纵坐标为t ,则t 的最大值为____________.二、解答题(满分90分,其中15、16、17题为14分,18、19、20题为16分) 15.设集合{}{}221|log (28),|21A x y x xB y y x x ==--+==+--,集合{}1|()(4)0C x ax x a=-+≤.⑴求A B ;⑵若RC A ⊆,求实数a 的取值范围.16.已知12a >且1a ≠,条件:p 函数(21)()log (5)a f x x -=-在其定义域上是减函数;条件:q Re 500.5250.6(50)int ad xIf x Then y x Elsey x End If pr y≤←←+-函数()g x =R. 如果“p 或q ”为真,试求a 的取值范围.17.设函数()f x 的定义域为R ,对,a b R ∀∈,总有()()()f a b f a f b +=且0x >时,0()1f x <<.⑴求证:(0)1f =且0x <时()1f x >; ⑵证明:()f x 在(,)-∞+∞上单调递减; ⑶设{}{}22(,)|()()(1),(,)|(2)1,A x y f x f y f B x y f mx y m R =⋅>=-+=∈,若A B =∅,试求实数m 的取值范围.18.如图所示,直立在地面上的两根钢管AB 和CD ,两根钢管相距1m ,m ,,现用钢丝绳对这两根钢管进行加固,在AB 上取一点E ,以C 为支点将钢丝绳拉直并固定在地面的F 处,形成一个直线型的加固. 设(),(),().BE x m EFD rad EF l m θ=∠==⑴试将()l m 分别表示成()x m ,()rad θ的函数;⑵选择其中一个函数模型求()l m 的最小值,并求相应的x (或θ)的值.(第18题图)19.如图,已知椭圆22:142y x C +=,Q 是椭圆的右准线l 上一动点,直线OQ 交椭圆C 于A 、B 两点,圆22:4O x y +=,QM 、QN 是圆O 的两条切线,M 、N 为切点. ⑴求证:直线MN 恒过椭圆C 的右焦点F ;⑵若点P 是椭圆上任意一点,且直线AP 、BP 的斜率都存在,分别记为12,k k ,探究12k k ⋅是否为定值?说明理由.(第19题图)20.设函数()3(*,,)n n f x x ax b n a b =-++∈∈N R . ⑴若1a b ==,求3()f x 在[]0,2上最大值和最小值;⑵若对任意[]12,1,1x x ∈-,都有3132|()()|1f x f x -≤,求a 的取值范围;⑶若4|()|f x 在[]1,1-上的最大值为12,求,a b 的值.高二数学(文)参考答案一、填空题(满分70分,每小题5分) 1.[]0,2 2.323.8- 4.[)2,+∞ 5.2 6.37.358.9109.2510.71311.3112.1a e≤-13.(17,311⎤⎥⎦14.11()2e e+二、解答题(满分90分,其中15、16、17题为14分,18、19、20题为16分) 15.解:⑴[)(](4,2),1,,3A B =-=+∞-∞-(][)4,31,2A B ∴=--………………………………………………………………7分⑵(][),42,RA =-∞-+∞,当0a >时,214,C a ⎡⎤=-⎢⎥⎣⎦,又RC A ⊆无解,当0a <时,(]21,4,C a ⎡⎫=-∞-+∞⎪⎢⎣⎭,又RC A ⊆,212a∴≥⇒212a ≤⇒0a ≤<………………………………………………………………14分16.解:⑴若p 真,则1021112a a <-<⇒<<…………………………………………………4分⑵若q 真,则||20x x a +--≥对x R ∀∈恒成立,设22()||22x a x ah x x x a a x a--≥⎧=+--=⎨-<⎩ ,[]()h x ∴最小2a ⇒-,故q 为真,而202a a -≥⇒≥………………………………10分⑶p q ∨为真112a ⇒<<或[]12(,1)2,2a a ≥⇒∈+∞………………………………14分17.解:⑴取0,0a b =>,则()(0)()f b f f b =,又()(0,1)f b ∈,(0)1f ∴=. 设0,0a x b x =<=->,则0()1f x <-<,()()()f x x f x f x ∴-=-1()1()f x f x =>-………………………………………4分 ⑵1212,(,),x x x x ∀∈-∞+∞<,则210x x ->,210()1f x x <-<, 于是[][]212121221()()()()()()10f x f x f x x x f x f x f x x -=-+-=--<,()f x ∴在R 上递减…………………………………………………………………………10分⑶2222()()(1)1f x f y f x y >⇔+<,(2)120f mx y mx y -+=⇔-+=2213320x y A B m mx y ⎧+=∴=∅⇔⇔-≤⎨-+=⎩无解…………………………………14分 18.…………………………………………4分 (8)分………………………………………………………16分………………………………………………………16分19.解:⑴:l x =)Q t ,则MN: 40ty +-=,令0y =,x MN ∴经过右焦点F …………………………………………………………………8分⑵设1122(,),(,)P x y A x y ,A 、B 关于原点对称,22(,)B x y ∴--2221222112222121211=2y y y y y y k k x x x x x x -+-∴=⋅=--+-……………………………………………………16分20.解:⑴33()31f x x x =-++,33()330f x x '=-+=,令3()0,1f x x '==,33(0,1)(1,2)()()x f x f x ' + -[][]33()(1)3,()1f x f f x ===-最大最小 (6)分⑵依题意3311|(1)(1)|162f f a --≤⇒≤≤,又23()33f x x a '=-+,3()f x ∴在1,⎡-⎣上,在⎡⎣上,在⎤⎦,33|(|1f f ∴-≤41a ⇒⇒≤,故16a ≤…………………………………………………………………………………10分 ⑶由44441111111|()|()(1),(1)2222222f x f x f f ≤⇒-≤≤⇒-≤≤-≤-≤,相加级413116,(10)2222f ≤≤-≤≤又,11622∴-≤=,从而162=代入级0a =,检验0a =,411,()22b f x x ==-合题意………………………16分。
安徽省阜阳市高二下学期第二次月考数学试卷含答案

数学试卷时量:120分钟 满分:150分一、选择题(本大题共12小题,每小题5分,共60分) 1.已知i z +=1,若43_2-+=z z ω,则ω为( )A.1B. 2C. 3D.22.已知命题p 、q ,如果p ⌝是q ⌝的充分而不必要条件,那么q 是p 的( ) A.必要不充分条件 B.充分不必要条件 C.充要条件 D.既不充分也不必要3.已知椭圆C 的右焦点为(1,0),离心率为0.5,则C 的方程是( )A.13422=+y xB. 14322=+y xC. 13222=+y xD.12322=+y x 4.在面积为S 的△ABC 的边AB 上任取一点P ,则△PBC 的面积大于4S的概率是( ) A.41 B.21 C.43 D.325.已知关于x 与y 的一组数据如下,则y 与x 的线性回归方程a x b y+=ˆˆ必过点( ). A .(2,2) B .(1,2)C .(1.5,4)D .(1.5,0)6.以下哪个K 2的观测值k ,在犯错误的概率不超过0.05的前提下,认为两个分类变量有关系( ).A .k =1B .k =2C .k =3D .k =47.曲线C 经过伸缩变换⎩⎨⎧='='y y x x 35后,变为了曲线18222=+y x ,则曲线C 的方程为( )A.1725022=+y x B.1100922=+y x C.12410=+y x D.19825222=+y x 8.抛物线x y 42=上一点A 到点)2,3(B 与焦点的距离之和最小,则点A 的坐标为( )A.)(22,2B.)(32,3C.)(2,5.0D.)(2,19.过椭圆右焦点的直线03=-+y x 交椭圆于A,B 两点,P 为AB 的中点,且OP 的斜率为0.5,则椭圆的方程为( )A.13422=+y xB.13622=+y xC.12422=+y x D.12622=+y x10.已知函数)(x f 的导函数为)(x f ',且满足x e f x x f ln )(2)(+'=,则=')(e f ( ) A.1-e B.-1 C.1--e D.e -11.21,F F 是椭圆1422=+y x 与双曲线C 的公共焦点,A,B 分别是椭圆与双曲线在第二、四象限的公共点,且四边形21BF AF 为矩形,则双曲线的离心率为( ) A.2 B. 3 C.23D.2612.定义在R 上的函数)(x f 满足:)()(x f x f <'恒成立,若21x x <,则)()(1221x f e x f e xx与的大小关系是( )A.)()(1221x f e x f e xx> B.)()(1221x f e x f e xx< C.)()(1221x f e x f e xx= D.不确定二、填空题(本大题共4小题,每小题5分,共20分)13.若p :1)1(,0>+>∀xe x x 有。
安徽省阜南县王店亲情学校高二数学下学期第二次月考试
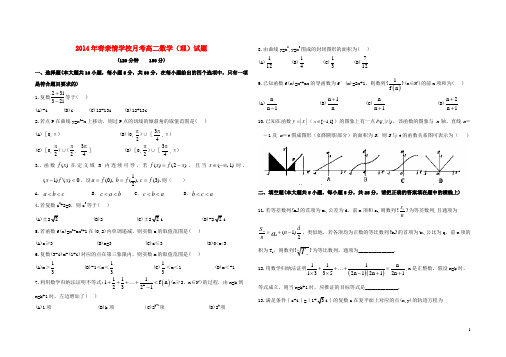
2014年春亲情学校月考高二数学(理)试题(120分钟 150分)一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.复数23i32i+-等于( ) (A)-i (B)i (C)12-13i (D)12+13i2.若点P 在曲线y=x 3-x 上移动,则过P 点的切线的倾斜角的取值范围是( )(A)[0,π) (B)(0,2π)∪[34π,π) (C)[0,2π)∪(2π, 34π] (D)[0,2π)∪[34π,π)3..函数)(x f 在定义域R 内连续可导,若)2()(x f x f -=,且当)1,(-∞∈x 时,0)()1(<'-x f x ,设).3(),21(),0(f c f b f a ===则( )A .c b a <<B .b a c <<C .a b c <<D .a c b <<4.若复数z 2+2=0,则z 3等于( )(A)±22 (B)2 (C)±22i (D)-22i 5.若函数f(x)=x 3-ax 2+1在(0,2)内单调递减,则实数a 的取值范围是( )(A)a ≥3 (B)a=3 (C)a ≤3 (D)0<a<3 6.复数(3-i)m-(1+i)对应的点在第三象限内,则实数m 的取值范围是( )(A)m >13 (B)-1<m <13 (C)13<m <1 (D)m <-1 7.利用数学归纳法证明不等式:()n 1111f n 2321+++⋯+<-(n ≥2,n ∈N *)的过程,由n=k 到n=k+1时,左边增加了( )(A)1项 (B)k 项 (C)2k-1项 (D)2k项8.由曲线y=x 2,y=x 3围成的封闭图形的面积为( ) (A)112 (B)14 (C)13 (D)7129.已知函数f(x)=x m+ax 的导函数为f ′(x)=2x+1,则数列{()1f n }(n ∈N *)的前n 项和为( ) (A)n n 1- (B)n 1n + (C)n n 1+ (D)n 2n 1++ 10.已知在函数||y x =([1,1]x ∈-)的图象上有一点(,||)P t t ,该函数的图象与 x 轴、直线x =-1及 x =t 围成图形(如图阴影部分)的面积为S ,则S 与t 的函数关系图可表示为( )二、填空题(本大题共5小题,每小题5分,共25分,请把正确的答案填在题中的横线上) 11.若等差数列{a n }的首项为a 1,公差为d ,前n 项和s n ,则数列{ns n }为等差数列,且通项为2)1(1dn na sn-+=,类似地,若各项均为正数的等比数列{b n }的首项为b 1,公比为q ,前n 项的积为T n ,则数列{nnT}为等比数列,通项为______________.12.用数学归纳法证明()()111n13352n 12n 12n 1++⋯+=⨯⨯-++,n 是正整数,假设n=k 时,等式成立,则当n=k+1时,应推证的目标等式是_____________.13.满足条件|z-i |=|3i |的复数z 在复平面上对应的点(x,y)的轨迹方程为____________________.14.函数f(x)=x 3+3ax 2+3[(a+2)x+1]有极大值又有极小值,则a 的取值范围是 __________________. 15.给出以下命题:①若()0baf x dx >⎰,则()0f x >;②20sin 4x dx π=⎰;③若函数()f x 为奇函数,则()0aaf x dx -=⎰;④函数()f x 的原函数为()F x ,且()F x 是以T 为周期的函数,则0()()aa Tf x dx f x dx +=⎰⎰.其中正确命题是 (写出所有正确命题的编号).三、解答题(本大题共6小题,共75分,解答时应写出必要的文字说明、证明过程或演算步骤) 16.(12分)(1)计算25i()34i 2++;(2)复数z=x+yi(x,y ∈R)满足z+2i z =3+i 求复数z.18.(12分)已知抛物线C:y=-x 2+2x,过点A(0,0),B(2,0)分别作抛物线的切线L 1,L 2. (1)求切线L 1和L 2的方程.(2)求抛物线C 与切线L 1和L 2所围成的图形面积S.19.(12分)已知a 为实数,且函数f(x)=(x 2-4)(x-a)(1)求导函数f ′(x);(2)若f ′(-1)=0,求函数f(x)在[-2,2]上的最大值、最小值. 20.(13分)已知数列{a n }的前n 项和为S n ,且a 1=1,S n =n 2a n (n ∈N *). (1)试求出S 1,S 2,S 3,S 4,并猜想S n 的表达式;(2)用数学归纳法证明你的猜想,并求出a n 的表达式. 21.(14分)设函数f(x)=lnx-错误!未找到引用源。
安徽省阜阳市阜南县第二中学高二数学理月考试卷含解析

安徽省阜阳市阜南县第二中学高二数学理月考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 设一个回归直线方程是,当变量增加一个单位时()A. 平均增加3个单位B. 平均减少5个单位C. 平均增5个单位D. 平均减少3个单位参考答案:B略2. 在等差数列{a n}中,已知a1=2,a2+a3=13,则a4+a5+a6等于( )A.40 B.42 C.43 D.45参考答案:B【考点】等差数列的性质.【专题】计算题.【分析】先根据a1=2,a2+a3=13求得d和a5,进而根据等差中项的性质知a4+a5+a6=3a5求得答案.【解答】解:在等差数列{a n}中,已知a1=2,a2+a3=13,得d=3,a5=14,∴a4+a5+a6=3a5=42.故选B【点评】本题主要考查了等差数列的性质.属基础题.3. 函数y=x+( )A.有最小值,无最大值B.有最大值,无最小值C.有最小值,最大值2D.无最大值,也无最小值参考答案:A4. 直线y=x-3与抛物线y2=4x交于A、B两点,过A、B两点向抛物线的准线作垂线,垂足分别为P、Q,则梯形APQB的面积为 ( )(A).72 (B).56 (C).64 (D).48参考答案:D5. 命题“若x>5,则x>0”的否命题是A.若x≤5,则x≤0 B.若x≤0,则x≤5C.若x>5,则x≤0 D.若x>0,则x>5参考答案:A略6. 四张卡片上分别标有数字其中可以当使用,则由这四张卡片可组成不同的四位数的个数为()A. B. C.D.参考答案:C7. 已知点F1,F2分别是椭圆C: +=1(a>b>0)的焦点,点B是短轴顶点,直线BF2与椭圆C 相交于另一点D.若△F1BD是等腰三角形,则椭圆C的离心率为()A.B.C.D.参考答案:B【考点】椭圆的简单性质.【分析】由题意画出图形,结合已知求出|DF1|、|DF2|,再由余弦定理列式求得答案.【解答】解:如图,由椭圆定义可得:|DF1|+|DF2|=2a,∵△F1BD是等腰三角形,∴|DF1|=|DB|=|DF2|+|BF2|,解得|DF2|=,|DF1|=.又|BF1|=a,∴cos∠F1DF2=,又cos∠F1DF2=,∴,化简得:a2=3c2,得.故选:B.8. 双曲线﹣=1(mn≠0)的离心率为2,有一个焦点与抛物线y2=4x的焦点重合,则mn的值为()A.B.C.D.参考答案:A【考点】圆锥曲线的共同特征;抛物线的简单性质;双曲线的简单性质.【分析】先根据抛物线方程求得抛物线的焦点,进而可知双曲线的焦距,根据双曲线的离心率求得m,最后根据m+n=1求得n,则答案可得.【解答】解:抛物线y2=4x的焦点为(1,0),则双曲线的焦距为2,则有解得m=,n=∴mn=故选A9. 已知,猜想的表达式为()A. B.C. D.参考答案:B∵∴,即.∴数列是以为首项,为公差的等差数列.∴∴故选B.10. 设偶函数对任意,都有,且当时,,则=A.10B.C.D.参考答案:B二、 填空题:本大题共7小题,每小题4分,共28分 11. 在如图所示的数阵中,第行从左到右第3个数是参考答案:略12.无论取何实数时,直线恒过定点,求定点的坐标为.参考答案:13. 以为中点的抛物线的弦所在直线方程为: .参考答案:14. 过双曲线的左焦点作圆的切线,切点为,延长交双曲线右支于点P ,若,则双曲线的离心率是 .参考答案:略15. 方程()所表示的直线恒过点_____________。
安徽省阜南县王店亲情学校高二政治下学期第二次月考试题(无答案)新人教版(1)
2014春亲情学校第二次月考高二政治试题说明:本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分100分;时间90分钟第Ⅰ卷(选择题共50分)本卷共有25小题,每小题2分,共50分。
在每题给出的四个选项中.只有一项是正确的。
请将正确答案的字母填到答题卡相应的位置上。
1.蔡元培曾说:“治自然科学者,局守一门,而不肯稍涉哲学,而知哲学之归宿,其中如自然哲学一部,尤为科学家所需要。
”这说明①自然科学与哲学是相互联系的②哲学是“科学之科学”,对自然科学研究具有指导作用③研究自然科学的目的在于推动哲学的进步和发展④自然科学研究离不开哲学所提供世界观和方法论的指导A.①② B.①④ C.②③ D.③④从哲学角度看,材料说明A.国家大力实施就业优先战略B.世界观决定方法论C.学生已经树立正确的就业观D.哲学是一种世界观3.《非诚勿扰2》捧红了一首小诗《见与不见》:“你见,或者不见我/我就在那里——不悲不喜……”下列与这句诗所蕴涵的哲理相一致的是A.心外无物 B.我在故我思C.理在事先,理生万物 D.古今异俗,新故异备4.有人曾问哲学家约翰·罗尔斯为什么要研究哲学,他说:“一个没有人去思考形而上学、知识论、道德与政治哲学的社会,其实是一个残缺不全的社会。
”这一观点意在强调哲学①能够使人善于思考,增长智慧②能够提供具体问题的解决方法③是时代精神上的精华④能够推动思想解放,促进社会变革A.①②B.③④C.①④D.②③5.哲学史上存在着唯物主义和唯心主义、辩证法和形而上学这“两个对子”。
下列对应关系能分别体现“两个对子”的是①理在事先—断章取义②形存神存—心外无物③掩耳盗铃—削足适履④沧海桑田—刻舟求剑A.①②B.③④C.①③D.②④6.改革开放的30多年是中国特色社会主义理论体系形成与发展的30年。
中国特色社会主义理论体系是马克思主义中国化的最新成果,是党最可宝贵的政治和精神财富。
由此可见A.任何哲学都是自己时代的精神上的精华B.任何哲学都是时代进步的助推器,推动着时代向前发展C.中国特色社会主义理论体系是当今时代精神上的精华D.真正的哲学是对具体科学的概括和总结7.世界著名人脑研究所的维得罗夫斯基教授近日表示,俄罗斯科学家经长期观测发现,人体死亡以后,从身体中发放出一种肉眼看不到的物质。
安徽省阜阳市阜南县王店孜乡亲情学校2024-2025学年高二上学期开学考物理试卷
安徽省阜阳市阜南县王店孜乡亲情学校2024-2025学年高二上学期开学考物理试卷一、单选题1.下列对自由落体运动的说法正确的是()A.物体做自由落体运动不受任何外力B.自由落体运动是初速度为零的匀加速直线运动C.“重的物体下落得快”是伽利略自由落体运动的结论D.做自由落体运动的物体,质量越大,下落越快v t图像中最有可能的是()2.某位运动员百米赛跑的成绩是10s,下列—A.B.C.D.3.如图所示,轻直杆BC的一端用铰链固定于竖直墙壁,另一端固定一个轻小滑轮C,轻细绳下端挂一重物,细绳的AC段水平。
忽略所有摩擦,若将细绳的端点A缓慢向下移动一小段距离,则移动过程中下列说法正确的是()A.直杆顺时针转动了一些B.直杆没有发生转动C.直杆逆时针转动了一些D.无法确定直杆是否转动4.如图甲所示,一根轻质弹簧栓连A、B物块中间静止在光滑水平面上,物块A的质量为1.5kg ,弹簧处于原长。
0t =时对物块A 施加水平向右的恒力F ,1s t =时撤去,在0~1s 内两物块的加速度随时间变化的情况如图乙所示。
弹簧始终处于弹性限度内,则( )A .F 大小为1NB .1s t =时弹簧弹力为1NC .物块B 的质量为1kgD .1s t =时物块A 的速度为0.8m/s5.随着无人机行业迅速发展,“无人机+”的潜力不断被挖掘。
某企业研发了一款可以灭火的重载无人机,可带50公斤水基弹飞行30分钟。
假如该型无人机悬停在火场上空,一枚水基弹从无人机上自由下落(忽略空气阻力),一小段时间后受一恒定水平向右的风力的影响,但着地前一段时间风突然停止,则水基弹的运动的轨迹可能是图中的( )A .B .C .D .6.人造卫星A 和人造卫星B 都绕地球做圆周运动,它们的质量之比为A B :1:2m m =,它们的轨道半径之比为2:1,则下面的结论中正确的是( )A .A 、B 的运行速度大小之比为A B :v v =B .A 、B 的运行周期之比为A B :2:1T T =C .A 、B 的运行角速度之比为A B :ωω=D .A 、B 受到地球的引力之比为A B :1:1F F =7.如图甲所示,农民用手抛撒谷粒进行水稻播种。
安徽省阜南县王店亲情学校2013-2014学年高二数学下学期第二次月考试题 文 新人教A版
亲情学校2014年春高二数学(文)月考试题(120分钟,150分)一、选择题(每题5分,共50分,在每小题给出的四个选项中只有一项是符合题目要求的) 1.复数2(2)+=i ( )A .34i --B .34i -+C .34i -D .34i + 2命题“所有能被2整除的整数都是偶数”的否定是( )A.所有不能被2整除的整数都是偶数B.所有能被2整除的整数都不是偶数C.存在一个不能被2整除的整数都是偶数D.存在一个能被2整除的整数不是偶数 3.设复数121,2z i z bi =+=+,若21z z 为纯虚数,则实数b = ( ) A .2B. 1C.1-D.2-4.设p :f (x )=x 3+2x 2+mx +1在(-∞,+∞)内单调递增,q :m ≥43,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件5.设x ,y ,z∈(0,+∞),a =x +1y ,b =y +1z ,c =z +1x,则a ,b ,c 三数( )A .至少有一个不大于2B .都小于2C .至少有一个不小于2D .都大于26.若函数32()f x ax bx cx d =+++有极值,则导函数()f x '的图象不可能是( )7.观察图示图形规律,在其右下角的空格内画上合适的图形为()A.B.C.D.8.一个算法的框图如图所示,若输出的结果为,则判断框中应填入的条件是( )A.i<5?B.i<6?C.i ≥5?D.i ≥6?9.在10个形状大小均相同的球中有6个红球和4个白球,不放回地依次摸出2个球,在第1次摸出红球的条件下,第2次也摸到红球的概率为( )A. B.C. D.10.把一个周长为12cm 的长方形围成一个圆柱,当圆柱的体积最大时,该圆柱的底面周长与高的比为 ( )A.1∶2B.1∶πC.2∶1D.2∶π 二、填空题(本大题共5小题,每小题5分,共25分).11.函数f(x)=x+e x的递增区间是 .12.设函数()f x 的导数为()f x ',且()2(1)ln (2)x f x f x f ''=-+,则(2)f '的值是 13.已知命题p:“存在x R ∈,使x 1420x m +++=” ,若“非p ”是假命题,则实数m 的取值范围是14已知复数z 1=-1+2i,z 2=1-i,z 3=3-2i,它们所对应的点分别为A,B,C,若错误!未找到引用源。
【数学】安徽省阜南县王店亲情学校2013-2014学年高一下学期第二次月考(理)
2014年春亲情学校高一数学(理)月考试题(120分钟 150分)一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.空间直角坐标系中,已知A(2,3,5),B(3,1,4),则A ,B 两点间的距离为( ) (A)62.经过点M(-2,m),N(m,4)的直线的斜率等于1,则m 的值为( )(A)1 (B)4 (C)1或3 (D)1或4 3.若二面角M-l-N 的平面角大小为π32,直线m ⊥平面M ,则平面N 内的直线与m 所成角的取值范围是( )][][A.[ B.]6242C.[ D.0]322πππππππ,,,,4.直线l 1与直线l 2:3x+2y-12=0的交点在x 轴上,并且l 1⊥l 2,则l 1在y 轴上的截距是( ) (A)-4(B)4(C)83-(D)835.一个底面是正三角形的三棱柱的正视图如图所示,则其体积等于( )(A)6(B)2(D)6.若直线(a+2)x+(1-a)y=3与直线(a-1)x+(2a+3)y+2=0互相垂直,则a 等于( ) (A)1 (B)-1 (C)±1 (D)-27.若圆C 与圆(x+2)2+(y-1)2=1关于原点对称,则圆C 的方程是( )(A)(x-2)2+(y+1)2=1 (B)(x-2)2+(y-1)2=1(C)(x-1)2+(y+2)2=1 (D)(x+1)2+(y-2)2=18.圆x 2+y 2+2kx+k 2-1=0与圆x 2+y 2+2(k+1)y+k 2+2k=0的圆心之间的最短距离是( )(A)2(B) (C)19.已知直线x=2及x=4与函数y=log 2x 图象的交点分别为A ,B ,与函数y=lgx 图象的交点分别为C ,D ,则直线AB 与CD( )(A)平行 (B)垂直 (C)不确定 (D)相交10.圆x2+y2+2x-4y-3=0上到直线x+y+1=0 )(A)1 (B)2 (C)3 (D)4二、填空题(本大题共5小题,每小题5分,共25分,请把正确答案填在题中的横线上)11.已知ABCD为平行四边形,且A(4,1,3),B(2,-5,1),C(3,7,-5),则点D的坐标为_______________.12.如图长方体中,AB=AD=23,CC1=2,则二面角C1-BD-C的大小为____13.圆x2+y2-2x-2y+1=0上的点到直线x-y=2的距离的最大值是_______ .14.如图,将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D-ABC中,给出下列三种说法:①△DBC是等边三角形;②AC⊥BD;③三棱锥D-ABC其中正确的序号是________(写出所有正确说法的序号).15.直线y=2x+3被圆x2+y2-6x-8y=0所截得的弦长等于_________三、解答题(本大题共6小题,共75分,解答时应写出必要的文字说明、证明过程或演算步骤)16.(12分)求过两条直线x-2y+4=0和x+y-2=0的交点P,且满足下列条件的直线方程.(1)过点Q(2,-1);(2)与直线3x-4y+5=0垂直.17.(12分)已知圆C:x2+y2-8y+12=0,直线l经过点D(-2,0),且斜率为k.(1)求以线段CD为直径的圆E的方程;(2)若直线l与圆C相离,求k的取值范围.18.(12分)如图,是一个几何体的三视图,请认真读图.(1)画出几何体的直观图.(2)当AB 的中点为M,PC 的中点为N 时,求证:MN ∥平面PAD.19. (12分)如图,在直三棱柱ABC-A 1B 1C 1中,AB=AA 1,∠CAB=2.(1)证明:CB 1⊥BA 1.(2)已知AB=2,BC=5,求三棱锥C 1-ABA 1的体积.20.(13分)已知圆M:x 2+(y-2)2=1,Q 是x 轴上的动点,QA ,QB 分别切圆M 于A,B 两点. (1)若点Q 的坐标为(1,0),求切线QA ,QB 的方程; (2)求四边形QAMB 的面积的最小值;(3)若,求直线MQ 的方程. 21.(14分)已知圆C 的圆心在直线l:3x-y=0上,且与直线l 1:x-y+4=0相切. (1)若直线x-y=0截圆C 所得弦长为26,求圆C 的方程. (2)若圆C 与圆x 2+y 2-4x-12y+8=0外切,试求圆C 的半径.(3)满足已知条件的圆显然不只一个,但它们都与直线l 1相切,我们称l 1是这些圆的公切线.这些圆是否还有其他公切线?若有,求出公切线的方程,若没有,说明理由.参考答案11.(5,13,-3) 12.30° 13.12+ 14.①② 15.416.解:由x 2y 40x y 20-+=⎧⎨+-=⎩,,解得x 0y 2=⎧⎨=⎩,,∴P(0,2).(1)∵k PQ =32-, ∴直线PQ:y-2=32-x,即3x+2y-4=0. (2)∵直线3x-4y+5=0的斜率k=34,∴所求直线的斜率k ′=43-,∴所求直线为y-2=4x 3-,即4x+3y-6=0.17.解:(1)将圆C 的方程x 2+y 2-8y+12=0配方得标准方程为x 2+(y-4)2=4, 则此圆的圆心为C(0,4),半径为2.所以CD 的中点E(-1,2),= ∴故所求圆E 的方程为(x+1)2+(y-2)2=5. (2)直线l 的方程为y-0=k(x+2), 即kx-y+2k=0.若直线l 与圆C 相离,则有圆心C 到直线l 2>,解得k<34.18.(1)由三视图推出几何体为一条侧棱PA 垂直于底面ABCD 的四棱锥,底面ABCD 为矩形,如图①.(2)如图②,取PD 的中点G,连接MN,NG,GA,则NG CD,而AB CD,AM=AB,所以NG AM,所以四边形AMNG为平行四边形,所以MN∥AG,又AG平面PAD,MN⊈平面PAD.所以MN∥平面PAD.18. (1)如图,连接AB1,CAB=,因为几何体ABC-A1B1C1是直三棱柱,∠所以AC⊥平面ABB1A1,故AC⊥BA1.又因为AB=AA1,所以矩形ABB1A1是正方形,所以BA1⊥AB1,又AC∩AB1=A,所以BA1⊥平面CAB1,又CB1平面CAB1,故CB1⊥BA1.(2)因为AB=AA1=2,BC=,所以AC=A1C1=1,由(1)知,A1C1⊥平面ABA1,所以=·A1C1=×2×1=..20.解:(1)设过点Q的圆M的切线方程为x=my+1,则圆心M到切线的距离为1,1=⇒m=43-或0,∴切线QA ,QB 的方程分别为 3x+4y-3=0和x=1. (2)∵MA ⊥AQ,∴S QAMB =|MA|·==(3)设AB 与MQ 交于点P , 则MP ⊥AB,MB ⊥BQ,13=. 在Rt △MBQ 中,|MB|2=|MP|·|MQ|,解得|MQ|=3.设Q(x,0),则x 2+22=9,x=∴Q(∴直线MQ 的方程为或21.设圆C 的圆心坐标为(a,3a),则它的半径r 2.==-(1)圆心C 到直线x-y=0的距离d ==,因而该直线截圆C 所得弦长为===所以11a ,r 2|44==-= 圆C 的方程为221349(x )(y ).448-+-= (2)2=-=因为两圆外切,所以(3)如果存在另一条公切线,则它必过l 与l1的交点(2,6).①若斜率不存在,则其方程为x=2,圆心C 到它的距离,由于方程需要对任意的a 都成立,因此无解,所以它不是公切线.②若斜率存在,设公切线的方程为y-6=k(x-2), 即kx-y+6-2k=0,所以d r 2,===-所以k2+6k-7=0,解出k=1或k=-7. k=1时直线与l1重合,k=-7时, 直线方程为7x+y-20=0.所以还存在一条公切线,其方程为7x+y-20=0.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
亲情学校2014年春高二数学(文)月考试题
一、选择题(每题5分,共50分,在每小题给出的四个选项中只有一项是符合题目要求的) 1.复数2(2)+=i ( )
A .34i --
B .34i -+
C .34i -
D .34i +
2命题“所有能被2整除的整数都是偶数”的否定是( )
A.所有不能被2整除的整数都是偶数
B.所有能被2整除的整数都不是偶数
C.存在一个不能被2整除的整数都是偶数
D.存在一个能被2整除的整数不是偶数 3.设复数121,2z i z bi =+=+,若2
1
z z 为纯虚数,则实数b = ( ) A .2
B. 1
C.1-
D.2-
4.设p :f (x )=x 3+2x 2+mx +1在(-∞,+∞)内单调递增,q :m ≥4
3,则p 是q 的( )
A .充分不必要条件
B .必要不充分条件
C .充分必要条件
D .既不充分也不必要条件
5.设x ,y ,z ∈(0,+∞),a =x +1y ,b =y +1z ,c =z +1
x ,则a ,b ,c 三数( )
A .至少有一个不大于2
B .都小于2
C .至少有一个不小于2
D .都大于2
6.若函数32()f x ax bx cx d =+++有极值,则导函数()f x '的图象不可能是 (
)
7.观察图示图形规律,在其右下角的空格内画上合适的图形为(
)
A. B. C. D.
8.一个算法的框图如图所示,若输出的结果为,则判断框中应填入的
条件是( )
A.i<5?
B.i<6?
C.i ≥5?
D.i ≥6?
9.在10个形状大小均相同的球中有6个红球和4个白球,不放回地依次摸出2个球,在第1次摸出红球的条件下,第2次也摸到红球的概率为( )
A.
B.
C.
D.
10.把一个周长为12cm 的长方形围成一个圆柱,当圆柱的体积最大时,该圆柱的底面周长与高的比为 ( )
A.1∶2
B.1∶π
C.2∶1
D.2∶π 二、填空题(本大题共5小题,每小题5分,共25分). 11.函数f(x)=x+e x 的递增区间是 .
12.设函数()f x 的导数为()f x ',且()2(1)ln (2)x f x f x f ''=-+,则(2)f '的值是
13.已知命题p:“存在x R ∈,使x 1
420x m +++=” ,若“非p ”是假命题,则实数m 的取值范
围是
14已知复数z 1=-1+2i,z 2=1-i,z 3=3-2i,它们所对应的点分别为A,B,C,若=x
+y
,则x+y 的值是
____________________
15.某工程的工序流程图如图(工时单位:天),现已知工程总时数为10天,则工序c 所需工时数为________天.
三、解答题。
(本大题共6小题,满分75分,解答应写出文字说明,推理过程或演算步骤) 16.(12分)已知:sin 230°+sin 290°+sin 2150°=
23,sin 25°+sin 265°+sin 2125°=2
3
,通过观察上述两等式的规律,请你写出一个一般性的结论,并给出证明.
17. (12分)已知曲线y =13x 3+4
3.求曲线过点P (2,4)的切线方程;
18.(12分)(1),,a b c 是不全相等的正实数,求证:3b c a a c b a b c
a b c
+-+-+-++>(综合法)
(2)已知 110,1,
a b a >->>
19.(12分)已知函数32(),()ln ,(0)f x x x bx g x a x a =-++=>.(1)当a x =时,求函数()g x 的单调区间;(2)若()f x 存在极值点,求实数b 的取值范围;
20. (13分)抛掷红、蓝两颗骰子,设事件A 为“蓝色骰子的点数为3或6”,事件B 为“两颗骰子的点数之和大于8”.
(1)求P(A),P(B),P(AB).
(2)当已知蓝色骰子点数为3或6时,问两颗骰子的点数之和大于8的概率为多少?
21. (14分)设.22131)(23ax x x x f ++-=(1)若)(x f 在),3
2
(+∞上存在单调递增区间,求a 的取值范围;(2)当20<<a 时,)(x f 在[]4,1上的最小值为3
16
-,求)(x f 在该区间上的最大值.
参考答案
一.
二.11. (-∞,+∞) 12.
ln 22
13. (- ,0) 14.5 15.4 三.16.一般性的结论为:
sin 2(α-60°)+sin 2α+sin 2(α+60°)=. 证明:左边=
+
+
=-[cos(2α-120°)+cos2α+cos(2α+120°)]
=-(cos2αcos120°+sin2αsin120°+cos2α+cos2αcos120°-sin2αsin120°) =-(cos2α-2×cos2α)==右边, 即该一般性结论成立.
17.解:设曲线y =13x 3+43与过点P (2,4)的切线相切于点A (x 0,13x 30+4
3),则切线的斜率k =y ′| x =x 0=x 20.∴切线方程为y -(13x 30+43)=x 20(x -x 0),即y =x 20·x -23x 30+43.∵点P (2,4)在切线上,∴4=2x 20
-23x 30+43
,即x 30-3x 2
0+4=0,解得x 0=-1或x 0=2.
故所求切线方程为4x -y -4=0或x -y +2=0; 18.略
19.
20.解:(1)设x为掷红骰子得的点数,y为掷蓝骰子得的点数,则所有可能的事件与(x,y)建立一一对应的关系,由题意作图,如图.
显然:P(A)==,
P(B)==,P(AB)=.
(2)方法一:P(B|A)==.
方法二:P(B|A)===.
21. 解:(1)已知()ax x x x f 2213123++-
=,()a x x x f 22'++-=∴,函数()x f 在⎪⎭
⎫
⎝⎛+∞,32上存在单调递增区间,即导函数在⎪⎭
⎫
⎝⎛+∞,32上存在函数值大于零的部分,91023
2
32322
'->⇒>++⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛∴a a f
(2)已知0<a<2, ()x f 在[]4,1上取到最小值3
16
-,而()a x x x f 22'++-=的图像开口向下,
且对轴2
1
=
x ,(),022111'>=++-=∴a a f (),012224164'<-=++-=a a f 则必有一点[],4,10∈x 使得(),00'=x f 此时函数()x f 在[]0,1x 上单调递增,在[]4,0x 单调递减,
()0261221311>+=++-=a a f ,()08340
8162164314<+-=+⨯+⨯-=∴a a f
()13
16
83404=⇒-=+-=∴a a f
此时,由()()
舍去或1-202002
00'
=⇒=++-=x x x x f ,所以函数()()3
102max =
=f x f。
