第五章 勒让德多项式
勒让德多项式的微分表达式

勒让德多项式的微分表达式
勒让德多项式是一种特殊的函数,它由最高次幂为N的N+1项组成,通常用来拟合曲线。
它和普通多项式的最大区别在于它的变量是
由不同的常数乘以指数x^n构成的,其形式如下:c(x)=a_N x^n +
a_(N-1) x^(N-1)+...+a_2 x^2 + a_1 x + a_0。
将上述表达式乘以n并将其代入原式中, 可以得出勒让德多项式
的微分表达式: c'(x)=Na_N x^(n-1)+ (N-1) a_(N-1) x ^(n-2)+…+
2a_2 x + a_1 。
对于勒让德多项式的求导,我们一般采用后面这种表达式,这也
是一种非常有效的方法,而不是一次使用n次链律法。
在使用这种表
达式之前,我们需要先记住最高次幂,即n,然后根据公式中的指数变化,从N开始,每次-1就可以得出每一项对应的指数,并且每一项前
面的系数也是可以直接把原多项式中相应系数带入即可。
因此,从上面可以看到,求勒让德多项式的导数的时候,需要我
们先找到最高次,然后根据指数的变化,再将每一项相应的系数带入,最后就可以得到她的微分表达式,这也是比较容易让人理解的一种方法。
勒让德多项式

k 2 3P3 ( x) 5xP2 ( x) 2P ( x) 15 x3 9 x 1 2 2
勒让德多项式的性质
奇偶性
Pl(-x) = (-1)l Pl(x) 零点定理 L阶勒让德多项式为L次多项式,有L个零点。 正交性
– 正交性公式 – 模 – 正交性应用例题
完备性
(35cos 4 20cos 2 9)
勒让德多项式的图象
勒 让 德 多 项 式 的 图 象
母函数和递推公式
母函数 – 定义:u(x, r) =∑ Pl (x) r l – 形式:u(x, r) = ( 1-2rx + r2 )-1/2 – 推导 – 应用 递推公式 – 基本递推公式 – 证明 – 应用
球内解要求u (0, )有界,半通解化为 u
l 0
Al r l Pl (cos )
2
由边界条件得: Ax
l 0
Al a l Pl ( x )
Ax2 P ( x)dx k
2k 1 根据完备性:Ak 2a k
1
1
勒让德多项式的应用
例题 2
半径为a的球面上电势分布为 f = Acos2θ,确定球外空 间的电势 u 。
2
由边界条件得: Ax
l 0
Bl a l 1Pl ( x )
2k 1 k 1 根据完备性: k B a 2
1
1
Ax2 P ( x)dx k
勒让德多项式的应用
例题 3
一空心圆球区域,内半径为a,外半径为b,内球面上电势为 f = cosθ,外球面上电势为零,确定区域内电势u 。
解:定解问题为:u 0, a r b u |r a cos , u |r b 0
勒让德多项式的微分表达式

勒让德多项式的微分表达式勒让德多项式(Lagrangepolynomial)可以被视为最普遍的多项式,在微积分,统计学,算法学,数值分析等数学应用领域有着重要的作用,广泛应用于现实生活中。
在本文中,我们将介绍勒让德多项式的微分表达式。
首先,我们需要介绍一下勒让德多项式。
它是一种多项式,其形式为:P(x) = sum_{i=0}^n f(x_i) L_i(x)其中,f(x_i)是某一个函数在某点X_i上的值,L_i(x)是勒让德多项式的基函数,对应于点x_i,一般表示为:L_i(x) = prod_{ieq j}^nfrac{x - x_j}{x_i - x_j}因此,当函数f(x)在点X_i处的值已知时,勒让德多项式的形式可以写成:P(x) = sum_{i=0}^n f(x_i) prod_{ieq j}^nfrac{x - x_j}{x_i - x_j}接下来,我们来讨论勒让德多项式的微分表达式。
由于求导的过程可能比较复杂,我们在此不对其具体表达式作详细讨论,而是直接给出结果:P(x) =sum_{i=0}^n f(x_i) left[ prod_{ieq j}^nfrac{x - x_j}{x_i - x_j} right]其中,()代表了基函数L_i(x)的导数形式,它可以表示为:left(prod_{ieq j}^n frac{x - x_j}{x_i - x_j} right) = sum_{i=0}^n prod_{ieq j}^n frac{x - x_j}{x_i - x_j} frac{1}{x_i -x_j}left( sum_{ieq j} frac{-1}{x - x_j} right)以上就是勒让德多项式的微分表达式。
从上面的表达式可以看出,它比较复杂,且计算过程比较耗时,容易出错。
因此,经常会使用相应的软件进行求解,以便减少计算量,提高计算精度和效率。
综上所述,勒让德多项式可以用于多种数学应用中,如微积分,统计学,算法学,数值分析等,是一种重要的多项式。
勒让德多项式递推公式推导

勒让德多项式递推公式推导
雷伯斯让德多项式递推公式是数学发展的一个里程碑。
它是一个可以用来快速计算高次多项式系数序列的重要公式,又称非递归式。
它以有趣的方式应用数学公式,使多项式系数序列计算变得更加合理、简单清晰。
雷伯斯让德多项式递推公式的形式为:
a_n=(n+ann+1+(n+2nn+2))*a_n-1
其中,a_n表示高次多项式的系数序列中的当前项系数,an+1表示高次多项式的系数序列中的下一项系数,同时还有nn+1和nn+2两个参数。
通常来说,我们可以很容易地计算第一项多项式系数序列a_1,但要计算多项式系数序列中的第n项,就需要比较复杂的计算过程。
雷伯斯让德多项式递推公式可以帮助我们快速计算第n项多项式系数序列,而不需要逐一计算每一项。
只要首先计算出a_1,然后将其与参数nn+1和nn+2相乘,再将所得的和再乘以上一项的系数a_n-1,即可获得当前项a_n的计算公式。
由此可见,雷伯斯让德多项式递推公式可以显著降低多项式计算的繁琐性,有效提升计算效率和准确性,也受到了数学家的一致欢迎。
它的出现使许多数学问题的解决变得更加轻松,再次推动了数学的发展,也为社会提供了不少便利。
勒让德多项式的微分表达式

勒让德多项式的微分表达式勒让德多项式的微分表达式是一个有趣的数学概念,它可以帮助我们推导出一个多项式在特定点处的导数。
与其他数学概念一样,尽管看起来可能很复杂,但当我们深入研究之后,发现它其实非常简单。
本文将探讨勒让德多项式的定义、示例以及其微分表达式的定义,并介绍其中的一些重要概念。
首先,什么是勒让德多项式?它是一种特定的数学表达式,它的形式为:f(x)=a0+a1x+a2x2+…+anxn,其中a0、a1、a2……an均为常数。
这种表达式很常见,它是多项式的一种特殊形式,可以用来描述一组数据的形状和走势。
它的特点是每项的指数均以x的n次方开头,这也是它得名的由来。
其次,可以看一个具体的勒让德多项式案例,如下:f(x)=(1/2)x2+4x+7。
可以看出,它包含三个指数:(1/2)x2、4x和7。
它的最大指数可以使用下面的公式求得:n=2,因此其最大次幂为2。
再次,什么是勒让德多项式的微分表达式?它可以描述一个多项式在特定点处的导数,以上面的示例来说,这个表达式是:f(x)=x2+4。
在这里,f(x)表示函数f(x)在x点处的导数。
与勒让德多项式有关的概念也同样有趣,比如最大次幂,它可以用来找出在特定点处函数的导数。
此外,还有一些重要概念与勒让德多项式有关,例如“微分指数表”,它可以用来计算特定点处函数的导数。
这里,指数表包含两个特别的操作:常数乘法微分和指数微分。
前者可以使用如下公式计算:[f(x)]=a0+a1x+a2x2+…+anxn,其中a0、a1、a2……an均为常数。
而指数微分也有自己的公式:[f(x)]=a0+a1x+a2x2+…+an(xn),其中a0、a1、a2……an均为常数。
最后,我们来看一下用勒让德多项式的微分表达式来求解特定点处函数的导数的实际案例。
假设我们的多项式为f(x)=(1/2)x2-2x+3,那么我们可以用以上公式来求出它在x=4处的导数:f(4)=2x+(-2)=2*4+(-2)=6,即该多项式在x=4处的导数为6。
勒让德多项式递推公式证明

勒让德多项式递推公式证明以勒让德多项式是数学中一类重要的特殊函数,其递推公式是证明其性质的关键。
本文将通过介绍以勒让德多项式的定义、性质和递推公式的证明,来解释这一标题。
以勒让德多项式是数学中的一类正交多项式,它们是解决物理和工程问题中的常微分方程的重要工具。
以勒让德多项式的定义如下:$$P_n(x) = \frac{1}{2^n n!} \frac{d^n}{dx^n} \left[(x^2 - 1)^n\right]$$其中,$n$为非负整数,$P_n(x)$表示以勒让德多项式的第$n$阶,$x$为自变量。
以勒让德多项式具有一系列重要的性质,如正交性、归一性等,这些性质使其在数学和物理学中得到广泛应用。
以勒让德多项式的递推公式是证明其性质的关键。
递推公式的形式如下:$$(n+1)P_{n+1}(x) = (2n+1)xP_n(x) - nP_{n-1}(x)$$下面我们来证明这个递推公式。
我们将以勒让德多项式的定义代入递推公式中,得到:$$(n+1)\left(\frac{1}{2^{n+1} (n+1)!} \frac{d^{n+1}}{dx^{n+1}} \left[(x^2 - 1)^{n+1}\right]\right) = (2n+1)x\left(\frac{1}{2^n n!} \frac{d^n}{dx^n} \left[(x^2 - 1)^n\right]\right) - n\left(\frac{1}{2^{n-1} (n-1)!} \frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right]\right) $$化简上式,可以得到:$$\frac{1}{2^{n+1} (n+1)!} \frac{d^{n+1}}{dx^{n+1}} \left[(x^2 - 1)^{n+1}\right] = \frac{2n+1}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right]$$我们将上式中的$n+1$分布到第一项中,并利用导数的链式法则进行化简,得到:$$\frac{1}{2^{n+1} (n+1)!} \frac{d}{dx}\left[(2n+1)x(x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$再次化简上式,得到:$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$继续化简上式,可以得到:$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right]$$再次化简上式,得到:$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$继续化简上式,可以得到:$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$再次化简上式,得到:$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$通过以上推导,我们证明了以勒让德多项式的递推公式。
勒让德多项式变换

勒让德多项式变换以勒让德多项式的变换 - 一首数学之歌在数学的世界里,有一种神奇的多项式,那就是以勒让德多项式。
它被广泛应用于物理学、工程学和计算机科学等领域,它的变换法则也是非常有趣的。
我们来一起探索一下以勒让德多项式的变换吧!首先,让我们从简单的例子开始。
假设我们有一个以勒让德多项式P(x),它可以表示为P(x) = a0 + a1x + a2x² + ... + anxn,其中ai是常数系数。
现在,我们希望对P(x)进行变换,使得它变成一个新的以勒让德多项式Q(x)。
那么,我们可以使用以下变换法则:1. 常数项的变换:Q(0) = P(1) - P(-1)。
2. 线性项的变换:Q'(x) = P(x) - P(-x)。
3. 高次项的变换:Q''(x) = P'(x) - P'(-x)。
通过这些变换法则,我们可以逐步将P(x)转化为Q(x),并得到一个全新的以勒让德多项式。
这种变换法则的背后是以勒让德多项式的奇偶性质。
以勒让德多项式具有奇偶对称性,即P(x) = P(-x)。
利用这一性质,我们可以通过差分的方式来消除奇偶项,最终得到一个新的以勒让德多项式。
不仅如此,以勒让德多项式的变换还可以帮助我们解决一些实际问题。
比如,在物理学中,以勒让德多项式可以用来描述球面上的势场分布;在工程学中,它可以用来处理信号的滤波和降噪等问题。
以勒让德多项式的变换是一种非常有趣而强大的数学工具。
它不仅可以帮助我们理解数学的本质,还可以应用于各个领域,解决实际问题。
希望通过这首数学之歌,你能对以勒让德多项式的变换有更深入的了解。
让我们一起在数学的海洋中畅游,探索数学的奥秘!。
勒让德多项式
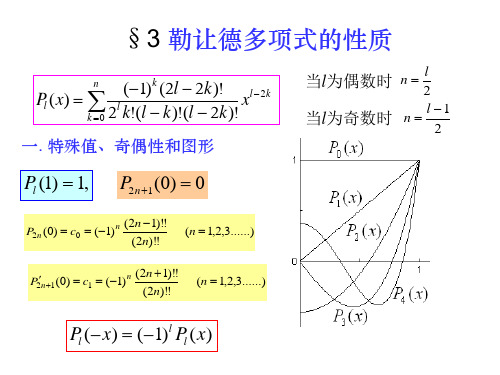
(1) k (2l 2k )! l 2 k Pl ( x) l x k 0 2 k!(l k )!(l 2k )!
n
一. 特殊值、奇偶性和图形
l 2 l 1 n 当l为奇数时 2
当l为偶数时 n
Pl (1) 1,
P2 n (0) c0 (1) n
六. 勒让德多项式的正交性、完备性与模
0, lk 2 1 Pl ( x)Pk ( x)dx Nl2 , l k 2l 1
1
勒让德多项式完备性 若f(x)是定义在[-1,1]区间上任意一个平方可积的函数,
那么
f ( x) cl Pl ( x)
l 0
(l 1) P l 1 ( x) lP l 1 ( x) (2l 1) xP l ( x)
2. P l ( x) P l 1 ( x) 2 xP l ( x) P l 1 ( x)
3. 4.
P l 1 ( x) xP l ( x) (l 1) P( x) Pl 1 ( x) P l 1 ( x) 2l 1P l ( x)
1 1 2rx r xr
2
r Pl ( x)
l l 0 2
(l 1) P l 1 ( x) lP l 1 ( x) (2l 1) xP l ( x)
1 2rx r 2
(1 2rx r ) lr l 1Pl ( x)
l 0
( x r ) r l Pl ( x) (1 2rx r 2 ) lr l 1Pl ( x)
证
2 l
1 dl 2 l Pl ( x) l ( x 1 ) 2 l! dx l
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勒让德方程
深圳大学电子科学与技术学院
二、勒让德方程的求解
(1 x ) y' '2xy'l (l 1) y 0
2
(8)
设此方程在x=0处有幂级数解 y Ck x k
y' kCk x k 1
k 1
y' ' k (k 1)Ck x k 2
k 2
C0与C1线性无关
y1 ( x) x
y0(x)只包含x的偶次幂,y1(x)只包含x的奇次幂。
勒让德方程有两个线性独立的解y0(x)和y1(x) , 称为勒让德函数,称为第一类勒让德函数。
深圳大学电子科学与技术学院
从系数的递推公式依据 幂级数收敛的达朗贝尔 判别法,这两个幂级数 的收敛半径为
k 5
(l 5)(l 3)(l 1)(l 2)(l 4)(l 6) C7 C1 7!
i
(l 2i 1) (l 3)(l 1)(l 2)(l 4)(l 6) (l 2i) C2i 1 (1) C1 (2i 1) !
深圳大学电子科学与技术学院
深圳大学电子科学与技术学院
第五章:勒让德多项式
深圳大学电子科学与技术学院
深圳大学电子科学与技术学院
本章提要:
• 几个微分方程的引入 • 勒让德方程的求解 • 勒让德多项式的性质
• 函数展成勒让德多项式的级数
参考了孙秀泉教授的课件
深圳大学电子科学与技术学院
一、几个微分方程的引入
三维波动方程: 三维热传导方程: 分离变量:
Ck k C k 2 2 1 (1 )(1 ) (k 2)(k 1) k k 1 lim lim k ( k l )(k l 1) k l l 1 (1 )(1 ) k k
R lim
l (l 1) 2 (l 2)l (l 1)(l 3) 4 y0 ( x) 1 x x 2! 4! y1 ( x) x (l 1)(l 2) 3 (l 3)(l 1)(l 2)(l 4) 5 x x 3! 5!
深圳大学电子科学与技术学院
1 d 2dR 1 d d 1 d 2 (r ) (sin ) R dr dr sin d d sin 2 d 2
(2)
左端只与r有关,右端只与、有关,要使两边相等, 只能等于常数。令该常数等于l(l+1),l为实数。
1 d 2dR (r ) l (l 1) R dr dr
k 0
代入式(8)
深圳大学电子科学与技术学院
(1 x ) k (k 1)Ck x
2 k 2
k 2
2 x kCk x
k 1 k
k 1
l (l 1) Ck x k
k 0 k
k (k 1)Ck x
k 2
k 2
k (k 1)Ck x 2 kCk x l (l 1) Ck x k
(2 l )(2 l 1) (l 2)l (l 1)(l 3) C4 C2 C0 (2 2)(2 1) 4!
(l 4)(l 2)l (l 1)(l 3)(l 5) C6 C0 6!
i
(l 2i 2) (l 2)l (l 1)(l 3) (l 2i 1) C2i (1) C0 (2i) !
m m 0 k 0
(k 2)(k 1)Ck 2 (k l )(k l 1)Ck x 0
k k 0
k (k 1) l (l 1) k2 l2 k l (k l )(k l 1)
求和为零的充分必要条件是任意项xk的系数为零
勒让德函数在 x<1内收敛
勒让德函数在x>1时发散。可以证明,在边界x=1上 是无界的。在实际问题中,又常常要求勒让德方程在 闭区间[-1,1]上有界。考虑将无穷级数y0(x)和y1(x)截 断,使它们变成多项式。多项式是一定有界的。
深圳大学电子科学与技术学院
Ck 2
(k l )(k l 1) Ck (k 2)(k 1)
k 2 k 1 k 0
k (k 1)Ck x k 2 k (k 1) 2k l (l 1)Ck x k
k 2 k 0
k=m+2
(m 2)(m 1)Cm 2 x k (k 1) l (l 1)Ck x k
2 2
2 2 2 2 2 2 2 a a 2 2 2 2 t y z x 2 2 2 2 2 2 a a 2 2 2 t y z x
(7)的通解为
( ) B1 cosm B2 sin m
(6)为连带勒让德方程。令x=cos,y(x)=(),则
2 m (1 x 2 ) y ' '2 xy' l (l 1) y0 2 1 x
2 ( 1 x ) y' '2xy'l (l 1) y 0 ) R(r )( )( )
d 2 d R R d d R d 2 (r ) 2 (sin ) 2 2 0 2 2 r dr dr r sin d d r sin d r2 两边同乘以 ,并移项,得 R 1 d 2dR 1 d d 1 d 2 (r ) (sin ) R dr dr sin d d sin 2 d 2
取: k ( x) 1 x 2、q 0、 1
d 2 dy (1 x ) y 0 dx dx
勒让德方程
深圳大学电子科学与技术学院
从拉普拉斯方程直接引入勒让德方程 球坐标系中的拉氏方程为:
2u 0
(1)
1 2 u 1 u 1 2u 0 r 2 sin 2 2 2 2 r r r r sin r sin
深圳大学电子科学与技术学院
(k 2)(k 1)Ck 2 (k l )(k l 1)Ck 0
Ck 2
k 0 k2 k4
(k l )(k l 1) Ck (k 2)(k 1)
(0 l )(0 l 1) l (l 1) C2 C0 C0 (0 2)(0 1) 2!
球贝塞尔方程
k=0
k=0
d 2 dR 2 r R 0 dr dr
欧拉方程
深圳大学电子科学与技术学院
2 1 d d m 2 sin ( 2 ) 0 sin d d sin
x cos y ( x) ( )
连带勒让德方程:
2 d dy m 2 2 ( 1 x ) ( )y 0 2 dx dx 1 x
m=0 勒让德方程:
d 2 dy 2 ( 1 x ) y0 dx dx
深圳大学电子科学与技术学院
Sturm-Liouville( 施 d d y k ( x) q ( x) y ( x) y 0 , (a x b) 图姆-刘维尔)型方程 dx d x
取: k ( x) 1、q ( x) 0、 ( x) 1
2 m 取: k ( x) x、q ( x) 、 ( x) x x
d2y y 0 dx2
亥姆霍兹方程
=1时
d dy m2 x y xy 0 dx dx x 参数形式的贝塞尔 d dy m2 x y xy 0 方程 dx dx x 贝塞尔方程
(r, t ) u(r )T (t )
u k u (亥姆霍兹方程) 0
深圳大学电子科学与技术学院
球坐标下:
z
r
y
x r sin cos y r sin sin z r cos
x
2u k 2u 0
1 2 u 1 u 1 2u 2 r sin k u0 2 2 2 2 2 r r r r sin r sin
当l=k时,Ck+2、Ck+4、…均为零,无穷级数y0(x)和 y1(x)中,必有一个退化为l次多项式。当实数l限于 l=0,1,2,3,…时,勒让德方程的解为多项式。
(k 2)(k 1) Ck Ck 2 (k l )(k l 1) (k 0,1,2,...,l 2) Cl 2 l (l 1) (2l 2)! Cl l 2(2l 1) 2 (l 1)!(l 2)! l (m 0,1,2,..., ) 2
(5)
深圳大学电子科学与技术学院
1 d d 1 d 2 2 sin (sin ) l (l 1) sin d d d2
1 d d sin (sin ) l (l 1) sin 2 m 2 d d
(5)
(6) (7)
1 d 2 2 m 0 2 d
深圳大学电子科学与技术学院
u(r , , ) R(r )( )( )
' ' ( ) m ( ) 0
2
1 d d m2 2 sin ( 2 ) 0 sin d d sin
d 2 dR 2 2 2 r (k r ) R 0 dr dr
(3)
(4)
1 d d 1 d 2 (sin ) l (l 1) 2 2 sin d d sin d
