结构力学分析案例
《结构力学》课程思政教学案例(一等奖)

《结构力学》课程思政教学案例(一等奖)一、引言结构力学是土木工程专业的一门重要课程,它是土木工程设计和施工的基础。
近年来,为了提高学生的思想道德素质和专业素养,并将思政教育融入专业课程教学中,我院积极探索课程思政的教学模式,开展了一系列思政教学案例的编写和实践活动。
本文结合《结构力学》课程的教学实践,介绍了一次教学案例的具体设计和实施情况,该案例得到了一等奖的荣誉,并取得了显著的教学效果。
二、教学目标1. 了解结构力学的基本理论和原理;2. 培养学生的分析和解决问题的能力;3. 增强学生的责任感和团队合作意识;4. 培养学生的创新意识和实践能力。
三、教学内容本案例主要围绕结构力学中的受力分析和结构设计展开,涉及到桥梁、楼房等结构的力学计算和设计。
通过实际案例的引入,让学生深入了解结构力学的实际应用,激发学生的学习兴趣和求知欲。
四、教学方法1. 课堂讲授:教师讲解结构力学的基本理论和方法,引导学生理解和掌握知识;2. 实例分析:以具体的桥梁或楼房结构案例进行力学分析和设计,让学生通过实例了解理论知识在实际中的应用;3. 团队合作:组织学生分组进行结构设计和计算,并进行团队展示和交流,培养学生的团队合作意识;4. 实地考察:组织学生到实际工程现场进行考察和调研,深化对结构力学的理解。
五、教学过程1. 引入实际案例:教师首先介绍一个真实的桥梁或楼房结构案例,引发学生对结构力学课程的兴趣和好奇心;2. 理论讲解与案例分析:教师讲解结构力学的基本理论和方法,然后引导学生根据案例进行力学分析和设计;3. 学生团队合作:学生分成若干小组,进行结构设计和计算,培养学生的团队合作意识和解决问题的能力;4. 学生展示与交流:小组成员展示他们的设计成果,并进行交流和讨论,促进学生之间的学习互动;5. 实地考察:组织学生到实际工程现场进行考察和调研,加深对结构力学理论的理解,激发学生的实践兴趣。
六、教学效果1. 学生的学习兴趣大大提高,课堂参与度明显增加;2. 学生的团队合作能力得到了锻炼和提升;3. 学生的实践能力和创新意识得到了培养和发展;4. 教师的教学效果得到了认可,获得了一等奖的荣誉。
结构工程师结构力学几何组成分析例题
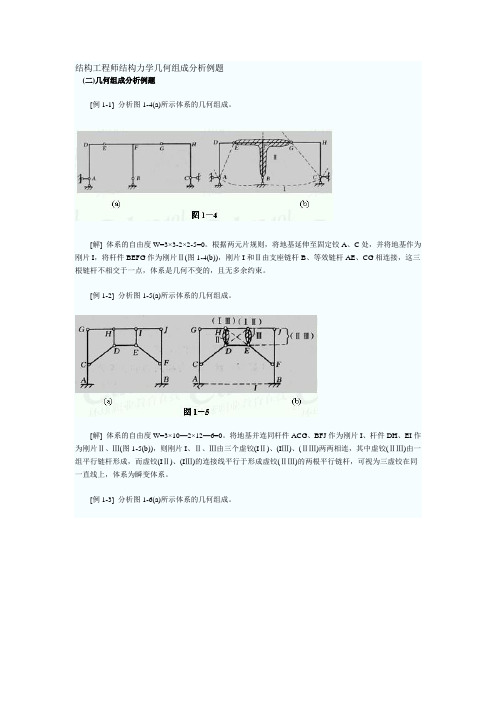
结构工程师结构力学几何组成分析例题(二)几何组成分析例题[例1-1] 分析图1-4(a)所示体系的几何组成。
[解] 体系的自由度W=3×3-2×2-5=0。
根据两元片规则,将地基延伸至固定铰A、C处,并将地基作为刚片I,将杆件BEFG作为刚片Ⅱ(图1-4(b)),刚片I和Ⅱ由支座链杆B、等效链杆AE、CG相连接,这三根链杆不相交于一点,体系是几何不变的,且无多余约束。
[例1-2] 分析图1-5(a)所示体系的几何组成。
[解] 体系的自由度W=3×10—2×12—6=0。
将地基并连同杆件ACG、BFJ作为刚片I、杆件DH、EI作为刚片Ⅱ、Ⅲ(图1-5(b)),则刚片I、Ⅱ、Ⅲ由三个虚铰(IⅡ)、(IⅢ)、(ⅡⅢ)两两相连,其中虚铰(ⅡⅢ)由一组平行链杆形成,而虚铰(IⅡ)、(IⅢ)的连接线平行于形成虚铰(ⅡⅢ)的两根平行链杆,可视为三虚铰在同一直线上,体系为瞬变体系。
[例1-3] 分析图1-6(a)所示体系的几何组成。
[解] 体系的自由度W=3×8—2×10-4=0。
根据两元片规则,将地基延伸至固定铰A处,并将地基作为刚片I,将CEF作为等效刚片Ⅱ,DB杆作为刚片Ⅲ,这三个刚片由三个虚铰(IⅡ)、(IⅢ)、(ⅡⅢ)两两相连,如图1-6(b)所示。
因形成无穷远处的两个虚铰(IⅢ)、(ⅡⅢ)的两组平行链杆不相互平行,故体系是无多余约束的几何不变体。
[例1-4] 分析图1-7(a)所示体系的几何组成。
[解] 体系的自由度W=3×9—2×12—3=0。
根据一元片规则,去除图1-7(a)所示体系的一元片,得图1-7(b)所示体系。
再将杆件AB、CE、DF分别作为刚片I、Ⅱ、ⅡⅢ,这三个刚片由三组平行链杆形成的三个无穷远处的虚铰(IⅡ)、(IⅢ)、(ⅡⅢ)两两相连,根据三刚片连接规则,体系为无多余约束的几何可变体系(无穷远处的三个点在一广义直线上)。
结构力学——静定桁架

静定桁架的稳定性分析方法
静定桁架的稳定性分析原理
静定桁架的稳定性分析方法: 能量法、力法、位移法等
静定桁架的定义和分类
静定桁架的稳定性提高静定桁架稳定性的措施
增加桁架的刚度:通过增加桁架的截面尺寸、材料强度等方法提高桁架的刚度,从而提高桁架的 稳定性。
静定桁架的杆 件受力可以分 为轴向力、剪 力和弯矩三种, 其中轴向力和 剪力是主要的
受力形式。
静定桁架的受 力特性还与桁 架的支座条件 有关,不同的 支座条件会影 响桁架的受力 分布和变形情
况。
03
静定桁架的组成与分类
静定桁架的基本组成
桁架:由杆件组成的结构,用于 承受荷载
荷载:施加在桁架上的力,包括 集中荷载和分布荷载
优化桁架制造工艺:通过优化桁架的制造工艺,提高桁架 的质量和生产效率
优化桁架安装工艺:通过优化桁架的安装工艺,提高桁架 的安装质量和效率
THNK YOU
汇报人:XX
静定桁架的应力计算方法: 截面法、图乘法、矩阵位移 法等
矩阵位移法:利用矩阵位移 法计算桁架的位移和内力,
适用于复杂桁架结构
静定桁架的变形计算
变形计算的基本原理:利用静定桁架的平衡条件求解 变形计算的方法:图乘法、解析法、有限元法等 变形计算的应用:预测桁架的变形情况,优化桁架设计 变形计算的注意事项:考虑桁架的材质、截面尺寸、载荷等因素的影响
静定桁架的内力分布规律
桁架的内力主要由轴力和剪力组成
轴力沿桁架的轴线方向分布,剪力沿桁架的横截面方向分布
桁架的内力分布与桁架的杆件布置、荷载分布等因素有关
通过静定桁架的内力分析,可以确定桁架各杆件的内力大小和方向,为桁架的设计和优 化提供依据
内力分析中的注意事项
【课程思政优秀案例】《结构力学I》:高铁建设中的结构力学——力法基本原理

课程思政优秀案例——《结构力学I》:高铁建设中的结构力学——力法基本原理一、课程和案例的基本情况课程名称:结构力学I授课对象:本科二年级课程性质:专业基础课课程简介:《结构力学I》是土木工程、铁道工程等专业学生必修的一门专业基础课。
该课程以培养“品德优秀、基础宽厚、思维创新、能力卓越”的土木工程人才为根本任务,主要研究工程上常见杆系结构的基本力学特征、内力分析与位移计算的基本原理和基本方法。
案例简介:本案例为结构力学教学大纲中的第38节课(共64节),时长50分钟,教学内容是介绍求解超静定结构的第一种基本方法—力法。
它是从静定结构过渡到超静定结构的第一节基本原理课,具有非常重要的承上启下作用。
本节课的教学目标主要包含以下三个层次:知识传授:重点掌握力法的基本原理和力法方程的物理含义能够应用力法基本原理求解一次超静定结构的内力能力培养:培养学生对超静定结构进行内力分析和计算的能力应用理论知识分析和解决实际工程问题的能力价值塑造:从我国高铁建设的巨大成就中厚植学生的家国情怀和职业使命通过启发引导培养学生的工程思维和解决实际问题的科学方法从不断的拓展思考中培养学生的深度学习能力和钻研精神二、案例蕴含的思政元素分析将结构力学课程与我国的高铁建设紧密结合,本案例打破“就力学谈力学”的局限性,从国家交通强国战略的角度充分挖掘了蕴含在力学基本原理中的育人元素,通过启发引导式的授课方式培养学生运用理论知识分析求解实际工程问题的工程思维和科学方法,拓展延伸培养学生的科研探索和创新精神,激发学生科技报国的家国情怀。
本案例主要包含以下思政元素:(1)交通强国、民族自信、职业使命通过北京奥运会、京张高铁引出中国速度和中国势力,一座座宏伟的高铁桥梁凝聚了一代又一代土木人的智慧和创新。
提出问题引入主题:如何计算连续梁桥的内力进行高铁桥梁的设计?让学生在感受民族自豪的同时思考土木工程师的职业使命。
(2)解决问题的工程思维和科学方法超静定结构的内力求解是面临的未知工程问题,如何利用已经掌握的静定结构的知识来分析求解呢?采用启发引导式的教学方法培养学生的工程思维和解决实际问题的科学方法。
结构力学 第二章 几何组成分析(典型例题)
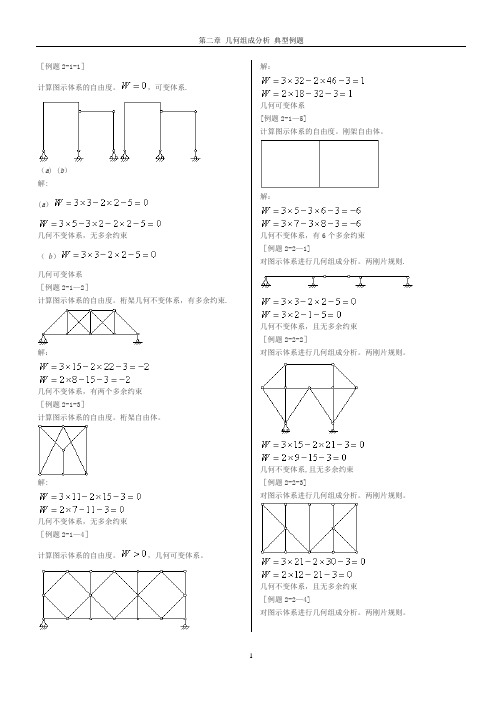
[例题2-1-1]计算图示体系的自由度。
,可变体系.(a) (b)解:(a)几何不变体系,无多余约束(b )几何可变体系[例题2-1—2]计算图示体系的自由度。
桁架几何不变体系,有多余约束. 解:几何不变体系,有两个多余约束[例题2-1-3]计算图示体系的自由度。
桁架自由体。
解:几何不变体系,无多余约束[例题2-1—4]计算图示体系的自由度。
,几何可变体系。
解:几何可变体系[例题2-1—5]计算图示体系的自由度。
刚架自由体。
解:几何不变体系,有6个多余约束[例题2-2—1]对图示体系进行几何组成分析。
两刚片规则.几何不变体系,且无多余约束[例题2-2-2]对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,且无多余约束[例题2-2-3]对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,且无多余约束[例题2-2—4]对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,有一个多余约束[例题2—2—5]对图示体系进行几何组成分析.二元体规则.几何不变体系,且无多余约束[例题2-2—6]对图示体系进行几何组成分析.两刚片规则,三刚片规则.几何不变体系,且无多余约束[例题2-2-7]对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束[例题2-2-8]对图示体系进行几何组成分析.三刚片规则.几何不变体系,且无多余约束[例题2-3-1]对图示体系进行几何组成分析.两刚片规则。
几何瞬变体系[例题2—3—2]对图示体系进行几何组成分析。
两刚片规则。
几何瞬变体系[例题2-3-3]对图示体系进行几何组成分析。
三刚片规则。
几何瞬变体系[例题2—3-4]对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束[例题2-3-5]对图示体系进行几何组成分析.三刚片规则.几何不变体系,且无多余约束[例题2-3—6]对图示体系进行几何组成分析。
二元体规则,三刚片规则.几何瞬变体系[例题2-3-7]对图示体系进行几何组成分析。
ANSYS经典案例分析

ANSYS经典案例分析ANSYS(Analysis System)是世界上应用广泛的有限元分析软件之一、它在数值仿真领域拥有广泛的应用,可以解决多种工程问题,包括结构力学、流体动力学、电磁学、热传导等。
本文将分析ANSYS的经典案例,并介绍其在不同领域的应用。
一、结构力学领域1.案例一:汽车碰撞分析汽车碰撞是一个重要的安全问题,对车辆和乘客都有很大的影响。
利用ANSYS进行碰撞分析可以模拟不同类型车辆的碰撞过程,并预测车辆结构的变形情况以及乘客的安全性能。
通过这些分析结果,可以指导汽车制造商改进车辆结构,提高车辆的碰撞安全性能。
2.案例二:建筑结构分析建筑结构的合理性和稳定性对于保证建筑物的安全和耐久性至关重要。
ANSYS可以对建筑结构进行强度和刚度的分析,评估结构的稳定性和安全性能。
例如,可以通过ANSYS分析大楼的地震响应,预测结构的位移和变形情况,以及评估建筑物在地震中的安全性。
二、流体动力学领域1.案例一:空气动力学分析空气动力学分析对于飞行器设计和改进具有重要意义。
利用ANSYS可以模拟飞机在不同速度下的气动性能,预测飞机的升阻比、空气动力学力矩等参数。
通过这些分析结果,可以优化飞机的设计,提高飞行性能和燃油效率。
2.案例二:水动力学分析水动力学分析对于船舶和海洋工程设计至关重要。
利用ANSYS可以模拟船舶在不同海况下的运动特性,预测船舶的速度、稳定性和抗浪性能。
通过这些分析结果,可以优化船舶的设计,提高船舶的性能和安全性能。
三、电磁学领域1.案例一:电力设备分析电力设备的稳定性和运行性能对电力系统的正常运行至关重要。
利用ANSYS可以模拟电力设备的电磁特性,预测电磁场分布、电磁场强度和电流密度等参数。
通过这些分析结果,可以评估电力设备的稳定性和运行性能,并指导电力系统的设计和改进。
2.案例二:电磁干扰分析电磁干扰是电子设备设计中常见的问题,特别是在通信和雷达系统中。
利用ANSYS可以模拟电磁干扰的传播路径和强度,预测设备的抗干扰能力。
结构力学典型例题

结构力学典型例题(共19页) -本页仅作为预览文档封面,使用时请删除本页-第2章平面体系的几何构造分析典型例题1. 对图体系作几何组成分析。
图分析:图等效图(去掉二元体)。
对象:刚片Ⅰ、Ⅱ和Ⅲ;联系:刚片Ⅰ、Ⅲ有虚铰A(杆、2);刚片Ⅱ、Ⅲ有虚铰C(无穷远)(杆3、4);刚片Ⅰ、Ⅱ有虚铰B(杆5、6);结论:三铰共线,几何瞬变体系。
2. 对图体系作几何组成分析。
图分析:去掉二元体(杆12、杆34和杆56图),等效图。
对象:刚片Ⅰ和Ⅱ;联系:三杆:7、8和9;结论:三铰不共线,无多余约束的几何不变体系。
3. 对图体系作几何组成分析。
图分析:图对象:刚片Ⅰ(三角形原则)和大地Ⅱ;联系:铰A和杆1;结论:无多余约束的几何不变体系。
对象:刚片Ⅲ(三角形原则)和大地Ⅱ;联系:杆2、3和4;结论:无多余约束的几何不变体系。
第3章静定结构的受力分析典型题1. 求图结构的内力图。
图解(1)支座反力(单位:kN)由整体平衡,得=100.= ,=.(2)内力(单位:制)取AD为脱离体:,,;,,。
取结点D为脱离体:,,取BE为脱离体:,,。
取结点E为脱离体:,,(3)内力图见图~d。
2. 判断图和b桁架中的零杆。
图分析:判断桁架零杆的常用方法是找出桁架中的L型结点和T型结点。
如果这两种结点上无荷载作用.那么L型纪点的两杆及T型结点的非共线杆均为零杆。
解:图:考察结点C、D、E、I、K、L,这些结点均为T型结点,且没有荷载作用,故杆件CG、DJ、EH、IJ、KH、LF均为零杆。
考察结点G和H,这两个结点上的两竖向链杆均已判断为零杆,故这两个结点的受力也已成为T型结点的情形.由于没有荷载作用,故杆件AG、BH也为零杆。
整个结构共有8根零杆.如图虚线所示。
图:考察结点D,为“K”型结点且无荷载作用,故;对称结构对称荷载(A支座处的水平反力为零),有,故杆件DE和DF必为零杆。
考察结点E和F,由于DE、DF已判断为零杆.故杆件AE、BF也是零杆。
结构力学例题

3
3ql3 3 200EI
进而可得
M 12 6 EI1 13ql 2 0.065ql 2 l 200
2 2 2 EI 4 EI ql 9 ql 1 2 M 21 M 21 M ' 21 0.18ql 2 8 l l 50
M 23 M 21 0.18ql
'
(3) (4)
N 32 N32
'
其中
M 12
v A
Pl ql 2 M 21 8 8
'
M 12
4 EI 2 EI 1 2 l l
M
' 21
2 EI 4 EI 1 2 l l
'
M 23 M 32源自ql 2 12M 23
4 EI 6 EI 2 EI 2 2 v3 3 l l l
弹性支座的应变能
2 3 1 F l 2 V2 AF 2 24 EI
系统的总应变能
V V1 V2
2 3 2 3 l3 3 P 3 P P l F l 2 2 [( F P) 3( F )( P F ) 3( F ) ] 6 EI 2 2 48EI 24 EI
M 32 0
2
弯矩图如下所示:
0.18ql 2
0.065ql 2
0.125ql 2
0.25ql
2
例4 用能量法求解如图所示梁的静不定 性。已知图中EI为常数,柔性系数 A l / (12EI ) 。
3
解:设弹性支座处的支反力为F,则有力 的平衡关系可得弯矩分布函数,如下:
3P (0 x l ) M ( x) ( F P) x ( F )l 2 3l (l x 3l / 2) M ( x) P( x) 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)计算截面惯性矩
0.12 (0.02)3 2 I1z 0.12 0.02 0.045 0.01 3.02 106 m 4 12 I2z 0.02 (0.12)3 2 0.02 0.12 0.08 0.045 5.82 106 m4 12
传动轴受竖向载荷 F FT Ft 4584kN
此力使轴在竖向平面内产生弯曲变形。
附加力偶矩: M e FT Ft
D 191N m 2
此外力偶矩使传动轴产生扭转变形。
M 0.1F 458.4 N m (2)内力分析:判断危险截面在B截面。危险截面上的弯矩:
• 4.弯曲梁强度计算
螺栓压板夹紧装置如图所示。已知板长3a=150mm,压板 材料的弯曲许用应力为[σ ]=140MPa。试确定压板传给工 件的最大允许压紧力F。 解析:压板可简化为图所示的外伸梁 作弯矩图如图所示。最大弯矩在截面B上
Mmax MB Fa
3 2 3 1.4 2 3 Iz 1.07cm 4 12 12 I 1.07 Wz z 1.07cm3 y max 1
• 1.概念分析求超静定结构的内力
分析图1-1所示组合结构的内力
解析:分析: 本例的组合结构若用一般 力法或位移法分析都比较繁琐, 但是利 用力学基本概念分析就十分简捷。首先 根据结构和荷载的对称性, 可判断横梁 无侧向位移 ( 属反对称位移 ) 。在忽略 受弯杆件轴向变形的前提下, 横梁也不 会有竖向位移。因此, 可以判定, 该结 构各结点处均无线位移。因横梁截面弯 曲刚度 , 所以两端结点上也不 会发生角位移。
图3-1
图3-2
解析: (1)确定截面形心位置 选参考坐标系z’oy如图3-3示,将截面分解为I和II两部分,形心C的纵坐标为:
0.12 0.02 0.01 0.02 0.12 0.02 0.06 yc 0.045m 0.12 0.02 0.02 0.12
解析:
(1)画弯矩图
z
(Mx)
y
F2l
y x ( M z) 2F1l
固定端截面为危险截面
(2)当横截面为矩形时,依据弯曲正应力强度条件:
M x M z F2 l 2F1 l 800 103 2 1.6 106 max 160 MPa 2 2 3 3 hb 2b b W x Wz b h 6 6 3 3 b 35.6 mm h 71.2 mm
图3-3
I z 3.02 106 5.0810-6 8.84 10-6 m4
(3)计算计算最大弯曲正应力
Nm 截面B—B的弯矩为: M B F 0.4 6000
在截面B的上、下边缘,分别作用有最大拉应力和最大压应力,其值 分别为:
σ l ,max σ c ,max 6000 0.045 7 3 . 05 10 P a 30.5MP a -6 8.8410 6000 0.12 0.02 0.045 7 6 . 45 10 P a 64.5MP a -6 8.8410
图 1-2
• 2.轴强度的计算
C B A
0.2m 0.1m
Me Ft
图2-1
FT
如图2-1所示传动轴所传递的功率P=2kW,转速n=100r/min,皮带轮 直径D=250mm,皮带轮张力FT=2Ft,轴材料的许用应力 80MPa 轴的直径d=45mm。按第三强度理论校核轴的强度。
3Ft
简化模型如图2-2所示
Me
解析: (1)外力分析:传动轴传递的外力偶矩为
M e 9550 P 2 9550 191N m n 100
M e ( FT Ft )
图2-2
D 2
( FT Ft )
D Me 2
2M e Ft 1528N, FT 2 Ft 3056N D
M max Wz
Wz 1.07 (102 ) 3 140 106 P 3000N 3kN a 5 102
• 5.根据应力确定截面形状
z F2 b
h
l l F1 y d
x
图5-1
如图5-1示悬臂结构,承受载荷F1与F2作用,已知F1=800 N,F2=1.6 kN,l=1 m,许用应力[σ] =160 MPa,试分别在下列两种情况下确定截面尺寸。 (1) 截面为矩形,h=2b; (2) 截面为圆形。
T M e 191N m 扭矩:
(3)按第三强度理论校核轴的强度
r3
(458.4 N m) 2 (191N m) 2 M 2 T2 55.5MPa 3 WZ d / 32
• 3.应用平行轴定理分析悬臂梁应力
如图3-1所示悬臂梁,自由端 承受集中载荷F=15kN作用。试 计算图3-2所示截面B--B的最 大弯曲拉应力与最大弯曲压应 力。
图1-1 组合结构
根据以上分析, 结构两侧斜杆的杆端弯矩可按照两端固定梁查表求得, 再根 据结点的力矩平衡条件易得横梁的端弯矩, 然后再叠加横梁的简支梁弯矩, 得结构弯矩图如图 1-2所示。此时, 两链杆中均无内力。 本例题值得注意的是: 横梁 的端弯矩是根据结点的力矩 平衡求得的, 因横梁为无限 刚性, 其杆端弯矩是无法直 接查表求得的。
结构力学实例分析
现代工程技术的日益进步和电子计算机的飞速发展对结 构力学学科产生了深远的影响。结构计算电子化后, 许 多传统的计算方法本身可能已逐步失去实际应用价值, 但其相应的基本概念和基本原理在结构分析中仍具有重 要的地位和价值。大型工程结构在各种复杂因素作用下 的分析, 要求强化结构力学基本概念的综合运用和概念 设计的理念。实际上, 力学基本概念和基本原理在工程 中的综合运用能力, 则正是当代结构工程领域科技人员 所应具备的最重要的素质。
(3)当横截面为圆形时,依据弯曲正应力强度条件:
max
M max W M x2 Mz2 W
2
F2 l 2F1 l 22ຫໍສະໝຸດ d3322
800 103 2 1.6 106
d3
32
160 MPa
d 52.4 mm
