读数显微镜测透镜曲率半径实验报告数据
工作报告之牛顿环物理实验报告

牛顿环物理实验报告【篇一:用牛顿环测量透镜的曲率半径实验报告】一、实验名称:用牛顿环测量透镜的曲率半径二、实验目的:1、观察光的等厚干涉现象,了解干涉条纹特点。
2、利用干涉原理测透镜曲率半径。
3、学习用逐差法处理实验数据的方法。
三、实验仪器:牛顿环装置(其中透镜的曲率未知)、钠光灯(波长为589.3nm)、读数显微镜(附有反射镜)。
四、实验原理:将一块曲率半径r较大的平凸透镜的凸面放在一个光学平板玻璃上,使平凸透镜的球面aob和平面玻璃cd面相切于o点,组成牛顿环装置,如图所示,则在平凸透镜球面和平板玻璃之间形成一个以接触点o为中心向四周逐渐增厚的空气劈尖。
当单色平行光束近乎垂直地向ab面入射时,一部分光束在aob面上反射,一部分继续前进,到cod面上反射。
这两束反射光在aob面相遇,互相干涉,形成明暗条纹。
由于aob面是球面,和o点等距的各点对o点是对称的,因而上述明暗条纹排成如图所示的明暗相间的圆环图样,在中心有一暗点(实际观察是一个圆斑),这些环纹称为牛顿环。
图(4)牛顿环装置图(5)牛顿环根据理论计算可知,和k级条纹对应的两束相干光的光程差为? 2?式中e为第k级条纹对应的空气膜的厚度,为半波损失。
2?由干涉条件可知,当??(2k?1)(k?0,1,2,3,?)时,干涉条纹为暗条纹。
即2解得??2e?e?k(2) 2设透镜的曲率半径为r,和接触点o相距为r处空气层的厚度为e,由图4所示几何关系可得r2??r?e??r2?r2?2re?e2?r2 由于r??e,则e2可以略去。
则r2e?(3)2r2?由式(2)和式(3)可得第k级暗环的半径为rk2?2re?kr? (4)由式(4)可知,如果单色光源的波长?已知,只需测出第k级暗环的半径rk,即可算出平凸透镜的曲率半径r;反之,如果r已知,测出rk后,就可计算出入射单色光波的波长?。
但是由于平凸透镜的凸面和光学平玻璃平面不可能是理想的点接触;接触压力会引起局部弹性形变,使接触处成为一个圆形平面,干涉环中心为一暗斑;或者空气间隙层中有了尘埃等因素的存在使得在光程差公式中附加了一项。
牛顿环和劈尖干——实验报告
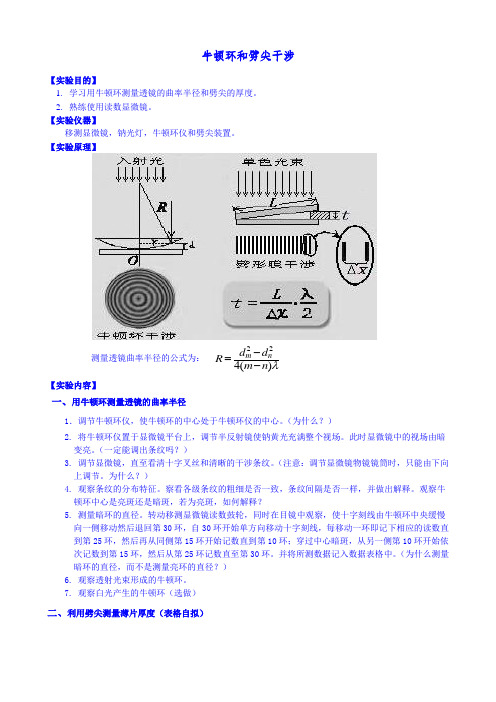
牛顿环和劈尖干涉【实验目的】1. 学习用牛顿环测量透镜的曲率半径和劈尖的厚度。
2. 熟练使用读数显微镜。
【实验仪器】移测显微镜,钠光灯,牛顿环仪和劈尖装置。
【实验原理】测量透镜曲率半径的公式为:224()m nd dRm nλ-=-【实验内容】一、用牛顿环测量透镜的曲率半径1.调节牛顿环仪,使牛顿环的中心处于牛顿环仪的中心。
(为什么?)2. 将牛顿环仪置于显微镜平台上,调节半反射镜使钠黄光充满整个视场。
此时显微镜中的视场由暗变亮。
(一定能调出条纹吗?)3. 调节显微镜,直至看清十字叉丝和清晰的干涉条纹。
(注意:调节显微镜物镜镜筒时,只能由下向上调节。
为什么?)4. 观察条纹的分布特征。
察看各级条纹的粗细是否一致,条纹间隔是否一样,并做出解释。
观察牛顿环中心是亮斑还是暗斑,若为亮斑,如何解释?5. 测量暗环的直径。
转动移测显微镜读数鼓轮,同时在目镜中观察,使十字刻线由牛顿环中央缓慢向一侧移动然后退回第30环,自30环开始单方向移动十字刻线,每移动一环即记下相应的读数直到第25环,然后再从同侧第15环开始记数直到第10环;穿过中心暗斑,从另一侧第10环开始依次记数到第15环,然后从第25环记数直至第30环。
并将所测数据记入数据表格中。
(为什么测量暗环的直径,而不是测量亮环的直径?)6. 观察透射光束形成的牛顿环。
7. 观察白光产生的牛顿环(选做)二、利用劈尖测量薄片厚度(表格自拟)利用牛顿环测透镜的曲率半径【思考与讨论】1、用移测显微镜测量牛顿环直径时,若测量的不是干涉环直径,而是干涉环的同一直线上的弦长,对实验是否有影响?为什么?2、透射光能否形成牛顿环?它和反射光形成的牛顿环有什么区别?。
[资料]用牛顿环测量透镜的曲率半径实验报告
![[资料]用牛顿环测量透镜的曲率半径实验报告](https://img.taocdn.com/s3/m/44dc84cd01f69e314232949d.png)
a,0a,0加了一项。假设附加厚度为a(有灰尘时,手压变形时),则光程差为
,,,,,2ea ,,2
22 rrmnR,,,(),mn
所以透镜的曲率半径为
22rr,mn R,,mn,,,又因为暗环的中心不易确定,故取暗环的直径计算
22DD,mn R,4,mn,,,由上式可知,只要测出与(分别为第与第条暗环的直径)的值,就能DDmnmn
,R算出或。
五、实验步骤:
1、调整测量装置
实验装置如图所示,读数显微镜的调整方法见重要仪器简介。
四、实验原理:
将一块曲率半径R较大的平凸透镜的凸面放在一个光学平板玻璃上,使平凸透镜的球面AOB与平面玻璃CD面相切于O点,组成牛顿环装置,如图所示,则在平凸透镜球面与平板玻璃之间形成一个以接触点O为中心向四周逐渐增厚的空气劈尖。当单色平行光束近乎垂直地向AB面入射时,一部分光束在AOB面上反射,一部分继续前进,到COD面上反射。这两束反射光在AOB面相遇,互相干涉,形成明暗条纹。由于AOB面是球面,与O点等距的各点对O点是对称的,因而上述明暗条纹排成如图所示的明暗相间的圆环图样,在中心有一暗点(实际观察是一个圆斑),这些环纹称为牛顿环。
由暗条纹条件
,,221eak,,,, ,,,,22
kea,,,得 2
,,,2 将上式代入式(4)得 rReRkakRRa222,,,,,,k,,2,,
上式中的不能直接测量,但可以取两个暗环半径的平方差来消除它,例如a
第环和第环,对应半径为 mn
牛顿环测透镜曲率半径实验报告

牛顿环测透镜曲率半径实验报告一、实验目的1、观察等厚干涉现象——牛顿环。
2、学习利用牛顿环测量平凸透镜的曲率半径。
3、掌握读数显微镜的使用方法。
二、实验原理将一块曲率半径较大的平凸透镜放在一块平面玻璃上,在透镜的凸面与平面玻璃之间就会形成一个厚度由中心向边缘逐渐增加的空气薄层。
当单色光垂直入射时,从空气薄层上下表面反射的两束光将会产生干涉。
在反射光中,相同厚度处的光程差相同,形成以接触点为中心的一系列明暗相间的同心圆环,即牛顿环。
设平凸透镜的曲率半径为$R$,与接触点$O$ 相距为$r$ 处的空气薄层厚度为$d$。
由于$R >> d$,可以将这一空气薄层近似看作一个楔形薄膜。
由几何关系可得:\d = r^2 / 2R\两束反射光的光程差为:\Delta = 2d +\frac{\lambda}{2}\其中,$\lambda$ 为入射光的波长。
当光程差为波长的整数倍时,出现亮条纹;当光程差为半波长的奇数倍时,出现暗条纹。
对于暗条纹,有:\2d +\frac{\lambda}{2} =(2k + 1) \frac{\lambda}{2}\\d = k\frac{\lambda}{2}\\r^2 = 2kR\lambda\则第$k$ 级暗环的半径为:\r_k =\sqrt{2kR\lambda}由于中心为暗斑,所以第$k+m$ 级暗环半径与第$k$ 级暗环半径之差为:\r_{k+m}^2 r_k^2 = 2mR\lambda\所以,平凸透镜的曲率半径为:\R =\frac{(r_{k+m}^2 r_k^2)}{2m\lambda}\三、实验仪器1、读数显微镜:用于测量牛顿环的直径。
2、钠光灯:提供单色光源。
3、牛顿环装置:由平凸透镜和平面玻璃组成。
四、实验步骤1、仪器调节将牛顿环装置放置在显微镜的载物台上,调节显微镜的目镜,使十字叉丝清晰。
调节显微镜的物镜,使其接近牛顿环装置,但不接触。
然后缓慢向上移动物镜,直到能清晰地看到牛顿环。
牛顿环测量曲率半径实验报告

牛顿环测量曲率半径实验报告实验目的1 观察等厚干涉现象,理解等厚干涉的原理和特点2 学习用牛顿环测定透镜曲率半径3 正确使用读数显微镜,学习用逐差法处理数据实验仪器读数显微镜,钠光灯,牛顿环仪,入射光调节架实验内容1.观察牛顿环将牛顿环放置在读数显微镜镜筒和入射光调节架下方,调节玻璃片的角度,使通过显微镜目镜观察时视场最亮。
调节目镜,看清目镜视场的十字叉丝后,使显微镜镜筒下降到接近牛顿环仪然后缓慢上升,直到观察到干涉条纹,再微调玻璃片角度和显微镜,使条纹清晰。
2.测牛顿环半径使显微镜十字叉丝交点和牛顿环中心重合,并使水平方向的叉丝和标尺平行(与显微镜移动方向平行)。
记录标尺读数。
转动显微镜微调鼓轮,使显微镜沿一个方向移动,同时数出十字叉丝竖丝移过的暗环数,直到竖丝与第N环相切为止(N根据实验要求决定)。
记录标尺读数。
3.重复步骤2测得一组牛顿环半径值,利用逐差法处理得到的数据,得到牛顿环半径R 和R的标准差数据处理及结果下图为在系统提供的表格内记录了相应的实验数据后由系统计算的结果下图为在仿真实验中先后调节好入射光调节架,显微镜镜筒,牛顿环位置及目镜位置后从目镜中观察到的衍射图样(牛顿环处于正中位置)思考题1.牛顿环产生的干涉属于薄膜干涉,在牛顿环中薄膜在什么位置?牛顿环的薄膜是介于牛顿环下表面(凸面)与下面的平面玻璃之间的一层空气薄膜。
2.为什么牛顿环产生的干涉条纹是一组同心圆环?干涉时薄膜等厚处光程差相等,产生的干涉现象也相同。
而牛顿环的薄膜等厚处相连在空间上是一个圆形,其圆心在凸面与平面的接触点上,所以干涉条纹是一组同心圆。
3.牛顿环产生的干涉条纹在什么位置上?相干的两束光线是哪两束?条纹产生在凸面的表面上。
测量曲率半径实验报告

一、实验目的1. 观察等厚干涉现象,了解等厚干涉的原理和特点。
2. 学习使用牛顿环测量透镜的曲率半径。
3. 正确使用读数显微镜,学习使用逐差法处理数据。
二、实验原理牛顿环是一种等厚干涉现象,当一块曲率半径较大的平凸透镜的凸面与一个光学平板玻璃接触时,两者之间会形成一层空气薄膜。
当单色光垂直照射到牛顿环上时,空气薄膜的上、下表面反射的光线会发生干涉,形成一系列明暗相间的同心圆环。
根据牛顿环的干涉原理,亮环对应的空气层厚度与1、3、5成比例,暗环对应的空气层厚度与0、2、4成比例。
通过测量亮环或暗环的半径,可以计算出透镜的曲率半径。
三、实验仪器1. 牛顿环装置(包括平凸透镜、光学平板玻璃、反射镜等)2. 钠光灯(波长为589.3nm)3. 读数显微镜(附有反射镜)4. 直尺5. 计算器四、实验步骤1. 将牛顿环装置放置在实验台上,调整钠光灯的位置,使其光线垂直照射到牛顿环上。
2. 使用读数显微镜观察牛顿环,记录下亮环和暗环的半径。
3. 记录实验数据,包括透镜的曲率半径、空气薄膜的厚度等。
4. 使用逐差法处理实验数据,计算透镜的曲率半径。
五、实验数据1. 亮环半径:r1 = 3.5mm2. 暗环半径:r2 = 5.2mm3. 透镜的曲率半径:R = 0.25m4. 空气薄膜的厚度:t = 0.2μm六、数据处理1. 计算亮环和暗环的厚度差:Δt = t2 - t12. 计算透镜的曲率半径:R = R0 (1 - Δt / λ)其中,R0为透镜的初始曲率半径,λ为钠光波长。
根据实验数据,计算透镜的曲率半径为:R = 0.25m (1 - 0.2μm / 589.3nm) ≈ 0.24999995m七、实验结果与分析1. 实验结果表明,使用牛顿环可以有效地测量透镜的曲率半径。
2. 实验过程中,由于仪器精度和人为误差的影响,测量结果存在一定的偏差。
3. 通过逐差法处理实验数据,可以减小误差,提高测量精度。
八、实验总结本次实验通过观察等厚干涉现象,学习了牛顿环的原理和应用。
用牛顿环测透镜曲率半径的数据处理方法

⽤⽜顿环测透镜曲率半径的数据处理⽅法⽤⽜顿环⼲涉测透镜的曲率半径实验⽬的1.观察⽜顿环产⽣的等厚⼲涉条纹,加深对等厚⼲涉现象的认识。
2.掌握测量平凸透镜曲率半径的⽅法。
实验仪器JXD —B型读数显微镜,⽜顿环仪,钠光灯。
仪器构造说明1.JXD —B型读数显微镜JXD —B型读数显微镜的构造、操作⽅法,见“光学常⽤仪器介绍”中常⽤仪器构造与调节的有关内容,请认真阅读。
2.⽜顿环仪⽜顿环仪是由曲率半径约为200~700厘⽶的待测平凸透镜L和磨光的平玻璃板P叠和装在⾦属框架F中构成,如图1所⽰。
框架边上有三个螺旋H,⽤来调节L和P之间的接触,以改变⼲涉条纹的形状和位置。
调节H时,螺旋不可旋得过紧,以免接触压⼒过⼤引起透镜弹性形变,甚⾄损坏透镜。
图 1实验原理如图2所⽰,在平⾯玻璃板BB '上放置⼀曲率半径为R 的平凸透镜AOA ',两者之间便形成⼀层空⽓薄层。
当⽤单⾊光垂直照射下来时,从空⽓上下两个表⾯反射的光束1和光束2 在空⽓表⾯层附近相遇产⽣⼲涉,空⽓层厚度相等处形成相同的⼲涉条纹,这种⼲涉现象称为等厚⼲涉。
此等厚⼲涉条纹最早由⽜顿发现,故称为⽜顿环。
在⼲涉条纹上,光程差相等处,是以接触点O 为中⼼,半径为r 的明暗相间的同⼼圆,r 、h 、R 三者关系为h R r h -=22(1)图 2因 R?h (R 为⼏⽶,h 为⼏分之⼀厘⽶)。
所以R r h 22≈光程差为22λδ-=h (2)即22λδ-=R r (3)(3)式是进⼊透镜的光束,光束1先由透镜凸⾯反射回去,光束2穿过透镜进⼊空⽓膜后,由平⾯玻璃板反射形成的光程差,式中λ/2为额外光程差。
在反射光中见到的亮环2222λλ?=-k R r k(4)在反射光中见到的暗环2)12(22λλ?-=-k R r k (5)式中k =0,1,2,…, 从上观察,以中⼼暗环为准,则有=R k r k λ2λ?=k r R k 2(6)可见,测出条纹的半径r ,依(6)式便可计算出平凸透镜的半径R 。
牛顿环测量曲率半径实验报告

实验名称:牛顿环测量曲率半径实验1.实验目的:1 观察等厚干涉现象,理解等厚干涉的原理和特点2 学习用牛顿环测定透镜曲率半径3 正确使用读数显微镜,学习用逐差法处理数据2.实验仪器:读数显微镜,钠光灯,牛顿环,入射光调节架3.实验原理图1如图所示,在平板玻璃面DCF上放一个曲率半径很大的平凸透镜ACB,C点为接触点,这样在ACB和DCF之间,形成一层厚度不均匀的空气薄膜,单色光从上方垂直入射到透镜上,透过透镜,近似垂直地入射于空气膜。
分别从膜的上下表面反射的两条光线来自同一条入射光线,它们满足相干条件并在膜的上表面相遇而产生干涉,干涉后的强度由相遇的两条光线的光程差决定,由图可见,二者的光程差等于膜厚度e的两倍,即此外,当光在空气膜的上表面反射时,是从光密媒质射向光疏媒质,反射光不发生相位突变,而在下表面反射时,则会发生相位突变,即在反射点处,反射光的相位与入射光的相位之间相差?,与之对应的光程差为?/2 ,所以相干的两条光线还具有?/2的附加光程差,总的光程差为(1)当?满足条件(2)时,发生相长干涉,出现第K级亮纹,而当(3)时,发生相消干涉,出现第k级暗纹。
因为同一级条纹对应着相同的膜厚,所以干涉条纹是一组等厚度线。
可以想见,干涉条纹是一组以C点为中心的同心圆,这就是所谓的牛顿环。
如图所示,设第k级条纹的半径为,对应的膜厚度为,则(4)在实验中,R的大小为几米到十几米,而的数量级为毫米,所以R >> e k,e k2相对于2Re k是一个小量,可以忽略,所以上式可以简化为(5)如果r k是第k级暗条纹的半径,由式(1)和(3)可得(6)代入式(5)得透镜曲率半径的计算公式(7)对给定的装置,R为常数,暗纹半径(8)和级数k的平方根成正比,即随着k的增大,条纹越来越细。
同理,如果r k是第k级明纹,则由式(1)和(2)得(9)代入式(5),可以算出(10)由式(8)和(10)可见,只要测出暗纹半径(或明纹半径),数出对应的级数k,即可算出R。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
读数显微镜测透镜曲率半径实验报告数据
一、实验目的
本实验旨在通过使用读数显微镜测量透镜曲率半径,深入了解透镜的性质和特点,提高实验操作技能和数据处理能力。
二、实验原理
透镜是一种光学器件,具有使光线聚焦或发散的作用。
透镜的曲率半径是描述其形状的一个重要参数。
在本次实验中,我们使用读数显微镜来测量透镜的曲率半径。
读数显微镜是一种精密测量仪器,它可以对物体进行高精度的测量。
在本次实验中,我们将使用读数显微镜来测量透镜两面的曲率半径,并计算出平均值作为最终结果。
三、实验步骤
1. 准备工作:将待测透镜放置在平整水平台上,并用纸巾轻轻擦拭干净。
2. 测量凸面:将读数显微镜放置于凸面上方,调节仪器使其垂直于透镜表面。
记录下初始读数,并向下移动仪器,直到观察到清晰的刻度线。
记录下此时的读数,并计算出凸面的曲率半径。
3. 测量凹面:将读数显微镜移至透镜的另一侧,重复步骤2,计算出
凹面的曲率半径。
4. 计算平均值:将凸面和凹面的曲率半径相加,并除以2,得到最终结果。
四、实验数据
1. 透镜直径:20mm
2. 凸面读数:
初始读数:6.20mm
最终读数:5.52mm
测量值:0.68mm
3. 凹面读数:
初始读数:6.10mm
最终读数:5.50mm
测量值:0.60mm
五、数据处理与分析
1. 计算凸面曲率半径:
由于透镜直径为20mm,因此凸面曲率半径为:
R1 = (L^2 + D^2) / 2L = (0.68^2 + 20^2) / 2*0.68 = 196.47mm
2. 计算凹面曲率半径:
由于透镜直径为20mm,因此凹面曲率半径为:
R2 = (L^2 + D^2) / 2L = (0.60^2 + 20^2) / 2*0.60 = 187.78mm
3. 计算平均值:
将凸面和凹面的曲率半径相加,并除以2,得到最终结果:
R = (R1 + R2) / 2 = (196.47 + 187.78) / 2 = 192.13mm
六、实验结论
通过使用读数显微镜测量透镜的曲率半径,我们得到了透镜的平均曲率半径为192.13mm。
本次实验结果较为准确,但仍存在一定误差。
在实际操作中,我们应该尽可能地避免人为误差,并进行多次测量取平均值来提高数据的可靠性。
