平行四边形知识结构图1
小学数学四年级知识结构图

垂直与平行,过 直线外一点画该 平行四边形和 直线的垂线,怎 梯形 样画平行线。平 行四边形和梯形
统计
复式条形统计图
数学 广角
优化思想
数学 广角
优化思想
数学四年级上册知识结构图源自例 题1. 读 出 下 面 各 数 。 1285000300 读 作 ( ) 10340500005读作( )2、写出下面各数。四万零九 十写作( )一百零三亿零三十写作( ) 3、一个 五位数四舍五入后约是8万,这个五位数最大是(), 最 小 是 ( ) 。 4 、 比 较 数 的 大 小 。 92504 和 103600 28906和28890 5、把下面的数改写成“万”或“亿” 作 单 位 的 数 。 7580000 1389000 300000000 20897000000 1、射线有()个端点,可以向()无限延伸。直线有 ()个端点,可以向()无限延伸。线段有()个端 点,不能向()无限延伸。2、角的大小与()有关, 与()无关。3、画25°130°的角。
1、口算。18×4 24×3 130×6 380×2 2 、笔算。145×12 425×36 237×82 3、学校准备发练习本,发给15个班,每个班144本,全校还需 要留40本作为备用。学校应发多少本练习本? 4、一个 粮店3天售出大米的数量分布是430千克、380千克、407千克, 这个粮店30天大约售出大米多少千克?
小学数学四年级上册知识结构图
单 元 标 题 具 体 容 内 例 题
亿以内数的认 识、亿以上数 大数的认识 的 认 识 、 用 计 算器计算探索 规律
角的度量
直线、射线、角 的定义,角的度 量,画角。
口算:两位数乘一 位数(进位)及相 应的几百几十乘一 位,笔算:包括“ 因数和积的变化规 律”
第十八章四边形章节复习辅导讲义

第十八章、四边形章节复习辅导讲义一、四边形知识框架: 1.四边形的知识结构 2.平行四边形的知识结构 二、四边形1. 定义:有不在同一直线上的四条首尾依次连接的线段构成的封闭图形。
2. 四边形的表示:四边形一般由依次的四个大写的字母表示,如四边形ABCD 等。
3. 四边形的分类:(1) 按照四边形的凹凸性将四边形分为凸四边形和凹四边形。
注意:中学阶段学习的四边形都是凸四边形。
(2) 按照四边形对边的平行性将四边形分为: ① 一般四边形:任何对边都不平行的四边形。
② 梯形:只有一组对边平行的四边形; A. 梯形分类: a .一般的梯形b .等腰梯形:一组对边平行,另一组对边相等的四边形。
c. 直角梯形:有一个内角为直角的梯形。
(3) 平行四边形:两组对边分别平行的四边形。
① 平行四边形的分类: A. 一般的平行四边形 B. 矩形(长方形):有一个较为直角的平行四边形。
C. 菱形:邻边相等的平行四边形。
D. 正方形:四条边都相等,四个内角也相等的四边形。
4. 四边形的内角和与外角和: (1) 四边形的内角和为360度 (2) 四边形的外角和为360度。
5. 四边形的性质:依次连接四边形各边中点所得的四边形称为中点四边形。
不管原四边形的形状怎样改变,中点四边形的形状始终是平行四边形【基础练习】1. 顺次连接一个任意四边形四边的中点,得到一个_______四边形. 2.顺次连接对角线相等的四边形的各边中点,所得四边形是_________.3. 如图1,已知:在ABCD 中,AB=4cm ,AD=7cm ,∠ABC 的平分线交AD•于点E ,交CD 的延长线于点F ,则DF=______cm .4. 如图,四边形ABCD 为正方形,△ADE 为等边三角形,AC 为正方形ABCD 的对角线,则∠EAC =___度.5. 四边形ABCD 的对角线AC BD ,的长分别为m n ,,可以证明当AC BD ⊥时(如图1),四边形ABCD 的面积12S mn =,那么当AC BD ,所夹的锐角为θ时(如图2),四边形ABCD 的面积S = .(用含m n θ,,的式子表示)1250°1 2A BC DB F C6.在如图所示的四边形中,若去掉一个50的角得到一个五边形,则12+=∠∠ 度.7.如图,已知AC 平分BAD ∠,12∠=∠,3AB DC ==, 则BC = . 8.已知四边形ABCD 中,90A B C ∠=∠=∠=︒,若添加一个条件即可判定该四边形是正方形,那么这个条件可以是____________.三、平行四边形(一) 平行四边形:1. 定义:两组对边分别平行的四边形。
三个角直角的平行四边形

三个角直角的平行四边形1.引言1.1 概述概述部分的内容可以从以下角度展开:平行四边形是一种具有特殊性质的四边形,它拥有三个角都是直角的特点。
在数学中,这种形状被广泛研究并应用于各个领域。
本文将着重探讨三个角都是直角的平行四边形,探究其性质以及与其他几何形状之间的关系。
首先,要明确的是,平行四边形是一种特殊的四边形。
它拥有两组平行的对边,即相对的两条边是平行的。
利用这个性质,我们可以简化很多几何计算和推理的过程。
加上三个直角的特点,三个角直角的平行四边形更具有特殊性和独特性。
其次,我们可以探究三个角都是直角的平行四边形在几何学中的应用。
首先,它可以作为建筑设计中的基本元素之一。
例如,在建筑的规划和设计过程中,平行四边形的概念被广泛应用于房屋的外形设计、室内空间布局以及家具的设计与摆放等方面。
平行四边形的特殊性质使得建筑师能够更好地利用和规划各个区域,使整体结构更加稳定和美观。
此外,平行四边形还在数学和物理学的研究中发挥了重要作用。
在数学领域中,平行四边形是解决图形证明和计算问题的常用工具。
通过研究平行四边形的性质和变换规律,我们可以推导出很多高级的几何定理和公式,为数学的发展提供了重要的支撑。
在物理学领域中,平行四边形的概念可以应用于物体的平衡分析和受力分析等方面。
通过将物体或力的作用效果抽象为平行四边形的形状,可以更好地理解物体的运动和受力情况,进而进行更精确的分析和预测。
总结来说,三个角直角的平行四边形是一种具有特殊性质的几何形状。
它在建筑设计、数学和物理学等领域中发挥着重要的作用。
通过研究和应用三个角直角的平行四边形,我们可以更深入地理解几何学的基本概念和原理,并将其运用于实际问题的解决中。
在接下来的正文部分,本文将进一步探讨三个角直角的平行四边形的性质和应用。
1.2 文章结构文章结构部分内容如下:本篇长文将按照以下结构进行讨论和分析:引言、正文和结论。
在引言部分,我们将首先对文中要讨论的主题进行概述,介绍平行四边形及其特点,并引入三个角都是直角的平行四边形这一特殊情况。
平行四边形的性质与应用

平行四边形的性质与应用平行四边形是一种具有特定性质和广泛应用的几何图形。
在本文中,我们将探讨平行四边形的性质以及它在现实中的应用。
一、平行四边形的定义与性质平行四边形是指具有两组对边平行的四边形。
它具有以下几个重要性质:1. 对边性质:平行四边形的对边相等。
即相对的两条边长度相等。
2. 对角线性质:平行四边形的对角线互相平分,并且互相垂直。
这意味着平行四边形的两条对角线长度相等且互相垂直。
3. 内角性质:平行四边形的内角之和为360度。
换句话说,平行四边形的任意两个相邻内角之和为180度。
4. 对顶角性质:平行四边形的对顶角相等。
即相对的两个内角大小相等。
二、平行四边形的应用平行四边形在几何学和实际生活中都有广泛的应用。
以下是一些常见的应用场景:1. 建筑设计:平行四边形的性质被广泛应用于建筑设计中,用于绘制平行四边形的模型,计算建筑物的面积和体积,以及确定建筑物内部布局的合理性。
2. 航空航天工程:在航空航天工程中,平行四边形的性质被用于计算飞机的机翼面积,帮助设计师设计出更加稳定和高效的飞行器结构。
3. 地理测量:在地理测量中,平行四边形的性质被应用于测量地表的形状、面积以及地表变动的研究。
同时,平行四边形也是测量工具中常用的标志物,用于校准和校正测量仪器。
4. 平行四边形的证明与运用:在数学课堂上,我们经常需要证明平行四边形的性质,通过证明和推理,培养学生的逻辑思维和问题解决能力。
此外,平行四边形的性质也应用于解决三角函数和向量等数学问题。
5. 平行四边形的网格结构:平行四边形的性质使其成为一种理想的结构形式,例如篮球场地板、瓷砖地板、蜂窝状网格等。
这些结构具有稳定性、坚固性和美观性。
结论平行四边形作为一种常见的几何图形,在我们的日常生活和学习中有着广泛的应用。
通过了解平行四边形的性质和运用,我们能够更好地理解和应用几何学知识,同时也能培养我们的逻辑思维和问题解决能力。
平行四边形不仅仅是数学课堂上的概念,它在各行各业中都发挥着重要的作用,为我们的生活和工作带来了便利和创造力。
四边形中的几何结构 (讲义及答案)
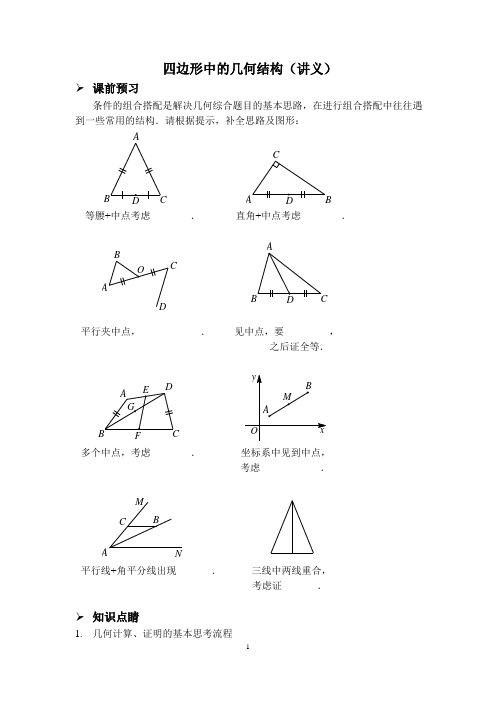
四边形中的几何结构(讲义)➢ 课前预习条件的组合搭配是解决几何综合题目的基本思路,在进行组合搭配中往往遇到一些常用的结构.请根据提示,补全思路及图形:等腰+中点考虑________. 直角+中点考虑________.C平行夹中点,____________. 见中点,要_________,_______之后证全等.多个中点,考虑________. 坐标系中见到中点,考虑____________.M NC BA平行线+角平分线出现_______. 三线中两线重合,考虑证_______.➢ 知识点睛1. 几何计算、证明的基本思考流程①标注条件,合理转化; ②组合特征,分析结构; ③由因导果,执果索因. 2. 特殊四边形中隐含条件①平行四边形中隐含条件:平行、中点;②菱形中隐含条件:平行、中点、角平分线、垂直; ③矩形中隐含条件:平行、中点、垂直;④正方形中隐含条件:平行、中点、角平分线、垂直. 3. 四边形中常见几何结构举例①中点结构:直角+中点,平行夹中点,多个中点; ②旋转结构:等线段共端点; ③弦图结构:外弦图,内弦图; ④面积结构:三个“一半”,平行转化.➢ 精讲精练1. 如图,在平行四边形ABCD 中,BC =2AB ,CE ⊥AB 于点E ,F 为AD 的中点,若∠AEF =54°,则∠B =__________.CDFBE AP A EB FDC第1题图 第2题图2. 如图,在菱形ABCD 中,∠A =110°,E ,F 分别是边AB ,BC 的中点,若EP⊥CD 于点P ,则∠FPC =__________.3. 如图,在四边形ABCD 中,∠ABC =∠ADC =90°,AD = CD ,DP ⊥AB 于点P .若 四边形ABCD 的面积是16, 则DP 的长为__________.4. DC5. 接BF ,与DE 相交于点G ,连接CG ,与BD 相交于点H .则下列结论:①△AED ≌△DFB ;②∠BGD =120°;③24BCDG S CG =四边形.其中正确的是__________.(填写序号)B E AF HCD G6. 已知,在平面直角坐标系中放置了5个如图所示的正方形,其中点B 1在y 轴上,点C 1,E 1,E 2,C 2,E 3,E 4,C 3均在x 轴上.若正方形A 1B 1C 1D 1的边长为1,∠B 1C 1O =60°,B 1C 1∥B 2C 2∥B 3C 3,则点A 3到x 轴的距离为___________.7. 如图,O ,在Rt △DCE中,∠CED ABCD 的面积为___________.EO DCBAPQFEABCD第7题图 第8题图8. 如图,在平行四边形ABCD 中,AB :BC =3:2,∠DAB =60°,点E 在AB 边上,且AE :EB =1:2,F 为BC 边的中点,过点D 作DP ⊥AF 于点P ,DQ ⊥CE 于点Q ,则DP :DQ 的值为__________.9. 如图,在边长为4的菱形ABCD 中,∠B =60°,点E ,G ,H ,F 分别在边AB ,BC ,CD ,AD 上,且AF =CG =1,BE =DH =2.P 是直线EF ,GH 之间的任一点,连接PE ,PF ,PG ,PH ,则△PEF 与△PGH 的面积之和为________________.D PFHCGBE A【参考答案】➢课前预习三线合一;斜边中线等于斜边的一半;延长证全等;倍长;倍长;中位线;中点坐标公式;等腰;等腰➢精讲精练1.72°2.55°3. 44.1 35.①②③6.7. 48.9.。
图形的变化知识结构图

称轴垂直平分.
画轴对称图形:〔2〕关于x轴对称: ;
〔3〕关于y轴对ห้องสมุดไป่ตู้: .
旋转的定义:把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转.
旋转的性质
图
图形的旋转定义:把一个图形绕着某一点旋转1800,如果它能够与另一个图形重合,那么就说这两个图形关于这个点
形中心对称 中心对称.
的中心对称图形:把一个图形绕着某一个点旋转1800,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心
称图形〔如线段、平行四边形〕.
变关于原点对称的点的坐标: .
相似多边形:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
化
相似三角形判定定理
图形的相似
定义:如果一个图形上的点A、B、…、P、…和另一个图形上的点 分别对应,并且它们的连线
位似 都经过同一点O, ,那么这两个图形叫做位似图形.
结论:在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,
那么与原图形上的点〔x,y〕对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
图形的变化 知识结构图
平移的定义
图形的平移点的平移:
图形的平移:
定义:一个平面图形沿一条直线折叠,直线两旁的局部能够互相重合.
轴对称图形:性质:轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
两个图形成轴对称:
图形的轴对称〔1〕线段垂直平分线上的点与这条线段两个端点的距离相等;
线段垂直平分线的性质〔2〕与一条线段两个端点的距离相等的点,在这条线段的垂直平分线上.
(完整版)人教版五年级数学上册全册知识结构图
人五数上教材知识点数
与
代
数
小数乘法
小数乘整数
小数乘法的计算方法
小数乘小数
积的近似数四舍五入、进一法、去尾法
运算定律推广加法、减法、乘法、除法
解决问题购物问题、租船问题
小数除法
除数是整数
小数除法的计算方法
除数是小数
商的近似数四舍五入、进一法、去尾法
循环小数意义、有限小数、无限小数
计算器探索规律
解决问题包装问题
简易方程
用字母表示数数、数量关系、运算定律、公式
解简易方程
方程的意义
等式的性质、解方程、实际问题与方程图
形
与
几
何
位置
多边形的面积
平行四边形的面积S=ah
三角形的面积S=ah÷2
梯形的面积S=(a+b)÷2
组合图形的面积
统计与概率
确定
不可能
一定
不确定
大多
小少
综合与实践
掷一掷
植树问题
封闭(一端植)全长÷间隔长=间隔数=棵数
不封闭
两端植全长÷间隔长+1=棵数
两端不植全长÷间隔长-1=棵数。
不同版本教材知识点设置的比较研究—以初中数学平行四边形为例
摘要随着课程改革不断推进,各地出现了各有特点的数学教材,教材的编写者有不同的思路,因此教材在各个方面也会存在一定的差异,同时不同版本的教材对比也有助于教师更好地教学与进行教学研究.通过对人教版、北师大版、苏科版中的“平行四边形”部分进行比较研究,从而帮助对该部分知识点的全面把握,以便更好地把握数学教材内容,优化教学设计.通过文献分析法、对比分析法、统计法、问卷调查法对不同版本初中数学教材从结构、引入、探究及习题设置进行了比较,从而发现三个版本教材的特色以及各自的异同点.通过对此课题的研究,提供一些有益的数学教学建议.关键词平行四边形教材对比人教版北师大版苏科版A comparative study on the set of knowledge points in different editionsof textbooks—— A case study of Parallelogram in junior middle schoolAbstract With the continuous advancement of the curriculum reform, mathematics textbooks with their own characteristics have appeared in various places. The compilers of the textbooks have different ideas, so there are certain differences in various aspects of the textbooks, at the same time, the comparison of different versions of teaching materials is helpful to teachers. This paper makes a comparative study of the "Parallelogram" section in the people s education press, the Beijing Normal University press and the Soviet section press, so as to help us grasp the knowledge points of this section in anall-round way, so as to better grasp the contents of the mathematics teaching materials and optimize the teaching design. Through literature analysis, Comparative Analysis, Statistics and Questionnaire survey, this paper compares the structure, Introduction, exploration and problem setting of different editions of junior middle school mathematics textbooks, thus discovered three edition teaching material's characteristic as well as respective similarities and differences. Through the research on this subject, some useful suggestions on mathematics teaching are provided.Key words Parallelogram textbook comparison People's Education Edition Beijing Normal University Edition Suke edition目录摘要 (II)Abstract (III)引言 (1)1绪论 (1)1.1问题的提出 (1)1.2国内外研究现状 (1)1.2.1国外研究概况 (1)1.2.2国内研究概况 (2)2研究对象、研究维度、研究思路与研究方法 (2)2.1研究对象 (2)2.2研究维度 (2)2.3研究思路 (2)2.4研究方法 (3)3平行四边形内容设置的比较研究 (3)3.1教材内容结构比较 (3)3.2引入的比较 (5)3.3探究活动的比较 (12)3.4习题的比较 (14)4初中不同版本数学教材比较的实证研究 (16)4.1问卷调查对象 (16)4.2问卷调查数据整理 (16)4.3问卷调查数据分析 (17)5结论 (17)5.1三个版本教材的横向比较 (17)5.2三个版本教材的纵向比较 (18)6建议 (18)6.1内容结构方面 (18)6.2引入方式方面 (18)6.3习题设置方面 (19)6.4探究活动方面 (19)结语 (20)参考文献 (21)致谢 (22)附录 (23)引言教育改革的核心是课程改革,课程改革促进了教材的优化 [1]P10.结合不同的地域特点和教育现状,国家支持相关部门编写不同特征的教材,不同教材的编写思路决定了教材在各个方面也会存在一定差异[2]P59-66.目前有很多专家学者对不同版本的初中数学教材进行了对比研究,很多一线教师也在关注不同教材下同一知识点的异同点.目前各种教材是怎样设计的,有什么样的优缺点、异同点,编写意图是什么?这些有待作进一步研究.在实际教学过程中应如何选用和使用教材是值得每一个基础教育工作者思考的问题.作为一名未来从事教育事业的毕业生,我结合自身学习的理论经验和实习期间的实践教学经验,对人民教育出版社[3]P41-67(以下简称人教版)、北京师范大学出版社[4]P135-140(以下简称北师版)、江苏风凰科学技术出版社[5]P56-90(以下简称苏科版)三个版本教材中“平行四边形”的内容进行比较研究,在研究过程中主要运用内容分析和统计分析法,并且结合一定的实践经验,通过对不同教材进行比较,希望可以深入的理解教材,找到不同之处,取长补短,对初中数学教材进行优化与反思.1绪论1.1问题的提出教科书是教师教和学生学的主要载体[6].现如今,越来越多的人去研究教材,新版本的初中数学教材有哪些特点,现在各种教材是怎样设计的,有什么样的优缺点、异同点?这些有待作进一步研究.平行四边形是四边形内容中的重要部分.它在教材中有着呈上启下的作用.研究发现,这部分研究较缺乏,因此,本文通过对三个版本初中数学教材中“平行四边形”部分进行对比研究,分析不同版本教材的特点.1.2 国内外研究现状现在对教材的研究较多,研究的方面也很多,作者搜集了大量的资料,通过分析整理,对国内外已有的教材对比研究现状进行了分析概括.1.2.1国外研究概况近年来,我国教育事业有了很大的发展,因为我们不断与国外教材进行比较研究,比较研究大多是对某一个具体的模块进行具体的分析比较,从而找出国内外教材之间的差异.2002年, Hoyles等学者,借助TIMSS这种手段对多国教材进行有针对性的比较,分析了这些国家的数学教科书与学生的成绩测试以及评价结果,对异同点进行了详细的比较[7]P61-P65;2006年,梁贯成等学者对日本、韩国等国家的教材进行了多方面比较,同时也对比了中澳数学教材中的价值观和中新数学教材的知识架构等等[8]P32-34;2007年,范良火等学者通过对三个国家的初中数学教材内容中的“问题解决步骤的呈现方式”进行比较,发现这三个国家在这方面的异同点,同时也提供了建议[9]P61-75;2013年,曹一鸣等人对不同国家初中数学的数与代数、统计与概率和图形与几何的整体布局进行了比较[10]P29-36。
平行四边形的概念
平行四边形的概念平行四边形是一种特殊的四边形,具有一些独特的性质和特点。
在几何学中,平行四边形是指具有两对对边平行的四边形。
本文将介绍平行四边形的定义、性质以及一些相关的应用。
一、定义平行四边形是指同时具有以下两个条件的四边形:1. 两对对边分别平行,即相对的两条边的延长线不会相交。
2. 相邻的两个角互补,即相邻的两个内角之和为180度。
二、性质1. 相对的两条边长度相等。
根据平行线的性质,平行四边形的相对边必须平行,因此长度也必须相等。
2. 相对的两个内角相等。
由于相邻的两个内角互补,因此相对的两个内角必须相等。
3. 对角线互相平分。
平行四边形的对角线共同平分对角线上的点,即将对角线分成两等分。
4. 对角线长度相等。
平行四边形的对角线长度相等,可以通过使用向量的方法证明。
5. 对边平行且等于对边。
平行四边形的对边必须平行,且相等。
6. 内角和等于360度。
由于平行四边形的内角互补,四个内角的和等于360度。
三、应用平行四边形在现实生活和工程中有着广泛的应用。
以下是一些常见应用的例子:1. 工程建筑:平行四边形的概念可以应用于建筑物的设计和结构,例如平行四边形的墙体和屋顶结构。
2. 地理测量:地理测量中的地图和地块常常涉及到平行四边形的性质,并且可以通过测量边长和角度来计算面积和周长。
3. 几何画图:平行四边形可以作为基本的几何图形之一,用于绘制其他复杂图形。
4. 数学证明:平行四边形的性质是许多数学证明的基础,例如证明四边形是平行四边形的充要条件等。
总结:平行四边形是一种具有两对平行边和相等对角线的四边形。
它具有一些独特的性质和应用。
了解平行四边形的概念可以帮助我们更好地理解几何学中其他相关的概念和定理,同时也有助于我们在实际生活和工程中应用几何学知识。
通过研究和应用平行四边形,我们可以更好地理解和掌握几何学的基本原理和应用技巧。
小学数学知识结构图(知识树PPT)
工程 问题
浓度 问题
溶液=溶剂+溶质
浓度=溶质÷溶液×100%
解决问题----列方程解决问题
*弄清题意,找出要求的的未知数用X表示 *找出题中数量间的等量关系,列出方程 *解方程 *检验或验算,写出答案
列 方 程 解 决 问 题
一般步骤
找等量关系 常用方法
关键语句 常见的加、减、乘、除的数量关系 常用的等量关系 利用图形周长、面积、体积公式
分数问题 类型
利息
*求a的几分之几(或百分之几)是多少 *一个数的几分之几(或百分之几)是a,求这个数 *求a是b的几分之几(或百分之几) *比a多(少)几分之几(或百分之几)的 数是多少 *a比b多(少)几分之几(或百分之几),求b *求a比b多(少)几分之几(或百分之几)。
利息=本金×利率×时间
图形的认识
测量 空间与图形 图形与位置
图形与变换
基本图形
线:直线,射线,线段,平行线, 垂线。(相交,垂直,平行) 角:角的概念,角的分类 平行四边形,长方形,正方形 三角形 梯形 圆和圆环 长方体,正方体 圆柱
图形的 认识
平面图形
立体图形
圆锥
球
基本图形
线 角 平行四边形,长方形,正方形的周长和面积 三角形的周长和面积
一般不给出具体的的工作总量用单位1表示用分数表示工效工作效率工作时间工作总量工作总量工作效率工作时间工作总量工作时间工作效率数量关系浓度问题溶液溶剂溶质浓度溶质溶液100解决问题列方程解决问题列方程解决问题题弄清题意找出要求的的未知数用x表示找出题中数量间的等量关系列出方程解方程检验或验算写出答案找等量关系常用方法关键语句常见的加减乘除的数量关系常用的等量关系利用图形周长面积体积公式一般步骤典型应用题平均数问题归一问题归总问题和差问题差倍问题和倍问题倍比问题行程问题流水问题还原问题植树问题盈亏问题年龄问题鸡兔同笼问题解决问题行程问题行程问题一般行程问题火车过桥问题相遇问题追及问题路程速度时间速度路程时间时间路程速度路程桥长车长车速桥长车长通过时间通过时间桥长车长车速桥长车速通过时间车长车长车速通过时间桥长相遇路程速度和相遇时间相遇时间相遇路程速度和速度和相遇路程相遇时间速度差追及时间追及路程追及路程速度差追及时间追及路程追及时间速度差量与计量常见的量计量进率与换算度量衡名数与名数的改写常见的量量计量单位及进率率长度
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形全章复习课一、知识结构图:二、平行四边形的性质边角对角线平行四边形对边平行且相等对角相等,邻角互补对角线互相平分矩形对边平行且相等四个角都是直角对角线相等且互相平分菱形对边平行,四边相等对角相等,邻角互补对角线互相垂直平分,每条对角线平分一组对角正方形对边平行,四边相等四个角都是直角对角线互相垂直平分且相等,每条对角线平分一组对角三、平行四边形的常用判定方法平行四边形1) 两组对边分别平行的四边形是平行四边形; 2) 两组对边分别相等的四边形;3) 一组对边平行且相等的;4)两组对角分别相等的四边形 5) 对角线互相平分的四边形;矩形1)有一个角是直角的平行四边形是矩形; 2)有三个角是直角的四边形是矩形;3)对角线相等的平行四边形是矩形。
4)对角线平分且相等的四边形是矩形菱形1)有一组邻边相等的平行四边形是菱形; 2)四条边都相等的四边形是菱形;3)对角线互相垂直的平行四边形是菱形。
4)对角线平分且垂直的四边形是菱形正方形1)有一个角是直角且有一组邻边相等的平行四边形是正方形;2)有一组邻边相等的矩形是正方形; 3)有一个角是直角的菱形是正方形。
1.三角形的中位线平行且等于第三边的一半2.直角三角形斜边上的中线等于斜边的一半3.菱形的面积公式:对角线乘积的一半练习题:1.不能判定四边形ABCD 为平行四边形的题设是( ) (A )AB 平行且等于CD 。
(B )∠A=∠C ,∠B=∠D 。
(C )AB=AD ,BC=CD 。
(D )AB=CD ,AD=BC 。
2.下面性质中菱形有而矩形没有的是( )(A )邻角互补(B )内角和为360°(C )对角线相等 (D )对角线互相垂直 3.正方形具有而菱形不一定具有的性质是( ) (A )四条边相等 (B )对角线互相垂直平分 (C )对角线平分一组对角 (D )对角线相等4、顺次连结任意四边形四边中点所得的四边形一定是( ) A 、平行四边形 B 、矩形 C 、菱形 D 、正方形5.如图,□ABCD 中,∠C=108°,BE 平分∠ABC,则∠ABE 等于( ) A.18° B.36° C.72° D.108° 6.下列命题中,真命题是( )A 、有两边相等的平行四边形是菱形B 、对角线垂直的四边形是菱形C 、四个角相等的菱形是正方形D 、两条对角线相等的四边形是矩形 7、□ABCD 中,∠A =50°,则∠B =__________,∠C =__________。
8.已知菱形两条对角线的长分别为5cm 和8cm ,则这个菱形的面积是______cm .9、菱形ABCD 的周长为36,其相邻两内角的度数比为1:5,则 此菱形的面积为_________。
10、对角线长为22的正方形的周长为___________,面积为__________。
11.如图,过矩形ABCD 的对角线BD 上一点K 分别作矩形两边的平行线MN 与PQ ,那么图中矩形AMKP 的面积S 1与矩形QCNK 的面积S 2的关系是S 1 S 2(填“>”或“<”或“=” )第11题图 第12题图12.如图,在矩形ABCD 中,点E 、F 分别在AB 、DC 上,BF ∥DE ,若AD=12cm ,AB=7cm ,NMQCBEDCB A•且AE :EB=5:2,则阴影部分的面积为_______cm例1:(1)如图,已知四边形ABCD 为平行四边形,∠A +∠C =80°,平行四边形ABCD 的周长为46 cm ,且AB -BC =3 cm ,求平行四边形ABCD 的各边长和各内角的度数.例2(1)如图,矩形ABCD 的对角线AC 、BD 相交于点O ,∠AOB=2∠BOC ,若对角线AC=6cm ,则该矩形的周长和面积各是多少?(2):如图,菱形ABCD 的边长为8㎝,∠BAD=120°,则菱形ABCD 的面积为例3:如图,矩形ABCD 的对角线AC 、BD 交于点O ,过点D 作DP ∥OC ,且 DP=OC ,连结CP 。
(1)试判断四边形CODP 的形状;(2)如果条件“矩形ABCD ”变为“正方形ABCD ”呢?例4:如图,已知四边形ABCD 中,AC=BD ,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 边上的中点。
(1)求证:四边形EFGH 是菱形;(2)添加一个条件,使四边形ABCD 是正方形,并说明理由。
D A BCO A B C DO发现:(1)顺次连接对角线既不相等也不垂直的四边形各边中点得 ;(2)顺次连接对角线相等但不垂直的四边形各边中点得 ; (3)顺次连接对角线互相垂直但不相等的四边形各边中点得 ; (4)顺次连接对角线相等且互相垂直的四边形各边中点得例5. 如右下图,把AD=12cm ,AB=8cm 的矩形沿着AE 为折痕对折使点D 落在BC 上点F 处,则DE=cm 。
例6.如图,△ABC 中,点O 为AC 边上的一个动点,过点O 作直线MN ∥BC ,设MN 交∠BCA的外角平分线CF 于点F ,交∠ACB 内角平分线CE 于E . (1)求证:EO=FO ;(2)当点O 运动到何处时,四边形AECF 是矩形?并证明你的结论; (3)若AC 边上存在点O ,使四边形AECF 是正方形,猜想△ABC 的形状并证明你的结论。
EAN MF C BO平行四边形单元检测一、选择题(每小题3分,共24分)1.在平行四边形ABCD 中,∠B =110°,延长AD 至F , 延长CD 至E ,连结EF ,则∠E +∠F =( ) A .110°B .30°C .50°D .70°2.菱形具有而矩形不具有的性质是 ( )CDFEA BA .对角相等B .四边相等C .对角线互相平分D .四角相等3.如图,平行四边形ABCD 中,对角线AC 、BD 交于点O ,点E 是BC 的中点.若OE =3 cm ,则AB 的长为 ( )A .3 cmB .6 cmC .9 cmD .12 cm 4.已知:如图,在矩形ABCD 中,E 、F 、G 、H 分别为边AB 、BC 、CD 、DA 的中点.若AB =2,AD =4,则图中阴影部分的面积为 ( )A .8B .6C .4D .35.用两块全等的含有30°角的三角板拼成形状不同的平行四边形,最多可以拼成 ( ) A .1个B .2个C .3个D .4个6.如图是一块电脑主板的示意图,每一转角处都是直角,数据如图所示(单位:mm ),则该主板的周长是 ( ) A .88 mm B .96 mm C .80 mmD .84 mm7.如图,平行四边形ABCD 中,对角线AC 、BD 相交于点O ,E 、F 是AC 上的两点,当E 、F 满足下列哪个条件时,四边形DEBF 不一定是平行四边形 ( ) A .∠ADE =∠CBF B .∠ABE =∠CDFC .OE =OFD .DE =BF8.如图是用4个相同的小矩形与1个小正方形镶嵌而成的正方形图案.已知该图案的面积为49,小正方形的面积为4,若用x 、y 表示小矩形的两边长(x >y ),请观察图案,指出以下关系式中不正确的是 ( ) A .7=+y x B .2=-y xC .4944=+xyD .2522=+y x 二、填空题(每小题4分,共24分)9.若四边形ABCD 是平行四边形,请补充条件 (写一个即可),使四边形ABCD 是菱形.10.如图,在平行四边形ABCD 中,已知对角线AC 和BD 相交于点O ,△ABO的周长为15,AB =6,那么对角线AC +BD = 11.如图,延长正方形ABCD 的边AB 到E ,使BE =AC ,则∠E= °.12.已知菱形ABCD 的边长为6,∠A =60°,如果点P 是菱形内一点,且PB =PD =32,那么AP 的长为 .13.在平面直角坐标系中,点A 、B 、C 的坐标分别是A (-2,5),B (-3,-1),第7题第10题第6题第8题第11题C(1,-1),在第一象限内找一点D,使四边形ABCD是平行四边形,那么点D的坐标是.14.如图,四边形ABCD的两条对角线AC、BD互相垂直,A1B1C1D1是中点四边形.如果AC=3,BD=4,那么A1B1C1D1的面积为三、解答题(52分)15.(8分)如图,在矩形ABCD中,AE平分∠BAD,∠1=15°.(1)求∠2的度数.(2)求证:BO=BE.16.(8分)已知:如图,D是△ABC的边BC上的中点,DE⊥AC,DF⊥AB,垂足分别为E、F,且BF=CE.当∠A满足什么条件时,四边形AFDE是正方形?请证明你的结论.17.(8分)如图,在平行四边形ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F.求证:四边形AFCE是菱形.18.(8分)已知:如图,在正方形ABCD中,AC、BD交于点O,延长CB到点F,使BF=BC,连结DF交AB于E.求证:OE=( )BF(在括号中填人一个适当的常数,再证明).19.(8分)在一次数学探究活动中,小强用两条直线把平行四边形ABCD分割成四个部分,使含有一组对顶角的两个图形全等.(1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有第14题组.(2)请在下图的三个平行四边形中画出满足小强分割方法的直线.(3)由上述实验操作过程,你发现所画的两条直线有什么规律?20.(12分)已知:如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.(1)试猜想线段AE与BF有何关系?说明理由.(2)若△ABC的面积为3cm2,请求四边形ABFE的面积.(3)当∠ACB为多少度时,四边形ABFE为矩形?说明理由.。
