第三章 釜式反应器
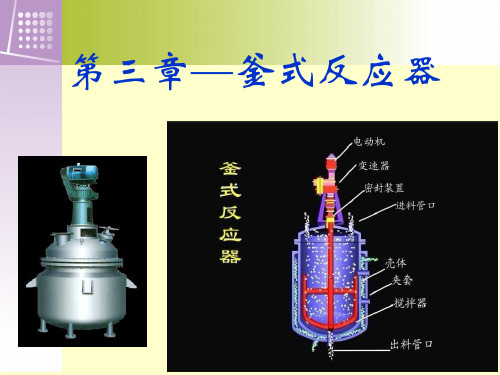
第三章-釜式反应器

3.1釜式反应器的物料衡算式
根据总的物料衡算式,则有:
写成 其中
M
i ijrj j 1
3.1釜式反应器的物料衡算式
连续釜式反应器
累积速率
代 数 方 程
间歇釜式反应器
微 分 方 程
3.2等温间歇釜式反应器的计算
特点
反应器内浓度处处相等,可排除传质的影响 反应器内温度处处相等,可排除传热的影响 物料同时加入,所有物料具有相同的反应时间
例3.1 酯化反应, 原料配比A:B:S=1:2:1.35, XAf=0.35, 密度1020kg/m3,辅助时间t0=1hr,装填 系数f=0.75,产量12000kg/Day, 求反应体积?
解: 原料处理量
FA0
12000 24M R xAf
12000 16.23 kmolA
2488 0.35
A
CA0
n=1
rA kC A
C A C A0e kt 或
kt
ln
CA0 CA
x A 1 e kt
n=2
rA
kC
2 A
CA
C A0 1 C A0kt
或
kt 1 1
xA
C A0kt 1 C A0kt
C A C A0
速率常数k值的提高将导致相应反应时间减少 即提高反应温度将使反应速率增加
Q 0.5cA2kmol /(m3 h)
反应开始时A和B的浓度均为2kmol/m3,目的产物 为P,试计算反应时间为3h时A的转化率和P的收率。 解:由题知
A p 2Q 2cA 20.5cA2 2cA cA2
将速率表达式代入等温间歇反应器的设计方程式 可有
第三章间歇釜式反应器知识讲解

数
需要设备的总容积为:
Q0t '
V
mVm
如果反应器容积V的计算值很大,可选用几个小的反应器
若以m表示反应釜的个数,
则每个釜的容积:Vm=V/m=Q0t’/( m)
为便于反应器的制造和选用,釜的规格由标准(GB 9845-88) 而定。在选择标准釜时,应注意使选择的容积与计算值相当或 略大。如果大,则实际生产能力较要求为大,富裕的生产能力 称为反应器的后备能力,可用后备系数δ来衡量后备能力的大
解: 每台锅每天操作批数: β=24/17=1.41 每天生产西维因农药数量:
1000×1000÷300=3330Kg(GD)
需要设备总容积: mVm=(3330/1.41)×200×10-3/12.5=37.8m3
取Va为10 m3的最大搪瓷锅4台。
δ=(4-3.78)/3.78×100%=5.82%
10
(3)反应体积VR
• 反应体积是指设备中物料所占体积,又称有效体积。
确定反应器的容积V的前提是确定反应器的有效容 积(反应容积)VR。
如果由生产任务确定的单位时间的物料处理量为Q0,
操作时间为t’(包括反应时间t和辅助操作时间t0 ),则
反应器的有效容积:
VR=Q0 t'
其中 t’ = t + t0
11
(4)*设备装料系数
实际生产中,反应器的容积要比有效容积大,以保 证液面上留有空间。
• 反应器有效体积与设备
实际容积之比称为设备
装料系数,以符号
表示,即:
=VR/V。其值视具体
情况而定
条
件
无搅拌或缓慢搅 拌的反应釜
带搅拌的反应釜
易起泡或沸腾状 况下的反应
第三章 釜式及均相管式反应器综述

x Af 0 CA dxA dCA C A0 rA rA
等容过程,液相反应
图解积分示意图
t C A0
x Af
0
CA dxA dCA C A0 rA rA
[rA]-1
[rA]-1
t/cA0 xA0 xAf x CA0
t CAf CA
二、间歇反应器的数学描述
Standardised stirred tank reactor sizes
标准尺寸( according to DIN)
反应釜规格 总容积 夹套容积 换热面积 400 L L m2 d1 h1 主要尺寸 (mm) d2 h2 533 120 2.5 800 1000 900 1250 630 847 152 3.1 1000 1000 1100 1300 1000 1447 216 4.6 1200 1200 1300 1550 2500 3460 368 8.3 1600 1600 1700 2060 4000 5374 499 11.7 1800 2000 1900 2500 6300 8230 677 15.6 2000 2500 2100 3050
4.155m / h
通过乙酸的起始浓度和原料中各组分的质量比,可求出乙 醇和水的起始浓度为
CB 0 3.908 60 2 10.2(mol / L) 46
3.908 60 1.35 CS 0 17.59(mol / L) 18
然后,将题给的速率方程变换成转化率的函数。
第三章 釜式及均相管式反应器
第一节 第二节 间歇釜式反应器 连续流动均相管式反应器
第一节 间歇反应器
一、釜式反应器的特征
(1)反应器内物料浓度达到分子尺度上的均匀,且反应 器内浓度处处相等,因而排除了物质传递对反应的影响;
第三章 釜式反应器

半间歇釜式反应器的物料衡算式:
设有反应:
A B R , r k ' c AcB
Q0c A0
QcA
( R A )V
d (V c A ) dt
Q 0 c A 0 Q c A R AV
d (V c A ) dt
式中V为反应器中混合物的体积,其值随时间而变。假定操作开始时先向反应器中注入 体积为V0的B,然后连续输入A,流量为Q,浓度为CA0,且不连续导出物料,即Q=0,即有
V V0 Q 0t
若将VCA看做变量,则该式为一阶线性微分方程,初始条件是t=0, VCA=0, Q0为常数时,一阶微分方程的解为:
VcA
Q0c A0 k
1 e x p ( k t )
将
V V0 Q 0t
cA cA0
代入
VcA
Q0c A0 k
1 e x p ( k t )
Q 0 c A 0 R AV
d (V c A ) dt
又设B大量过剩,则该反应可按一级反应处理,即 rA kc A
,代入上式有:
Q 0 c A 0 k c A 0V
任意时间下反应混合物的体积:
d (V c A ) dt
V V0
t 0
Q0dt
若为恒速加料,则Q0为常数,所以
FA 0 v0 c A 0
= T (v c p + K A )-(v c p T 0 + K A T m )
(v c p + K A )
-(v c p T 0 + K A T m )
= T (v c p + K A )-(v c p T 0 + K A T m )
第三章 釜式反应器

连串反应组分浓度与反应时间关系示意图
3.4 等温CSTR 的计算
对连续釜式反应器,稳态操作,有: 则物料衡算通式变为:
Q0 ci 0 Qci Vr
dni dt
0
j 1
M
ij
rj
i 1,2, K
无时间变量,液相反应体积变化不显著,
假定进出口流量相等连续釜式反应器反应体积计算公式
21
cQ
等温 BR 的计算
c A0
AP AQ
A
P
cP k1 cQ k2
成立的条件: 各反应的速率方程形 式相同; 反应物中各反应组分 的化学计量系数均相 等
22
c
Q
0
t
平行反应物系组成与反应时间关系示意图
等温 BR 的计算
复合反应
将上述结果推广到含有M个一级反应的平行反应系统:
累积速率=0, dni
dt
0
可简化为代数方程:
Q0ci 0 Qci iVr i 1,2, K
7
间歇釜式反应器的特点是分批装料和卸料,因此操作方式灵活,
特别适用于多品种、小批量的化学品生产。因此,在医药、试 剂、助剂、添加剂等精细化工部门得到了广泛的应用。
间歇反应器操作时间由两部分组成:一是反应时间,即装料完
连续釜式反应器操作:定态 等温、等浓度下反应等反应速率下反应,rA定值
28
3.4 等温CSTR 的计算
对连续釜式反应器体积计算公式
单一反应
Q0 (c A0 c A ) Vr rA
对连续釜式反应器体 积由物料衡算式可直 接计算得到
Vr
Q0 c A0 X Af rA ( X Af )
3-釜式反应器
反应器的参数不随时间变化 不存在时间自变量,也没有空间自变量 多用于液相反应,恒容操作
出口处的C, T=反应器内的C, T 。由物料恒算式
得 (3.40)
假定物料进出口的流量相等, 则
(3.41)
3.4连续釜式反应器的反应体积
若反应器内只有一个反应,且关键组分为A,则
最后得到连续釜式反应器的计算方程为
最后解出:
(3-
38)
(3-39)
反应物系组成随时间的变化关系如图3-4所示,如果P 是目的产物,其值有最优解。通过CP 对时间求导数,可 以得到:
3.3等温间歇釜式反应器的计算(复合 反应)
如果 例题3.3
3.4连续釜式反应器的反应体积
•间歇釜:,有进有出。
该式可用于均相、多相,等温或非等温过程。
对于间歇反应器,由于dV=0,若为均相
则
(否则不行)
3.2等温间歇釜式反应器的计算(单一 反应)
设反应速率方程为
(不可逆反应),
则
,在等温下有
XAf
∫ 1
t=
0
kcA0a-1
dXA (1-XA)a
=
(1-XAf)1-a-1
(a-1) kcA0a-1
(a≠1)
3.3等温间歇釜式反应器的计算(复合 反应)
对于均相,恒容过程方程进一步变为:
设初值条件为:t=0时,CA=CAO,CP=0,CQ=0,则方程的解为 进一步:
3.3等温间歇釜式反应器的计算(复合 反应)
反应物系的组成随时间的变化关系如图3.3所示,由图可见,t ↑,CA↓, 而CP↑、CQ↑。 图3-3 平行反应组成随时间的变化关系
当温度T↑时,反应速率常数k↑,导致达到规定转化率所 用的反应时间t↓。对于可逆放热反应,是上面的结论仍然 正确吗?
第三章 釜式反应器

等温间歇反应器反应时间的解析计算
由于反应在等温条件下进行,则反应速率常数在反应 过程中保持不变。
对于n级不可逆反应 将反应速率方程变换为转化率的函数并积分得到:
对于一级不可逆反应积分结果为:
14
影响间歇反应器反应时间的因素分析
从间歇反应器反应时间的计算公式可以看出: 反应时间随反应组分的初始浓度(一级反应除外)的提
rAVr
nA0
dxA dt
分离变量积分:
t
t
0 dt nA0
dx x A f
A
0 rAVr
11
间歇反应器的反应时间计算 (单一反应)
恒容条件下(多数情况)
t
cA0
xAf 0
dxA rA
or
t cA dcA
r cA0 A
如果动力学方程形式为: rA kCAn
i
反应生成
物质量 物质量 i物质量
通式为
7
间歇釜式反应器的物料衡算式
由于间歇反应器在反应过程中无物料的进出,因此
Q0=Q=0,即:
单位时间 单位时间内积
反应掉的
=累在反应器内
i物质量 的i物质量
由间歇反应器的设计方程可得一个极为重要的结论:反应物达 到一定的转化率所需的反应时间,只取决于过程的反应速率, 也就是说取决于动力学因素,而与反应器的大小无关。
第三章 釜式反应器
釜式反应器是工业上应 用广泛的反应器之一。
可以用来进行均相反应 (主要是液相均相反应), 又可用于多相反应,如 气液、液固、液液及气 液固等反应。
在操作方式上,既可以 是进行连续操作,也可 以进行间歇或半间歇操 作。
第三章 釜式反应器(复习)

3.釜式反应器3.1 釜式反应器的物料衡算式说明:(1)定态下(连续)操作(2)非定态下(间歇)操作3.2 等温间歇釜式反应器的特点(1)反应器内浓度处处相等,可排除传质的影响; (2)反应器内温度处处相等,可排除传热的影响;(3)物料同时加入并同时停止反应,所有物料具有相同的反应时间。
3.3 等温间歇釜式反应器单一反应的计算(1)反应时间结论:反应物达到一定的转化率所需要的反应时间,只取决于过程的反应速率,也就是说取决于动力学因素,而与反应器的大小无关。
(2)反应体积 反应器有效体积 反应器实际体积说明:①间歇釜式反应器操作时间由反应时间t 和辅助时间t 0K i dt dn V QC C Q iR i i i ,,2,1,00=+ℜ-=∑==ℜMj jiji r 1υKi r V QC C Q Mij jij R i i ,,2,1,00 =-=∑=υKi dtdn r V i Mij j ij R ,,2,1,0 ==+-∑=υ⎰-ℜ=AfA x x A A A dx C t 0)(0)(00t t Q V R +=fV V R /=组成;②f 为装填系数,取0.4-0.85,根据反应物料的性质选。
③反应器的大小是由反应物料的处理量决定的。
(3)最优反应时间以单位时间内产品产量为目标函数以单位质量产品的生产费用为目标函数3.4 连续釜式反应器的反应体积(1)定态下操作的连续釜式反应器的特点和特征 等温,等浓度,等反应速率。
①物料进出口体积流量相等(恒容) ②反应器内温度均匀且不变化 ③反应器内浓度均匀且等于出口浓度 (2)设计方程3.5 空时说明:空时用来衡量连续反应器的生产能力,空时越小,表示该反应器的处理物料量越大,空时大则相反。
若在进出口物料组成相同的条件下比较两个连续反应器,空时小者,生产能力大。
AffA A AA A r x C Q r C C Q R V 0000)(==-0t t C dtdC R R +=aa t a t C dtdC f RR )(00++=进料体积流量反应体积==Q V Rτ对于等容均相反应过程,空时也等于物料在反应器内的平均停留时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t0 pt
ln( k1 / k 2 ) 代入式( 6 ) k1 k 2 k
cP max
k1 c A0 k2
k k 2 1
2
cP max YP max = cA0
3.4 连续釜式反应器反应体积的计算
物料衡算式:Q0Ci0=QCi-RiV r 因为釜式反应器大多数进行液相反应 所以视作为恒容过程 Q=Q0
dcA 对A : ( RA ) k1cA (1) dt dcP 对P : RP k1cA k2cP (2) dt
cA cA0 exp(k1t )(4)
dcP 带入式(2)得: k1cA0 exp(k1t ) k2cP dt
dcP k2cP k1c A0 exp(k1t )(5) dt
Vr=
Q 0( c i,0 - c 0 )
-R
i
i = 1,2,...,k
Q0( c A,0 - c A ) Q0( c A,0 - c A ) Q0c A,0( x A, f - c A,0 ) = = 2 - R Ac A, f -R A x A, f
Vr=
-R
A
空时 V r
Q0
单位时间处理单位体积无聊所需的空间体积 空时越大,反应器的生产能力越小
∵ cA0 cA cP cQ
k2 c A0 ∴ cQ cA0 cA cP 1 exp (k1 k2 )t k1 k2
cP k1 常数 cQ k2
可推广到M个一级平行反应: 对反应物A:
cA cA0 exp ( - k1 +k2 +... +km)t
二.最优反应时间
t↑→(-RA)↓→生产能力/单位时间↓ t↑→产品产量↑ ①产品产量/单位操作时间最大
Vr CR FR t t0
dc R cR dt t t0
dc VR t t0 R cR dFR dt 0 2 dt t t0
多釜
τ1 V r,1 x A,1 = 对于第一釜: = c A,0 Q 0 c A,0 - R A x A,1
τ V x x A,1 2 r,2 A,2 对于第二釜: = = c A,0 Q 0 c A,0 - R A x A,2
因为 V r,1 +V r,2 < V r 所以采用两釜串联比采用单釜操作有利
定组分 M=2 K=2
对 A:
RA
dc 1 dnA A Vr dt dt
( RA ) rp rQ (k1 k2 )cA
dcA dt
对 P:
cA0 1 1 1 积分t ln ln k1 k 2 cA k1 k 2 1 x A
dc p 1 dn f Rp cA cA0 exp(k1 k2 )t Vr dt dt dc RP rp k1c A P k1c A0 exp (k1 k2 )t dt
2 化简 : 1 - X A,2 = 1 - X A,1
XA, 2 = 1 - (1 - X A,1 )
2
V r1 X A,1 = X A,1 = Q 0 c A,0 - R A,1 k c A,0(1 - X A,1 ) V r2 X X A,2 - X A,1 A,2 - X A,1 = = - R A,2 Q 0 c A,0 k c A,0(1 - X A,2 ) 1 - 1 - X A,1 - X A,1 X A,1 = = 2 k (1 - X A,1 ) 1 k c A,0 X A,1
dAT dcR 1 ac at a t a 0 R 0 0 f 2 dt Vr c R dt
dcR cR dt t (a0t0 a f ) / a
3.3等温间歇反应器中进行复合反应时的计算
一、平行反应 A→P A→Q rP=k1cA rQ=k2CA i=1,2……k
对P: R = 1 dn f = - dc p p Vr dt dt
cA cA0 exp (k1 k2 )t
dcP RP rp k1c A k1c A0 exp (k1 k2 )t dt
积分:t:0-t
c P,0 0
k1cA0 cP 1 exp (k1 +k2 )t k1 k2
3.5.1 串联釜式反应器的计算
Q0
c A,0 x A,0
c A,1 x A,1
c A,p-1 x A,p-1
c A,N X A,N
V r,1
V r,2
V r,p
V r,N
对第P釜进行计算: τ p = V r = c A,p-1 c A,p Q0 -R A,p
p = 1, 2,...N
对P=1, 1
ki C A 0 产物i: Ci 1 exp( t k j ) j 1 kj j 1
(t t 0 )Q 0 Vr
二、连串反应
2) A (1) P ( Q
N3
M2
K2
1 c A0 1 1 t ln ln (3) k cA k 1 xA
若各釜进行二级反应
p 1, 2,..., N
R A k c A f ( x A ) 动力学方程 c A,p 1 c A,p p R A,p c A,0 c A,0 R A ( x p) x A,p x A,p 1 p p
两种情况
1.X N 和 Vr, p已知,求 N
2. X N 和 N 已知,求 Vr, p
先假设 p
若各釜体积同,1=2=...=p ...= N
各操作线平行
3.5.2 串联釜式反应器各釜的最佳反应体积比
Q
0
c
A,0
c x
A ,1
A ,1
c x
A ,2
A ,2
V r1 x A,1 V r2 x A,2 - x A,1 = = - R A,2 Q 0 c A,0 - R A,1 Q 0 c A,0 V r总 V r1 V x x -x = + r2 = A,1 + A,2 A,1 - R A,2 Q 0 c A,0 Q 0 c A,0 Q 0 c A,0 - R A,1
关于cP 的一级线性常微分方程的初始条件: t = 0,cP = cP0 = 0
∴ cP k1cA0 k2t k1t (e e ) k1 k0 (6)
k2e k1t k1e k2t cQ cA0 cA cP cA0 1 k k 2 1
MB cR ( M ) dcR M 点斜率= t t d t AB 0 pt 0 M
②单位产品消耗费用最小 a:费用/单位反应时间 a0:费用/单位辅助时间 af:固定费用 AT :费用/单位产品质量
AT at a0t0 a f Vr cR min
c A,0 c A,1 R A,1
若进行一级反应
R A k1cA
c A,0 c A,1 1 k1c A,1 c A,1 c A,2 对P=2 2 k 2c A,2
对P=N
c A,0 c A,1 1 k11
c A,2
c A,N
c A,1 c A,0 1 k 2 2 (1 k11)(1 k 2 2)
t nA0
xA
vAA+vBB→vRR
d xA ( RA )Vr
M=1 K=1
积分: 0 x d xA t c A0 间歇反应釜当作恒容过程: 0
A
RA
结论:为了达到一定的转化率所需要的反应时间 仅与反应速率有关,而与反应器大小无关。
( RA ) rA kcA
t c A0
对一级反应,- R A,1 = k c A,1 = k c A,0 (1- x A,1) - R A,2 = k c A,2 = k c A,0 (1- x A,2) 1 d( ) 1 R A,1 = k c A,0 (1- x A,1) = 2 d x A,1 d x A,1 k c A,0 (1- x A,1) 1 1 1 1 1 - R A,1 - R A,2 = x A,1 x A,1 k c A,0 (1- x A,1) kc A,0 (1- x A,2) 1
c A,N 1 c A,0 1 k N N (1 k11)(1 k 22) ... (1 k N N)
N
c A,N 1 c A,N k Nc A,N
若各釜反应温度相同 k1 k 2 k N k 若各釜反应体积相同 Vr1 Vr2 ... VrN Vr (单釜) 即
2
V r1 = V r2
对一级反应,采用相同体积的釜串联,可使总反 应体积最小 对 R A k c 为了使总反应体积最小 A 1 α>1 ,则小釜在前,大釜在后 2 0<α<1 ,大釜在前,小釜在后 3 α=1 ,釜体积相当 4 α<0 ,单釜操作有利 5 α=0 ,串联不必要
0
Ri对于反应物而言为负,对产物而言为正 连续反应器: dni Q c = Qc - RV
dt
0 i0 i
i i
间歇反应器:Байду номын сангаасQ0 0
Q0
dn i R i Vr 0 i=1, ……k dt
3.2 等温间歇釜式反应器
一.单一反应:
d xA dnA ( RA )Vr nA0 dt dt
V r c A,0( x A, f - x A,0 ) = - R A x A, f Q0
