第二章 结构图等效化简
合集下载
2.4 系统框图及其等效变换
绘制图1所示 所示R-C网络的系统框图 例1 绘制图 所示 网络的系统框图
解: 1）列写该网络的运动方程
U r (s ) − U c (s ) 1 I (s ) = , U c (s ) = I (s ) R CS
2）画出上述两式对应的方框图 3）将两方框图按信号的流向依次 连接，求得c为系统的方框图 图1 R-C网络
G (s )H ( s ) G (s ) = = 1 + G (s )H ( s ) 1 + G (s )
C R (s ) U (s ) G (s )的分子 = = R(s ) V (s ) + U (s ) G (s )的分母 + G (s )的分子
2012-5-2 第二章 控制系统的数学模型
(2 - 51)
正反馈
2012-5-2
+
G1 ( s) G(s) = 1 − G1 ( s ) H ( s )
第二章 控制系统的数学模型 11
图6 环节的反馈连接
2012-5-2
第二章 控制系统的数学模型
12
如果H(s)=1,称为单位反馈系统
C (s ) R (s )
U (s ) 若令G (s ) = , 则上式改写为 V (s )
R2
图2 R-C滤波网络
,
1 U c (s ) = I 2 (s ) C 2s
2）画出上述四式对应的方框图，如图2 a所示 3）根据信号的流向，将各方框单元依次连接起来，就得到 图2 b所示的方框图
2012-5-2 第二章 控制系统的数学模型 7
图3 图 2 所示电路的系统框图
2012-5-2 第二章 控制系统的数学模型 8
1. 化简的关键是解除环路与环路的交叉 或形成大环 化简的关键是解除环路与环路的交叉,或形成大环 套小环的形式. 套小环的形式 2. 解除交叉连接的有效方法是移动比较点或引出点. 解除交叉连接的有效方法是移动比较点或引出点 要向同类移动
第2章 力系的等效简化
2
My Mx cos cos M M
cos
Mz M
S D
例题2.2 五面体作用三个力偶， F1 F1 5N，F2 F2 10N， a 0.2m, 求三个力偶的合成结果。 F3 F3 10 2 N，
m 解： M x F1a F3a sin 45 1N ·
R 2 x 2 cos R 2 4 4
3.整体重心的x坐标：
弧线边重心的x坐标：
x1
R cos Rd
4 4
3 2R xC 4
R
2
2 2
R
S D
主矢：FR = F1 + F2 + + Fn = Fi
M = Mo F 1 + Mo F 2 + + Mo F n = Mo Fi 主矩：
S D
2. 空间任意力系的简化结果讨论 1）主矢 FR = ，主矩 M o 。原力系简化为一个合力偶。
2）主矢 FR ，主矩 M o 。力系简化一合力。
例：平面固定支座约束力分析
FAy
合力投影定理
A
MA FAx
S D
3 6 例题2.3 已知水压力 F1 8 10 N , 泥沙压力 F2 15010 N ,
坝重 W 10106 N , 试将三力向O点简化最后结果。
解： 主矢
FRx F1 F2 8.15 10 N
6
FRy W 10 10 6 N
S D
2.1 力系的分类 二.力偶系 作用于刚体的一群力偶称为力偶系。若力偶系中的各力偶 都位于同一平面。则为平面力偶系，否则为空间力偶系。
自动控制原理课后答案,第二章(西南科技大学)
第2章 控制系统的数学模型
思考题：双RC网络 课题练习:2-9 作业题： 2-2、2-4、2-5、2-7、2-11、2-14 精讲例题：2-12
思考题：求双 RC 网络图的微分方程、传递函数来自解：ui i1R1 u
u 1
C1
iC dt
R1
R2
i1
ic i2
ui
C1 u C2
uo
uo
1 C2
dt
R
R2C
2
d
2uC (t dt2
)
3RC
duC (t dt
)
uC
(t)
R
2C
2
d
2ur (t dt2
)
2RC
dur (t dt
)
ur
(t
)
(d) 解：列微分方程组得
ur
(t)
uc
(t)
1 C
i1dt
ur (t) uc (t) (i2 i1)R
i1 C
i2
RR
ur
C ic
uc
(d)
uc
(t
)
i1R
1 C
icdt
ic i1 i2
微分方程为：
R 2C 2
d
2uc (t) dt2
3RC
duc (t) dt
uc (t)
R2C
2
d
2ur (t) dt2
2RC
dur (t) dt
ur
(t)
2-4 若某系统的单位阶跃响应为c(t)=1-2e-2t+e-t, 试求 系统的传递函数和脉冲响应。
1 G1G2 G1G2G3 (1
1
)
1 G1G2 G1
思考题：双RC网络 课题练习:2-9 作业题： 2-2、2-4、2-5、2-7、2-11、2-14 精讲例题：2-12
思考题：求双 RC 网络图的微分方程、传递函数来自解：ui i1R1 u
u 1
C1
iC dt
R1
R2
i1
ic i2
ui
C1 u C2
uo
uo
1 C2
dt
R
R2C
2
d
2uC (t dt2
)
3RC
duC (t dt
)
uC
(t)
R
2C
2
d
2ur (t dt2
)
2RC
dur (t dt
)
ur
(t
)
(d) 解：列微分方程组得
ur
(t)
uc
(t)
1 C
i1dt
ur (t) uc (t) (i2 i1)R
i1 C
i2
RR
ur
C ic
uc
(d)
uc
(t
)
i1R
1 C
icdt
ic i1 i2
微分方程为：
R 2C 2
d
2uc (t) dt2
3RC
duc (t) dt
uc (t)
R2C
2
d
2ur (t) dt2
2RC
dur (t) dt
ur
(t)
2-4 若某系统的单位阶跃响应为c(t)=1-2e-2t+e-t, 试求 系统的传递函数和脉冲响应。
1 G1G2 G1G2G3 (1
1
)
1 G1G2 G1
第二章结构图化简
•时滞环节
微分方程：Xo（t）= Xi（t -τ） 传递函数：G（S）= e –τs 具体对象: 延时环节
延迟环节是一个非线性的函数，有延迟的系统是很难分 析和控制的。为简单起见，化简如下：
es
1 es
1 1
1s ... 1s
4.建立复杂系统的传递函数： • 由系统的微分方程取拉氏变换 • 电路系统，由复阻抗直接建立 • 动态结构图化简
f (0)
L
d
2f dt
(t
2
)
s2F(s)
sf
(0)
f
' (0)
从微分方程模型到传递函数
RC
du c
u
u
dt
c
r
设初始值uc(0)=0
(RCs 1)U (s) U (s)
c
r
U (s) c
1
U (s) RCs 1
r
2．零初始条件的含义：
•输入作用是在t=0 以后才作用于系统，
r(0) r(0) r(0) 0
1t
1t 1t
uc C'e RC ure RC e RC
1t C'e RC ur
Ur(t) 1
0
Uc(t) 1
t
t
0
方法2. 用拉氏变换求解线性微分方程
Laplace变换
L[f(t)]=F(s) 从时域→复域
定义： 举例：
F(s) f (t)estdt
0
f (t) 1(t)
F(s) estdt 1 est 1
2
1
s
RC
RC c
s 1
s RC
u
(t )
1(t )
自动控制原理02结构图及其等效变换课件
G1 (s)
N (s)
G2 (s)
C (s)
B(s) H (s)
（1）R(s)作用下的系统闭环传递函数
此时， N(s) 0
R(s) E(s)
G1 (s)
B(s)
G2 (s) C1(s)
(s) C1(s) R(s)
H (s)
C1
(s)
(s)R(s)
1
G1 (s)G2 (s) G1 (s)G2 (s)H
d)
2.3.3 结构图的等效变换和简化
例2-9 R(s)
G2G3G4
C(s)
G1
1 G2G3H1 G3G4H 2
e)
R(s)
G1G2G3G4
C(s)
1G1G2G3G4 G2G3H1 G3G4H 2
f)
2.3 控制系统的结构图及等效变换
2.3.4 系统传递函数
典型闭环控制系统 的结构图:
R(s) E(s)
I (s)
1 Ls U L (s)
U0
(s)
1 Cs
I (s)
Ui (s)
UL (s) UR (s)
Uo (s)
a)
UR (s) 1/ R I (s)
b)
UL (s) 1/ Ls I (s)
c)
I (s) 1 / Cs U o (s)
d)
2.3.2 结构图的建立
例2-7 按照信号的流向将以上各个环节连接起来。就构成了 系统的动态结构图。
（6）多个比较点与引出点的交换与合并
R(s)
C(s)
G(s)
B1(s) B2(s) a)
R(s)
C(s)
G(s) R(s)
R(s)
N (s)
G2 (s)
C (s)
B(s) H (s)
（1）R(s)作用下的系统闭环传递函数
此时， N(s) 0
R(s) E(s)
G1 (s)
B(s)
G2 (s) C1(s)
(s) C1(s) R(s)
H (s)
C1
(s)
(s)R(s)
1
G1 (s)G2 (s) G1 (s)G2 (s)H
d)
2.3.3 结构图的等效变换和简化
例2-9 R(s)
G2G3G4
C(s)
G1
1 G2G3H1 G3G4H 2
e)
R(s)
G1G2G3G4
C(s)
1G1G2G3G4 G2G3H1 G3G4H 2
f)
2.3 控制系统的结构图及等效变换
2.3.4 系统传递函数
典型闭环控制系统 的结构图:
R(s) E(s)
I (s)
1 Ls U L (s)
U0
(s)
1 Cs
I (s)
Ui (s)
UL (s) UR (s)
Uo (s)
a)
UR (s) 1/ R I (s)
b)
UL (s) 1/ Ls I (s)
c)
I (s) 1 / Cs U o (s)
d)
2.3.2 结构图的建立
例2-7 按照信号的流向将以上各个环节连接起来。就构成了 系统的动态结构图。
（6）多个比较点与引出点的交换与合并
R(s)
C(s)
G(s)
B1(s) B2(s) a)
R(s)
C(s)
G(s) R(s)
R(s)
理论力学 第二章 力系的等效简化(20P) (2)
矩形均布载荷： 矩形均布载荷：
Fq = ql
三角形分布载荷： 三角形分布载荷：
1 Fq = ql 2
AB的分布载荷对 例7：如图所示，求作用于悬臂梁AB的分布载荷对A点 ：如图所示，求作用于悬臂梁AB的分布载荷对A 的矩。 的矩。 解：
L 2L M A = − Fq1 − Fq 2 2 3 1 2 = − (q1 + 2q2 )L 6
V
A
A 积分法 A A 均质细杆： 长度L×截面积A) 均质细杆：P=γLS, (比重γ ×长度 ×截面积 比重
∫ =
A
xd A
∫ =
A
yd A
∫ =
A
zd A
xc=∑Li xi/L ∑
yc=∑Li yi/L ∑
zc=∑Li zi/L ∑
∫ =
L
xd L L
积分法
∫ =
L
ydL L
∫ =
L
L
zdL L
OO′ = d = FR × M O
2 FR
2、平面任意力系的简化
F1 A1 A2 An
主矢： 主矢： 主矢， 主矢，主矩
F2 Fn
F1 M1
=
简化中心
M2 F2 Mn O
Fn
=
附加力偶
FR MO
F R = Σ Fi
FRx = ∑ Fix FRy = ∑ Fiy
FRX FRY cos α = , sin α = FR FR
合力： 合力：
Fq = ∫ q ( x )d x
b
作用点： 作用点：
xc
∫a q( x )dx ⋅ x =
Fq
a b
∫a xq( x )dx = b ∫a q( x )dx
第二章 (2.3,2,4)动态结构图、反馈系统的传递函数
研究控制系统的性能，主要的传 递函数为： 一、系统的开环传递函数 一、系统的开环传递函数 二、系统的闭环传递函数 二、系统的闭环传递函数 三、系统的误差传递函数 三、系统的误差传递函数
一、系统的开环传递函数
D(s)
闭环控制 系统的典型 结构：
R(s)
E(s) E(s)
_
B(s)
G1(s)
+
C(s) G2(s)
Y2(s)
(3) 反馈
R(s)
G(s) H(s)
C(s)
R(s)
C(s) G( s) ( s) 1 H ( s)G ( s)
C ( s ) E ( s ) G( s ) [ R( s) C ( s) H ( s)]G ( s)
C ( s) G( s) ( s) R( s) 1 H ( s)G ( s)
H2 G1 G2 H1
1 G4
G3 a G4 H3
b
例2：综合点移动
综合点与引出 点互换位置了
G 33 G G 11 G
G2
G 22 G H 11 H
错！ 向同类移动
1并联
G3 G1
3串联
2反馈
G2 H1
G1
G4 G1 H1 输入 G1 H1 H1
两个
例3 作用分解
G2
a b
两个 输出
G3 H3
4
绘制双T网络结构图
R1
U1(s)
R2
urr(t) U (s)
I1(s)
sc1
I2(s)
1 C 1
I2(s)
sc2
1 C 2
ucc(t) U (s)
Ur(s)
一、系统的开环传递函数
D(s)
闭环控制 系统的典型 结构：
R(s)
E(s) E(s)
_
B(s)
G1(s)
+
C(s) G2(s)
Y2(s)
(3) 反馈
R(s)
G(s) H(s)
C(s)
R(s)
C(s) G( s) ( s) 1 H ( s)G ( s)
C ( s ) E ( s ) G( s ) [ R( s) C ( s) H ( s)]G ( s)
C ( s) G( s) ( s) R( s) 1 H ( s)G ( s)
H2 G1 G2 H1
1 G4
G3 a G4 H3
b
例2：综合点移动
综合点与引出 点互换位置了
G 33 G G 11 G
G2
G 22 G H 11 H
错！ 向同类移动
1并联
G3 G1
3串联
2反馈
G2 H1
G1
G4 G1 H1 输入 G1 H1 H1
两个
例3 作用分解
G2
a b
两个 输出
G3 H3
4
绘制双T网络结构图
R1
U1(s)
R2
urr(t) U (s)
I1(s)
sc1
I2(s)
1 C 1
I2(s)
sc2
1 C 2
ucc(t) U (s)
Ur(s)
《自动控制原理》第二章传递函数
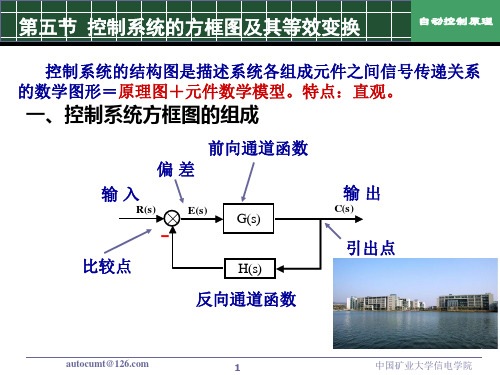
一、控制系统方框图的组成
方框图（结构图）的四要素：
R( s)
G (s) C (s)
自动控制原理
R (s ) +
R( s) C ( s)
c(t )
C (s) C (s)
r (t )
C (s)
R( s)
(d )
(a)
(b)
(c )
（1）方框（方块）:表示输入到输出单向传输间 的函数关系。
r(t)
R (s) G (s)
1 R2
I 2 (s)
U 2 (s)
U 3 (s)
U1 ( s )
1 I1 ( s ) R1
I 2 (s)
1 U 3 (s) sC1
1 R2
I 2 ( s) 1 U 2 (s) sC2
autocumt@
7
中国矿业大学信电学院
一、控制系统方框图的组成
建立方框图的步骤：
自动控制原理
H3
H3
二、系统方框图的等效变换和化简
自动控制原理
例2.21
用方框图的等效法则，求如图所示 系统的传递函数C(s)/R(s)
解：这是一个具有交叉反馈的多回路系统，如果不对它作 适当的变换，就难以应用串联、并联和反馈连接的等效变 换公式进行化简。本题的求解方法是把图中的点A先前移 至B点，化简后，再后移至C点，然后从内环到外环逐步 化简，其简化过程如下图。
X(s) Y(s) Z(s) C(s) X(s) Z(s)
自动控制原理
C(s) Y(s)
（7）引出点之间互移
X(s)
a
b
C(s) Z(s)
X(s)
a
b
C(s) Y(s) C(s)
工程力学 第2章 力系的等效与简化
第2章 力系的等效与简化 作用在实际物体上的力系各式各样，但是，都可用归纳为两大类：一类是力系中的所有力的作用线都位于同一平面内，这类力系称为平面力系；另一类是力系中的所有力的作用线位于不同的平面内，称为空间力系。
这两类力系对物体所产生的运动效应是不同的。
同一类力系，虽然其中所包含的力不会相同，却可能对同一物体产生相同的作用效应。
在就是前一章中提到的力系等效的概念。
本章将在物理学的基础上，对力系的基本特征量加以扩展，引入力系主矢与主矩的概念；以此为基础，导出力系等效定理；进而应用力向一点平移定理以及力偶的概念对力系进行简化。
力系简化理论与方法将作为分析所有静力学和动力学问题的基础。
§2-1 力系等效定理 ２－１－１ 力系的主矢和主矩 ２－１－２ 力系等效定理 §2-2 力偶与力偶系 ２－２－１ 力偶与力偶系 ２－２－２ 力偶的性质 ２－２－３ 力偶系的合成 §2-3 力系的简化 ２－３－１ 力向一点平移定理 ２－３－２ 空间一般力系的简化 ２－３－３ 力系简化在固定端约束力分析中的应用 §2-4 结论和讨论 ２－４－１ 关于力矢、主矢、力矩矢、力偶矩矢以及 主矩矢的矢量性质 ２－４－２ 关于合力之矩定理及其应用 ２－４－３ 关于力系简化的最后结果 ２－４－４ 关于实际约束的简化模型 ２－４－５ 关于力偶性质推论的应用限制 习 题 本章正文 返回总目录第2章 力系的等效与简化 §２－１ 力系等效定理 物理学中，关于质点系运动特征量已有明确论述，这就是：质点系的线动量和对某一点的角动量。
物理学中还指明线动量对时间的变化率等于作用在质点系上的合外力；角动量对时间的变化率等于作用在质点系上外力对同一点的合力矩。
这里的合外力，实际上只有大小和方向，并未涉及作用点或作用线。
因而，需要将其中的合外力与外力的合力矩扩展为力系的主矢和主矩。
２－１－１ 力系的主矢和主矩 主矢：一般力系（F 1，F 2，…，F n ）中所有力的矢量和（图2—1），称为力系的主矢量，简称为主矢（principal vector ），即∑=ni i1R FF ＝(2－1)图2－1力系的主矢其中F R 为力系主矢；F i 为力系中的各个力。
自动控制原理2.4 结构图的等效变换及简化计算
Pk—从R(s)到C(s)的第k条前向通道增益 △k —第k条前向通道的余子式
在△中，去掉与第k条前向通 道相接触的回路对应的项后
剩余的部分。
求法: 去掉第k条前向通路后所求的△ 用梅森公式求上例信号流图对应的传函。
南京工业职业技术学院机械工程学院——自动控制原理
梅森公式例1
GG44((ss))
R(s)
注：比较点和引出点之间不能换位。 3. 通过在被变换的支路上乘或除某个传函来保持等效。 4. 根据环节方框的连接方式（串联、并联和反馈）进行简化
计算。
南京工业职业技术学院机械工程学院——自动控制原理
结构图三种连接形式及其计算
串联
G1
G2
G1 G2
n
G(s) Gi (s) i 1
并联 G1 G2
反馈 G1
G5
R –
X1 G1
– G2 X2 –
G3 X3
G4
C
X3
G6
G7
南京工业职业技术学院机械工程学院——自动控制原理
G8 G5
R – G1 X1
X2 – G2
–
X3
G3
G4
C
X3 G6
G7
（2）求传函。用梅逊公式：
1 G1G2G3G4G7 G1G2G3G4G8 G2G3G6 G3G4G5
R(s)
-
G4
A
G1
-
B
G2
H1
G3 H2
C C(s)
P1 G1G2G3 1 1
P2 G1G4 2 1
C(S) P(S) P11 P22
P11 P22
R(S)
1 (L1 L2 L3 L4 L5 )
在△中，去掉与第k条前向通 道相接触的回路对应的项后
剩余的部分。
求法: 去掉第k条前向通路后所求的△ 用梅森公式求上例信号流图对应的传函。
南京工业职业技术学院机械工程学院——自动控制原理
梅森公式例1
GG44((ss))
R(s)
注：比较点和引出点之间不能换位。 3. 通过在被变换的支路上乘或除某个传函来保持等效。 4. 根据环节方框的连接方式（串联、并联和反馈）进行简化
计算。
南京工业职业技术学院机械工程学院——自动控制原理
结构图三种连接形式及其计算
串联
G1
G2
G1 G2
n
G(s) Gi (s) i 1
并联 G1 G2
反馈 G1
G5
R –
X1 G1
– G2 X2 –
G3 X3
G4
C
X3
G6
G7
南京工业职业技术学院机械工程学院——自动控制原理
G8 G5
R – G1 X1
X2 – G2
–
X3
G3
G4
C
X3 G6
G7
（2）求传函。用梅逊公式：
1 G1G2G3G4G7 G1G2G3G4G8 G2G3G6 G3G4G5
R(s)
-
G4
A
G1
-
B
G2
H1
G3 H2
C C(s)
P1 G1G2G3 1 1
P2 G1G4 2 1
C(S) P(S) P11 P22
P11 P22
R(S)
1 (L1 L2 L3 L4 L5 )
2-4结构图及其等效变换
i= 1
n
C(s)
（3）反馈连接 ：闭环系统
R E
±
C
G
R
B
G(s) 1mG(s)H(s)
C
H
G (s)—前向通道传递函数；H (s)—反馈通道传递函数。
Q (s) =G s)E(s) =G s)(R(s) ± B(s)) C ( ( =G s)R(s) ±G s)B(s) =G s)R(s) ±G s)H(s)C(s) ( ( ( ( ∴ (s)(1mG s)H(s)) =G s)R(s) C ( (
Ur –
1 ( R1 C 1 s + 1)
1 ( R2 C 2 s + 1)
串联结构 Uc
R1C 2 s
Ur –
反馈结构 Uc
1 ( R1C1s + 1)(R2C2 s + 1+ R2C2 + R1C2 )s +1
动态结构图化简的要领： 动态结构图化简的要领： 1.通过比较点、 1.通过比较点、引出点的移动 通过比较点 打开复杂交叉 2.利用三种基本结构进行化简 2.利用三种基本结构进行化简
§2-4 结构图及其等效变换
一．基本概念： 基本概念：
网络为例： 以RC 网络为例：
i
R
ur = Ri + uc 1 uc = ∫ idt c
ur
C
uc
i ur − uc = R 即 1 uc = ∫ idt c
Ur (s)
∆U(s) 1 I(s)
R
Uc (s)
R
G
R
G
C
C
±
1 G
±
Q
Q
第2章4传递函数方块图及其化简ppt课件
G1
+ (+-)
A G1
G2 AG2
AG1 AG1+ AG2
++
1 G1
G2 AG2
A G1
1 G1
AG1 AG2
G2 + +
分支点移动 A G2
1 G2
AG1 AG1+ AG2 G1 + +
AG2
(2)反馈化成单位反馈
A+ -
G1 A G1 1 + G1G2
A1+
G2
-
G1
G1 G2 1+ G1G2
(3)根据因果关系，确定各个原始微分方程分中的输入量与 输出量，并将拉斯变换的结果表示成传递函数方框图的形 式；
(4)按信号的传递过程，依次将上述各个方框图连接起来， 构成整个系统的传递函数方框图，一般输入在左边，输出 在右边。
jik 04
2
例2： 绘制电枢控制式直流电动机的传递函数
方框图 。
R
i1 (t)
G1 +
G2 +
1 G3
-A
G3
Xo(s)
C
H2
H1
H3
Xi 1(s)
+
-
G1 +
G2
-
1 G3
G3 1+H2 G3
Xo(s)
C
略
H1
jik 04
15
X (s) 0 求 Xo(s) 。令
Xi2(s)
i1
Xi 1(s)
H3
+
-
-
G1 B +
G2
,
Xi
自动控制原理(2-2)2.5 框图及其化简方法
根据系统中信息的传递方向，将各个子系统的函数 方块用信号线顺次连接起来，就构成了系统的结构 图，又称系统的方块图。 系统的结构图实际上是系统原理图与数学方程的 结合，因此可以作为系统数学模型的一种图示。
一、结构图的组成
① 结构图的每一元件用标有传递函数的方框表示。
R(s)
G (s)
C (s)
元件的结构图
G2 ( s )
(a)
X 2 ( s)
G3 ( s)
X 3 ( s)
X 0 (s)
G1 ( s )G2 ( s )G3 ( s)
(b)
X 3 ( s)
图2－10 串联环节的简化
n个环节（每个环节的传递函数为Gi(s) ，i=1,2,3,…） 串联的等效传递函数等于各传递函数相乘。
G(s) G1 (s)G2 (s) Gn (s)
R( s) G(s)
+
相加点前移
C (s) Q( s)
(a)
R( s)
+
C (s) G(s)
Q( s)
1 G ( s)
(b)
图2－13 相加点前移
1 C ( s ) R ( s )G ( s ) Q ( s ) R ( s ) Q ( s ) G (s) G (s)
分支点前移
C (s) G (s) C (s)
(a)
R( s)
R( s) G (s)
C ( s)
G(s)
(b)
C ( s)
图2－15 分支点前移
C ( s ) R ( s )G ( s )
分支点后移
C (s) G (s) R( s ) R( s ) G (s) C (s)
《自动控制原理》（卢京潮，西北工业大学）第二章习题及答案
第 2 章习题及解答
2-1 建立图 2-33 所示各机械系统的微分方程 （其中 F (t ) 为外力，x (t ) 、 y (t ) 为位移；
k 为弹性系数， f 为阻尼系数， m 为质量；忽略重力影响及滑块与地面的摩擦） 。
图 2-33 系统原理图
解. （a）以平衡状态为基点，对质块 m 进行受力分析（不再 考虑重力影响） ，如图解 2-1(a)所示。根据牛顿定理可写出
微分方程为
duc2 du r2 3 du c 1 2 du r 1 u + + = + + 2 2 ur c 2 2 2 2 dt CR dt C R dt CR dt C R
(c) 由图解 2-2（c）可写出
U r ( s ) = R1 [ I1 ( s ) + I 2 ( s ) ] + ( Ls + R2 ) I 2 ( s )
对 B 点有
dx1 dy − ) dt dt
（1）
f(
dx1 dy − ) = k2 y dt dt
（ቤተ መጻሕፍቲ ባይዱ）
联立式（1） 、 （2）可得：
k1 k 2 k1 dx dy + y= dt f (k1 + k 2 ) k1 + k 2 dt
(c) 如图解 2-1(c)所示，取 A,B 两点分别进行受力分析。对 A 点有
2
图 2-37 单摆系统
将上式中非线性项 sin θ 在平衡点 θ 0 = 0 附近进行泰勒级数展开， 取一次近似有
sin θ = sin θ 0 +
d sin θ |θ0 ⋅Δθ = sin θ 0 + cos θ 0 ⋅ Δθ dt
将 θ 0 = 0 代入上式，得： sin θ − sin θ 0 = Δθ 。代入原方程可得线性化后的单摆方程
2-1 建立图 2-33 所示各机械系统的微分方程 （其中 F (t ) 为外力，x (t ) 、 y (t ) 为位移；
k 为弹性系数， f 为阻尼系数， m 为质量；忽略重力影响及滑块与地面的摩擦） 。
图 2-33 系统原理图
解. （a）以平衡状态为基点，对质块 m 进行受力分析（不再 考虑重力影响） ，如图解 2-1(a)所示。根据牛顿定理可写出
微分方程为
duc2 du r2 3 du c 1 2 du r 1 u + + = + + 2 2 ur c 2 2 2 2 dt CR dt C R dt CR dt C R
(c) 由图解 2-2（c）可写出
U r ( s ) = R1 [ I1 ( s ) + I 2 ( s ) ] + ( Ls + R2 ) I 2 ( s )
对 B 点有
dx1 dy − ) dt dt
（1）
f(
dx1 dy − ) = k2 y dt dt
（ቤተ መጻሕፍቲ ባይዱ）
联立式（1） 、 （2）可得：
k1 k 2 k1 dx dy + y= dt f (k1 + k 2 ) k1 + k 2 dt
(c) 如图解 2-1(c)所示，取 A,B 两点分别进行受力分析。对 A 点有
2
图 2-37 单摆系统
将上式中非线性项 sin θ 在平衡点 θ 0 = 0 附近进行泰勒级数展开， 取一次近似有
sin θ = sin θ 0 +
d sin θ |θ0 ⋅Δθ = sin θ 0 + cos θ 0 ⋅ Δθ dt
将 θ 0 = 0 代入上式，得： sin θ − sin θ 0 = Δθ 。代入原方程可得线性化后的单摆方程
第二章结构图的等效变换求系统的传递函数
△k称为第k条前向通路的余子式 △k求法: 去掉第k条前向通路后所求的△ △k=1-∑LA+ ∑LBLC- ∑LDLELF+…
R(s)
a b
c
G4(s) G11(s) (s) G H1(s)
d e
梅逊公式例R-C
G G22(s) (s)
f
G G33(s) (s)
g H3(s)
h
C(s)
△1=1
R(s)
梅逊公式介绍
R-C :
C(s) = R(s)
∑Pk△k △
其中:
△称为系统特征式 △= 1 - ∑La + ∑LbLc -∑LdLeLf+…
所有单独回路增益之和 ∑LbLc—所有两两互不接触回路增益乘积之和 ∑LdLeLf—所有三个互不接触回路增益乘积之和
— ∑La
Pk—从R(s)到C(s)的第k条前向通路传递函数
1 1
G 2(s) G (s) G (s) 2 2 H 2(s) H (s) H (s) 2 2
H 1(s) H (s) H (s) 1 1 G1(s)
H3(s)
H 3(s) H (s) H (s) 3 3
C(s)
R(s)
G2 H3 E(S) P1= – P =1 1 H1(s)
1= 1 H △△ =1+G 1 2 H 2 2(s)P1△1= ?
E(s)=
R(s)[ (1+G2H2) + (- G3G2H3) ] + (–G2H3) N(s)
1 - G1H1 + G2H2
+ G1G2H3 -G1H1G2 H2
综合点移动
G3
G1
G2
向同类移动 无用功
R(s)
a b
c
G4(s) G11(s) (s) G H1(s)
d e
梅逊公式例R-C
G G22(s) (s)
f
G G33(s) (s)
g H3(s)
h
C(s)
△1=1
R(s)
梅逊公式介绍
R-C :
C(s) = R(s)
∑Pk△k △
其中:
△称为系统特征式 △= 1 - ∑La + ∑LbLc -∑LdLeLf+…
所有单独回路增益之和 ∑LbLc—所有两两互不接触回路增益乘积之和 ∑LdLeLf—所有三个互不接触回路增益乘积之和
— ∑La
Pk—从R(s)到C(s)的第k条前向通路传递函数
1 1
G 2(s) G (s) G (s) 2 2 H 2(s) H (s) H (s) 2 2
H 1(s) H (s) H (s) 1 1 G1(s)
H3(s)
H 3(s) H (s) H (s) 3 3
C(s)
R(s)
G2 H3 E(S) P1= – P =1 1 H1(s)
1= 1 H △△ =1+G 1 2 H 2 2(s)P1△1= ?
E(s)=
R(s)[ (1+G2H2) + (- G3G2H3) ] + (–G2H3) N(s)
1 - G1H1 + G2H2
+ G1G2H3 -G1H1G2 H2
综合点移动
G3
G1
G2
向同类移动 无用功
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1. 飞豹战机的俯仰角控制系统是由中航工业西安飞行自动控制研究所主持研制的。
其系统的
简化结构图如图1所示，试求其闭环传递函数()/()C s R s 。
(等效化简or Mason 均可，都用也行，但不加分)。
飞机
陀螺
()
R s ()
C s -
+
21
0.31
s s ++0.5
1
-0.421
s +0.4
0.7
s
K +
图1. 系统结构图
2. 某控制系统的结构图如图2，试求其闭环传递函数()/()C s R s 与()/()C s N s (等效化简or
Mason 均可，都用也行，但不加分)。
()
R s ()
C s -
-
+
+
1
H 2
H 3
H 1G 2
G ()N s
图2. 系统结构图
厦门大学《自动控制原理》课程作业
航空航天学院 航 空 系 2018年级 飞动 专业
主讲教师： 董一巍 作业内容：（第五讲）
3.试求闭环传递函数()/()
C s R s(等效化简or Mason均可，都用也行，但不加分)。
)s
图3. 系统结构图。