第二章 结构图化简
《自动控制原理》典型考试试题
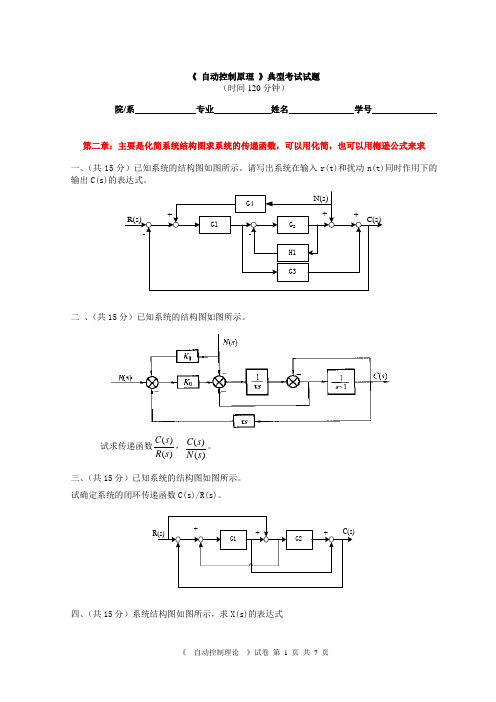
《 自动控制原理 》典型考试试题（时间120分钟）院/系 专业 姓名 学号第二章：主要是化简系统结构图求系统的传递函数，可以用化简，也可以用梅逊公式来求一、（共15分）已知系统的结构图如图所示。
请写出系统在输入r(t)和扰动n(t)同时作用下的输出C(s)的表达式。
G4H1G3G1G 2N(s)C(s)R(s)--+++二 、（共15分）已知系统的结构图如图所示。
试求传递函数)()(s R s C ，)()(s N s C 。
三、（共15分）已知系统的结构图如图所示。
试确定系统的闭环传递函数C(s)/R(s)。
G1G2R(s)-++C(s)-+四、（共15分）系统结构图如图所示，求X(s)的表达式G4(s)G6(s)G5(s)G1(s)G2(s)N(s)C(s)R(s)--G3(s)X(s)五、（共15分）已知系统的结构图如图所示。
试确定系统的闭环传递函数C(s)/R(s)和C(s)/D(s)。
G1G2R(s)-++C(s)-+D(s)G3G4六、（共15分）系统的结构图如图所示，试求该系统的闭环传递函数)()(s R s C 。
七、（15分）试用结构图等效化简求题图所示各系统的传递函数)()(s R s C一、（共15分）某控制系统的方框图如图所示，欲保证阻尼比ξ=0.7和响应单位斜坡函数的稳态误差为ss e =0.25,试确定系统参数K 、τ。
二、（共10分）设图（a ）所示系统的单位阶跃响应如图（b ）所示。
试确定系统参数,1K 2K 和a 。
三、（共15分）已知系统结构图如下所示。
求系统在输入r(t)=t 和扰动信号d(t)=1(t)作用下的稳态误差和稳态输出)(∞C2/(1+0.1s)R(s)-C(s)4/s(s+2)E(s) D(s)四、（共10分）已知单位负反馈系统的开环传递函数为：2()(2)(4)(625)KG s s s s s =++++试确定引起闭环系统等幅振荡时的K 值和相应的振荡频率ω五、（15分）设单位反馈系统的开环传递函数为12 )1()(23++++=s s s s K s G α若系统以2rad/s 频率持续振荡，试确定相应的K 和α值第三章：主要包括稳、准、快3个方面稳定性有2题，绝对稳定性判断，主要是用劳斯判据，特别是临界稳定中出现全零行问题。
2019_2020学年高中数学第二章框图本章整合课件北师大版选修1_2
…
…
最后输出S=N-T=1−
1 2
+
1 3
−
1 4
+
⋯
+
1 99
−
1 100
,
一次处理
1 ������
与
1 ������+1
两项,故
i=i+2.
答案:B
1234567 89
3(2018·天津高考)阅读右边的程序框图,运行相应的程序,若输入N 的值为20,则输出T的值为( ) A.1 B.2 C.3 D.4
综合应用
专题一 专题二 专题三
应用试设计《数学选修1-1》第三章“变化率与导数”的知识结构 图.
解:
1234567 89
1(2018·北京高考)执行如图所示的程序框图,输出的s值为( )
A. 1 B. 5 C. 7 D. 7
2
6
6
12
1234567 89
解析:运行程序框图,s=1,k=1;s=1+(-1)1×
1 2
=
1 2
,
������
=
2;
������
=
1 2
+
(−1)2 × 1 = 5 , ������ = 3; 此时满足k≥3,跳出循环,输出的 s= 5 . 故选B.
36
6
答案:B
1234567 89
2(2018·全国 2 高考)为计算 S=1− 1 + 1 − 1 + ⋯ + 1 − 1 ,
234
本章整合
-1-
知识建构
算法流程图
流程图 工序流程图
框图
实际问题流程图 数学问题及其他问题的解决
第二章传递函数案例
解：
系统的结构图为
3. 结构图化简 (结构图的等效变换）
化简目的：
将结构图化简为一个方块，即传递函数。
化简原则：
保证化简前后的代数等价关系不变
等效变换法则
环节串联
环节并联
反馈回路化简
负反馈
正反馈
相加点移动
分支点移动
前移
后移
信号的分支点与相加点不可以互换
例：化简结构图，求取传递函数
阶跃响应曲线
七、比例积分环节 （P-I）
定义：环节输出正比于输入信号和它对时间的积分。
微分方程
1 c( t ) K r t Ti
0 r t dt
t
传递函数
1 G( s) K 1 T s i
阶跃响应曲线
八 、延迟环节
四、惯性环节
定义：环节的输出不能立即复现输入，而是经过 一定时间后才能复现输入的变化。
微分方程 传递函数
dc( t ) T c( t ) Kr ( t ) dt
K G( s) Ts 1
运算放大器
1 1 Rf Rf Cf s Cf s U 2 ( s) U1 ( s ) R1 Rf R1 K Rf Cf s 1 Ts 1
dr ( t ) c( t ) K r ( t ) TD d t
微分方程
传递函数
G( s)
c s r s
K 1 TD s
在放大器上加以 RC 网 络 反 馈 , 当 增益K足够大时
U 2 ( s) U1 ( s ) K 1 1 K RCs 1 K RCs 1 RCs 1 K RCs 1 RC 1 s 1 K K RCs 1 s1
自动控制原理-夏超英-第2章+习题解答
第二章 习题解答2-1试求下列各函数的拉氏变换。
（a ）()12f t t =+，（b ）2()37()f t t t t δ=+++，（c ）23()2ttt f t e ete ---=++，（d ）2()(1)f t t =+，（e ）()sin 22cos 2sin 2tf t t t e t -=++，（f ）()2cos tf t te t t -=+，（g ）()sin32cos f t t t t t =-，（h ）()1()2cos 2f t t t t =+ 解：（a ）212()F s s s =+（b ）23372()1F s s s s=+++（c ）2121()12(3)F s s s s =+++++ （d ）2()21f t t t =++，3221()F s s s s=++（e ）222222()44(1)4s F s s s s =++++++ （f ）2222211621()11(1)s d s s F s s ds s s ⎛⎫ ⎪++⎝⎭=+=++++ （g ）2222222223262231()(3)(1)s d d s s s s F s ds ds s s ⎛⎫⎛⎫ ⎪ ⎪+++⎝⎭⎝⎭=-+=-++（h ）2222211684()(4)s d s s F s s ds s s ⎛⎫ ⎪++⎝⎭=+=++2-2试求图2.54所示各信号的拉氏变换。
（a ） （b ） （c ） （d ）图2.54 习题2-2图解：（a ）021()t s e X s s s -=+（b ）000221()t s t se e X s t s s s--=-+- （c ）33112212()()t s t st s t s t s t s t s t s a ae be be ce ce a b a c b ce X s e e s s s s s s s s s s----------=-+-+-=++-（d ）11()1()1()1()()1()1()11()1()(2)1(2)1(2)1111()21()2()1()(2)1(2)1(2)x t t t T t t t T t T t T T Tt T t T t T t T t T T Tt t T t t T t T t T t T t T T T T=--+--------+--+-=-⨯-+---+--+-所以22222222211111111()222Ts Ts TsTsTs Ts s s s e e e e T T T X s e e s s T s T s T s s s s s------+++=-+-++=-+2-3运用部分分式展开，求下列各像函数的原函数。
2-3-2 结构计算简图的简化内容.
慢的荷载，如结构的自重、水压力和土压力等。动力荷载是指
其大小、方向和作用位置随时间迅速变化的荷载，如冲击荷载、 突加荷载以及动力机械运动时产生的荷载等。有些动力荷载如 车辆荷载、风荷载和地震作用荷载等，一般可将其大小扩大若 干倍后按静力荷载处理，但在特殊情况下要按动力荷载考虑。
国家共享型教学资源库
江苏建筑职业技术学院
2. 结点的简化 结构中各杆件间的相互连接处称为结点。结点可简化为 以下两种基本类型。
国家共享型教学资源库
江苏建筑职业技术学院
（1）铰结点
铰结点的特征是所连各杆都可以绕结点自由转动，即在结点
处各杆之间的夹角可以改变。
国家共享型教学资源库
江苏建筑职业技术学院
（2）刚结点
刚结点的特征是所连各杆不能绕结点作相对转动，即各
座、定向支座和固定端支座。对于重要结构，如公路和铁路桥梁， 通常制作比较正规的典型支座，以使支座反力的大小和作用点的 位置能够与设计情况较好地符合；对于一般结构，则往往是一些 比较简单的非典型支座，这就必须将它们简化为相应的典型支座。
下面举例说明。
国家共享型教学资源库
江苏建筑职业技术学院
国家共享型教学资源库
杆之间的夹角在变形前后保持不变。
国家共享型教学资源库
江苏建筑职业技术学院
●当一个结点同时具有以上两种结点的特征时，称为组 合结点，即在结点处有些杆件为铰接，同时也有些杆件为刚性
连接。
国家共享型教学资源库
江苏建筑职业技术学院
3. 支座的简化 把结构与基础或支承部分连接起来的装置称为支座。平面结
构的支座根据其支承情况的不同可简化为固定铰支座、活动铰支
国家共享型教学资源库
江苏建筑职业技术学院
高二数学选修12第二章《结构图》课件解读
市深杭 场圳州 营办办 销事事 部处处
例2 阅读框图，对其进行解释说明。
解析： 艺术分为7个门类：音乐、戏剧戏曲、
舞蹈、电影、美术、书法和摄影： 音乐可分为：音乐学、作曲与作曲
理论、音乐表演艺术和音乐其他学科； 戏剧戏曲分为：戏剧戏曲史、戏剧
戏曲理论、戏剧戏曲表演和戏剧戏曲其 他学科；
舞蹈可分为：舞蹈史、舞蹈理论、 舞蹈编导、舞蹈表演和舞蹈其他学科；
的表现为“树”形结构，也会用一些“环”形结构，来表达 逻辑先后关系。
总结
流程图和结构图有什么区别和联系？？
1.联系： 它们的共同点：都是框图， 框图是表示一个系统各部分和各环节之间
关系的图示，能清晰地表达比较复杂的系统各部分之间的关系，是表达和 交流思想的有力工具。
2.区别： 流程图描述动态过程，结构图刻画系统结构。流程图通常会有一个
回归分析
相关系数
可线性化的回归分析
独立性检验
条件概率与独立事件 独立性检验 独立性检验的基本思想 独立性检验的应用
＊ 结构图： 结构图一般由构成系统的若干要素和表达各要素之
间的连线（或方向箭头）构成，连线通常按从上到下、 从左到右的方向表示要素的从属关系或逻辑先后关系。
＊ 分类： 结构图一般有知识结构图和组织结构图。它们更多
“起点”，一个或多个“终点”，其基本单元之间有流程线连接；结构图 则更多地表现为“树”形结构，其基本要素之间一般为概念上的从属关系 或逻辑上的先后关系。
动手做一做
1. 请画出《三角函数》一章的结构图。 2. 阅读下列结构图，你可以得到什么信息？
总经理
总工程师
副总经理
专家、顾问
研发部 信息部 监理部 咨询部 财务部 编辑部
动态结构图的等效变换和化简
等 R(s)
效
C(s) G(s)
1Gs
B(s)
Cs
Rs
GBssGs
RsGs Bs
二、综合点的移动和互移
（二）综合点后移
R(s)
B(s)
C(s) G(s)
Cs Rs BsGs
等 R(s) 效
B(s)
G(s) G(s)
C(s)
Cs RsGs BsGs
二、综合点的移动和互移
（三）综合点互移
R(s)
C(s)
G(s)
等
R(s)
效
Cs RsGs
R(s)
C(s)
G(s)
R(s)
11GGss
Cs RsGs
三、引出点的移动和互移
（三）引出点互移
R(s)
R(s)
等 R(s)
R(s)
效
例题
试化简下图所示两级RC电路的动态结构图，并求出传 递函数。
Ui s
1
R1
-
-
1 C1s
1 R2
-
Uo s
G2 (s) C2 (s)
C1s RsG1s C2s RsG2s Cs C1s C2s
Cs G1s G2sRs
结论：n个环节并联后总的传递函数是各环节传递函数的代数和。
一、环节的合并
（三）反馈连接
如下图所示，系统的输出信号C(s)在经过某个环节H(s)后，反 送到输入端，这种连接方式成为反馈连接。
R(s)
C(s)
B(s) D(s)
Cs Rs Bs Ds
等
R(s)
C(s)
效
D(s) B(s)
Cs Rs Ds Bs
三、引出点的移动和互移
高中数学北师大版选修2-1第二章《结构图》ppt课件
[例1] 设计“数列”一章的知识结构图． [思路点拨] 画“数列”的知识结构图，首先要明确知 识点以及各个知识点的从属关系，其次要明确各个知识点 是否有“并列”关系．
[精解详析] 知识结构图如图 所示．
[一点通] 绘制知识结构图，首先要对所画结构图 的每一部分有一个深刻的理解，从头到尾抓住知识的主 要脉络进行分解，然后将每一部分进行归纳与提炼，形 成一个个知识点并逐一写在矩形框内，最后按其内在的 逻辑顺序将它们排列起来并用线段相连，要注意实际问 题的逻辑顺序和概念上的从属关系．
1．下列关于函数、函数的定义域、函数的值域、函数的对
应法则的结构图正确的是
()
答案：A
2．将下列概念进行分类，画出结构图． 正方形、平行四边形、矩形、菱形、梯形、等腰梯形、 四边形、直角梯形． 解：结构图如下：
3．设计《数学选修1－1》第三章“变化率与导数”的知识 结构图．
解：
[例2] 某公司的组织结构是：总经理之下设执行经理、 人事经理和财务经理．执行经理领导生产经理、工程经理、 品质管理经理和物料经理．生产经理领导线长，工程经理 领导工程师，工程师管理技术员，物料经理领导计划员和 仓库管理员．
⑤ 搁置问题抓住老师的思路。碰到自己还没有完全理解老师所讲内容的时候，最好是做个记号，姑且先把这个问题放在一边，继续听老师讲后面的 内容，以免顾此失彼。来自：学习方法网
⑥ 利用笔记抓住老师的思路。记笔记不仅有利于理解和记忆，而且有利于抓住老师的思路。
2019/8/29
最新中小学教学课件
24
谢谢欣赏！
③ 根据老师的提示抓住老师的思路。老师在教学中经常有一些提示用语，如“请注意”、“我再重复一遍”、“这个问题的关键是····”等等，这些 用语往往体现了老师的思路。来自：学习方法网
框图化简、梅逊公式习题
梅森公式
例：使用Mason公式计算下述结构图的传递函数
G4
R
E
-
G1
G2
+ -
G3
C
+
H1
H2
C(s) , E(s) R(s) R(s)
[解]：在结构图上标出节点，如上。然后画出信号流图，如下：
G4
R
E G1 G2
H1
G3 H2
C
H1H2
梅森公式
G4
C(s) R
求
：
R(s)
E G1
G2
H1
P
1
2
Pk k
k 1
G1G2G3 G3G4 G1G3G4 H1
1 G1H1 G3H 2 G1G2G3H1H 2 G1G3H1H 2
梅森公式
G4
C(s) R
求
：
R(s)
E G1
G2
H1
H1H2
G3 H2
C
前向通道有二，分别为: P1 G1G2G3, P2 G3G4
回路有三，分别为： G1H1,G3H2 ,G1G2G3H1H2
G4
R
E
-
G1
G2
+ -
G3
C
+
H1
H2
C(s) , E(s) R(s) R(s)
[解]：在结构图上标出节点，如上。然后画出信号流图，如下：
G4
R
E G1 G2
H1
G3 H2
C
H1H2
梅森公式
G4
C(s) R
求
：
R(s)
E G1
G2
H1
H1H2
结构图化简
例2
化简方块图，求传递函数。
7
8
9
10
11
例3
12
13
14
15
16
C(s)
C(s)
R(s)
G(s)
R(s)
C(s)
R(s)
G(s)
引出点后移
R( s) R( s)G( s)
1/G(s)
R(s)
1 G( s) C (s) R(s)G(s)
3
结构图化简规则（续表）
原方块图
R1(s) E(s) R3(s) ± C (s ) R1(s)
等效方块图
R3(s) ± E (s ) R2(s) ± C(s) R3(s) C(s) R1(s) ± C(s) ± R2(s) R2(s) C(s) C(s) R2(s)
C ( s) G1 ( s ) R( s ) 1 G1 ( s )G2 ( s )
2
结构图化简规则（续表）
原方块图
R(s)
等效方块图
C (s ) ± Q(s) R(s) ± R(s) Q(s)
G(s)
G(s)
C(s) Q(s) C(s) ±
等效运算关系 比较点前移
C ( s ) R( s )G ( s ) Q( s ) [ R( s ) Q( s ) ]G ( s ) G( s)
5
Ui
UR1 -
1/R
I
1/[RC2C3;C2)s]
Uo
RC2s+1
1 1 R C1 s( RC 2 s 1) C 2 s ( s ) 1 1 1 ( RC 2 s 1) R C1 s( RC 2 s 1) C 2 s
第二章-2 结构图的组成和绘制 自动控制原理 课件 ppt
(1) 串联方框的简化
3 信号流图的组成及性质
ቤተ መጻሕፍቲ ባይዱ
5梅逊(Mason)增益公式：
梅逊(Mason)增益公式：
P 1
pkk
P----从源节点到阱节点的传递函数（总增益） n----从源节点到阱节点的前向通道总数 Pk ----从源节点到阱节点的的第k条前向通道总增益
(2)扰动作用下的闭环传递函数
N (s)C N ((s s))1G 1(s G )G 2(2 s()s)H (s)
C (s) N (s)N (s) 1 G 1 (s G )G 2 (2 s ( )s)H (s)N (s)
输入信号和扰动同时作用下的输出为
C(s)(s)R(s)N(s)N(s)
G1(s)G2(s)R(s)G2(s)N(s)
1G1(s)G2(s)H(s)
(3)闭环系统的误差传递函数
e(s)E R ((s s))1G 1(s)G 1 2(s)H (s) e(n s)N E ((s s)) 1 G 1 G (s 2 )(G s)2 H (s()s H )(s)
前向通道相接触的回路增益项 （包括回路增益的乘积项）以后
的余项式。
6闭环系统的传递函数
(1)输入信号下的闭环传递函数
(s)C(s) G 1(s)G 2(s) R(s) 1G 1(s)G 2(s)H(s)
C (s) (s)R (s) G 1(s)G 2(s) R (s) 1G 1(s)G 2(s)H (s)
1 L a---L -a 所有L 单b L c独回L a 路L b L 增c 益 之-和---流图特征式
LbLc ----在所有互不接触的单独回路中，每次取其中两个
回路的回路增益的乘积之和。
结构图简化
解：
R
G1 C G2
G3
30
G1 R G2
C
G3 G1 R 1/G2
G2
C
G3
31
2-7 信号流图及梅逊公式
2.7.1 信号流图的基本概念
1.定义：信号流图是表示一组联立线性代数方程的图。 先看最简单的例子。有一线性系统，它由下述方程 式描述： x2 = a12 x1
式中，为输入信号(变量)；x2为输出信号(变量)；a12为两
49??????????基本方法直接列写法原始方程组线性化消中间变量化标准形转换法由传递函数微分方程式由结构图传递函数微分方程由信号流图传递函数微分方程?????基本概念物理化学及专业上的基本定律中间变量的作用简化性与准确性要求1微分方程式?????50基本概念??????????定义线性定常系统零初始条件一对确定的输入输出典型环节传递函数零极点分布图单位阶跃响应特性?????基本方法定义法由微分方程传递函数图解法由结构图化简传递函数由信号流图梅逊公式传递函数?????2传递函
信号之间的传输(增益)。即输出变量等于输入变量乘上 传输值。若从因果关系上来看，x1为“因”，x2为 “果”。这种因果关系，可用下图表示。 a12 x1 x2
32
下面通过一个例子，说明信号流图是如何构成的。 设有一系统，它由下列方程组描述：
x2 = a12 x1 + a32 x3 x3 = a23 x2 + a43 x4 x4 = a24 x2 + a34 x3 + a44 x4 x5 = a25 x2 + a45 x4
17
(2) 并联
R(s) R(s)
G1(s)
C1(s)
+
自控控制原理习题 王建辉 第2章答案
2—1 什么是系统的数学模型?在自动控制系统中常见的数学模型形式有哪些？ 用来描述系统因果关系的数学表达式，称为系统的数学模型。
常见的数学模型形式有：微分方程、传递函数、状态方程、传递矩阵、结构框图和信号流图。
2-2 简要说明用解析法编写自动控制系统动态微分方程的步骤。
2—3 什么是小偏差线性化?这种方法能够解决哪类问题？在非线性曲线(方程）中的某一个工作点附近，取工作点的一阶导数，作为直线的斜率，来线性化非线性曲线的方法。
2-4 什么是传递函数？定义传递函数的前提条件是什么？为什么要附加这个条件？传递函数有哪些特点？传递函数：在零初始条件下，输出量的拉氏变换与输入量的拉氏变换之比. 定义传递函数的前提条件:当初始条件为零.为什么要附加这个条件：在零初始条件下，传递函数与微分方程一致. 传递函数有哪些特点：1．传递函数是复变量S 的有理真分式，具有复变函数的所有性质；n m ≤且所有系数均为实数。
2．传递函数是一种有系统参数表示输出量与输入量之间关系的表达式，它只取决于系统或元件的结构和参数,而与输入量的形式无关,也不反映系统内部的任何信息。
3．传递函数与微分方程有相通性.4．传递函数)(s W 的拉氏反变换是系统的单位脉冲响应。
2-5 列写出传递函数三种常用的表达形式.并说明什么是系统的阶数、零点、极点和放大倍数。
nn n n mm m m a s a s a s a b s b s b s b s W ++++++++=----11101110)( ()()∏∏==++=nj jmi i s T s T K s W 1111)( 其中nma b K =()()∏∏==++=nj jm i i g p s z s K s W 11)( 其中0a b K g =传递函数分母S 的最高阶次即为系统的阶数,i z -为系统的零点,j p -为系统的极点。
K 为传递函数的放大倍数，g K 为传递函数的根轨迹放大倍数。
自动控制原理(2-2)2.5 框图及其化简方法
根据系统中信息的传递方向，将各个子系统的函数 方块用信号线顺次连接起来，就构成了系统的结构 图，又称系统的方块图。 系统的结构图实际上是系统原理图与数学方程的 结合，因此可以作为系统数学模型的一种图示。
一、结构图的组成
① 结构图的每一元件用标有传递函数的方框表示。
R(s)
G (s)
C (s)
元件的结构图
G2 ( s )
(a)
X 2 ( s)
G3 ( s)
X 3 ( s)
X 0 (s)
G1 ( s )G2 ( s )G3 ( s)
(b)
X 3 ( s)
图2－10 串联环节的简化
n个环节（每个环节的传递函数为Gi(s) ，i=1,2,3,…） 串联的等效传递函数等于各传递函数相乘。
G(s) G1 (s)G2 (s) Gn (s)
R( s) G(s)
+
相加点前移
C (s) Q( s)
(a)
R( s)
+
C (s) G(s)
Q( s)
1 G ( s)
(b)
图2－13 相加点前移
1 C ( s ) R ( s )G ( s ) Q ( s ) R ( s ) Q ( s ) G (s) G (s)
分支点前移
C (s) G (s) C (s)
(a)
R( s)
R( s) G (s)
C ( s)
G(s)
(b)
C ( s)
图2－15 分支点前移
C ( s ) R ( s )G ( s )
分支点后移
C (s) G (s) R( s ) R( s ) G (s) C (s)
自动控制理论第二章传递函数_图文
§2.6 一般反馈控制系统
传递函数的各种术语 误差传函 扰动传函 一般控制作用
1. 一般控制系统
前向通道传函 闭环系统的开环传函 系统闭环传递函数 系统在给定作用下的输出
1、由系统输入到系统输出端的信号通路定义为系统 前向主通路(道)[简称主通路或前向通路]
②方框：表示输入、输出信号之间的传递 关系。
③引出点(测量点)：表示信 号引出或测量位置，从同一 点引出的信号完全相同。
④比较点(综合点)：表示两个或两个以上 的信号，在该点相加、减。注意，比较点 处信号的运算符号必须标明正(+)、负(-)， 一般不标者取正号。同时进行运算的信号 必须具有相同的量纲。
梅逊公式
回路总增益 (闭环传函)
第i条前向通 道余子式
第i个前向 通道增益
特征式
例：三级RC滤波网络如
图所示，求传递函数G(s)。
解： 前向通路1条 独立回路5个
两两不接触回路6个
三三不接触回路 特征式 余子式 传递函数
例：试求取图示系统的传递函数
解：前向通路3条
独立回路2个
例：系统结构图如图所示，试求其传递函数
积分器框图
特性：调节系统稳态误差，也称为无差 环节。
电压的传递函数
三、纯微分环节
定义：环节的输出响应正比于输入信号的变化率 。
微分方程 传递函数
测速发电机
四、惯性环节
定义：环节的输出不能立即复现输入，而是经过 一定时间后才能复现输入的变化。
微分方程
传递函数
运算放大器
五、振荡环节
定义：在输入作用下，环节输出响应随时间变化的 过渡过程总是在某一稳定值上下出现衰减振荡，而 最终趋于稳定值。
《自动控制原理》（卢京潮，西北工业大学）第二章习题及答案
2-1 建立图 2-33 所示各机械系统的微分方程 （其中 F (t ) 为外力，x (t ) 、 y (t ) 为位移；
k 为弹性系数， f 为阻尼系数， m 为质量；忽略重力影响及滑块与地面的摩擦） 。
图 2-33 系统原理图
解. （a）以平衡状态为基点，对质块 m 进行受力分析（不再 考虑重力影响） ，如图解 2-1(a)所示。根据牛顿定理可写出
微分方程为
duc2 du r2 3 du c 1 2 du r 1 u + + = + + 2 2 ur c 2 2 2 2 dt CR dt C R dt CR dt C R
(c) 由图解 2-2（c）可写出
U r ( s ) = R1 [ I1 ( s ) + I 2 ( s ) ] + ( Ls + R2 ) I 2 ( s )
对 B 点有
dx1 dy − ) dt dt
（1）
f(
dx1 dy − ) = k2 y dt dt
（ቤተ መጻሕፍቲ ባይዱ）
联立式（1） 、 （2）可得：
k1 k 2 k1 dx dy + y= dt f (k1 + k 2 ) k1 + k 2 dt
(c) 如图解 2-1(c)所示，取 A,B 两点分别进行受力分析。对 A 点有
2
图 2-37 单摆系统
将上式中非线性项 sin θ 在平衡点 θ 0 = 0 附近进行泰勒级数展开， 取一次近似有
sin θ = sin θ 0 +
d sin θ |θ0 ⋅Δθ = sin θ 0 + cos θ 0 ⋅ Δθ dt
将 θ 0 = 0 代入上式，得： sin θ − sin θ 0 = Δθ 。代入原方程可得线性化后的单摆方程
第二章：实数知识结构图
第二章：实数知识结构图一、实数的概念及分类1、实数的分类正有理数有理数零有限小数和无限循环小数实数负有理数正无理数无理数无限不循环小数负无理数2、无理数：无限不循环小数叫做无理数。
在理解无理数时，要抓住“无限不循环”这一实质，归纳起来有四类：（1）开方开不尽的数，如32,7等；（2）有特定意义的数，如圆周率π，或化简后含有π的数，如3π+8等；（3）有特定结构的数，如0.1010010001…等；（4）某些三角函数值，如sin60o等。
二、实数的倒数、相反数和绝对值1、相反数实数与它的相反数是一对数（只有符号不同的两个数叫做互为相反数，零的相反数是零），从数轴上看，互为相反数的两个数所对应的点关于原点对称，如果a 与b 互为相反数，则有a+b=0，a=-b ，反之亦成立。
2、绝对值在数轴上，一个数所对应的点与原点的距离，叫做该数的绝对值。
（|a|≥0）。
零的绝对值是它本身，也可看成它的相反数，若|a|=a ，则a ≥0；若|a|=-a ，则a ≤0。
3、倒数如果a 与b 互为倒数，则有ab=1，反之亦成立。
1和-1的倒数等于本身。
零没有倒数。
4、数轴规定了原点、正方向和单位长度的直线叫做数轴（画数轴时，要注意上述规定的三要素缺一不可）。
实数与数轴的点是一一对应的。
三、平方根、算数平方根和立方根1、算术平方根：一般地，如果一个正数x 的平方等于a ，即x 2=a ，那么这个正数x 就叫做a 的算术平方根。
特别地，0的算术平方根是0。
表示方法：记作“a ”，读作根号a 。
性质：正数和零的算术平方根都只有一个，零的算术平方根是零。
2、平方根：一般地，如果一个数x 的平方等于a ，即x 2=a ，那么这个数x 就叫做a 的平方根（或二次方根）。
表示方法：正数a 的平方根记做“a ”，读作“正、负根号a ”。
性质：一个正数有两个平方根，它们互为相反数；零的平方根是零；负数没有平方根。
3、开平方：求一个数a 的平方根的运算，叫做开平方。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
导出输入量和输出量之间的数学表达式，从而建立数学模 型。
实验法： 对实际系统加入一定形式的输入信号，求取系统 输出响应，从而建模 。
二、控制系统的微分方程模型
微分方程的编写应根据组成系统各元件工作过程中所遵 循的物理定理来进行。例如：电路中的基尔霍夫电路定 理，力学中的牛顿定理，热力学中的热力学定理等。
将诸待定常数求出后代入F (s)式，取反变换求得f (t)
f (t ) L1 [ F ( s)] Cm C m1 C m1 Cn C1 L m m 1 s s1 s s m1 s sm ( s s1 ) ( s s1 )
1 RC
t
e
1 RC
t
Ur(t) 1 t 1
Uc(t)
t
0
0
方法2. 用拉氏变换求解线性微分方程
Laplace变换 L[f(t)]=F(s) 从时域→复域 定义： 举例：
F ( s ) f (t )e st dt
0
f (t ) 1(t )
1 st 1 F ( s) e dt e s 0 s 0
1
C m1 m2 C m m 1 s1t n t t C 2 t C1 e Ci e si t (m 2)! i m (m 1)!
1 1 L [ ] t n 1e at ( n 1)! ( s a) n
1
注：
如上例：
例：RC无源网络 解： Uc是被控量，Ur是给定量 列出方程组如下：
Ur=UC+ RI
dUc I=C dt
R Ur
i
C
Uc
du RC u u dt
c c
r
例： 列写直流调速系统的微分方程
解： 输入：Ur 输出：w
列出方程如下：
e u r u f u a K a e d Tm dt K m u a u f K f Tm：电动机的时间常数
PD调节器 (Proportion Differential)
•二阶振荡环节 微分方程
T
2
d c(t ) dt 2
2
dc(t ) 2T c(t ) r (t ) dt
传递函数
1 G ( s) 2 2 T s 2Ts 1
具体对象：
RLC无源网络
•二阶微分环节
微分方程
d r (t ) dr (t ) r (t ) 2 r (t ) dt dt
传递函数分母多项式= 0 的根——极点
例：系统的闭环传递函数为
S+2 G（S）= --------------------------------（S+3）（S+1+j）(S+1- j ) 零点：-2 极点：-3，-1-j, -1+j
3、 典型元部件的传递函数
比例环节（无惯性环节） 微分方程：Xc（ t ）= k Xr（ t ） 传递函数：G（S）= k 具体对象：比例放大器、 电位器
数学模型
定义：控制系统的输入输出变量以及中间变量之间关系的 数学表达式即为数学模型。数学模型是分析和设计自动控 制系统的基础。
为什么要建立数学模型：我们需要了解系统的具体的性能
指标，希望能够从理论上对系统的性能进行定量的分析和 计算。
常用的有微分方程、传递函数、动态结构图、状态方程等
建模的方法
il
ul
一阶惯性环节
dxc (t ) xc (t ) kxr (t ) 微分方程： T dt k 传递函数： G ( s ) Ts 1
具体对象：具有一个储能元件的电路
•一阶微分环节
dr (t ) 微分方程： c(t ) r (t ) dt
传递函数：
G ( s) s 1
反拉氏变换
三、控制系统的传递函数模型
1、 传递函数的概念和定义
定义：线性定常系统在零初始条件下，输出量 的拉氏变 换与输入量的拉氏变换之比。
微分定理：
d L f (t ) sF ( s ) f (0) dt
d f (t ) L s F ( s) sf (0) f (0) dt
Kf： 测速机输出电压斜率
Km：电动机增益时间常数（电压转速传递函数）
消去中间变量得
d Tm (1 K ) K m K a ur dt K Ka Km K f
建立系统微分方程模型的一般步骤：
根据实际工作情况，确定系统和各元件的输入，输 出变量； 从输入端开始，按照信号的传递顺序，依照各变量 所遵循的物理（或化学）定律，列写处在变化（运 动）过程中的动态方程（一般为微分方程）； 消去中间变量，写出输入、输出变量的微分方程； 标准化：与输入有关的各项放在等号右侧，与输出 有关的各项放在等号左侧，并按降幂排列，最后将 系数回代为具有一定物理意义的形式。
•用拉氏变换求解微分方程
1. 将微分方程进行拉氏变换(积分下限为0-），得到 以S为变量的代数方程； 2． 解代数方程，得系统输出变量的象函数表达式； 3． 进行拉氏反变换，得微分方程的解。
•用拉氏变换求解微分方程的优点
微分方程转化为多项式
拉氏变换
Uc(t)微分方程
s的多项式
求解
Uc(t)
Uc(s)
2 2
2
传递函数
• 积分环节
微分方程：
xc (t ) kxr (t )dt
k G (s) s
传递函数：
具体对象： a. 电容
b．运算放大器电路
c．比例积分(PI调节器 proportion integral)
•微分环节
微分方程： 传递函数： 具体对象： a 电感 b. 理想微分
dxr (t ) xc (t ) k dt G ( s) ks
s si
n Ci L1[ F ( s)] f (t ) L1 i 1 s si
Ci e sit
i 1
n
2. 有重根情况
Cm C m 1 C1 C m 1 Cn F(s) m m 1 (s s1) (s s1) s s1 s sm 1 s sn
m
m 1
首先将F（s）的分母多项式A（s）进行因式分解，即写为
A(s) (s s1)(s s2)(s sn)
1．A（s）= 0无重根
c c c c F ( s) ss ss ss ss
1 2 i n 1 2 i
n
Ci lim s si) (s) ( F
st
•常用函数的Laplace变换：
(t ) 1
1 t 2 s
1 1(t ) s
1 1 t 2 s
2
3
e
t
1 s
sin t 2 2 s
•拉普拉斯变换基本定理：
初值定理
f (0 ) lim sF ( s)
s
终值定理：
f () lim s F ( s)
求线性微分方程的解
由给定输入信号时的输出信号来分析系统性能。 方法1：常规解法 例：求 RC 网络中，当Ur为单位阶跃输入信号时， 被控信号Uc的变化曲线。
解：方法一
（1）先求对应齐次线性方程的通解
du 1 u 0 dt RC
c c
du 1 dt u RC
c c
两端积分得
1 ln uc dt lnC ' RC
uc C ' e
1 t RC
（2）使用常数变易法求非齐次线性方程的特解
即
uc C (t )e
1 RC
t
1 RC
duc C ' (t )e dt
t
C (t )e
1 RC
t
1 ( ) RC
代入非齐次方程中得
C ' (t )e
1 RC
t
C (t )e
1
1 RC
t
t 1 1 ur RC ( ) C (t )e RC RC RC
3 2 3 2 3 3 s 1
d [( s 1) F ( s )] C lim 0 dt 1 d [( s 1) F ( s )] C lim 1 2 dt 5 1 F (s) ( s 1) s 1 5 f (t ) t e e 2
3 2 s 1 2 3 1 s 1 2 3 2 t t
2 2 ' 2
从微分方程模型到传递函数
du RC u u dt
c c
r
设初始值uc(0)=0
( RCs 1)U ( s) U ( s)
c r
U ( s) 1 U ( s) RCs 1
c r
2．零初始条件的含义： •输入作用是在t=0 以后才作用于系统，
r (0) r (0) r (0) 0
第二章 控制系统的数学模型
本章主要内容： 控制系统的模型 建立系统的微分方程模型 建立系统的传递函数模型 建立系统的动态结构图并化简 自动控制系统的传递函数定义
一、控制系统的模型 模型：经原系统简化了的系统，并能反映 系统所代表的全部重要特征。 模型的分类
数字模型 数学模型 图形模型 模型 计算机程序 物理模型：模拟
•系统在输入作用前相对静止，