框图化简、梅逊公式习题
自动控制复习题
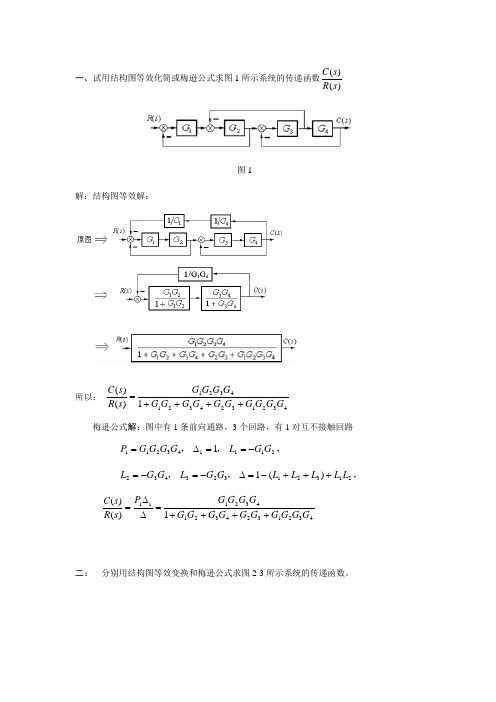
一、试用结构图等效化简或梅逊公式求图1所示系统的传递函数)()(s R s C图1解:结构图等效解:所以:432132432143211)()(G G G G G G G G G G G G G G s R s C ++++= 梅逊公式解:图中有1条前向通路,3个回路,有1对互不接触回路,,,2111432111G G L G G G G P -==∆= ,,,21321323432)(1L L L L L G G L G G L +++-=∆-=-=43213243214321111)()(G G G G G G G G G G G G G G P s R s C ++++=∆∆=二: 分别用结构图等效变换和梅逊公式求图2-3所示系统的传递函数。
)(s R )(2s G )(1s G )(s C -)(3s G -图2-3解:用梅逊公式求取系统传递函数。
由图2-3知,系统有1个回路,有2条前向通路。
因此有)()(321s G s G L =∑-=-=)()(1132s G s G L a ∆1)(1)(222111=-===∆∆s G P s G P 根据梅逊公式,系统的传递函数为)()(1)()()()(322121s G s G s G s G P s R s C k kk --==∑=∆∆三、试用结构图等效化简和梅逊增益公式求图1所示各系统的传递函数)()(s R s C图1解:所以: 2321212132141)()(H G G H G H G G G G G G s R s C ++++= (e )图中有2条前向通路,3个回路,,,,∆=∆==∆=242132111G P G G G P ,,,,)(132123*********L L L H G G L H G L H G G L ++-=∆-=-=-= 2321212132141122111)()(H G G H G H G G G G G G P P P P s R s C ++++=∆∆+=∆∆+∆=二、 设图2(a )所示系统的单位阶跃响应如图2(b )所示。
《自动控制原理》典型考试试题
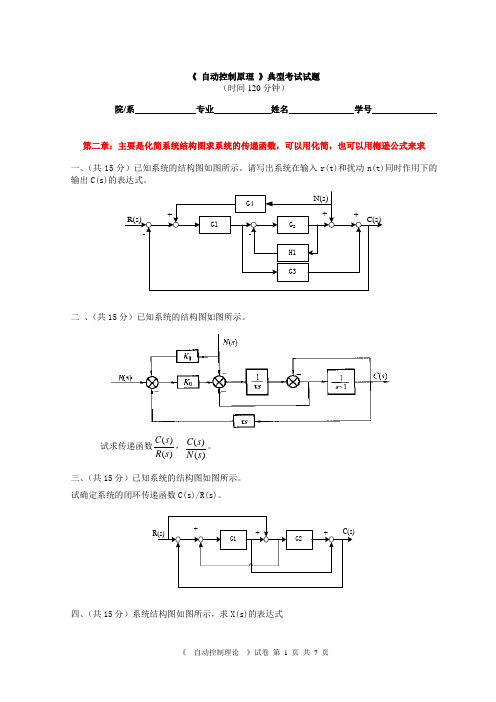
《 自动控制原理 》典型考试试题(时间120分钟)院/系 专业 姓名 学号第二章:主要是化简系统结构图求系统的传递函数,可以用化简,也可以用梅逊公式来求一、(共15分)已知系统的结构图如图所示。
请写出系统在输入r(t)和扰动n(t)同时作用下的输出C(s)的表达式。
G4H1G3G1G 2N(s)C(s)R(s)--+++二 、(共15分)已知系统的结构图如图所示。
试求传递函数)()(s R s C ,)()(s N s C 。
三、(共15分)已知系统的结构图如图所示。
试确定系统的闭环传递函数C(s)/R(s)。
G1G2R(s)-++C(s)-+四、(共15分)系统结构图如图所示,求X(s)的表达式G4(s)G6(s)G5(s)G1(s)G2(s)N(s)C(s)R(s)--G3(s)X(s)五、(共15分)已知系统的结构图如图所示。
试确定系统的闭环传递函数C(s)/R(s)和C(s)/D(s)。
G1G2R(s)-++C(s)-+D(s)G3G4六、(共15分)系统的结构图如图所示,试求该系统的闭环传递函数)()(s R s C 。
七、(15分)试用结构图等效化简求题图所示各系统的传递函数)()(s R s C一、(共15分)某控制系统的方框图如图所示,欲保证阻尼比ξ=0.7和响应单位斜坡函数的稳态误差为ss e =0.25,试确定系统参数K 、τ。
二、(共10分)设图(a )所示系统的单位阶跃响应如图(b )所示。
试确定系统参数,1K 2K 和a 。
三、(共15分)已知系统结构图如下所示。
求系统在输入r(t)=t 和扰动信号d(t)=1(t)作用下的稳态误差和稳态输出)(∞C2/(1+0.1s)R(s)-C(s)4/s(s+2)E(s) D(s)四、(共10分)已知单位负反馈系统的开环传递函数为:2()(2)(4)(625)KG s s s s s =++++试确定引起闭环系统等幅振荡时的K 值和相应的振荡频率ω五、(15分)设单位反馈系统的开环传递函数为12 )1()(23++++=s s s s K s G α若系统以2rad/s 频率持续振荡,试确定相应的K 和α值第三章:主要包括稳、准、快3个方面稳定性有2题,绝对稳定性判断,主要是用劳斯判据,特别是临界稳定中出现全零行问题。
2.4框图化简及梅逊公式

C(s)
有1组三个互不接触回路: L3 abefij
不存在四个互不接触回路: L4 0
1 L1 L2 L3
k 第k个前向通道的余子式;其值为 中除去与第k个前
向通道接触的回路后的剩余部分;
1 1 L1 L2 L3 ... 1
R(S ) E (S )
G1 G2
C (S )
R(S ) 1 E (S ) G1 C (S ) 1 C (S )
G2
信号流图是由定向线段(支路)将一些节点(变量)连接起来 组成的。支路上的传递函数称为支路增益
[几个术语]:
输入节点(源点):只有输出支路的 节点。如: R,N。
R
1
N 1 E P G Q G1 2
补充例题1
g
h b
R(s ) 1
a
c
d
1
2
3
i
4
5
l
e j6
7f
k
1 C (s )
8
9
m
Байду номын сангаас
补充例题2
R(s )
G1
1 1
G2
C (s )
3) 反馈联接:
R(s ) E (s)
G (s )
C (s )
H (s )
称为闭环传递函数
C ( s) G( s) ( s ) R( s ) 1 G ( s ) H ( s )
H (s)G2 (s)
①
R(s)
G1 ( s)
G2 ( s)
-
G3 ( s)
H ( s)G2 ( s)
梅森公式经典例题

梅森公式经典例题摘要:一、梅森公式简介二、梅森公式经典例题解析1.基本形式2.乘积形式3.复合形式4.应用场景三、梅森公式在实际问题中的应用四、总结与拓展正文:一、梅森公式简介梅森公式(Mason"s formula)是一种在概率论和统计学中广泛应用的公式,用于计算离散随机变量概率密度函数的积分。
梅森公式以数学家梅森(Mason)的名字命名,其一般形式如下:若离散随机变量X有n个可能的结果,对应的概率分别为p1, p2, ..., pn,则X的概率密度函数F(x)可以通过梅森公式计算:F(x) = Σ[pi * (1 - p1^(n-i))]二、梅森公式经典例题解析1.基本形式例题1:已知离散随机变量X有3个可能的结果,分别对应的概率为1/3,1/4,1/5。
求X的概率密度函数。
解:根据梅森公式,计算得到:F(x) = (1/3) * (1 - 1/3^2) + (1/4) * (1 - 1/4^2) + (1/5) * (1 - 1/5^2)2.乘积形式例题2:已知离散随机变量X有2个可能的结果,分别为A和B,对应的概率分别为1/2和1/3。
若事件A和事件B互斥,求X的概率密度函数。
解:根据梅森公式,计算得到:F(x) = (1/2) * (1 - 1/2^2) * (1 - 1/3^2)3.复合形式例题3:已知离散随机变量X有两个可能的结果A和B,对应的概率分别为1/2和1/3。
若随机变量Y = X + 1,求Y的概率密度函数。
解:根据梅森公式,计算得到:F(y) = (1/2) * (1 - 1/2^2) * (1 - 1/(y-1)^2)4.应用场景梅森公式在概率论和统计学中有广泛的应用,例如计算离散随机变量的累积分布函数、概率密度函数等。
此外,梅森公式还可以用于求解马尔可夫链、泊松分布等问题。
三、梅森公式在实际问题中的应用在实际问题中,梅森公式可以用于解决各种概率论和统计学问题。
梅逊增益公式及应用

-H2
1
②
G1 G2
G3
1 C(s)
① -H1
-1 ③
3
1 Li 1 G1G2H1 G2G3H2 G1G2G3
i 1
1 1
T
C(s) R( s )
1
P11
1
G1G2 H1
G1G2G3 G2G3H2
G1G2G3
例:求系统的总增益。
G(s) C(s) P11
G1G2G3G4
R(s) 1 G2G3G6 G3G4G5 G1G2G3G4G7
R(s)+ +
H2(s)
—
G1(s) +
G2 ( s )
G3 ( s )
C(s)
——
H1(s)
R(s) 1
-H2
1
G1 G2
G3
1 C(s)
-H1
-1
R(s) 1
P1 G1G2G3
G1G2G3 G1G4 G2G3H2 G1G2G3
G1G4
G4H2
② E(s)/R(s) E(s)
1
R(s)
1 1 G1
-H1
④⑤
G4
G2
G3
① -H2 ②
前向通道: P1 1
-1 ③
L1 G1G2H1 L2 G2G3 H2
反馈回路: L3 G1G2G3
1 1 G1G2H1 G2G3H2 G4H2
梅逊增益公式及应用
信号流图上从输入节点(源节点)输出节点到(汇节点)的总增 益公式,即梅逊公式(Mason),表达式为:
T
G(s)
C(s) R( s )
梅逊公式的应用

0
H
2
Y0
解上述方程组,得
Y0
X i
X
0
X
0
G 1 G 2
X
0
X
0
H
2
1 G2H1
X i
G 1 G 2
H
2
1 G2H1
G4
X i
X
0
G 1 G 3
X
0
整理得:
1 G 2 H 1 G 4 H 2 G 1 G 2 G 4 G 1 G 3 H 2 G 1 G 2 G 4 G 1 G 3 G 1 G 2 G 3 H 1 X i ( s )
-H2
②
2.6
P1=G1G2G3; P2=G1G4
系统信号流图及梅逊公式
该系统有二个前向通路,其传递函数分别为: 有5个反馈回路,其传递函数分别为:L1=−G1G2H1; L2=−G2G3H2; L3=−G1G2G3H3; L4=−G1G4H3; L5=−G4H2 5个反馈回路都相互接触,即没有互不接触的反馈回路,则:
G4(s)
X0(s)
-
G6(s) G7(s)
前向通道(一条): 回路3个(互有接触):
P1 G1G 2 G 3 G 4
1 1
1 G 2 G 3 G 5 G 3 G 4 G 6 G 1G 2 G 3 G 4 G 7 G3
3个回路 具有的公共传递函数:
G (s)
1 G1G 2 H 1 G 2 G 3 H 2 G1G 2 G 3 H 3 G1G 4 H 3 G 4 H 2
5个反馈回路均与两条前向通道接触,故: 1 1 则:
2 1
第二章补充习题
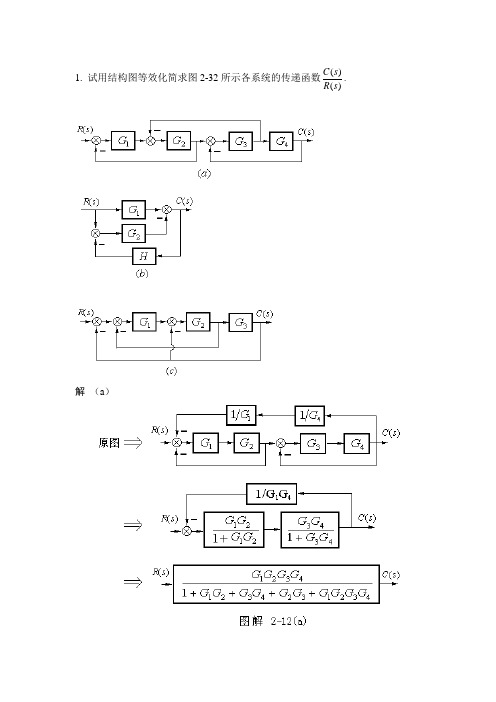
1. 试用结构图等效化简求图2-32所示各系统的传递函数)()(s R s C .解 (a )所以: 432132432143211)()(G G G G G G G G G G G G G G s R s C ++++= (b )所以: HG G G s R s C 2211)()(--=(c )2. 试用梅逊增益公式求上题中各结构图对应的闭环传递函数。
解 (a )图中有1条前向通路,3个回路,有1对互不接触回路,,,2111432111G G L G G G G P -==∆=,,,21321323432)(1L L L L L G G L G G L +++-=∆-=-=43213243214321111)()(G G G G G G G G G G G G G G P s R s C ++++=∆∆=(b )图中有2条前向通路,1个回路,,,,,H G L G P G P 2122211111==∆-==∆= 11L -=∆HG G G P P s R s C 22122111)()(--=∆∆+∆=(c )图中有1条前向通路,3个回路,,,211132111G G L G G G P -==∆=,,,)(132********L L L G G G L G G L ++-=∆-=-=3213221321111)()(G G G G G G G G G G P s R s C +++=∆∆=3. 求图中系统从v 到y的传递函数。
解:4. 已知系统方程组如下:⎪⎪⎩⎪⎪⎨⎧=-=-=--=)()()()()]()()([)()]()()()[()()()]()()[()()()(3435233612287111s X s G s C s G s G s C s X s X s X s G s X s G s X s C s G s G s G s R s G s X 试绘制系统结构图,并求闭环传递函数)()(s R s C 。
自动控制原理--信号流图及梅逊公式应用例题

La d eg bcg
有两个互不接触回路
Lb Lc deg
则 1 d eg bcg deg
f
1. X1 X 4 , p1 aef , p2 abcf
1 1 d, 2 1
X4 X1
1 ( p1 1
p2 2 )
aef (1 d ) abcf 1 d eg bcg deg
4. 闭环系统的误差传递函数 [ 定义误差 E(s)=R(s)-B(s) ]
e (s)
E(s) R(s)
en (s)
E(s) N(s)
1
G 1
1
, N(s) 0
1 (s)G 2 (s)H(s)
E(s)
G 2 (s)H(s) , R(s) 0
G1 (s)G 2 (s)H(s)
e
(s)R(s)
Tr1
x1 xr
1 (d
a(1 e) e cf ) de
Ty1
x1 y
1 (d
bf e cf
)
de
例2.15 已知系统信号流图,求传递函数。
• 解:三个回路:L1 G2H2
-H1
L2 G1G2H2
L3 G 2G 3H1
• 回路相互均接触,则:
R
G1
G2
G3
H2 -H2
G4
例2.13 绘制结构图对应的信号流图(1) 。
Ui(s) (-)
(-)
1 I1(s)
1 U(s)
R1
IC(s) C1s
(-)
1
1
R2 I2(s) C2 s
Uo(s)
Ui(s)
-1
1/R1
1/C1s
IC(s)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H3 s H (s) 2 G1 s G2 s G3 s H3 s H1 s G4 s
C s
– 首先将 G3 s , G4 s 间的引出点后移到方框的输出端
H 3(s) s H 2 G1 s G2 s 1 G4 s G3 s H3 s H1 s G4 s C s
C (s) 求 : R(s)
R
G4 E G1 H1
G2
H1H 2
G3 H2
C
1 La Lb Lc 1 G1H1 G3 H2 G1G2G3 H1H2 G1G3 H1H2
1 1, 2 1 G1H1 G1G2G3 G3G4 G1G3G4 H1 1 2 P Pk k k 1 1 G1H1 G3 H 2 G1G2G3 H1H 2 G1G3 H1H 2
△k称为第k条前向通路的余子式
求法: 去掉第k条前向通路后所求的△
梅逊公式例R-C
R(s)
G (s) G (s) 44
G1 1(s) H1(s) G2 2(s) G3 (s) 3 3
H3(s)
△2=1+G1H1
C(s)
△1=1
G4(s) G1(s)C(s) =? G2(s) R(s)
L3= – G1G2G3H3H1
1 1
L2 G1G2G3 H2
P 1 G 1G2G3G4 L1 G2G3 H3
C P R
P
k 1 k
n
L3 G1G2G3G4 H1 L4 G3G4 H 4 1 ( L1 L2 L3 L4 )
k
L2 G1G2G3 H2
P 1 G 1G2G3G4 L1 G2G3 H3
H1
C (s)
R( s )
_
G1
G2G3G4 1 G3G4 H 3 G2G3 H 2
C (s)
H3
R( s )
G1G2G3G4 1 G3G4 H 3 G2G3H 2 G1G2G3G4 H1
C (s)
( s )
G1 ( s)G2 ( s)G3 ( s)G4 ( s) 1 G2 ( s)G3 ( s) H 2 ( s) G3 ( s)G4 ( s) H 3 ( s) G1 ( s)G2 ( s)G3 ( s)G4 ( s) H1 ( s)
1 G4 s G3 s H3 s G4 s C s
G1 s
G2 sபைடு நூலகம்
H1 s
– 得到图为
H2(s)/G4(s) H 3 s G4 s
R s
G1 s
G2 s H1 s
G34 s
C s
27
H2(s)/G4(s) H 3 s G4 s
G2
H1H 2
G3 H2
C
1 La Lb Lc 1 G1H1 G3 H2 G1G2G3 H1H2 G1G3 H1H2
1 1, 2 1 G1H1 G1G2G3 G3G4 G1G3G4 H1 1 2 P Pk k k 1 1 G1H1 G3 H 2 G1G2G3 H1H 2 G1G3 H1H 2
R s
25
H2 H s 3 (s)
R s
1 G4 s G3 s H3 s G4 s C s
G1 s
G2 s
H1 s
HH 2(s)/G 4(s) 3 s G4 s
R s
G1 s
G2 s H1 s
R
G4 E G1 H1
G2
H1H 2
G3 C H2
梅森公式
前向通道有二,分别为: P 1 G 1G2G3 , P 2 G3G4
回路有三,分别为: G1H1 ,G3 H 2 ,G1G2G3 H1H 2 有两个不接触回路,所以:
C (s) 求 : R(s)
R
G4 E G1 H1
解:(1)找出上图中所有的前向通路 只有一条前向通路
T1 G1G2G3G4
(2)找出系统中存在的所有的回路 共有三个回路,三个回路的传输之和为
1 L1 L2 L3 (3)这三个回路都存在公共节点,即不存在不接触回路。故系统的特征方程 式为: 1 L
G23 s G2 s G3 s G4 s 1 G3 s G4 s H3 s +G2 s G3 s H 2 s
28
R s
G1 s H1 s
G23 s
C s
G2 s G3 s G4 s 其中: G23 s 1 G s G s H s +G s G s H s 3 4 3 2 3 2
梅逊公式介绍 R-C : △称为系统特征式
C(s) = R(s)
∑Pk△k △
△=1- ∑La+ ∑LbLc-∑LdLeLf+…
其中:
∑La
—
所有单独回路增益之和
∑LbLc—所有两两互不接触回路增益乘积之和 ∑LdLeLf—所有三个互不接触回路增益乘积之和
Pk—从R(s)到C(s)的第k条前向通路传递函数
框图化简、梅逊公式习题
A
B C
求下列由弹簧-质量-阻尼器组成的机械系统传递函数。
m
k
f
(a)
(b)
例 绘制如图所示 RC 无源网络的结构图
解 将无源网络视为一个系 统,组成网络的元件就对应于系 统的元部件。应用复阻抗概念, 根据基尔霍夫定律写出以下方程:
RC无源网络
按照这些方程可分别绘制相 应元件的方框图如图(a) - (d)所 示。然后用信号线按信号流向 依次将各方框连接起来,便得 到无源网络的结构图,见图(e).
最后将求得其传递函数为:
GA ( s ) = G1 ( s ) G 2 ( s ) G 3 ( s ) G 4 ( s )
1 +G 2 ( s ) G3 ( s ) H 2 ( s ) +G 3 ( s ) G 4 ( s ) H 3 ( s ) +G1 ( s ) G 2 ( s ) G 3 ( s ) G 4 ( s ) H 1 ( s )
G 3(s) G 3(s)
P2= G4G3
L4= – G4G3
P1=G1G2G3
L1= –G1 H1 L5 = – G1G2G3 L2= – G3 H3 L1L2= (–G1H1) (–G3H3) = G1G3H1H3
L1L4=(–G1H1)(–G4G3)=G1G3G4H1
用梅逊公式求下图中信号流图的传递函数。
1 1, 2 1 G1H1 G1G2G3 G3G4 G1G3G4 H1 1 2 P Pk k k 1 1 G1H1 G3 H 2 G1G2G3 H1H 2 G1G3 H1H 2
例:使用Mason公式计算下述结构图的传递函数
G4
R E
1 1, 2 1 G1H1 G1G2G3 G3G4 G1G3G4 H1 1 2 P Pk k k 1 1 G1H1 G3 H 2 G1G2G3 H1H 2 G1G3 H1H 2
G34 s
C s
– 接着将 G3 s , G4 s , H3 s 组成的内反馈网络简化,其等效传 递函数为
G3 s G4 s G34 s 1 G3 s G4 s H3 s
26
H2 H s 3 (s)
R s
第二章 自动控制系统的数学模型
最终结果:
例 试简化如图的结构图,并求系统传递函数C(s)/R(s).
系统结构图
R( s )
_ _
G1
H2
G2
H1
G3
G4
H3
C (s)
H2
R( s )
_
G1
_
G4
G2
H1
-
G3
G4
H3
C (s)
H2
R( s )
_
G1
_
G4
G3G4 1 G3G4 H 3
G2
试应用梅森公式求取下图所示方框图的传递函数。
H 4(s)
R(s)
G1(s)
G 2(s) G 3(s) G 4(s)
C(s)
-
H 3(s)
-
+
H 2(s)
H 1(s)
解. 本题信号流图为 R( s ) 1 G1
G2
-H4 -H3
G3
G4
1
C (s)
-1
-H2
-H1
L3 G1G2G3G4 H1 L4 G3G4 H 4 1 ( L1 L2 L3 L4 )
-
C ( s) E ( s) , R( s) R( s)
C
G1
H1
+
G2
+ -
G3
H2
[解]:在结构图上标出节点,如上。然后画出信号流图,如下:
R
G4 E G1 H1
G2
H1H 2
G3 C H2
梅森公式
前向通道有二,分别为: P 1 G 1G2G3 , P 2 G3G4
回路有三,分别为: G1H1 ,G3 H 2 ,G1G2G3 H1H 2 有两个不接触回路,所以:
梅森公式
前向通道有二,分别为: P 1 G 1G2G3 , P 2 G3G4
回路有三,分别为: G1H1 ,G3 H 2 ,G1G2G3 H1H 2 有两个不接触回路,所以:
