等积变形练习题 - 副本
四下奥数-等积变形.doc
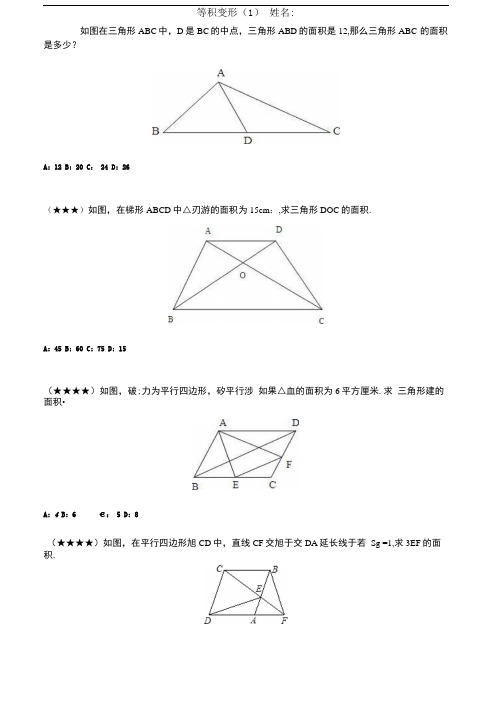
等积变形(1)姓名:如图在三角形ABC中,D是BC的中点,三角形ABD的面积是12,那么三角形ABC 的面积是多少?A: 12 B: 20 C: 24 D: 26(★★★)如图,在梯形ABCD中△刃游的面积为15cm:,求三角形DOC的面积.A: 45 B: 60 C: 75 D: 15(★★★★)如图,破;力为平行四边形,矽平行涉如果△血的面积为6平方厘米.求三角形建的面积•A: 4 B: 6 €: 5 D: 8(★★★★)如图,在平行四边形旭CD中,直线CF交旭于交DA延长线于若Sg =1,求3EF的面积.A: 1 B: 2 C: 3 D: 4(★★★★)如图:已知三角形ABC的面积是88平方厘米,是平行四边形Z)EFC的2倍, 求阴影部分的面积。
A: 44 B: 31 C: 22 D; 30(★★★)如图是由大、小两个正方形组成的,小正方形的询长是占厘米,求三角形NBC 的面积.A: 4 B: 8 C: 16 D: 20(★★★)如图,与AEFG均为正方形,三角形如丑的面积为6平方厘米,图中阴影部分的面积为•DA: 3 B: 6 C:9 D: 123 D等积变形(2) 姓名:BD 长4厘米,DC 长16厘米,B 、C 和D 在同一条直线上.则三角形ABC 的面积是三角 形ABD 面积的( )倍;三角形ADC 的面积是三角形ABD 面积的( )倍。
A; 3 , 4 B; 4 , 3 C : 5 , 3 D; S , 4如图,在三角形ABC 中,BC=10厘米,高是6厘米,D 、E 分别为AB 和AC 的中点,那么三角形DEB 的面积是( )平方厘米。
A: 6 B: 6, 5 (': 7 D: 7. 5三角形.4SC 中,DC = 23D, CE = 3北,三角形如)E 的面积是20平方厘米,三角形.45(? 的面积是( )平方厘米。
A:90 B: 100 C; 120 D: 150A; 30B;40 C : 50 D : 60 如图, 的面积是( 三角形ECD 的面积为3,其中CE=3AE, 3D = 4CD,三角形ABC)0 A: 10B; 12 C : 15 P: 16 如图, X13C 的面积是10平方厘米,将一纺、BC 、 得到一个新的SDEF ,则少EF 的面积为( 分别延长一倍到D 、E. F 且两两 )平方厘米。
等积变形(复习)
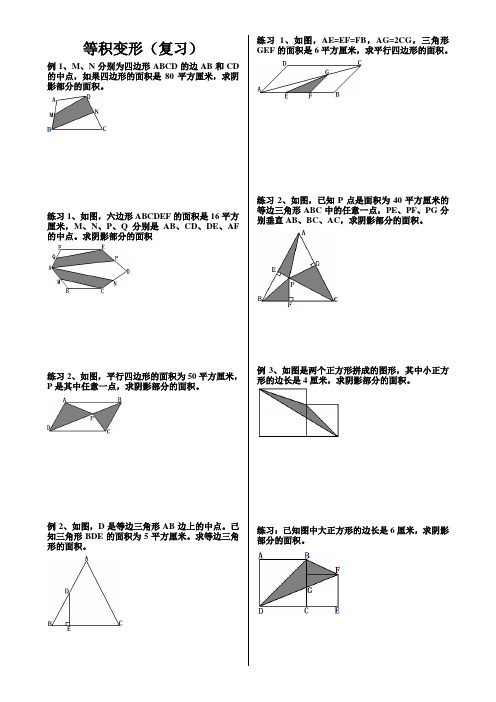
等积变形(复习)例1、M、N分别为四边形ABCD的边AB和CD 的中点,如果四边形的面积是80平方厘米,求阴影部分的面积。
练习1、如图,六边形ABCDEF的面积是16平方厘米,M、N、P、Q分别是AB、CD、DE、AF 的中点。
求阴影部分的面积练习2、如图,平行四边形的面积为50平方厘米,P是其中任意一点,求阴影部分的面积。
例2、如图,D是等边三角形AB边上的中点。
已知三角形BDE的面积为5平方厘米。
求等边三角形的面积。
练习1、如图,AE=EF=FB,AG=2CG,三角形GEF的面积是6平方厘米,求平行四边形的面积。
练习2、如图,已知P点是面积为40平方厘米的等边三角形ABC中的任意一点,PE、PF、PG分别垂直AB、BC、AC,求阴影部分的面积。
例3、如图是两个正方形拼成的图形,其中小正方形的边长是4厘米,求阴影部分的面积。
练习:已知图中大正方形的边长是6厘米,求阴影部分的面积。
ABCD 中,EF 与AC 平行,如果三角形BFC 的面积是35平方厘米,那么三角形AEB 的面积是多少平方厘米?2、在三角形ABC 中,AD 与BC 垂直,CE 与AB 垂直,AD=8厘米,CE=7厘米,AB+BC=21厘米,求三角形ABC 的面积。
3、如图,三角形ABC 的面积是30平方厘米,D 是BC 的中点,AE=2ED ,求阴影部分的面积。
4、三角形ABC 的面积是180平方厘米,D 是BC 的中点,AD=3AE ,EF=3BF ,求阴影部分的面积。
5、如图,BD=2DC ,AE=BE ,已知三角形ABC 的面积是18平方厘米,求四边形AEDC 的面积。
6、两个边长为2厘米的正方形,其中一个的顶点在另一个的中心上,求两个正方形不重合部分的面积和。
7、在正方形中,A 、B 、C 分别是所在边的中点,三角形COD 的面积是三角形AOB 的面积的几倍?8、如图,长方形ABCD 的长为10厘米,宽为6厘米,E 、F分别为所在边的中点,FG=2GE。
【小升初专项训练】04 等积变形

第5讲等积变形第一关三角形的等积变形【例1】如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为 平方厘米。
【答案】12.25【例2】如图,E、F分别是梯形ABCD两腰上的中点,已知阴影部分的面积是43c㎡,那么梯形ABCD 的面积是多少?【答案】172【例3】如图:三条直线互相平行,l1与l3之间的距离是7厘米,l2上AB=4厘米.求阴影部分三角形的面积是多少平方厘米? 【答案】14【例4】你能看出下面两个阴影部分A与B面积的大小关系吗?(两个长方形面积相等)【答案】A与B的面积相等【例5】如图,在斜边长为20cm的直角三角形ABC中去掉一个正方形EDFB,留下两个阴影部分直角三角形AED和DFC.若AD=8cm,CD=12cm,则阴影部分面积为多少?给出答案并说明你的计算依据.【答案】48【例6】如图,在直角三角形中有一个正方形,已知BD=10厘米,DC=7厘米,阴影部分的面积是多少?【答案】35平方厘米【例7】如图,梯形ABCD的面积是36,下底长是上底长的2倍,阴影三角形的面积是多少?【答案】16【例8】下图中阴影部分甲的面积与阴影部分乙的面积哪个大?【答案】图中甲乙的面积相等【例9】如图,在三角形ABC中,D是BC上靠近C的三等分点,E是AD中点,已知三角形ABC的面积为1,那么图中两个阴影三角形面积之和是多少?【答案】0.4【例10】已知△ABC面积为5,且BD=2DC,AE=ED,求阴影部分面积.要求写出关键的解题推理过程.【答案】2【例11】如图,将一个梯形分成四个三角形,其中两个三角形的面积分别为10与12.已知梯形的上底长度是下底的.请问:阴影部分的总面积是多少?【答案】23【例12】如图,已知梯形ABCD中,CD=10,梯形ABCD的高是4,那么阴影部分的面积是多少。
【答案】20【例13】(1)如图1,阴影部分的面积是多少?(2)如图2,一个长方形长4厘米,宽3厘米.A为长方形内的任意一点,阴影部分的面积是多少?【答案】(1)100;(2)6【例14】如图,在图中△ABE、ADF和四边形AECF面积相等.阴影部分的面积是多少?【答案】15【例15】如图,两个正方形(单位:厘米)中阴影部分的面积是多少平方厘米?【答案】8【例16】由面积为1,2,3,4的矩形拼成如图的长方形,图中阴影部分的面积为多少?【答案】【例17】如图所示,正方形ABCD的对角线BD长20厘米,BDFE是长方形.那么,五边形ABEFD的面积是多少平方厘米。
小学数学《三角形的等积变形》练习题(含答案)

内容概述
我们已经知道三角形面积的计算公式:三角形面积=底×高÷2
从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积.
如果三角形的底不变,高越大(小),三角形面积也就越大(小);
如果三角形的高不变,底越大(小),三角形面积也就越大(小);
这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的1/3,则三角形面积与原来的一样。这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.
于是:三角形ABD的面积=12×高÷2=6×高
三角形ABC的面积=(12+4)×高÷2=8×高
三角形ADC的面积=4×高÷2=2×高
所以,三角形ABC的面积是三角形ABD面积的4/3倍;三角形ABD的面积是三角形ADC面积的3倍。
巩固理解结论:两个三角形等高时,面积的倍数=底的倍数
【例2】如右图,E在AD上,AD垂直BC,AD=12厘米,DE=3厘米。
【例6】如右图所示,在平行四边形ABCD中,E为AB的中点,AF=2CF,三角形AFE(图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?
【例7】图中△AOB的面积为15cm2,线段OB的长度为OD的3倍,求梯形ABCD的面积.
【例8】(北京市第一届“迎春杯”刊赛)如右图.将三角形ABC的BA边延长1倍到D,CB边延长2倍到E,AC边延长3倍到F.如果三角形ABC的面积等于l,那么三角形DEF的面积是?
例题精讲
小学数学《三角形的等积变形》练习题(含答案)

又由于三角形AED与三角形AEC的高相等,而CD=1/4AC,于是AD=3/4AC,
所以,三角形AED的面积=3/4×三角形AEC的面积
=
.
=
【附4】(北京市第四届“迎春杯”刊赛)下图中三角形ABC的面积为1,其中AE=3AB,BD=2BC,那么三角形BED的面积是________.
分析:连接辅C助线E.
(三角形BCE的面积)︰(三角形DCE的面积)=BC﹕CD=1﹕1,
所以三角形BCE的面积等.于三角形DCE的面积.
又因为(三角形BCE的面积)︰l=BE﹕AB=2﹕1,
所以三角形BCE的面积等于2.
因此三角形BDE的面积等于2+2=4.
【附5】(第四届《小数报》数学竞赛初赛)如图,梯形ABCD被它的一条对角线BD分成了两部分.三角形BDC的面积比三角形ABD的面积大l0平方分米.已知梯形的上底与下底的长度之和是15分米,它们的差是5分米.求梯形ABCD的面积.
【例6】如右图所示,在平行四边形ABCD中,E为AB的中点,AF=2CF,三角形AFE(图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?
【例7】图中△AOB的面积为15cm2,线段OB的长度为OD的3倍,求梯形ABCD的面积.
【例8】(北京市第一届“迎春杯”刊赛)如右图.将三角形ABC的BA边延长1倍到D,CB边延长2倍到E,AC边延长3倍到F.如果三角形ABC的面积等于l,那么三角形DEF的面积是?
【附2】如图,在△ABC中,DC=3BD,DE=EA,若△ABC面积是2,则阴影部分的面积是多少?
分析:连结FD,由AE=ED可知:S△AFE=S△EFD,S△AEC=S△DCE
小学五年级数学思维专题训练—等积变形(含答案解析)
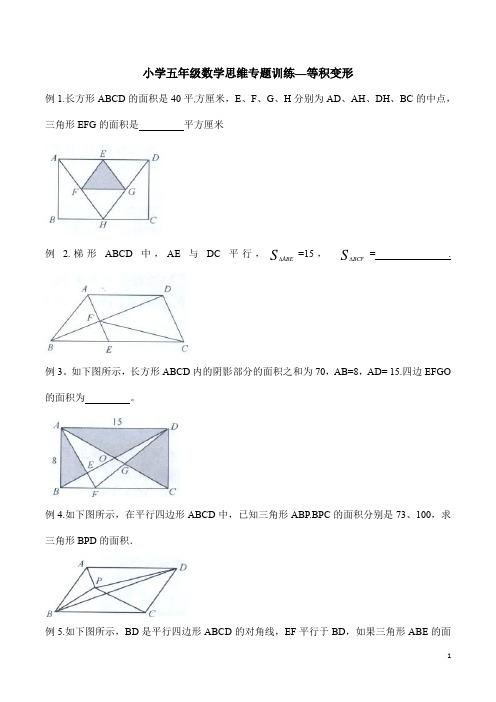
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米,E、F、G、H分别为AD、AH、DH、BC的中点,三角形EFG的面积是平方厘米例 2.梯形ABCD中,AE与DC平行,S ABE∆=15,S BCF∆= .例3。
如下图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD= 15.四边EFGO 的面积为。
例4.如下图所示,在平行四边形ABCD中,已知三角形ABP.BPC的面积分别是73、100,求三角形BPD的面积.例5.如下图所示,BD是平行四边形ABCD的对角线,EF平行于BD,如果三角形ABE的面积是12平方厘米,那么三角形AFD的面积是平方厘米。
例6.如下图所示,已知AE=EC,CD=DB,S ABC =60,求四边形FDCE的面积.例7.如右图所示,正方形ABC D和正方形ECGF并排放置,BF与CD相交于点H,已知AB=6厘米,则阴影部分的面积是平方厘米.例8.如下图所示,E、F、G、H分别是四边形ABCD各边的中点,EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积.试比较S1+S3与S2+S4的大小.例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如右图所示,则阴影部分的面积是 平方厘米.例10.右图所示ABCD 是个直角梯形(∠DAB=∠ABC= 900),以 , AD 为一边向外作长方形ADEF ,其面积为6.36平方厘米,连接BE 交AD 于P ,再连接PC .则图中阴影部分的面积是 平方厘米。
A.6.36B.3.18C.2.12D.1.59例11.如下图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的 。
A .21B .32C .52D .125例12.如下图所示,矩形ABCD 的面积是24平方厘米,三角形ADM 与三角形BCN 的面积之和是7.8平方厘米,则四边形PMON 的面积是 平方厘米.例13.一个矩形分成4个不同的三角形(如下图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?例14.如下图所示,正方形每条边上的三个点(端点除外)都是这条边的四等分点,则阴影部分的面积是正方形面积的。
等积变形附答案

三角形的等积变形我们已经掌握了三角形面积的计算公式:三角形面积=底x高十2这个公式告诉我们:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小).同样若三角形的高不变,底越大(小),三角形面积也就越大(小).这说明;当三角形的面积变化时,它的底和高之中至少有一个要发生变化. 但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原耒的;.贝!I三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.本讲即研究面积相同的三角形的各种形状以及它们之间的关系.为便于实际问题的研究,我们还会常常用到以下结论:①等底等高的两个三角形面积相等.②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.③若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.例如在右圈中,若^ABD-^A AEC的底边相等(£D=DE=EC=|E.C)3它们所对的顶点同为A点,(也就是它们的高相等)那么这两个三角形的面积相等.同时也可以知道^ ABC勺面积是△ ABD或△ AEC面积的3倍.例如在图中,△ ABC与△ DBC的底相同(它们的底都是BC),它所对的两个顶点A D在与底BC平行的直线上,(也就是它们的高相等),那么这两个三角形的面积相等.例如图中,△ ABC与△ DBC的底相同(它们的底都是BC),AABC的高是△ DBC 高的2倍(D是AB中点,AB=2BD有AH=2DE)则^ ABC的面积是△ DBC面积的2倍.上述结论,是我们研究三角形等积变形的重要依据.例1、用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.方法1=如右图,将RC边四等分(KD =DE=EF=FC=|B C),连结△ABE、△AEF、△AF对积*方法2:如右图,先将BC二等分,分点D连结AD得到两个等积三角形,即△ ABD与△ ADC等积.然后取AC AB中点E、F,并连结DE DF.以而得到四个等积三角形,即△ ADF △ BDF △ DCE △ ADE等积.C方法务如右图,先將BC四攀分,即:BD二一BC,连结直A再将AB三等分,aPAE-EF=FD--AD,连结CE、CF,从而得到四个尊积的三角形 ,即^AKD, △CDF, △CEE △ACE等积.例2、用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比为及1 : 3 : 4.方法1 :如下左图,将BC边八等分,取1 : 3 : 4的分点D E,连结AD AE 从而得到^ ABD △ ADE △ AEC的面积比为1 : 3 : 4.方法厶如上右圈,先取EC中点D,再取yVB的才分点民连结AD、DE从而得到三个三角形:△ ADE △ BDE △ ACD其面积比为1 : 3 : 4.方法玉如右图,先恥止中点D,连结CD,再取CD上;分点兔连结4从而得到三个三角形;△ACE △ADE、△BCD,其面积比为1 ; 3 :4.C当然本题还有许多种其他分法,同学们可以自己寻找解决.例3、如图,在梯形ABCD中,AC与BD是对角线,其交点0,求证:△ A0B与△ CODS积相等.c证明:•••△ ABC与△ DBC等底等高, /. S^AB(=S A DBC又S △ AOB=S A ABC—S A BOC S △ DOC=S^ DBC—BOC/. S AAOB=S ACOD例4、如图,把四边形ABCDfe成一个等积的三角形.分析本题有两点要求,一是把四边形改成一个三角形,二是改成的三角形与原四边形面积相等.我们可以利用三角形等积变形的方法,如右图,把顶点A移到CB的延长线上的A'处,△ A BD与△ ABD面积相等,从而△ A DC面积与原四边形ABC®积也相等.这样就把四边形ABCD等积地改成了三角形^ A DC问题是A'位置的选择是依据三角形等积变形原则.过A 作一条和DB平行的直线与CB的延长线交于A'点.解:①连结BD②过A作BD的平行线,与CB的延长线交于A'.③连结A。
三角形的等积变形2

习题十三解答一、选择题:1.(D) 2.(D) 3.(D) 4.(A) 5.(C).提示:以KH为边,再在对边的五个点A、B、C、D、E中任取一点为顶点,可分别构成5个面积为3平方厘米的三角形.同理,以JG、AD、BE为边也各自可以构成5个面积为3平方厘米的三角形.又因为△AFI、△BFJ、△CFK、△ELI、△DLH和△CLG也是面积为3平方厘米的三角形.所以面积为3平方厘米的三角形一共有26个.二、填空题:提示:如右图连结BD,设Ⅰ=S△BEG,Ⅱ=S△CEG,Ⅲ=S△CFG,Ⅳ=S△DFG,设S1=Ⅰ+Ⅱ,S2=Ⅲ+Ⅳ,S3=S△BDG.∵Ⅲ=Ⅳ∴F为CD中点,有:S△BCF=S△BDF,又∵Ⅲ=Ⅳ,∴ S△BGD=S△BCG,即 S3=S1,由已知Ⅰ为Ⅱ的2倍,∴BE=2EC,S△BDE=2S△CDE,两边分别减去Ⅰ和2Ⅱ,可得:S△BDG=2S△CDG,即 S3=2S2,因此:4.甲∶乙∶丙=1∶2∶6,提示:∵ EF∥BC, AB=2AE∴ AC=3AF,BC=3EF,∵甲∶乙=1∶2,又∵(甲+乙)∶丙=1∶2∴甲∶乙∶丙=1∶2∶6.三、解答题:4.如右图所示,连结AB'、AC,∴ S△AA'B'=S△ABB'即 S△A'BB'=2S△ABC同理 S△D'DC'=2S△ADC∴ S△A'BB'+S△C'DD'=2△C'DD'=2S四边形ABCD同理 S△AA'D'+S△B'CC'=2S四边形ABCD∴四边形A'B' C' D' 的面积=5×S四边形ABCD=5.5.解:连结AG、CG,如右图所示,∵ AF=EC,有S△AGF=S△CGE,又∵ED=BG,有S△AED=S△ABG且 S△CDE=S△BCG,由此可见:△EFG的三个部分中S△ABG补到了S △EAD,S△AFG补到了S△CEG之后,又将其中的S△BCG补到了S△CDE 而S△AEG的位置不变,由此一来相当于将△EFG等积变形到了四边形ABCD,两者面积相同,即:S△EFG=1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:神通广大的平行线
活动:请画出一个三角形,要求同时满足:
(1)与△ABC 有一条公共边. (2)与△ABC 面积相等但形状不同.
练一练:
1.如图,△ABC 和△DCE 是面积分别为a ,b 的等边三角形,其中点B 、C 、E 在同一条直线上,则△ADE 的面积是———.
2.如图,正方形ABFG 和BCDE 的边长分别为a ,b ,其中点 A 、B 、C 在同一条直线上,则△AFD 的面积是———.
3.如图,网格中小正方形的边长为1,则△ABC 的面积是_____
拓展运用: 4.如图,四边形ABCD 、BEFG 、PQFM 都是正方形,顶点A 、B 、E 在同一条直线上,顶点G 、F 、Q 也在同一条直线上,则阴影部分的面积是________________.
B E
G C D
F M B A B A B
A
5.如图,抛物线与坐标轴相交于点A (2,0)、B (6,0)、C (0,6),点D 是抛物线的顶点.
(1)△BCD 的面积是___________.
(2)点P 在抛物线上,且△BCP 的面积为24,则点P 的坐标是———.
课外作业: 1.如图,由7个形状、大小完全相同的正六边形组成网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC 的顶点都在格点上,则△ABC 的面积是______.
2.如图,四边形ABCD ,请将它变成一个面积与它相等的三角形。
你有哪些方法?能过四边形ABCD 上的一点P 画一条直线将四边形ABCD 分成面积相等的两个部分吗?
A B C
O x
y
D P。
